Samvirke mellom rullende materiell og spor
Lenke til PDF-filen: Samvirke mellom rullende materiell og spor
INNLEDNING
Studiet av de dynamiske bevegelser til det rullende materiell ved framføring på et skinnegående spor er meget komplisert. Dette har sammenheng med de dynamiske belastninger som hjulsettet utsettes for når det beveger seg på skinnegangen. Men bevegelsen til det rullende materiell følger allikevel grunnleggende dynamiske prinsipper. Dette gjelder både vertikalt og lateralt samt rulling.
Temaet samvirke rullende materiell/bane er delt inn i to kapitler. Denne første delen omhandler vognens bevegelser på sporet, herunder konisitet og vogndynamikk. Forhold knyttet til adhesjonsegenskaper og kryp er beskrevet i del 2.
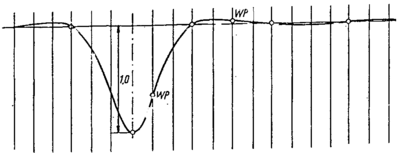
Et spor blir aldri helt perfekt. Ved meget lange bølgelengder vil den geometriske linjeføringen mht. sporet lateralt og vertikalt samt i lengderetning påvirke bevegelsene til vogn og boggi . Ved korte bølgelengder vil uregelmessigheter i skinnene føre til urolige bevegelser. Riktig konstruksjon og oppbygging av sporet og underbygningen samt definert og planlagt vedlikehold vil redusere amplitudene på sporfeilene.
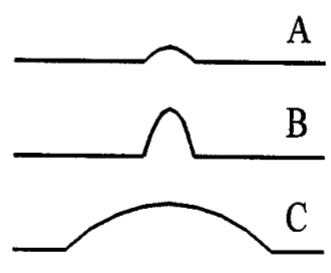
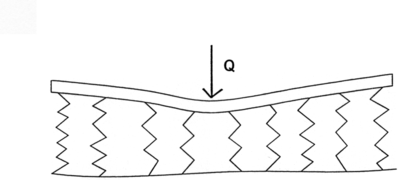
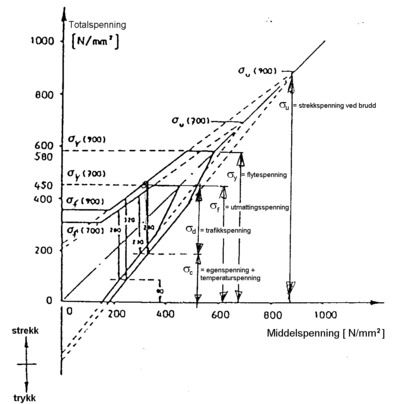
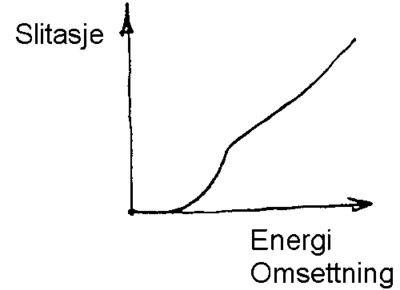
Det er gjennom lang tid observert at amplituden for ulike sporfeil er en funksjon av bølgelengder. Jo større bølgelengden er, jo større er vanligvis amplituden i sporfeilen. Dette er illustrert i figur 2.1 En sporfeil av type A vil oppstå langt oftere enn en sporfeil av type B for samme bølgelengde. Videre vil en sporfeil av type C med større amplitude ved lang bølgelengde oppstå like lett som en sporfeil av type A ved kort bølgelengde. Som en første tilnærming kan gjøres den antakelse at størrelsen på amplituden til en sporfeil er en funksjon av sporets bølgelengde.
SAMVIRKE RULLENDE MATERIELL/BANE
Samvirke mellom det rullende materiell og bane er et meget vidt begrep, men skal i det etterfølgende begrenses til det som kalles gangdynamikkeller gangegenskaper.
Dette omfatter:
- Bevegelser av det rullende materiell på skinnebundet spor
- Krefter mellom rullende materiell og spor (sporkrefter)
Følgende hendelser kan relateres til ovenstående:
- Avsporinger
- Slitasjeav f.eks. hjul og skinner
- Komfortfor de reisende
Følgende aspekter er relatert til gangdynamiske prinsipper:
- Sikkerhetsom en funksjon av hastighetog sporstandard
- Tillatt lastkapasitettil det rullende materiell som funksjon av påkjenninger på sporet
- Togets tillatte hastighetpå grunn av sporgeometrisk linjeføring
- Passasjerenes opplevelser av reisen samt risiko for forskyvning av lasten og dermed skader på gods
- Vedlikeholdskostnader på det rullende materiell og på sporet
Kjøreegenskapene til det rullende materiell har stor betydning for:
- Sikkerhet
- Komfortog skader på gods
- Økonomi
Gjeldende utviklingstendenser er framføring av tog med tyngre laster og med
større hastigheter. Disse aspektene er i høy grad avhengig av god
kjøredynamikk.
I forbindelse med kjøreegenskapene til det rullende materiell på skinnebundet
spor skal det beskrives noen grunnleggende begreper:
- Statisk tilstandinntreffer når det rullende materiell står stille på et perfekt spor.
- Kvasistatisk tilstander den tilstand som opptrer når det rullende materiell framføres med konstant hastighetpå et perfekt spor. Det forutsettes atdette sporet har konstant kurveradiusmed konstant overhøyde. Videre eksisterer det konstante friksjonsforhold mellom hjul og skinne. Dette medfører at alle krefter eller forskyvninger i det rullende materiell og mellom det rullende materiell og sporet er konstant hele tiden.
- Dynamisk tilstand definerer de bevegelser og tilleggskreftersom det rullende materiell utøver på grunn av sporfeil, endring av opprinnelig sporgeometri, endring av hastighetog friksjoni sporet. Selvgenererende bevegelser som f.eks. sinusforløpog ustabilt løpinngår i begrepe
Vognenes vibrasjonsmønster
I dette avsnittet skal det gis en beskrivelse av bevegelsene til det rullende materiell.
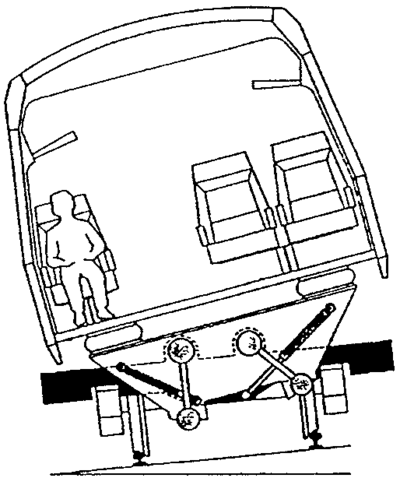
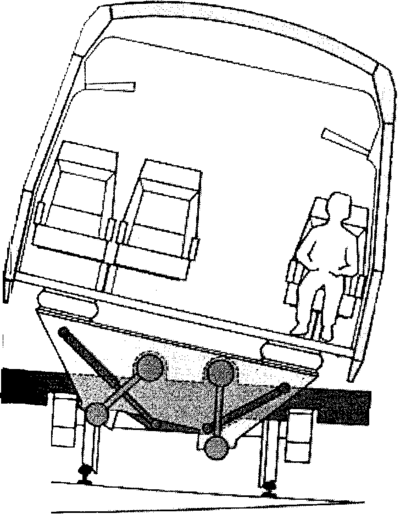
Det er 6 mulige bevegelser for alle komponenter til det rullende materiell ved framføring på et skinnegående spor. Dette gjelder for selve vognkassen, boggirammenog hjulsettet. Bevegelsene er vist samlet i figur 2.2.
| Bevegelser | Engelsk betegnelse | Norsk betegnelse | |
|---|---|---|---|
| Translasjonsbevegelse i kjøreretningen (X -retning) | Langsgående bevegelse eller longitudinell bevegelse | X Longitudinal | Rykk i kjøreretningen |
| Translasjonsbevegelse i tverretningen (Y -retning) | Sidebevegelse eller lateral bevegelse | Y Lateral | Sidesleng |
| Translasjonsbevegelse vinkel rett mot sporplanet | Vertikalbevegelse | Z Vertical, bounce | Hopping |
| Rotasjons -bevegelse i et plan tvers på lengderetninge) | Vognbevegelse | φ Roll, sway | Rulling |
| Rotasjons bevegelse i et langsgående vertikalplan | χ Pitch | Galoppering elle
vipping | |
| Rotasjons - bevegelse i selve sporplanet | ψ Yaw | Svingning |
Langsgående bevegelser eller rykkav vognene har sammenheng med
stivhetsparametre i forbindelse med buffere i en togformasjon.
Jernbanevogner er vanligvis symmetriske om den vertikale akse. Dette er
illustrert i figur 2.3. Vertikale ujevnheter i sporet kan antas å påvirke vognens
bevegelser symmetrisk om denne aksen.
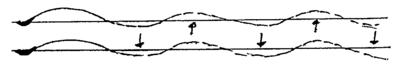
Bevegelser mht. hoppingog galopperinger overveiende uavhengige av laterale ujevnheter i sporet og rulling. Hopping og galoppering opptrer derim i spor med ujevnheter i vertikal retning og er illustrert i figurene 2.4 og 2.5.
På grunn av jernbanevognenes konstruksjon er vognmateriellet ikke symmetrisk om noen lateral akse. Lateral bevegelse og rulling vil derfor oppstå samtidig. Disse 2 sammenkoblede bevegelsene kan beskrives som øvre rulling og nedre rulling. Bevegelsene er vist i figurene 2.6 og 2.7.
Ved nedre rulling har rotasjonssenteret et lavt nivå, mens for øvre rulling ligger rotasjonssenteret høyere oppe. Frekvensen for den øvre liggende rulling vil vanligvis være høyere enn for den lavere liggende rulling.
Svingningsmønsteret (yaw) er vist i figur 2.8
Typiske frekvensområder for ulike bevegelser er:
- Lavere rulling: 0,6 Hz
- Svingning: 0,9 Hz
- Hopping: 1,0 Hz
- Galoppering: 1,4 Hz
- Øvre rulling: 1,6 Hz
Reaksjonsmønsteret til en virkelig vogn er meget komplekst. Dette gjelder også når vognen framføres på et idealisert spor. Denne kompleksiteten er sammensatt av et antall av fysiske effekter. Det er nødvendig å beskrive samspillet av disse fysiske effektene for å få innsikt i forståelsen av hvordan vognen oppfører seg i et spor.
VOGN I FJÆR/DEMPER-SYSTEM
I det foregående avsnittet er bevegelsene til det rullende materiell beskrevet og illustrert. I dette avsnittet skal bevegelsene uttrykkes matematisk. Dette er særlig tilfelle for den vertikale bevegelse.
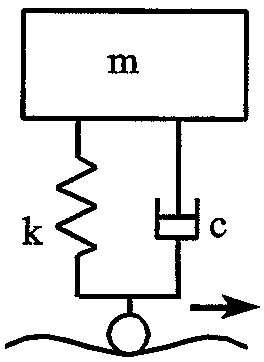
Masse med et enkelt fjær/demper-system
En masse som sitter på et fjæropplegg, har et system med en frihetsgrad. Bevegelsen til massen vil bli påvirket av vertikale ujevnheter i sporet. Dette er vist i figur 2.9.
Denne massen vil utøve resonansved en naturlig frekvens som er gitt ved formelen:
| (2.1) |
Her betyr:
- fn = naturlig frekvens [Hz], [s -1]
- k = fjærstivhet[N/m]
- m = masse [kg]
Uten dempingi systemet vil bevegelsen gå mot uendelig ved den naturlige
frekvensen. Systemet utføres derfor med en demper med gitte
karakteristikker:
- c = demperkonstant[N/v], [N/m/s], [Ns/]
Det er mulig å påvirke området for resonansfrekvenser gjennom parametrene k og m. En stiv fjær vil gi høye frekvenser og en tung masse vil medføre lave frekvenser.
Det defineres følgende parameter:
| (2.2) |
Dette gir:
| (2.3) |
Videre defineres:
| (2.4) |
Dette gir:
| (2.5) |
ω0 kan identifiseres som systemets resonansfrekvens(egenfrekvens) ved en
dempingsfaktorlik 0 (ingen dempingi systemet).
ζ defineres som den relative dempingi forhold til kritisk demping:
| (2.6) |
hvor
| (2.7) |
Den dempede naturlige frekvens blir:
| (2.8) |
Ved lave frekvenser vil massen følge uregelmessighetene i sporet ved
langsgående bevegelse. Dette gjelder både for vertikal forskyvning og for
akselerasjonsbevegelser til vognkassen. Ved massens egenfrekvens vil
aktivitetene oppnå særdeles høye verdier. Ved økende frekvenser avtar
verdiene igjen.
Det er mulig å øke nivået på dempingen. Det må imidlertid bemerkes at dempere i motsetning til fjærer er meget sensitive i høyere frekvensområder. Dette har sammenheng med at dempere reagerer som funksjon av hastighet. Fjærene får forskyvninger på grunn av uregelmessigheter i sporet.
Disse forholdene er vist i figur 2.10. Diagrammet viser forsterkningen i akselerasjonen uttrykt ved ÿ/w0til en masse som funksjon av frekvensområdet w(opptredende frekvenser). Forsterkningen i akselerasjonen er illustrert ved ulike nivåer på dempingen.
Egenskapene blir:
- lav dempingmedfører stor forsterkning ved resonans
- høy dempinggir stor forsterkning i akselerasjonen ved høye frekvenser
- høy dempingoppleves som vibrerende ved høyfrekvente forstyrrelser
En viktig oppgave er derfor å konstruere den optimale demping.
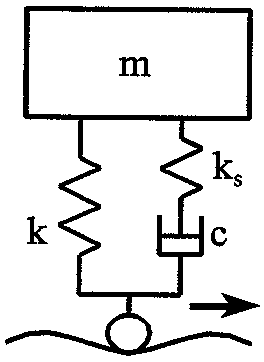
Masse med fjær og demper med innebygget fjær
Overføring av energi til massen m kan reduseres betydelig ved innføring av fjær i dempersystemet. Dette er illustrert i figur 2.11. Litt elastisitet vil alltid opptre i hydrauliske dempere på grunn av sammentrykkingen av olje samt fleksible innfatningskomponenter i dempersystemet. Det er vanligvis verdifullt å benytte slike fleksible innfatningskomponenter for å få kontroll over systemet.
Kombinasjonen av demper og en fjær i dempersystemet har bruddfrekvens som er definert iht. følgende formel:
| (2.9) |
Her betyr:
- kss= stivhet i fjæren til dempersystemet
- c= demperkonstant
- fb= bruddfrekvens
Ved frekvenser lavere enn bruddfrekvensen vil systemet opptre hovedsakelig
som demper. Ved frekvenser høyere enn fb vil systemet virke som en fjær. Et
passende valg av bruddfrekvens vil gi akseptabel demping ved naturlig
frekvens. Dermed vil overføring av vibrasjoner ved høyere frekvenser bli
redusert.
En verdi av kss = 10 k vil medføre et meget stivt system. Ved lavere verdier av kss blir systemet mykere. Dette medfører at overføring av energi til massen m ved høyere frekvenser minsker betraktelig. Imidlertid vil forholdet føre til en viss økning i overføring av energi ved resonansfrekvens. Det vises til figur 2.12. Y-aksen illustrerer akselerasjonen uttrykt ÿ/ω0 og x-aksen frekvensområdet uttrykt ved ω.
Det kan vises matematisk at for et system med én frihetsgrad vil den optimale
oppførselen til massen skje ved et nivå i dempingen på 20 % og en stivhet i
dempersystemet kss som er 2 ganger større enn fjærstivheten k.
Effekten av primærfjær i systemet
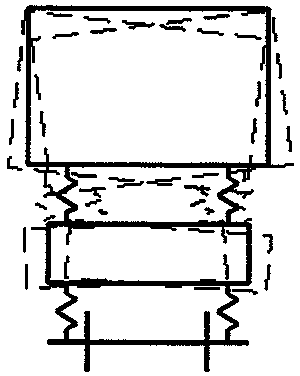
Dersom det innføres en primærfjær, dannes et system med 2 masser. Dette systemet har 2 frihetsgrader og dermed 2 egenfrekvenser (naturlige frekvenser). Egenfrekvensene vil være avhengige av stivhetene til de 2 elastiske fjærene. Det vises til figur 2.13.
Den dynamiske bevegelse til et slikt system som beveger seg på et idealisert
spor, er vist i figur 2.14.
Betydningen av 2 separate resonansfrekvenser kan observeres. Massen av boggien er mye mindre enn massen av. Samtidig er den primære fjæren mye stivere. Dette medfører at den naturlige frekvensen til sekundærfjæren blir høyere (7 Hz).
Primærfjæren filtrerer bort mye av de høyfrekvente bevegelsene som oppstår på grunn av ujevnheter i sporet. Jo mykere primærfjæren er, jo større blir effekten av filtreringen.
Det må imidlertid bemerkes at kontakten hjul - skinne i tillegg introduserer høyere frekvenser som må isoleres (beskrevet ved Hertzian-fjæren).
Toakslede vogner
En lang masse har normalt opplegg mot sporet i 2 punkter. En to-akslet vogn er et slikt eksempel. Vognen har de 2 frihetsgradene hopping og vipping (galoppering). Generelt vil disse frihetsgradene opptre i forskjellige frekvenser og ha forskjellige nivåer mht. demping. I tillegg vil de geometriske egenskapene til vognen filtrere effekter av påvirkninger fra uregelmessigheter i sporet. Ved bestemte bølgelengder i sporet vil hoppingen av vognen skje med full amplitude iht. sporets uregelmessigheter. Ved andre bølgelengder vil den vertikale amplitude i forbindelse med hoppingen bli mindre.
Vippingen av vognen vil ved bestemte bølgelengder kunne skje med full amplitude.
Det vises til figurene 2.15 og 2.16.
Det forutsettes en lengde mellom akslene til vognen lik L. Den maksimale
hoppingen til vognen inntreffer ved definerte bølgelengder i sporet. Likeledes
vil det ved andre bølgelengder i sporet ikke være hopping i det hele tatt. Dette
er vist i tabellen under. Det samme gjelder for vipping. For den illustrerte
vognen vil det være 2 tilfeller av vibrasjonsmuligheter med forskjellige
egenfrekvenser og nivåer på demping som oppstår på grunn av ulike
bølgelengder.
Bølgelengdene som forårsaker hoppingen og vippingen, er bare avhengige av avstanden mellom punktene for uregelmessighetene i sporet. Frekvensene for når vibrasjonene opptrer, vil derfor være avhengig av hastigheten. Siden hvert tilfelle har en spesifisert egenfrekvens, vil hoppingen av vognen (massen) bli utøvet ved en bestemt hastighet. Ved andre hastigheter vil avstanden mellom uregelmessighetene i sporet kunne forårsake en filtrerende effekt ved sammenligning med et system med ekvivalent enhetsmasse.
Tabell 2.1 Hopping og vipping ved ulike bølgelengder
| Bølgelengde | Hopping av vogn | Vipping av vogn |
|---|---|---|
| Uendelig | Maksimum | Null |
| 2 L | Null | Maksimum |
| L | Maksimum | Null |
| 2L/3 | Null | Maksimum |
| L/2 | Maksimum | Null |
| 2L/5 | Null | Maksimum |
Effekten av den geometriske filtreringen er meget kompleks, selv for idealisert
spor. Dette er illustrert i diagram 2.17. Diagrammene illustrerer
vertikalbevegelser og galoppering(vipping) for en to-akslet vogn med avstand
mellom akslene på 9 m.
Virkelige opptredende sporfeil kan forårsake mer komplekse bevegelser.
Bevegelsene til to-akslede vogner kan forverres betydelig ved bestemte
hastigheter dersom en bølgelengdeved maksimal hendelse mht. hopping eller
vipping sammenfaller med en bølgelengde hvor uregelmessighetene i sporet
er særdeles store.
Det faktum at både hopping og vipping opptrer i en vognkasse, medfører for passasjeren at akselerasjonen varierer langs vognkassen. En passasjer som sitter midt i vognen, vil bare føle hoppingen. En annen passasjer i endene av vognen vil i tillegg føle vertikal bevegelse fra vippingen. På grunn av dette vil sannsynligvis komforten oppfattes å være betydelig bedre midt i vognen enn i vognende. Dette er anskueliggjort i diagram 2.18.
Et annet forhold er at vognen blir utsatt for momentbøyning. Amplituden av
bøyebevegelsen er naturligvis størst i vognmidt. Bøyningen kan føre til
opplevelser av vibrasjoner for passasjeren.
Effekten av boggier
En boggi vil utøve tilsvarende løpeegenskaper ved framføring som en toakslet vogn. Hopping og vipping vil også for en boggi være avhengig av bølgelengder for ujevnheter i sporet samt avstand mellom hjulsatsene til boggiene. Imidlertid vil normalt vogner med boggier være betydelig lenger enn to-akslede vogner.
Et annet viktig aspekt er at selve boggien vil utøve et geometrisk tilleggsfilter for å ta opp uregelmessigheter i sporet. Bølgelengder som påvirker hoppingen av en boggi, vil normalt ikke bli overført til vognkassegjennom sekundærfjæringen. Det vises til figur 2.19
Boggiene introduserer flere frihetsgrader enn de som påvirker hopping og
vipping. Dermed oppstår flere resonansfrekvenser i systemet. Vipping av
boggien ved resonansfrekvensene vil bare ha liten innflytelse på bevegelsen
av selve vognkassen. Derimot vil hoppingen av boggien i frekvensområdene
for resonans ha stor virkning på bevegelsen i vognkassen.
Løpeegenskapene til en vogn med boggier som framføres på et idealisert spor, er vist i figur 2.20. Som eksempel er avstanden mellom boggiene blitt holdt den samme som for en to-akslet vogn med akselavstand lik 9,0 m. I tillegg er avstanden mellom akslene i boggien lik 2,0 m. Det framkommer at bevegelsen til vognen med boggier er sammenfallende med bevegelsene til den to-akslede vognen. Det er imidlertid et fall i aktiviteten ved en frekvens på 7,5 Hz som tilsvarer en bølgelengde på 4,0 m ved hastighet lik 30 m/s. Dette er et resultat av den geometriske filtreringen av boggien. Togframføring mht. komfort blir bl.a. betydelig forbedret.
I denne diskusjonen er så langt effekten av kontakten hjul/skinne ikke berørt.
Kontakten mellom hjul og skinne influerer særlig på den vertikale bevegelse.
Lateral bevegelse oppstår i prinsippet av samme grunn. Men i tillegg vil det for
den vertikale bevegelse genereres kinematiske bevegelser på grunn av
vibrasjoner i boggiene. Frekvensen i disse vibrasjonene samt dempingen vil
være avhengig av hastigheten. Noen av bevegelsene vil bli overført til
vognkassen, andre ikke.
Det er allerede påpekt at høy demping oppleve s som vibrerende ved høyfrekvente bevegelser eller forstyrrelser. En viktig oppgave er derfor å optimalisere dempingen.
Én mulighet er å gjennomføre fjæring i 2 trinn, slik at fjæringen i det første trinnet virker på den mellomliggende masse (f.eks. boggier). Det andre trinnet i fjæringen skal virke på den massen (dvs. vognkasse) som isoleres fra underlagets ujevnheter (sporet). Det er nettopp dette som skjer ved et rullende materiell som er utstyrt med primær- og sekundærfjæring med mellomliggende boggimasse. Massen i boggien virker som et filter for høyfrekvente forstyrrelser.
Matematiske vibrasjonsmodeller
I den klassiske fysikken eller mekanikken blir det beskrevet matematiske modeller for bevegelser av legemer som vibrerer eller som blir utsatt for forstyrrelser på grunn av ujevnheter i underlaget. Modellene tar gjerne utgangspunkt i bevegelsesforløp som funksjon av tiden.
Et enkelt ekvivalent system for beskrivelse av vibrasjoner består av en konsentrert masse med et fjærsystem. Denne massen blir utsatt for en framføringskraft og samtidig en retarderende kraft som forårsakes av demperelementet. Et slikt system er vist i figur 2.21. Massen m kan tenkes plassert i en generell posisjon som er forskjøvet i en avstand x fra nøytralstillingen. Kraften i fjæren med stivhet k er i denne stillingen (nøytralstillingen) lik 0. Det forutsettes at fjæren er tilknyttet et ubevegelig og udeformerbart fundament. Massen beveger seg iht. en kraft F = f(t) som altså blir uttrykt som en funksjon av tiden. Men samtidig blir bevegelsen til massen retardert i demperelementet ved en kraft som vil være proporsjonal med hastigheten. Denne type av såkalt friksjonsretardasjon blir betegnet som viskosiøs demping. Denne viskosiøse dempingen kan framstilles på flere måter.
I figur 2.21betyr:
- m = masse til legemet (kg)
- F = kraft som massen m blir utsatt for (kN)
- kx = retarderende kraft (kN)
- k = fjærstivhet(kN/mm)
- x = tilbakelagt vei fra nøytralstilling til fjæren (mm)
- c = den viskosiøse demperkonstant(N/m/s)
- x = hastighet(m/s)
Newton’ s 2. lov lyder:
| (2.10) |
Ved anvendelse av denne lov kan bevegelsen i x-retningen beskrives:
| (2.11) |
Denne likningen kan omformes til:
| (2.12) |
Et system som ligner på det foregående, er vist i figur 2.22. Det forutsettes at fjæren er forbundet med et underlag eller et fundament som har fått en forskyvning som funksjon av tiden lik δ = δ (t). Denne forskyvningen kan enten ha framkommet ved bevegelse av fundamentet eller ved deformasjon. Dersom x er den absolutte forskyvning av massen m målt fra nøytral posisjon ved δ = 0, vil fjæren få en spenning:
| (2.13) |
For øvrig er betegnelsene de samme som i foregående figur.
Dersom hastigheten til deformasjonen av underlaget neglisjeres, blir formelen:
| (2.14) |
Denne kan omskrives til:
| (2.15) |
Vi ser at kraften F i figur 2.15 er erstattet av uttrykket kδ , dvs. produktet av
fjærstivhet og bevegelse av fjæren på grunn av forskyvning av fundamentet.
Likningene
| (2.16) |
og
| (2.17) |
er lineære differensiallikninger av 2. grad og blir benyttet til å beskrive
bevegelsene til mange systemer, bl.a. også i jernbaneteknikk i forbindelse
med framføring av rullende materiell.
Differensiallikningene lar seg løse ved standardprosedyrer. Noen eksempler relatert til jernbaneteknikk vises i det etterfølgende.
Grunnleggende prinsipper
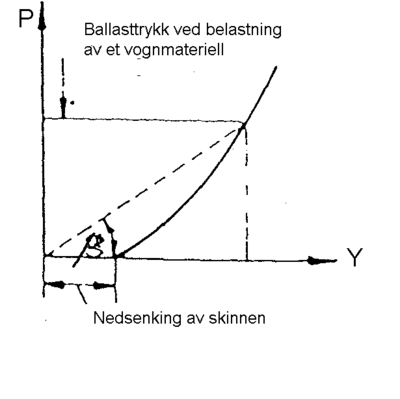
Som kjent framføres det rullende materiell på et spor med diverse komponenter. Sporet utgjør et byggverk som lar seg opprette mer eller mindre jevnt, men sporfeil i vertikal retning vil alltid være tilstede. Komforten ville naturligvis bli meget god i et feilfritt spor. Men en idealisert jevnhet er ikke mulig å oppnå uten at kostnadene blir enormt store.
Nettopp av kostnadsgrunner både ved nybygging og ved vedlikeholdsarbeider vil sporet alltid bli overlevert med sporfeil innenfor definerte toleransegrenser. Dette medfører at det er det skinnegående materiell som må bli utformet på en slik måte at virkningen av uregelmessighetene i sporet blir redusert mht. komfort. Dette skal imidlertid ikke oppfattes dit hen at et spor kan ferdigstilles med sporfeil. Det skal innenfor akseptable kostnader søkes å bygge et spor så feilfritt som mulig og sporet skal ved overtagelse i alle fall være i samsvar med definerte toleransegrenser.
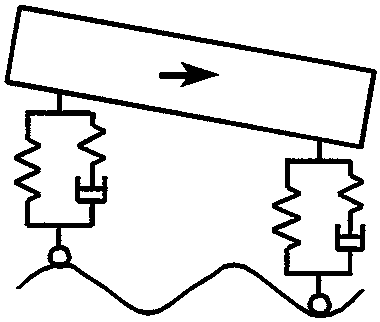
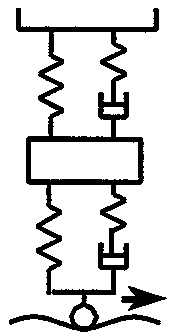
Uregelmessigheter og ujevnheter under eller på rullende hjul vil føre til støtbevegelser som merkes. Av den grunn er vognmateriellet fjæret. Materiell for frakt av passasjerer har alltid to fjærer i seriekopling. Dette betyr at de har en primærfjær for boggirammen og en sekundærfjær for selve vognkassen.
Selv med fjærer i seriekopling vil vognkassen bli utsatt for bevegelser og akselerasjoner ved ujevnheter i sporet. Det skal beskrives hvordan ujevnheter i sporet kan skape akselerasjoner i vognkassen.
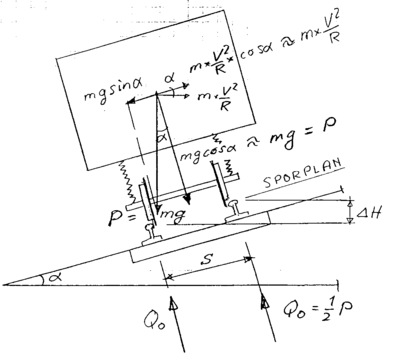
Fjærer medfører at en masse m tilbakelegger en bestemt veg. Denne bevegelsen vil resultere i en kraft. Fjærstivhet er definert som forholdet mellom kraft og veg. Jo mykere fjæren er, jo mindre blir fjærkraften ved bevegelse over samme veg. Dersom en masse m med hjul ruller over en vertikal ujevnhet med høyde h, kan kraften under forutsetning av gitt fjærstivhet beregnes:
| (2.18) |
h er ujevnhet i høyde
c er fjærstivhet til et legeme
m er legemets masse
Newtons lover sier at aksjon er lik reaksjon. Dette medfører at fjærkraften F virker i motsatt retning på hjulet og massen i samsvar med følgende uttrykk:
| (2.19) |
Figur 2.23 viser at fjæren vil overføre ujevnhetene ved hjulet til massen m1 over fjærkraften F1 i bevegelser med en akselerasjon ¨z1:
| (2.20) |
Derav kan utledes:
| (2.21) |
Uttrykket c1/m1 er proporsjonalitetsfaktoren og i denne inngår både
fjærstivheten og massen.
I en seriekobling av fjærer gjentar den samme effekten seg for sekundærtrinnet. Den vertikale bevegelse z1 til den mellomliggende masse m1 forårsaker sammen med sekundærfjæren med stivhet c2 en akselerasjon ¨z2 til massen m2 som beregnes til:
| (2.22) |
Igjen er c2/m2 en proporsjonalitetsfaktor og i denne inngår både fjærstivheten
og massen.
Det er naturligvis om å gjøre å konstruere vognen på en slik måte at
akselerasjonene ¨z1
og ¨z2 blir så lave som mulig ved passering av en ujevnhet
med høyde h. De to proporsjonalitetsfaktorene c1/m1
og c2/m2 har en
avgjørende betydning.
Likningene ovenfor kan omskrives:
| (2.23) |
Samme relasjoner gjelder naturligvis også for masse m2.
Forholdet fjærstivhet/masse indikerer hvilken akselerasjon i m/s 2 som den avfjærede masse vil få med en gang (i første øyeblikk) når fotpunktet til fjæren blir løftet plutselig 1 mm. Denne kvotienten (generelt c/m) virker som overføringsfunksjon for intensiteten eller forsterkningen i akselerasjonen ¨z/h (generelt).
Neste steg er å undersøke hvordan akselerasjonen fører til svingninger. Med en sammentrekkende bevegelse til fjæren ved ujevnheten h blir den potensielle energi til fjæren ved fjærkraft F og fjærveg h:
| (2.24) |
I uttrykket for fjærkraften inngår akselerasjonen ¨z. Denne er igjen avhengig av hastigheten z til massen m. Den potensielle energi som er lagret i fjæren, går over til kinetisk energi på grunn av bevegelsen til massen:
| (2.25) |
Den bevegelige massen gjør at fjæren strekker seg ut. Denne massen avgir energi til fjæren helt til fjæren ikke strekker seg mer ut. Deretter starter en pendling av energien i motsatt retning. Dermed oppstår de karakteristiske svingningene til massen. Slike svingninger er dynamiske hendelser med regelmessige bevegelser mellom bestemte grenser og periodisk veksel mht. energiformen. Den frie udempede svingning vil teoretisk aldri opphøre. Og det vil gjelde:
| (2.26) |
Det må gjelde:
| (2.27) |
| (2.28) |
Det kan utledes:
| (2.29) |
Forholdet z (prikk)/h angir den hastighet som massen m får når fotpunktet til fjæren blir løftet en høyde h på grunn av den vertikale ujevnhet i sporet. Denne hastigheten er avhengig av størrelsen som igjen er avhengig av den spesifikke fjærstivheten c/m. Uttrykket kan bli betraktet som overføringsfaktor til den hastigheten som svingningene får.
I moderne skinnegående materiell ligger de spesifikke fjærstivhetene ev. overføringsfaktorene eller intensiteten i akselerasjonene i størrelsesorden:
| (2.30) |
| (2.31) |
Det framgår at intensiteten eller forsterkningen i akselerasjonene i de 2 fjærstegene atskiller seg med mer enn 102. Primærfjæren pådrar seg relativt store akselerasjoner ved små ujevnheter. Sekundærfjæren bevirker på massen m2små akselerasjoner som er ønskelig mht. komfort. En forutsetning for dette er bevegelse eller løfting av begge fotpunktene samtidig.
For svingningshastighetene gjelder:
| (2.32) |
| (2.33) |
Ved en samtidig løfting av fotpunktene til begge fjærene ved passering av ujevnheten med høyde h får primærfjæren en svingningshastighet som er ca. 15 ganger høyere enn svingningshastigheten til sekundærfjæren. Til nå er det foretatt betraktninger mht. til passering av en hindring i sporet av kvasistatisk natur. For å komme over hindringen må hjulet bli løftet og fjæren blir trykt sammen. Det oppstår dermed en kraft i selve fjæren uttrykt ved fjærstivheten og fjærvegen. Ved passering av hindringen vil hjulet bli senket og kraften samt energien i fjæren forsvinner. Den tiden som hjulet bruker på nedsenkingen, har avgjørende betydning for de dynamiske bevegelser. Jo tidligere en nedsenking av hjulet følger etter et løft på grunn av hindringen, jo mindre blir bevegelsen av selve massen som framføres og dermed også svingningen.
Dette gjelder så lenge som at fjæren ikke har overført en vesentlig del av energien (i fjæren) til massen som er i bevegelse. Dersom fjæren ved nedsenkingen etter passering av hindringen ikke rekker å bli avfjæret, vil fjæren fra nedre stilling bli trukket opp igjen og ny energi vil bli lagret og overført til massen. Energien vil akselerere massen og forårsake videre svingninger.
Den svingningsdyktige kombinasjonen av fjær og masse og tidsintervallet mht. serie av ujevnheter står i et definert forhold til hverandre. Så lenge ujevnhetene i sporet opptrer i en serie med større avstand enn det som tilsvarer den beregningsmessige varigheten av svingningene, vil svingningsbevegelsene holde seg på lavt nivå. Varigheten av svingningene beregnes ut fra den opptredende svingningshastighet. Opptrer ujevnhetene i sporet i en serie med en avstand som tilnærmet er lik varigheten i svingningene, vil dette medføre kraftige bevegelser mht. svingninger. Blir disse parametrene like, vil svingningene fortsette uten stans og det blir resonans.
Svingninger og virkningene av disse kan påvirkes på forskjellig vis. Uten særlige tiltak blir i et udempet fjærmasse system den tilførte energien lagret av fjæren og overført som bevegelsesenergi til massen.
Den mest virksomme metoden mht. å utøve innflytelse på energiopptaket i forbindelse med svingningene er å redusere ujevnhetene på skinnene i sporet. Ujevnheten med en høyde h inngår kvadratisk (i 2. potens) i energiopptaket. En feilfri kjørevei uten ujevnheter er derfor den mest effektive form for å eliminere svingninger i massen og å skape best mulig komfort. Dessverre blir gjennomføringen av et slikt tiltak svært dyrt.
Lave akselerasjoner til massen m iht. likningene
| (2.34) |
og
| (2.35) |
kan realiseres med lave verdier av c/m. Myke fjærer med liten fjærstivhet reduserer energiopptaket i forbindelse med passering av ujevnheter i sporet. Svingningshastigheten og framfor alt svingningsakselerasjonen til massen m blir ved et slikt tiltak redusert.
Effekten av et system med 2 svingningsmasser blir tydeliggjort. Mellommassen m1etter primærtrinnet gjør det vanskelig å bygge opp akselerasjonene, svingningshastighetene og svingbreddene. Mellommassen skjermer det etterfølgende sekundærtrinnet mot forstyrrelser. Denne massen sammen med myke primærfjærer fungerer derfor som en sperre for opptak av bevegelsesenergi. Redusering av energi med dempere og spesielt hydrauliske svingningsdempere med dempekraft som er proporsjonalt med hastigheten, er benyttede metoder for kontroll av svingningene.
Formålet med fjærene er å redusere akselerasjonen til massen ved samtidig opptak av energi når hindringer skal passeres. Dempere skal fjærne energiopptaket ved en uønsket kraft som opptrer i denne forbindelse. Disse forhold må kombineres på en slik måte at fordelene blir framhevet og ulempene fjernet.
Trykkreftene i dempere forsterker oppbyggingen av akselerasjonen til massen, mens strekkreftene reduserer akselerasjonen. Omvendt vil det være ved nedbyggingen av akselerasjonen etter passering av hindringen. Bevegelsene blir forstørret ved strekkreftene og redusert ved trykkreftene.
Det er tilstrekkelig å gjøre trykk- og strekkegenskapene til demperen avhengig av den opptredende fjærkraft i den hensikt å forbedre komforten. Akselerasjonen til massen ved oppbyggingen i forbindelse med passeringen av hindringen forsvinner når summen av fjærkraft og dempekraft blir lik null:
| (2.36) |
Den optimale svingningskomfort blir oppnådd når:
| (2.37) |
dvs. når:
| (2.38) |
Hydrauliske dempere framskaffer dempekrefter S som vil være proporsjonal
med dempehastigheten:
| (2.39) |
Dette gir:
| (2.40) |
Hastigheten i forbindelse med dempingen er på grunn av bevegelsene ikke
mulig å påvirke. Dempekraften S kan derimot tilpasses forholdene gjennom k.
Denne dempeverdien k må fortløpende innstilles i takt med de varierende
forholdene:
| (2.41) |
Tekniske forhold begrenser imidlertid verdien av k og den tillatte dempekraft
S:
| (2.42) |
| (2.43) |
Dette betyr at den fjærkraftorienterte styringen av dempekraften stemmer overens med den størst mulige redusering av energien ved minimumsverdien for akselerasjonen i forbindelse med oppbyggingen og dermed den best mulige komforten mht. svingningsforløpet.
Enkel vibrasjonsmodell relatert til rullende materiell på spor
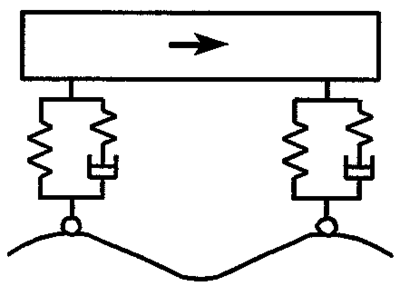
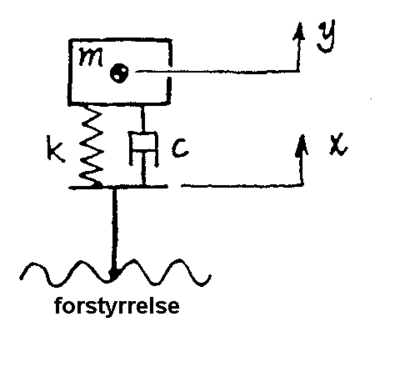
De teoretiske grunnmodellene som ble beskrevet i avsnittet foran, skal benyttes til å beskrive vibrasjoner i det rullende materiell. I stedet for en idealisert horisontal bevegelse skal det studeres den vertikale bevegelse til en vognmasse som består av fjærer og demper. Vognmassen beveger seg på sporet med ujevnheter i vertikalretning og har en frihetsgrad. Det vises til figur 2.24.
De idealiserte modellene i foregående avsnitt ble utsatt for en horisontal bevegelse. I tilfellet hvor underlaget eller fundamentet til fjæren fikk en forskyvning eller deformasjon, ble hastigheten av deformasjonen ikke tatt med i betraktningen. Dette fordi egenvekten til massen (vertikallast) ikke hadde innflytelse på fundamentets bevegelse.
I vertikalretningen har massen innflytelse på deformasjonen til underlaget eller undergrunnen. Følgelig må hastigheten av deformasjonen til underlaget tas med i modellen. Følgende betegnelser inngår:
- y = forskyvning til massen (mm)
- x = underlagets forskyvning (mm)
- c = demperkonstantfor viskosiøs lineær demper(N/m/s) = (Ns/m)
- k = fjærstivhet(N/mm)
- m = massen
- x = hastighettil demperelementet på grunn av underlagets forskyvning
- y = hastigheten til forskyvningen av massen
- ÿ = massens akselerasjon
Iht. Newtons 2. lov kan følgende formel utledes:
| (2.44) |
Denne formelen kan skrives om på følgende måte:
| (2.45) |
Formelen er en differensiallikning av 2. grad og derfor matematisk komplisert å behandle. Det er utviklet matematiske metoder (Pierre Simon de Laplace) hvor en spesiell type integralfunksjon kan transformere en funksjon til en annen funksjon iht. formel:
| (2.46) |
Laplace-transformasjonen har anvendelser innen teorien for lineære
differensiallikninger med konstante koeffisienter. Transformasjonen er ren
matematisk teknikk for å kunne omgjøre en komplisert funksjon til en enklere
funksjon.
En Laplace-transformasjon av likning i (2.45) gir:
| (2.47) |
Som tidligere nevnt defineres følgende:
| (2.48) |
og
| (2.49) |
Dette kan også uttrykkes som:
| (2.50) |
Iht. ovenstående gir:
| (2.51) |
ω0 kan identifiseres som systemets resonansfrekvens eller egenfrekvens ved demping ζ = 0.
ζ er relativ demping i forhold til den kritiske demping:
| (2.52) |
Likning
| (2.53) |
kan også skrives på formen:
| (2.54) |
Denne kan utvikles videre:
| (2.55) |
| (2.56) |
| (2.57) |
Dette gir:
| (2.58) |
Med
| (2.59) |
| (2.60) |
| (2.61) |
| (2.62) |
blir
| (2.63) |
Denne likningen beskriver forsterkningen til forskyvningen til massen m på grunn av ujevnhetene i underlaget. Den dynamiske bevegelse av massen i forhold til den statiske bevegelse av underlaget uttrykkes som:
| (2.64) |
I ovennevnte brøk framstiller telleren den dynamiske bevegelse til massen og
nevneren framstiller den statiske bevegelse til underlaget (undergrunnen) på
grunn av ujevnheter.
Uttrykkene 2.37 og 2.38 kombineres ved følgende omskrivning rent matematisk:
| (2.65) |
Det defineres en fasevinkel mellom y og x lik θ :
| (2.66) |
Det gjentas at ω er opptredende frekvens til massen på grunn av ujevnheter og at ω0 er resonansfrekvensen eller egenfrekvensen til massen m.
Dersom
- ζ << 1 og ω<< ω0 blir θ tilnærmet lik 0o
og
- ζ << 1 og ω>> ω0 blir θ tilnærmet lik 1800 eller π
Dette betyr at ved lav demping(ζ << 1) vil svingningen skje i fase med
ujevnhetene i underlaget dersom opptredende frekvens ω er vesentlig mindre
enn resonansfrekvensen.
Videre vil ved lav demping svingningen skje i motfase om opptredende
frekvens er høyere enn resonansfrekvensen.
Med
| (2.67) |
blir 1. deriverte, dvs. hastigheten
| (2.68) |
Den 2. deriverte gir akselerasjonen:
| (2.69) |
Med
| (2.70) |
kan på samme vis utledes at akselerasjonen på grunn av ujevnhetene blir
| (2.71) |
Forholdet mellom massens akselerasjon og bevegelsen av vognen på grunn
av ujevnhetene i underlaget kan uttrykkes iht.
| (2.72) |
Forsterkningen i akselerasjonen kan uttrykkes ved
| (2.73) |
Innsatt i ovenstående likning med matematisk omskrivning blir:
| (2.74) |
Endelig kan den normerte akselerasjonsforsterkning uttrykkes:
| (2.75) |
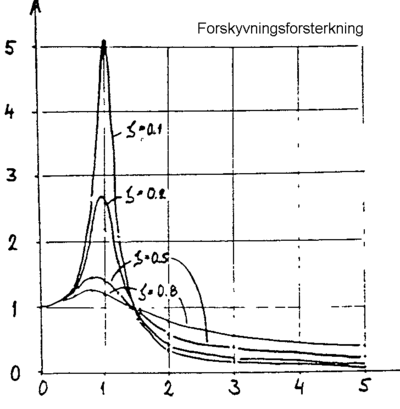
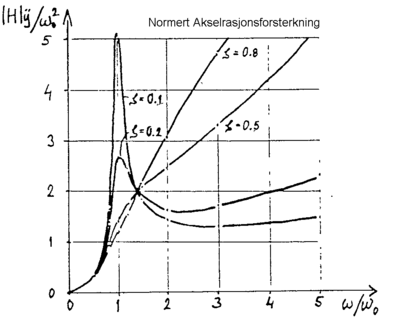
Forsterkningen eller intensiteten mht. forskyvning |H| y og normert
forsterkning mht. akselerasjonen |H|ÿ/ω02
er vist på figurene 2.25 og 2.26.
En viktig oppgave er derfor å optimere dempingen.
En mulighet er å etablere fjærkonstruksjon i to trinn. Den første fjærkomponenten skal virke på en mellomliggende masse (for eksempel en boggi) og den andre komponenten skal virke på den massen som må isoleres fra underlagets ujevnheter.
Det er nettopp dette som er tilfelle for en vogn med primærfjær og sekundærfjær. Vognen ha da en mellomliggende masse som er boggien. Denne boggimassen virker som et filter for høyfrekvente forstyrrelser.
Eksempel – ujevnheter i undergrunnen
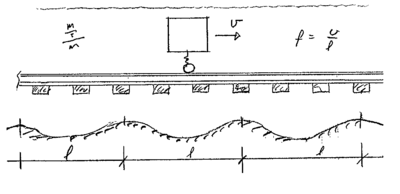
Det skal illustreres et eksempel på hvordan vertikale bevegelser kan opptre i det rullende materiell ved framføring. Vognen har en hastighet lik v (m/s). I underbygningen eksisterer periodiske ujevnheter med avstand L mellom disse. Vognmateriellet vil da passere ujevnhetene med en frekvens lik
| (2.76) |
Her betyr:
- f = frekvens (Hz), (s-1)
- v = hastighet(m/s)
- L = avstand mellom de periodiske ujevnheter (m)
Dette er vist i figur 2.27.
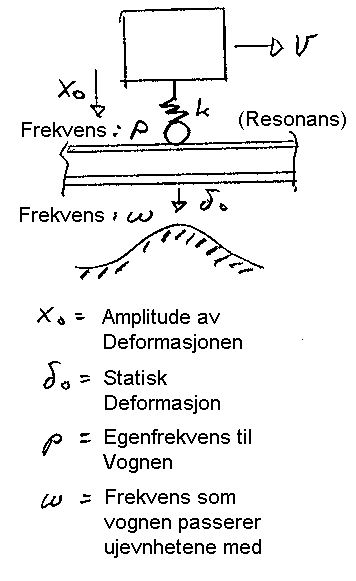
På grunn av variasjon av elastisiteten i overbygningen vil det opptre en endring av den vertikale statiske deformasjon x0(jω)= δ0 i underlaget til sporkonstruksjonen ved passering av det rullende materiell. Vognen kan da anta en dynamisk bevegelse i vertikalretningen lik y0(jω)= x0.
Her betyr:
- δ0 er amplitude for den statiske deformasjon i vertikal retning i underlaget når et legeme med masse m passerer
- x0 er amplitude for den dynamiske bevegelse i vertikal retning i til legemet med masse m
- ω0 = p er massens egenfrekvens
- ω = frekvens som det rullende materiell passerer de periodiske ujevnhetene med
Forholdet
| (2.77) |
er vist i figur 2.28og 2.29. ζ er dempingsfaktor i forhold til kritisk demping for
det rullende materiell. ζ = 1 medfører
| (2.78) |
for alle ω/p0
For f = v/L = w> p0 vil tallverdien av H – funksjonen anta en lav verdi. Dette er
meget gunstig mht. å unngå resonans og gjelder for alle dempingsforhold i
forhold til kritisk demping. Forholdet medfører at det er fordelaktig å passere
de periodisk opptredende ujevnheter med stor hastighet.
For f = v/L = ω< p0 vil tallverdien av den samme funksjonen anta en lavere
verdi enn verdien for resonans. Effekten mht. til å unngå resonans ved lavere
hastigheter er ikke så gunstig som ved høyere hastigheter.
For f = v/L = ω= 0 blir forholdet lik 1. Da står vognen stille.
Det eksisterer ulike tiltak for å redusere vibrasjonene. Det mest effektive tiltaket er å eliminere den utøvende kraft som er årsak til vibrasjonene:
- jevn og homogen elastisitet i sporkonstruksjonen
- introdusere dempingselementer som myk mellom leggsplate(i gummi) mellom skinne og sville
- sørge for tilstrekkelig minimumshøyde i ballastlaget
- toget tvinges til en framføringshastighet hvor frekvensen ved passering av ujevnhetene i overbygningen er forskjellig fra egenfrekvensene til togets komponenter
Innvirkning på kjøredynamikken lateralt på grunn av feil i sporet
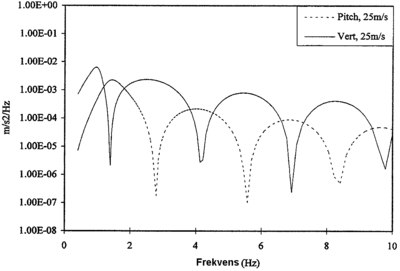
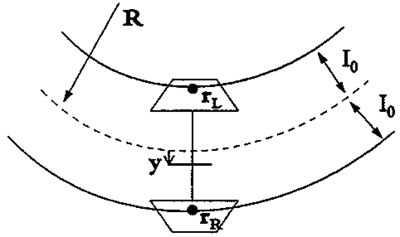
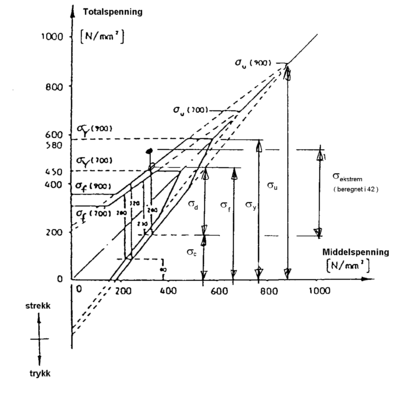
En type sporfeil som må vies oppmerksomhet, er langbølgede sidefeil med bølgelengderover ca. 30 m. Disse finnes spesielt i kurver og er vanligvis av periodisk karakter. Feilene er årsak til forstyrrelse av komforten. For krengetogene er krengeteknikken en funksjon av den ukompenserte sideakselerasjon i sporplanet og disse togtypene vil derfor være svært ømfintlige overfor langbølgede sidefeil. Dette er vist i figur 2.30. Eksemplet illustrerer en langbølget sidefeil på 80 m og en lateral forskyvning av sporet på 0,028 m ved kilden til sporfeilen..
Kilden til langbølgede sidefeil er en alvorlig lateral sporfeil. Denne feilen
forårsaker bevegelser sideveis av vognen som overfører dempede periodiske
laterale bevegelser mot sporet.
Dersom bølgelengdene korresponderer med resonansfrekvensen til en vogn i
lateral retning, kan det oppstå ubehagelige situasjoner. I figur 2.31 støter
vognen sideveis mot sporet med en kraft F0 der hvor den alvorlige sporfeil er
oppstått. Stivheten til sporet sideveis kan betegnes med k. ω er den frekvens
som vognmateriellet passerer de periodiske ujevnhetene med. p er vognens
resonansfrekvens. Sideveis bevegelse til vognmateriellet er x som vil variere
som funksjon av avstand fra den alvorlige sporfeil. Uttrykket F0/k beskriver den
statiske deformasjonen i sporet. Iht. litteraturen kan følgende uttrykk utledes:
| (2.79) |
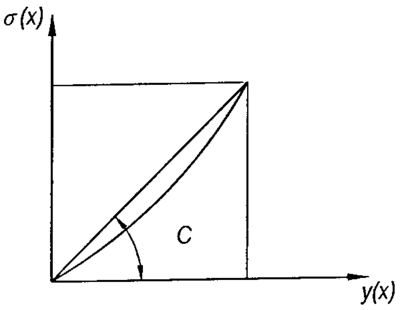
Det dannes dempede svingninger. Disse kan beskrives av en omhyllingskurve. Det vises til figur 2.32.
Bevegelseslikning for det rullende materiell
I de foregående avsnitt er det blitt diskutert utførlig den vertikale bevegelse til et enkelt legeme eller masse. En enkel svingningsteori for kun en bevegelse er betraktet. Forsterkningen av forskyvningen til massen i forhold til underlagets endring av deformasjonen på grunn av varierende elastisitet og tilfelle for resonansbevegelser er diskutert.
Det er påpekt at det er til sammen 6 mulige bevegelser for en masse eller
legeme som beveger seg langs sporet:
- langsgående bevegelseell er rykk i kjøreretningen
- lateral bevegelseeller sidesleng
- vertikalbevegelseeller hopping
- rotasjonsbevegelseeller rulling
- galoppering eller vipping
- svingning
Ved å betrakte alle disse bevegelsene til et legeme blir naturligvis forholdet vesentlig mer komplisert og omfangsrikt enn når bare en bevegelse (den vertikale) betraktes.
Et rullende materiell kan tenkes sammensatt av flere enkeltstående legemer som er forbundet med fjærer og dempere. I en slik sammensatt modell hvor bevegelsen til hver del beskrives av 6 frihetsgrader, kan den resulterende bevegelse av modellen beskrives av en vektor med forskyvning
| (2.80) |
av alle frihetsgrader.
Legemene og deres systemtregheter med hver frihetsgrad kan bli uttrykt ved
en matrise
| (2.81) |
og forholdet mellom forskyvning og hastigheten til frihetsgradene. Stivhetene og dempingen kan uttrykkes ved matrisene
| (2.82) |
| (2.83) |
Likninger for bevegelse av en modell kan skrives på følgende form:
| (2.84) |
F er eksterne krefter som virker på vognen.
Matrisen for demping må skrives på formen
| (2.85) |
Dette fordi dempingen tar i betraktning stivhet og hastighetsavhengige elementer.
Løsningen av disse likningene i matrisene gjør det mulig å beregne stabilitet, kjøreegenskaper og evnen til å gjennomløpe kurver til et rullende materiell ved å ta hensyn til materiellets ulike komponenter (ikke bare et legeme med en masse).
Dynamisk modell av vogn-spor
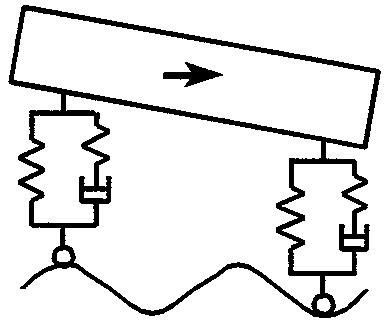
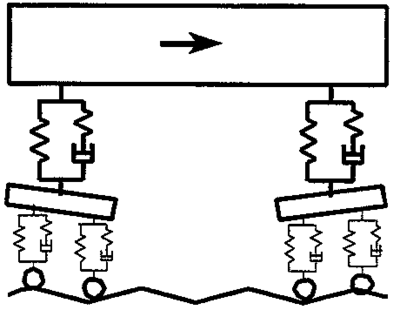
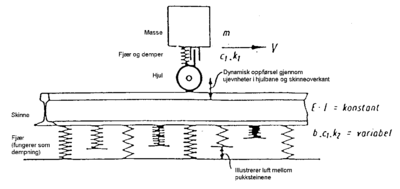
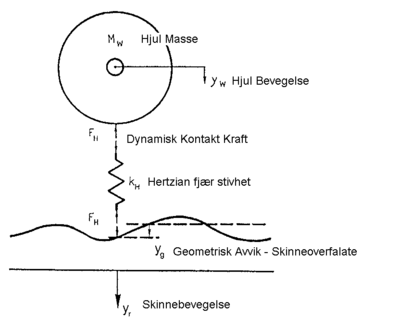
Den gjensidige dynamiske påvirkning mellom rullende materiell og spor kan matematisk beskrives meget godt og definert i vertikal retning. Figur 2.33gir et eksempel på en slik modell som består av et diskret (avsondret) masse - fjær system for det rullende materiell og en diskret opplagret bjelke på elastisk underlag. I kontaktflaten mellom hjul og skinne eksisterer den såkalte Hertzian fjæren.
Den dynamiske oppførsel opptrer i et meget vidt bånd fra lave frekvenser i størrelsesorden 0,5 - 1,0 Hz for vertikale og laterale akselerasjoner opp til 2000 Hz i vognkasse som en konsekvens av geometriske ujevnheter i skinner og på hjulbane.
Det skal i det etterfølgende bli forsøkt å skape en forståelse for de dynamiske
krefters natur ved beskrivelse av sporets og det rullende materiellets
dynamiske karakter.
Et dynamisk system som består av fjærer og masser har i det minste en
egenfrekvens. Ved denne frekvensen vil systemet vibrere. Det er allerede
nevnt at et enkelt system med én masse og én fjær med stivhet k har
egenfrekvens iht. følgende formel:
| (2.86) |
Her betyr:
- f0 = egenfrekvens(Hz), (s-1)
- k= fjærkonstant(kN/mm)
- m= masse i kg
Det kan utledes av formelen at en stor masse med myk fjær gir lave frekvenser. Omvendt vil en liten masse med stiv fjær forårsake høye frekvenser.
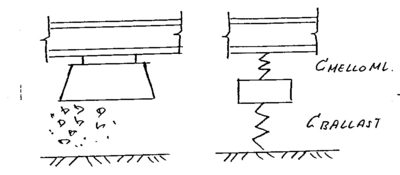
Sporet er bygd opp av flere komponenter. Et konvensjonelt spor består av skinner, befestigelse med fjærer og mellomleggsplater (elastisk skinnebefestigelse), sviller og endelig ballast samt underbygning. På samme måte kan det rullende materiell deles opp i vognkasse, boggiramme og hjulsats.
Et system bestående av sporet og det rullende materiell kan illustreres som vist i figur 2.25. I denne formen er vognmateriellet forbundet med fjæroppheng og demper mellom vognkasse og boggi(sekundærfjær) og et nytt fjæroppheng med demper mellom boggi og hjulsats. Den direkte kontaktflaten mellom hjul og skinne kan beskrives ved den såkalte Hertzian-fjæren. Det høyelastiske mellomlegget mellom skinne og sville kan også betraktes som en fjær med gitt stivhet og demper. Under sville hviler ballasten på en underbygning. Alt etter undergrunnens beskaffenhet har ballasten forskjellige stivheter.
Systemet består altså av flere legemer som er forbundet med hverandre gjennom fjærer og dempere. Hvert av disse legemene kan da tilordnes hver sin egenfrekvens. Dessuten er det nødvendig å betrakte systemet som en helhet med en resulterende egenfrekvens. Det er påvist at hver komponent i sporet blir utsatt for ulik påkjenning fra samme dynamiske kraft mot skinnens kjøreflate. Dette henger sammen med at sporet og det rullende materiell kan betraktes som et dynamisk system som beskrevet. De opptredende frekvenser for de enkelte legemer i systemet kan beregnes iht. følgende formel:
| (2.87) |
hvor
- f = det enkelte legemets egenfrekvens
- k= legemets stivhet (N/m)
- m= legemets masse (kg)
Normalt vil vognkassen ha den største massen og det mykeste fjæropphenget
i systemet. Med tilordnet demper medfører dette lave frekvenser i vertikal
bevegelse. Boggirammen har mindre masse og som regel stivere fjær. Dette
medfører høyere frekvenser. Hertzian-fjæreni kontaktflaten mellom hjul og
skinne er meget stiv og fører til særdeles høye frekvenser.
Den resulterende masse bestående av komponentene i sporet opptrer som
ekvivalent medsvingende masse. Denne ekvivalente medsvingende masse er
normalt mindre enn vognkassens masse og har også en høyere fjærstivhet.
Dette fører som regel til høyere frekvenser for sporet enn for vognkassen. Spesielt i tunneler med lav ballasthøyde og uten ballastmatter kan frekvensene bli til dels meget store.
Det rullende materiell forårsaker resulterende egenfrekvenser i området 0 < f < 30 Hz. Den resulterende svingende masse er bestemt ut fra vekten av vognkasse, boggiramme, og hjulsats. I den nedre delen av dette frekvensområdet kan sporet antas å være stivt og ubevegelig.
I frekvensområdet 20 < f < 60 Hz oppstår en sone hvor hjulsats og spor danner et felles svingende system. Den svingende masse blir summen av hjulmasse og ekvivalent medsvingende spormasse.
For høyere frekvenser vil sporet igjen stivne og det oppstår resonanssvingninger mellom hjul og skinne. Dette medfører store overflatespenninger på hjul og skinne.
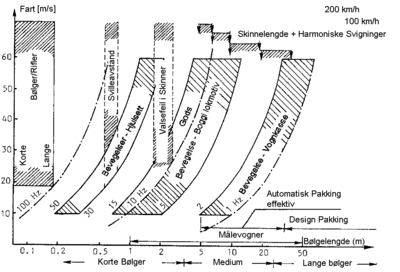
Figur 2.34viser hvilke deler i vognmateriellet som antar bestemte typer av resonansbevegelser ved gitte hastigheter og ved hvilke bølgelengder disse bevegelsene inntreffer.
I diagrammet er angitt bølgelengde langs abscissen og ordinaten viser
hastighetsnivået. Intervallområdene for resonansbevegelser for de ulike deler
av vognmateriellet er inntegnet. Det framgår f.eks. at vognkassen til en vogn
vil anta vertikalbevegelser(hopping) i frekvensområdet 1 - 2 Hz. Avhengig av
framføringshastighet(10 m/s til 60 m/s) vil den periodiske bølgelengde variere
fra 5 m opp til 50 m.
Et lokomotiv vil anta resonansbevegelser mht. hopping og galoppering i frekvensområdet 5 til 15 Hz. Dette skjer i bølgelengdeområdet 0,5 m til 5,0 m i angitt hastighetsområde.
Tilsvarende vil det opptre hopping av hjulsett til en boggi i frekvensområdet 30 - 50 Hz i samme hastighetsintervall (10 m/s - 60 m/s) ved bølgelengder i området 0,2 m til 2,0m. Det gjøres oppmerksom på at svilleavstanden er 0,6 m. Svillene representerer en plutselig forandring i elastisitetsforholdene i sporkonstruksjonen, spesielt ved for lav ballasthøyde. Dette kan under ekstreme forhold føre til resonansbevegelser.
Det skal gis en teoretisk betraktning mht. bevegelse av en partikkel på sporet hvor en bølge i sporets overflate i en idealisert tilstand tenkes beskrevet ved følgende funksjon:
- z = z0 cos kx
hvor
- k = 2π/L
Her betyr:
- L = bølgens lengde (m)
- z0= bølgens amplitude
En massepartikkel beveger seg på bølgens overflate med hastighet
- v(m/s)
Med tilbakelagt vei
- x = vt
vil massepartikkelen i tidsperioden bevege seg
- z = z0 cos kvt
I en definert tidsperiode T beregnes bølgelengden til:
- L = vt (m)
eller
- L = v/f
hvor
- f = 1/T (s-1) eller (Hz)
Dersom sporet tenkes helt stivt, dvs. i frekvensområdet f < (20 - 30) Hz, vil bølgelengder iht.
- L = vf-1
variere i området 2 m < L < 60 m ved hastighet ca. 60 m/s.
Tilsvarende oppnås aktuelle bølgelengder i frekvensområde 30 < f < (60 - 100) Hz lik 0,60 m < L < 2 m.
Hertzian - fjæren
Gjennom den gjensidige påvirkningen i vogn - sporsystemet blir krefter overført ved kontaktflaten mellom hjul og skinne. Denne kraften F forårsaker en vertikal bevegelse av hjulet til boggien og sammenhengen mellom bevegelse og kraft uttrykkes ved den såkalte Hertzian-fjæren. Den antatte lineariserte stivheten til Hertzian-fjæren kan beskrives ved differensialligningen
| (2.88) |
Dette betyr at stivheten kH
beskriver en lineær forandring av kraft over en gitt
lengdeenhet. Egentlig er denne stivheten ikke lineær, men dette blir altså
antatt i den matematiske modell.
Stivheten kH er i litteraturen angitt som en funksjon av aksellast og hjuldiameter. Som eksempel kan nevnes at for en hjuldiameter på 1,00 m og en statisk hjullast lik 75 kN er det beregnet en verdi for kH lik:
- 1,4 x 109 N/m for nye hjul
- 1,6 x 109 N/m for eldre hjul
Det blir altså antatt en stivere verdi for eldre hjul enn for yngre hjul.
Iht. figur 2.35 kan sammenhengen mellom den gjensidige påvirkningskraften FH og forandringen i lengden til Hertzian-fjæren bestemmes ved følgende ligning:
| (2.89) |
Her betyr:
- yW= den vertikale forskyvning av hjulet i nivå med aksel
- yR= den vertikale forskyvning av skinnen under påvirkning av kraft FH
- yG= vertikal geometri av skinnen
- kH= den lineariserte stivhet i Hertzian-fjæren
- FH= vertikal dynamisk kraft i kontaktflate hjul–skinne
For å holde de dynamiske kreftene så lave som mulig er det nødvendig å
vektlegge forskjellige aspekter ved konstruksjon av vognmateriell.
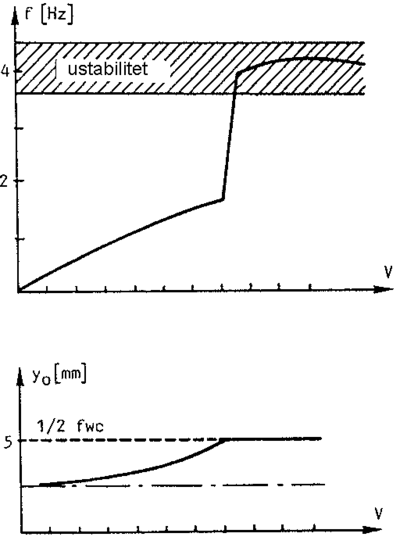
Vognen må utøve stabilitet innenfor det hastighetsområde den er dimensjonert for. Dette betyr at det må være tilstrekkelig nivåer på alle dempere i relevante vibrasjonsområder. Over tid slites hjulflensen og forandring av konisiteten oppstår. Spesielt ved høyere hastigheter kan forandring av konisitet føre til ustabilitet ved framføring av det rullende materiell.
Mht. komfort for passasjerene er det nødvendig å innføre myke fjæroppheng. Sammen med stor vognmasse medfører dette lave vertikale egenfrekvenser.
Store sporkrefter og derved utmatting samt slitasje oppstår på sporet på grunn av stor vognmasse og spesielt på grunn av den uavfjærede masse. Uavfjæret masse er massen under det primære fjæropphenget til vognen og er derfor massen som hviler direkte på kontaktflaten mellom hjul og skinne.
Det må av den grunn gjøres avveininger eller kompromisser mht. konstruksjon av vognmateriell. Tunge vogner vil bevirke god komfort fordi de reagerer tregt på ujevnheter i sporet. På den annen side vil tung masse føre til utmatting på sporets komponenter.
Det er helt nødvendig å unngå flate hjul for å hindre hjulslag.
Men det må også stilles krav til overbygningen. Overbygningen må ha jevn og homogen elastisitet. Ballastlaget må derfor være ensartet og ha konstant høyde. Videre bør ballastlaget legges på en underbygningskonstruksjon hvor formasjonsplaneter lagt ut med stor nøyaktighet mht. jevnhet (helt plant). Ujevnheter i formasjonsplanet kan føre til uheldige bevegelser av materiellets ulike deler i vertikalretningen med resonansfrekvenser som følge.
HJULSETTPÅ SKINNEBUNDET SPOR
Bevegelsesmønsteret til hjulsettet til et vognmateriell på skinnebundet spor er fundamentalt for forståelsen av kjøredynamikken. I dette avsnittet skal det gis en beskrivelse av bevegelsene. I neste avsnitt følger de matematiske likninge som er forbundet med framføring av det rullende materiell.
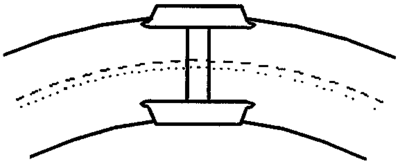
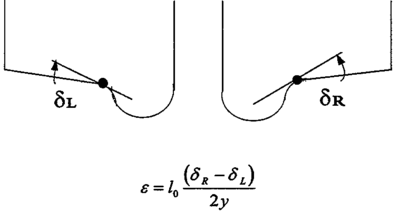
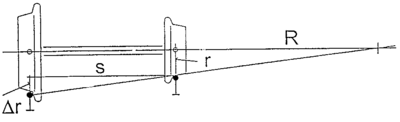
Differanse i rulleradius til hjulene i hjulsettet
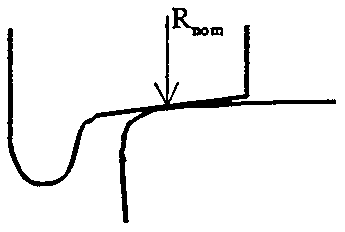
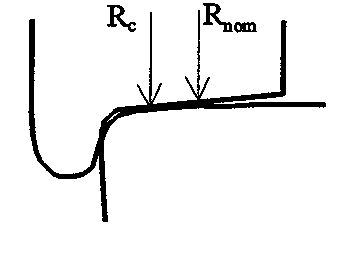
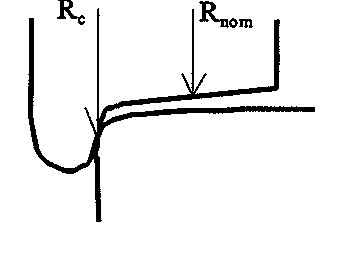
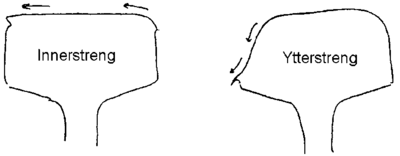
Hjulbanene til hjulene i et hjulsett er formet konisk. Når hjulsettet antar en lateral bevegelse i forhold til spormidt, vil rulleradius bli endret. Dette er illustrert i figurene 2.36,2.37 og 2.38. Figur 2.36 viser tilfellet når hjulsettet beveger seg med nominell hjulradius rNOM . Når flensen til hjulet flytter seg mot innvendig kant av skinnehodet, vil rulleradius til hjulbanen i kontaktpunktet mellom hjul og skinne rc. øke. Beveger flensen til hjulet seg vekk fra innvendig skinnekant, blir rulleradius mindre enn rNOM .
I figur 2.38 er vist et tilfelle hvor rulleradius rC kan bli meget stor.
Etter som hjulsettet beveger seg lateralt fra den midtre eller nominelle
posisjon, vil en hjulflens nærme seg innvendig kant av skinnehodet. Den
andre hjulflensen vil fjerne seg fra skinnehodet. Dette medfører at rulleradius
til hjulbanen i kontaktpunktet for det ene hjulet vil øke. Tilsvarende vil
rulleradius til hjulbanen i kontaktpunktet til det andre hjulet avta. Dermed
oppstår det en differanse i rulleradius til de 2 hjulene i hjulsettet.
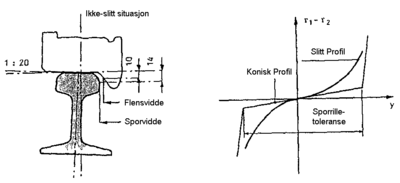
Dersom hjulprofilene var helt koniske, ville gravitasjonssenteret til hjulsettet ha samme høyde ved lateral bevegelse. Men vanligvis er hjulsettene utsatt for slitasje som fører til hult profil. Dette medfører en kraftig endring av hjulradius for det hjulet hvor flensen nærmer seg innvendig kant av skinnehodet. Differensen i rulleradius til hjulbanene for de 2 hjulene vil da bli meget stor. Gravitasjonssenteret til hjulsettet vil løfte seg litt. Forholdet kan medføre klatring som til slutt kan ende i avsporing. Dette vil imidlertid bli forsøkt hindret av hjulsettets treghet og stivhet til primærfjæren. I figur 2.39er det vist forskjellen mellom et korrekt konisk profil og et slitasjeprofil.
Effekt av lateral bevegelse av hjulsettet
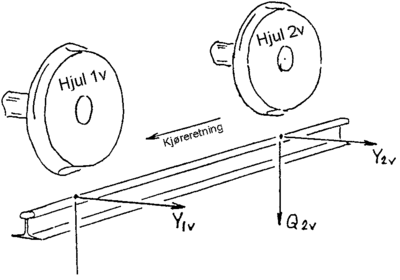
Dersom et hjulsett beveger seg f.eks. lateralt til venstre i forhold til sporet i kjøreretningen, så vil rulleradius til hjulbanen til det venstre hjulet rL øke. Det vises til figur 2.40. Rulleradius til hjulbanen til det høyre hjulet derimot vil avta når hjulet beveger seg fra skinnen. Når omkretsen til det venstre hjulet blir større, vil det prøve å rulle videre ved en gitt rotasjonshastighet. Når fjæringen til slutt utøver motstand, vil det oppstå motsatt like store langsgående krefter på de 2 hjulene. Dette medfører et dreiemoment som forsøker å bringe hjulsettet tilbake til senterlinjen i sporet.
Dersom hjulsettet beveger seg med en anløpsvinkel i sporet, vil hjulene i
hjulsettet prøve å fortsette rullingen i den angitte retning. Dette er vist ved de
svake angitte dobbeltpilene i figur 2.41. Dersom hjulsettet i denne stillingen b
tvunget til å fortsette den parallelle bevegelsen i sporet (angitt ved de svarte
dobbeltpilene), vil det oppstå laterale krefter på hjulbanen til hvert hjul.
Dersom det er hjulflensen som framtvinger hjulsettet til å løpe parallelt med
sporet med anløpsvinkel, så vil det fremdeles være en lateral kraft F på
hjulbanen til hvert hjul. Hjulflensen på det venstre hjulet må imidlertid utvikle
en kraft på 2 F i retning mot høyre for å overvinne hjulbanekreftene. Når
hjulbane- og hjulflenskreftene summeres på det venstre hjulet, vil det oppstå
en netto kraft lik F mot høyre på det venstre hjulet. Det vil da bli en
rotasjonsbevegelse mot høyre. Dette er vist i figur 2.42.
Kreftene vist i figur 2.42 er de resulterende krefter på hjulene. Kreftene på skinnene vil bli like store og motsatt rettet. Dette betyr at hjulsettetvil generere krefter som vil trekke skinnene fra hverandre og dermed føre til større sporvidde.
Bevegelse av et fritt hjulsett på rett linje
Det antas at et fritt hjulsett beveger seg på et spor. Videre forutsettes at hjulsettet starter denne bevegelsen fra en forskjøvet posisjon. På grunn av forskjell i rulleradius til hjulbanene på de 2 hjulene vil hjulsettet av seg selv styre inn mot senterlinjen av sporet. Når hjulsettet når senterlinjen av sporet, vil det danne en anløpsvinkel i forhold til skinnene. Av den grunn vil hjulsettet gå mot den andre siden av sporet og bevegelsene vil fortsette på denne måten. Bevegelsesmønsteret er vist i figur 2.43.
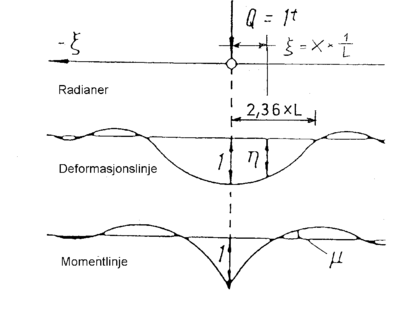
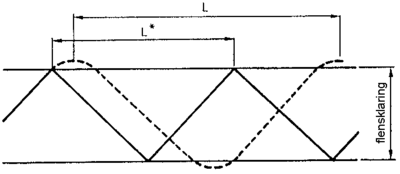
Denne trigonometriske bevegelsen på sporet betegnes som hjulsettets kinematiske bevegelse og er kun en funksjon av det geometriske systemet. Bestemmende parametre er den effektive konisitet til hjulsettet, hjulradius og sporvidde. Den effektive konisitet utledes av helningen på skinnene og de koniske hjulene på hjulsettet. Den bølgelengde som oppstår, kalles den kinematiske bølgelengde og er uavhengig av hastighet. Dette medfører at frekvensen av den kinematiske bevegelse øker lineært med økende hastighet.
Denne bevegelsen kan i siste konsekvens føre til ustabilitet og såkalt hunting (hjulflensen støter mot skinnekantens innside).
I en kurve vil den ytre skinnen være lenger enn den indre skinnen. Dersom
hjulsettet beveger seg tilstrekkelig langt nok lateralt mot den ytre skinne ved
framføring, vil differensen i rulleradius til hjulbanene til de 2 hjulene utligne
forskjellen i lengde. Et hjulsett som følger en slik bevegelse i en kurve,
betegnes å følge den ideelle linje. Dette er illustrert i figur 2.44.
Et hjulsett som har radielle egenskaper og som følger den ideelle linje, vil løpe
perfekt gjennom kurven. Dermed vil tilleggskrefter ikke genereres. Imidlertid er
det viktig å være klar over at størrelsen av tilgjengelig lateral bevegelse vil bli
begrenset ved hjulflensens tilstedeværelse. For et hjul med konisitet lik 1 : 20
vil det være nødvendig med en radius lik 1700 m for at hjulsettet skal følge
den ideelle linje uten flenskontakt.
Rullende friksjon
Friksjonskrefter oppstår på grunn av differanse i rulleradius til hjulbanene i hjulene og på grunn av anløpsvinkel. Disse friksjonskreftene er forskjellig fra den klassiske glidende friksjon. Dette har sin bakgrunn i at hjulsettet ruller langs sporet.
Teorien og forståelsen av den rullende kontakt er fundamental for utviklingen av den teoretiske forståelse av kontakten hjul/skinne.
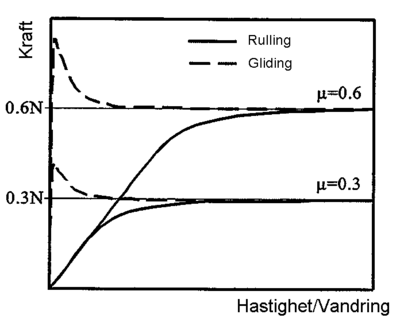
Den rullende kontakt eller den relative bevegelse mellom hjul og skinne benevnes kryp. Kryp er hastigheten av overflatekontakten til det ene legemet relativt til overflatekontakten til det andre legemet. Krefter på grunn av kryp kalles krypkrefter.
Et typisk krypkraft/krypforhold er vist i figur 2.45. Ved den glidende friksjon bygges kraften opp til et høyt nivå med en gang. Men med en gang den er oppstått, synker den glidende krypkraft med økende relativ hastighet. Mht. den rullende friksjon vil kraften være proporsjonal med den relative hastighet eller kryp ved lave verdier. Ved høyere verdier av hastighet/kryp vil kraften nærme seg asymptotisk mot et nivå som er gitt ved friksjonskoeffisienten multiplisert med normallast lik N.
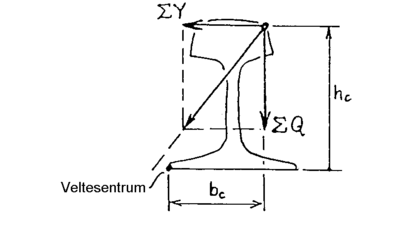
SAMVIRKE MATERIELL - BANE, KONISITET
I det foregående avsnitt ble bevegelsen av hjulsettet beskrevet. I dette avsnittet skal de matematiske sammenhenger diskuteres.
Generelt har hjulene følgende oppgaver:
- Bære det rullende materiell
- Styre det rullende materiell i lateral retning
- Overføre trekk- og bremsekrefter
Hjulsatsen
Hjulsatsen er et av jernbaneteknikkens grunnleggende konstruksjonselement. Hvert av hjulene har en hjulbane som er i kontakt med skinnen og en flens. Hjulflensens oppgave er å styre hjulsettet lateralt i sporet.
De 2 hjulene i et hjulsett er forbundet med en aksel. En hjulsats kan dermed beskrives som et par konede hjul med flenser hvor hjulene er stivt forbundet med akselen.
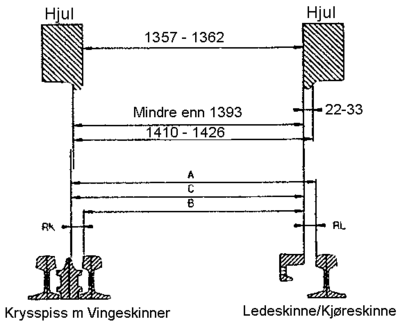
Figur 2.46 illustrerer et hjulsett på sporet.
Følgende parametre defineres:
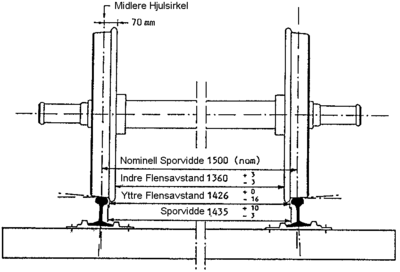
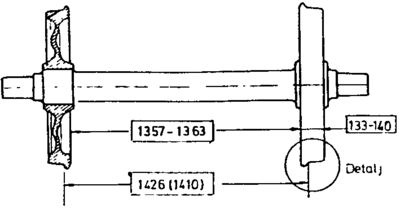
- Nominell sporvidde som er avstanden mellom kontaktpunktene for
løpebanenes middellinjer (sirkellinjer) på skinnene. Denne parameteren er meget viktig og må ikke forveksles med sporvidde. Nominell sporvidde skal være 1500 mm.
- Sporvidde som er avstanden mellom innsiden til de 2 skinnene målt 14 mm
under skinnetopp. Sporvidden skal være 1435 mm. Toleranseverdier er vanligvis + 10 mm og - 3 mm for et spor av vanlig bra standard. Detaljerte toleransemål i de ulike hastighetsavhengige kvalitetsklaser er gitt i regelverket.
- Flensvidde som er avstanden mellom hjulflensene mot innside av
skinnekant målt 10 mm under overkant av skinnetopp for et spor med nominell sporvidde. Det forutsettes at hjulsettet er i sentrert posisjon. Flensvidden er 1426 mm med toleranseverdier lik + 0 mm og -16 mm.
- Hjulvidde som er avstanden mellom innside av hjulene og er 1360 mm på
et standard spor med nominell sporvidde lik 1500 mm. Toleranseverdiene er + 3 mm og - 3 mm.
- Sporspillet er klaringen mellom hjulsettet og sporet og er dermed den
avstand hjulsettet kan bevege seg lateralt. Denne avstanden er ikke den samme som avstanden mellom sporvidde og flensvidde.
- Andre viktige parametre for hjulet er flenstykkelse, flenshøyde og det
såkalte qR målet.
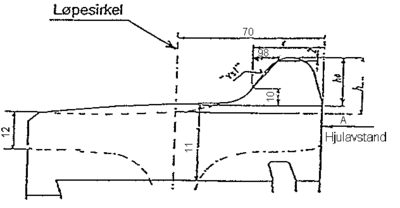
qR måletdefineres som horisontal avstand målt fra et punkt i en høyde på 2 mm fra underkant hjulflenstil et punkt som er 10 mm over hjulbanen ved løpesirkelen. Det vises til figur 2.47.
Ved Jernbaneverket skal qR
ikke underskride 6,5 mm. Ved en lavere verdi vil
innvendig side av flensen bli meget bratt. Dette øker faren for avsporing.
Hjulets konisitet
Det er nevnt at hjulets løpebane er konisk formet.
Årsaken til dette er at konisiteten gir en styremulighet for hjulsatsen i sporet på rett linje og i kurver. I den etterfølgende betraktning skal det antas at hjulenes hjulbaner har en rak konisk form.
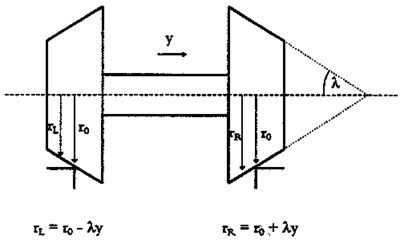
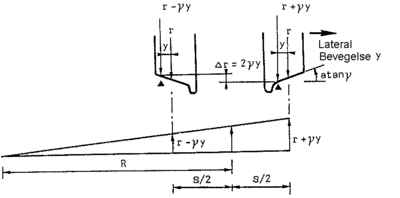
Figur 2.48 viser kontaktpunktene mellom hjulene til et hjulsett og skinnene. Det er antatt at hjulsettet er sentrert. Dersom hjulsettet beveger seg lateralt mot høyre på grunn av klaringen, vil rulleradius til det høyre hjulet, rH , bli større. Likeledes vil rulleradius til det venstre hjulet, r V , bli mindre.
Dersom hjulsettet derimot beveger seg mot venstre, vil rV bli større og rH vil anta en lavere verdi.
Denne differansen mellom størrelsen på de 2 hjulradiene til hjulene er en meget viktig parameter for å kunne beskrive hjulsettets bevegelser. Under antakelse av at hjulets hjulbane er ideelt konisk utformet, kan følgende enkle matematiske sammenhenger iht. betegnelser i figur 32 utledes ved lateral bevegelse av hjulparet mot høyre:
| (2.90) |
| (2.91) |
Her betyr:
- rV er rulleradius til det venstre hjulet i kontaktpunktet med skinne
- rH er rulleradius til det høyre hjulet i kontaktpunktet med skinne
- r0 er midlere rulleradius til hjulet
- λ er hjulbanens konisitet eller helning
- y er lateral forskyvning av hjulsettet
For et konisk hjulsett er verdien av λ gitt ved vinkelen til det koniske kjegleutsnittet. For l lik 0,05 er konisiteten eller helningen til hjulbanen med horisontalen lik 1 : 20. Tilsvarende er for λ lik 0,025 konisiteten til hjulbanen lik 1 : 40.
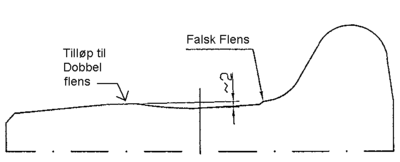
Imidlertid i praksis er variasjonen eller endringen i hjulradius for hvert hjul en meget kompleks funksjon. Viktige parametre er hjulets og sporets geometri. Dette har sammenheng med at hjul med rak konisitet i hjulbanen etter hvert vil bli utsatt for slitasje i hjulbanen. Det kan danne seg en dobbelflens som vist i figur 2.49. Et annet fenomen er dannelse av en falsk flens. Et slikt slitasjeprofil vil kunne oppstå relativt hurtig, bl.a. på grunn av bremsing. Men når det først har oppstått, vil profilet være ganske stabilt og det opptrer da som et slitasjetilpasset profil.
Både dobbelflens og falsk flens vil i varierende grad føre til tvangsstyring av hjulsettet.
Kontaktpunktsgeometri
Mellom hjul og skinne dannes en kontaktflate. Dersom normalkraften i kontaktflaten går mot null, vil kontaktflaten bare bli et punkt. Dette punktet kalles kontaktpunktet.
Den geometriske formen på kontaktflaten mellom hjulbane og skinnehode er normalt elipseformet.
Kontaktellipsens størrelse kan beregnes ved hjelp av Hertz’ kontaktteori. Kontaktellipsens flateinnhold er ca. 1 - 2 cm2. Dette er illustrert i figur 2.50.
Dersom det dannes kun ett kontaktpunkt mellom hjul og skinne, råder ettpunktskontakt. Det vises til figur 2.51.
2 kontaktpunkter mellom hjul og skinne betegnes topunktskontakt. Dette er
illustrert i figur 2.52.
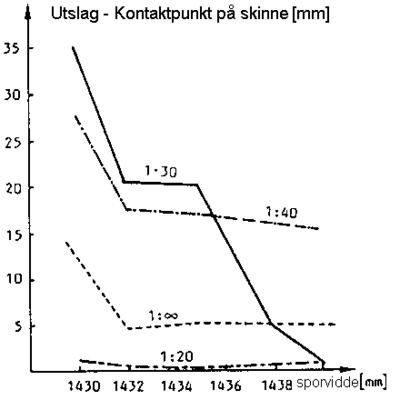
Det skal bemerkes at for et hjul med slitasjetilpasset hjulbane på en slitt skinne forflyttes kontaktpunktet som regel kontinuerlig mot hjulflensen når hjulet forskyves lateralt i forhold til skinnen.
Ekvivalent konisitet
Når et hjul forskyves lateralt i forhold til skinnen, medfører dette en endring av flere parametre som har betydning for kontaktpunktet mellom hjul og skinne.
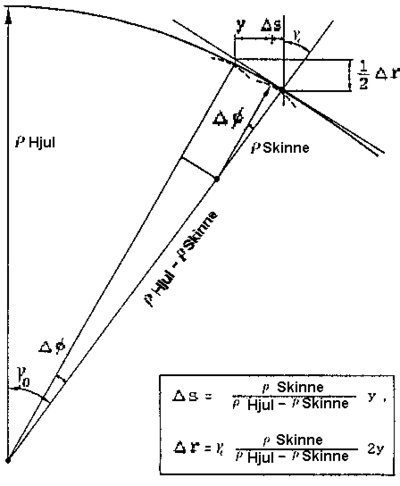
Den laterale forskyvning til hjulsettet betegnes y. Flere parametre vil være avhengig av denne bevegelsen. Det innføres:
- r0 er hjulradius i løpesirkelen
- Δr er økning i hjulradius
- γ er kontaktpunktsvinkelen
- ΔZH er hjulløftet
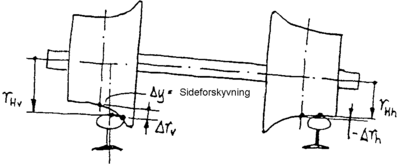
- Δy er sideforskyvning av kontaktpunktet hjul – skinne, denne defineres som positiv når hjulets flens nærmer seg skinnen
Figur 2.53 viser definisjonen av disse parametrene.
Med bakgrunn i ovennevnte vil det for en gitt hjul/skinne kombinasjon dannes
de tre kontaktpunktsfunksjonene:
| (2.92) |
| (2.93) |
| (2.94) |
Med effektiv konisitet for et hjul menes kvotienten mellom økning i rulleradius og den laterale forskyvning mellom hjul og skinne:
| (2.95) |
Oftest er det imidlertid den effektive konisiteten for et hjulsett som er av
interesse. Denne konisiteten uttrykkes som kvotienten mellom den halve
forskjellen i rulleradius mellom de 2 hjulene og den laterale forskyvning
mellom hjul og skinne:
| (2.96) |
Det vises til figur 2.54.
Dersom hjulbanene til de 2 hjulene har den samme konisitet(rak konus), er
den effektive konisitet identisk med konusvinkelen dvs. kontaktpunktsvinkelen.
For dette tilfelle gjelder:
| (2.97) |
| (2.98) |
| (2.99) |
Dette gir:
| (2.100) |
Det vises til figur 2.55.
Det framgår av ovennevnte at med et slitt profil vil den aktuelle konisitet være
avhengig av formen på skinnehodet og hjulbanen samt slitasje på øvrige
komponenter. Sporvidde og skinnehelning har også innflytelse.
Uttrykket (rL-rR) gjenspeiler den øyeblikkelige differanse i rulleradius til hjulbanene for et hjulsett. I praksis er denne differansen en ikke-lineær funksjon av den laterale forskyvning Δy av hjulsettet mht. senterstillingen.
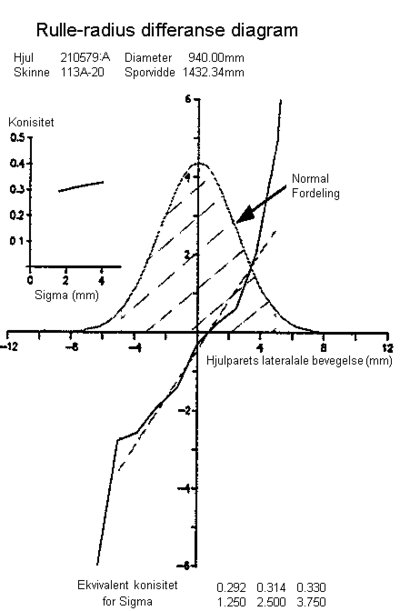
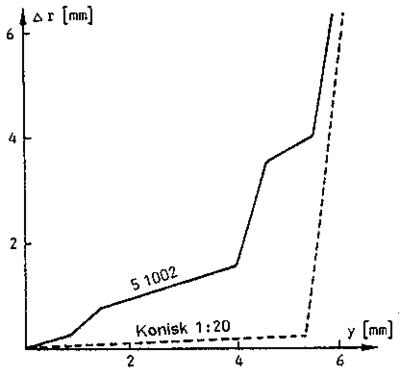
Et diagram som beskriver differansen i rulleradiusuttrykt ved (rV - rH) i forhold til den laterale bevegelse Dy av hjulsettet kan opptegnes. Et eksempel er vist i figur 2.56.
Det framgår at funksjonen ikke beskriver en rett linje. For å oppnå en “ ekvivalent konisitet” vil det være nødvendig å trekke en rett linje gjennom den ikke-lineære grafen for best mulig tilpassing. Dette kan gjøres ved å benytte en veiet funksjon som tar hensyn til den tiden som hjulsettet bruker for hver verdi av den laterale posisjon hjulsettet har. Den mest normale veide funksjon er normalfordelingsfunksjonen sentrert om sporets senterlinje og med et standardavvik lik 2,5 mm. Ved å bruke en slik veiet funksjon kan den best tilpassede rette linje for å beskrive den ekvivalente konisitet uttrykkes ved:
| (2.101) |
N representerer normalfordelingsfunksjonen mht. hyppighet av den enkelte
laterale forskyvning ved en bestemt verdi av differanse i rulleradius.
Når hjulsettet gjennomløper en kurve, vil de 2 hjulene ha forskjellig distanse tilbakelegge. Dette fordi den ytre skinnestrengen er lengre enn den indre skinnestrengen i kurven. Dersom differansen i rulleradius til de 2 hjulene forholder seg til differansen i lengde til skinnestrengene, så vil hjulsettet gjennomløpe kurven på en perfekt måte. Dette er illustrert i figur 2.57.
Hjulsettets laterale posisjon i en riktig stilling i kurven kan uttrykkes ved følgende formel:
| (2.102) |
Her betyr:
- rV = rulleradius til det venstre hjulet
- R = kurvens radius
- l0= halv sporavstand
- rH = rulleradius til det høyre hjulet
Dersom hjulbanene til hjulene er teoretisk formet med riktig konisitet, kan
beliggenheten til den nøytrale linjen i kurven beregnes mht. forskyvning fra
spormidt:
| (2.103) |
Her betyr:
r0= sentersirkel i hjulbanen til hjulet
l = konisitet til hjulene
Kontaktpunktvinkelen er allerede nevnt. Størrelsen på kontaktpunktsvinkelen
er meget viktig da kraften normalt på kontaktpunktet gir opphav til en lateral
komponent. Kraften normalt på kontaktpunktet skal bære vekten av det
rullende materiell som framføres. Dersom hjulsettet har hjul som er teoretisk
konisk utformet, så vil konisiteten til hjulet i kontaktpunktet være den samme
som kontaktpunktsvinkelen. Dette gjelder under forutsetning av at flenskontakt
blir unngått. For et profilert hjul vil den opptredende kontaktpunktsvinkelen d
variere etter som hjulsettet beveger seg langs skinnene. På samme måte som
en differanse i rulleradiustil hjulene i et hjulpar oppstår, vil det oppstå en
differanse i størrelsen på kontaktpunktsvinkelen til de samme hjulene. Denne
differansen kan uttrykkes ved
| (2.104) |
Denne differansen i kontaktpunktsvinkelenkan beregnes og en lineær
kontaktpunktsvinkel som parameter kan bestemmes relatert til (γR - γL) som
funksjon av den laterale forskyvning y:
| (2.105) |
Dette er antydet i figur 2.58.
Det er allerede nevnt at hjulbaner på hjul med rak konus etter hvert vil
forandre form på grunn av slitasje. For små sideforskyvninger mellom hjul og
skinne kan hjulflaten og skinneflaten i området for det nominelle
kontaktpunktet med en viss tilnærming anses å ha konstante krumningsradier
i tverrplanet. Det forutsettes videre at kontaktpunktsvinkelen i normal stilling
ved forskyvning y=0 er λ=γ0.
Under forutsetninger av små laterale forskyvninger kan den effektive
konisitetenberegnes iht.:
| (2.106) |
Her betyr:
- rTH = krummningsradius til hjulbanen
- rTR = krummningsradius til skinnehodet
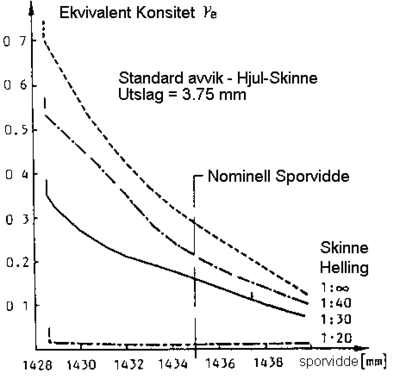
Det kan av ovennevnte formel avleses at den effektive konisitet kan bli meget stor dersom hjulbanens og skinnehodets krummningsradier er tilnærmet like store. Ved oppstått slitasje i hjulbanen til hjulet kommer derfor den effektive konisiteten til å øke.
Den effektive konisitet kommer også til å bli stor når sporspillet er lite i normalstilling til hjulet. Dette henger sammen med at Kontaktpunktvinkelen g 0 blir høy. Det vises til figur 2.59.
I ovenliggende formel ble det forutsatt at krummningsradiene for hjulbanen til hjulet og til skinnehodet i tverrplanet var konstant. Dette har tilnærmet gyldighet for små bevegelser av hjulsettet i lateral retning i området rundt normalstillingen, dvs. i området + 2 mm til - 2 mm.
I praksis må størrelsene Δr, γ og ΔZH beregnes med numeriske metoder. For ikke-lineære funksjoner kan benyttes metoden som tar i bruk normalfordelingsfunksjonen som veid funksjon. Det vises til foregående redegjørelse.
Det kan konkluderes med at ved lite sporspill dvs. trangt spor kan den effektive konisiteten bli meget høy. Spesielt gjelder dette når det samtidig er full tykkelse av hjulflensen på begge hjulene.
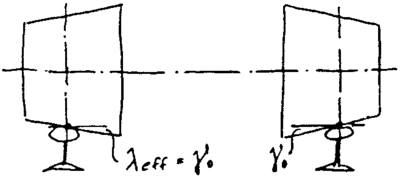
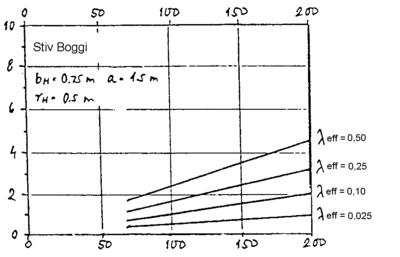
Spørsmålet blir hvor stor bør konisiteten være. Det er naturligvis vanskelig å konstruere et løpeverk som utøver gode løpeegenskaper under alle forhold. Normal konstruksjonspraksis er at det rullende materiell skal klare en effektiv konisitet i området
0,05 ≤ λEFF. ≤ 0,35.
Dette gjelder for framføring av rullende materiell med høyere hastigheter.
For lavere hastigheter bør kanskje gjelde λEFF. ≤ 0,50.
Hjulparets bevegelse i sporet
Rett linje
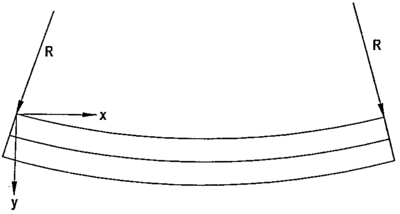
Et hjulsett med hjul som har teoretisk riktig konisitet mht. hjulbanen, beveger seg på rett linje. På grunn av klaringen i sporet (sporspillet) vil hjulet bli forskjøvet lateralt. Denne laterale bevegelsen vil bli møtt eller motvirket av en kraft som gjør at hjulsettet beveger seg mot den andre siden. Det oppstår en periodisk bevegelse, en såkalt sinusbevegelse. Denne pendlingen av hjulsettet er beskrevet teoretisk av Klingel i 1883 og betegnes derfor som Klingels bevegelse. I figur 2.60er hjulsettet modifisert og følgende parametre inngår i den matematiske formuleringen:
- λ eller γ = konisitet(helning) til hjulbanen
- r = radius av hjulbanens sirkel i senter
- R = radius i sinuskurven til den periodiske bevegelse på rett linje
- s = sporvidde
- y = lateral forskyvning av hjulsettet fra senter
- v = hastighet
- x = distanse som tilbakelegges
I en teoretisk riktig bevegelse vil hjulsettet bli forskjøvet lateralt over en distanse y med utgangspunkt i senter til hjulbanens løpesirkel. Dette på grunn av rullingen til hjulsettet ved framføring. Videre vil differansen i rulleradius til hjulsettet være 2yγ .
Det kan utledes følgende matematiske sammenhenger:
| (2.107) |
| (2.108) |
Dette gir:
| (2.109) |
| (2.110) |
| (2.111) |
| (2.112) |
Med disse 4 utrykkene kan følgende sammenhenger utledes:
| (2.113) |
som er definisjon av ekvivalent konisitet.
| (2.114) |
Det er påpekt at den hjulsettet følger en tilnærmet sinusbevegelse med en
radius R på grunn av klaringen eller sporspillet når det beveger seg på ret
linje. Det må være kjent fra mekanikken at et element inntar en form ved
sentrisk belastning på grunn av trykkrefter som kan beskrives ved:
| (2.115) |
Dette betyr at den annen deriverte av en funksjon beskriver krumningen til elementet i et x-y koordinatsystem ved sentrisk belastning av elementet. Det vises til figur 2.61. Denne relasjonen kan overføres til den tilnærmede sinusbevegelse til et hjulsett som på grunn av hjulbanenes konisitet beveger seg langs sporet på en rett linje.
Det kan dermed utledes:
| (2.116) |
| (2.117) |
| (2.118) |
| (2.119) |
| (2.120) |
| (2.121) |
Denne differensiallikningen har en generell løsning som kan skrives på
formen:
| (2.122) |
α kan beskrives ved uttrykket:
| (2.123) |
For y(x = 0) = 0, blir løsningen:
| (2.124) |
Her betyr:
- y0 = amplitude av den lateral forskyvning av hjulsettet
- L = bølgelengde i den periodiske sinusbevegelse på rett linje
Den kinematiske bølgelengde L er vist i figurene 2.62 og 2.63 og beskrives
ved formelen:
| (2.125) |
Den maksimale laterale akselerasjon uttrykkes ved:
| (2.126) |
Frekvensen til den laterale akselerasjon:
| (2.127) |
Dersom denne frekvensen sammenfaller med en av resonansfrekvensene til
det rullende materiell, vil vognen bli ustabil ved framføring. Den laterale
akselrasjonen er et mål for størrelsen på de laterale krefter. Det framgår at
den laterale kraften vil øke ved større hastigheter og/eller ved mindre
bølgelengder, dvs. ved større konisiteter. Det framgår også at størrelsen på
bølgelengden er uavhengig av hastigheten. Parametre som bestemmer
bølgelengdens størrelse, er radius i senter til hjulbane, sporvidde og konisitet.
En konisitet lik 1 : 40 vil gi en større bølgelengde og en lavere lateral
akselerasjon enn en konisitet lik 1 : 20 ved samme hastighet. Den progressive
økende konisitet i tilfellet av slitte profiler på hjulbane og skinnehode vil
forårsake kortere bølgelengder og økende akselerasjoner.
”Hunting”
Det er utledet at bevegelsesligningen til Klingel kan skrives på formen:
| (2.128) |
Det forutsettes at y = 0 ved stedet x = 0, dvs. der hvor bevegelsen til hjulsettet
starter.
Størrelsen på amplituden y0er en funksjon av sporets kvalitet mht.
uregelmessigheter (laterale sporfeil), dynamisk oppførsel av vognmateriellet
og hastigheten til det rullende materiell. Generelt på grunn av glidning vil y0
øke som funksjon av voksende hastighet inntil den laterale forskyvning antar
halve verdien av sporspillet (flangeway clearance). Hjulflensen vil da støte mot
innsiden av skinnehodet og hjulsettet vil “ bykse” eller “ sprette” tilbake. Dette
medfører at den laterale bevegelse vil innta en helt annen karakter og denne
bevegelsen er kjent som hunting. Dette er illustrert i figur 2.64.
Bevegelsen til hjulsettet skifter fra en harmonisk sinusbevegelse til en form for sikksakk bevegelse. Bølgelengden blir kortere og frekvensen til den laterale akselerasjonen uttrykt ved hastighet over bølgelengde(v/L) øker. Til slutt kan resonans inntreffe. Dette er illustrert i figur 2.65. Boggien eller hjulsettet må derfor konstrueres på en slik måte at løpeegenskapene blir stabile. Parametre som må vies oppmerksomhet, er konisitet og sporspillet.
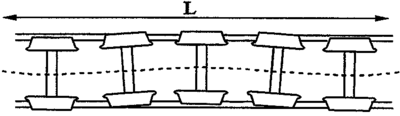
Slitte hjulprofiler
Et absolutt perfekt konisk hjulprofil vil være ustabilt dersom bare formen betraktes. Men under påvirkning av slitasje vil profilet anta en form som gjør profilet stabilt. I tillegg vil de teoretisk riktige hjulprofilene ha den ulempe at en lateral bevegelse på grunn av 2-punkt kontakt, vil føre til støtbevegelse. Dersom det antas at profilet i kontaktpunktet mellom skinnehodet og hjulbane er sirkulært, så kan det utledes at ved en lateral forskyvning y til hjulsettet mht. sporet vil kontaktpunktet på skinnehodet overføres over en distanse:
| (2.129) |
Her betyr:
- Δs = forskyvning av kontaktpunktet på skinne på grunn av
forskyvning av hjulsettet
- y = forskyvning av hjulsettet
- rHJUL = krummningsradius til hjulbanen
- rSKINNE =krummningsradius til skinnehodet
Videre kan det utledes:
| (2.130) |
Det vises til figur 2.66 og figur 2.67.
Med koniske profil er radius uendelig og kontaktpunktet på skinnehodet beveger seg derfor ikke. Dette medfører at slitasje på skinnehodet blir mye konsentrert på et punkt. Et meget interessant punkt opptrer dersom radiene på hjulbanen og skinnen nesten blir den samme. Dersom det bare er en liten lateral forskyvning på akselen, så vil kontaktpunktet hoppe. Dette fører til mangel på kjørekomfort. I kurven for Dr manifesterer seg dette i et hopp.
Praktiske forsøk gjort i ORE Committee C 116har vist at over en gitt tidsperiode så stabiliserer seg slitasjen ved ekvivalent konisitet på ca. 0,2 til 0,3. Under hensyntagen til stabil løpsdynamikk må den ekvivalente konisitet være mindre 0,4, i alle fall ved høyere hastigheter. Og for å garantere sentereffekten må den ekvivalent konisitet være større enn 0,1. Figur gir en oversikt over verdier av den ekvivalente konisitet for profilet S 1002 i kombinasjon med skinne av type UIC60 for forskjellige sporvidder og skinnehelninger. Med unntakelse av skinnehelning1 : 20 øker konisiteten når sporvidden minker. Særlig ved stor skinnehelning øker konisiteten ved minkende sporvidde. Med skinnehelning 1 : 20 er konisiteten meget liten og nærmest uavhengig av sporvidden i området 1428 - 1438 mm.
Forskyvningene i kontaktpunktet på skinnehodet for gitte verdier er vist i figur 2.68. Videre er de illustrert i figur 2.69. Det vises at ved skinnehelning1 : 20 så arbeider ikke prinsippet med slitte profiler. Med skinnehelning 1 : 40 forblir hjulprofilene stabile skinnene slites lineært dersom sporvidden er mellom 1432 mm og 1436 mm.
Anløpsvinkler
Det skal beskrives bevegelsesforløpet i en kurve for en boggiramme og for to akslede vogner.
Boggiramme
Anløpsvinkler opptrer ved gjennomkjøring i kurver med små radier. Under forutsetning av en stiv konstruert boggi holdes akslene parallelle. Boggien vil derfor forsøke å kjøre rett fram. Hjulet i fremre aksel vil da gjennomløpe sirkelkurven med flenskontakt mot ytre skinnestreng. Skinnestrengen presser hjulet tilbake og tvinger dermed boggien til å følge sporets krumning. Det oppstår en vinkel som defineres som anløpsvinkel. Det vises til figur 2.70. Anløpsvinkelen er vinkelen mellom skinnestrengen og hjulflaten. Denne vinkelen er lik vinkelen mellom hjulakselen og kurvens radius. Anløpsvinkelen angir forskjellen mellom vognakselens virkelige stilling og en teoretisk radialstilling. Størrelsen på anløpsvinkelen er avhengig av parametrene kurveradius og avstand mellom akslene i en boggie iht. følgende formel:
| (2.131) |
Her betyr:
- α= anløpsvinkel til fremre aksel i boggi mot skinnestreng
- l = avstand mellom akslene
- R = radius i kurve
Formelen gir vinkelen i radianer. Omregning til grader og minutter blir:
| (2.132) |
eller
| (2.133) |
Dersom avstanden mellom akslene i en boggier f.eks. 2500 mm (B5 - materiell) og kurveradiuser 300 m, beregnes anløpsvinkelen til :
| (2.134) |
| (2.135) |
Dette under forutsetning av stiv boggiramme med aksler som holdes nøyaktig parallelle. Den bakre aksel i boggiløper gjennom kurven uten flenskontakt og føres dermed radielt.
Det er utviklet boggikonstruksjoner hvor oppleggene for hjulsettene er bygget elastiske og som dermed muliggjør radiell innstilling av hjulsettene.
Hjulsatsene er konstruert slik at det alltid er et sporspill ved framføring. Den forreste aksel i en boggikonstruksjon med stiv ramme vil da anta en anløpsvinkel som beregnes etter følgende formel:
| (2.136) |
Her betyr f sporspillet. Ved økende sporviddeblir anløpsvinkelen dermed
større.
En stor anløpsvinkelmedvirker til økt slitasje på skinner og hjul samt til økt energiforbruk ved framføring av det rullende materiell. Det er derfor av interesse å holde anløpsvinkelen så lav som mulig.
To-akselede vogner
Dersom to-akslede vogner(godsvogner) ble bygget på en tilsvarende måte som boggier med stiv ramme (begge aksler holdes nøyaktig parallelle), ville anløpsvinkelen bli for stor. Dette fordi to-akslede vogner har en avstand mellom akslene opp til 10,0 m. Disse vognene blir bygget på en slik måte at akslene er svingbare i forhold til vognkassen. Hjulsatsene er derfor i stand til å dreie seg litt fra midtstillingen som de inntar på rettlinjet spor. Men akslene oppnår likevel ikke den radiale innstillingen. Det innstiller seg en anløpsvinkel som vist i figur 2.71.
Den bakre aksel vil som oftest rulle gjennom kurven uten flenskontakt med skinnene. Men hjul nr. 4 på bakre aksel av en vogn med stor akselavstand kan ved lave hastigheter i kurver med små radier få flenskontakt med den indre skinnestreng.
Hjulsats i kurver
Overskriftstekst
Det skal betraktes 2 tilstander:
- Ideell gjennomløping av hjulsett i kurve
- Kinematisk rullebevegelse
Ideell gjennomløping av hjulsett i kurver
Betingelse for radiell innstilling av ytre hjul i første hjulsats skal diskuteres. Det vises til figur 2.72.
Følgende begreper inngår:
- R = radius i sirkelkurve
- S = avstand mellom hjulflensene i hjulsettet
- a = akselavstand i sporets senterlinje
- Δx = avstand for radiell innstilling
Følgende matematiske utledning kan gjøres:
| (2.137) |
Dette gir mht. ΔX:
| (2.138) |
Uttrykket viser at jo større a er, jo større må Δx være for at hjulsettet skal
gjennomløpe kurven radielt.
Vinkelen kan beregnes:
| (2.139) |
I figurene 2.73 og 2.65 er vist diagrammene mht. berøringsgeometrien for
hjul/skinne i et gjennomløp i en kurve. Øverste figur (figur2.64) angir
nødvendig Δx som funksjon av radius R ved forskjellig avstand mellom
akslene. Nederste figur (figur 2.74) viser vinkel som funksjon av radius og
avstand a.
Kinematisk rullebetingelse i kurveradier
Det ytre hjulet må følge en lengre vei enn det hjulet som går på innerstrengen. Dette betyr at radius til løpesirkel til det ytre hjulet må være større enn radius til løpesirkel til det indre hjulet. Forskjellen betegnes Dr. Dette er illustrert i figur 2.75 under.
Følgende betegnelser gjelder:
- R = radius i sirkelkurve
- s = avstand mellom hjulflensene
- r = radius i løpesirkel i sentrum av hjulbane
- Δr = differanse i løpesirkel til hjulbanene i hjulsettet
- y = lateral forskyvning av hjulsettet
Det kan utledes følgende matematiske relasjoner:
| (2.140) |
Iht. utledninger utført i kapittel, gjelder:
| (2.141) |
Dvs. nødvendig differanse avtar med økende radius i kurve.
Videre er det tidligere vist følgende relasjon:
| (2.142) |
Dette viser at det er 2 muligheter til å oppnå tilstrekkelig differanse i
rulleradius:
- øke konisiteten
- oppnå større verdi av den laterale forskyvning y av hjulsettet ved for eksempel assymetrisk sliping
I figur 2.76er Δr framstilt som funksjon av rs/R ved forskjellige radier i
løpesirkelen.
Dynamisk stabilitet – gangstabilitet
Det vises til foregående kapitler om konisitet og gangdynamikk. Flere konklusjoner kan trekkes.
Jo større konisiteten blir i forhold til hjulradius og sporvidde, jo mindre blir bølgelengden i sinusgangen. Jo mindre bølgelengden blir og jo større hastigheten er, desto høyere blir frekvensen i svingningene og desto kraftigere blir bevegelsene. Det vises til grunnleggende formler.
Når bevegelsene i svingningene dempes, konkluderes det med at hjulsatsen har stabil gange eller gangstabilitet. Dette gjelder også for vognen som er montert på hjulsatsen.
I motsatt tilfelle vil bevegelsens amplitude i svingningene øke inntil det er hjulflensene som begrenser bevegelsene. Hjulflensene vil da få kontakt med skinnene. Dette medfører ustabilitet eller ustabil gange.
Et fri hjulsats har ustabil gange ved meget lave hastighet. Teoretisk oppstår den ustabile gange ved hastighet lik 0. Den hastighet som forårsaker ustabil gange, benevnes kritisk hastighet.
En vedvarende bevegelse i svingningene i lateral retning hvor hjulflensene til hjulsatsen får kontakt med skinnene, kan naturligvis ikke aksepteres. Bevegelsene vil forplante seg opp i selve vognen og gi opphav til kraftige forstyrrelser. Ofte blir også de laterale kreftene på sporet meget store i et slikt tilfelle. Dette gjelder særskilt ved høye hastigheter og dersom andre komponenter i vognen er stivt koplet til hjulsatsen. Spesielt er rammeverket i boggien utsatt. Ved en slik stiv kopling vil komponentene i vognkonstruksjonen følge med bevegelsene til hjulsatsen i lateral retning.
Risikoen for ustabilitet øker som regel med høyere hastigheter.
Generelt eksisterer det 2 typer av ustabilitet:
- Ved høy hjulkonisitet blir frekvensene til sinusbevegelsene meget store.
Her virker bl.a. uavfjæret masse i hjulsats og tilkoplet boggirammeverk destabiliserende. Denne ustabiliteten i hjulsatsen har normalt en svingningsfrekvens i området 4 – 8 Hz.
- Ved relativt lav hjulkonisitet blir bevegelsene i sinusgangen også meget
lav. Frekvensene ligger i nærheten av egenfrekvensen til vognens avfjæring, dvs. sekundærfjæringen. Selve vognen samvirker dynamisk på et meget komplisert måte med løpeverket og løpeverkets naturlige sinusgang.
Denne ustabiliteten gir ofte mindre kraftige bevegelser enn den høyfrekvente ustabilitet. Men etter som vognen i høy grad deltar i svingningene, blir ofte bevegelsene i svingningene i vognen uakseptable høye sammenlignet med de høye krav som gjelder i dag.
Ustabilitet for en vogn har en svingningsfrekvens på 1 – 2 Hz.
Hjulprofil-spor
Hjulsatsens viktigste grensemål er angitt i figur 2.77. I figur 2.78er vist detaljmål av hjulprofilet. Målene i parentes gjelder som ytterste slitasjegrenser.
Flenstykkelsen for et enkelt hjul etter slitasje ikke bli mindre enn 22 mm. Dessuten kreves at summen av flenstykkelsen til begge hjulene i hjulsatsen ikke må underskride 50 mm. Videre må flenshøyden ikke bli større enn 36 mm. Det kreves også at det såkalte qR– målet ikke må underskride grenseverdien på 6,5 mm. Blir denne verdien underskredet, betyr dette at hjulflensen er blitt altfor steil. Ved en slik steil hjulflenser det stor fare for at hjulet klatrer opp mot tungespissene i sporveksler.
Et annet forhold som må vies oppmerksomhet, er dannelse av falsk eller dobbelflens i hjulbanen.
Overholdelse av disse grensemålene er av stor betydning for sikker framføring av det rullende materiell i sporet og ved passering av bl.a. sporveksler. NSB BA benytter et såkalt P8A-B-C hjulprofil i sitt rullende materiell. Dette hjulprofilet er tilpasset en skinnehelning lik 1 : 20 samt avrundingsradius på skinnehodet til de skinnetyper (bl.a. S49, S54, UIC60) som benyttes ved Jernbaneverket.
Hjulprofilene er vist i figurene 2.79, 2.80og 2.81.
Av ovennevnte figurer framgår at hjulprofilene har forskjellig bredde. P8A har bredde 135 mm, P8B har bredde 140 mm og P8C har bredde 145 mm. For øvrig er profilene identiske.
For å hindre skjevgang er det fastsatt grensemål mht. tillatt hjuldiameterdifferanse innen en boggi og mellom boggiene til det rullende materiell. Disse målene er gitt i regelverket (bl.a. trykk 741.1.2 av juli 1995). For lokomotiv av type El17 gjelder et grensemål på 3 mm innenfor en boggi og 50 mm mellom boggiene. El17 har hjulprofil P8B.
Normal sporvidde ved Jernbaneverket er 1435 mm. Det er definert hastighetsavhengige kvalitetsklasser(K0, K1,K2, K3, K4, K5. K0 er den strengeste kvalitetsklasse og gjelder for framføring av rullende materiell i høye hastigheter. Det er definert tillatte toleranseverdier for bl.a. normal sporvidde i hver kvalitetsklasse. Jo høyere kvalitetsklassen er, jo strengere er toleranseverdiene i avvik. Holder avvikene på de sporgeometriske parametre seg innenfor de definerte toleranseverdier i den aktuelle kvalitetsklasse, medvirker dette til en sikker framføring av det rullende materiell.
I det etterfølgende skal beskrives situasjoner hvor avvikene mht. hjulmål og
sporet ikke overholdes. Følgene tilfeller skal diskuteres:
- Stor sporvidde
- Trang sporvidde
- Falsk flens og dobbel flens i hjulbanen
- Konfliktområder i sporvekselen
Stor sporvidde
I figur 2.82er vist bilde av et hjulprofil av type P8A. Dette profilet beskrives av hjulflens og avrundinger på innsiden med varierende radius (R13, R100, R330). Området for R13 sammenfaller med området for R13 på skinnehodet til profilene S49, S54 og UIC60. Dette betyr at kontaktpunktet hjul/skinne ved øvrige riktige sporgeometriske forhold (bl.a. skinnehellning 1 : 20) er tilpasset hverandre. Videre består hjulprofilet av et rett parti på hjulbanen med lengde 10 mm. På den resterende del av hjulbanen er det bygd en konisitet lik 1:10.
Det største tillatte avvik i sporviddeer +30 mm som gjelder for klassene K3,
K4 og K5. Dette gir en sporvidde lik 1475 mm. Spørsmålet er hva som skjer
når sporvidden blir større. Dette skal diskuteres.
Det antas at summen av hjulflensene til hjulene i hjulsatsen har minste tillatte verdi lik 50 mm. Videre antas at det ene hjulet som har flenstykkelse lik 28 mm, har flenskontakt med skinnehodet. Dette kan inntreffe for eksempel ved gjennomkjøring i kurver for det ytre hjulet og på rett linje for begge hjul på grunn av sporspillet. Det vises til figur 2.83.
For det andre hjulet med flenstykkelse22 mm, framgår at hjulbanens berøringspunkt i den horisontale projeksjon på skinnehodet har en lengde på 9 mm. Størrelsen på kontaktflaten vil i virkeligheten bli mindre på grunn av avrundingsradius på skinnehodet. Det som imidlertid er avgjørende, er at det er det flate partiet på 10 mm på hjulbanen til dette hjulet som har kontakt med skinnehodet.
Ved større sporvidde enn 1475 mm vil kontaktpunktet til hjulet med flenstykkelse lik 22 mm på skinnehodet være konisitetsflaten med helning 1 : 10. Dette forårsaker en for stor differanse i hjulradius for de 2 hjulene i hjulsatsen. Dr blir med andre ord for stor. Denne økningen i Dr vil kunne føre til skjevstilling av hjulakselen og medfører dermed en fare for framføring av det rullende materiell.
Ovenstående er den vesentligste årsak til at maksimal sporvidde er 1475 med mer i akuttgrense. Akuttgrense medfører at sporvidden må korrigeres øyeblikkelig.
Trang sporvidde
I figur 2.84er det vist forholdene for et hjulsett på et spor med minste tillatte sporvidde i akuttgrense. Sporvidden er 1428 mm. Dersom bredde mellom innsiden av hjulene er 1363 mm inkludert toleranser (± 3mm), blir sporspillet bare 5 mm dersom hjulsatsen har nydreide hjul med flenstykkelse30 mm. Et sporspill på bare 5 mm er altfor lite for å hindre ustabilitet ved framføring av det rullende materiell. Et for lite sporspill vil også føre til høy ekvivalent konisitet. Videre blir friksjonskreftene mellom hjul og skinne større. Dette øker faren for avsporing. Feilen må derfor utbedres raskt.
Falsk flens og dobbel flens
Bl.a. på grunn av bremsing med klosser av kunstmateriale kan det dannes dobbelflens og også en falsk flens på hjulbanen. En slik slitt hjulbane er meget uheldig da:
- Løpeegenskapene til boggien eller hjulsatsen hindres på grunn av tvangsstyring
- Fare for avsporingøker
- Ugunstig belastning av komponenter i sporet (sporveksel)
Det er av den grunn fastsatt krav om at maksimal slitasjehøyde i hjulbanen ikke skal overskride 2 mm. Det vises til figur 2.85.
En hjulbane med dobbelflens i kombinasjon med falsk flens vil kunne belaste
komponenter i sporet ugunstig dersom slitasjehøyden overskrider
grenseverdier.
Spesielt vil deler av krysspartiet som ikke er konstruert for belastning, bli belastet. Forholdet fører over tid til sprekkdannelser i disse delene. Det vises til figur 2.86
Også stokkskinne blir unødvendig slitt ved anliggende tunge der hvor tungepartiet i sporvekselen skal ta over hele belastningen ved framføring av det rullende materiell i avvik. Slitasjeforløpet kan bli meget ugunstig på skinnehodet til stokkskinnen. Dette kan naturligvis ha uheldige konsekvenser for framføring av materiellet i hovedspor. Det vises til figur 2.87.
LØPEVERKSPRINSIPPER FOR VOGNER
I dette avsnittet skal behandles grunnleggende egenskaper mht. løpeverk for to-akslede vogner og for vogner med boggier.
Det er gjort rede for at en hjulsats bør ha evnen til å løpe gjennom en kurve uten flenskontakt og med så liten anløpsvinkel som mulig.
Videre må det tilstrebes at det rullende materiell skal framføres i sporet uten at dette materiellet selv genererer laterale svingninger. En lateral bevegelse i sporet skal dempes.
Egenskapene til en hjulsatser grunnleggende for framføring i sporet, men den er i virkeligheten bare en del av det rullende materiell. Et visst antall hjulsatser skal bære vogn og øvrige komponenter samtidig som de skal styre vognkassen med de laster vognen inneholder.
Den komponent som har til oppgave å bære og å styre det rullende materiell, er løpeverket. Løpeverkets deler er hjul og hjulaksler i form av hjulsats, lagring av aksel i akselboks og dessuten et fjærsystem.
To-akslet vogn
I sin aller enkleste form består løpeverket av en hjulsats(hjul og hjulaksel) som er lagret og innspent i vognens hovedrammeverk i selve vognkassen. Det vises til figur 2.88.
Denne type av rullende materiell er den enkleste i utførelse og har derfor en del begrensninger.
For det første blir selve lasteevnen begrenset. Av de komponenter (rammeverk, aksel etc.) som bestemmer den totale vekten til materiellet, blir gjerne aksellasten dimensjonerende. Denne parameteren fastsetter svært ofte tillatt last.
For det andre må to-akslede vogner gjøres relativt korte. Selve lengden av vognen begrenses av den største mulige akselavstand. Dette fordi akselavstanden blir bestemt ut fra den evnen som den to-akslede vognen har til å gjennomløpe en kurve. Ved for store akselavstander vil hjulsatsene ikke kunne vri seg tilstrekkelig i kurver med små radier. Dette vil medføre store anløpsvinkler. Det blir ingen radiell styring i kurven. Dersom hjulsatsen ved stor akselavstand skulle innstille seg radielt ved gjennomløp i kurver med små radier, ville hjulsatsens vridningsvinkel i forhold til vognkassens rammeverk bli for stor. Denne vridningsvinkelen begrenses på grunn av den stivhet i innspenningen som alltid må være mellom hjulsats og vognkasse.
For det tredje vil en to-akslet vognlett innta en ustabil gange ved høyere hastigheter (V > 100 km/h). Dette har sammenheng med at styringen av hjulsatsen i rammeverket må være myk for å oppnå en tilfredsstillende evne til gjennomløp i kurver. Hjulsatsene må være svingbare i forhold til vognkassen. Men et slikt forhold vil lett kunne forårsake ustabilitet i forbindelse med hjulparets sinusbevegelser ved høyere hastigheter.
En stivere innspenning av hjulparet gir dårlige gangegenskaper ved gjennomløp i kurver. Dette kan medføre at den store massen av vognkassen ved stiv forbindelse til hjulparet virker destabiliserende. Dette resulterer i store sporkrefter.
I tillegg må nevnes at slike typer vogner bare har et fjærnivå. Alt i alt må det konkluderes med at en to-akslet vogn har relativt mindre bra gangegenskaper. Akselavstanden begrenses til ca. 10,0 m og hastigheten til ca. 100 km/h. Det må altså tilstrebes en balansegang mellom myk forbindelse (radielt innstilt hjulpar) og stiv forbindelse (sikre stabilitet ved høy hastighet på rett spor) for to-akslede vogner.
Vogn med boggier
Boggier er oftest i to-akslet utførelse. Det vises til figur 2.89. Hjulsatsene eller hjulparene er lagret og innspent i et rammeverk på en slik måte at de blir vridbare i forhold til vognkassen. Da en vogn som regel har 2 boggier, vil det rullende materiell gjennomløpe kurven på en langt bedre måte enn en to akslet vogn. Innføring av boggier mht. virkemåte har naturligvis også den fordel at vognkassen kan gjøres mye lengre.
Det forekommer også boggier med 3 eller flere hjulsatser. I slike konstruksjoner (boggi med 3 hjulsatser) vil den midte hjulsatsen utøve særlig store laterale krefter mot sporet med mindre tiltak settes inn. Disse består i å utstyre opplageret for den midtre akselen med et fjærkonstruksjon.
Det er 2 grunnleggende prinsipper for styring av hjulsatser i rammeverket:
- Stiv styring av hjulsats
- Myk styring av hjulsats hvor hjulsatsen oppnår radiell innstilling i kurvene
Det er velkjent at en fri hjulsats ha ustabil gange ved relativt liten hastighet. Det er også kjent at stabiliteten kan forbedres og dermed den kritiske hastigheten økes ved å spenne inn hjulsatsen i et stivt rammeverk. Dette kan skje på den måten at hjulsatsens frie bevegelser begrenses ved for eksempel å gi styringen til hjulsatsen et definert spillerom. Eller hjulsatsen kan innspennes med en kontinuerlig fjær som gir kontinuerlig voksende fjærkraft ved økende deformasjon.
Ved den ene ytterlighet er altså hjulsatsen helt fri, ved den andre ytterlighet er hjulsatsen helt innspent i et rammeverk.
I en vogn kan styringen av hjulsatsen verken være helt fri eller helt stiv. Styringen må ligge mellom disse ytterlighetene.
I figur 2.90er vist en konvensjonell boggi med stiv styring av hjulsatsene for å oppnå stabil gange.
I figur 2.91er vist en boggi med gode løpeegenskaper i en kurve ved radiell innstilling av hjulene i hjulsatsen.
Dersom hjulsatsene spennes inn i rammeverket, hindres hjulsatsens frie
sinusbevegelse. Samtidig vil evnen til å gjennomløpe kurven hindres i mer
eller mindre grad. Dermed oppstår det kryp og krypkrefter mellom hjul og
skinner. På rett spor vil dette medføre 2 effekter:
- Sinusgangens svingningsbevegelser dempes
- Sinusgangens bølgelengde øker
Det er allerede nevnt at Klingel på 1880 - tallet utviklet de formler som
beskriver hjulsatsens sinusgang på rett linje. Formlene beskriver også
sinusgangen for en boggi med 2 stivt innspente hjulsatser.
For et fritt hjulpar gjelder:
| (2.143) |
For boggi med stiv akselstyring gjelder:
| (2.144) |
Her betyr:
- L = bølgelengdefor sinusbevegelse på rett linje
- bH= den halve laterale avstand mellom hjulenes kontaktpunkter
- rH= hjulradius
- λ = effektiv konisitet
- a = den halve akselavstand i boggien
Det er tidligere redegjort for at den effektive konisitet kan beregnes etter
formel:
| (2.145) |
Sinusbevegelsens bølgelengde L er avhengig av konisiteten i kontaktpunktet
hjul/skinne. Videre er svingningsfrekvensen til sinusbevegelsen en funksjon av
framføringshastigheten til toget.
I figur 2.92er vist sinusbevegelsens frekvens for ulike ekvivalente konisiteter og dessuten hastighet for et fritt hjulpar ved bruk av ovennevnte formler. Formlene er tilnærmede spesielt for høyere hastigheter. På grunn av opptredende krypkrefter blir frekvensen i virkeligheten lavere ved høyere hastigheter.
Figur 2.93 viser det samme for en stiv boggi.
Det skal belyses egenskaper ved stiv akselstyring i boggien.
En boggi med stiv styring av akslene medfører en større bølgelengde i sinusbevegelsen og dermed redusert risiko for ustabil gange. Det er også vektlagt å holde konisiteten mellom hjul og skinne på et lavt nivå av samme årsak. Den effektive konisitet må da velges til å være i området 0,025 – 0,10. Det må bemerkes at ved å innføre styreanordninger uten spill har den effektive konisiteten kunne økes ganske betydelig. Dette betyr effektiv konisitet opp til 0,3 – 0,5 ved 200 km/h.
Den laterale sekundærfjæren mellom vognkasse og boggi må avstemmes slik at egenfrekvensen(resonansfrekvensen) ligger under frekvensen til sinusbevegelsen til boggien ved begynnende ustabilitet. Gjennom et slikt tiltak blir samvirke mellom vognkassens og boggiens dynamikk minst mulig.
Imidlertid finnes en nedre grense for hvor lavt vognkassens laterale egenfrekvenser kan legges. Sekundærfjæringen kan selvfølgelig ikke gjøres så myk at den ikke kan ta opp de sentrifugalkrefter som oppstår ved gjennomløp i kurver. Det er også av betydning at vognkassens fjæring ikke oppleves som svaiende da dette kan bevirke tendenser til togsyke.
Den altoverveiende fordel med stiv føring av hjulsatsene i en boggier økt stabilitet ved høyere hastigheter og at det kan tillates slitte hjulprofil som fører til høyere konisitet. Dette har naturligvis gyldighet bare på rett linje.
Ulempen med stiv akselføringer naturligvis at evnen til å gjennomløpe kurver blir mye dårligere. Dette fordi styringen vil føre til flenskontakt med skinnehodet. Det ytre hjulet i første hjulsats i boggien blir presset med en stor kraft, den såkalte føringskraft, mot ytterskinne i kurven. Som beskrevet i kapittel xx dannes det en anløpsvinkel mellom flensen til ytterhjulet og skinnehodet til ytterstrengen. Dermed vil boggien utøve en kraftig motstand ved gjennomløp da boggien må ”presse” seg gjennom kurven for å overvinne friksjonen.
På tørt spor (uten smøring verken på hjulflenseller skinnehodet) kan motstanden ved framføring bli så stor som 1,0 – 2,0 kN for hver vogn i kurver med radius 300 – 400 m.
Det bygges dermed opp en energiomsetning som blir omsatt i varme og i slitasje på hjul og skinner.
Tiltak er naturligvis å smøre sporet i tørt vær. Dette kan skje ved faste installerte smøreapparater i kurver hvor erfaringsmessig slitasjen er stor. Eller traksjonsmateriell kan utstyres med smøreapparater. Vanskeligheten består i å smøre riktig mengde på riktig plass slik at friksjonsforholdene ikke forsvinner helt. For store smøremengder fører til risiko for sluringog dårlige bremseforhold.
Vanning av skinnegangen kan også være en løsning.
Energiomsetning og slitasje i kontaktpunkt hjul/skinne
Slitasje på hjul og skinner opptrer ved framføring av det rullende materiell. En årsak er ganske sikkert tørt spor som gir høy friksjon. Friksjonen kan i stor grad elimineres ved flenssmøring eller ved at olje smøres på riktig sted på overkanten av skinnehodet.
Det eksisterer ulike former for hjulslitasje:
- Flensslitasje 1: flensens tykkelse Ft blir redusert
- Flensslitasje 2: qR målet blir brattere (steilere)
- Slitasje på løpebanen: blir målt gjennom flenshøyden FH
- Urunde hjul: oppstår for eksempel ved eksentrisiteter og ved bruk av bremseklosser
Flere faktorer bidrar til flensslitasje. Ved liten radius i sirkelkurven blir
anløpsvinkelen mellom hjul og skinne større. Dette medfører mer kryp og
dermed større krypkrefter som igjen gir økt slitasje.
Høy friksjon fører også til større krypkrefter og dermed økt slitasje.
Endelig har løpeverkets egenskaper også betydning. Ved stiv styring av hjulsettet og ved stor akselavstand i for eksempel boggien blir anløpsvinkelen større. Dermed øker kryp og krypkrefter samt slitasje.
Slitasje av hjulbanen skyldes trykk i kontaktpunktet mellom hjul og skinner i kombinasjon med normale krypkrefter. Det samme gjelder ved sluring. Vedvarende bremsing med bremseklosser mot hjulbanen vil også føre til slitasje på hjulbanen.
Hjul kan være eksentriske eller ha bølgedannelser langs hjulets omkrets. Antall bølger kan variere fra 2 til ca. 10. Bølgedannelsene antas å oppstå på grunn av regelbundne sykliske variasjoner i vertikallaster i kombinasjon med en viss sluring. Vertikallastvariasjonene kan oppstå på grunn av vibrasjoner i systemet hjul-spor.
Ved låsing av hjul i forbindelse med bremsing forekommer hjulslag. Skinneslitasje forekommer både på innerstreng og ytterstreng. Det vises til figur 2.94.
På innerstrengen dannes ” skjegg” og på ytterstrengen slites innsiden av skinnehodet.
Slike slitasjeforløp kan forklares med de krefter som virker mellom hjul og skinne ved gjennomkjøring i kurver.
Materialkombinasjonen mellom hjul og skinne har også betydning for slitasjeforholdet.
I en modell som beskriver slitasjen (bortfall av materiale), antas at denne slitasjen er nær proporsjonal med energiomsetningen i kontaktpunktet mellom hjul og skinne.
I virkeligheten er forholdet som beskrevet i figur 2.95.
Generelt kan energiomsetningen beskrives ved følgende uttrykk:
| (2.146) |
Energi pr. tidsenhet finnes ved derivasjon:
| (2.147) |
| (2.148) |
Her betyr:
- F = friksjonskraft
- M = friksjonsmoment
- s = glistrekning
- F = glidningsvinkel
- Δv = glihastighet
- Δw= rotasjonshastighet i forbindelse med glidning
Det vises til figur 2.96.
Glihastigheten dekomponeres i en x-retning (ΔvX) og i en y-retning (ΔvY).
Friksjonskreftene (krypkrefter) dekomponeres også i en x-retning (FX) og i en y-retning (FY).
Kryp i x-retning betegnes υX og i y-retning υY(i kontaktflaten mellom hjul og skinne). Φ er spinn.
Dette gir:
| (2.149) |
Energiomsetning kan skrives på vektorform:
| (2.150) |
Energiutvikling pr. meter løpestrekning:
| (2.151) |
I x- og y-retning:
| (2.152) |
| (2.153) |
Energiomsetningen kan verbalt uttrykkes slik:
Energiomsetning = Kraft · Kryp(X,Y) + Moment · Spinn
Myk styring av hjulsatser – radiell styring
Myk styring av hjulsatsen i en boggi betyr at hjulsatsen har selvstyrende evne til å gjennomløpe kurver bedre enn ved stiv styring. Dette medfører at energiomsetningen avtar og dermed blir motstand ved gjennomløp i kurver samt slitasje mindre. Videre vil de laterale sporkrefter bli mindre.
De lavere sporkreftene er en følge av:
- Forbedret evne til å gjennomløpe kurver
- Mykere avfjæring mellom hjulsats og boggiramme
Det er særlig de dynamiske tilleggskreftene som oppstår ved sporfeil, som er
blitt redusert.
Energiomsetningen ved gjennomløp i kurver kan beregnes:
| (2.154) |
Her betyr:
- E er energiomsetning(Nm/m spor)
- Fξ er longitudinell krypkraft
- νξ er longitudinelt krypdefinert som relativ hastighet mellom hjul og skinne i kontaktflaten og aktuell framføringshastighet
- Fη er lateral krypkraft
- νη er lateralt kryp
- M er sluremomentet mellom 2 legemer
- Φ er slurevinkel
Det er påvist store forskjeller i energiomsetning mht. forholdet mellom en stiv
konstruert boggi og en boggi med radielt innstilte hjulsatser.
Forholdet kan være 4:1.
Fordelen ved boggier med radielt styrte hjulsatser er altså lavere laterale
sporkrefter og dermed mindre slitasje på hjul og skinner.
Ulempen er imidlertid at gangstabiliteten blir dårligere ved høyere hastigheter.
Tiltak for å bedre denne kan gjennomføres:
- Fjærsystemet både longitudinelt og lateralt i styringen av hjulsatsen må avstemmes med nøyaktig stivhet
- Boggien må utøve riktige egenskaper mht. vridningsdemping. Dette inkluderer tilpasset demping av boggiens styringsegenskaper i forhold til vognkassen. Demping må også innføres lateralt i primærfjæringen, dvs. i hjulsatsstyringen.
Prinsippløsninger for boggikonstruksjoner
Det skal redegjøres for konstruksjonsløsninger for boggier mht. løpeegenskaper.
Følgende boggikonstruksjoner blir beskrevet:
- Stiv akselføring
- Elastisk styrte hjulsatser
- Gjensidig koblede hjulsatser
- Hjulsatser som blir styrt av vognkassen
- SIG-NAVIGATOR
- Sammenligning av de forskjellige boggikonstruksjonene
- Three-piece boggi til vogner med tunge aksellaster
Stiv akselføring
Figur 2.97 viser en boggikonstruksjon med stiv akselføring.
Boggier med stiv akselføring gir stor stabilitet ved framføring av det rullende materiell på rett strekning. Ved gjennomløp i kurver vil imidlertid slitasjen på hjul og skinner bli relativt høy. Dette skyldes store anløpsvinkler og høy lateral føringskraft.
Ved smøring av hjulflensmed smøringsapparat vil slitasjen bli betydelig mindre på grunn av redusert friksjon mellom hjul og skinne.
Elastisk styrte hjulsatser
Figur 2.98 viser prinsippet mht. konstruksjonsløsning for en boggi med elastisk styrte hjulsatser.
Akselboksen til hjulsatsen bindes til boggirammen på en slik måte at opplageret til denne (akselboksen) blir myk i lengderetningen. En slik konstruksjon skaper elastisitet mellom hjulsatsens aksel og boggirammen i denne retningen og gir dermed hjulsatsen den nødvendige frihet til å innstille seg radielt. En slik radiell innstilling betinger konisitet mellom hjulbanens berøringsflate på skinnehodet og skinnen.
Elastisk styrte hjulsatser vil kunne innstille seg radielt i kurver og på den måten blir slitasje på hjul og skinner redusert. Det må imidlertid bemerkes at radiell innstilling av hjulsatsene betinger tørre skinner.
Ulempen er at boggier med radielt styrte hjulsatser ved høye hastigheter ikke løper tilstrekkelig stabilt. En absolutt forutsetning for stabil gange er nøyaktig paring av skinnehode og hjulbane.
Gjensidig koblede hjulsatser
Figur 2.99 viser konstruksjonsprinsippet til en boggi med gjensidig koblede hjulsatser.
Hjulsatsene i en boggi blir koblet sammen på en slik måte at de hjelper
hverandre og støtter hverandre i tendensen til å oppnå radiell styring.
Imidlertid er det nødvendig å ha innretninger som hindrer uønskede rotasjoner
om hovedaksen. Dette blir oppnådd ved innføring av definerte stivheter i
konstruksjonen mellom hjulsatsene mht. å unngå fordreining og
saksbevegelser.
Hjulsatser som blir styrt av vognkassen
Figur 2.100viser prinsippet for en boggikonstruksjon hvor hjulsatsenes bevegelse blir styrt av vognkassen.
Det er den relative bevegelse mellom boggikonstruksjon og vognkasse som framtvinger den radiale innstillingen til hjulsatsene. Dette skjer ved hjelp av mekaniske innretninger.
SIG-NAVIGATOR
Denne konstruksjonen er utviklet av SIG. Figur 2.101 viser prinsippet.
Løsningen bygger på det prinsipp at boggikonstruksjonen reagerer på den relative bevegelse mellom vognkasse og boggi. Denne bevegelsen forårsaker en radiell innstilling av hjulsatsene ved gjennomløp av kurver. Mekaniske innretninger bevirker at akselboksene som befinner seg ved innerstrengen i kurven, beveger seg mot hverandre. På samme måte vil akselboksene som befinner seg på den ytre skinnestrengen, bevege seg fra hverandre. Langsgående og tverrgående glidning blir dermed eliminert.
Konstruksjonen medfører lave anløpsvinkler og føringskrefter og dermed lite slitasje på hjul og skinner.
Sammenligning av de forskjellige boggikonstruksjonene
Figur 2.102 angir størrelsen på anløpsvinkel, føringskraft, slitasje på hjul og slitasjevolum samt urundhet for de forskjellige boggikonstruksjonene under sammenlignbare forhold.
"Three-piece" boggier til vogner for tunge aksellaster
Det vises til figur 2.103.
I denne boggikonstruksjonen består rammeavstivningen av 2 kryssede
stenger som har forbindelse med sidebjelkene i rammen. De 2 stengene er
forbundet med hverandre. Elastiske hylser er benyttet på forbindelsesstedene.
Ofotbanen har en kurvatur med små radier og fall i kjøreretningen ned til Narvik. Malmtogene må derfor kjøre i bremset tilstand med 30 tonn (framtidig aksellast) aksellast. Det er derfor av betydning at det benyttes en boggikonstruksjon som fungerer radielt mht. styring av hjulsettene også i bremset tilstand, dvs. at bremsingen ikke må låse hjulsettene i en ukontrollert skjev stilling.
I forbindelse med anskaffelse av nye malmvogner har MT AB valgt en three piece boggikonstruksjon som vist i figur 2.103. Spoornet i Sør-Afrika benytter denne type av vogner for framføring av tunge aksellaster.
AVSPORINGSMEKANISMER
Avsporing mht. gangdynamiske forhold kan inndeles flere grupper:
- Flensklatring
- Togvelting
- Skinnevelting
- Sporforskyvning
- Sporvidde
- Solslyng
- Viktige mål i sporveksler
- Feil mht. lange bølgelengder vertikalt i sporet
- Avlastning
Flensklatring
Flensen på et hjul klatrer opp på skinnehodets kjørekant dersom sidekraften blir for stor i forhold til vertikalkraften.
Følgende kriterium gjelder:
| (2.155) |
Dette betyr at det defineres en største verdi i forholdet mellom lateral kraft og
vertikal kraft på et hjul.
I figur 2.104 er framstilt de krefter som virker på et hjul. Hjulet har en flensvinkel mot skinnen lik β. I figuren betyr:
Q er vertikal hjulkraft(kN)
Y er lateral kraft (kN)
Ved klatringdrei er det seg alltid om ettpunktsberøring. For å belyse problemet dekomponeres resultanten av de 2 kreftene Q og Y i en tangentialkraft Fνη langs tangenten mellom hjul og skinne og i en normalkraft Nf normalt til tangenten i berøringspunktet.
Hjulet kan bare løfte seg dersom hjulflensen finner tilstrekkelig friksjon mot
skinnens kjørekant, dvs. når:
| (2.156) |
hvor γf er friksjonskoeffisient mellom hjulflens og kjørekant på skinnehodet.
Dersom
| (2.157) |
vil klatring ikke finne sted.
Den kritiske grenseverdi oppnås ved
| (2.158) |
Klatring forhindres dersom hjullasten Q blir større den vertikale komponenten
av flenskreftene:
| (2.159) |
dvs. når
| (2.160) |
Normalkraften i flensen kan uttrykkes som en funksjon av den laterale kraft Y på hjulet:
| (2.161) |
| (2.162) |
Dermed kan det utledes:
| (2.163) |
| (2.164) |
For at klatring ikke skal skje, må:
| (2.165) |
Denne formelen kalles Nadals formel.
β er hjulets flensvinkel. Denne vinkelen defineres som vinkelen mellom
fellestangenten i berøringspunktet og sporplanet.
Ovenstående viser at stor friksjon mellom hjul og skinne begunstiger faren for
avsporing. Stor friksjon oppstår i trange spor, ved tørre og nye rustede skinner
og ved liten flensvinkel. qR– målet er også av betydning. I Norge skal dette
målet ikke underskride 6,5 mm.
Flenssmøring vil motvirke tendensen til klatring.
Det framgår av uttrykket i ovennevnte formel at faren for avsporing oppstår
ved et for stort forhold mellom føringskraften Y og hjulkraften Q. Når dette
forholdet overskrider en bestemt grenseverdi, kan hjulflensen klatre opp mot
skinnens kjørekant. Det er vognens eller boggiens ledende hjul som kan få
denne tendensen. Dette betyr at hjulet i forreste aksel ruller på ytterstrengen i
en kurve.
Togvelting
Det skal betraktes et forenklet tilfelle og et mer sammensatt tilfelle.
Forenklet tilfelle
Her behandles velting under forutsetning av at bare sentrifugalkraften er medvirkende. Velting inntreffer når den resulterende kraft av vognens tyngde og sentrifugalkraft går gjennom det ytre hjulet. Det vises til figur 2.105.
I figur 2.105 betyr:
g er tyngdens akselerasjon
α er vinkel til sporplanet i forhold til et horisontalt plan
s er sporvidde
h er høyde fra overkant skinne til vognens tyngdepunkt
R er kurveradius
Følgende gjelder:
| (2.166) |
Da α er relativt liten, kan ovenstående uttrykk forenkles:
| (2.167) |
| (2.168) |
Dette gir følgende uttrykk:
| (2.169) |
Velting inntreffer når
| (2.170) |
eller
| (2.171) |
Dette skal belyses med et eksempel:
R = 600 m
g = 9,81 m/s2
s = 1,5 m
h = 2,5 m
Velting inntreffer ved beregnet hastighet :
| (2.172) |
Et mer sammensatt tilfelle
Det rullende materiellet vil velte når de laterale krefter blir for store. Slike krefter er for eksempel sentrifugalkraft og vindkraft. Det vises til figur 2.106.
Det innføres følgende begreper:
FY VIND er resulterende lateral vindkraft(kN)
FZ VIND er resulterende vertikal løftekraft (kN)
FG er vognens tyngdekraft vertikalt mot sporplanet (kN)
m er vognens masse (kg)
ÿS er kvasistatisk sideakselerasjon i sporplanet
ÿDYN er dynamisk sideakselerasjon i sporplanet
HTP er momentarm for vognkassens tyngdepunkt i forhold til sporplanet
HV er momentarm for resulterende laterale vindkraft i forhold til sporplanet
bH er halve sporvidde
δY er vognkassens laterale bevegelse i forhold til spormidt vinkelrett på sporplanet
δZV er avstand fra resultanten av den løftede vindkraft til spormidt
A er senter for velting i betraktningsmodellen
Sikkerhetsfaktor for velting defineres ved forholdet:
| (2.173) |
Iht. betegnelser i figur 2.106 blir forholdet:
| (2.174) |
I telleren er angitt de stabiliserende momenter og i nevneren inneholder de
momenter som forårsaker velting.
Det bemerkes at for det rullende materiell er det bare vognkassensom er blitt betraktet. Dersom en nøyaktig beregning er påkrevet, må også vekt og masse for boggi og hjulpar tas med. For disse delene kan vindlasten settes lik 0. Det rullende materiell vil begynne å velte når:
| (2.175) |
Tradisjonelt er følgende forenklede formel benyttet:
| (2.176) |
I denne formelen er δY kvasistatisk forskyvning.
Det legges merke til at for å oppnå tilstrekkelig sikkerhet mot velting kreves en sikkerhet lik 4 ved bruk av den forenklede formel.
Skinnevelting
For en skinne med en viss lengde som ikke er fastholdt eller innspent, gjelder at skinnen kan velte dersom kraftresultanten for de opptredende vertikale og laterale krefter havner utenfor skinnefoten. Dette kan uttrykkes ved følgende ulikhet:
| (2.177) |
hC er høyden på skinnen regnet fra hjulets angrepspunkt på skinnehodet
bC er lateral avstand fra hjulets angrepspunkt på skinnehodet til veltesenteret.
Det vises til figur 2.107.
For de befestigelser som ikke holder skinnen innspent, benyttes vanligvis de krefter som virker fra en boggi.
Et kort skinneparti under et individuelt hjul bedømmes ikke å kunne velte uansett hva som hender under nærmeste hjul på samme boggi. Det vises til figur 2.108.
Kriteriet for sikkerhet mot velting av skinne som ikke blir fastholdt av befestigelsen, kan uttrykkes ved:
| (2.178) |
Det er nevnt at det benyttes krefter fra en boggi. For en tenkt venstre side i
sporet i kjøreretningen gjelder da:
| (2.179) |
Tilsvarende formel kan uttrykkes for høyre side i kjøreretningen.
Intervallet RV < 0.5 – 0,7 beror på type av skinne som benyttes.
Ovennevnte betraktninger er gjort for befestigelsestype som ikke holder skinnen fastholdt eller innspent i befestigelsen, dvs. befestigelser av type skinnespiker. Ved bruk av moderne høyelastiske skinnebefestigelser er skinnen innspent og sikkerhet mot velting av skinne er derfor ivaretatt på en langt mer sikker måte.
Sporforskyvning
Risiko for sporforskyvning lateralt beror på den totale sidekraften mellom hjulsett og sporet. Nivået på de krefter som sporet kan tåle lateralt, er vel definert ved en definert grenseverdi for den såkalte S-kraften. Utgangspunktet er de laterale Y-krefter fra hvert hjul i hjulsettet på begge skinner i sporet ved framføring av det rullende materiell. Det vises til figur 2.109.
Iht. figur 2.109 beregnes S-kraften:
| (2.180) |
S er lateral sideforskyvningskraft mot sporet.
YV er lateral hjul-skinnekraft på venstre skinne
YH er lateral hjul-skinnekraft på høyre skinne
Det finnes en grenseverdi for tillatt sporforskyvningskraft:
| (2.181) |
Denne formelen benevnes Prud’ hommes formel og er utviklet empirisk med
grunnlag i omfangsrike forsøk for undersøkelse av stabiliteten i sporet.
Q0statisk eller nominell hjullast.
α er en faktor som er avhengig av type av vognmateriell:
α er 1,00 for lokomotiv, passasjervogner og togsett med traksjonsenhet. α er 0,85 for godsvogner.
Årsaken til de ulike verdiene for faktor α beror på kvaliteten til vogn og ikke
minst til boggikonstruksjon for forskjellig typer materiell. Det finnes ennå mye
eldre godsvogner i trafikk med dårlige løpeegenskaper som forårsaker stor
spredning mht. belastning på sporet og dermed store krefter. Av
sikkerhetsmessige årsaker settes derfor α lik 0,85 for denne type materiell.
Lokomotivene og passasjervogner samt togsett med traksjonsenhet er som
regel av nyere dato. I takt med utviklingen er disse materielltypene utstyrt med
moderne boggikonstruksjoner og andre komponenter som bevirker mindre
dynamiske krefter ved framføring. α lik 1,0 kan derfor benyttes i slike tilfeller.
Med faktor α = 0,85 kan formelen skrives:
| (2.182) |
Dette er den opprinnelige formelen og gjelder egentlig for et spor med tresviller med senteravstand lik 65 cm og skinner med vekt minst 46 kg/m samt grusballast i et ikke-stabilisert spor. I et spor med betongsviller og pukkballast blir naturligvis sikkerhet mot sporforskyvning vesentlig bedre. α lik 1,00 er for nyere materiell er nettopp utledet av dette faktum.
For at S-kraften skal kunne forårsake forskyvning av sporet med avsporing som resultat, må denne kraften ha en viss varighet og virke over en tilsvarende lengde på sporet. Det regnes med en varighet som tilsvarer en lengde på 2 meter. Dette betyr at sporforskyvning og dermed avsporing ikke vil inntreffe når:
| (2.183) |
Dette medfører at innenfor 2 meters verdiene kan S-kraften være høyere enn
grenseverdien.
Dette er illustrert i figur 2.110.
Sporvidde
Sporutvidelseskjer hvor skinnene ikke er i stand til å motstå virkningen av laterale krefter fra hjulene til det rullende materiell ved framføring. Det er stor forskjell på løpeegenskaper til forskjellige typer av rullende materiell og noen vogner utøver høyere laterale krefter enn andre. Kreftene kan også øke når nivået på friksjonen mellom hjul og skinne øker. Videre er det vanligvis ikke til å unngå at de laterale kreftene blir store i kurver med små radier. Sporkonstruksjonen må derfor være i stand til å motstå disse kreftene for å sikre en forsvarlig framføring.
Dersom evnen til skinnene når et punkt hvor de ikke lenger kan motstå systemet av laterale krefter som skyver skinnene fra hverandre, vil skinnene bevege seg utover eller rotere i befestigelsen. Hjulsettet har da ikke lenger noe underlag (skinnene) å bli framført på.
Dersom sporvidden i utgangspunktet er meget stor i statisk tilstand, er risikoen for avsporing selvsagt til stede. Men også i dynamisk tilstand dvs. når det rullende materiell passerer, er det risiko for avsporing. Dette beror naturligvis på bl.a. befestigelsens og svillens tilstand. Avsporingsrisikoen er da tilstede selv om den statiske sporvidde er innenfor toleransegrensene. Spesielt vil tendensen til avsporing være større for materiell med 3 eller flere hjulsatser på boggien.
Årsaker som medfører sporutvidelse, kan være slitte eller ødelagte komponenter i sporet. Dette gjelder i særlig grad befestigelsens deler og sviller. Løse bolter i tresviller på grunn av avlange hull og brutte komponenter i befestigelsen vil kunne føre til for stor sporvidde og dermed avsporing. Betongsviller i oppsprukket tilstand i befestigelsesleiet og riss i betongen med fare for korrosjon i armeringen vil også være årsaker til avsporing.
Solslyng
Solslyng inntreffer når hele sporkonstruksjonen sammen med svillene beveger seg sideveis i ballasten.
Denne type avsporingskjer ved meget store longitudinelle krefter i skinnene. Kreftene oppstår ved at skinnene utvider seg ved meget høye temperaturer.
Det er derfor av avgjørende betydning at sporet er støttet sideveis ved tilstrekkelig lengde på ballastskuldrene.
Videre er det nødvendig at den laterale motstand mot forskyvning er tilnærmet konstant. Dette betyr at det kreves kontinuerlig og homogen elastisitet i sporet sideveis. Endring i denne elastisiteten og dermed motstandskapasiteten kan føre til solslyng. Et eksempel på et sted med endring av sporets elastisitet sideveis er overgangen fra vanlig spor til brukonstruksjon med stålbjelker og tresviller.
Svillens vekt er også av betydning. Betongsviller vil medvirke til bedre lateral motstand mot sideforskyvning for sporkonstruksjonen enn tresviller.
Konfliktområder i sporveksler
Det er påpekt at et qR – mål mindre enn 6,5 mm betyr for steil flens på hjulet og at dette kan medføre fare for klatring. Spesielt i det området for tungespissensom er underhøvlet og som derfor blir liggende under stokkskinnens kjørekant, er faren stor for avsporing ved for steil flens på hjulets hjulbane. Flensen kan klatre opp på tungespissen og resultatet er avsporing. Det vises til figur 2.111.
Et annet mulig konfliktområde er krysspartiet i en sporveksel. Krysspartiet består av krysspissen, vingeskinnen og ledeskinnen. Disse danner en konstruktiv enhet. Den innbyrdes beliggenhet av disse konstruksjonsdelene er fastsatt på grunnlag av hjulsatsens mål og bestemmes i det vesentligste av 4 hovedmål. Det vises til figur 2.112.
Betegnelsene i figur 2.112er:
A = sporvidde(mellom 1433 og 1450 mm)
C = ledeviddesom må være så stor at hjulflensen ikke kan klatre opp mot krysspissen. Dette betinger et mål C > 1393 med mer
B = avstand mellom ledeflatene. Denne skal ikke være så stor at en hjulsatskan klemme seg fast mellom ledeskinnen og vingeskinnen. Målet må være mindre enn 1356 mm.
RL og
RK = rillebredder som må være tilstrekkelig store for å skaffe plass til de tykkeste (dvs. nydreide) hjulflenser. Målene må være større enn 35 mm og utføres normalt i en størrelse på 41 mm.
Hovedmålene må kontrolleres jevnlig.
Feil mht. vertikale bølgelengder i sporet
Dersom det oppstår en serie av vertikale dybder i sporet (skinnene) med jevne mellomrom, kan dette føre til avsporing av det rullende materiell. Slike langbølgede feil i vertikalretning i toppen av sporkonstruksjonen har vanligvis sin årsak i periodisk ujevnhet i elastisitetsforholdene. Årsaken kan være lokale våte steder i sporkonstruksjonen.
Risikoen for avsporing blir desto større dersom avstanden mellom de periodiske feilene tilsvarer vognens resonansfrekvens mht. galoppering eller vipping samt svingning. Spesielt er to-akslede vogner med høy vertikal fjærstivheter utsatt.
Det må bemerkes at de vertikale sykliske ujevnheter alene ikke er tilstrekkelig til å bevirke avsporing. Hjulsettet må også anta en samtidig lateral bevegelse. En lateral bevegelse av hjulsettet kan imidlertid oppstå på grunn av krefter i kurver og fordi laterale resonansbevegelser til vognen opptrer i samsvar med periodiske laterale feil i sporet.
Et lasket spor vil kunne forårsake en slik avsporing dersom de to tilstøtende skinneendene ikke har samme høyde.
Avlastning
Dette avsnittet har bakgrunn i det arbeidet som er utført av utvalget i ORE B 55 mht. sikkerhet mot avsporing av godsvogner i vindskjevt spor. Avsnittet bygger på en artikkel av J. Maulmann i NSB – teknikk 2, 1980.
Det skal betraktes forholdet Y/Q i en overhøyderampe med justeringsfeil.
En overhøyderampe er en kombinasjon av en overhøyde og en vindskjevhet. Under forutsetning av lav hastighet dvs. når sentrifugalkraften er neglisjerbar, vil overhøyden forårsake reduksjon av hjulkreftene på ytre skinnestreng for alle hjul som antydet i figur xx. Vindskjevheten forårsaker en ekstra avlastning av hjulkraften på ytre skinnestreng av det hjulet som befinner seg på det laveste sted på denne strengen, dvs. hjul nr. 1.1 i figur 2.113. Iht. denne figuren gjelder følgende betegnelser:
Q0 er den gjennomsnittlige hjulkraft, dvs. 25 % av vognens tyngde for en 2- akslet vogn
ΔQh er forandring av hjultrykk på grunn av overhøyde hA
ΔQg er forandring av hjultrykk på grunn av sporets vindskjevhet g
ΔQL er forandringer av hjultrykk på grunn av lastens eksentrisitet
For de 4 hjulene i en 2-akslet vogn kan det settes opp følgende formler for hjulbelastning:
Forreste hjul i ytterstreng (det hjul som befinner seg lavest på denne
strengen):
| (2.184) |
Forreste hjul i innerstreng:
| (2.185) |
Bakerste hjul i ytterstreng:
| (2.186) |
Bakerste hjul i innerstreng:
| (2.187) |
Som formel 2.91 viser, kan en sporfeil i stor grad influere på størrelsen av forandringen av hjultrykket på grunn av sporets vindskjevhet(ΔQg). Vognen befinner seg i en vindskjevhet på g promille som på grunn av for eksempel utilstrekkelig justering eller setninger etter at justeringen er foretatt, er blitt betraktelig større enn den tilsiktede rampestigningen som skal være gt promille.
Hjulkraftforandringen ΔQg skyldes både sporets og vognens konstruktive utførelse og kan uttrykkes ved følgende formel:
| (2.188) |
Faktoren CtA er vognens totale torsjonsstivhet i kN/promille. Denne faktoren kan i stor grad influeres av vognkonstruktøren.
Hjulkraftforandringen ΔQh skyldes praktisk talt bare sporet, og det framgår av figur xx at hjulkraftforandringen kan uttrykkes ved:
| (2.189) |
Her betyr:
h er overhøyden
S er avstand mellom skinnene
H er høyden av vognens tyngdepunkt over sporplan
Vognkonstruktøren kan bare i meget liten grad influere på faktoren H som vil
være avgjørende for størrelsen av forandringen av hjulkraften.
Hjulavlastningen kan ytterligere bli redusert som følge av sideveis eksentrisite
av vognens last. Ved lav hastighet har dette tilsvarende virkning som
overhøyden når vognens stilling er slik at eksentrisiteten er rettet mot sporets
indre streng. Dette er vist i figur 2.114.
Forholdet kan uttrykkes ved følgende formel:
| (2.190) |
GL er vognens last
eL er lastens eksentrisitet
Ved lav hastighet vil det forreste hjulet i ytterstreng ha den største
hjulavlastningen:
| (2.191) |
Tilsvarende blir påtrykket størst for det forreste hjulet i innerstreng:
| (2.192) |
Størrelsen av føringskraften Ya er ved lave hastigheter i stor grad avhengig av
tverrkraften som virker på det motsatte hjul, dvs. hjulet på indre streng. Og
denne kraften Yi er en friksjonskraft som øker proporsjonalt med hjulkraften på
indre streng, dvs. med Qi. Med økende påtrykk blir også Yi større.
Ved lave hastigheter, dvs. uten påvirkning av sentrifugalkraften gjelder
tilnærmet:
| (2.193) |
Tverrkraften på den indre streng kan uttrykkes ved:
| (2.194) |
Tverrkraften på den ytre streng uttrykkes ved:
| (2.195) |
Dette gir:
| (2.196) |
Ved å innføre
| (2.197) |
kan ovennevnte formel uttrykkes på følgene måte:
| (2.198) |
Dette gir:
| (2.199) |
γi er vinkelen i forhold til sporplan av fellestangenten i berøringspunktet
hjul/skinne på indre streng. Denne vinkelen er meget liten.
ρi er friksjonsvinkelen hjul/skinne som er avhengig akselens anløpsvinkel α. Ved stor anløpsvinkel kan f oppnå størrelser over 0,5.
Overhøydens innflytelse kan medføre en liten reduksjon av Ya, men dette
medfører ikke at vognen legger seg mot indre streng. Dette fordi den positive
faktoren i ovennevnte formel alltid er betraktelig større enn den negative
komponenten som er faktoren av akselkraften i sporplanet. Videre influerer
overhøyden på faktoren f som vil øke noe. Dette fordi overhøyden bevirker en
økning av anløpsvinkelen ved lav hastighet.
Iht. ovenstående kan Y/Q-forholdet uttrykkes på følgende måte:
| (2.200) |
Det skal i det etterfølgende gjennomgås en prosedyre for beregning av
sikkerhet mot avsporing under definerte forutsetninger. Det antas en tom
godsvogn i en kurve med radius 150 m uten overhøyde og med en feil i
vindskjevhet av størrelse gLIM. Det forutsettes at et av hjulene kan løfte seg
inntil 5 mm, slik at vognens torsjon gT ikke blir større enn g*.
Videre forutsettes at vognen har hjul med flensvinkler lik 70o . Forholdet Ya/Qa skal ikke overskride 1,2.
Da overhøyde og last er satt lik null, kan ovenstående formel uttrykkes som:
| (2.201) |
Uttrykket er det samme som over, men i samsvar med forutsetningene faller
ΔQh (ingen overhøyde) og ΔQL (ingen last) ut. Leddet ΔQg= CtA· g erstattes av
ΔQt= CtA· gt. f150= tg(γi+ ρi) for en kurve med radius 150 m.
g er sporets vindskjevhet og gt er vognens torsjon. Begge størrelsene er uttrykt i promille. Da det ene hjulet tillates å løfte seg 5 mm, vil g og gt anta forskjellige verdier.
Denne formelen gjelder en feilfri vogn og innflytelse av torsjonsfriksjonen er ikke medtatt. Det er imidlertid ønskelig å ta med alle faktorene som kan influere på sikkerheten mot avsporing av en tom vogn i en kurve uten overhøyde. Disse faktorene er:
ΔQeb er sideveis eksentrisitet av vognens tyngdepunkt.
ΔQto er vognens egen vindskjevhet
ΔQμ er torsjonsfriksjonen
Videre er det lagt inn den forutsetning at vindskjevheten i sporet kan forårsake
at vognen allikevel befinner seg i et spor med liten overhøyde. Denne
overhøyden forårsaker en hjulkraftforandring med benevnelsen ΔQüg.
Summen av alle ovennevnte faktorer som altså kan forårsake en hjulkraftforandring, skal holde seg innenfor en bestemt grense som benevnes ΔQlim:
| (2.202) |
Størrelsen av ΔQlim bestemmes iht. følgende uttrykk:
| (2.203) |
Faktoren
| (2.204) |
settes lik 0 da det forutsettes overhøyde lik 0 (eller meget liten overhøyde).
Faktoren f150 er som allerede nevnt lik tg(γi+ ρi) for en kurve med radius 150
m. Størrelsen av denne faktoren kan bestemmes ved å foreta målinger av
føringskreftene Ya i en kurve med radius 150 m uten overhøyde.
Det må forlanges:
| (2.205) |
Dette uttrykket løses mht. ΔQlim:
| (2.206) |
Når det gjelder 2-akslede vogner med UIC dobbeltlenkopphenging og med
akselavstander 6 – 9 m, har det blitt foreslått følgende formel for faktoren f150:
| (2.207) |
hvor A er akselavstanden angitt i meter.
For slike vogner kan ΔQlim uttrykkes som:
| (2.208) |
For A = 6 m blir ΔQlim= 0,64Q0.
For A = 9 m blir ΔQlim= 0,50Q0.
I formel
| (2.209) |
forekommer forskjellige faktorer som er fastlagt på grunn av nødvendige
sikkerhetsmarginer. Disse tar hensyn til vedlikeholdstoleranser og følgende
blir antatt:
| (2.210) |
| (2.211) |
Videre gjelder:
| (2.212) |
Settes dette inn i formelen, oppnås følgende betingelse:
| (2.213) |
Når akselavstanden A er gitt, kan vognkonstruktøren praktisk talt bare influere
på størrelsen av ΔQt som uttrykker hjulkraftforandring på grunn av vognens
torsjon.
Løsning av ulikheten over gir største maksimale verdi for ΔQtlim:
| (2.214) |
Vognens totale vindskjevhet skal ikke overskride:
| (2.215) |
Ifølge retningslinjene kan tillatt hjulavlastning ΔQlim beregnes når vognen har
UIC-dobbeltlenker som antatt her. For akselavstand A = 9 m er det iht. formel
| (2.216) |
beregnet at
| (2.217) |
Godsvogner må være i stand til å gjennomkjøre vindskjevheter inntil
størrelsen glim som er grenseverdien for sporets vindskjevhet. For 2-akslede
vogner gjelder:
| (2.218) |
hvor A er akselavstanden i meter.
Med A lik 9 m blir glim = 5,22 promille. Det ledende hjul vil da løfte seg 5 mm
og vognens totale torsjon kan beregnes:
| (2.219) |
Vognen befinner seg da i en overhøyde
| (2.220) |
Som allerede angitt er den totale torsjonsstivhet for en vogn:
| (2.221) |
I ovenstående er det altså forutsatt en største overhøyde lik 23,5 mm. Imidlertid kan det forekomme større overhøyder üg i kurver med små radier (150 – 180 m). Dette betyr at vognen allikevel ikke er avsporingssikker. For kurver med liten radius og stor overhøyde må det stilles større krav til sporets justeringsstandard enn det som blir forlangt i formelen til faktoren glim.
Med gitt akselavstand er det påpekt at vognkonstruktøren bare i liten grad kan influere på størrelsen ΔQt som altså er hjulkraftforandringen på grunn av vognens torsjon. Det finnes også en grense for de krav som kan settes til godsvognenes konstruksjon. Problemet bør heller angripes på en slik måte at det undersøkes hvilke krav som må stilles til sporet for å oppnå sikkerhet mot avsporinger i spor med stor overhøyde.
Det er fastsatt i regelverket en maksimal overhøyde som funksjon av kurvens radius:
| (2.222) |
R er kurvens radius i meter
hmaks framkommer i mm.
Grenseverdi for rampestigning er 1 : 400 eller 2,5 promille.
VOGNENES RULLING
Vognenes rullvinkelkoeffisient
Når et tog kjører gjennom en kurve, vil det oppstå sidekrefter som oppleves som ubehagelige av passasjerene. Disse sidekreftene øker proporsjonalt med andre potens av hastigheten og har benevnelsen sentrifugalkraft. Kraften uttrykkes vanligvis ved sideakselerasjonen:
| (2.223) |
Her betyr:
au er ukompensert sideakselerasjon i sporplanet (m/s2)
v er hastighettil det rullende materiell i kurven (m/s)
R er radius i kurve (m)
g er tyngdens akselerasjon (m/s2)
D er overhøyde(mm)
S er sporvidde(mm)
Med en masse m blir sentrifugalkraften:
| (2.224) |
Størrelsen på denne kraften fordeles på akslene på vognens boggier eller på begge akslene i en 2-akslet vogn.
Det vises til figur 2.115.
Det framgår av uttrykket for den ukompenserte sideakselerasjon at denne (au) reduseres ved å øke overhøyden i kurven. Den ytre skinnestreng legges høyere enn den indre skinnestreng i kurven. Overhøyden skal i Norge ikke overskride 150 mm.
Ideelt sett burde hastigheten i kurven ikke være større enn at
sideakselerasjonen blir tilnærmet lik null (som på rett linje). En slik hastighet
benevnes likevektshastighet.
Nå er det imidlertid slik at ut fra et komfortsynspunkt kan passasjerene
utsettes for en ukompensert sideakselerasjon i sporplanet av en viss størrelse.
Erfaring tilsier at aU
kan anta en viss størrelse uten at passasjerene opplever
komforten som dårlig. Dette gir grunnlag for økt hastighet.
Nå er det imidlertid slik at denne sideakselerasjonen i sporplanet ikke alene
bestemmer komforten. Sideakselerasjonen som passasjerene opplever, er
altså ikke bare betinget av togets hastighet og kurvens overhøyde. Også
togmateriellets konstruksjon er av betydning. På grunn av materiellets
fjærkonstruksjoner vil konvensjonelt materiell rulle eller krenge utover i kurven
når toget gjennomløper kurven med en større hastighet enn
likevektshastigheten. Dette medfører at vognens helning i forhold til det
horisontale plan blir mindre enn sporplanets helning. Vognens ” overhøyde” blir
mindre enn kurvens overhøyde. Dermed blir effekten av overhøyden i sporet
redusert. Rulling oppstår både i sekundærfjæringen (fjæring mellom boggi og
vognkasse) og i noe mindre grad i primærfjæringen (fjæring mellom hjul og
boggi). Den samlede grad av rull uttrykkes ved rullvinkelkoeffisienten r.
Sideakselerasjonen blir på grunn av rulling normalt høyere i vognkassen enn i sporplanet. Denne sideakselerasjonen som betegnes kompensert sideakselerasjon, benevnes aK.
Iht. ovennevnte gjelder at aK påvirker komforten til passasjerene. aU gir opphav til de krefter som oppstår mellom hjul og skinne ved framføring av det rullende materiell.
Den effektive rullingsfaktor fr uttrykkes ved rullvinkelkoeffisienten r på denne måten:
| (2.225) |
Sammenhengen mellom ak, au og fr (ev. r) kan angis:
| (2.226) |
Det framgår at r bør anta liten verdi. Dette betinger harde fjærkonstanter.
For norsk materiell gjelder følgende verdier:
- Vogn litra B3: r = 0,6
- Vogn litra B5: r = 0,4
- Vogn type B7: r = 0,2
På grunn av de store forskjellene i rullvinkelkoeffisient framføres vognene med
ulike hastigheter av hensyn til komforten.
De 2 øverste vogntypene (Vogn litra B3 og vogn litra B5) framføres med
kurvehastigheter (normalhastighet) som tilsvarer aU lik 0,65 m/s2. Rent
unntaksvis kan vognene framføres med ukompensert sideakselerasjon i sporplanet lik 0,85 m/s2.
Dette gir følgende verdier for sideakselerasjonen i vognkasse som passasjerene utsettes for:
- Vogn litra B3:
- aK= 0,65 (1 + 0,6) = 1,0 m/s2
- aK= 0,85 (1 + 0,6) = 1,4 m/s2
- Vogn litra B5:
- aK= 0,65 (1 + 0,4) = 0,9 m/s2
- aK= 0,85 (1 + 0,4) = 1,2 m/s2
Anbefalt verdi av komforthensyn er 1,0 m/s2. Ukompensert sideakselerasjoni sporplanet lik 0,65 m/s2 tilfredsstiller dette kravet. aU lik 0,85 m/s2 medfører at komfortkravet overskrides. Særlig for vogn litra B5 blir den kompenserte sideakselerasjon i vognkassefor høy.
Vogner av type B7 framføres med en hastighet i kurvene (plusshastigheter)som tilsvarer aU = 0,85 m/s2 til 1,00 m/s2. Dermed blir sideakselerasjonen i vognkassen for denne vognen:
- Vogn type B7:
- aK= 0,85 (1 + 0,2) = 1,0 m/s2
- aK = 1,00 (1 + 0,2) = 1,2 m/s2
Verdien av denne akselerasjonen i vognkasse er også høy for B7-vogner. Det
må imidlertid bemerkes at vognen er utstyrt med meget god fjæring sideveis.
Denne fjæringen fører til reduserte laterale akselerasjoner i vognkasse som
følge av ujevnheter i sporet.
Av hensyn til komfort kan altså konvensjonelt materiell ikke framføres med
høyere hastigheter enn de som tilsvarer en ukompensert sideakselerasjon i
sporplanet lik 1,00 m/s2. Imidlertid moderne vognmateriell (for passasjerer) er
utstyrt med gode boggier. Slikt vognmateriell kan framføres med høyere
hastigheter og dermed høyere ukompensert sideakselerasjon i sporplanet enn
angitt over før grenseverdier for sporkrefter blir nådd. Dersom en slik
hastighetsøkning er ønskelig, må av komforthensyn vognen krenge innover i
kurven i stedet for utover (som for konvensjonelt materiell). Dette betyr at
rullvinkelkoeffisienten må være negativ. Vognkassen får dermed en større
helning i forhold til horisontalplanet enn sporplanet. Vognkassens ” overhøyde”
blir større enn overhøyden i sporet. En slik oppførsel lar seg bare gjennomføre
dersom vognkassen utstyres med et krengesystem.
Et aktivt krengesystem(motordrevet krengebevegelse) kan for eksempel gi en
rullvinkelkoeffisient r = - 0,6. Dersom vognen framføres med ukompensert
sideakselerasjon i sporplanet lik 1,8 m/s2, blir den kompenserte
sideakselerasjon i vognkasse:
| (2.227) |
Gjennomkjøring i kurver med så høy ukompensert sideakselerasjon medfører
ca. 30 % hastighetsøkning i forhold til de hastigheter som kan oppnås med
konvensjonelt materiell.
Det bør videre poengteres at den kompenserte sideakselerasjon aK
ikke bør overskride 1,0 m/s2. Dette har sammenheng med den økte negative effekten
av ujevnheter i sporet. Denne effekten øker med tredje potens av
hastighetsøkningen.
Det er allerede nevnt at høyere komfort oppnås i togmateriell hvor vogner
utstyres med krengesystem og at dette forhold tillater økt hastigheter i kurver.
I figur 2.116 er vist krengesystemet på vogner i X2.
Ved gjennomføring av omfattende forsøk med dette togsettet har det vist seg at en maksimal helning eller krenging av vognen på 6,5° gir meget god komfort for de reisende passasjerer. For å oppnå en effektiv krenging av vognkasse på 6,5° er det på grunn av fjæringen nødvendig med en effektiv helning på 8° mellom boggirammen og vognkassen. Dette framkommer ved helninger på følgende måte:
Boggiramme – boggibjelke: 8 grader
Boggibjelke – vognkasse: - 0,5 grader
Boggiramme – jernbanespor: - 1,0 grad
Effektiv helning på vognkasse: 6,5 grader
Denne helningen medfører ca. 70 % kompensasjon av sentrifugalkraften ved gjennomkjøring i kurver. Under forutsetning av at komforten ikke skal bli dårligere, betyr dette at hastigheten kan økes med ca. 30 %. Selve rotasjonen av vognkasse skjer i nærheten av vognens tyngdepunkt og dette har en meget gunstig effekt mht. opptredende sporkrefter.
Ovennevnte skal belyses med et eksempel. Det tas utgangspunkt i en vogn av type Vogn litra B3 med rullvinkelkoeffisient r lik 0,6 og vogn i X2 med r = -0,7. Iht. tidligere betraktninger skal den kompenserte sideakselerasjon i vognkasse av hensynet til komfort ikke overstige 1,0 m/s2.
Med utgangspunkt i uttrykket:
| (2.228) |
kan den ukompenserte sideakselerasjon i sporplanet beregnes:
| (2.229) |
Dette gir følgene verdier for den ukompenserte sideakselerasjon i sporplanet
for de 2 vogntypene:
Vogn litra B3:
| (2.230) |
Vogn i X2:
| (2.231) |
aU lik 3,33 m/s2 er for høy og medfører risiko for avsporing eller velting.
Akselerasjonen begrenses til 1,8 m/s2 av sikkerhetsgrunner. Den opptredende
kompenserte sideakselerasjon i vognkasse beregnes da til å være:
| (2.232) |
Dette gir meget god komfort i forhold til konvensjonelt materiell.
Det kan vises at aU = 1,80 m/s2 tilsvarer manglende overhøyde I = 280 mm. Helningen til vognkasse i forhold til sporplanet beregnes:
| (2.233) |
Innsatt i formel gir dette:
| (2.234) |
Ved å ta utgangspunkt i uttrykket for den ukompenserte sideakselerasjonen i
sporplanet kan hastighetsøkningen beregnes:
| (2.235) |
Uttrykket løses mht. hastighet:
| (2.236) |
Dersom R er 500 m og D er 150 mm blir hastighetene:
Vogn litra B3.
| (2.237) |
Dette gir tilsvarende en hastighet for krengetog på 37 m/s2.
Hastighetsøkningen er på over 30 % og gir bedre komfort.
Det må imidlertid gjøres oppmerksom på at krenging opp til 8o (tilsvarende en kompensasjonsgrad på 70 %) krever lange overgangskurver. I korte overgangskurver vil rullvinkelhastigheten bli så stor (over 6 grader) at forholdet kan medføre risiko for togsyke.
Sporet i Sverige har lange overgangskurver og det er derfor berettiget å benytte en så høy kompensasjonsgrad. I Norge er overgangskurvene kortere og for det norske krengetoget er det derfor valgt en kompensasjonsgrad på 55 % som kompromiss.
Bevegelseslikninger for rullende materiell
Det skal betraktes et tilfelle med kvasistatisk gjenomløp av det rullende materiell i kurven. Kvasistatisk gjenomløp betyr at det ikke finnes sporfeil eller andre forstyrrelser. Det antas at vognkassen har et tyngdepunkt som ligger høyere enn den laterale kraftresultanten i fjærsystemet.
Dersom vognen gjennomløper kurven med en høyere hastighet enn den
balanserte hastighet, virker den resulterende laterale kraft utover. Vognkassen
påvirkes da av et moment som virker i et tverrstilt vertikalplan. Forholdet fører
til deformasjoner i fjærsystemet som bevirker at vognkassen vil helle utover i
kurven, dvs. i samme retning som den resulterende sentrifugalkraften med
fradrag av sporets overhøyde. Denne krengingen av vognkassen medfører
som nevnt en redusering av helningen til det rullende materiell. Og nettopp det
å skape en slik helning er hele hensikten med å bygge spor med overhøyde i
kurve. En del av den kompenserte sideakselerasjonen som skapes ved
overhøyde i sporet i en kurve, går dermed tapt.
Ved et kvasistatisk gjenomløp i kurve innføres følgende betegnelser:
ay = lateral sideakselerasjoni sporplanet (m/s
2
)
ayz = lateral akselerasjon i gulvet i vognkassen (m/s 2 )
az = vertikal akselerasjon i sporplanet (m/s 2 )
azk = vertikalakselerasjon i gulvet i vognkasse (m/s 2 )
b = halve avstand mellom hjulenes løpesirkler (m)
D = overhøyde i sirkelkurve (m)
g = tyngdens akselerasjon (m/s 2 )
R = radius i kurve (m)
v = hastighet (m/s)
φD = helning til sporplanet (radianer)
φfr = helning til vognkasse i forhold til sporplanet (radianer)
φfr er definert til å være positiv dersom helningen av vognkassener motsatt av helningen av sporplanet.
Det antas at sporplanet er referansesystemet. Da dannes følgende likninger:
| (2.240) |
| (2.241) |
Med vognkassensom referansesystem beregnes de akselerasjoner som
oppleves av personer i vognen:
| (2.242) |
| (2.243) |
Det påpekes at vinklene som regel er små (≤ 0,1 radianer). Med tilnærmelse
kan da skrives:
| (2.244) |
| (2.245) |
Forholdet mellom de laterale akselerasjonene i vognkasse og sporplanet kan uttrykkes:
| (2.246) |
| (2.247) |
| (2.248) |
Det er blitt utledet økningen av den laterale akselerasjon i vognkassen i
forhold til sporplanet:
| (2.249) |
r er rullvinkelfaktoren og er altså en funksjon av rullvinkelen uttrykt i radianer til
vognmateriellet og den laterale akselerasjon i sporplanet.
Den effektive rullfaktor kan beregnes:
| (2.250) |
r settes inn med positivt fortegn ved helning innover i kurven og med negativt
fortegn ved helning utover i kurven.
Sammenstilling av bevegelseslikninger i kurver
Med betegnelsene i foregående avsnitt gjelder: Den effektive rullefaktor:
| (2.251) |
Lateral akselerasjon i sporplanet:
| (2.252) |
Denne kan også uttrykkes som:
| (2.253) |
Lateral akselerasjon i vognkassens gulv:
| (2.254) |
Denne kan også uttrykkes som:
| (2.255) |
Det laterale rykk i overgangskurven kan beregnes:
| (2.256) |
Rullvinkel forårsaket ved overhøyde:
| (2.257) |
Rullvinkel forårsaket ved vognens rulling:
| (2.258) |
Den samlede rulling:
| (2.259) |
Rullvinkelhastigheten blir:
| (2.260) |
Her betyr.
Lt er overgangskurvens lengde
I er manglende overhøyde
Krengeteknikk
Den maksimale tillatte kjørehastighet til det rullende materiell i en kurve blir bestemt av hensynet til en sikker framføring. Faktorer som kommer i betraktning og som er bestemmende, er sikkerhet mht. avsporing og stabilitet i overbygningen samt kvaliteten på selve sporet og den komfort som passasjerene utsettes for. Vogner som blir utstyrt med innretninger slik at vognkassen beveger seg innover i kurven, kan tillates å ha høyere hastigheter enn konvensjonelt materiell ut fra hensynet til komfort. Dette har sammenheng med at den resulterende laterale akselerasjon i slike tog (krengetog) blir mindre enn for konvensjonelt materiell. Krengeteknikken med de nødvendige innretninger er derfor en metode som kan benyttes til å øke hastigheten i kurver. Det er imidlertid en forutsetning at sporet har tilfredsstillende stabilitet.
Uttrykkene passiv og aktiv krengeteknikkfinnes. Ved passiv krengeteknikk har vognkassen oppheng som en pendel og utøver helning mot innside av kurven på grunn av de opptredende sentrifugalkrefter. Ved aktiv krengeteknikk blir vognkassen styrt innover i kurven ved en driv(kraft)enhet og kunstig styreenhet.
Installering av innretning for krengeteknikk har kun betydning for komfort. Men
i sammenheng med krengeteknikken blir det gjort også andre tiltak. Disse kan
være redusering av aksel- og hjullast på vognmateriellet og en moderne boggi
med radiell innstilling av hjulsatsene samt redusering av uavfjæret masse.
Dette medfører at den samlede belastning på sporet som består av
kvasistatiske og dynamiske krefter, i hvert fall ikke behøver å bli større ved
krengetog enn ved konvensjonelt materiell. Dette til tross for at hastighetene i
kurvene er større.
På strekninger hvor krengetog skal trafikkere, er det flere hensyn å ta. Mht.
trasseringen er det viktig å vurdere forholdet mellom overgangskurvens
lengde, størrelsen på sirkelkurven samt overhøyde i sirkelkurven. Sporveksler
er å oppfatte som tvangspunkter ved kjøring i avvik. Minste tverrsnitt samt
beliggenhet av kjøreledningen må også tas hensyn til. Sikkerhet ved
framføring for overvåking av hastighet og sikring av planoverganger er andre
viktige aspekter.
Kombinasjonen av krengeteknikk i seg selv og tiltak på det rullende materiell
samt i infrastrukturen må sees på som et lukket og samlet driftssystem.
Innretninger for krenging av vognkassen
Det er utviklet flere systemer mht. til aktiv krenging som skal ivareta krengingen til vognkassen. Det er da hensiktsmessig å betrakte forskjeller i den mekaniske oppbyggingen til systemene. En viktig forskjell består i om det er en funksjonell elle en ikke funksjonell kombinasjon med andre komponenter til det rullende materiell (Fahrwerk:luftfjærer, Wankstütze).
Det kan nevnes at Bombardier/Talbot har et system for aktiv krengeteknikk
som kalles ” Cont-Roll” . Den funksjonelle integrasjon for dette systemet består i
at krenging gjennomføres i sammenheng med ” Wankstützenverstellung”.
For alle andre systemer er det en funksjonell atskillelse. Den mekaniske
tilkoplingen av vognkassen til boggien i bevegelsesflaten skjer for nesten alle
systemer ved en trapesformet pendel. Dette gjelder løsninger fra Adtranz,
Fiat, Siemens-SGP og Alstom. Det vises til figur 2.117.
Noen systemer baserer seg på en bjelke i boggien som er formet som en sirkel. Vognkassen har opplegg og beveger seg på et bueformet rullelager. Slike trapesformede pendler og bueformede bjelker er robuste komponenter og tar opp den vertikale lasten fra vognkassen samt de opptredende sentrifugalkrefter.
Inngripen i vognkasse
Standardutvikling er at drivenheten for krengesystemene er plassert under vognkassegulvet i boggien. Dermed blir inngripen i selve vognkassen unngått.
Strømavtaker
Ved de elektrifiserte krengetogene må det sørges for at strømavtakeren ikke krenger når toget gjennomløper kurven. Den enkleste måten å gjøre dette på er å ha en traksjonsenhet i togsettet som ikke krenger. Det eksisterer løsninger hvor det er montert en bærerygg på den primærfjærede boggirammen. Denne løsningen medfører at strømavtakeren blir uavhengig av vognkassen og den helning som vognkassen får.
Drivenhet for krenging
Det er standard å benytte hydrauliske drivenheter i forbindelse med et aktivt krengesystem. Disse enhetene har den fordel at de ved høye trykk i driftsituasjon lar seg bygge inn kompakt i boggirammeverket. Hydrauliske drivenheter kan utøve høye krefter for å framskaffe krengingen. Gjennom elektromagnetiske ventiler er det mulig å gjennomføre en fin og tilpasset styring. Det trengs imidlertid et eget system for tilførsel av energi for å besørge krengingen.
Det er også utviklet elektriske drivenheter for å besørge krengingen av vognkassen. Fordelen med slike systemer er flere. Vedlikeholdsbehovet er lite samt at styringen er enkel. Videre kan krengehastigheten varieres.
Høyde på dreiepol
Forskjellige undersøkelser og forsøk viser at dreieaksen for krengingen mht. vognkassens lengdeakse ideelt bør ligge i området ved sitteflaten i setene eller litt over. Magehøyde for sittende passasjerer er en passende høyde for dreiepolen. Det er overveiende sannsynlig at passasjerene vil føle dreiebevegelsen minst ubehagelig ved en slik plassering av dreiepolen.
Er dreiepolenplassert ved gulvet i vognkassen, vil dreiebevegelsen lett bli
oppfattet som vakling. Dette forhold kan føre til togsyke.
Nyttig krengevinkel
Ved bruk av innretningen for krenging av vognkassenkan en maksimal krengevinkelbestemmes. På grunn av fjæregenskapene til primær- og sekundærfjæren vil vognkassen ved høy hastighet i kurven få helning utover i kurven på grunn av store sentrifugalkrefter. Dette forholdet medfører at den effektive krengevinkel blir ca. 1,5 grader mindre enn den krengevinkel som kan innstilles på grunn av innretningen til krengesystemet.
Lateral føring og tilbakeføring av vognkasse
Det er påpekt at det er ønskelig å ha dreiepolenknapt over tyngdepunktet i vognkassen og i høyde med sitteflaten på setene. Det er derfor nødvendig ved siden av den reine dreiebevegelse å ha en lateral bevegelse av vognkassen i forhold til boggirammen i bevegelsesflaten mellom vognkasse og boggi. Denne laterale forskyvningen kan realiseres med den mekaniske innretningen til krengesystemet. Det er også mulig å anordne tilleggskomponenter.
Videre må det sørges for at vognkassenetter gjennomløpet i kurven blir
nøyaktig rettet opp, dvs. vognkassen må tilbake til nullstillingen. Dette gjelder
også for det tilfelle at drivenheten for krengesystemet skulle slutte å virke.
Lateral fjæring
Den laterale fjæringen skjer som regel ved sekundærfjæringen. Dersom innretningen for helningen til vognkassen ligger over sekundærfjæringen, så blir delvis en aktiv lateral fjæring og en tverrsentrering bygget inn. Dette tiltaket begrunnes med en for sterk belastning på sekundærfjæren i tverretningen. Dessuten påpekes det at tiltaket er nødvendig for å øke kjørekomforten. Formen på denne innretningen har også betydning for tillatt bredde på vognkassen.
Sensorer for krenging
Krengetogene er utrustet med sensorer som muliggjør krengingen. Metoden går ut på at den laterale akselerasjon i gulvet i vognkassen blir målt og som funksjon av hastigheten blir krengevinkelen bestemt. På minst en boggi for hver vogn i toget er det montert akselerometre som måler den ukompenserte laterale akselerasjon. Ved en slik løpende måling må det kartlegges om den målte laterale akselerasjon er bevirket sentrifugalkrefter eller en uregelmessighet i bevegelsen på grunn av sporfeil i overbygningen. For å unngå utilsiktede bevegelser på grunn av disse uregelmessighetene må de høye frekvensene til signalene for akselerasjonen filtreres. Et slikt tiltak bevirker imidlertid en tidsmessig forsinkelse av signalflyten og resultatet er en forsinket helning av vognkassen. Dette resulterer i en høyere lateral akselerasjon ved innkjøring til eller ved utkjøring av kurver enn i kurvene selv. Denne høyere akselerasjonen i trasseringspunktene medvirker til husking eller gynging av vognkassen og kan under omstendighetene føre til togsyke. Spesielt vil det være den første vognen som blir utsatt for en slik forsinket hendelse. For de etterfølgende vognene finnes det flere muligheter til å korrigere denne forsinkelsen. Bl.a. kan sensorer i forangående vogn gi signaler slik at forsinkelse i krengingen til den vognen som skal inn i kurven, unngås. En annen metode er å benytte et overordnet ledesystem. Jo kortere overgangskurven er, jo hurtigere må styringen reagere, dvs. at hastigheten til innretningen for krengingen må bli høyere.
Målingen av den laterale akselerasjon i gulvet til vognkassener altså ikke nok.
Dette selv om det bare er denne (vognkassen) som skal krenge.
Måleinstrumenter som gyroskop må installeres i den hensikt å oppdage
kurvens begynnelse og slutt tidsnok slik at krengingen til vognkassen kan
starte umiddelbart i trasseringspunktene. Med trasseringspunkter menes
overgangskurvens begynnelse (OB) og overgangskurvens slutt (OE). Bruk av
sensorer krever et meget høy intensitetsnivå. Dette gjelder også
grunnalgoritmen i sensorsystemet. Utvikling og forsøk av slike grunnalgoritmer
krever mye tid. Det må også bemerkes at en slik grunnalgoritme på ingen
måte er universell. Den regelalgoritme som gjelder for en region eller land,
behøver ikke å gjelde ved andre forvaltninger. Dette har naturligvis
sammenheng med at trasseringsregler kan være forskjellige i ulike land. I
ytterste konsekvens vil en grenseoverskridende trafikk med krengetog kunne
føre til uheldige målkonflikter ved utarbeidelse av regelalgoritmer.
Krenging med støtte fra datateknikk
På grunn av det nødvendige høye intensitetsnivået i bruk av sensorer og den nødvendige tid for å utvikle regelalgoritmer i forbindelse med krengesystemer er det fremmet forslag om å bruke datateknikk, dvs. bruk av datastøttede programmer for å styre krengingen til krengetogene. Slike systemer tar utgangspunkt i strekningsdata som må lagres i programmene. Slike programmer skal kunne medføre at vognene (også første vogn) starter bevegelsene mer presist.
LITTERATURHENVISNINGER
1. Die Eisenbahnschiene
Fritz Fastenrath 1977
2. Modern Railway Track C Esveld 1989
3. Engineering Mechanics Volume 2 J.L.Meriam 1980
4. Samverkan Fordon – Bana Evert Andersson 1990
5. Railway Vehicle Dynamics AEA Technology 1998
6. Komfortverbesserungen an Schienenfahrzeugen für den Personenverkehr Manfred Mitschke ZEV + DET Glas. Ann. 123 (19999) 4 April
7. ORE B 55 Hjulavlastning