Samvirke mellom rullende materiell og spor
Lenke til PDF-filen: Samvirke mellom rullende materiell og spor
1 INNLEDNING
Studiet av de dynamiske bevegelser til det rullende materiell ved framføring på et skinnegående spor er meget komplisert. Dette har sammenheng med de dynamiske belastninger som hjulsettet utsettes for når det beveger seg på skinnegangen. Men bevegelsen til det rullende materiell følger allikevel grunnleggende dynamiske prinsipper. Dette gjelder både vertikalt og lateralt samt rulling.
Temaet samvirke rullende materiell/bane er delt inn i to kapitler. Denne første delen omhandler vognens bevegelser på sporet, herunder konisitet og vogndynamikk. Forhold knyttet til adhesjonsegenskaper og kryp er beskrevet i del 2.
Et spor blir aldri helt perfekt. Ved meget lange bølgelengder vil den geometriske linjeføringen mht. sporet lateralt og vertikalt samt i lengderetning påvirke bevegelsene til vogn og boggi . Ved korte bølgelengder vil uregelmessigheter i skinnene føre til urolige bevegelser. Riktig konstruksjon og oppbygging av sporet og underbygningen samt definert og planlagt vedlikehold vil redusere amplitudene på sporfeilene.
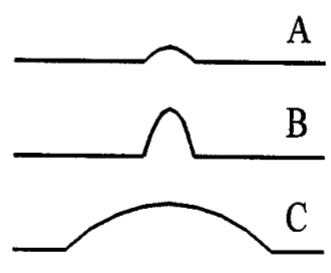
Det er gjennom lang tid observert at amplituden for ulike sporfeil er en funksjon av bølgelengder. Jo større bølgelengden er, jo større er vanligvis amplituden i sporfeilen. Dette er illustrert i figur 2.1 En sporfeil av type A vil oppstå langt oftere enn en sporfeil av type B for samme bølgelengde. Videre vil en sporfeil av type C med større amplitude ved lang bølgelengde oppstå like lett som en sporfeil av type A ved kort bølgelengde. Som en første tilnærming kan gjøres den antakelse at størrelsen på amplituden til en sporfeil er en funksjon av sporets bølgelengde.
2 SAMVIRKE RULLENDE MATERIELL/BANE
Samvirke mellom det rullende materiell og bane er et meget vidt begrep, men skal i det etterfølgende begrenses til det som kalles gangdynamikkeller gangegenskaper.
Dette omfatter:
- Bevegelser av det rullende materiell på skinnebundet spor
- Krefter mellom rullende materiell og spor (sporkrefter)
Følgende hendelser kan relateres til ovenstående:
- Avsporinger
- Slitasjeav f.eks. hjul og skinner
- Komfortfor de reisende
Følgende aspekter er relatert til gangdynamiske prinsipper:
- Sikkerhetsom en funksjon av hastighetog sporstandard
- Tillatt lastkapasitettil det rullende materiell som funksjon av påkjenninger på sporet
- Togets tillatte hastighetpå grunn av sporgeometrisk linjeføring
- Passasjerenes opplevelser av reisen samt risiko for forskyvning av lasten og dermed skader på gods
- Vedlikeholdskostnader på det rullende materiell og på sporet
Kjøreegenskapene til det rullende materiell har stor betydning for:
- Sikkerhet
- Komfortog skader på gods
- Økonomi
Gjeldende utviklingstendenser er framføring av tog med tyngre laster og med
større hastigheter. Disse aspektene er i høy grad avhengig av god
kjøredynamikk.
I forbindelse med kjøreegenskapene til det rullende materiell på skinnebundet
spor skal det beskrives noen grunnleggende begreper:
- Statisk tilstandinntreffer når det rullende materiell står stille på et perfekt spor.
- Kvasistatisk tilstander den tilstand som opptrer når det rullende materiell framføres med konstant hastighetpå et perfekt spor. Det forutsettes atdette sporet har konstant kurveradiusmed konstant overhøyde. Videre eksisterer det konstante friksjonsforhold mellom hjul og skinne. Dette medfører at alle krefter eller forskyvninger i det rullende materiell og mellom det rullende materiell og sporet er konstant hele tiden.
- Dynamisk tilstand definerer de bevegelser og tilleggskreftersom det rullende materiell utøver på grunn av sporfeil, endring av opprinnelig sporgeometri, endring av hastighetog friksjoni sporet. Selvgenererende bevegelser som f.eks. sinusforløpog ustabilt løpinngår i begrepe
2.1 Vognenes vibrasjonsmønster
I dette avsnittet skal det gis en beskrivelse av bevegelsene til det rullende materiell.
Det er 6 mulige bevegelser for alle komponenter til det rullende materiell ved framføring på et skinnegående spor. Dette gjelder for selve vognkassen, boggirammenog hjulsettet. Bevegelsene er vist samlet i figur 2.2.
| Bevegelser | Engelsk betegnelse | Norsk betegnelse | |
|---|---|---|---|
| Translasjonsbevegelse i kjøreretningen (X -retning) | Langsgående bevegelse eller longitudinell bevegelse | X Longitudinal | Rykk i kjøreretningen |
| Translasjonsbevegelse i tverretningen (Y -retning) | Sidebevegelse eller lateral bevegelse | Y Lateral | Sidesleng |
| Translasjonsbevegelse vinkel rett mot sporplanet | Vertikalbevegelse | Z Vertical, bounce | Hopping |
| Rotasjons -bevegelse i et plan tvers på lengderetninge) | Vognbevegelse | φ Roll, sway | Rulling |
| Rotasjons bevegelse i et langsgående vertikalplan | χ Pitch | Galoppering elle
vipping | |
| Rotasjons - bevegelse i selve sporplanet | ψ Yaw | Svingning |
Langsgående bevegelser eller rykkav vognene har sammenheng med
stivhetsparametre i forbindelse med buffere i en togformasjon.
Figur 2.2 Frihetsgrader mht. bevegelser til en jernbanevogn og vognens
hovedkomponenter
Jernbanevogner er vanligvis symmetriske om den vertikale akse. Dette er
illustrert i figur 2.3. Vertikale ujevnheter i sporet kan antas å påvirke vognens
bevegelser symmetrisk om denne aksen.
Figur 2.3 Det rullende materiell er vanligvis symmetrisk om den vertikal
akse.
Bevegelser mht. hoppingog galopperinger overveiende uavhengige av
laterale ujevnheter i sporet og rulling. Hopping og galoppering opptrer derim
i spor med ujevnheter i vertikal retning og er illustrert i figurene 2.4 og 2.5.
Figur 2.4 Illustrasjon mht. hoppingav vogn.
Figur 2.5 Eksempel på galoppering av vogn
På grunn av jernbanevognenes konstruksjon er vognmateriellet ikke
symmetrisk om noen lateral akse. Lateral bevegelse og rulling vil derfor
oppstå samtidig. Disse 2 sammenkoblede bevegelsene kan beskrives som
øvre rulling og nedre rulling. Bevegelsene er vist i figurene 2.6 og 2.7.
Figur 2.6 Eksempel på øvre rulling av vognmateriellet
Figur 2.7 Eksempel på nedre rulling av vognmateriellet
Ved nedre rulling har rotasjonssenteret et lavt nivå, mens for øvre rulling ligger
rotasjonssenteret høyere oppe. Frekvensen for den øvre liggende rulling vil
vanligvis være høyere enn for den lavere liggende rulling.
Svingningsmønsteret (yaw) er vist i figur 2.8
Figur 2.8 Svingningsmønsteret for en vogn
Typiske frekvensområder for ulike bevegelser er:
- Lavere rulling: 0,6 Hz
- Svingning: 0,9 Hz
- Hopping: 1,0 Hz
- Galoppering: 1,4 Hz
- Øvre rulling: 1,6 Hz
Reaksjonsmønsteret til en virkelig vogn er meget komplekst. Dette gjelder også når vognen framføres på et idealisert spor. Denne kompleksiteten er sammensatt av et antall av fysiske effekter. Det er nødvendig å beskrive samspillet av disse fysiske effektene for å få innsikt i forståelsen av hvordan vognen oppfører seg i et spor.
3 VOGN I FJÆR/DEMPER-SYSTEM
I det foregående avsnittet er bevegelsene til det rullende materiell beskrevet og illustrert. I dette avsnittet skal bevegelsene uttrykkes matematisk. Dette er særlig tilfelle for den vertikale bevegelse.
3.1 Masse med et enkelt fjær/demper-system
En masse som sitter på et fjæropplegg, har et system med en frihetsgrad. Bevegelsen til massen vil bli påvirket av vertikale ujevnheter i sporet. Dette er vist i figur 2.9.
Figur 2.9 Masse med et enkelt fjæropplegg og dempe
Denne massen vil utøve resonansved en naturlig frekvens som er gitt ved
formelen:
| (2.1) |
Her betyr:
- fn = naturlig frekvens [Hz], [s -1]
- k = fjærstivhet[N/m]
- m = masse [kg]
Uten dempingi systemet vil bevegelsen gå mot uendelig ved den naturlige
frekvensen. Systemet utføres derfor med en demper med gitte
karakteristikker:
- c = demperkonstant[N/v], [N/m/s], [Ns/]
Det er mulig å påvirke området for resonansfrekvenser gjennom parametrene k og m. En stiv fjær vil gi høye frekvenser og en tung masse vil medføre lave frekvenser.
Det defineres følgende parameter:
| (2.2) |
Dette gir:
| (2.3) |
Videre defineres:
| (2.4) |
Dette gir:
| (2.5) |
ω0 kan identifiseres som systemets resonansfrekvens(egenfrekvens) ved en
dempingsfaktorlik 0 (ingen dempingi systemet).
ζ defineres som den relative dempingi forhold til kritisk demping:
| (2.6) |
hvor
| (2.7) |
Den dempede naturlige frekvens blir:
| (2.8) |
Ved lave frekvenser vil massen følge uregelmessighetene i sporet ved
langsgående bevegelse. Dette gjelder både for vertikal forskyvning og for
akselerasjonsbevegelser til vognkassen. Ved massens egenfrekvens vil
aktivitetene oppnå særdeles høye verdier. Ved økende frekvenser avtar
verdiene igjen.
Det er mulig å øke nivået på dempingen. Det må imidlertid bemerkes at dempere i motsetning til fjærer er meget sensitive i høyere frekvensområder. Dette har sammenheng med at dempere reagerer som funksjon av hastighet. Fjærene får forskyvninger på grunn av uregelmessigheter i sporet.
Disse forholdene er vist i figur 2.10. Diagrammet viser forsterkningen i akselerasjonen uttrykt ved ÿ/w0til en masse som funksjon av frekvensområdet w(opptredende frekvenser). Forsterkningen i akselerasjonen er illustrert ved ulike nivåer på dempingen.
Figur 2.10 Forsterkning av akselerasjonen som funksjon av svingningsfrekvens samt nivå på dempere
Egenskapene blir:
- lav dempingmedfører stor forsterkning ved resonans
- høy dempinggir stor forsterkning i akselerasjonen ved høye frekvenser
- høy dempingoppleves som vibrerende ved høyfrekvente forstyrrelser
En viktig oppgave er derfor å konstruere den optimale demping.
3.2 Masse med fjær og demper med innebygget fjær
Overføring av energi til massen m kan reduseres betydelig ved innføring av fjær i dempersystemet. Dette er illustrert i figur 2.11. Litt elastisitet vil alltid opptre i hydrauliske dempere på grunn av sammentrykkingen av olje samt fleksible innfatningskomponenter i dempersystemet. Det er vanligvis verdifullt å benytte slike fleksible innfatningskomponenter for å få kontroll over systemet.
Figur 2.11 Modell av vogn med fjær i dempersystemet
Kombinasjonen av demper og en fjær i dempersystemet har bruddfrekvens
som er definert iht. følgende formel:
| (2.9) |
Her betyr:
- kss= stivhet i fjæren til dempersystemet
- c= demperkonstant
- fb= bruddfrekvens
Ved frekvenser lavere enn bruddfrekvensen vil systemet opptre hovedsakelig
som demper. Ved frekvenser høyere enn fb vil systemet virke som en fjær. Et
passende valg av bruddfrekvens vil gi akseptabel demping ved naturlig
frekvens. Dermed vil overføring av vibrasjoner ved høyere frekvenser bli
redusert.
En verdi av kss = 10 k vil medføre et meget stivt system. Ved lavere verdier av kss blir systemet mykere. Dette medfører at overføring av energi til massen m ved høyere frekvenser minsker betraktelig. Imidlertid vil forholdet føre til en viss økning i overføring av energi ved resonansfrekvens. Det vises til figur 2.12. Y-aksen illustrerer akselerasjonen uttrykt ÿ/ω0 og x-aksen frekvensområdet uttrykt ved ω.
Det kan vises matematisk at for et system med én frihetsgrad vil den optimale
oppførselen til massen skje ved et nivå i dempingen på 20 % og en stivhet i
dempersystemet kss som er 2 ganger større enn fjærstivheten k.
Figur 2.12 Effekt av fjæropplegg i dempersystemet.
3.3 Effekten av primærfjær i systemet
Dersom det innføres en primærfjær, dannes et system med 2 masser. Dette systemet har 2 frihetsgrader og dermed 2 egenfrekvenser (naturlige frekvenser). Egenfrekvensene vil være avhengige av stivhetene til de 2 elastiske fjærene. Det vises til figur 2.13.
Figur 2.13 System med 2 masser og innebygget primærfjær og sekundærfjær
Den dynamiske bevegelse til et slikt system som beveger seg på et idealisert spor, er vist i figur 2.14.
Betydningen av 2 separate resonansfrekvenser kan observeres. Massen av boggien er mye mindre enn massen av. Samtidig er den primære fjæren mye stivere. Dette medfører at den naturlige frekvensen til sekundærfjæren blir høyere (7 Hz).
Primærfjæren filtrerer bort mye av de høyfrekvente bevegelsene som oppstår på grunn av ujevnheter i sporet. Jo mykere primærfjæren er, jo større blir effekten av filtreringen.
Figur 2.14 Dynamisk oppførsel til system med 2 masser
Det må imidlertid bemerkes at kontakten hjul - skinne i tillegg introduserer høyere frekvenser som må isoleres (beskrevet ved Hertzian-fjæren).
3.4 Toakslede vogner
En lang masse har normalt opplegg mot sporet i 2 punkter. En to-akslet vogn er et slikt eksempel. Vognen har de 2 frihetsgradene hopping og vipping (galoppering). Generelt vil disse frihetsgradene opptre i forskjellige frekvenser og ha forskjellige nivåer mht. demping. I tillegg vil de geometriske egenskapene til vognen filtrere effekter av påvirkninger fra uregelmessigheter i sporet. Ved bestemte bølgelengder i sporet vil hoppingen av vognen skje med full amplitude iht. sporets uregelmessigheter. Ved andre bølgelengder vil den vertikale amplitude i forbindelse med hoppingen bli mindre.
Vippingen av vognen vil ved bestemte bølgelengder kunne skje med full amplitude.
Det vises til figurene 2.15 og 2.16.
Figur 2.15 To-akslet vogn som utsettes for hopping.
Figur 2.16 To-akslet vogn som utsettes for vipping(galoppering)
Det forutsettes en lengde mellom akslene til vognen lik L. Den maksimale hoppingen til vognen inntreffer ved definerte bølgelengder i sporet. Likeledes vil det ved andre bølgelengder i sporet ikke være hopping i det hele tatt. Dette er vist i tabellen under. Det samme gjelder for vipping. For den illustrerte vognen vil det være 2 tilfeller av vibrasjonsmuligheter med forskjellige egenfrekvenser og nivåer på demping som oppstår på grunn av ulike bølgelengder.
Bølgelengdene som forårsaker hoppingen og vippingen, er bare avhengige av avstanden mellom punktene for uregelmessighetene i sporet. Frekvensene for når vibrasjonene opptrer, vil derfor være avhengig av hastigheten. Siden hvert tilfelle har en spesifisert egenfrekvens, vil hoppingen av vognen (massen) bli utøvet ved en bestemt hastighet. Ved andre hastigheter vil avstanden mellom uregelmessighetene i sporet kunne forårsake en filtrerende effekt ved sammenligning med et system med ekvivalent enhetsmasse.
Tabell 2.1 Hopping og vipping ved ulike bølgelengder
| Bølgelengde | Hopping av vogn | Vipping av vogn |
|---|---|---|
| Uendelig | Maksimum | Null |
| 2 L | Null | Maksimum |
| L | Maksimum | Null |
| 2L/3 | Null | Maksimum |
| L/2 | Maksimum | Null |
| 2L/5 | Null | Maksimum |
Effekten av den geometriske filtreringen er meget kompleks, selv for idealisert
spor. Dette er illustrert i diagram 2.17. Diagrammene illustrerer
vertikalbevegelser og galoppering(vipping) for en to-akslet vogn med avstand
mellom akslene på 9 m.
Figur 2.17 Dynamisk opptreden av en typisk to-akslet vogn mht. vertikalbevegelse og galoppering.
Virkelige opptredende sporfeil kan forårsake mer komplekse bevegelser. Bevegelsene til to-akslede vogner kan forverres betydelig ved bestemte hastigheter dersom en bølgelengdeved maksimal hendelse mht. hopping eller vipping sammenfaller med en bølgelengde hvor uregelmessighetene i sporet er særdeles store.
Det faktum at både hopping og vipping opptrer i en vognkasse, medfører for passasjeren at akselerasjonen varierer langs vognkassen. En passasjer som sitter midt i vognen, vil bare føle hoppingen. En annen passasjer i endene av vognen vil i tillegg føle vertikal bevegelse fra vippingen. På grunn av dette vil sannsynligvis komforten oppfattes å være betydelig bedre midt i vognen enn i vognende. Dette er anskueliggjort i diagram 2.18.
Figur 2.18 Akselerasjoner i vognkassemidt på og i ende.
Et annet forhold er at vognen blir utsatt for momentbøyning. Amplituden av
bøyebevegelsen er naturligvis størst i vognmidt. Bøyningen kan føre til
opplevelser av vibrasjoner for passasjeren.
3.5 Effekten av boggier
En boggi vil utøve tilsvarende løpeegenskaper ved framføring som en toakslet vogn. Hopping og vipping vil også for en boggi være avhengig av bølgelengder for ujevnheter i sporet samt avstand mellom hjulsatsene til boggiene. Imidlertid vil normalt vogner med boggier være betydelig lenger enn to-akslede vogner.
Et annet viktig aspekt er at selve boggien vil utøve et geometrisk tilleggsfilter for å ta opp uregelmessigheter i sporet. Bølgelengder som påvirker hoppingen av en boggi, vil normalt ikke bli overført til vognkassegjennom sekundærfjæringen. Det vises til figur 2.19
Figur 2.19 Vogn med 2 boggier
Boggiene introduserer flere frihetsgrader enn de som påvirker hopping og vipping. Dermed oppstår flere resonansfrekvenser i systemet. Vipping av boggien ved resonansfrekvensene vil bare ha liten innflytelse på bevegelsen av selve vognkassen. Derimot vil hoppingen av boggien i frekvensområdene for resonans ha stor virkning på bevegelsen i vognkassen.
Løpeegenskapene til en vogn med boggier som framføres på et idealisert spor, er vist i figur 2.20. Som eksempel er avstanden mellom boggiene blitt holdt den samme som for en to-akslet vogn med akselavstand lik 9,0 m. I tillegg er avstanden mellom akslene i boggien lik 2,0 m. Det framkommer at bevegelsen til vognen med boggier er sammenfallende med bevegelsene til den to-akslede vognen. Det er imidlertid et fall i aktiviteten ved en frekvens på 7,5 Hz som tilsvarer en bølgelengde på 4,0 m ved hastighet lik 30 m/s. Dette er et resultat av den geometriske filtreringen av boggien. Togframføring mht. komfort blir bl.a. betydelig forbedret.
Figur 2.20 Akselerasjonsegenskaper for vognkasse med boggier
I denne diskusjonen er så langt effekten av kontakten hjul/skinne ikke berørt. Kontakten mellom hjul og skinne influerer særlig på den vertikale bevegelse. Lateral bevegelse oppstår i prinsippet av samme grunn. Men i tillegg vil det for den vertikale bevegelse genereres kinematiske bevegelser på grunn av vibrasjoner i boggiene. Frekvensen i disse vibrasjonene samt dempingen vil være avhengig av hastigheten. Noen av bevegelsene vil bli overført til vognkassen, andre ikke.
Det er allerede påpekt at høy demping oppleve s som vibrerende ved høyfrekvente bevegelser eller forstyrrelser. En viktig oppgave er derfor å optimalisere dempingen.
Én mulighet er å gjennomføre fjæring i 2 trinn, slik at fjæringen i det første trinnet virker på den mellomliggende masse (f.eks. boggier). Det andre trinnet i fjæringen skal virke på den massen (dvs. vognkasse) som isoleres fra underlagets ujevnheter (sporet). Det er nettopp dette som skjer ved et rullende materiell som er utstyrt med primær- og sekundærfjæring med mellomliggende boggimasse. Massen i boggien virker som et filter for høyfrekvente forstyrrelser.
3.6 Matematiske vibrasjonsmodeller
I den klassiske fysikken eller mekanikken blir det beskrevet matematiske modeller for bevegelser av legemer som vibrerer eller som blir utsatt for forstyrrelser på grunn av ujevnheter i underlaget. Modellene tar gjerne utgangspunkt i bevegelsesforløp som funksjon av tiden.
Et enkelt ekvivalent system for beskrivelse av vibrasjoner består av en konsentrert masse med et fjærsystem. Denne massen blir utsatt for en framføringskraft og samtidig en retarderende kraft som forårsakes av demperelementet. Et slikt system er vist i figur 2.21. Massen m kan tenkes plassert i en generell posisjon som er forskjøvet i en avstand x fra nøytralstillingen. Kraften i fjæren med stivhet k er i denne stillingen (nøytralstillingen) lik 0. Det forutsettes at fjæren er tilknyttet et ubevegelig og udeformerbart fundament. Massen beveger seg iht. en kraft F = f(t) som altså blir uttrykt som en funksjon av tiden. Men samtidig blir bevegelsen til massen retardert i demperelementet ved en kraft som vil være proporsjonal med hastigheten. Denne type av såkalt friksjonsretardasjon blir betegnet som viskosiøs demping. Denne viskosiøse dempingen kan framstilles på flere måter.
Figur 2.21 Bevegelse av masse m i en avstand x fra nøytral posisjon.
I figur 2.21betyr:
- m = masse til legemet (kg)
- F = kraft som massen m blir utsatt for (kN)
- kx = retarderende kraft (kN)
- k = fjærstivhet(kN/mm)
- x = tilbakelagt vei fra nøytralstilling til fjæren (mm)
- c = den viskosiøse demperkonstant(N/m/s)
- x = hastighet(m/s)
Newton’ s 2. lov lyder:
| (2.10) |
Ved anvendelse av denne lov kan bevegelsen i x-retningen beskrives:
| (2.11) |
Denne likningen kan omformes til:
| (2.12) |
Et system som ligner på det foregående, er vist i figur 2.22. Det forutsettes at fjæren er forbundet med et underlag eller et fundament som har fått en forskyvning som funksjon av tiden lik δ = δ (t). Denne forskyvningen kan enten ha framkommet ved bevegelse av fundamentet eller ved deformasjon. Dersom x er den absolutte forskyvning av massen m målt fra nøytral posisjon ved δ = 0, vil fjæren få en spenning:
| (2.13) |
For øvrig er betegnelsene de samme som i foregående figur.
Figur 2.22 Bevegelse av masse m i en avstand x fra nøytral posisjon når
opplageret til fjæren får en forskyvning.
Dersom hastigheten til deformasjonen av underlaget neglisjeres, blir formelen:
| (2.14) |
Denne kan omskrives til:
| (2.15) |
Vi ser at kraften F i figur 2.15 er erstattet av uttrykket kδ , dvs. produktet av
fjærstivhet og bevegelse av fjæren på grunn av forskyvning av fundamentet.
Likningene
| (2.16) |
og
| (2.17) |
er lineære differensiallikninger av 2. grad og blir benyttet til å beskrive
bevegelsene til mange systemer, bl.a. også i jernbaneteknikk i forbindelse
med framføring av rullende materiell.
Differensiallikningene lar seg løse ved standardprosedyrer. Noen eksempler
relatert til jernbaneteknikk vises i det etterfølgende.
3.7 Grunnleggende prinsipper
Som kjent framføres det rullende materiell på et spor med diverse
komponenter. Sporet utgjør et byggverk som lar seg opprette mer eller mindre
jevnt, men sporfeil i vertikal retning vil alltid være tilstede. Komforten ville
naturligvis bli meget god i et feilfritt spor. Men en idealisert jevnhet er ikke
mulig å oppnå uten at kostnadene blir enormt store.
Nettopp av kostnadsgrunner både ved nybygging og ved vedlikeholdsarbeider vil sporet alltid bli overlevert med sporfeil innenfor definerte toleransegrenser. Dette medfører at det er det skinnegående materiell som må bli utformet på en slik måte at virkningen av uregelmessighetene i sporet blir redusert mht. komfort. Dette skal imidlertid ikke oppfattes dit hen at et spor kan ferdigstilles med sporfeil. Det skal innenfor akseptable kostnader søkes å bygge et spor så feilfritt som mulig og sporet skal ved overtagelse i alle fall være i samsvar med definerte toleransegrenser.
Uregelmessigheter og ujevnheter under eller på rullende hjul vil føre til støtbevegelser som merkes. Av den grunn er vognmateriellet fjæret. Materiell for frakt av passasjerer har alltid to fjærer i seriekopling. Dette betyr at de har en primærfjær for boggirammen og en sekundærfjær for selve vognkassen.
Selv med fjærer i seriekopling vil vognkassen bli utsatt for bevegelser og akselerasjoner ved ujevnheter i sporet. Det skal beskrives hvordan ujevnheter i sporet kan skape akselerasjoner i vognkassen.
Fjærer medfører at en masse m tilbakelegger en bestemt veg. Denne bevegelsen vil resultere i en kraft. Fjærstivhet er definert som forholdet mellom kraft og veg. Jo mykere fjæren er, jo mindre blir fjærkraften ved bevegelse over samme veg. Dersom en masse m med hjul ruller over en vertikal ujevnhet med høyde h, kan kraften under forutsetning av gitt fjærstivhet beregnes:
| (2.18) |
h er ujevnhet i høyde
c er fjærstivhet til et legeme
m er legemets masse
Newtons lover sier at aksjon er lik reaksjon. Dette medfører at fjærkraften F virker i motsatt retning på hjulet og massen i samsvar med følgende uttrykk:
| (2.19) |
Figur 2.23 Kjøretøy som masse-fjærsystem hvor fjærkrefter og
forskyvninger opptrer ved passering av en enkel ujevnhet.
Figur 2.23 viser at fjæren vil overføre ujevnhetene ved hjulet til massen m1 over fjærkraften F1 i bevegelser med en akselerasjon ¨z1:
| (2.20) |
Derav kan utledes:
| (2.21) |
Uttrykket c1/m1 er proporsjonalitetsfaktoren og i denne inngår både
fjærstivheten og massen.
I en seriekobling av fjærer gjentar den samme effekten seg for sekundærtrinnet. Den vertikale bevegelse z1 til den mellomliggende masse m1 forårsaker sammen med sekundærfjæren med stivhet c2 en akselerasjon ¨z2 til massen m2 som beregnes til:
| (2.22) |
Igjen er c2/m2 en proporsjonalitetsfaktor og i denne inngår både fjærstivheten
og massen.
Det er naturligvis om å gjøre å konstruere vognen på en slik måte at
akselerasjonene ¨z1
og ¨z2 blir så lave som mulig ved passering av en ujevnhet
med høyde h. De to proporsjonalitetsfaktorene c1/m1
og c2/m2 har en
avgjørende betydning.
Likningene ovenfor kan omskrives:
| (2.23) |
Samme relasjoner gjelder naturligvis også for masse m2.
Forholdet fjærstivhet/masse indikerer hvilken akselerasjon i m/s 2 som den avfjærede masse vil få med en gang (i første øyeblikk) når fotpunktet til fjæren blir løftet plutselig 1 mm. Denne kvotienten (generelt c/m) virker som overføringsfunksjon for intensiteten eller forsterkningen i akselerasjonen ¨z/h (generelt).
Neste steg er å undersøke hvordan akselerasjonen fører til svingninger. Med en sammentrekkende bevegelse til fjæren ved ujevnheten h blir den potensielle energi til fjæren ved fjærkraft F og fjærveg h:
| (2.24) |
I uttrykket for fjærkraften inngår akselerasjonen ¨z. Denne er igjen avhengig av hastigheten z til massen m. Den potensielle energi som er lagret i fjæren, går over til kinetisk energi på grunn av bevegelsen til massen:
| (2.25) |
Den bevegelige massen gjør at fjæren strekker seg ut. Denne massen avgir energi til fjæren helt til fjæren ikke strekker seg mer ut. Deretter starter en pendling av energien i motsatt retning. Dermed oppstår de karakteristiske svingningene til massen. Slike svingninger er dynamiske hendelser med regelmessige bevegelser mellom bestemte grenser og periodisk veksel mht. energiformen. Den frie udempede svingning vil teoretisk aldri opphøre. Og det vil gjelde:
| (2.26) |
Det må gjelde:
| (2.27) |
| (2.28) |
Det kan utledes:
| (2.29) |
Forholdet z (prikk)/h angir den hastighet som massen m får når fotpunktet til fjæren blir løftet en høyde h på grunn av den vertikale ujevnhet i sporet. Denne hastigheten er avhengig av størrelsen [math] \sqrt { c/m } [/math] som igjen er avhengig av den spesifikke fjærstivheten c/m. Uttrykket [math] \sqrt { c/m } [/math] kan bli betraktet som overføringsfaktor til den hastigheten som svingningene får.
I moderne skinnegående materiell ligger de spesifikke fjærstivhetene evt. overføringsfaktorene eller intensiteten i akselerasjonene i størrelsesorden:
| (2.30) |
| (2.31) |
Det framgår at intensiteten eller forsterkningen i akselerasjonene i de 2 fjærstegene atskiller seg med mer enn 102. Primærfjæren pådrar seg relativt store akselerasjoner ved små ujevnheter. Sekundærfjæren bevirker på massen m2små akselerasjoner som er ønskelig mht. komfort. En forutsetning for dette er bevegelse eller løfting av begge fotpunktene samtidig.
For svingningshastighetene gjelder:
| (2.32) |
| (2.33) |
Ved en samtidig løfting av fotpunktene til begge fjærene ved passering av ujevnheten med høyde h får primærfjæren en svingningshastighet som er ca. 15 ganger høyere enn svingningshastigheten til sekundærfjæren. Til nå er det foretatt betraktninger mht. til passering av en hindring i sporet av kvasistatisk natur. For å komme over hindringen må hjulet bli løftet og fjæren blir trykt sammen. Det oppstår dermed en kraft i selve fjæren uttrykt ved fjærstivheten og fjærvegen. Ved passering av hindringen vil hjulet bli senket og kraften samt energien i fjæren forsvinner. Den tiden som hjulet bruker på nedsenkingen, har avgjørende betydning for de dynamiske bevegelser. Jo tidligere en nedsenking av hjulet følger etter et løft på grunn av hindringen, jo mindre blir bevegelsen av selve massen som framføres og dermed også svingningen.
Dette gjelder så lenge som at fjæren ikke har overført en vesentlig del av energien (i fjæren) til massen som er i bevegelse. Dersom fjæren ved nedsenkingen etter passering av hindringen ikke rekker å bli avfjæret, vil fjæren fra nedre stilling bli trukket opp igjen og ny energi vil bli lagret og overført til massen. Energien vil akselerere massen og forårsake videre svingninger.
Den svingningsdyktige kombinasjonen av fjær og masse og tidsintervallet mht. serie av ujevnheter står i et definert forhold til hverandre. Så lenge ujevnhetene i sporet opptrer i en serie med større avstand enn det som tilsvarer den beregningsmessige varigheten av svingningene, vil svingningsbevegelsene holde seg på lavt nivå. Varigheten av svingningene beregnes ut fra den opptredende svingningshastighet. Opptrer ujevnhetene i sporet i en serie med en avstand som tilnærmet er lik varigheten i svingningene, vil dette medføre kraftige bevegelser mht. svingninger. Blir disse parametrene like, vil svingningene fortsette uten stans og det blir resonans.
Svingninger og virkningene av disse kan påvirkes på forskjellig vis. Uten særlige tiltak blir i et udempet fjærmasse system den tilførte energien lagret av fjæren og overført som bevegelsesenergi til massen.
Den mest virksomme metoden mht. å utøve innflytelse på energiopptaket i forbindelse med svingningene er å redusere ujevnhetene på skinnene i sporet. Ujevnheten med en høyde h inngår kvadratisk (i 2. potens) i energiopptaket. En feilfri kjørevei uten ujevnheter er derfor den mest effektive form for å eliminere svingninger i massen og å skape best mulig komfort. Dessverre blir gjennomføringen av et slikt tiltak svært dyrt.
Lave akselerasjoner til massen m iht. likningene
| (2.34) |
og
| (2.35) |
kan realiseres med lave verdier av c/m. Myke fjærer med liten fjærstivhet reduserer energiopptaket i forbindelse med passering av ujevnheter i sporet. Svingningshastigheten og framfor alt svingningsakselerasjonen til massen m blir ved et slikt tiltak redusert.
Effekten av et system med 2 svingningsmasser blir tydeliggjort. Mellommassen m1etter primærtrinnet gjør det vanskelig å bygge opp akselerasjonene, svingningshastighetene og svingbreddene. Mellommassen skjermer det etterfølgende sekundærtrinnet mot forstyrrelser. Denne massen sammen med myke primærfjærer fungerer derfor som en sperre for opptak av bevegelsesenergi. Redusering av energi med dempere og spesielt hydrauliske svingningsdempere med dempekraft som er proporsjonalt med hastigheten, er benyttede metoder for kontroll av svingningene.
Formålet med fjærene er å redusere akselerasjonen til massen ved samtidig opptak av energi når hindringer skal passeres. Dempere skal fjærne energiopptaket ved en uønsket kraft som opptrer i denne forbindelse. Disse forhold må kombineres på en slik måte at fordelene blir framhevet og ulempene fjernet.
Trykkreftene i dempere forsterker oppbyggingen av akselerasjonen til massen, mens strekkreftene reduserer akselerasjonen. Omvendt vil det være ved nedbyggingen av akselerasjonen etter passering av hindringen. Bevegelsene blir forstørret ved strekkreftene og redusert ved trykkreftene.
Det er tilstrekkelig å gjøre trykk- og strekkegenskapene til demperen avhengig av den opptredende fjærkraft i den hensikt å forbedre komforten. Akselerasjonen til massen ved oppbyggingen i forbindelse med passeringen av hindringen forsvinner når summen av fjærkraft og dempekraft blir lik null:
| (2.36) |
Den optimale svingningskomfort blir oppnådd når:
| (2.37) |
dvs. når:
| (2.38) |
Hydrauliske dempere framskaffer dempekrefter S som vil være proporsjonal
med dempehastigheten:
| (2.39) |
Dette gir:
| (2.40) |
Hastigheten i forbindelse med dempingen er på grunn av bevegelsene ikke
mulig å påvirke. Dempekraften S kan derimot tilpasses forholdene gjennom k.
Denne dempeverdien k må fortløpende innstilles i takt med de varierende
forholdene:
| (2.41) |
Tekniske forhold begrenser imidlertid verdien av k og den tillatte dempekraft
S:
| (2.42) |
| (2.43) |
Dette betyr at den fjærkraftorienterte styringen av dempekraften stemmer overens med den størst mulige redusering av energien ved minimumsverdien for akselerasjonen i forbindelse med oppbyggingen og dermed den best mulige komforten mht. svingningsforløpet.
3.7 Enkel vibrasjonsmodell relatert til rullende materiell på spor
De teoretiske grunnmodellene som ble beskrevet i avsnittet foran, skal benyttes til å beskrive vibrasjoner i det rullende materiell. I stedet for en idealisert horisontal bevegelse skal det studeres den vertikale bevegelse til en vognmasse som består av fjærer og demper. Vognmassen beveger seg på sporet med ujevnheter i vertikalretning og har en frihetsgrad. Det vises til figur 2.24.
Figur 2.24 Et dynamisk system med en frihetsgrad som utsettes for
vibrasjoneri vertikalretning
De idealiserte modellene i foregående avsnitt ble utsatt for en horisontal
bevegelse. I tilfellet hvor underlaget eller fundamentet til fjæren fikk en
forskyvning eller deformasjon, ble hastigheten av deformasjonen ikke tatt med
i betraktningen. Dette fordi egenvekten til massen (vertikallast) ikke hadde
innflytelse på fundamentets bevegelse.
I vertikalretningen har massen innflytelse på deformasjonen til underlaget eller undergrunnen. Følgelig må hastigheten av deformasjonen til underlaget tas med i modellen. Følgende betegnelser inngår:
- y = forskyvning til massen (mm)
- x = underlagets forskyvning (mm)
- c = demperkonstantfor viskosiøs lineær demper(N/m/s) = (Ns/m)
- k = fjærstivhet(N/mm)
- m = massen
- x = hastighettil demperelementet på grunn av underlagets forskyvning
- y = hastigheten til forskyvningen av massen
- ÿ = massens akselerasjon
Iht. Newtons 2. lov kan følgende formel utledes:
| (2.44) |
Denne formelen kan skrives om på følgende måte:
| (2.45) |
Formelen er en differensiallikning av 2. grad og derfor matematisk komplisert å behandle. Det er utviklet matematiske metoder (Pierre Simon de Laplace) hvor en spesiell type integralfunksjon kan transformere en funksjon til en annen funksjon iht. formel:
| (2.46) |
Laplace-transformasjonen har anvendelser innen teorien for lineære
differensiallikninger med konstante koeffisienter. Transformasjonen er ren
matematisk teknikk for å kunne omgjøre en komplisert funksjon til en enklere
funksjon.
En Laplace-transformasjon av likning i (2.45) gir:
| (2.47) |
Som tidligere nevnt defineres følgende:
| (2.48) |
og
| (2.49) |
Dette kan også uttrykkes som:
| (2.50) |
Iht. ovenstående gir:
| (2.51) |
ω0 kan identifiseres som systemets resonansfrekvens eller egenfrekvens ved demping ζ = 0.