Mekanisk systembeskrivelse av kontaktledningsanlegg
Innhold
- 1 Mekanisk systembeskrivelse
- 1.1 Kontaktledning
- 1.2 Utliggere
- 1.3 Master, fundamenter og åk
- 1.4 Dimensjonering av master, fundamenter og åk.
- 1.5 Returkrets
- 1.6 Ledningsføring
- 1.7 Beskyttelsesjording
- 1.8 ISOLATORER
1 Mekanisk systembeskrivelse
1.1 Kontaktledning
Generelt
Kontaktledningen har to oppgaver
1. Å overføre elektrisk energi fra matestasjoner og frem til toget.
2. Å overføre elektrisk energi fra ledningen og til toget (strømavtaking).
Oppgave 1 er en ren elektrisk oppgave og er enkel å løse og er omtalt i "Elektrisk systembeskrivelse”.
Oppgave 2 er en mekanisk/dynamisk oppgave. Dynamiske krav til strømavtaker og kontaktledning er nærmere omtalt i ”Dynamisk systembeskrivelse”.
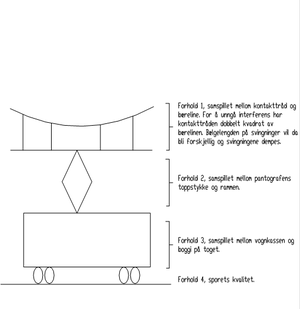
Det er flere elementer som påvirker strømavtakingen:
1. Kontaktledningens kvalitet (forhold 1).
2. Sporets kvalitet (forhold 4).
3. Vind.
4. Kontaktkraft.
5. Hastighet og hvordan vognkassen oppfører seg (forhold 3).
6. Profil (tvangspunkter som tunneler osv).
7. Hvordan toppstykket er lagret opp i forhold til rammen og trykket som toppstykket utøver på kontaktråden (forhold 2).
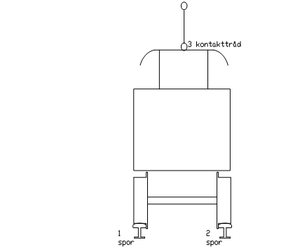
Det er flere faggrupper enn kontaktledning som har innvirkning på strømavtakingen. Det er viktig at det vises tverrfaglig forståelse for dette. Toget berører infrastrukturen på tre punkter. Alle punktene er viktige for at vi skal få en god strømavtaking:
1. Sporstreng 1.
2. Sporstreng 2.
3. Kontakttråd.
Se figur 2.
Systemer
Teknisk regelverk kontaktledning [1] fastsetter rutiner for utvelgelse av kontaktledningssystemer. Kriteriene for systemvalg ligger i hastighetsprofilet, strømavtakerkonfigurasjon for togene, togtetthet og sporklasse. To kontaktledninger som går parallelt i vekslingsfelt eller seksjonsfelt må ikke være mer enn en klasse fra hverandre. Eksempel: System 35 og 25 kan ikke går parallelt , da må man bygge en ”bro” mellom dem med System 20.
Ved bygging av nytt kontaktledningsanlegg er det tre klasser å velge mellom:
| 1. | System 35, kan brukes på alle spor utenom:
|
| 2. | System 20 og 25 brukes på:
|
I tillegg til disse tre klassene med kontaktledningsanlegg finnes det flere eldre typer kontaktledningsanlegg ute på banestrekningene. Hastighetene for de eldre typene er vist i tabell .1 sammen med hastighetene for de nye klassene.
System 35 System 35 deles i to grupper, System 35 (med Y-line) og System 35 MS (uten Y-line). Systemet egner seg for hastighetsområder rundt 130 km/t for flere strømavtakere og er således ikke et alternativ til høyhastighet. Maksimal ledningslengde er 2 x 800 m. Strekkfordelingen er bæreline 7,1 kN, kontakttråd 7,1 kN.
System 20
System 20 er delt i tre systemløsninger, avhengig av byggemåte og kjørehastighet.
Standard A, er beregnet for kjørehastigheter opptil 200 km/t med en strømavtaker. Systemet er med Y-line og er beregnet for strekninger med kurveradius > 800 m. Maksimal ledningslengde er 2 x 750 m. Strekkfordelingen er bæreline 10 kN, kontakttråd 10 kN.
Standard B, er beregnet for kjørehastigheter opptil 160 km/t med en strømavtaker. Systemet er uten Y-line og kan kan brukes på strekninger med kurveradius < 800 m. Maksimal ledningslengde er 2 x 650 m. Strekkfordelingen er bæreline 10 kN ,kontakttråd 10 kN.
Standard C1, er beregnet for tunneler med hastighet opptil 200 km/t med en strømavtaker, det kan bygges både med og uten Y-line. Systemet har en systemhøyde på minimum 0,75 m og er beregnet for strekninger med kurveradius 5000 m. Strekkfordelingen er bæreline 13 kN, kontakttråd 13 kN.
Standard C2, er beregnet for tunneler med hastighet opptil 160 km/t med en strømavtaker, det bygges uten Y-line. Systemet har en systemhøyde på minimum 0,30 m. Strekkfordelingen er bæreline 13 kN, kontakttråd 13 kN.
System 25
System 25 er beregnet for kjørehastigheter opptil 250 km/t med en strømavtaker. Systemet er med Y-line og er beregnet for strekninger med kurveradius > 1200 m. Maksimal ledningslengde er 2 x 600 m. Strekkfordelingen er bæreline 15 kN, kontakttråd 15 kN.
Hastighet
| Kontaktlednings-systemer | Toghastighet i km/t for en pantograf eller der innbyrdes avstand mellom pantografene er a > 200 m. | Toghastighet i km/t for en pantograf eller der innbyrdes avstand mellom pantografene er 73 > a > 200 meter. |
| Tabell 3 til 79 | 80 | 80 |
| System 35 MS | 140 | 120 |
| System 35 | 150 | 130 |
| Dynamisk standardforbedret
m. piggisolator |
140 | 130 |
| Dynamisk standardforbedret
m. stavsolator |
150 | 130 |
| System 20, standard A og C1 | 200 | 160 |
| System 20, standard B og C2 | 160 | 130 |
| System 25 | 250 | 200 |
Ved valg av kontaktledningssystem er det viktig at anlegget fremstår som en systematisert helhet. Man kan ikke trappe mer enn en systemklasse av gangen. Anlegget skal ha en utforming og teknisk løsning slik at feil ikke oppstår.
1.1.1 Liner og tråd
Plassering
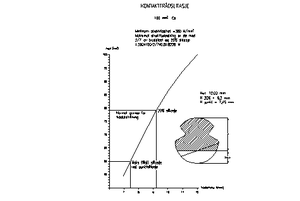
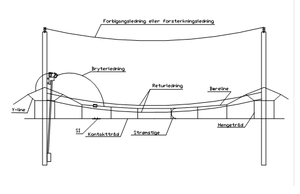
De fleste tråder og liner som brukes er vist på figuren under. Kontakttråd, bæreline, Y-line og hengetråd er deler av kontaktledningsanlegget og henges opp i utliggere eller tilsvarende festepunkter. Det er kontakttråden og strømavtakerens slepekull som er det dynamiske kontaktpunkt for overføring av energi fra ledning til forbruker. Det er disse to komponentene som er de mest utsatte med tanke på slitasje. Strømavtakeren blir regelmessig kontrollert av NSB. Krav til maksimum slitasje på kontakttråden er beskrevet i Teknisk regelverk.Figur 8 viser et eksempel på hvor mye en kontakttråd kan slites før den må byttes ut.
Strømstiger og Strømbruer, skal presses fast med godkjent pressutstyr. I parallell felt er viktig å passe på at de ikke blir montert i klemmefritt rom (se kap. 1.6.1 Ledningsføring over sporveksler.). Bryterledning, den skal ha presset kabelsko i begge ender. Forsterknings-, mate-, og forbigangsledning henges på kontaktledningsmastene eller monteres på spir på åk. Hvis det avspennes i mast må det alltid monters bardun i masten. Forsterknings-, mate-, forbigangskabel legges i kablekanal eller annen godkjent mekanisk beskyttelse. På svært fuktutsatte plasser skal man bruke en egen type. Returledning henges på kontaktledningsmastene eller monteres på spir på åk.
Mekanisk krav
Maksimal tillatt spenning i fastavspente ledninger (returledning, forbigangsledning og fjernledning) er oppgitt i tabellens siste kolonne. Tabellen er laget ut fra egenvekt og gitt ytre last på ledningen. Vindlasten vil som regel være dimensjonerende i forhold til snølast. Det er derfor sett bort fra snølasten ved utarbeidelse av tabellen.
Snø- og islast
Det regnes ikke snølast på vertikale ledninger.
| [math]q=\frac {(200 + 50\cdot d)}{100}[/math] | (1) |
der
- qs = snø- og islast pr. meter ledning [N/m].
- d = ledningen diameter [mm].
Vindlast
Når det regnes vindlast regnes ikke snølast da det er veldig liten sannsynlighet for at begge tilfellene oppstår samtidig. Vindlast beregnes på alle ledninger og tråder.
| [math]q_v=\frac {1}{2} \cdot \rho v^2 \cdot c_W \cdot d[/math] | (2) |
der
- qv = vindlast pr. meter ledning [N/m]
- [math]\rho[/math] = lufttetthet (p = 1,25 kg/m3).
- v = vindhastighet [m/s].
- cw = luftformfaktor (cw = 1,07).
- d = ledningens diameter [m].
Typer
Tabellene under viser noen data på liner og tråder for de systemene som benyttes ved bygging av nye anlegg..
| System 35 | Type | Egenvekt [N/m] | Diameter [mm] | Tverrsnitt [mm2] | Strekk [kN] | Maks tillatt spenning
[N/mm2] |
|---|---|---|---|---|---|---|
| Bæreline | Cu 50/7 | 4,46 | 9,0 | 49,48 | 7,06 | |
| Kontakttråd | Ri 100 Cu | 8,9 | 12,0 | 100 | 7,06 | |
| Fixline | Bz II 50/19 | 4,37 | 9,0 | 48,35 | 10 | |
| Forbigangs-ledning | Al 240/61 | 6,7 | 20,3 | 222,35 | 50 | |
| Retur-ledning | Al 240/61 m/isolasjon | 9,2 | 25 | 242,54 | 50 | |
| Fjern-ledning | SAHF 120 26/7 | 7,77 | 19,38 | 222,35 | 50 | |
| Y-line1) | Bz II 35/7 | 3,10 | 7,5 | 34,36 | ||
| Hengetråd | Bz II 10/49 | 0,89 | 4,5 | 9,6 |
- 1) Lengden på Y-linen = 14 m for kurveradius > = 800 m
| System 20A | Type | Egenvekt [N/m] | Diameter [mm] | Tverrsnitt [mm2] | Strekk [kN] | Maks tillatt spenning
[N/mm2] |
|---|---|---|---|---|---|---|
| Bæreline | Bz II 50/19 | 4,37 | 9,0 | 48,35 | 10 | |
| Kontakttråd | Ri 100 Cu | 8,9 | 12,0 | 100 | 10 | |
| Fixline | Bz II 50/19 | 4,37 | 9,0 | 48,35 | 10 | |
| Forbigangs-ledning | Al 240/61 | 6,7 | 20,3 | 222,35 | 50 | |
| Retur-ledning | Al 240/61 m/isolasjon | 9,2 | 25 | 242,54 | 50 | |
| Fjern-ledning | SAHF 120 26/7 | 7,77 | 19,38 | 222,35 | 50 | |
| Y-line1) | Bz II 25/7 | 2,20 | 6,3 | 24,36 | ||
| Hengetråd | Bz II 10/49 | 0,89 | 4,5 | 9,6 |
- 1) Lengden på Y-linen = 14 m for kurveradius > = 800 m
| System 20B | Type | Egenvekt [N/m] | Diameter [mm] | Tverrsnitt [mm2] | Strekk [kN] | Maks tillatt spenning
[N/mm2] |
|---|---|---|---|---|---|---|
| Bæreline | Bz II 50/19 | 4,37 | 9,0 | 48,35 | 10 | |
| Kontakttråd | Ri 100 Cu | 8,9 | 12,0 | 100 | 10 | |
| Fixline | Bz II 50/19 | 4,37 | 9,0 | 48,35 | 10 | |
| Forbigangs-ledning | Al 240/61 | 6,7 | 20,3 | 222,35 | 50 | |
| Retur-ledning | Al 240/61 m/isolasjon | 9,2 | 25 | 242,54 | 50 | |
| Fjern-ledning | SAHF 120 26/7 | 7,77 | 19,38 | 222,35 | 50 | |
| Hengetråd | Bz II 10/49 | 0,89 | 4,5 | 9,6 |
| System 25 | Type | Egenvekt [N/m] | Diameter [mm] | Tverrsnitt [mm2] | Strekk [kN] | Maks tillatt spenning
[N/mm2] |
|---|---|---|---|---|---|---|
| Bæreline | Bz II 70/19 | 5,96 | 10,5 | 65,81 | 15 | |
| Kontakttråd | Ri 120
RiS 120 CuAg |
10,7
10,7 |
13,2
13,2 |
120
120 |
15
15 |
|
| Fixline | Bz II 70/19 | 5,96 | 10,5 | 65,81 | 10 | |
| Forbigangs-ledning | Al 240/61 | 6,7 | 20,3 | 222,35 | 50 | |
| Retur-ledning | Al 240/61 m/isolasjon | 9,2 | 25 | 242,54 | 50 | |
| Fjern-ledning | SAHF 120 26/7 | 7,77 | 19,38 | 222,35 | 50 | |
| Y-line1) | Bz II 35/7 | 3,10 | 7,5 | 34,36 | ||
| Hengetråd | Bz II 10/49 | 0,89 | 4,5 | 9,6 |
- 1) Lengden på Y-linen = 18 m for kurveradius [math]\ge [/math] = 1200 m
- 2) Det regnes med 8 m hengetråd for et 60 m spenn.
1.1.2 Avspenning (seksjonering)
Avspenninger Normalt deler vi avspenningene inn tre grupper:
- Bevegelig avspenning
- Fast avspenning
- Fixavspenning
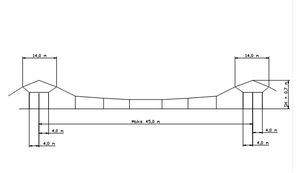
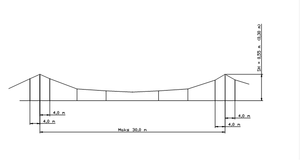
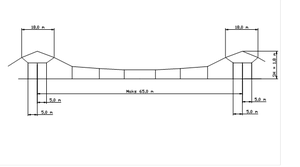
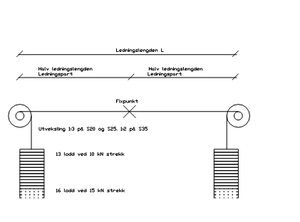
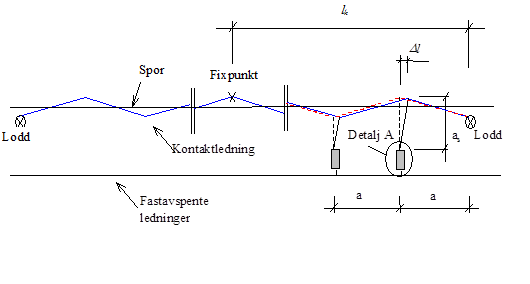
Normalt oppheng av en kontaktledning er som vist i skissen under. Det er en loddavspenning i hver ende og en fixavspenning på midten som vist på figur 10.
Loddavspenninger
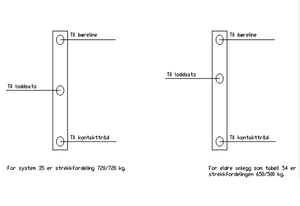
Loddavspenningens oppgave er å til en hver tid sørge for konstant strekk i kontaktråden og bærelinen. Utførelsen av loddavspenningen varierer fra system til system. For System 35 og eldre er det en loddsats for hver avspenning. Utvekslingen i loddhjulene er 1 til 2. I avspenningswiren er det satt opp en balansearm for å fordele strekket mellom bæreline og kontakttråd, fordelingen er vist på figur 11.
For System 20 og System 25 er det to loddsatser, en for bæreline og en for kontakttråden. Utvekslingen er 1 til 3. Loddsatser som er beregnet til System 20 og 25 har også en sperrehake som gjør at hvis en av ledningene ryker, detter ikke loddsatsen i bakken.
For mer inngående studier av hvordan disse fungerer kan man se på systemtegningene.
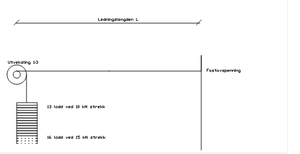
Fastavspenninger
På kortere ledninger hvor det ikke anvendes fixavspenning avspennes ledningen i et fastpunkt. Ved fastavspenninger føres ledningene inn i en mast på samme måte som ved loddavspenning, men her har man ikke lodd, loddhjul og balansearm.
Fixavspenninger
Fixavspenningen monteres ”midt” på ledningen.
For å beregne plasseringen av fixavspenningen skal formelen nedenfor anvendes. Plasseringen av fixpunktet velges og kraftlikevekten sjekkes. Kraftdifferansen skal ikke være større mellom ledningspartene enn +/- 10%.
| [math]\frac {1}{x}= \frac {9,5}{n+1} + \frac {33,3}{L_{1/2}} [/math] | (3) |
der
- n = antall bevegelige utliggere
- L1/2 = halv ledningslengde
- x = utnyttelsen av den halve ledningslengden
1.2 Utliggere
{ Kapittelet er ikke ferdigstilt }
1.3 Master, fundamenter og åk
{ Kapittelet er ikke ferdigstilt }
1.4 Dimensjonering av master, fundamenter og åk.
1.4.1 Sikkerhetsfilosofi
Ved innføring av NS3052 ”Beregning av belastninger” i 1970, ble begrepet lastkoeffisienter eller lastfaktorer innført i regelverket. NS3052 ble i 1979 erstattet av NS3479 ”Prosjektering av bygningskonstruksjoner, dimensjonerende laster”. Med innføringen av disse standardene, samt NS3472 Prosjektering av stålkonstruksjoner” i 1973, ble sikkerhetsfilosofien for statiske beregninger endret. NS3479 opererer med grensetilstander som bruddgrensetilstand og bruksgrensetilstand. Det ble innført ulike lastfaktorer og materialfaktorer avhengig av de ulike grensetilstandene. Karakteristiske laster blir multiplisert med sine respektive lastfaktorer, og resulterende spenninger blir kontrollert mot materialets dimensjonerende fasthet. Dimensjonerende fasthet er materialets flytegrense dividert med en materialfaktor.
Forgjengeren til NS3472 var NS424A. Denne standarden hadde en annen sikkerhetsfilosofi der opptredende spenninger ble benyttet i kapasitetskontrollen. Sikkerhetsfaktoren, S, var definert som forholdet mellom materialets strekkfasthet, [math]\sigma_B[/math], og tillatte spenninger, [math]\sigma_{till}[/math], i materialet.
| [math]S = \frac {\sigma_B}{\sigma_{till}} [/math] | (4) |
NS424A angir en sikkerhetsfaktor S=2,75 i konstruksjonsklasse 1 (NS424A tabell 1”), mens FEA-F [3] krever en sikkerhetsgrad S=2,50 for stål.
Forskrifter for elektriske anlegg, FEA-F, tar utgangspunkt i sikkerhetsfilosofien i NS424A. Her defineres sikkerhet i forhold til brudd i materialet. I Jernbaneverket sine beregninger for kontaktledningsanlegg brukes lastfaktorer og materialfaktorer slik det er definert i NS3472 og NS3479. For å sammenligne disse to sikkerhetsfilosofiene, beregnes en faktor, S, som kan kalles ”sikkerhet”. ”Sikkerhet” skal defineres i forhold til brudd i materialet (bruddgrensetilstanden). Derfor inneholder formel 5 lastfaktoren [math]\gamma_f[/math]. I NS3472 brukes uttrykket dimensjonerende materialfasthet, fd = fy/[math]\gamma_f[/math]. Betegnelsen fy er flytegrense og tilsvarer uttrykket [math]\sigma_f[/math] i NS424A. Betegnelsen fd tilsvarer uttrykket tillatte spenninger, [math]\sigma_{till}[/math], slik det er brukt i NS424A. NS424A pkt. 4.5.4 sier at forholdet mellom bruddspenning (strekkfasthet) og flytegrense er 1,75 ([math]\sigma_B = 1,75 \sigma_f[/math]). Da kan vi beregne en ”sikkerhet”, S, etter sikkerhetsfilosofien i NS3479 og NS3472 på følgende måte:
| [math]S = \frac {\sigma_B}{\sigma_{till}} \cdot \gamma_f = \frac {\sigma_B}{f_d} \cdot \gamma_f = \frac {\sigma_B}{f_y/\gamma_m} \cdot \gamma_f = \frac {\sigma_B}{\sigma_f/\gamma_m} \cdot \gamma_f = \frac {1,75 \cdot \sigma_f \cdot \gamma_m}{\sigma_f} \cdot \gamma_f = 1,75 \cdot \gamma_m \cdot \gamma_f [/math] | (5) |
| [math]\gamma_m[/math] = materialfaktor. | Denne faktoren kan for stål variere fra 1,0 til 1,15.
Ved beregning av ”sikkerheten” S brukes [math]\gamma_m[/math]=1,1 |
| [math]\gamma_f[/math]= lastfaktor. | For egenvekt, [math]\gamma_f[/math] = 1,2
For nyttelast, [math]\gamma_f[/math] = 1,6 |
Med disse verdiene innsatt i formel 5 får man:
| For egenvekt:
For nyttelast: |
[math]S=1,75 \cdot 1,1 \cdot 1,2 = 2,31[/math]
[math]S=1,75 \cdot 1,1 \cdot 1,6 = 3,08[/math] |
- Ved å anta at egenvekt utgjør 2/3 av totallasten får man en ”sikkerhetsfaktor” på
| [math]S=2,31 \cdot \frac {2}{3} + 3,08 \cdot {1}{3} = 2,57[/math] |
- Ved å anta at egenvekt utgjør ½ av totallasten får man en ”sikkerhetsfaktor” på
| [math]S=2,31 \cdot \frac {1}{2} + 3,08 \cdot {1}{2} = 2,70[/math] |
NS424A angir en sikkerhetsfaktor på 2,75 i konstruksjonsklasse 1 mens FEA-F krever en sikkerhetsgrad på 2,50, ( FEA-F bruker uttrykket sikkerhetsgrad). Beregningene ovenfor viser at man oppnår ”sikkerhetsfaktorer” tilsvarende verdiene i NS424A ved å bruke sikkerhetsfilosofien i NS3479 og NS3472.
1.4.2 Laster
Følgende laster virker på et kontaktledningsanlegg:
- Egenvekt
- Snø- og islast
- Vindlast
- Temperaturlast
- Differansestrekk
- Montasjelast
1.4.2.1 Egenvekt
Her medtas egenvekt fra alle komponenter i kontaktledningsanlegget, både ledninger,loddsats, master, åk, utliggere osv.
1.4.2.2 Snø- og islast
Verdien for snø- og islast er hentet fra FEA-F §73. De samme lastene er også benyttet i SIEMENS forskrifter for System 20.
Snø- og islast på ledninger:
| Snø- og islast ved 0°C: | [math]q=\frac {(900 + 225 \cdot d)}{100}[/math] | (6) |
| Snø- og islast ved -25°C: | [math]q=\frac {(200 + 50 \cdot d)}{100}[/math] | (7) |
der
- q = snø- og islast pr. meter ledning [N/m].
- d = ledningens diameter [mm]
FEA-F §73 gjelder høyspenningslinjer og er nødvendigvis ikke helt relevant for kontaktledningsanlegg med hyppige togpasseringer. Det er derfor valgt å bruke snø- og islasten for -25°C i beregningene. Dette er i samsvar med SIEMENS forskrifter for System 20.
Snø- og islast på andre komponenter På komponenter som utliggere, master, åk regnes snø- og islast lik 20 % av komponentens stålvekt. Trykk 504 pkt. 4.1.
1.4.2.3 Vindlast
| [math]q= \frac {1}{2} \rho v^2 \cdot c_w \cdot d [/math] | (8) |
der
- q = vindlast pr. meter på aktuell komponent (N/m)
- [math]\rho[/math] = lufttetthet ([math]\rho[/math] = 1,25 kg/m3)
- v = vindhastighet [m/s]
- cw = luftformfaktor:
Denne varierer fra komponent til komponenet. For ledninger regnes cw = 1,07. For gitterkonstruksjoner ligger verdien i området fra 2 til vel 3. Luftformfaktorene beregnes etter NS3479. Dette samsvarer godt med krav til vindtrykk i FEA-F §72.
- d = ledningens diameter [m] eller effektivt areal pr. m for gitterkonstruksjoner [m2/m].
1.4.2.4 Temperaturlast
Kontakttråd og bæreline er loddavspente ledninger og strekkraften påvirkes ikke av endringer i temperatur. Ledningene er frie til å bevege seg. Temperaturendringer fører derfor til at loddsatsen beveger seg opp og ned langs masten uten at kreftene i ledningen endres.
Fastavspente ledninger derimot påvirkes av temperaturendringer. Ved lave temperaturer kan strekkraften i disse ledningene bli svært stor. Se avsnittet om strekkraft i fastavspente ledninger.
1.4.2.5 Differansestrekk
Dette er krefter som virker parallelt med sporet dersom det er ulike spennlengder på hver side av en mast. I bruddgrensetilstand og bruksgrensetilstand er det særlig temperaturendringer som fører til differansestrekk. I en ulykkesgrensetilstand kan differansestrekk oppstå ved at ledninger slites av og masten blir utsett for strekk til en side.
Bane NOR har regler om at forskjell i spennvidde mellom to nabofelt endres for minimum hver sjette spennlengdene i ledningsparten med mellom 10 % og 15 % for å unngå galopperende ledning (resonans, gjelder for ledningsutformingene S20 og S25). I bruddgrensetilstand og bruksgrensetilstand neglisjeres derfor differansestrekket vanligvis. I ulykkesgrensetilstand (brudd i ledninger) må det imidlertid tas hensyn til at masten eller åket utsettes for strekk parallelt sporet.
1.4.2.6 Montasjelast
Dette er krefter som oppstår i systemet under montering. Snø- og islaster dekker vanligvis montasjelast slik at det ikke er nødvendig å regne med disse lastene.
1.4.3 Strekkraft i ledninger
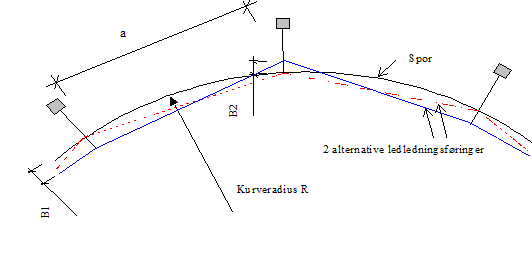
På grunn av ledningens sikksakk og kontaktledningsanleggets (sporets) kurvatur vil ledningens strekkraft gi en kraftkomponent normalt på sporet. Denne kraften blir overført til mast og fundament som moment og skjærkraft.
Formel 9 benyttes for å beregne kurvekraft/ sidekraft fra ledninger.
| [math]K=H \cdot (\frac {a}{R} \pm \cdot \frac {B2 - B1}{a})[/math] | (9) |
der
- K = kurvekraft/ sidekraft grunnet strekk i ledningen
- H = strekkraft i ledningen
- a = masteavstand
- B1 og B2 = ledningens sikksakk. På figuren er B1 og B2 positive for verdier på utsiden av sporet (kurven) og negative for verdier på innsiden av sporet.
Første leddet i formelen gir kraften fra en ledning som følger samme jevne kurvatur som sporet (stiplet linje). Andre ledd i formelen er et justeringsledd for ledningens sikksakk. Formel 9 representerer da alternativet med heltrekt ledningsføring slik det er vist på figur 13. På rettlinje representeres kurvekreftene kun av andre ledd i formelen.
1.4.3.1 Strekkraft i kontaktledning
Kontaktledningen er loddavspent og strekkraften varierer fra system til system.
| System 20A: | Bæreline 10 kN, | Kontakttråd 10 kN |
| System 20B: | Bæreline 10 kN, | Kontakttråd 10 kN |
| System 25: | Bæreline 15 kN, | Kontakttråd 15 kN |
| System 35: | Bæreline 7,1 kN, | Kontakttråd 7,1 kN |
1.4.3.2 Strekkraft i fastavspente ledninger
| Spennlengde | 30 m | 35 m | 40 m | 45 m | 50 m | 55 m | 60 m | 65 m | 70 m | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Temp. (oC) | f(m) | P(kg) | f(m) | P(kg) | f(m) | P(kg) | f(m) | P(kg) | f(m) | P(kg) | f(m) | P(kg) | f(m) | P(kg) | f(m) | P(kg) | f(m) | P(kg) |
| -40 | 0,09 | 1198 | 0,14 | 1041 | 0,21 | 879 | 0,33 | 731 | 0,48 | 615 | 0,66 | 534 | 0,88 | 481 | 1,12 | 444 | 1,38 | 418 |
| -35 | 0,10 | 1039 | 0,16 | 893 | 0,25 | 751 | 0,38 | 632 | 0,54 | 544 | 0,73 | 486 | 0,95 | 486 | 1,19 | 419 | 1,44 | 399 |
| -30 | 0,12 | 885 | 0,19 | 755 | 0,29 | 639 | 0,43 | 549 | 0,60 | 488 | 0,80 | 446 | 1,01 | 417 | 1,25 | 397 | 1,51 | 382 |
| -25 | 0,14 | 741 | 0,23 | 634 | 0,34 | 546 | 0,49 | 484 | 0,66 | 442 | 0,86 | 413 | 1,08 | 393 | 1,31 | 378 | 1,57 | 367 |
| -20 | 0,17 | 612 | 0,27 | 532 | 0,40 | 473 | 0,55 | 433 | 0,73 | 405 | 0,92 | 385 | 1,14 | 371 | 1,37 | 361 | 1,63 | 353 |
| -15 | 0,21 | 504 | 0,32 | 453 | 0,45 | 416 | 0,61 | 392 | 0,78 | 375 | 0,98 | 362 | 1,20 | 353 | 1,43 | 346 | 1,69 | 341 |
| -10 | 0,25 | 419 | 0,37 | 392 | 0,50 | 372 | 0,66 | 359 | 0,84 | 349 | 1,04 | 342 | 1,26 | 337 | 1,49 | 333 | 1,75 | 330 |
| -5 | 0,30 | 356 | 0,42 | 345 | 0,56 | 338 | 0,72 | 332 | 0,90 | 328 | 1,09 | 325 | 1,31 | 323 | 1,55 | 321 | 1,80 | 319 |
| 0 | 0,34 | 310 | 0,46 | 310 | 0,61 | 310 | 0,77 | 310 | 0,95 | 310 | 1,15 | 310 | 1,36 | 310 | 1,60 | 310 | 1,86 | 310 |
| 5 | 0,38 | 275 | 0,51 | 282 | 0,65 | 287 | 0,82 | 291 | 1,00 | 294 | 1,20 | 297 | 1,42 | 299 | 1,65 | 300 | 1,91 | 301 |
| 10 | 0,42 | 249 | 0,55 | 260 | 0,70 | 269 | 0,86 | 275 | 1,05 | 281 | 1,25 | 285 | 1,47 | 288 | 1,71 | 291 | 1,96 | 293 |
| 15 | 0,46 | 228 | 0,59 | 242 | 0,74 | 253 | 0,91 | 262 | 1,09 | 269 | 1,30t | 274 | 1,52 | 279 | 176 | 283 | 2,01 | 286 |
| 20 | 0,50 | 212 | 0,63 | 227 | 0,78 | 240 | 0,95 | 250 | 1,14 | 258 | 1,34 | 265 | 1,56 | 270 | 1,80 | 275 | 2,06 | 279 |
| 25 | 0,53 | 198 | 0,67 | 215 | 0,82 | 228 | 0,99 | 239 | 1,18 | 248 | 1,39 | 256 | 1,61 | 263 | 1,85 | 268 | 2,11 | 273 |
| 30 | 0,57 | 187 | 0,71 | 204 | 0,86 | 218 | 1,04 | 230 | 1,22 | 240 | 1,43 | 248 | 1,66 | 255 | 1,90 | 261 | 2,16 | 267 |
| 35 | 0,60 | 177 | 0,74 | 194 | 0,90 | 209 | 1,07 | 221 | 1,27 | 232 | 1,47 | 241 | 1,70 | 249 | 1,94 | 255 | 2,21 | 261 |
| 40 | 0,63 | 168 | 0,77 | 186 | 0,94 | 201 | 1,11 | 214 | 1,31 | 225 | 1,52 | 234 | 1,74 | 242 | 1,99 | 250 | 2,25 | 256 |
Strekkraften i fastavspente ledninger (returledning, forbigangsledning, fjernledning) er avhengig av:
- Egenvekt av ledning
- Last (snø/is og vind) på ledning
- Temperatur
- Geometriske forhold som pilhøyde og masteavstand
Strekkraften i fastavspente ledninger kan beregnes. Dette er gjort for en ledning av type AHF 150 med isolasjon. Resultatet er vist i tabell .6. Strekktabellene vil være forskjellige for ulike ledningstyper (ulik vekt og ulike materialegenskaper), men tabell .6 er representativ for de fleste fastavspente ledninger som brukes i kontaktledningsanlegget. Dersom det ligger snø og is på ledningene vil strekkreftene bli større enn det som er vist i tabell 6.
- Utgangspunktet for tabell 6 er:
- Ledningen henger i en parabelform
- Ledningens strekkraft er 310 kg ved 0 oC
- Ledningen er 100 % innspent i begge ender.
Forutsetningen om at ledningen er 100 % innspent i begge ender er oftest ikke oppfylt. Både mast og åk er elastiske og vil få små deformasjoner ved pålasting. En mer realistisk modell vil være å modellere innfestingen med fjærer. Det er ikke gjort nærmere studier for å vurdere størrelsen av en slik fjærkonstant og heller ikke hvilken betydning en fjærinnspenning har på strekkraften i ledningen. Men ved å regne med full innspenning, regnes det konservativt. I praksis blir nok strekkraften i de fastavspente ledningene mindre enn det som vises i tabell 6.
Etter vurdering av pilhøyder velges som utgangspunkt for beregningene at ledningens strekkraft skal være 310 kg ved 0 oC. Sammenhengen mellom ledningens strekkraft og pilhøyde er gitt som:
| [math]P=\frac {q\cdot l^2}{8\cdot f}[/math] | 10 |
Det forutsettes at ledningen har en parabelform. Da kan ledningens buelengde finnes som:
| [math]s =l\cdot (1+ \frac {8}{3}\cdot (\frac {f}{l})^2)[/math] | 11 |
Så gis ledningen en temperaturendring. Buelengden (og pilhøyden) vil da endres. Det fører til at strekkraften i ledningen også endres. Den totale endring i buelengde blir da summen av et ledd grunnet temperaturendring, et ledd grunnet elastisk tøyning og et siste ledd f(k) som er lengdeendringens bidrag fra fjærinnspenning. Som forklart tidligere neglisjeres dette leddet i de videre beregningene.
| [math]\Delta s =\alpha \cdot \Delta t \cdot l + \frac {\Delta P \cdot l}{E\cdot A} + f(k)[/math] | 12 |
der f(k) = 0
Følgende betegnelser er brukt i formlene 10, 11 og 12:
| P | = strekkraft i ledningen. |
| q | = vertikallast (inkl. egenvekt) på ledningen. |
| l | = masteavstand |
| f | = pilhøyde |
| s | = ledningens buelengde |
| [math]\Delta s[/math] | = endring av buelengde pga. temperaturtøyning og elastisk tøyning. |
| [math]\Delta t[/math] | = temperaturendring |
| [math]\Delta P[/math] | = endring i ledningens strekkraft pga. endret buelengde. |
| E | = ledningens elastisitetsmodul. |
| A | = ledningens tverrsnittsareal. |
| [math]\alpha[/math] | = ledningens lengdeutvidelseskoeffisient. |
| f(k) | = strekkraft i ledningen. |
Verdiene i tabell 6 beregnes ved å iterere mellom formel 10, 11 og 12.
Strekktabell for fastavspent ledning type AHF 150 med isolasjon.
| Returledning, diameter | = 25 mm |
| Vekt | = 9,22 N/m = 0,94 kg/m |
| Lengdeutv. koeff. Al | = 2E-5 1/oC |
| E-modul | = 61000 N/mm2 |
| Tverrsnittsareal | = 238,8 mm2 |
Hvor store spenninger representerer disse strekkreftene og hvor store spenninger kan aksepteres? Tabellen viser at ved -40°C og en spennlengde på 30 m er strekkraften P=1.198 kg. Med et tverrsnittsareal på 238,8 mm2 blir spenningen 49,2 N/mm2. Produsenten Alcatel opplyser at elastisk grense (høyere spenninger kan føre til varig deformasjon av ledningen) for rene aluminiumsliner [math]\sigma_{0-0,1}[/math]=80 N/mm2. En spenning [math]\sigma[/math] = 50 N/mm2 tilsvarer en strekkraft på ca. 1.200 kg og er samtidig så lav at det ikke er noen fare for varig (plastisk) deformasjon av ledningen. Fra eldre tilsvarende strekktabeller (tabell 73) finner vi opplysninger om at maksimal tillatt spenning [math]\sigma[/math] 5,12 kp/mm2 som tilsvarer [math]\sigma[/math]= 50,2 N/mm2.
I de videre beregningene antas rene aluminiumsliner og det velges å bruke maksimal tillatt spenning [math]\sigma[/math] = 50 N/mm2 for alle fastavspente ledninger, både forbigangsledning, returledning og fjernledning. Ledningenes egenvekt er tilnærmet den samme, og det er naturlig å henge opp alle ledninger i samme felt med lik pilhøyde. Da blir opptredende spenninger tilnærmet like for alle ledningene. Som fjernledning brukes ofte aluminiumsliner med stålkjerne (type SHAF). Disse linene har en høyere elastisk grense, men måten linene henges opp på (pilhøyde, spennlengde, egenvekt) gjør at det kan regnes med maksimal tillatt spenning [math]\sigma[/math] = 50 N/mm2 også for disse.
1.4.3.3 Strekkraft i fixline
Fixline er også en fastavspent line der strekkraften er avhengig av temperatur. Beregninger av strekkraft i fixliner er utført og presentert i en tabell på tegning E-7195. Tabellen viser at strekkraften i fixline kan komme opp i 10 kN ved -40°C. I de videre beregningene brukes en strekkraft på 10 kN for fixliner (uavhengig av kontaktledningssystem).
1.4.4 Grensetilstander og lastfaktorer
Ved beregning av kontaktledningssystemer vurderes følgende 4 grensetilstander:
- Bruddgrensetilstand
- Bruksgrensetilstand for forskyvning av kontaktledning
- Bruksgrensetilstand for totale forskyvninger
- Ulykkesgrensetilstand
For alle laster unntatt snø/is og vind defineres en gunstig og en ugunstig lastvirkning. På den måten tas det hensyn til at lastenes størrelse kan variere innenfor et gitt område. Med gunstig lastvirkning får man frem en minimumslast og med ugunstig lastvirkning fås en maksimumslast. I enkelte tilfeller kan for eksempel en returledning bidra til å støtte opp en kontaktledningsmast. For å eliminere/redusere en slik ”støtteeffekt” regnes det i den aktuelle lastkombinasjonen, med minst mulig strekkraft i ledningen. Det gjøres beregningsmessig ved å velge lastfaktorer for gunstig lastvirkning.
1.4.4.1 Bruddgrensetilstand
Krefter fra bruddgrensetilstanden skal brukes for kapasitetskontroll av konstruksjonselementene. Lastfaktorer for denne grensetilstanden er i hovedsak hentet fra NS3479 ”Prosjektering av bygningskonstruksjoner, dimensjonerende laster”.
| Lastfaktor | |
| Egenvekt utligger og ledninger, gunstig: | 1,0 |
| Egenvekt utligger og ledninger, ugunstig: | 1,2 |
| Snø/is, vind | 1,6 |
| Strekk i loddavspente ledninger, inkl. egenvekt av loddsats, gunstig: | 0,9 |
| Strekk i loddavspente ledninger, inkl. egenvekt av loddsats, ugunstig: | 1,2 |
| Strekk i fastavspente ledninger, gunstig: | 0 |
| Strekk i fastavspente ledninger, ugunstig: | 1,2 |
| Strekk i fixledninger, gunstig: | 0 |
| Strekk i fixledninger, ugunstig: | 1,2 |
|
Strekk i fjernledning m/hengeisolator, gunstig: |
0 |
| Strekk i fjernledning m/hengeisolator, ugunstig: | 1,2 |
For fastavspente ledninger forutsettes det at ledningene skal kunne fjernes uten at det er behov for nye beregninger. Derfor velges lastfaktor = 0 for gunstig lastvirkning.
1.4.4.2 Bruksgrensetilstand for forskyvning av kontaktledning
Jernbaneverket setter krav til maksimal forskyvning av kontaktledningen. Kravet er todelt og er sammensatt av et bidrag fra fundamentets rotasjon og horisontalforskyvning og et bidrag fra mastens forskyvning. Krefter fra grensetilstanden ”bruksgrense for forskyvning av kontaktledning” skal brukes for å kontrollere dette kravet.
| Lastfaktor | |
| Egenvekt utligger og ledninger | 0 |
| Snø/is, vind | 1,0 |
| Strekk i loddavspente ledninger, inkl. egenvekt av loddsats: | 0 |
| Strekk i fastavspente ledninger, gunstig: | -0,25 |
| Strekk i fastavspente ledninger, ugunstig: | 0,7 |
| Strekk i fixledninger, gunstig: | -0,25 |
| Strekk i fixledninger, ugunstig: | 0,7 |
|
Strekk i fjernledning m/hengeisolator, gunstig: |
-0,25 |
| Strekk i fjernledning m/hengeisolator, ugunstig: | 0,7 |
Det defineres en «nulltilstand» etter at alle ledninger er hengt opp i masten og kontaktledningen er strammet og justert. Bare krefter som oppstår i systemet etter en slik «nulltilstand» bidrar til forskyvning av kontaktledningen. Derfor velges lastfaktor = 0 for egenvekt og for strekk i loddavspente ledninger. Snø/is- og vindlaster inngår med full effekt i denne grensetilstanden; derfor lastfaktor = 1,0.
Når det gjelder fastavspente ledninger, vil temperaturendringer påvirke strekkreften i ledningene. Det forutsettes i strekktabellene at fastavspente ledninger monteres med en strekkraft på ca. 300 kg ved 0 °C. Maksimalt opptredende strekkraft varierer iflg. strekktabellene fra ca. 400 kg opp til ca. 1200 kg avhenging av kurveradius og masteavstand. Strekkraften som brukes i beregningene, finnes som produktet av maksimalt tillatt spenning og ledningens tverrsnittsareal. For ledning type AL 240/61 blir det 50 N/mm2 x 242,54 mm2 [math]\approxeq[/math] 1200 kg. Ved temperaturstigning vil strekkraften i fastavspente ledninger avta. For gunstig lastvirkning regnes at stekkraften i fastavspente ledninger reduseres fra 300 kg til 0 kg. Det oppnås ved å velge lastfaktor –0,25 (300 + 1200 x (-0,25) = 0). For ugunstig lastvirkning regnes det at strekkraften i fastavspente ledninger øker fra 300 kg til 1140 kg (en økning på 840 kg). Det oppnås ved å velge lastfaktor 0,7 (1200 x 0,7 = 840).
1.4.4.3 Bruksgrensetilstand for totale forskyninger
Krefter fra grensetilstanden ”bruksgrensetilstand for totale forskyvninger” kan brukes for å beregne forskyvningene av kontaktledningen fra ubelastet system til maksimalt belastet system (i motsetning til ”bruksgrensetilstand for forskyvning av kontaktledning” hvor kreftene brukes for å regne forskyvninger fra en definert ”nulltilstand” til maksimalt belastet system).
| Lastfaktor | |
| Egenvekt utligger og ledninger | 1, 0 |
| Snø/is, vind | 1,0 |
| Strekk i loddavspente ledninger, inkl. egenvekt av loddsats: | 1,0 |
| Strekk i fastavspente ledninger, gunstig: | 0 |
| Strekk i fastavspente ledninger, ugunstig: | 1,0 |
| Strekk i fixledninger, gunstig: | 0 |
| Strekk i fixledninger, ugunstig: | 1,0 |
|
Strekk i fjernledning m/hengeisolator, gunstig: |
0 |
| Strekk i fjernledning m/hengeisolator, ugunstig: | 1,0 |
Denne kontrollen er i praksis lite interessant fordi Jernbaneverket ikke har sett krav til en slik total forskyvning.
1.4.4.4 Ulykkesgrensetilstand
Krefter fra ulykkesgrensetilstanden brukes for å kontrollere kapasitet ved ekstrordinære tilstander som nedriving av kontaktledning eller andre former for brudd i ledningene. I en slik grensetilstand forutsettes det at sporet ikke trafikkeres av tog som er avhengige av kjørbar kontaktledning. I denne grensetilstanden kontrollerer man bare at master og åk ikke faller ned eller får skadelige deformasjoner. Det aksepteres store forskyvninger i kontaktledningssystemet.
| Lastfaktor | |
| Egenvekt utligger og ledninger | 1, 0 |
| Snø/is, vind | 1,0 |
| Strekk i loddavspente ledninger, inkl. egenvekt av loddsats: | 1,0 |
| Strekk i fastavspente ledninger, gunstig: | 0 |
| Strekk i fastavspente ledninger, ugunstig: | 1,0 |
| Strekk i fixledninger, gunstig: | 0 |
| Strekk i fixledninger, ugunstig: | 1,0 |
|
Strekk i fjernledning m/hengeisolator, gunstig: |
0 |
| Strekk i fjernledning m/hengeisolator, ugunstig: | 1,0 |
I en ulykksgrensetilstand regnes det med materialfaktor [math]\gamma_m[/math] = 1,0.
Brudd i kontaktledning: En kontaktledningspart er loddavspent i hver ende og fastholdt i et fixpunkt midt mellom loddsatsene. I fixpunktet er utliggeren festet til to bardunerte master (fastpunktforankringsmaster) ved hjelp av fixline. Bærelinen (men ikke kontakttråden) er fastholdt i fixpunktet. I feltene på hver side av fixpunktet er det en slakk fixforbindelse mellom kontakttråd og bæreline. System 20 og System 25 har egne loddsatser for kontakttråden og for bærelinen. Systemet har låsemekanisme for loddsatsene slik at disse ikke faller i bakken ved ledningsbrudd. System 35 har en felles loddsats som mater strekkraft både inn i bæreline og kontakttråd (en halvpart i hver). De to linene henger sammen i en vippe. Derfor må både bæreline og kontakttråd slites av før kraften føres inn i fixpunktet. Systemet har ikke låsemekanisme for loddsatsen.
Brudd i kontaktledning kan deles i 2 faser:
1. Nedrivingsfasen.
2. Skadefasen.
1. Nedrivingsfasen
Dette er fasen da selve nedrivingen skjer. Kontaktledningssystemet får et rykk idet ledningene slites av. Ved rykk i kontakttråden vil kreftene føres til avspenningsmasten dersom ikke ledningen tøyes så mye at fixforbindelsen strammes. Ved stram fixforbindelse vil krefter også overføres til fixmastene. Et rykk i bærelinen fører til at kreftene forplanter seg til fixmastene eller til en av avspenningsmastene avhengig av hvor på ledningen togets pantograf griper tak. Både fixmastene og avspenningsmastene er bardunerte. Master og fundamenter for utsvingbare utliggere pådrar seg ikke krefter i sporets lengderetning, men kan påføres krefter normalt på sporet. Sikksakk, kurve og ledning som går til avspenning gir trykk/strekk-krefter i utliggerne. Idet ledningene slites av vil loddsatsene i System 20 og System 25 gå i låsestilling. For System 35 vil vippen legge seg og fixforbindelsen overfører krefter mellom bæreline og kontakttråd inntil begge ledninger eventuelt slites av.
2. Skadefasen
I denne fasen er ledningene slitt av og en ny statisk likevektstilstand er etablert. Ved brudd i kontakttråden for System 20 og System 25 vil begge loddsatsene gå i låsestilling. Ved brudd i bæreline vil loddsatsen på bruddsiden av fixpunktet gå i låsestilling. Da vil kraften fra loddsatsen i den andre enden føres inn i fixpunktet og videre til en av de to bardunerte mastene. For System 35 vil hele strekkraften føres inn i fixpunktet dersom både bæreline og kontakttråd er slitt av. Ved brudd i bare en av linene vil vippen ved loddavspenningen legge seg og forskyve ledningen ca. 20 cm uten at det overføres krefter til fixpunktet. Dersom begge ledninger i System 35 slites av, vil loddet gå i bakken. Da vil utliggerne kunne svinge 90° og mastene utsettes for krefter i sporets lengderetning. For System 20 og System 25 vil loddsatsene gå i låsestilling ved brudd , og systemet påføres ikke krefter i sporets lengderetning.
Det er ikke foretatt beregninger av selve nedrivingsfasen. Erfaring viser imidlertid at belastning på master og fundamenter fra nedriving av kontaktledning sjelden er et problem. I skadefasen er kreftene generelt mindre enn det som beregnes i bruddgrensetilstand. For det første skal det regnes med lavere lastfaktorer i ulykkesgrensetilstand, og for det andre føres mindre krefter inn i systemet fordi loddsatser enten har gått i låsestilling eller har gått i bakken.
Brudd i fastavspente ledninger
Som beskrevet tidligere under avsnitt om laster, neglisjeres differansestrekket fra fastavspente ledninger ved dimensjonering av kontaktledningsanlegg i bruddgrensetilstand og i bruksgrensetilstand. Det kan gjøres fordi Jernbaneverket har en bestemmelse om at forskjellen i spennlengde på hver side av en mast ikke skal være mer enn 20 % (System 20 og System 25). Ved brudd i fastavspente ledninger vil det nødvendigvis oppstå et differansestrekk, det vil si krefter i sporets lengderetning. I en ulykkesgrensetilstand kan det aksepteres noe deformasjon av masten, noe som fører til redusert differansestrekk. Det må vurderes hvor stort differansestrekk det skal regnes med.
1.4.5 Lastkombinasjoner
Ved beregning av kontaktledningsanlegg skal det kontrolleres for følgende 3 lastkombinasjoner:
- Vind mot spor sammen med strekk i fastavspente ledninger ved -40°C
- Vind fra spor sammen med strekk i fastavspente ledninger ved -40°C
- Snø/is ved -25°C sammen med strekk i fastavspente ledninger ved -40°C
Det regnes ikke med lastkombinasjoner hvor både vind og snø/is inngår samtidig. Dette er i henhold til anbefalinger fra SIEMENS forskrifter (System 20 kapittel 10.3 lasttilfeller) og FEA-F § 72. Når det gjelder lastkombinasjonen vind, regnes det vind mot en flate som er lik ledningens diameter fri for snø- og islast (kfr. FEA-F §72).
1.4.6 Fundamenter
Som grunnlag for dimensjonering av fundament beregnes et kraftsett (moment, skjærkraft og normalkraft) i fundamenttoppen. Laster, grensetilstander og lastkombinasjoner er som beskrevet ovenfor. Forhold som påvirker kreftene i fundamenttoppen er:
- Masteavstand
- Kurveradius
- Type kontaktledningssystem
- Hvor mange ledninger som henger i masten, både loddavspente og fastavspente.
- Om masten har tilleggsfunksjoner som avspenningsmast, fastpunktmidtmast eller fastpunktforankrigsmast.
- Om mastene bytter side av sporet eller ikke.
- Om masten står i ytterkurve eller innerkurve (strekkutligger eller trykkutligger).
- Geometriske data som mastehøyde og hvor på masten de ulike ledningene henger.
Aktuelle kontroller for fundamenter.
1. Kapasitet. Krefter normalt på sporet i bruddgrensetilstand. Det må vurderes om det i tillegg er nødvendig å kontrollere for krefter i sporets lengderetning og for torsjon. Vanligvis er disse kreftene så små at de kan neglisjeres.
2. Deformasjoner. Fundamentets bidrag til kontaktledningens forskyvning i bruksgrensetilstand.
3. Kapasitet etter brudd i fastavspente ledninger. Ulykkesgrensetilstand. Det må vurderes om det er nødvendig å kontrollere for denne grensetilstanden.
Jernbaneverket Ingeniørtjenesten har utviklet et Excel/Visual Basic program (KL_fund) som beregner krefter i topp av mastefundament.
Ved bruk av nedborede fundamenter kan det settes opp en regnemodell der jorda modelleres med fjærer som støtter en nedboret betongsylinder. Et slikt fundament blir ofte boret 4–5 m ned i bakken. Boring kan utføres både i løsmasse og fjell. Beregninger som er utført for kontaktledningsfundamentet Mofix [4] viser at fundamentet vanligvis ikke er kritisk med hensyn til kapasitet (bruddgrensetilstand). Deformasjonskravet (bruksgrensegrensetilstand for forskyvning av kontaktledning) er oftest dimensjonerende. Dette kravet er vanskelig å dokumentere fordi deformasjonene er helt avhengig av forholdene i bakken. Grunnforholdene modelleres med jordfjærer, og det er vanskelig å finne gode verdier for disse jordfjærene.
Det tradisjonelle mastefundamentet med en betongsøyle støpt på en nedgravd fundamentplate beregnes etter tradisjonelle geotekniske prinsipper for dimensjonering av søylefundament. Fundamenteringen kan gjøres grunnere enn for nedborede betongfundamenter. Beregningene tar ikke hensyn til sidestøtte mot betongsøyla fra omkringliggende masse. Også for disse beregningene er deformasjonskravet vanskelig å dokumentere.
1.4.7 Master
Ved dimensjonering av mastefot og innfesting brukes de samme kreftene som i fundamenttoppen. Dersom det er ønskelig å kontrollere masten i et snitt høyere oppe, må kreftene regnes på nytt for det aktuelle snittet. Det kan gjøres ved hjelp av programmet KL_fund ved å velge fiktive verdier for mastehøyde og for avstand opp til ledningene. Man tenker seg rett og slett sporet flyttet opp til det aktuelle snittet og kjører en beregning med nye, fiktive høyder.
Ved beregning av fundamenter blir differansestrekk og torsjonsmoment vanligvis neglisjert. Det gjøres fordi kreftene er små og har liten innvirkning på fundamentet. Når det gjelder master, er forholdet et annet. Mastene er slanke konstruksjoner med liten motstand mot vridning og deformasjon. Dette gjelder særlig B-masten. Derfor kan små differansekrefter og vandringskrefter1 føre til uakseptabel deformasjon og vridning av masten. Jernbaneverket setter krav til mastens bidrag til forskyvning av kontaktledningen og til maksimal vridning av masten.
Ved dimensjonering av master må effekten av differansestrekk og torsjon vurderes i tillegg til kreftene som beregnes i programmet KL_fund.
Aktuelle kontroller for master:
1. Kapasitet. Krefter (inklusiv torsjon) normalt på sporet og i sporets lengderetning i bruddgrensetilstand.
2. Deformasjoner. Forskyvning og vridning i bruksgrensetilstand.
3. Kapasitet etter brudd i fastavspente ledninger. Ulykkesgrensetilstand. Det må vurderes om det er nødvendig å kontrollere for denne grensetilstanden.
Alminnelig bæremast med enkel utligger. Det er to effekter som gir bidrag til krefter i sporets lengderetning og dermed også til torsjonsmoment i kontaktledningsmast:
1. Differansestrekk.
Fastavspente ledninger henger vanligvis i bakkant av masten. Eventuelt differansestrekk vil føre til krefter i sporets lengderetning og torsjon i masten.
2. Vandringskrefter.
Fordi kontaktledningen er loddavspent vil ledningen forlenges og trekke seg sammen ved henholdsvis temperaturøkning og temperaturfall. Utliggeren vil svinge og trykk-/strekkreftene fra kontaktledningen vil føres skrått inn i masten. Dette fører til torsjonsmoment i masten samtidig som det påføres krefter både i retning mot sporet og i retning parallelt sporet (vandringskrefter1).
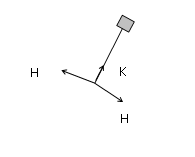
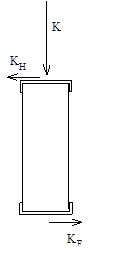
Figur 15 og 16 viser effekter som fører til torsjonsmoment og vridning av masten.
Kontaktledning stiplet linje: Kontaktledning før temperaturøkning (utligger står normalt på masten). Kontaktledning heltrekt linje: Kontaktledning etter temperaturøkning.
| a | = Masteavstand. |
| as | = Lengde av utligger. |
| lk | = Lengde av halv kontaktledningspart. |
| [math]\Delta l[/math] | = Forlengelse av kontaktledning og utsving av utligger (utliggervandring). |
| K | = Trykk- /strekkraft i utligger grunnet sikksakk eller kurve. |
| KH | = Kraft i sporets lengderetning grunnet skråstilt utligger (vandringskraft). |
| KF | = Kraft i sporets lengderetning grunnet differansestrekk. |
Kraft i sporets lengderetning grunnet skråstilt utligger (vandringskraft), KH::
| [math]\Delta l = \alpha \cdot \Delta t \cdot l_k[/math] | (13) |
hvor [math]\Delta t[/math] er temperaturendring.
Strengt tatt skal formelen være når det regnes for siste bæremast før loddavspenning. Men for å regne mest mulig generelt tenkes siste bæremast plassert så nær loddavspenningen at verdien a settes til null. Dette er til sikker side.
| [math]K = 2 \cdot H \cdot (\frac {a}{R} \pm 2 \cdot \frac {B2 - B1}{a})[/math] | (14) |
hvor det første 2 tallet indikerer at dette er kraft både fra bæreline og fra kontakttråd. B2 og B1 er sikksakk og R er kurveradius, se formel 9 for nærmere forklaring.
| [math]K_H = K \cdot \frac {\Delta l}{a_s}[/math] | (15) |
Som eksempel settes følgende verdier inn i formelverket:
| [math]\alpha[/math] | = 1,7 x 10-5 1/°C |
| [math]\Delta t[/math] | = (50-5)°C = 45 °C |
| lk | = 750 m |
| H | = 15 kN (System 25) |
| a | = 65 m |
| as | = 3,5 m |
| R | = [math]\infty[/math] (rett linje) |
| B2 = -B1 | = 0,3 m (sikksakk) |
Dette gir:
- Utliggervandring [math]\Delta l[/math] = 0,57 m
- Trykk-/strekk i utligger K = 0,55 kN
- Vandringskraft KH = 0,09 kN
For en B3 mast med bredde 577 mm gir dette et torsjonsmoment Mt = 26 Nm. I kurve bli torsjonsmomentet større.
Kraft i sporets lengderetning grunnet differansestrekk, KF. Denne kraften kan være vanskelig å bestemme. Jernbaneverket har en bestemmelse om at maksimal forskjell i spennlengde på hver side av en mast ikke skal være større enn 20 % (System 20 og System 25). Med dette kravet blir differansestrekk fra fastavspente ledninger lite, og effekten neglisjeres vanligvis ved beregninng av fundamenter. Men master, særlig B3 master, er slanke konstruksjoner. Ved dimensjonering av master må man vurdere effekten av differansestrekk særlig med hensyn til vridning, men også med hensyn til kapasitet (brudd).
Mast med dobbel utligger: Det som er sagt om alminnelig bæremast med enkel utligger gjelder også her. Men mast med dobbel utligger får i tillegg et bidrag fra eksentrisk innføring av kraft grunnet den doble utliggeren. Følgende effekter gir altså bidrag til krefter i sporets lengderetning og torsjonsmoment i en mast med dobbel utligger:
1. Differansestrekk
2. Vandringskrefter
3. Eksentrisk kraftresultant i masten grunnet dobbel utligger.
1.4.8 Åk
Som grunnlag for beregning av åk brukes laster, grensetilstander og lastkombinasjoner som beskrevet ovenfor. Forhold som påvirker kreftene i åket er:
- Avstand mellom åkene / ledningenes spennlengde
- Om ledninger føres på skrå inn i åket eller ikke. (ledninger til avspenning, kurver, sikksakk osv.)
- Type kontaktledningssystem
- Åkets spennlengde
- Hvor mange ledninger som henges i åket, både loddavspente og fastavspente.
- Utstyr som henger i åket slikt som tomtelys og lignende.
Aktuelle kontroller for åk.
1. Kapasitet. Krefter i bruddgrensetilstand.
2. Deformasjoner. Nedbøying i bruksgrensetilstand.
3. Kapasitet etter brudd i fastavspente ledninger. Ulykkesgrensetilstand.
Det må vurderes om det er nødvendig å kontrollere for denne grensetilstanden.
Jernbaneverket Ingeniørtjenesten har dimensjonert nye utgaver av de gamle åkene type 12 og type 14. Åkene er beregnet i bruddgrensetilstand og bruksgrensetilstand.
I analyseprogrammet RM-Spaceframe er det laget en romlig modell av åkene. Åkene er beregnet med en vindhastighet på 30 m/s. Det er kontrollert for vind både normalt på sporet og langs sporet. I beregningene er det foruten ledninger og oppheng også tatt med tomtelys. Det er tatt hensyn til sidekrefter fra kurvestrekk og at et par av kontaktledningene føres skrått inn i åket (for eksempel ledninger til avspenning). I beregningene er det tatt hensyn til noe differensialstrekk i fastavspente ledninger. For videre omtale av lastforutsteningene vises det til heftet ”Utvikling av åk, lastgrunnlag” [5].
Selve dimensjoneringen av åkene er utført som håndberegninger i heftet ”Utvikling av åk, statiske beregninger, åk type 12 og åk type 14” [6].
1.5 Returkrets
1.5.1 Returledning/kabel
Returledningen skal i frie spenn ikke påkjennes mer enn 50% av de høyeste tillatte påkjenninger for høyspenningsledninger i ugunstigste belastningstilfelle. Ledningens fester skal tilfredsstille gjeldende forskrifter for lavspenningsanlegg. [1]
1.5.2 Sugetransformator
Sugetransformatorene skal lages av materialer som skal være motstandsdyktige mot korrosjon. I sugetransformatorkassen skal det brukes en materialkvalitet (tettet stål) som gir godt feste for sinkbelegget. Delene skal varmforsinkes som foreskrevet i NS 1970 og med noen tilleggskrav. Sugetransformatoren skal i normal drift ikke lekke olje, selv ved langvarig bruk i inntil 40 år. Dersom transformatoren skal monteres i master, skal totalvekten ikke overskride 3500 kg. For montering på bakken tillates noe høyre vekt. [7]
Krav til is- og snølast skal minimum være lik 1,5 kg/m2 ved 5 °C. Utstyret skal ha en hensiktsmessig utforming slik at vibrasjoner ikke oppstår. [7]
1.5.3 Filterimpedans
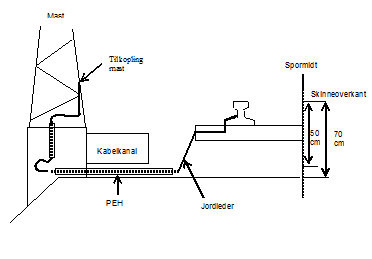
Filterimpedansene plasseres pukken, minimum 2,5 m fra spormidt, med lokket i plan med svillens overkant slik at den er synlig. De skal ha deksel som beskytter tilkoblingspunktene mot fuktighet, støv og mekaniske påkjenninger. Filterimpedanser må ha vanntett kasse for at ikke vann skal trenge inn til impedansspolen og eventuelt forårsake kortslutninger. Kassen må være av korrosjonsbestandig materiale slik at det ikke ruster hull i kassen eller at dekselet ruster fast. Filterimpedansen må tåle de klimatiske forhold som den kan bli utsatt for.
1.6 Ledningsføring
Innledning
Ved prosjektering og bygging av kontaktledningsanlegg er man nødt til å ta hensyn til tvangspunkter i forholdet mellom spor og kontaktledningsanlegget. Med tvangspunkter mener man her steder der sporet binder både master og ledningsføring opp mot en bestemt plassering. Eksempler på tvangspunkter kan være signaler, sporveksler, sporsløyfer, kurvatur, plattformer og lignende. En god tommelfingerregel ved prosjektering av kontaktledningsanlegg vil naturligvis være å identifisere alle slike tvangspunkter før selve prosjekteringen starter. Det er viktig å ta hensyn til alle disse punktene. Det er eksempler på at slike punkter i ettertid har medført problemer med ekstra kostnader i forbindelse med større feilfrekvens enn normalt, samt mer eller mindre ombygginger av ferdige anlegg.
1.6.1 Ledningsføring over sporveksler
Et av de viktigste og vanskeligste tvangspunktene for kontaktledningsanlegg er sporveksler. Dette kapitlet vil forsøke å beskrive ledningsføring og masteplassering ved sporveksler og sporsløyfer. Før det gås inn på den rent prosjekteringsmessige biten er det nødvendig å kjenne til noen begreper og begrensninger som influerer ledningsføringen ved sporveksler og sporsløyfer.
Tangentiell og kryssende ledningsføring.
Uavhengig av hvilket prinsipp det velges for ledningsføring over veksler vil kontakttråden heves ved strømavtakerpassering. Hevingen er avhengig av type kontaktledningssystem og toghastighet. Ved tangentiell ledningsføring legges ledningene inntil hverandre, noe som betyr at de ikke knyttes fysisk sammen på noe sted. Her vil ikke løfting av en tråd medføre løfting av den andre. Tangentiell ledningsføring vil da bli begrensende i forhold til kontakttrådens dynamiske heving, og dermed være hastighetsavhengig. Ved kryssende ledningsføring vil ledningene være mekanisk forbundet med hverandre i krysningspunktet via et svevende kryss. Ved samtidig å benytte seg av krysshengere vil løfting av den ene kontakttråden alltid forårsake løfting av den andre. På denne måten elimineres muligheten for at den tråden som det ikke kjøres på kommer inn under hornet på en passerende strømavtaker. Dette betyr at kryssende ledningsføring over veksler er tilnærmet hastighetsuavhengig. I prinsippet gjelder dette for alle hastigheter som tog har eller vil ha i Norge. I Jernbaneverkets anlegg skal det i utgangspunktet kun benyttes kryssende ledningsføring.
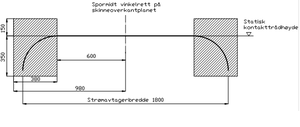
Klemmefritt rom.
Dette rommet må være definert. Klemmefritt rom for Jernbaneverket er foreløpig definert til å strekke seg fra 600 mm til 980 mm ut på hver side av midte strømavtaker. Høyden på det klemmefrie rommet er i utgangspunktet gitt av systemtype og hastighet. Det er videre definert at klemmefritt rom har en høyde på 150 mm over og 300 mm under statisk kontakttrådhøyde. I det klemmefrie rommet skal det ikke befinne seg kontakttrådklemmer, strømstiger, strømbruer eller krysshengere. Hengetråder kan plasseres i klemmefritt rom. Det tillates også Y-linehengetrådklemmer ved behov.
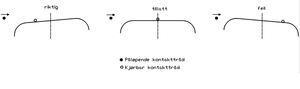
Av- og påløpende ledninger.
På en del steder i kontaktledningsanlegget er strømavtakeren nødt til å betjene 2 kontakttråder samtidig. I vekslings- og seksjonsfelt der man ”bytter” ledning vil ny ledning komme ovenfra og ned på strømavtakeren, samtidig som gammel ledning vil forsvinne opp fra strømavtakeren. Ved sporveksler kommer og går ledninger av og på strømavtakeren også i horisontalplanet, altså fra siden. Dersom en strømavtaker beveger seg med stor hastighet vil kontaktkraften mellom kontakttråd og strømavtaker føre til at kullstykkene blir presset ned på det punktet kontakttråden til en hver tid befinner seg på kullstykket. Kontakttrådens sikksakk gjør videre at dette presspunktet flytter seg fra side til side. Dersom kontakttråden ligger til venstre for midten av strømavtakeren vil kontaktkraften føre til at slepekullene trykkes ned på venstre side, med den følge at de går litt opp på høyre side. Dersom kontakttråden ligger til høyre for midten av strømavtakeren skjer det motsatte, det vil si at slepekullene trykkes ned på høyre side og går litt opp på venstre side. En ledning som kommer inn fra siden skal møte minst mulig problemer når den kommer inn på strømavtakeren. Derfor er det viktig at den ledningen som allerede befinner seg på strømavtakeren er på samme side av midten på strømavtakeren som den innkommende ledning. Det samme vil gjelde for ledninger som forlater strømavtakeren. Dersom en ledning forlater strømavtakeren er det viktig at den ledningen som blir igjen er på samme side av midten av strømavtakeren som den utgående ledning. I praksis er det følgende forhold som gjelder for å sikre seg for korrekt plassering av av- og påløpende ledninger: Ledning for avviksspor skal aldri befinne seg på den siden av spormidt som er lengst vekk fra hovedsporet. Likeledes skal ledning for hovedspor aldri befinne seg på den siden av spormidt som er lengst vekk fra avvikssporet.
Fritt profil for strømavtaker
Fritt profil for strømavtaker definerer det rommet som strømavtakeren kan befinne seg i under kontaktledningsanlegget. Inne i fritt profil for strømavtaker skal det ikke befinne seg faste anleggsdeler. Fritt profil for strømavtaker er et dynamisk profil, det vil si at det følger kontakttrådens høydevariasjoner som skyldes kontakttrådens dynamisk løft ved strømavtakerpassering.
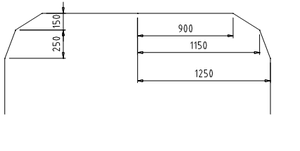
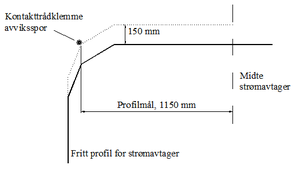
Profilmål
Master med seksjonsutliggere for flere spor krever spesiell oppmerksomhet. Dersom en mast har en kjørbar utligger for både hoved- og avviksspor er det viktig å sørge for at det ikke oppstår konflikter med hensyn til den plass strømavtakeren trenger for en problemfri passering, det vil si fritt profil for strømavtaker. Det må videre sørges for at når strømavtakeren passerer i det ene sporet, så må utliggeren for det andre sporet ikke komme i veien for strømavtakeren. Dette gjøres ved å sørge for tilstrekkelig avstand mellom spormidt for det spor som det kjøres på og kontakttrådklemmen til utliggeren for det andre sporet. Det er imidlertid vanskelig å gi noen eksakt verdi på denne avstanden. Profilmålet for Jernbaneverket er satt til 1150 mm. Bakgrunnen for denne verdien ligger i utformingen av fritt profil for strømavtaker. Anta at kontakttrådklemmen for avviksspor ligger 1150 mm fra spormidt for hovedspor. Det kan nå tillates et dynamisk løft på 150 mm for ledningen for hovedspor før kontakttrådklemmen for avviksspor kommer inn i hovedsporets fritt profil for strømavtaker. Dersom avstanden fra kontakttrådklemmen i hovedspor ligger 1150 mm fra spormidt for avviksspor tillates tilsvarende dynamisk løft for ledningen i avvikssporet. Figur 20 viser dette for hovedspor. Profilmålet på 1150 mm er å anse som et minimumsmål. Det er ingenting i veien for at denne avstanden er større. Et større profilmål vil imidlertid føre med seg at utliggeren for avvikssporet blir svært lang dersom utliggerne for både hoved- og avviksspor er i samme mast.
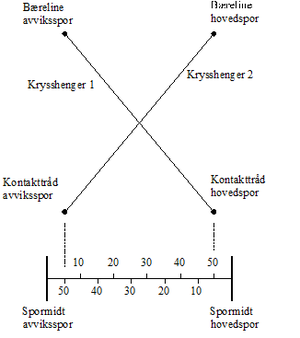
Krysshengere.
Krysshengere brukes i forbindelse med sporveksler og er hengetråder som er festet i kontakttråden for det ene sporet og bærelinen for det andre sporet. Hensikten med krysshengere er å overføre noe av den dynamiske hevingen fra den ledningen strømavtakeren kjører på til den ledningen som kommer inn på strømavtakeren. Krysshengere erstatter ikke andre hengetråder. De skal monteres etter at anlegget er montert og justert og skal i ubelastet tilstand ikke overføre bærekrefter mellom kontakttråd og bæreline. Krysshengere plasseres før det svevende krysset sett fra bakkant kryss (BK). Krysshenger 1 plasseres der hvor avstanden mellom spormidt avviksspor og kontakttråd hovedspor = 500 mm. Denne festes i kontakttråd for hovedspor og bæreline for avviksspor. Krysshenger 2 plasseres der hvor avstanden mellom spormidt hovedspor og kontakttråd for avviksspor = 500 mm. Denne festes i kontakttråd for avviksspor og bæreline for hovedspor. Figur 21 viser hvordan krysshengere plasseres og monteres. Anta en strømavtakerpassering i høy fart på kontakttråd 1. Dynamisk løft i kontakttråd 1 vil føre til at bæreline 1 hever seg. Bæreline 1 og kontakttråd 2 er forbundet via krysshenger 2. Når bæreline 1 heves vil krysshenger 2 dra med seg kontakttråd 2 oppover. Dette fører til at høydeforskjellen mellom kontakttråd 1 og kontakttråd 2 reduseres i det kontakttråd 2 kommer inn på strømavtakeren. Kjøring på kontakttråd 2 vil på samme måte redusere høydeforskjellen mellom kontakttråd 2 og kontakttråd 1. Innbyrdes avstanden mellom krysshengerne må minimum være forskjellen i ledningsvandring pluss 15 - 20 cm. Dersom forskjellen i ledningsvandring er stor, mer enn 250 med mer, kan krysshengeren festes til bærelinen med en trinse.
Hovedprinsipper ved ledningsføring over sporveksler.
Ved alle sporveksler er det 5 forhold som man søker å ta hensyn til. Disse er:
1. Overholde reglene for fritt profil for strømavtaker.
2. Overhold reglene for klemmefritt rom.
3. Overholde reglene for av- og påløpende ledninger.
4. Overholde regelen for profilmål.
5. Prøve å ha kun 1 kjørbar utligger på alle master med seksjonsutliggere.
Ovenstående punkter er forsøkt satt opp i en prioritert rekkefølge, der punktene 1 og 2 skal betraktes som ufravikelige. Forskjellen i viktighet er imidlertid marginal. Punkt 5 sees på som svært viktig ved hastigheter høyere enn 160 km/t. Dersom et punkt ikke lar seg gjennomføre helt til fulle skal det likevel betraktes som et mål man skal komme så nærme som mulig. Det er i disse tilfellene viktig å tenke konsekvenser da uheldige løsninger kan ende opp med hastighetsreduksjoner eller i verste fall ombygging av anlegget.
Tegning av vekselen, målestokk. Ved beregning av ledningsføring over sporveksler er det viktig å ha en fornuftig tegning av den aktuelle sporvekselen. Vekselen kan for eksempel tegnes med spormidt i følgende målestokk:
Vertikal: 1 : 50
Horisontal: 1 : 500
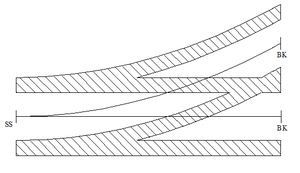
I tillegg inntegnes klemmefritt rom for begge spor, samt stedene SS og BK. SS, stokkskinneskjøt, er vekselens begynnelse, og er ikke det samme som tungespiss. BK, bakkant kryss, er det punktet hvor vekselen ender i avvik og hovedspor.
For å forstå de videre fremgangsmåtene er det først nødvendig å definere noen nye begreper, nemlig UP1, UP2 og XP. UP1, utliggerpunkt 1, er masteplassering nærmest stokkskinneskjøt, SS. UP2, utliggerpunkt 2, er masteplassering nærmest bakkant kryss, BK. XP, krysningspunkt, er det punktet kontakttrådene krysser hverandre mellom UP1 og UP2.
1.6.2 Ledningsføring over sporveksler, hastigheter opp til 160 km/t
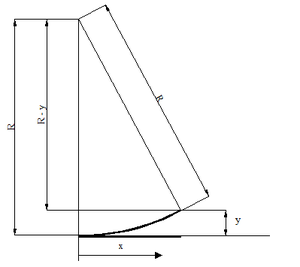
I hastighetsområde opp til 160 km/t kan ”20-cm”-metoden benyttes. Denne går i korte trekk ut fra at UP1 plasseres ved det punktet på sporvekselen der hovedspor og avviksspor har en innbyrdes avstand på 20 cm. Normalt vil da både hovedspor og avviksspor ha egen mast med utligger i retning BK, det vil si at man ikke har noen UP2 med seksjonsutligger men i stedet en UP2 for hvert spor. Videre har metoden den svakhet at begge utliggerne ved UP1 blir kjørbare. Dette er grunnen til hastighetsbegrensningen på 160 km/t da høyhastighetskjøring på 2 utliggere samtidig representerer dårlige dynamiske forhold med stor fare for fraslag, for store krefter mellom kontakttråd og strømavtaker samt forsert slitasje. Det er i prinsippet flere måter å finne det punktet på sporvekselen der hoved- og avviksspor er 20 cm fra hverandre. En metode vil være å fysisk måle på vekselen ute på det stedet som den, eller en tilsvarende sporveksel, ligger. Den andre vil være å regne ut avstanden eller å bruke en tegning eller tabell der avstandene for de forskjellige vekslene er angitt. Figur .23 og formel .16 viser hvordan man kan regne ut avstanden dersom sporvekselen har konstant radius og denne er kjent. Tabell 7 viser avstand fra stokkskinneskjøt til det punktet hvor avstanden mellom hoved- og avviksspor er 20 cm for en del typiske konstante vekselradier.
For figur 23 gjelder følgende utregningsmetode:
| [math]R^2 = x^2 + (R-y)^2[/math] | (16) |
| [math]x = \sqrt {R^2 - (R-y)^2}[/math] |
der
- R = Sporvekselradius, i [m]
- y = Ønsket avstand mellom hoved- og avviksspor i, [m]
- x = Avstand fra stokkskinneskjøt til punkt med avstanden y mellom
hoved- og avviksspor, i [m]
| Sporvekselradius, [m] | Avstand fra stokkskinneskjøt til 20 cm sprik, [m] |
| 190 | 8,72 |
| 300 | 10,95 |
| 500 | 14,14 |
| 760 | 17,43 |
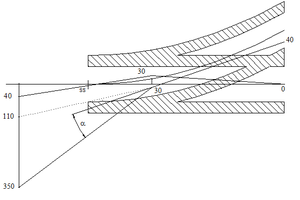
Valg av sikksakk og plassering av kontakttråder for hoved- og avviksspor.
Grunnregelen for valg av sikksakk er at ledningen for hovedspor legges i spormidt for avvikssporet og at ledningen for avviksspor legges i spormidt for hovedspor. Figur .24 viser dette. Plassering av kontakttråden for avviksspor følger reglene for av- og påløpende ledninger. Det er i de fleste tilfeller naturlig at både hoved- og avvikssporet har en egen mast for neste utligger, UP2. Dersom UP2 for hovedspor har sikksakk ”0” og ledningen for avvikssporet alltid er på hovedsporssiden av spormidt vil regelen for av- og påløpende ledninger alltid overholdes. Det kan være gunstig at vinkelen mellom ledning i hovedspor og ledning i avviksspor gjøres så liten som mulig. Jo mindre denne vinkelen er desto større avstand blir det mellom XP, det svevende krysset, og UP1.
Vinkel på ledninger som går til avspenning.
Når det nyttes 2 kjørbare utliggere ved samme mast stilles det krav til avbøyningsvinkelen for kontakttrådene. For spor med hastighet > 100 km/t er maksimal avbøyningsvinkel 5o. For spor med hastighet < 100 km/t er maksimal avbøyningsvinkel 15o. Velges en for stor vinkel vil dynamikken reduseres i for stor grad. Figur .24 viser hvilken vinkel det er snakk om, her kalt [math]\alpha[/math]. Dersom vinkelen er for stor kan det benyttes en føringsutligger i masten før. Dette er vist med stiplet linje i figur 24. Husk at eventuelle føringsledninger som kommer inn i klemmefritt rom må være minimum 150 mm høyere enn kontakttrådhøyden for den kjørbare ledningen for å komme klar av det klemmefrie rommet.
Dersom det velges sikksakk som vist på figur 24 så blir avstanden mellom UP1 og det svevende krysset forholdsvis liten. For å gjøre denne avstanden noe større er det mulig å øke sikksakk-verdiene ved UP1. Ved for eksempel å øke til 30 sikksakk både for hoved-og avviksspor vil det svevende krysset flyttes lenger vekk fra UP1. Dette er vist i figur 25. Dersom sikksakkverdiene forandres utover det som er gjeldende i tabellverket må spennlengdene kontrolleres med hensyn på tillatt vindutblåsning. Videre finnes det også justeringsmuligheter for sikksakk-verdier ved UP2. Det er imidlertid mange forhold som spiller inn ved forskjellige valg av sikksakk. Lag en skikkelig tegning, skriv opp alle forhold som kan komme til å ha innvirkning, ta hensyn til disse og fremfor alt: bruk litt tid på jobben.
1.6.3 Ledningsføring over sporveksler, hastighet over 160 km/t
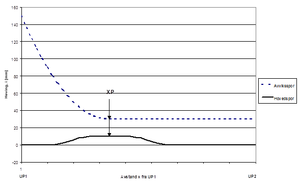
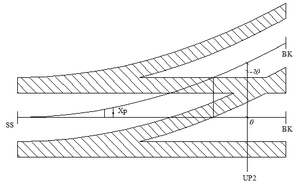
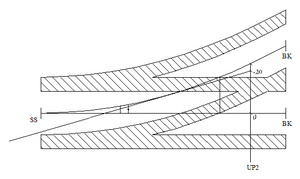
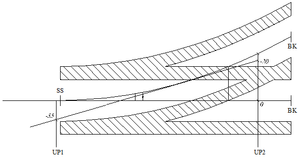
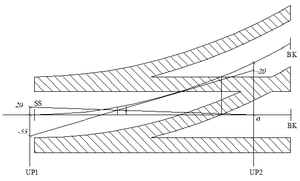
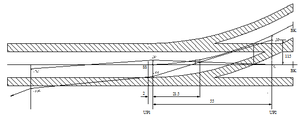
Banestrekninger som bygges for større hastigheter enn 160 km/t skal bygges med kontaktledningsanlegg System 20 (S20), System 25 (S25) eller tilsvarende. Det er selvsagt også fult mulig å benytte teoriene for ledningsføring over sporveksler for hastigheter over 160 km/t også for lavere toghastigheter med andre systemer. Ved toghastigheter fra 160 km/t og oppover stilles det store krav til anleggets dynamiske egenskaper. Harde punkter i anlegget fører til store krefter mellom strømavtaker og kontaktledningsanlegg. Størrelsen på de kreftene som oppstår ved et dynamisk hardt punkt øker ikke lineært med hastigheten men snarere eksponensielt. Dette betyr at økningen i absoluttverdien for en slik kraft er mye større ved en hastighetsøkning fra 160 til 180 km/t enn den er ved en hastighetsøkning fra 60 til 80 km/t. To kjørbare utliggere ved samme mast vil representere et dynamisk hardt punkt. Ved hastigheter over 160 km/t skal derfor alle master med seksjonsutliggere ha bare en kjørbar utligger. Det er i prinsippet to måter å gjøre dette på. Den ene måten er å sørge for at avstanden mellom hoved- og avviksspor ved masten er så stor at det kun er en kjørbar utligger for hvert spor, det vil si at man overholder regelen for profilmålet på 1150 mm. Den andre måten vil da være at man ved masten har forskjellig kontakttrådhøyde for de to sporene. Dersom kontakttrådhøyde-forskjellen mellom to utliggere i en seksjonsmast er 150 mm eller mer kan man betrakte det som at masten har bare en kjørbar utligger. Et dynamisk løft på 150 mm er imidlertid ikke helt umulig, derfor skal utliggere med 150 mm løft alltid ha lett direksjonsstag. Med bakgrunn i ovenstående gjelder følgende høydeforløp for kontakttråd og bæreline mellom UP1 og UP2:
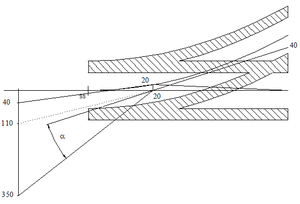
Ved UP1 er tråden som går til avspenning hevet med 15 cm i forhold til kontakttrådhøyden i hovedspor. Ved XP er tråd for hovedtogspor hevet med 1 cm, og tråd for avvik hevet med 3 cm. På dette punktet monteres det et svevende krysset for å forbinde de to kryssende kontakttrådene. Hevingen på 1 cm i hovedtogspor gjelder fra og med begge hengetrådene på hver side av XP. Hevingen av de to kontakttrådene ved XP gir en forhåndsløfting i anlegget som forbedrer dynamikken ved strømavtakerpassering. UP2 plasseres slik at kjøring på to ledninger ikke lar seg gjøre, det vil si på et sted der avstanden mellom hoved- og avviksspor er større eller lik summen av profilmålet på 1150 mm og sikksakkverdi for avvikssporet. I tillegg er tråden for avvik hevet med 3 cm også ved UP2. Figur .26 viser høydeforløpet til kontaktledningene for hoved- og avviksspor.
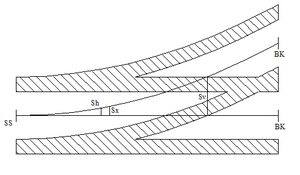
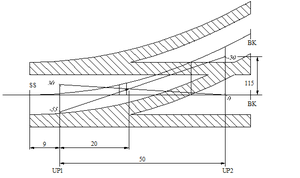
Vekslingsområde og nødvendige avstander. For å avklare begrensningene i forhold til plassering av kontakttråder og svevende kryss definerer man først et vekslingsområde. I dette vekslingsområde skal kontakttrådene for hoved- og avviksspor krysse hverandre. Området begrenses i endene av størrelsene Sv og Sh. Sv, start vekslingsområde, er det punkt på vekselen hvor avstanden mellom de to sporenes spormidt er lik avstanden fra midte slepekull til enden på det klemmefrie rommet. Hos Jernbaneverket er Sv = 980 mm. Sh er maksimal sikksakkverdi for ledningen i hovedsporet, det vil si 0.2 m dersom det bygges S20 og 0.3 m dersom det bygges S25. Vekslingsområdet begrenses da til slutt av Sv, Sx og begge sporenes spormidt. I vekslingsområdet må begge ledningene hele tiden være på samme side i forhold til midte strømavtaker i henhold til regel om av- og påløpende ledninger. Sted for optimalt krysningspunkt, Sx, ligger i det stedet på vekselen hvor avstanden mellom de to sporenes spormidt er lik verdien fra formel 17.
| [math]S_x = \frac {2}{3} \cdot S_a + \frac {1}{2} \cdot S_h[/math] | (17) |
der
- Sa = største sikksakk i avviksspor.
- Sh = største sikksakk i hovedspor.
| System | Strekk
N |
Kontakttråd
mm2 |
Tyngde
N/m |
X
m |
| 35 | 7060 | 80 | 7,1 | 15,5 |
| 35 | 7060 | 100 | 8,9 | 13,8 |
| 20A og 20B | 10000 | 100 | 8,9 | 16,5 |
| 20 C | 13000 | 100 | 8,9 | 18,5 |
| 25 | 15000 | 120 | 10,7 | 18,4 |
Optimalt kryssningspunkt vil da ligge på Sx der hvor de to addendene i formel 17 møter hverandre.
Videre skal vi nå ta for oss nødvendig avstand mellom UP1 og XP, og definerer denne som x. I henhold til avsnittet om kontakttrådhøydeforløp for avvikssporet, fig. 26, så har denne en høydeendringen fra XP til UP1 på 12 cm. Dette betyr at avstanden x mellom UP1 og XP må minimum være den avstanden som trengs for å heve avviksledningen med 12 cm (fra 3 cm ved XP til 15 cm ved UP1). Denne avstanden er systemavhengig og regnes ut fra strekket i og tyngden av kontakttråden. Det er viktig å merke seg at dersom x er større enn nødvendig, så skal allikevel ikke ledningen heves med mer enn 15 cm i forhold til den kjørbare ledningen. Dette fordi ledning for avviksspor ved UP1 ellers lett kan komme i konflikt med horisontalrøret i utliggeren for hovedsporet. Størrelsen på x (avstand) eller y (høydeendring) finnes ved bruk av formel 18 og 19.
| [math]x = 0,5 \cdot \sqrt {\frac {8 \cdot H_F \cdot y}{q_F}}[/math] | (18) |
| [math]y = \frac {x^2 \cdot q_F}{2 \cdot H_F}[/math] | (19) |
der
- x = avstand mellom UP1 og XP, i [m].
- HF = strekket i kontakttråden, i [N].
- y = ønsket heving, i [m].
- qF = tyngden av kontakttråden, i [N/m].
Etter formel 18 gir en ønsket heving på y = 0.12 meter verdiene i tabell 8.
Valg av sikksakk, masteplassering og plassering av kontakttråder for hoved- og avviksspor
Det finnes egentlig ingen fasitløsning når det gjelder sikksakk, masteplassering og kontakttrådføringer. Det vil hele tiden være flere måter å gjøre det på som alle kan være riktige i forhold til de regler som gjelder. Allikevel vil noen løsninger være bedre enn andre. Vurdering av hvilke løsninger som er mest optimal må gjøres av den som prosjekterer anlegget. Det viktigste i denne sammenheng er å ha klart for seg hvilke begrensninger og krav som gjelder. Som regel vil det være gunstigere å holde seg godt innenfor gjeldende krav og begrensninger i stedet for å holde seg så vidt innenfor. Dersom enkelte krav og begrensninger ikke lar seg overholde skal konsekvensene av dette straks vurderes. I praksis menes her en vurdering av anleggets mulige hastighetsbegrensninger som følge av ikke optimale løsninger. Nedenfor er det prøvd å lage en ”oppskrift” for valg av sikksakk, masteplassering og plassering av kontakttråder. Det er forutsatt at mastene plasseres langs sporvekselens rettlinjede hovedspor.
1. Tegne inn Sv, Sx og Sh.
Avstandene merkes av på tegning.
2. Merke tidligste plassering av UP2, samt foreløpig sikksakkverdi for hoved- og avviksspor.
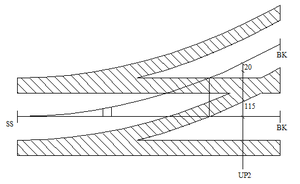
UP2 kan tidligst stå ved det punktet på sporvekselen der avstanden mellom hoved- og avviksspor er lik profilmålet, 115 cm, pluss sikksakkverdi for avvikssporet. Ved UP2 er det lurt å begynne med en sikksakkverdi på 0 cm for hovedspor og en sikksakkverdi på –20 cm for avviksspor.
3. Merke av optimalt teoretisk XP.
Optimalt teoretisk XP ligger der hvor de to addendene i formel .17 møtes på Sx.
4. Legge foreløpig ledning i avviksspor.
Dette gjøres ved å legge ledningen i avviksspor fra –20 cm sikksakk ved UP2, deretter som tangent til spormidt for avvikssporet og videre mot UP1.
5. Bestemme foreløpig plassering av UP1.
For at kontakttrådklemmen for avvikssporet ved UP1 skal komme tilstrekkelig klar av klemmefritt rom skal sikksakkverdi for avvikssporet ved UP1 aldri overstige - 55 cm. Foreløpig plassering av UP1 blir da ved det punktet hvor foreløpig ledning for avviksspor har en sikksakkverdi på – 55 cm.
6. Legge ledning i hovedspor.
Ledning for hovedspor legges med sikksakkverdi på 0 ved UP2 og derfra mot UP1. Sikksakkverdien ved UP1 velges etter hvilket kontaktledningssystem som benyttes. Normalt betyr dette en sikksakkverdi på 20 cm ved bygging av S20 og en sikksakkverdi på 30 cm ved bygging av S25.
7. Sjekke at avstanden x mellom UP1 og XP er stor nok for tilstrekkelig heving av kontakttråd for avviksspor.
Etter at punktene 1 til 7 er gjennomført kommer finjusteringen, optimaliseringen og etterkontrollen. Nedenfor er det satt opp en del punkter til bruk for dette. Figur 27 viser en ferdig prosjektert sporveksel fra UP2 til avspenning for S20.
- Avstanden mellom UP1 og UP2 kan maksimalt være 60 meter. Det må i alle fall kontrolleres for vindutblåsning både for hoved- og avviksspor.
- Ledning for hoved- og avviksspor bør gå gjennom teoretisk optimalt kryssningspunkt XP. Ledning for hovedspor skal ikke under noen omstendig*heter krysse spormidt for hovedspor mellom UP1 og UP2. Likeledes skal ikke ledning for avviksspor krysse spormidt for avviksspor mellom de samme punktene.
- Sikksakkverdi for ledning for avviksspor kan ved UP2 økes til –30 cm selv om det bygges S20 dersom dette medfører at krysningspunktet blir gunstigere sett i forhold til teoretisk optimalt XP.
- Man skal alltid prøve å la virkelig XP ligge nærmere spormidt for hovedspor enn spormidt for avviksspor. Ved strømavtakerpassering er det ideelt at XP kommer så nær midten av slepekullet som mulig. Ved å holde XP nærmest midten av slepekullet i hovedspor sørger man for de beste dynamiske forholdene i det sporet der hastigheten er høyest.
- Ved UP1 bør utligger for avviksspor være en strekkutligger mens utligger for hovedspor bør være en trykkutligger. Dersom begge utliggerne er av samme type vil man få problemer med plassen da liner og tråder for en utligger skal ”tres” gjennom den andre utliggeren. For at utligger for avviksspor ved UP1 skal være en strekkutligger så må ledning for avviksspor gå gjennom en føringsutligger før den kommer til loddavspenningen.
- Ved UP2 vil utligger for avviksspor få en stor utliggerlengde. For å stive opp utliggeren bør denne ha et diagonalrør. Ved bygging av S25 har alle utliggere diagonalrør.
Ved bygging av kontaktledningsanlegg S25 over sporveksler skal det i utgangspunktet brukes andre verdier for sikksakk. Det er imidlertid fult mulig å bruke sikksakk som for S20. En forutsetning som alltid vil være til stede er overholdelse av krav til tillatt vindutblåsning, samt krav til minimum kraft i direksjonsstaget. Figur .28 viser et forslag til ledningsføring for S25 over en enkel sporveksel.
1.6.4 Sporsløyfer
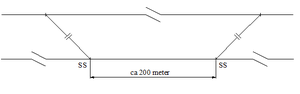
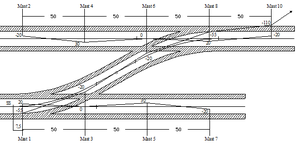
Sporsløyfer benyttes på dobbeltsporede strekninger for å kunne ha en mer smidig togtrafikkavvikling. Særlig ved feil kan sporsløyfene ofte forhindre en total stopp i toggangen. Et komplett sett med sporsløyfer består av 4 sporveksler og gjør det mulig å kjøre fra det ene sporet og over til det andre uavhengig av hvilket spor toget kommer i og hvilken retning det har. Figur .29 viser elektrisk kobling ved en komplett sporsløyfe. Kontaktledningsmessig er det viktig at avstanden mellom de to stokkskinneskjøtene som ligger nærmest hverandre er tilstrekkelig for en fornuftig ledningsføring og masteplassering. Bruk av føringsutligger før avspenning fører til at avstanden fra stokkskinneskjøten til avspenningsmasten blir om lag 100 meter. Dersom begge sløyfeledningene avspennes i samme mast midt i sporsløyfearrangementet bør avstanden mellom de to sporsløyfene være ca. 200 meter målt fra stokkskinneskjøt til stokkskinneskjøt.
I hovedsporene deles kontaktledningsanlegget elektrisk ved bruk av seksjonsfelter, mens det mellom vekslenes avviksspor deles opp ved hjelp av seksjonsisolatorer. Ofte benyttes sporsløyfene på strekninger der hastighetene i hovedspor er store, det vil si opp til 200 - 250 km/t. Sporvekslene har også blitt vesentlig større og har nå hastigheter opp mot 140 km/t i avvikssporet. Det er derfor viktig at ledningsføringen gjøres på en slik måte at den ikke blir dimensjonerende for hastigheten. Ved ledningsføring over sporsløyfer benyttes det samme teorigrunnlag som for enkeltsporveksler.
Figur 30 viser en del av en komplett sporsløyfearrangement. Sporvekslene her har en stigning på 1:18.5 og en radius på 1200 m. Avstanden mellom de to hovedsporene er 5,4 m. Kontaktledningssystemet er S20A. Masteplassering i forhold til stokkskinneskjøt er den samme for begge vekslene samtidig som spennlengdene er valgt slik at alle mastene står rett ovenfor hverandre. Seksjonsisolatoren er plassert midt mellom mast 3 og mast 6 og vil på grunn av symmetri ha sikksakkverdi 0 cm. Det er vist føringsutligger for avvikssporet ved mast 10. Denne er benyttet for at det skal være både trykk-og strekkutligger ved mast 8. Det samme vil gjelde for den andre sporvekselen, men dette er ikke vist på figuren. Mast 4 og mast 5 har tilsynelatende gal sikksakk, men verdien 30 cm er valgt for at kreftene i direksjonsstagene for hovedspor ved mastene 3 og 6 skal komme over grenseverdien på 80 N. Ved enkelte sporsløyfer kan sporvekslene ligge slik at prosjekteringen fører til at mastene for de to sporene ikke blir stående rett ovenfor hverandre. Det viktigste er plasseringen av UP1 og UP2 ved hver enkelt veksel. De andre spennlengdene justeres slik at mastene etter en viss avstand igjen står rett ovenfor hverandre. Regelen om [math]\plusmn[/math] 20 % endring av spennlende mellom to påfølgende spenn kan fravikes for selve sløyfesporet. UP1 og UP2 bør refereres til de respektive vekslenes stokkskinneskjøter.
1.7 Beskyttelsesjording
På grunn av fare for høye berøringsspenninger ved brudd i kretsen for beskyttelsesjording, skal alle beskyttelsesledere, skjøter, avgreininger og koblingspunkter som inngår i kretsen, legges slik at de ikke utsettes for unødvendige mekaniske påkjenninger. Samtidig må de legges slik at eventuelle skader er lette å oppdage ved inspeksjon.
Den langsgående jordlederen bør legges i kabelkanal. Kabelkanalen vil beskytte den mot mekanisk skade. I kabelkanalen skal den langsgående jordlederen ligge øverst, slik at den er lett tilgjengelig for inspeksjon. Dette skal gjøres fordi det da er enkelt å sjekke om jordlederen er hel eller om den er ødelagt. Dersom den er ødelagt er det fare for høye berøringsspenning på ledende konstruksjoner. Ved at jordlederen ligger lett tilgjengelig er det også enkelt å koble til eller fra utstyr. Hovedutjevningsforbindelsen skal beskyttes med plastrør i pukken og legges loddrett på svillekant inn til jernbaneskinne. Røret skal legges 0,5 meter under skinneoverkant.
Ved direkte jording mellom utsatt anleggsdel og skinnegangen skal jordledningen legges 0,5 m under skinneoverkant. Dersom det er kabelkanal skal jordledningen beskyttes av et plastrør med diameter 32 mm i pukken, ellers skal jordledningen graves ned. Ved kryssinger skal jordledningene ligge over kabler, men under kabelkanal. Ved direkte jording skal også utjevningsforbindelsene legges slik at de er lett tilgjengelig for inspeksjon samtidig som de er best mulig beskyttet mot mekaniske påkjenninger. Årsaken er den samme som nevnt ovenfor.
Utfra erfaringer kan ikke beskyttelsesjordledningene ha mindre tverrsnitt enn 50 mm2. Dersom de har mindre tverrsnitt er det fare for at de blir mekanisk skadet ved forlegning.
Alle tilkoblingene på skinnene skal utføres med godkjent skruforbindelse. Forbindelsen skal være skrudd fordi det skal være muligheter for frakobling ved arbeider i sporet, som for eksempel ballastrensing, og ved målinger. Skruforbindelsene skal i tillegg korrosjonsbeskyttes for at de ikke skal ruste. Skruforbindelsen må være godkjent slik at den ikke løsner når tog kjører forbi, og det oppstår vibrasjoner i skinnegangen.
Når det gjelder den mekaniske systembeskrivelsen av filterimpedansen som benyttes ved tilkobling til skinnegangen, så henvises det til punkt 1.5.3 Filterimpedans.
1.8 ISOLATORER
Isolatorer brukes der hvor to anleggsdeler skal være elektrisk atskilt samtidig som de er mekanisk sammenhengende. Dette stiller både elektriske og mekaniske krav til isolatorer. Isolatorer som benyttes i kontaktledningsanlegget må være laget av slike materialer og ha en slik utforming at de tåler de elektriske, mekaniske, termiske og klimatiske påvirkninger de blir utsatt for. Den elektriske beskrivelsen av isolatorer finnes i ”Elektrisk systembeskrivelse”. Dette kapittelet beskriver også hvor i kontaktledningsanlegget de forskjellige isolatortypene benyttes. Isolatorer skal i utgangspunktet ha slike mekaniske egenskaper at de ikke endrer form eller styrke, selv om de skulle svikte elektrisk. På samme måte er det ønskelig at isolatoren har slike mekaniske egenskaper at følgeskader unngås om isolatoren skulle bli utsatt for hærverk. Det vil si at den ikke deler seg når den knuses, slik at utliggeren eller ledningen faller ned. Det er viktig at isolatorer behandles med forsiktighet på byggeplasser slik at de ikke er skadet ved montering. Teknisk regelverk krever at isolatorene beholder emballasjen på til anleggsplassen er ryddet og rengjort.
Mekaniske krav til isolatorer.
Tekniske spesifikasjoner for kontaktledningsanlegg [7] og Teknisk regelverk beskriver mekaniske minstekrav til isolatorer i kontaktledningsanlegg. Her gjengis kun noen av kravene. De mekaniske kravene er forskjellige alt etter hvor isolatoren skal benyttes.
- Isolatorer i kontakttråd og bæreline skal minimum tåle 4 ganger strekkraften i den line der de skal monteres og ha minimum 1,6 ganger linens bruddstyrke. Av standardiseringshensyn skal isolatorer til samme formål være ombyttbare. De må derfor dimensjoneres etter den line som har størst strekkraft og bruddstyrke.
- Isolatorer i utliggere har ulik belastning avhengig av om utliggeren de er montert i, står på trykk eller strekk. I tillegg varierer kreftene på isolatoren alt etter om den er montert i strekkstaget eller trykkstaget på utliggeren. Fordi isolatorene skal være ombyttbare må de dimensjoneres etter 4 ganger det største belastningstilfellet.
- Isolatorer i retur-, mate-, forbigangs- og forsterkningsledning dimensjoneres for 3 ganger de vertikale og horisontale krefter som de kan utsettes for.
- Isolatorer i barduner skal dimensjoneres for 3 ganger den belastning som de utsettes for.
- Seksjonsisolatorer skal ha mekaniske egenskaper som gjør at de kan settes inn i strekk for alle kontaktledningssystemer. De må ha dynamiske egenskaper som gjør at kraften mellom strømavtaker og isolator ikke overskrider 150 N ved alle aktuelle hastigheter. Isolatoren må ikke miste sin isolasjonsevne som følge av forurensning eller kullavsetning fra strømavtaker.
Isolatorer som benyttes i kontaktledningsanlegget skal prøves i henhold til gjeldende IEC publikasjoner, se Tekniske spesifikasjoner [7].
LITTERATURHENVISNINGER
1. Jernbaneverket – Teknisk regelverk JD 540, rev.1, Jernbaneverket (jan. 1999)
2. Jernbaneverket – Teknisk regelverk JD 542, rev.1, Jernbaneverket (jan. 1999)
3. Produkt- og elektrisitetstilsynet – Forskrifter for elektriske anlegg. Forsyningsanlegg FEA-F, (aug. 1994)
4. Tormod Dyken – Styrke- og deformasjonsbeegning av KL-fundamentet Mofix, Jernbaneverket Ingeniørtjenesten, (des. 1998)
5. Oddbjørn Jorde – Utvikling av åk. Lastgrunnlag, Jernbaneverket Ingeniørtjenesten (jan. 1997) 6. Oddbjørn Jorde – Utvikling av åk. Statiske beregninger, åk type 12 og åk type 14, Jernbaneverket Ingeniørtjenesten (jan. 1997)
7. Jernbaneverket – Teknisk spesifikasjoner KL-anlegg, Jernbaneverket (1998)