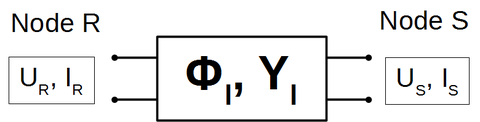Elektrisk systembeskrivelse av kontaktledningsanlegg ver01

__NUMBEREDHEADINGS__

Generelt

Kontaktledningsanlegget overfører effekt mellom matestasjonen og traksjonsmateriell og andre belastninger tilknyttet kontaktledningen. I eldre anlegg skjer overføringen i kontaktledning ved 15 kV nominell spenning, med retur i kjøreskinner ved 0 kV. I nyere anlegg er det innført returledere eller AT-system med positivleder og negativleder. Følgende ledere er vanlige i et kontaktledningsanlegg. Det kan finnes ytterligere ledere parallelt med jernbanetraseen som påvirker eller påvirkes av kontaktledningsanlegget.

<figtable id="tab:Ledere_oversikt">

Ledere oversikt

Leder	Forklaring	Nominell spenning
KL	Kontaktledningsanlegg, omfatter kontakttråd og bæreline	15 kV
RR	Kjøreskinner	0 kV
RL	Returleder	0 kV
FSL	Forsterkningsleder	15 kV
PL	Positivleder (for AT-system)	+ 15 kV
NL	Negativleder (for AT-system)	- 15 kV

</figtable>

I dette kapittelet beskrives en matematisk modell som beregner hvordan strøm og spenning fordeler seg mellom ulike ledere i et slikt flerledersystem som et kontaktledningsanlegg utgjør. Denne modellen er det teoretiske grunnlaget for beregning av:

• impedansen mellom matestasjon og belastning i kontaktledningssystemet,
• potensial i returkretsen,
• indusert spenning i ledere som går parallelt med jernbanetraseen,
• belastning på enkeltledere og komponenter i kontaktledningsnettet.

I praktisk bruk er regnemodellen programmert inn i et regneprogram der numeriske parametre for beregningen angis og resultatet presenteres i form av grafer og tabeller.

Lineær modell

Et kontaktledningsanlegg har en tilnærmet lineær oppførsel og kan derfor for mange formål modelleres som et lineært system.

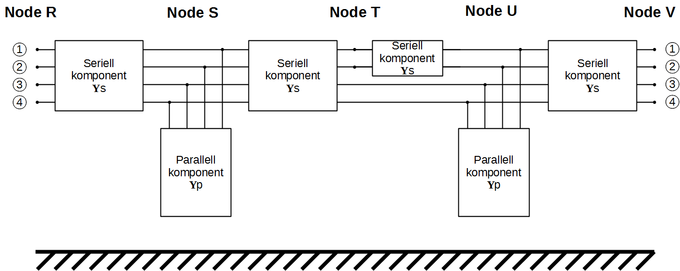
<xr id="fig:LinearModell"/> viser skjematisk en linje med serielle og parallelle komponenter for et system med fire ledere. Serielle komponenter har koplingspunkter til en eller flere av lederne på hver side av komponenten, mens parallelle komponenter kun har en kopling til hver leder.

<figure id="fig:LinearModell">

Linje med 5 noder, 4 ledere og 6 lineære kretselementer. Strekningen har 18 koplingspunkter: 2 for node T og 4 for hver av de andre nodene. </figure> En lineær elektrisk modell av en komponent eller et system kan uttrykkes ved hjelp av en admittansmatrise. Admittansmatrisen angir strømmen som påtrykkes alle systemets koplingspunkter, som funksjon av spenningen ved hver enkelt node, der både strømmen og spenningen er viserverdier. Skrevet på matriseform: ${\begin{pmatrix}I_{1}\\\vdots \\I_{18}\end{pmatrix}}={\begin{pmatrix}Y_{1,1}&\cdots &Y_{1,18}\\\vdots &\ddots &\vdots \\Y_{18,1}&\cdots &Y_{18,18}\end{pmatrix}}\cdot {\begin{pmatrix}U_{1}\\\vdots \\U_{18}\end{pmatrix}}$ For systemet i <xr id="fig:LinearModell"/> har vektorene $\mathbf {I}$ og $\mathbf {U}$ 18 elementer hver, mens admittansmatrisen $\mathbf {Y}$ har (18 x 18) elementer. Hver komponent i systemet kan uttrykkes ved sin admittansmatrise. Systemets admittansmatrise er summen av matrisene for alle komponentene. Det er noen viktige fordeler med å beskrive systemer og komponenter ved sin admittansmatrise framfor alternative beskrivelser:

• Admittansmatrisen for en komponent eller et system er alltid definert (i motsetning til noen av de alternative beskrivelsene).
• Admittansmatrisen for alle systemets komponenter kan enkelt kombineres til en felles admittansmatrise for et helt system.
• Admittansmatrisen for et system er glissen, som gjør at den kan lagres uten at det krever svært stor lagringsplass.
• Ved beregning av lastflytanalyse i et kraftsystem, beskrives kraftsystemet ved systemets admittansmatrise.

Under forutsetning av at systemet har minst en jordforbindelse er admittansmatrisen $\mathbf {Y}$ inverterbar. Det er da mulig å uttrykke alle systemets spenninger som funksjon av påtrykket strøm i alle systemets koplingspunkter, via den inverse admittansmatrisen, som kalles impedansmatrisen. De aller fleste av systemets koplingspunkter blir ikke påtrykket strøm, og i de resterende koplingspunktene er strømmen kjent. Derfor er det ofte av størst interesse å beregne spenning på bakgrunn av kjente verdier for strøm. ${\begin{pmatrix}U_{1}\\\vdots \\U_{18}\end{pmatrix}}={\begin{pmatrix}Z_{1,1}&\cdots &Z_{1,18}\\\vdots &\ddots &\vdots \\Z_{18,1}&\cdots &Z_{18,18}\end{pmatrix}}\cdot {\begin{pmatrix}I_{1}\\\vdots \\I_{18}\end{pmatrix}}$ Ved å sette inn belastninger fra tog eller kortslutninger ved aktuelle noder/koplingspunkter får man som resultat spenningen ved samtlige andre noder i systemet. Dette kan så benyttes til videre å beregne strøm- og spenningsprofil for hver enkelt komponent. Forhold som ikke er lineære, og som derfor må tilnærmes i en lineær modell, er:

• magnetiske egenskaper for stålskinner, som gjør stålets indre reaktans ulineært avhengig av strøm og frekvens,
• strømfortrengning i ledere, som gjør den elektriske motstanden i en leder ulineært avhengig av frekvens, og
• aktivt styrte belastninger, for eksempel tog.

I de kommende avsnittene beskrives hvordan admittansmatrisen etableres for de ulike komponenttypene i et kontaktledningssystem:

• Seriell komponent: Transmisjonslinje
• Seriell komponent: Sugetransformator
• Seriell komponent: Seksjonering eller brudd
• Parallell komponent: Autotransformator
• Parallell komponent: Jordforbindelse
• Parallell komponent: Kilde og belastning

Transmisjonslinje

Enkel linjesløyfe

Den enkleste formen for problemet er ei enkel linjesløyfe. Det finnes mye teori som beskriver problemet, og problemet har kjent analytisk løsning. Det tas i avsnittet en rask gjennomgang av den grunnleggende teorien, fordi den samme framgangsmåten benyttes for analyse av et flerledersystem.

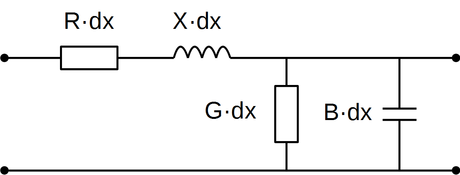
En kontaktledning med retur i kjøreskinner kan forenklet betraktes som ei linjesløyfe, hvis man ser bort fra lekkasje til jordsmonn. Telegraflikningen tar utgangspunkt i et svært kort segment $\mathrm {d} x$ av linjesløyfa. Linjesegmentet har en seriell resistans $R\cdot \mathrm {d} x$ og reaktans $X\cdot \mathrm {d} x=\omega \cdot L\cdot \mathrm {d} x$, og en parallell konduktans $G\cdot \mathrm {d} x$ og susceptans $B\cdot \mathrm {d} x=\omega \cdot C\cdot \mathrm {d} x$. Her er L, C og $\omega$ henholdsvis linjens induktans, kapasitans og vinkelfrekvens.

<figure id="fig:Telegraflikningene">

Telegraflikningene - Kretsskjema for et linjesegment dx </figure> Parametrene kan skrives om om slik at impedansen blir $Z=R+jX$ og admittansen blir $Y=G+jB$. Parametrene kan finnes ved beregning eller ved måling. Det serielle spenningsfallet dU over dette linjesegmentet er gitt av Ohms lov: (i) ${\frac {\mathrm {d} U}{\mathrm {d} x}}=-Z\cdot I$ Strømmen som lekker gjennom admittansen $Y$ utgjør forskjellen i strøm over linjesegmentet. Denne strømmen er proporsjonal med spenningen: (ii) ${\frac {\mathrm {d} I}{\mathrm {d} x}}=-Y\cdot U$ Likningene (i) og (ii) danner et koplet likningssett som i litteraturen kalles for telegraflikningene. Likningssettet kan ordnes med matriserepresentasjon på følgende måte: ${\frac {\mathrm {d} }{\mathrm {d} x}}{\begin{pmatrix}U\\I\end{pmatrix}}={\begin{pmatrix}0&-Z\\-Y&0\end{pmatrix}}\cdot {\begin{pmatrix}U\\I\end{pmatrix}}=\mathbf {A} \cdot {\begin{pmatrix}U\\I\end{pmatrix}}$ Her har systemmatrisen A dimensjonene (2 x 2). Løsningen på et slikt likningssett er beskrivet i flere lærebøker i lineæralgebra, for eksempel i Referanse [1]. En rask innføring er gitt i Wikipedia. Egenverdiene $\lambda$ til systemet er: $\lambda _{1}=+{\sqrt {Z\cdot Y}}=\gamma$ $\lambda _{2}=-{\sqrt {Z\cdot Y}}=-\gamma$ der $\gamma ={\sqrt {Z\cdot Y}}$ er linjens forplantningskonstant. De tilhørende egenvektorene kan finnes til å være: $\mathbf {v_{1}} ={\begin{pmatrix}1\\-{\sqrt {\tfrac {Y}{Z}}}\end{pmatrix}}={\begin{pmatrix}1\\-{\tfrac {1}{Z_{0}}}\end{pmatrix}}$ $\mathbf {v_{2}} ={\begin{pmatrix}1\\{\sqrt {\tfrac {Y}{Z}}}\end{pmatrix}}={\begin{pmatrix}1\\{\tfrac {1}{Z_{0}}}\end{pmatrix}}$ der $Z_{0}={\sqrt {\tfrac {Z}{Y}}}$ er linjens karakteristiske impedans. Forplantningskonstanten $\gamma$ er en kompleks størrelse og et mål på hvordan en strøm/spenning dempes og forandrer fase langs en transmisjonslinje. Den karakteristiske impedansen $Z_{0}$ er et mål på sammenhengen mellom strøm og spenning i en transmisjonslinje. Egenvektorene $\mathbf {v_{1}}$ og $\mathbf {v_{1}}$ ordnes så i en egenvektormatrise $\mathbf {V}$: $\mathbf {V} ={\begin{pmatrix}\mathbf {v_{1}} &\mathbf {v_{2}} \end{pmatrix}}={\begin{pmatrix}1&1\\-{\tfrac {1}{Z_{0}}}&{\tfrac {1}{Z_{0}}}\end{pmatrix}}$ Egenvektormatrisen $\mathbf {V}$ har følgende inverse: $\mathbf {V^{-1}} ={\frac {1}{2}}{\begin{pmatrix}1&-Z_{0}\\1&Z_{0}\end{pmatrix}}$ Løsningen er gitt av følgende uttrykk: ${\begin{pmatrix}U\\I\end{pmatrix}}(x)=\mathbf {V} \cdot e^{\mathbf {\Lambda } x}\cdot \mathbf {V^{-1}} \cdot {\begin{pmatrix}U_{0}\\I_{0}\end{pmatrix}}=\mathbf {\Phi } (x)\cdot {\begin{pmatrix}U_{0}\\I_{0}\end{pmatrix}}$ der:
$U_{0}$ og $I_{0}$ er strøm og spenning ved posisjonen $x=0$,
$e^{\mathbf {\Lambda } x}$ er en diagonal 2x2-matrise med diagonale elementer $e^{\gamma x}$ og $e^{-\gamma x}$ , og
$\mathbf {\Phi } (x)$ er den resulterende løsningsmatrisen. Skrevet fullt ut er løsningsmatrisen: $\mathbf {\Phi } (x)={\begin{pmatrix}\cosh {(\gamma x)}&-Z_{0}\sinh({\gamma x)}\\-{\tfrac {1}{Z_{0}}}\sinh {(\gamma x)}&\cosh {(\gamma x)}\end{pmatrix}}$ Løsningen gir en komplett beskrivelse av strøm og spenning i alle punkter langs en transmisjonslinje, dersom strømmen og spenningen ved posisjon $x=0$ er kjent. <figure id="fig:Admittansbeskrivelse_2porter">

Et linjesegment med lengde $l$ har lineære karakteristikker og kan beskrives komplett ved en 2x2 løsningsmatrise $\mathbf {\Phi _{l}}$ eller admittansmatrise $\mathbf {Y_{l}}$ </figure> For en linje av lengde $l$ som vist i <xr id="fig:Admittansbeskrivelse_2porter" /> mellom punktene $R$ og $S$ kan man finne sammenhengen mellom strøm og spenning ved de to linjeendene ved: ${\begin{pmatrix}U_{S}\\-I_{S}\end{pmatrix}}=\mathbf {\Phi } (l)\cdot {\begin{pmatrix}U_{R}\\I_{R}\end{pmatrix}}=\mathbf {\Phi _{l}} \cdot {\begin{pmatrix}U_{R}\\I_{R}\end{pmatrix}}$ der $U_{S}=U(0),\;U_{R}=U(l),\;I_{S}=I(0),\;I_{R}=-I(l)$. Grunnen til det negative fortegnet for $I_{R}$ er at vi nå definerer strømmen som positiv inn i linja ved begge linjeender. Man vil i mange tilfeller kjenne spenningen ved de to linjeendene, og ønske å beregne strømmen. Da kan likningssettet skrives om på admittansmatriseform slik at: ${\begin{pmatrix}I_{R}\\I_{S}\end{pmatrix}}=\mathbf {Y_{l}} \cdot {\begin{pmatrix}U_{R}\\U_{S}\end{pmatrix}}$ Man kan finne at matrisen $\mathbf {Y_{l}}$ er: $\mathbf {Y_{l}} ={\frac {1}{Z_{0}\sinh {(\gamma l)}}}{\begin{pmatrix}\cosh {(\gamma l)}&-1\\-1&\cosh {(\gamma l)}\end{pmatrix}}$

Transmisjonslinje med flere parallelle ledere

Ved flere parallelle ledere blir framgangsmåten svært lik den som er skissert for en linjesløyfe, men matematikken blir så komplisert at den ikke kan gjøres analytisk. Den må derfor i stedet gjennomføres numerisk, vanligvis ved hjelp av en datamaskin.

I tillegg til resistans og selvinduktans for hver enkelt leder vil det også være en gjensidig induktans mellom hver enkelt leder. Den gjensidige induktansen gir et tillegg til spenningen over en leder som følge av strømmen i hver av de andre lederne. For et system med n (1, 2, ... n) ledere kan dette beskrives med matriser på følgende måte:

${\frac {\mathrm {d} }{\mathrm {d} x}}{\begin{pmatrix}U_{1}\\\vdots \\U_{n}\end{pmatrix}}=-\left[{\begin{pmatrix}R_{11}&\cdots &R_{1n}\\\vdots &\ddots &\vdots \\R_{n1}&\cdots &R_{nn}\end{pmatrix}}+j\cdot {\begin{pmatrix}X_{11}&\cdots &X_{1n}\\\vdots &\ddots &\vdots \\X_{n1}&\cdots &X_{nn}\end{pmatrix}}\right]\cdot {\begin{pmatrix}I_{1}\\\vdots \\I_{n}\end{pmatrix}}=-{\begin{pmatrix}Z_{11}&\cdots &Z_{1n}\\\vdots &\ddots &\vdots \\Z_{n1}&\cdots &Z_{nn}\end{pmatrix}}\cdot {\begin{pmatrix}I_{1}\\\vdots \\I_{n}\end{pmatrix}}$

På tilsvarende måte kan det være en konduktiv eller kapasitiv lekkasje mellom hver leder i et ledningssystem. Dette kan beskrives på matriseform på følgende måte for de samme lederne:

${\frac {\mathrm {d} }{\mathrm {d} x}}{\begin{pmatrix}I_{1}\\\vdots \\I_{n}\end{pmatrix}}=-\left[{\begin{pmatrix}G_{11}&\cdots &G_{1n}\\\vdots &\ddots &\vdots \\G_{n1}&\cdots &G_{nn}\end{pmatrix}}+j\cdot {\begin{pmatrix}B_{11}&\cdots &B_{1n}\\\vdots &\ddots &\vdots \\B_{n1}&\cdots &B_{nn}\end{pmatrix}}\right]\cdot {\begin{pmatrix}U_{1}\\\vdots \\U_{n}\end{pmatrix}}=-{\begin{pmatrix}Y_{11}&\cdots &Y_{1n}\\\vdots &\ddots &\vdots \\Y_{n1}&\cdots &Y_{nn}\end{pmatrix}}\cdot {\begin{pmatrix}U_{1}\\\vdots \\U_{n}\end{pmatrix}}$

På kompakt matriseform kan dette skrives:

${\frac {\mathrm {d} }{\mathrm {d} x}}{\begin{pmatrix}\mathbf {U} \\\mathbf {I} \end{pmatrix}}={\begin{pmatrix}\mathbf {0} &\mathbf {-Z} \\\mathbf {-Y} &\mathbf {0} \end{pmatrix}}\cdot {\begin{pmatrix}\mathbf {U} \\\mathbf {I} \end{pmatrix}}=\mathbf {A} \cdot {\begin{pmatrix}\mathbf {U} \\\mathbf {I} \end{pmatrix}}$

Her er systemmatrisen $\mathbf {A}$ en matrise med dimensjoner (2n x 2n). Parametermatrisene $\mathbf {R}$, $\mathbf {X}$, $\mathbf {G}$ og $\mathbf {B}$ er bestemt ut ifra benyttede ledermaterialer, isolasjonsmaterialer, jordsmonn, systemets geometri og driftsfrekvens. Bestemmelse av parametermatrisene er beskrevet i Lenke: Parametre for flerledersystem

Systemmatrisen $\mathbf {A}$ har 2n egenverdier $\lambda _{i}$ med 2n tilhørende egenvektorer $\mathbf {v_{i}}$. Disse må finnes numerisk av datamaskiner for aktuelle parametermatriser. Systemets løsning blir på formen:

${\begin{pmatrix}\mathbf {U} \\\mathbf {I} \end{pmatrix}}(x)=\mathbf {V} \cdot e^{\mathbf {\Lambda } x}\cdot \mathbf {V^{-1}} \cdot {\begin{pmatrix}\mathbf {U_{0}} \\\mathbf {I_{0}} \end{pmatrix}}=\mathbf {\Phi } (x)\cdot {\begin{pmatrix}\mathbf {U_{0}} \\\mathbf {I_{0}} \end{pmatrix}}$

der:
$\mathbf {U_{0}}$ og $\mathbf {I_{0}}$ er strøm og spenning ved posisjonen $x=0$,
$e^{\mathbf {\Lambda } x}$ er en diagonal (2n x 2n)-matrise med diagonale elementer $e^{\lambda _{i}x}$,
$\mathbf {V}$ er (2n x 2n) egenvektormatrisen der kolonne nr. i er egenvektoren $\mathbf {v_{i}}$ til egenverdien $\lambda _{i}$ , og
$\mathbf {\Phi } (x)$ er den resulterende løsningsmatrisen med dimensjoner (2n x 2n).

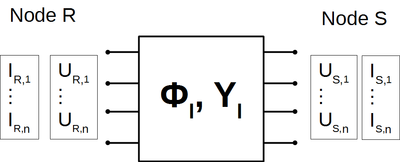
<figure id="fig:Admittansbeskrivelse_nlinjer">

Et linjesegment med lengde $l$ har lineære karakteristikker og kan beskrives komplett ved en 2nx2n løsningsmatrise $\mathbf {\Phi _{l}}$ eller admittansmatrise $\mathbf {Y_{l}}$ </figure> På samme måte som for den enkle linjesløyfa kan man for en linje med lengde $l$ som vist i <xr id="fig:Admittansbeskrivelse_nlinjer" /> mellom nodene $R$ og $S$ finne sammenhengen mellom strøm og spenning ved de to linjeendende ved: ${\begin{pmatrix}\mathbf {U_{S}} \\-\mathbf {I_{S}} \end{pmatrix}}=\mathbf {\Phi } (l)\cdot {\begin{pmatrix}\mathbf {U_{R}} \\\mathbf {I_{R}} \end{pmatrix}}=\mathbf {\Phi _{l}} \cdot {\begin{pmatrix}\mathbf {U_{R}} \\\mathbf {I_{R}} \end{pmatrix}}$ For å finne admittansmatrisebeskrivelsen deles løsningsmatrisen $\mathbf {\Phi _{l}}$ inn i fire (n x n) submatriser på følgende måte: ${\begin{pmatrix}\mathbf {U_{S}} \\-\mathbf {I_{S}} \end{pmatrix}}={\begin{pmatrix}\mathbf {\Phi _{l,11}} &\mathbf {\Phi _{l,12}} \\\mathbf {\Phi _{l,21}} &\mathbf {\Phi _{l,22}} \end{pmatrix}}\cdot {\begin{pmatrix}\mathbf {U_{R}} \\\mathbf {I_{R}} \end{pmatrix}}$ En kan da finne at beskrivelsen på admittansmatriseform $\mathbf {Y_{l}}$ blir: ${\begin{pmatrix}\mathbf {I_{R}} \\\mathbf {I_{S}} \end{pmatrix}}=\mathbf {Y_{l}} \cdot {\begin{pmatrix}\mathbf {U_{R}} \\\mathbf {U_{S}} \end{pmatrix}}={\begin{pmatrix}\mathbf {Y_{l,11}} &\mathbf {Y_{l,12}} \\\mathbf {Y_{l,21}} &\mathbf {Y_{l,22}} \end{pmatrix}}\cdot {\begin{pmatrix}\mathbf {U_{R}} \\\mathbf {U_{S}} \end{pmatrix}}$ der ${\begin{aligned}\mathbf {Y_{l,11}} &=-\mathbf {\Phi _{l,12}^{-1}} \cdot \mathbf {\Phi _{l,11}} \\\mathbf {Y_{l,12}} &=\mathbf {\Phi _{l,12}^{-1}} \\\mathbf {Y_{l,21}} &=\mathbf {\Phi _{l,22}} \cdot \mathbf {\Phi _{l,12}^{-1}} \cdot \mathbf {\Phi _{l,11}} -\mathbf {\Phi _{l,21}} \\\mathbf {Y_{l,22}} &=-\mathbf {\Phi _{l,22}} \cdot \mathbf {\Phi _{l,12}^{-1}} \end{aligned}}$

Sugetransformator

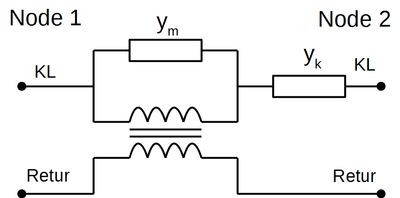
Ekvivalentskjema for en sugetransformator kan tegnes som vist i <xr id="fig:Sugetransformator_skjema"/>, der y_m er magnetiseringsadmittansen og y_k er kortslutningsadmittansen.

<figure id="fig:Sugetransformator_skjema">

Ekvivalentskjema for sugetransformator. </figure> Basert på dette skjemaet kan en admittansmatrise etableres som følger: ${\begin{pmatrix}I_{1-KL}\\I_{1-Retur}\\I_{2-KL}\\I_{2-Retur}\end{pmatrix}}={\begin{pmatrix}(y_{m}+y_{k})&-y_{k}&-(y_{m}+y_{k})&y_{k}\\-y_{k}&y_{k}&y_{k}&-y_{k}\\-(y_{m}+y_{k})&y_{k}&(y_{m}+y_{k})&-y_{k}\\y_{k}&-y_{k}&-y_{k}&y_{k}\end{pmatrix}}\cdot {\begin{pmatrix}U_{1-KL}\\U_{1-Retur}\\U_{2-KL}\\U_{2-Retur}\end{pmatrix}}$ For å finne verdiene for parametrene y_m og y_k leser man datablad for en sugetransformator. I Norge benyttes to typer sugetransformator: 600 A og 800 A, og dataene for disse er gjengitt under. For de fleste praktiske formål kan y_m settes til 0 S, kun ved analyse av brudd i returkretsen kan denne få betydning. <figtable id="tab:Data_for_sugetransformatorer">

Data for sugetransformatorer

Parameter	Symbol	Enhet	Sugetransformator 600 A	Sugetransformator 600 A	Sugetransformator 800 A
Merkeytelse (datablad)	Sn	kVA	55	55	95
Merkestrøm (datablad)	Ir	A	600	600	800
Merkespenning (datablad)	Ur	V	91,7	91,7	118,75
Merkeimpedans (beregnet)	Zr	Ω	0,1528	0,1528	0,1484
Kortslutningstap (målt)	Pk	W	1 099	4 429	7 012
Tomgangstap (målt)	Po	W	9	39	40
Tomgangsstrøm (målt)	Io	A	0,2	0,6 (antatt)	0,5 (antatt)
Kortslutningsimpedans (målt)	ez / ek	%	22,89	20,24	18,2
Kortslutningsresistans (beregnet)	er	%	10,47	8,05	7,38
Kortslutningsreaktans (beregnet)	ex	%	20,36	18,57	16,64
Magnetiseringsadmittans (beregnet)	ym	mS	2,18	6,55	4,21
Magnetiseringskonduktans (beregnet)	gm	mS	1,07	4,64	2,84
Magnetiseringsreaktans (beregnet)	bm	mS	1,90	4,61	3,11
Produsent			ABB	Møre Trafo	Møre trafo
Kilde			EK.800131	EK.800207	EK.800208
Kortslutningsadmittans	yk	S	13,08 - j 25,42	12,84 - j 29,65	14,62 - j 32,87
Magnetiseringsadmittans	ym	mS	1,07 + j 1,90	4,64 + j 4,61	2,84 + j 3,11

</figtable>

Seksjonering

En seksjonering kan tegnes som en seriell admittans som vist i <xr id="fig:Seksjonering_skjema"/>.

<figure id="fig:Seksjonering_skjema">

Ekvivalentskjema for seksjonering. </figure> Admittansmatrisen for en slik seriell admittans er: ${\begin{pmatrix}I_{1}\\I_{2}\end{pmatrix}}={\begin{pmatrix}y&-y\\-y&y\end{pmatrix}}\cdot {\begin{pmatrix}U_{1}\\U_{2}\end{pmatrix}}$ For en ren seksjonering er motstanden svært stor, og admittansen y kan settes til $y=0$ S.

Autotransformator

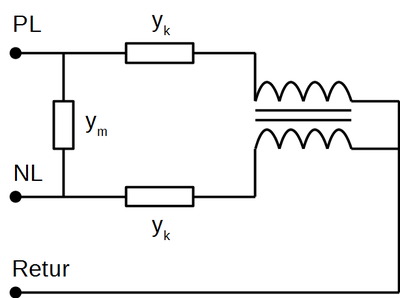
En seksjonering kan tegnes som vist i <xr id="fig:Autotransformator_skjema"/>.

<figure id="fig:Autotransformator_skjema">

Ekvivalentskjema for autotransformator. </figure> Den tilhørende admittansmatrisen kan finnes ut fra skjmaet til å være: ${\begin{pmatrix}I_{NL}\\I_{PL}\\I_{Retur}\end{pmatrix}}={\begin{pmatrix}(y_{k}+y_{m})&(y_{k}-y_{m})&(-2\cdot y_{k})\\(y_{k}-y_{m})&(y_{k}+y_{m})&(-2\cdot y_{k})\\(-2\cdot y_{k})&(-2\cdot y_{k})&(4\cdot y_{k})\end{pmatrix}}\cdot {\begin{pmatrix}U_{NL}\\U_{PL}\\U_{Retur}\end{pmatrix}}$ Parametrene y_k og y_m kan beregnes ut ifra transformatorens datablad. Merk: For krestsskjemaet og admittansmatrisen som er angitt over, må verdiene autotransformatorens høyspentvikling brukes. Datablad for en 5 MVA autotransformator fra ABB angir (kilde: EB.800106). <figtable id="tab:Data_for_sugetransformatorer">

Data for sugetransformatorer

Parameter	Symbol	Enhet	Autotransformator 5 MVA
			Høyspent- vikling	Lavspent- vikling
Merkeytelse (datablad)	Sn	kVA	5000
Merkespenning (datablad)	Ur	V	33 000	16 500
Merkestrøm (beregnet)	Ir	A	151,5	303,0
Merkeimpedans (beregnet)	Zr	Ω	217,8	54,45
Kortslutningstap (datablad)	Pk	W	10 600
Tomgangstap (datablad)	Po	W	2 600
Tomgangsstrøm	Io	A	Ikke angitt
Kortslutningsimpedans (datablad)	ez / ek	%	0,4
Kortslutningsimpedans (beregnet)	ez / ek	Ω	0,8712	0,2178
Kortslutningsresistans (beregnet)	er	Ω	0,4617	0,1154
Kortslutningsreaktans (beregnet)	ex	Ω	0,7388	0,1847
Magnetiseringskonduktans (beregnet)	gm	µS	2,3875	9,5501
Magnetiseringssusceptans antatt lik 2,5 · gm	bm	µS	5,9688	23,875
Produsent			ABB
Kilde			EK.800106
Kortslutningsadmittans	yk	S	0,6082 - j 0.9735	2,4330 - j 3,8941
Magnetiseringsadmittans	ym	µS	2,3875 + j 5,9688	9,5501 + j 23,875

</figtable>

Jordforbindelse

En jordforbindelse er en forbindelse mellom et tilkoplingspunkt i systembeskrivelsen, og fjernt jordsmonn. Jordforbindelsen omfatter overgangsmotstanden i en jordelektrode. Admittansbeskrivelsen av en jordforbindelse er:

$i_{R}=y_{RE}\cdot u_{R}$

der

i_R er strømmen i jordforbindelsen tilknyttet tilkoplingspunkt R.

y_RE er admittansen mellom tilkoplingspunkt R og jordpotensialet e.

u_R er spenningen mot jord ved tilkoplingspunkt R.

Verdien for y_RE i et tilkoplingspunkt er den inverse overgangsmotstanden:

$y_{RE}={\frac {1}{r_{RE}}}$

Verdien for overgangsmotstand må måles eller anslås ved beregning. For modellering er det antatt at matestasjoner har en admittans på 0,1 S, og for AT-kiosker er det antatt en admittans på 0,02 S for hver AT-kiosk.

Referanser

[1] Edwards, Penney: Elementary Linear Algebra, Pearson, 1987. ISBN 9780132582605.