Elektrisk systembeskrivelse av kontaktledningsanlegg ver01

__NUMBEREDHEADINGS__

Generelt

Kontaktledningsanlegget overfører effekt mellom matestasjonen og traksjonsmateriell og andre belastninger tilknyttet kontaktledningen. I eldre anlegg skjer overføringen i kontaktledning ved 15 kV nominell spenning, med retur i kjøreskinner ved 0 kV. I nyere anlegg er det innført returledere eller AT-system med positivleder og negativleder. Følgende ledere vil bli omtalt videre i dette kapittelet:

<figtable id="tab:Ledere_oversikt">

Ledere oversikt

Leder	Forklaring	Nominell spenning
KL	Kontaktledningsanlegg, omfatter kontakttråd og bæreline	15 kV
RR	Kjøreskinner	0 kV
RL	Returleder	0 kV
FSL	Forsterkningsleder	15 kV
PL	Positivleder (for AT-system)	normalt + 15 kV
NL	Negativleder (for AT-system)	normalt - 15 kV

</figtable>

I dette kapittelet vil det bli beskrevet en matematisk modell som beskriver hvordan strøm og spenning fordeler seg mellom ulike ledere i et slikt flerledersystem som et kontaktledningsanlegg utgjør. En slik modell kan brukes til å beregne:

• impedansen mellom matestasjon og belastning i kontaktledningssystemet,
• potensial i returkretsen,
• indusert spenning i ledere som går parallelt med jernbanetraseen,
• belastning på enkeltledere og komponenter i kontaktledningsnettet.

Introduksjon: Telegraflikningene

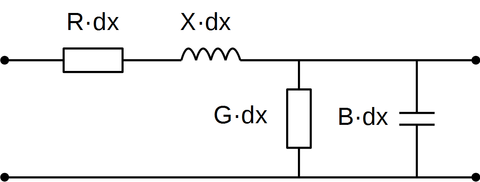
Den enkleste formen for problemet er ei enkelt linjesløyfe. En kontaktledning med retur i kjøreskinner kan forenklet betraktes på denne måten, hvis man ser bort fra lekkasje til jordsmonn. Telegraflikningen tar utgangspunkt i et svært kort linjesegment dx av linjesløyfa. Linjesegmentet har en seriell resistans R · dx og reaktans X · dx, og en parallell konduktans G · dx og susceptans B · dx.

<figure id="fig:Telegraflikningene">

Telegrafilikningen: Kretsskjema for et linjesegment dx </figure> Det serielle spenningsfallet dU over dette linjesegmentet er gitt av Ohms lov: <equation id="eqn:Telegrafilikningene - spenningsfall"> $\mathrm {d} U=-\left(R\cdot \mathrm {d} x+jX\cdot \mathrm {d} x\right)\cdot I$ </equation> Strømmen som lekker gjennom admittansen (konduktansen G og susceptansen B) utgjør forskjellen i strøm over linjesegmentet. Denne strømmen er proporsjonal med spenningen ved det aktuelle linjesegmentet: <equation id="eqn:Telegrafilikningen - endring i strom"> $\mathrm {d} I=-\left(G\cdot \mathrm {d} x+jB\cdot \mathrm {d} x\right)\cdot U$ </equation> Omskrevet og ordnet blir dette et koplet likningssett, som i litteraturen kalles for telegraflikningen. (i) ${\frac {\mathrm {d} U}{\mathrm {d} x}}=-\left(Z\right)\cdot I$
(ii) ${\frac {\mathrm {d} I}{\mathrm {d} x}}=-\left(Y\right)\cdot U$ Her er parametrene skrevet om slik at impedansen blir $Z=R+jX$ og admittansen blir $Y=G+jB$ Likningssettet kan løses for en lang linje ved å derivere (ii) og sette inn resultatet i (i) (ii) ${\frac {\mathrm {d} ^{2}I}{\mathrm {d} x^{2}}}=-Y\cdot {\frac {\mathrm {d} U}{\mathrm {d} x}}$ (ii) ${\frac {\mathrm {d} U}{\mathrm {d} x}}={\frac {-1}{Y}}\cdot {\frac {\mathrm {d} ^{2}I}{\mathrm {d} x^{2}}}$ Setter inn i (i) og skriver om: (iii) ${\frac {\mathrm {d} ^{2}I}{\mathrm {d} x^{2}}}=Y\cdot Z\cdot I$ Løsningen på en slik andre ordens differensiallikning finnes ved å anta at strømmen I har formen: (iv) $I=I_{0}\cdot e^{\gamma x}$ Ved å dobbeltderivere denne og sette inn i (iii) finner man: (iii) $I_{0}\cdot \gamma ^{2}\cdot e^{\gamma x}=Y\cdot Z\cdot I_{0}\cdot e^{\gamma x}$ Man ordner (iii) og finner: $\gamma =\pm {\sqrt {Y\cdot Z}}$ Ved å derivere (iv) og sette uttrykket inn i (ii) finner man: (ii) $I_{0}\cdot \gamma \cdot e^{\gamma x}=-\left(Y\right)\cdot U$ Uttrykket kan så ordnes: (ii) $U=I_{0}\cdot {\frac {\gamma }{-Y}}$