Effektflyt

__NUMBEREDHEADINGS__

Effektflyt

Generelt

Kontaktledningsanlegget i Norge er samkjørt, slik at alle omformerstasjonene i Norge er elektrisk forbundet på et 1-fase 15 kV og 16 2/3 Hz system. Kontaktledningsanlegget er tilknyttet 3-fase-nettet via transformatorer og frekvensomformere. Det fins to typer omformere i Norge, enten roterende aggregater som utgjør hoveddelen eller statiske omformere.

Effektflyten i kontaktledningsanlegget blir styrt av de samme fysiske prinsippene som effektflyten i et 3-fase-nett. I et 3-fase overføringssystem vil forholdet mellom resistans, R, og reaktans, X, være forskjellig fra et 1-fase kontaktledningssystem. X på R forholdet i en 3-fase overføringslinje vil i størrelsesorden være fra 1 – 15, avhengig av spenningsnivå (forholdet er størst ved høyest spenningsnivå). X på R forholdet i et kontaktledningssystem vil som regel være ca. 1.

Utledning av utrykk for aktiv og reaktiv effekt

Effektflyten i et fordelingssystem er styrt av spenningsforskjeller og vinkelforskjeller i nettet. Et enkelt fordelingssystem er vist i figur 1. Dette fordelingsnettet er brukt til å utlede et fullstendig uttrykk for den aktive og reaktive effektflyten.

Figur 1 Fordelingsnett brukt for å utlede uttrykk for aktiv- og reaktiv effektflyt

Tilsynelatende effekt, S, inn til en samleskinne er bestemt matematisk ved hjelp av likning 1.

(2.1)

Strømmen er bestemt av spenningene i samleskinne A og B, og er matematisk gitt av likning .2.

(2.2)

Setter inn uttrykket for strømmen i systemet og får (2.3)

Omformer, konjugerer og får (2.4) Fra matematiske formelsamlinger finner vi at

(2.5)

Bruker dette og setter inn i likning .4, og får

(2.6)

Konjugerer og multipliserer ut parentesene

(2.7)

Ved hjelp av regler for omgjøring av sinus og cosinus funksjoner kan uttrykket i likning .7 skrives

(2.8)

For å kunne splitte likning .8 opp i en real del og en imaginær del, må man utvide brøken med R+jX slik at det blir en reell nevner. Får da et utrykk for effekten, PA som ser slik ut:

(2.9)

Utrykket for reaktiv effekt, QA vil se slik ut:

(2.10)

Som en ser av likning .9 og .10 er effektflyten inn til en samleskinne avhengig av spenningsforskjeller og vinkelforskjeller. Ut fra de samme likningene kan en også se at effektflyten er avhengig av forholdet mellom R og X.

Til sammenligning kan en se på likningene som blir brukt for å beskrive effektflyt i et vanlig 3-fase høyspent fordelingssystem. Her blir ofte forenklingen med å si at R<<X, slik at likningene .9 og .10 kan skrives som dette:

(2.11)

(2.12)

Som en ser vil en slik forenkling gjøre likningene langt enklere, men en må huske på at i kontaktledningsanlegget er ikke de rette forutsetningene til stede. Derfor er en nødt til å bruke de fullstendige uttrykkene i likning .9 og .10.

Vinkelforskjell mellom omformerstasjonene

Generelt

Mellom omformerstasjoner vil det være vinkelforskjeller. Grunnen til dette er at det er vinkelforskjeller i tilkoblingspunktene på 3-fase siden, samt at de roterende omformerstasjonene har en iboende vinkelkarakteristikk som gjør at lastvinkelen vil synke når omformeren blir belastet. Vinkelforskjellen på grunn av forskjeller i vinkel på 3-fase siden blir 1/3 så stor på 1-fase siden som den er på 3-fase siden på grunn av poltallet på motor og generator er 3 til 1.

Beregning ved hjelp av simuleringsprogram (Simpow)

For å vise hvordan lastdeling mellom to omformerstasjoner endrer seg ved forskjellig spenningsvinkel på 3-fase-siden er det laget en enkel modell i et dataverktøy (Simpow). Modellen består av to like omformerstasjoner med ytelse 2x5,8 MVA. Avstanden mellom omformerstasjonen er 80 km, og det er plassert en last på 4 MVA midt mellom omformerstasjonene. Lasten har enten cos$\varphi$=1 eller cos$\varphi$=0,8 (induktiv), og vinkelen på 3-fase-siden i omformerstasjon benevnt A er 0 for alle simuleringene, mens vinkelen på 3-fase-siden i omformerstasjon benevnt B endres fra –10º til 10º. Resultatene for simuleringene er vist i tabellene 1 og 2 nedenfor.

Tabell 1 Effektflyt ved forskjellige vinkler, cos$\varphi$= 1,0

Spennings-vinkel på 3-fase-siden i omformer-stasjon B Aktiv effekt fra omf. A [MW] Reaktiv effekt fra omf. A [MVAr] Aktiv effekt fra omf. B [MW] Reaktiv effekt fra omf. B [MVAr] -10º 2,34 0,01 1,97 0,31 -5º 2,24 0,07 2,06 0,23 0º 2,15 0,15 2,15 0,15 5º 2,06 0,23 2,24 0,07 10º 1,97 0,31 2,34 0,01

Som en ser i tabell 1 vil opplastningen til den enkelte omformerstasjon endre seg avhengig av spenningsvinkel på 3-fase siden. En ser at opplastningen av omformerstasjon B blir mindre dersom vinkelen dreies i negativ retning, dette gjelder både aktiv og reaktiv effekt.

Tabell 2 Effektflyt ved forskjellige vinkler, cos= 0,8

Spennings-vinkel på 3-fase-siden i omformer-stasjon B Aktiv effekt fra omf. A [MW] Reaktiv effekt fra omf. A [MVAr] Aktiv effekt fra omf. B [MW] Reaktiv effekt fra omf. B [MVAr] -10º 1,95 1,18 1,58 1,54 -5º 1,85 1,27 1,67 1,45 0º 1,76 1,36 1,76 1,36 5º 1,67 1,45 1,85 1,27 10º 1,58 1,54 1,95 1,18

Resultatene i tabell 2 viser det samme som resultatene i tabell 1, bare at her har lasten cos$\varphi$=0,8.

Det er også gjort en simulering i tomgang, med spenningsvinkel på 3-fase-siden i omformerstasjon B på 10º, mens vinkel i A er 0º. Resultatene fra denne simuleringen er vist i tabell .3 nedenfor.

Tabell 3 Effektflyt i tomgang ved vinkel på 10º i B

Spennings-vinkel på 3-fase-siden i omformer-stasjon B Aktiv effekt fra omf. A [MW] Reaktiv effekt fra omf. A [MVAr] Aktiv effekt fra omf. B [MW] Reaktiv effekt fra omf. B [MVAr] 10º 0,19 -0,19 -0,19 0,19

Resultatet i tabell .3 viser at en kan ha en effektflyt mellom omformerstasjoner som går i tomgang bare på grunn av en vinkelforskjell på 10 fra 3-fase nettet. Også i situasjoner der det er last på linjen vil det kunne oppstå reaktiv effektflyt mellom omformerstasjoner. Denne uønskede effektflyten fører følgelig til økede energikostnader.

Beregningseksempel

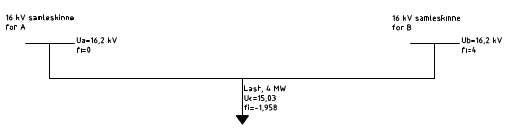
For å vise hvordan en regner ut en effektflyt er det tatt utgangspunkt i et enkelt eksempel, se figur 2. Systemet består av to 1-fase samleskinner, med en last på midten. Avstanden mellom samleskinnene er 80 km og impedansen i kontaktledningen er Z=0,21+j0,21 /km. Lasten er på 4 MVA og cos$\varphi$=1,0. I den ene samleskinnen er det brukt U=16,2 kV og vinkel 0º, mens i den andre samleskinnen er U=16,2 kV og vinkel 4º.

Figur 2 Skisse for illustrasjon av regne eksempel

Først følger resultatene for systemet utført ved hjelp av beregningsprogram, vist i tabell 4, etterfulgt av utregning for hånd.

Tabell 4 Resultater fra beregningsprogram

Last U [kV] Vinkel Aktiv effekt, P, fra ssk A Reaktiv effekt, Q, fra ssk A Aktiv effekt, P, fra ssk B Reaktiv effekt, Q, fra ssk B 4 MW 15,03 -1,958 1,53 0,54 2,47 -0,54

Bruker formlene utledet i kapittel 1.2 for å regne ut effektflyten for hånd. Siden lasten er matet fra to sider, benytter man superposisjonsprinsippet og beregner en side av gangen. Regner først effektflyten fra A, bruker ligning 9 og 10 for å henholdsvis beregne P og Q. Finner først P, setter verdier inn i ligning 9 og får:

(2.13)

Dette gir:

(2.14) På tilsvarende måte finner man effekten fra B som blir:

(2.15)

Dette gir:

(2.16)

Regner så ut den reaktive effekten, Q, på samme måte som ovenfor, bare at en nå bruker ligning .10. Dette gir:

(2.17)

Dette gir:

(2.18)

På tilsvarende måte finner man reaktiv effekt fra B som blir:

(2.19)

Dette gir:

(2.20)

Som en ser fra resultatene stemmer de simulerte verdiene godt overens med de beregnede verdier. Legger man sammen verdiene for P og Q fra A og B, ser man at lasten trekker 4 MW, mens den reaktive delen blir matet forbi lasten og til samleskinne B.

Spenningsforskjell mellom omformerstasjonene

Beregning ved hjelp av simuleringsprogram (Simpow)

Forskjeller i spenning mellom to omformerstasjoner vil gi effektflyt mellom omformerstasjonene. Dette gjør seg sterkest gjeldene når det ikke er last, det vil si at omformerstasjonene går i tomgang. Da vil omformerstasjonen med lavest spenning motta både aktiv og reaktiv effekt, mens omformerstasjonen med høyest spenning vil levere effekt. Dette er vist i tabell .5 som viser resultater fra beregningsprogram, og ved utregning. Utgangsspenningen fra omformerstasjon A er 16,2 kV mens utgangsspenningen fra omformerstasjon B er 16,5 kV. Begge stasjonene har lastvinkel på 0º.

Tabell 5 Effektflyt ved spenningsforskjeller mellom omformerstasjoner i tomgang

Aktiv effekt fra omf. A [MW] Reaktiv effekt fra omf. A [MVAr] Aktiv effekt fra omf. B [MW] Reaktiv effekt fra omf. B [MVAr] -0,145 -0,145 0,147 0,147

Beregningseksempel

La oss bruke likning 9 og 10 til å regne ut aktiv og reaktiv effekt i samleskinne A. Bruker at UA=16,2 kV og UB=16,5 kV, R=X=0,21 $\Omega$/km og avstanden mellom omformerstasjonene er 80 km gir R=X=16,8 $\Omega$. Dette gir aktiv effekt inn i samleskinne A:

(2.21)

Regner ut og får:

(2.22)

Utrykket for reaktiv effekt, QA vil se slik ut:

(2.23)

Regner ut og får: (2.24)

Som en ser utfra resultatene fra likning 22 og 24 stemmer de beregnede verdiene og simulerte verdiene fra tabell 5 meget godt overens.

Regulering stigende/synkende/FLAT

Mye av stoffet i dette delkapittelet er hentet fra ”Systemstudie, samkörning och trafiksimuleringar”, [2]

For å regulere spenningen ut fra en roterende omformer er det en spenningsregulator. Denne består av et stabiliserings ledd og et kompounderings ledd. Regulatoren henter sine innsignaler fra den reaktive delen av strømmen og regulerer på spenningen avhengig av hvilken reguleringsfilosofi som er valgt. Dette kan enten være stigende-, synkende- eller flat karakteristikk, det vil si at er det valgt en stigende karakteristikk vil spenningen øke ved økende reaktiv strømuttak. Som en følge av høyere spenning ut vil stasjonen ta på seg større last og bli hardere belastet. Er karakteristikken synkende vil det motsatte skje og er den flat vil regulatoren prøve å holde flat spenning ut uavhengig av reaktiv strøm.

I Oslo-området er det valgt å ha en synkende karakteristikk i alle roterende omformerstasjoner. Fra simuleringer vist i [2] kommer det frem at ved en slik innstilling vil dette gi det beste resultatet for Oslo-området, basert på tap i fordelingssystemet, samt at ingen omformerstasjoner blir overbelastet. Grunner til dette er at en får bedre lastdeling mellom omformerstasjonene og at den reaktive effektflyten reduseres.

Tilbakemating

I forbindelse med nytt trekkmateriell er det blitt vanlig at lokomotivene har tilbakemating når de bremser, regenerativ brems. Dette gjelder EL 17, EL 18, BM70, BM71, BM72, BM73 og de nye malmlokomotivene. Måten elektrisk brems virker på er forenklet sagt at motoren i lokomotivet går som generator og leverer effekt ut på kontaktledningsanlegget. Som en følge av dette vil det bli en lokal spenningsheving (maksimalt 17,25 kV), og effekt blir transportert ut på kontaktledningsanlegget. Denne effekten kan enten bli brukt av nærliggende trekkmateriell, bli tilbakematet gjennom en roterende omformer eller statisk omformer med mulighet for tilbakemating (eksisterer ikke i den norske banestrømforsyningen, bortsett fra i Sarpsborg omformerstasjon).

I forbindelse med tilbakematet effekt er det viktig å skille mellom roterende og statiske omformere. I en roterende omformer vil den aktive effekten bli overført via akslingen og matet ut til 3-fasenettet. Siden akslingen naturlig nok bare overfører aktiv effekt vil den eventuelle reaktive delen blant annet gå til å magnetisere 1-fase maskinen.

Ved tilbakemating av togets bremseenergi snus effektretningen i omformeren og motoren fungerer som generator mot 3-fase systemet. Spesielle vern er innført for å klare problemene som kan oppstå hvis man mister tilkoblingen med 50 Hz nettet. Man er først og fremst bekymret over øket påkjenning i motoren ved automatisk gjeninnkobling etter spenningsbortfall på 3-fase matingen.

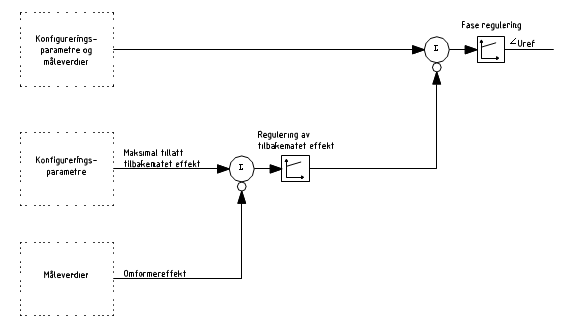
Figur 3 Skisse som viser reguleringsprinsippet for tilbakematet effekt for en statisk omformer

De statiske omformerne som eksisterer i strømforsyningen i dag har ikke mulighet for tilbakemating (med unntak av i Sarpsborg omformerstasjon). Prøver en å mate effekt fra 1-fase nettet til 3-fase nettet vil den statiske omformer regulere vinkel og amplitude til spenningen. Den vil øke vinkelen og amplitude slik at effekten vil flyte forbi til enten et annet lokomotiv eller en roterende omformer. Er det så mye effekt som tilbakemates at den statiske omformeren ikke klarer å styre effekten bort fra seg vil den overskytende effekten bli ”brent” opp over en motstand. Er dette fortsatt ikke tilstrekkelig vil omformeren koble ut. Reguleringsprinsippet for dette er vist i fig 3.