Parametre for flerledersystem

__NUMBEREDHEADINGS__

Generelt

Dette kapittelet beskriver parametrisering av et linearisert flerledersystem for bruk i en admittansbeskrivelse som beskrevet i Lenke: Transmisjonslinje med flere parallelle ledere.

I et system med flere parallelle elektriske ledere med felles retur i jord er systemets lineære elektriske egenskaper komplett beskrevet av fire parametermatriser:

• Matrise for serieresistanser: R [Ω/km]
• Matrise for seriereaktanser: X [Ω/km]
• Matrise for parallell konduktiv avledning: G [S/km]
• Matrise for parallell susceptiv avledning: B [S/km]

Hver av matrisene har dimensjonene (n x n) der n er antallet parallelle ledere i systemet. Matrisene er alltid symmetriske.

Matrisene kan sammenstilles til en kompleks matrise for serieimpedans Z og en kompleks matrise for parallell admittans Y:

${\begin{matrix}\mathbf {Z} =\mathbf {R} +j\cdot \mathbf {X} \\\mathbf {Y} =\mathbf {G} +j\cdot \mathbf {B} \end{matrix}}$

Dette kapittelet inneholder et regneeksempel for hvordan man bestemmer verdiene for parametermatrisene for et konkret linjesett for AT-system med PL, NL, kl og skinner. Med det aktuelle regneeksempelet er matrisene R, X, G og B for dette AT-systemet beregnet til å være (ved driftsfrekvens 16 2/3 Hz):

<figtable id="tab:Serieimpedans_redusert_innledning">

Matrise for serieimpedans Z [Ω/km]

Resistans R [Ω/km]						Reaktans X [Ω/km]
	NL	PL	Kontakt- ledning	Kjøre- skinner			NL	PL	Kontakt- ledning	Kjøre- skinner
NL	0,0906	0,0164	0,0163	0,0164		NL	0,2928	0,1957	0,1596	0,1463
PL	0,0164	0,0906	0,0162	0,0164		PL	0,1957	0,2928	0,1621	0,1469
Kontaktledning	0,0163	0,0162	0,1449	0,0166		Kontaktledning	0,1597	0,1621	0,2632	0,1586
Kjøreskinner	0,0164	0,0164	0,0166	0,0464		Kjøreskinner	0,1463	0,1469	0,1586	0,2607

</figtable>

<figtable id="tab:Kapasitansmatrise_redusert_innledning">

Matrise for parallell admittans Y [µS/km]

Konduktans G [µS/km]						Susceptans B [µS/km]
	NL	PL	Kontakt- ledning	Kjøre- skinner			NL	PL	Kontakt- ledning	Kjøre- skinner
NL	0	0	0	0		NL	0,9570	-0,3700	-0,1152	-0,0055
PL	0	0	0	0		PL	-0,3700	0,9643	-0,1469	-0,0060
Kontaktledning	0	0	0	0		Kontaktledning	-0,1152	-0,1469	1,1642	-0,0294
Kjøreskinner	0	0	0	100 000		Kjøreskinner	-0,0055	-0,0060	-0,0294	2,6309

</figtable>

Beregningsforutsetninger

Følgende parametre behandles i beregningene som kjente verdier.

<figtable id="tab:Beregningsforutsetninger">

Beregningsforutsetningerlederen

Parameter	Symbol	Verdi	Enhet	Kilde
Magnetisk permeabilitet i tomt rom	µ0	4·π·10-7	H/m	[A]
Elektrisk permittivitet i tomt rom	ε0	8.8542·10-12	F/m	[A]
Jordresistivitet	ρe	5000	Ωm	[G]

</figtable>

Jordresistiviteten varierer mye for ulike typer jordsmonn. Den valgte verdien på 5000 Ωm representerer et nivå som er lavere enn hva man kan forvente ved fjellgrunn, samtidig som det er mye høyere enn hva man kan forvente i grunn med fuktig sand og leire. Det finnes flere lett tilgjengelige angivelser over tallverdier for jordresistivitet i ulike typer jordsmonn i Norge, for eksempel ved søk på nett. Her er tallverdiene angitt i referanse [G] lagt til grunn:

<figtable id="tab:Jordresistivitet">

Jordresistivitet som angitt i referanse [G]

Jordsmonn	Resistivitet ρe [Ωm]
Sjøvann (saltholdig)	< 1
Ferskvann (elv, innsjø)	10 - 1 000
Fuktig myrjord	20 - 200
Dyrket jord, leire (fuktig)	50 - 200
Fuktig sandjord	100 - 300
Tørr sandjord	1 000 - 50 000
Fjellgrunn med vannfylte sprekker	1 000 - 10 000

</figtable>

Geometrisk konfigurasjon

Linjesettet defineres med følgende geometriske konfigurasjon, der x-aksen ligger horisontalt på tvers av sporet slik at x=0 er midt mellom de to kjøreskinnene, og y-aksen står vertikalt på sporet slik at y=0 er ved jordoverflaten. Konfigurasjonen gjengir omtrent den konfigurasjonen som er angitt i Teknisk regelverk: AT-system med seksjonert kontaktledning.

<figtable id="tab:Geometri">

Geometrisk konfigurasjon

Leder	x-koordinat [m]	y-koordinat [m]
Negativleder, NL	4	10
Positivleder, PL	3	10
Bæreline, bl	0	6,6
Kontakttråd, kt	0	5,8
Skinne 1, S1	-0,7175	0,2
Skinne 2, S2	0,7175	0,2

</figtable>

Den angitte høyden er lederens gjennomsnittshøyde. Lengdeøkningen som følge av nedheng er i størrelsesorden 0,25%, og er neglisjert her. Tilsvarende gjelder for sikksakk-formen til kontakttråd og bæreline.

Serieimpedans

Generelt

Seriempedansen består av:

• egenimpedansen til hver leder, og
• gjensidig impedans mellom lederne.

Serieimpedansen kan skrives som:

$\mathbf {Z} =\mathbf {Z_{egen}} +\mathbf {Z_{gjensidig}}$

J. R. Carson beskrev først teoretisk bølgeforplantning i lange ledere med retur i jord, i en artikkel i Bell System Technical Journal i 1926 (Referanse [B]). Ved utledning av likningene er jordsmonnet antatt som uniformt ledende med fast jordresistivitet, og jordoverflaten er anttatt å være flat. Fordelen med metoden er at det gjør det mulig å finne tilnærmete verdier for disse impedansene uten å gjennomføre en detaljert modellering av landskapet, samtidig som det gir rimelig nøyaktighet. Mer nøyaktige metoder for å fastsette impedansen til ledere over jordsmonn omfatter detaljert modellering av landskapet og jordsmonnet som lederen henger over, og kan ikke gjennomføres generelt.

Formelverket fra referanse [B] har blitt skrevet om på en mer lesbar form i senere kilder og lærebøker, og for resten av denne artikkelen refereres det til referanse [C] og [G].

Egenimpedans

Beskrivelse

Egenimpedansen $\mathbf {Z_{egen}}$ kan deles inn i den indre impedansen $\mathbf {Z_{indre}}$ som følge av resistans og magnetfelt i ledermaterialet, og den ytre impedansen $\mathbf {Z_{ytre}}$ som følge av resistans i jordretur og magnetfeltet i mediet utenfor lederen. I dette dokumentet antas det at mediet utenfor lederen alltid er luft.

$\mathbf {Z_{egen}} =\mathbf {Z_{indre}} +\mathbf {Z_{ytre}}$

Det er vanlig å angi kombinerte formler for den indre og den ytre impedansen. Kun ved angivelse av kjøreskinnenes egenimpedans deler vi her opp egenimpedansen på denne måten, fordi den indre impedansen for skinnene er fastsatt ved måling, mens den ytre må beregnes [C].

$\mathbf {Z_{egen}}$ er en diagonal matrise med et diagonalt element tilhørende hver leder. For en leder i umagnetisk materiale med retur i jord, er egenimpedansen til lederen tilnærmet gitt av:

$Z_{egen,ii}=r_{i}+r_{E}+j\cdot f\cdot \mu _{0}\cdot \ln {\left({\frac {D_{j}}{g_{i}}}\right)}$

der:

f er strømmens frekvens,

$\mu _{0}$ er den magnetiske permeabiliteten i tomt rom,

$r_{i}$ er lederens resistans,

$r_{E}$ er resistansen for strømmens returvei i jordsmonnet,

$D_{j}$ er jordavstanden,

$g_{i}$ er lederens geometriske middelavstand.

Lederens resistans r_i

Lederresistansen r_i er avhegig ledermateriale, geometri, temperatur, og strømmens frekvens. Frekvensavhengigheten opptrer på grunn av strømfortrengning, og for normale ledere er frekvensavhengigheten svak ved driftsfrekvenser. For ledere angis vanligvis lederens likestrømsresistans ved 20°C, og vekselstrømsresistans ved driftsfrekvens på 50 Hz. Fordi strømfortrengningen har mindre innvirkning ved 16 2/3 Hz enn ved 50 Hz anbefales det å benytte lederens likestrømsresistans for beregninger ved 16 2/3 Hz for alle ledere bortsett fra kjøreskinner. Dersom denne resistansen har stor påvirkning på resultatet, bør frekvensavhengigheten modelleres mer detaljert for høyere frekvenser, ettersom strømfortrengning da får mer å si.

Der lederresistansen ikke er oppgitt, kan likestrømsresistansen beregnes på bakgrunn av ledermaterialets resistivitet og lederens tverrsnitt:

$r_{i,DC}={\frac {1}{A\cdot \sigma }}$

der:

A er lederens tverrsnitt, og

$\sigma$ er ledermaterialets ledeevne.

Resistansen for strømmens returvei i jord r_E

For et ikke-magnetisk jordsmonn med uniform ledeevne kan resistansen r_E tilnærmes med formelen:

$r_{E}={\frac {\pi \cdot f\cdot \mu _{0}}{4}}$

Det vil si at frekvensen er den eneste variabelen som påvirker jordresistansen. r_E er 0,01645 Ω/km ved 16 2/3 Hz driftsfrekvens, og 0,04935 Ω/km ved 50 Hz driftsfrekvens.

Jordavstanden D_j

Jordavstanden D_j er en beregnet dybde ned i jordsmonnet der tyngdepunktet av returstrømmen i jord går. Ifølge [G] kan den tilnærmet angis med formelen:

$D_{j}=660\cdot {\sqrt {\frac {\rho _{e}}{f}}}$

Det vil si at jordavstanden er avhengig av driftsfrekvensen f og av jordresistiviteten ρ_E. Ved 16 2/3 Hz og jordresistivitet på 5000 Ωm blir jordavstanden 11 432 m.

Geometrisk middelavstand g_i

Den geometriske middelavstanden for en leder kan beregnes for ledere med enkel geometri, men for virkelige ledere blir den normalt oppgitt. Referanse [H] angir beregnet geometrisk middelavstand for sirkulære ledere med kordeller som vist i <xr id="tab:GeometriskMiddelavstand"/>. En massiv rund leder har eksakt geometrisk middelavstand lik $g_{i}=e^{-{\frac {1}{4}}}\cdot a=0,7788\cdot a$ der a er lederens radius.

<figtable id="tab:GeometriskMiddelavstand">

Geometrisk middelavstand for ledere med flere kordeller

Antall kordeller	1	3	7	19	37	61	∞
Geometrisk middelavstand g	0,7788 · a	0,6778 · a	0,7254 · a	0,7576 · a	0,7680 · a	0,7720 · a	0,7788 · a

</figtable>

Kjøreskinner:

Ifølge referanse [C] kan ikke strømfortrengning neglisjeres for kjøreskinner på samme måte som for øvrige ledere uten å gjøre en stor feil, på grunn av skinnens store dimensjoner og skinnens magnetiske egenskaper. Referanse [C] anbefaler derfor at impedansen bestemmes basert på målinger. Det angis at for en kjøreskinne ved 16 2/3 Hz kan den indre impedansen angis som en verdi som varierer lineært fra 0,060 + j 0,075 Ω/km ved 100 A, til 0,125 + j 0,110 Ω/km ved 1000 A strømbelastning i hver kjøreskinne, og deretter konstant impedans for høyere strømmer. Her legges i det videre til grunn strømmen som er angitt for 100 A i hver skinne, for bruk ved driftsstrømmer i AT-system. I tillegg til denne indre impedansen må det legges til en ytre impedans som følge av magnetfeltet som ikke påvirkes av skinnematerialet. Den totale egenimpedansen for en kjøreskinne blir:

$Z_{egen,ii}=0,060+0,01645+j0,075+j\cdot f\cdot \mu _{0}\cdot \ln {\left({\frac {D_{j}}{a}}\right)}\cdot 1000\;\left[{\frac {\mathrm {\Omega } }{\mathrm {km} }}\right]$

I dette uttrykket er a en tenkt radius for skinnen. Referanse [H] angir at en studentoppgave har foreslått å bruke 0,2 m for denne radien basert på målinger, men angir at det er stor usikkerhet forbundet med forslaget. Referanse [C] angir denne radien til 0,04935 m for en S60 skinne basert på radien for en sirkulær leder med like stort tverrsnitt. Vi legger her til grunn angivelsen i referanse [C] for denne radien.

Oppsummering

<xr id="tab:Egenimpedans" /> inneholder beregnete verdier for egenimpedans for beregningseksempelet med et AT-system med PL, NL, kl og kjøreskinner:

<figtable id="tab:Egenimpedans">

Egenimpedans for aktuelle ledere

Parameter	PL,NL a,b	Kontakttråd a,c	Bæreline a,c	Kjøreskinne d
Ledermaterial	AL-1	CuAg 0,1	CuMg 0,5	Stål (R260Mn)
Ledertverrsnitt [mm2]	381	100	50	7670
Ytre diameter [mm]	25,3	12,0	9,0	-
Kordeller	37	1	19	-
Diameter for hver kordell [mm]	3,62	-	1,80	-
Geometrisk middelavstand g [mm]	9,72	4,67	3,41	-
Ledeevne % av IACS (5,8001·107 S/m) (IACS: International Annealed Copper Standard, 1914)	61,0	97,0	80,0	9,6
Relativ permeabilitet	1	1	1	60
Likestrømsresistans rDC [Ω/km]	0,0742	0,1777	0,4310	0,0234
Resistans, basert på målinger (referanse [C]) [Ω/km]	-	-	-	0,060
Vekselstrømsresistans 50 Hz r50Hz [Ω/km]	-	-	-	-
Reaktans, basert på målinger (referanse [C]) [Ω/km]	-	-	-	0,075
Resistans Re(Zii,egen) ved 16 2/3 Hz [Ω/km]	0,0906	0,1942	0,4475	0,0765
Reaktans Im(Zii,egen) ved 16 2/3 Hz [Ω/km]	0,2928	0,3081	0,3147	0,3334
Kilder: [a] Bane NOR: Teknisk spesifikasjon [b] EN 50182 [c] EN 50149. For Bz II er materialdata for CuMg 0,5 antatt [d] Bane NOR: Teknisk regelverk, overbygning, sporkonstruksjoner

</figtable>

Gjensidig impedans

Beskrivelse

Gjensidig impedans mellom to ledere i og k er gitt av:

$Z_{gjensidig,ik}=r_{E}+j\cdot f\cdot \mu _{0}\cdot \ln {\left({\frac {D_{j}}{g_{ik}}}\right)}$

der

$r_{E}$ er resistansen for strømmens returvei i jordsmonnet,

f er strømmens frekvens,

$\mu _{0}$ er den magnetiske permeabiliteten i tomt rom,

$D_{j}$ er jordavstanden,

$g_{ik}$ er den geometriske middelavstanden mellom de to lederne.

Geometrisk middelavstand mellom to ledere

Dersom begge lederne er runde er den geometriske middelavstanden $g_{ik}$ mellom lederne lik avstanden mellom senter for de to lederne. Dersom avstanden mellom lederne er stor sammenliknet med ledernes dimensjoner, kan den geometriske middelavstanden tilnærmes til avstanden mellom senter for lederne også for ledere som ikke er runde.

Oppsummering

<xr id="tab:Serieimpedans" /> inneholder beregnete verdier for gjensidige impedanser for beregningseksempelet med et AT-system med PL, NL, kl og kjøreskinner:

<figtable id="tab:Serieimpedans">

Matrise for serieimpedans Z [Ω/km]

Resistans R [Ω/km]								Reaktans X [Ω/km]
	NL	PL	Kontakt- tråd	Bære- line	Kjøre- skinne 1	Kjøre- skinne 2			NL	PL	Kontakt- tråd	Bære- line	Kjøre- skinne 1	Kjøre- skinne 2
NL	0,0906	0,0164	0,0164	0,0164	0,0164	0,0164		NL	0,2928	0,1957	0,1589	0,1610	0,1457	0,1468
PL	0,0164	0,0906	0,0164	0,0164	0,0164	0,0164		PL	0,1957	0,2928	0,1613	0,1640	0,1465	0,1473
Kontakttråd	0,0164	0,0164	0,1942	0,0164	0,0164	0,0164		Kontakttråd	0,1589	0,1613	0,3081	0,2004	0,1595	0,1595
Bæreline	0,0164	0,0164	0,0164	0,4475	0,0164	0,0164		Bæreline	0,1610	0,1640	0,2004	0,3147	0,1567	0,1567
Kjøreskinne 1	0,0164	0,0164	0,0164	0,0164	0,0765	0,0164		Kjøreskinne 1	0,1457	0,1465	0,1595	0,1567	0,3334	0,1881
Kjøreskinne 2	0,0164	0,0164	0,0164	0,0164	0,0164	0,0765		Kjøreskinne 2	0,1468	0,1473	0,1595	0,1567	0,1881	0,3334

</figtable>

Ekvivalente ledere

To ledere kan representeres med en ekvivalent leder. Dette er ofte en god ide dersom lederne driftes på samme potensial, og spesielt dersom de er parallellkoplet underveis. I kontaktledningsanlegg vil man gjerne representere kontakttråd og bæreline som en felles leder "kontaktledning", og man vil gjerne representere de to kjøreskinnene som en felles leder.

Leder i og j kan slås sammen til en ny leder k ved følgende matriseoperasjoner:

${\frac {\mathrm {d} \mathbf {U} }{\mathrm {d} x}}=\mathbf {Z} \cdot \mathbf {I}$

$\mathbf {I} =\mathbf {Z^{-1}} \cdot {\frac {\mathrm {d} \mathbf {U} }{\mathrm {d} x}}=\mathbf {r} \cdot {\frac {\mathrm {d} \mathbf {U} }{\mathrm {d} x}}$

der

${\frac {\mathrm {d} \mathbf {U} }{\mathrm {d} x}}$ er vektoren for spenningsforskjeller over en strekning dx.

Matrisen $\mathbf {r}$ tilpasses ved å sette:

${\frac {\mathrm {d} U_{k}}{\mathrm {d} x}}={\frac {\mathrm {d} U_{i}}{\mathrm {d} x}}={\frac {\mathrm {d} U_{j}}{\mathrm {d} x}}$

$I_{k}=I_{i}+I_{j}$

Da blir alle elementene i den reduserte matrisen $\mathbf {r_{red}}$ som ikke har k som subskript uforandret, og for øvrig:

$r_{red,kk}=r_{ii}+r_{jj}+r_{ij}+r_{ji}$

Og for hver enkelt øvrige leder (markert med subskript m):

$r_{red,km}=r_{im}+r_{jm}$

$r_{red,mk}=r_{mi}+r_{mj}$

Den nye matrisen $\mathbf {r_{red}}$ inverteres så tilbake for å finne den nye serieimpedansmatrisen $\mathbf {Z_{red}} =\mathbf {r_{red}^{-1}}$. Ved å gjøre den operasjonen og slå sammen kjøreskinnene til en ny leder, og kontakttråd og bæreline til en annen ny leder, blir den resulterende matrisen $\mathbf {Z_{red}}$ som vist i neste avsnitt.

Resultat for serieimpedans Z

<figtable id="tab:Serieimpedans_redusert">

Redusert matrise for serieimpedans Z [Ω/km]

Resistans R [Ω/km]						Reaktans X [Ω/km]
	NL	PL	Kontakt- ledning	Kjøre- skinner			NL	PL	Kontakt- ledning	Kjøre- skinner
NL	0,0906	0,0164	0,0163	0,0164		NL	0,2928	0,1957	0,1596	0,1463
PL	0,0164	0,0906	0,0162	0,0164		PL	0,1957	0,2928	0,1621	0,1469
Kontaktledning	0,0163	0,0162	0,1449	0,0166		Kontaktledning	0,1597	0,1621	0,2632	0,1586
Kjøreskinner	0,0164	0,0164	0,0166	0,0464		Kjøreskinner	0,1463	0,1469	0,1586	0,2607

</figtable>

Parallell admittans

Den parallelle admittansen består av konduktiv kopling G og susceptiv kopling B mellom ledere.

$\mathbf {Y} =\mathbf {G} +j\cdot \mathbf {B}$

Konduktiv kopling

Ettersom kun forbindelser mellom ledere og jord modelleres, er G en diagonal matrise med et diagonalt element som representerer jordforbindelsen for hver leder. I vårt regneeksempel modelleres kun jordforbindelsen mellom kjøreskinner og jord, og da blir elementene i matrisen G:

<figtable id="tab:Konduktans_redusert">

Matrise for konduktans G [S/km]

Konduktans G [S/km]
	NL	PL	Kontakt- ledning	Kjøre- skinner
NL	0	0	0	0
PL	0	0	0	0
Kontaktledning	0	0	0	0
Kjøreskinner	0	0	0	gE

</figtable>

Verdien for g_E varierer mye avhengig av jordsmonn og utforming av fundamenter og jordelektroder. Enten må denne estimeres for hver enkelt strekning, eller så må det benyttes en konservativ verdi. Videre i dette regneeksempelet settes g_E til 0,1 S/km, som vil være konservativt i de fleste tilfeller, men i noen særlige tilfeller (fjellgrunn eller kontaktledningsfundamenter med svært dårlig kontakt med jord) vil denne verdien kunne bli enda lavere. Teknisk regelverk: Verdier for avledning mellom returkrets og jord oppsummerer kjent informasjon om verdien til g_E.

Kapasitiv kopling

Det oppstår en kapasitiv kopling C mellom leder og jord, og innbyrdes mellom ledere. Den frekvensavhengige susceptansen B beregnes fra kapasitansen C ved:

$\mathbf {B} =\omega \cdot \mathbf {C}$

der

• ω er spenningens vinkelfrekvens

Det elektriske feltet E rundt en elektrisk ladet sylindrisk leder kan beregnes fra Gauss' lov:

$\oint \mathbf {E} \;\operatorname {d} \mathbf {A} ={\frac {Q_{omsl}}{\epsilon _{0}}}$

der

• A er en tenkt overflate i rommet rundt lederen [m²],
• Q_omsl er den elektriske ladningen omsluttet av den tenkte overflaten A [C],
• ε₀ er den elektriske permittivitet for tomt rom, 8,854187817·10^-12 [F/m]

For en sylindrisk leder kan det elektriske feltet kun være i den radielle retningen. I en avstand r fra lederen er det elektriske feltet konstant i omkretsen rundt lederen. Likningen kan derfor løses ved å velge overflaten A til en sylindrisk overflate konsentrisk rundt lederen, med radius r. For dette tilfellet kan sirkelintegralet reduseres til:

$\oint \mathbf {E} \;\operatorname {d} \mathbf {A} =E\cdot 2\cdot \pi \cdot r\cdot l$

og Q_omsl kan reduseres til:

Q_omsl = λ · l

der

• E er styrken på det elektriske feltet ved radius r fra lederens senter [N/C],
• l er lengden for et kort linjesegment [m],
• λ er antall ladninger per lengdeenhet for lederen [C/m]

Lengden l kan forkortes fra likningen, og den elektriske feltstyrken E kan bestemmes som funksjon av r og λ:

$E={\frac {\lambda }{2\cdot \pi \cdot r\cdot \epsilon _{0}}}$

Spenningen U_r mellom lederen og et punkt i avstand r fra lederens senter er da gitt av:

$U_{r}=\int _{r_{i}}^{r}E\;\operatorname {d} r={\frac {\lambda }{2\cdot \pi \cdot \epsilon _{0}}}\cdot \int _{r_{i}}^{r}{\frac {1}{r}}\;\operatorname {d} r$

og med løst integral:

$U_{r}={\frac {\lambda }{2\cdot \pi \cdot \epsilon _{0}}}\cdot \ln {\left({\frac {r}{r_{0,i}}}\right)}=\lambda \cdot \beta ={\frac {\lambda }{C}}$

der

• r_0,i er ytre radius for leder i [m].
• β er elastansen mellom lederens overflate og punktet r [m/F]
• C er kapasitansen mellom lederens overflate og punktet r [F/m]

Spenningen mellom to ledere i og j kan beregnes ved:

$U_{ij}=U_{i}-U_{j}=\beta _{ij}\cdot (\lambda _{i}-\lambda _{j})={\frac {1}{2\cdot \pi \cdot \epsilon _{0}}}\cdot \ln {\left({\frac {D_{ij}}{(r_{0,i}+r_{0,j})}}\right)}\cdot \left(\lambda _{i}-\lambda _{j}\right)$

der

• D_ij er avstanden mellom senter for leder i og leder j.

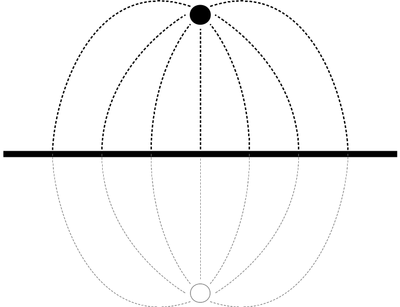
Der lederen er over jord med overflatepotensial tilnærmet lik 0, påvirker overflatepotensialet det elektriske feltet slik at lederen også får en kapasitans mot jord. Betingelsen ved jordoverflaten er at det elektriske feltet står vinkelrett på jordoverflaten. Den matematiske teknikken som brukes for å beregne dette feltbildet, er å tenke seg at det finnes en speilet leder under bakken med lik og motsatt ladning. <xr id="fig:Kapasitans_lederOverJord" /> viser hvordan man kan se for seg dette.

<figure id="fig:Kapasitans_lederOverJord">

Leder over jord med feltlinjer mot jord. En tenkt speilet leder under jordoverflaten med tilhørende tenkte feltlinjer er tegnet grått.

</figure>

Spenningen mellom jord og en leder i som henger i høyden h_i over jord kan da beregnes ved:

$U_{i}={\frac {1}{2\cdot \pi \cdot \epsilon _{0}}}\cdot \ln {\left({\frac {2\cdot h_{i}}{r_{i}}}\right)}\cdot \lambda _{i}$

Der det er flere ledere i et system, er spenningen i en leder en funksjon av ladningen i alle ledere i systemet og alle de tenkte speilede lederne under bakken:

$U_{i}={\frac {1}{2\cdot \pi \cdot \epsilon _{0}}}\cdot \left[\ln {\left({\frac {2\cdot h_{i}}{r_{i}}}\right)}\cdot \lambda _{i}-\ln {\left({\frac {D_{ij}}{(r_{i}+r_{j})}}\right)}\cdot \lambda _{j}+\ln {\left({\frac {D'_{ij}}{(r_{i}+r_{j})}}\right)}\cdot \lambda _{j}+...\right]$

Etter en forenkling blir uttrykket:

$U_{i}={\frac {1}{2\cdot \pi \cdot \epsilon _{0}}}\cdot \left[\ln {\left({\frac {2\cdot h_{i}}{r_{i}}}\right)}\cdot \lambda _{i}+\ln {\left({\frac {D'_{ij}}{D_{ij}}}\right)}\cdot \lambda _{j}+...\right]$

der

• h_i er høyden for leder i over jordoverflaten,
• r_i er ytre radius for leder i,
• D_ij er avstanden i rett linje mellom leder i og leder j,
• D'_ij er avstanden i rett linje mellom leder i og det tenkte speilbildet for leder j.

Dette kan videre ordnes på matriseform for alle ledere i systemet:

$\mathbf {U} =\mathbf {\beta } \cdot \mathbf {\lambda }$

der

• U er vektoren med spenning mot jord for systemets ledere,
• β er matrisen med elastanser mellom systemets ledere, ofte kalt potensialmatrisen, og
• λ er vektoren med ladninger i systemets ledere

Elementene i potensialmatrisen β blir:

$\beta _{ii}={\frac {1}{2\cdot \pi \cdot \epsilon _{0}}}\cdot \ln {\left({\frac {2\cdot h_{i}}{r_{i}}}\right)}$

og

$\beta _{ij}={\frac {1}{2\cdot \pi \cdot \epsilon _{0}}}\cdot \ln {\left({\frac {D'_{ij}}{D_{ij}}}\right)}$

Kapasitansmatrisen C kan finnes ved å invertere potensialmatrisen β slik at:

$\mathbf {\lambda } =\mathbf {\beta ^{-1}} \cdot \mathbf {U} =\mathbf {C} \cdot \mathbf {U}$

For de 6 lederne i eksempelet med AT-system finner man på bakgrunn av dette følgende kapasitansmatrise (der det er antatt at kjøreskinnene er runde ledere med radius på 5 cm):

<figtable id="tab:Kapasitansmatrise">

Matrise for kapasitans C [nF/km]

Kapasitans C [nF/km]
	NL	PL	Kontakt- tråd	Bære- line	Kjøre- skinne 1	Kjøre- skinne 2
NL	9,161	-3,542	-0,631	-0,472	-0,024	-0,029
PL	-3,542	9,231	-0,826	-0,581	-0,027	-0,030
Kontakttråd	-0,631	-0,826	8,444	-2,743	-0,061	-0,060
Bæreline	-0,472	-0,581	-2,743	8,187	-0,081	-0,080
Kjøreskinne 1	-0,024	-0,027	-0,061	-0,081	12,699	-0,106
Kjøreskinne 2	-0,029	-0,030	-0,060	-0,080	-0,106	12,699

</figtable>

På tilsvarende måte som for serieimpedans kan også denne kapasitansmatrisen reduseres slik at ledere som er på samme potensial kombineres. Det gjøres ved å sette:

${\begin{matrix}U_{kl}=U_{bl}=U_{kt}\\\lambda _{kl}=\lambda _{bl}+\lambda _{kt}\end{matrix}}$

og

${\begin{matrix}U_{RR}=U_{S1}=U_{S2}\\\lambda _{RR}=\lambda _{S1}+\lambda _{S2}\end{matrix}}$

Ved å sette inn disse betingelsene blir den reduserte kapasitansmatrisen:

<figtable id="tab:Kapasitansmatrise_redusert">

Redusert matrise for kapasitans C [nF/km]

Kapasitans C [nF/km]
	NL	PL	Kontakt- ledning	Kjøre- skinner
NL	9,161	-3,542	-1,103	-0,052
PL	-3,542	9,231	-1,407	-0,057
Kontaktledning	-1,103	-1,407	11,145	-0,282
Kjøreskinner	-0,052	-0,057	-0,282	25,186

</figtable>

Resultat for parallell admittans Y

Sammenstilt kan man finne matrisen $\mathbf {Y} =\mathbf {G} +j\cdot \mathbf {B} =\mathbf {G} +j\cdot \omega \cdot \mathbf {C}$:

<figtable id="tab:Kapasitansmatrise_redusert">

Matrise for parallell admittans Y [µS/km]

Konduktans G [µS/km]						Susceptans B [µS/km]
	NL	PL	Kontakt- ledning	Kjøre- skinner			NL	PL	Kontakt- ledning	Kjøre- skinner
NL	0	0	0	0		NL	0,9570	-0,3700	-0,1152	-0,0055
PL	0	0	0	0		PL	-0,3700	0,9643	-0,1469	-0,0060
Kontaktledning	0	0	0	0		Kontaktledning	-0,1152	-0,1469	1,1642	-0,0294
Kjøreskinner	0	0	0	100 000		Kjøreskinner	-0,0055	-0,0060	-0,0294	2,6309

</figtable>

Referanser

[A] Young H., Freedman R.: Sears and Zemansky's University Physics - with modern physics. Tenth edition. Addison Wesley Longman Inc., 2000

[B] Carson, J. R: Wave Propagation in Overhead Wires with Ground Return, Bell System Technical Journal, 5: 4. Oktober 1926 side 539-554. (Lenke)

[C] Kießling, Puschmann, Schmieder: Fahrleitungen elektrischer Bahnen, 3. Auflage. Publicis Publishing, 2014, ISBN 978-3-89578-407-1.

[D] United States Department of Commerce: Circular of the Bureau of Standards, No. 31, Copper Wire Tables, 1914 (Lenke)

[E] CENELEC, EN 50149:2012: Railway applications - Fixed installations - Electric traction - Copper and copper alloy grooved contact wires, 2012

[F] CENELEC, EN 50182:2001 Conductors for overhead lines - Round wire concentric lay stranded conductors, 2001

[G] Høidalen H.K: Kurskompendium: Elektromagnetisk sameksistens i jernbaneanlegg, kapittel 9: Kontaktledningsnettet - Impedanser og induserte spenninger, NTNU, 2006.

[H] TET09 - Prosjektering av elektriske anlegg - Parametere for linjer, kabler og skinneføringer - Beregning av tap, induktans og kapasitans, Utdrag fra kompendium i faget Elektriske kraftsystemer del II, 1993. Institutt for elkraftteknikk, NTNU.