Impedans i jernbanenettet

__NUMBEREDHEADINGS__

Impedans i jernbanenettet

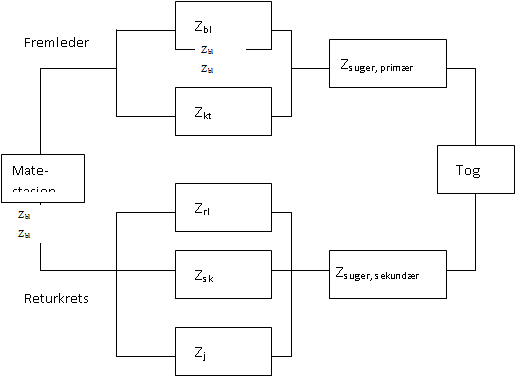
Kontaktledningsanlegget består av flere elektriske elementer som sammen gir den totale impedansen i jernbanenettet. Hovedelementene i kretsen er vist i figur 1.

Figur 1 Elementer som inngår i jernbanenettets impedans

Forklaringer til figur 1:

bl:	bæreline
kt:	kontakttråd
suger, primær:	primærside sugetransformator
suger, sekundær:	sekundærside sugetransformator
rl:	returledning
sk	skinne
j	jord

Fremlederen i kretsen består i tillegg til elementene i figuren av en matekabel/ledning fra omformerstasjonen og til kontaktledningsanlegget. Returkretsen består også av returkabel fra kontaktledningsanlegget og til omformerstasjonen. I jernbanen brukes kontaktledning for å dekke kontakttråd og bæreline.

Som det fremkommer i figur 1 består kretsen av mange elementer. En del av returstrømmen vil gå i jorden, og impedansen i denne delen av kretsen er den det er vanskeligst å identifisere. Denne impedansen vil variere med ulike jordsmonn. For komponenter som ledninger og transformatorer oppgis impedansen fra produsent. For skinnene vil impedansen kunne måles eller oppgis av leverandør. I tillegg kommer impedansen ved overgangen fra skinne til jord, denne er ofte kalt avledning. Skinnens impedans er avhengig av strømfortrenging og frekvens. Strømfortrenging er et uttrykk for hvor i skinnen strømmen går. Dette vil gi usikkerhet for de verdiene som oppgis.

Elementenes innvirkning på impedans

For banestrømforsyningen er det vesentlig at impedansen i jernbanenettet er minst mulig, da dette gir lave tap i energioverføringen. De enkelte leddene i fremkretsen og returkretsen vil ha innvirkning her. Redusert impedans i kretsen gir mindre spenningsfall på overføringen og dermed reduserte tap.

Tverrsnitt på kontakttråd og bæreline, og ledningsevnen til materialet de er laget av har innvirkning. En annen måte å redusere impedansen er å koble inn en tredje fremleder i parallell med kontaktledningen. Endring av tverrsnitt og fremføring av flere ledere i fremkretsen har vanligvis en positiv innvirkning på den resistive delen i impedansen.

For å få redusere den induktive delen mest mulig må det henges opp returledning på kontaktledningsmastene. Ved opphenging av returleder blir avstanden mellom fremleder og returleder redusert og dette reduserer koblingen mellom lederne, og dermed også induktiviteten.

Beregning av impedans

Mye av stoffet i dette kapittelet er hentet fra hovedoppgaver utarbeidet ved NTNU, [1], [2] og [3].

Teori for beregning av serieimpedans

Kontaktledningsanlegget er et system der en har strømsløyfer med jord som returvei. I litteraturen finnes det flere metoder å beregne impedansen i denne strømsløyfen. Her er Carsons tilnærmede formler benyttet. Disse formlene forutsetter at jorden er homogen med uendelig utbredelse til sidene og nedover. For å finne forenklede beregningsmetoder er det hensiktsmessig å ekvivalere jorden med en konsentrert leder. Det vil her bli gitt en kort gjennomgang av det viktigste teoretiske grunnlaget for å beregne kontaktledningsanleggets serieimpedans.

I beregningene innføres det usikkerhet ved å ekvivalere jorden med en konsentrert leder. I tillegg modelleres også skinnene som runde ledere ved denne beregningen. Dette gir en annen strømfortrengning enn i en reell skinne. Antagelsen av at 50 % av strømmen går i jorden bringer også unøyaktighet inn i beregningene.

Jordsmonn med uendelig ledningsevne

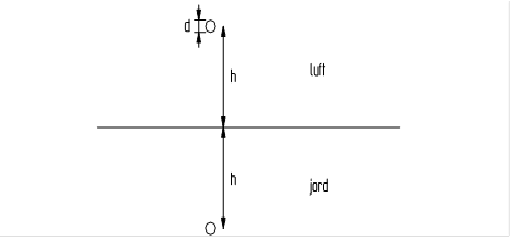
Når jorden har uendelig ledningsevne blir det magnetiske feltet i jorden lik null. For å tilfredsstille dette må jordoverflaten falle sammen med en feltlinje. Dette skjer ved at en fremleder er plassert i en høyde h over bakken og jordsmonnet blir erstattet med en leder i avstand 2h fra fremlederen, se figur 2.

Figur 2 Leder over jordplan med speilet returleder, avstand 2h mellom lederne

Induktiviteten til sløyfen som består av fremlederen i høyde h over jordoverflaten og returlederen i høyden h under jordoverflaten, kan beregnes ut fra likning 1.

$L={\frac {\mu _{0}}{2\pi }}\cdot ln{\frac {2h}{g_{11}}}$ H/m

1

hvor

L:	induktansen i jord [H/m]
g11:	geometrisk middelavstand for en leder med hensyn på seg selv [m] (se kapittel 2.2)
h:	fremlederens høyde over bakken [m]
$\mu _{0}$:	permeabiliteten i vakuum, $4\pi \cdot 10^{-7}$ [H/m]

Ved uendelig ledningsevne blir det ikke effekttap i jorden (returveien), og den eneste reelle komponenten i serieimpedansen er motstanden i fremlederen, altså rfremleder i likning 2. Impedansen pr. meter for sløyfen leder-jord blir:

$Z_{11-j}=r_{fremleder}+jx_{total}=r_{fremleder}+j\mu _{0}f\cdot ln{\frac {2h}{g_{11}}}$ [$\Omega$/m]

2

Z11-j:	impedans [$\Omega$/m]
rfremleder:	fremlederes vekselstrømresistans [$\Omega$/m]
xtotal:	sløyfens reaktans [$\Omega$/m]
f:	frekvens

Den totale reaktansen for sløyfen, xtotal, kan deles opp i to deler, en indre reaktans xindre og en ytre reaktans xytre , den ytre reaktansen kalles også for gjensidig reaktans. Den indre reaktansen skyldes indre induktivitet i lederen, mens den ytre reaktansen skyldes luftfeltet mellom fremleder og jord. Likning 3 gir total impedans pr. meter for systemet:

$Z=r_{fremleder}+j(x_{indre}+x_{ytre})$ [$\Omega$/m]

3

Jordsmonn med endelig ledningsevne

Når jordsmonnet har endelig ledningsevne vil jordstrømmene fordele seg nedover i jorden slik at feltlikninger og grensebetingelser blir tilfredsstilt. Dersom man går ut fra at jorden har konstant ledningsevne og en uendelig utbredelse, kan likningen for impedansen til sløyfen leder - jord skrives:

$Z_{11-j}=r_{fremleder}+j\mu _{0}f\cdot ln{\frac {2h}{g_{11}}}+2\mu _{0}f\cdot (P+jQ)$ [$\Omega$/m]

4

hvor

Z11-j:	impedans [$\Omega$/m]
$\mu _{0}f\cdot ln$ (2h/g11 :	sløyfens reaktans, se likning 1
$\mu _{0}f\cdot P$:	tap i jorden
$\mu _{0}f\cdot Q$:	jordstrømmens bidrag til reaktansen

Istedenfor å beregne P og Q er det i likning .5 innført et tilnærmet uttrykk for impedansen for sløyfen leder-jord.

$Z_{11-j}=r_{fremleder}+r_{e}+j\mu _{0}f\cdot ln{\frac {D_{j}}{g_{11}}}$ [$\Omega$/m]

5

hvor

r_e er samlet tap i jorden:

$r_{e}={\frac {1}{4}}\mu _{0}\pi f$ [$\Omega$/m]

6

Størrelsen D_j i likning 5 kan tolkes som avstanden til en ekvivalent returleder som fører hele jordstrømmen.

$D_{j}=1,31\cdot {\sqrt {\frac {2\rho }{\mu _{0}\omega }}}=1,31\cdot {\sqrt {\frac {\rho }{\mu _{0}\pi f}}}=1,31\cdot \sigma$ [m]

7

hvor

$\sigma$:	inntrengningsdybden for jordsmonnet [m]
$\rho$:	jordresistiviteten $\Omega$m

Likning 5 har en begrensning når det gjelder frekvens og resistiviteten i jorden. Likningen gir liten feil på frekvenser opp til 50-60 Hz og resistivitet i jorden på mellom 50 og 500 $\Omega$m. I tillegg er likningen begrenset til å gjelde for en leder med en høyde over jorden som er mye større enn lederens radius.

Det er viktig å legge merke til at den tilnærmede likningen for serieimpedansen (likning 5) er uavhengig av lederens høyde over bakken, fordi inntrengningsdybden i jorden er så mye større enn lederens høyde over bakken.

Flere ledere med felles retur gjennom jord

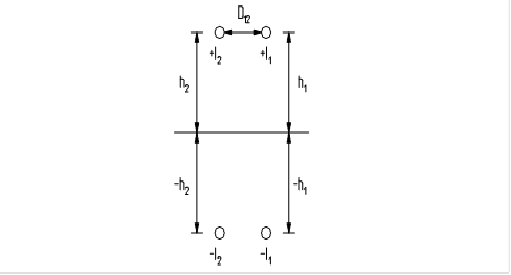
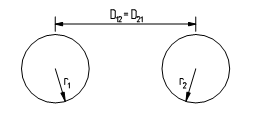
Når det er flere parallelle ledere med felles retur i jord, se figur 3, vil avstanden mellom lederne innvirke på impedansen mot jord og den gjensidige impedansen mellom lederne.

For å kunne sette opp et uttrykk for gjensidig impedans mellom fremlederne må jorden ekvivaleres med et speil. Fremlederne vil da bli speilet, og hver fremleder får sin egen konsentrerte returleder i avstanden 2h, se figur 3.

Figur 3 Prinsippskisse av to parallelle ledere med returleder i jord

En tilnærmet formel for gjensidig impedans mellom to ledere som har felles retur gjennom jord kan skrives:

$Z_{12-j}=r_{e}+jx_{12-j}=r_{e}+j\mu _{0}f\cdot ln{\frac {D_{j}}{D_{12}}}$ [$\Omega$/m]

8

hvor

re	jordens resistans [$\Omega$/m
x12-j	jordens reaktans [$\Omega$/m
Dj	strømmens inntrengningsdybde, se likning 7 [m]
D12	lederavstand, se figur 3 [m]

Strømmen som går i den ene lederen, 1, vil indusere en spenning i den andre lederen, 2. Formelen for å finne den induserte spenningen i leder 1 som en følge av at det går en strøm, I2, i leder 2 er:

$\Delta U_{1-j}=Z_{12-j}\cdot I_{2}$

9

Verdien på $\Delta$U_1-j representerer indusert langsspenning i leder 1 siden det ikke regnes med noe spenningsfall i jorden.

Ved beregning på flere ledere kan den samme fremgangsmåten benyttes. En generell formel for den induserte langsspenningen er:

$\Delta U_{k-j}=\sum _{l=1}^{n}Z_{kl-j}\cdot I_{j}$ [V/m]

10

Geometrisk middelavstand

I dette kapitelet er det bare de mest brukte middelavstandene som vil blir beskrevet. For å bruke de geometriske middelavstandene i reaktansberegninger forutsettes det at det er jevn strømtetthet over ledertverrsnittet. Formlene for de geometriske middelavstandene forutsetter også at lederen er av et umagnetisk materiale ($\mu _{r}$ = 1) og at lederen er sirkulær.

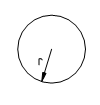
Den geometriske middelavstanden for en massiv sirkulær leder med hensyn på seg selv er gitt i likning 11. I figur 4 er det vist en skisse over hvilke verdier som skal brukes.

$g_{11}=0,39\cdot d=0,78\cdot r$ [m]

11

Figur 4 En massiv sirkulær leder

Når lederen som leder strøm er delt opp i flere delledere, er den geometrisk middelavstanden et mål på hvor tyngdepunktet er for strømmen. I figur 5 er det illustrert et tilfelle hvor lederen består av to delledere. På denne figuren er det også skissert hvilke verdier som skal benyttes.

Figur 5 Leder som består av to delledere

Den geometrisk middelavstanden for dette tilfellet er:

$g_{aa}={\sqrt[{4}]{g_{11}\cdot D_{12}\cdot g_{22}\cdot D_{21}}}$ [m]

12

hvor

g11:	$0,78\cdot r_{1}$ [m]
g22:	$0,78\cdot r_{2}$ [m]
D12:	D21 = lederavstanden [m]

Hadde lederen bestått av tre delledere ville den geometriske middelavstanden blitt:

$g_{aa}={\sqrt[{9}]{g_{11}\cdot g_{22}\cdot g_{33}\cdot D_{12}^{2}\cdot D_{13}^{2}\cdot D_{23}^{2}}}$ [m]

13

Total impedans i kontaktledningsanlegget

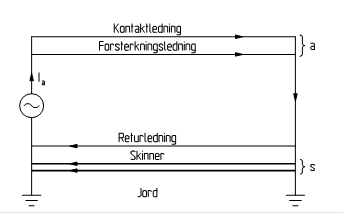
Ved å bruke de likningene som er nevnt i kapittel 2.1 kan en komme frem til likninger som gjelder spesifikt for kontaktledningsanlegget. I figur 6 er det tatt for seg de mest aktuelle lederne som finnes i kontaktledningsanlegget.

Det er viktig å nevne at de likningen som er satt opp i kapittel 2.1 gjelder for lange parallelle overføringer. Dette betyr at lengden på overføringen må være større enn inntrengningsdybden i jord og i tillegg må overføringen være lenger enn overgangssonene. Det forutsettes da at strømfordelingen og impedansen er lik i hele overføringen. Dette fører til at det i beregningene ses bort ifra den påvirkning sugetransformator og returledning vil ha på strømfordelingen.

Figur 6 Fremledere og returledere i kontaktledningsanlegget

Impedans for kontaktledningsanlegg uten returleder

Det mest brukte systemet i det norske jernbanenettet er å ha en fremleder, a, som består av kontakttråd og bæreline, og en returleder, s, som består kun av skinnene. For dette systemet er det følgende likninger som gjelder:

$\Delta U_{a-j}=Z_{aa-j}\cdot I_{a}+Z_{as-j}\cdot I_{s}$ [V/m]

14

$\Delta U_{s-j}=Z_{ss-j}\cdot I_{s}+Z_{as-j}\cdot I_{a}$ [V/m]

15

hvor

Zaa-j:	impedansen mellom fremleder og jord [$\Omega$/m]
Zas-j:	gjensidig impedans mellom ledere og jord [$\Omega$/m]
Zss-j:	impedans mellom skinne og jord [$\Omega$/m]

Når skinnene er ideelt jordet i begge endene, er $\Delta$U_s-j = 0. Skinnestrømmen kan da finnes ut fra følgende sammenheng:

$I_{s}={\frac {Z_{as-j}}{Z_{ss-j}}}\cdot I_{a}$ [A]

16

Ved å sette inn likning 16 i likning 14, elimineres I_s og en vil da ha:

$\Delta U_{a-j}=Z_{aa-j}\cdot I_{a}-{\frac {Z_{as-j}^{2}}{Z_{ss-j}}}\cdot I_{a}=(Z_{aa-j}-{\frac {Z_{as-j}^{2}}{Z_{ss-j}}})\cdot I_{a}$ [V/m]

17

Den totale serieimpedansen for kontaktledningsanlegget finnes så ved å dele spenningen på strømmen.

$Z_{tot}={\frac {\Delta U_{a-j}}{I_{a}}}=Z_{aa-j}-{\frac {Z_{as-j}^{2}}{Z_{ss-j}}}$ [$\Omega$/m]

18

Impedans for kontaktledningsanlegg med returleder

I henhold til regelverk for kontaktledningsanlegg skal strekninger som bygger om kontaktledningsanlegget nå bygge nytt anlegg med returledning. I dette systemet vil fremlederen, a, bestå av kontakttråd og bæreline og en returleder som består av to deler, s, som består kun av skinnene, og r, som består av returlederen. For dette systemet er det følgende likninger som gjelder:

$\Delta U_{a-j}=Z_{aa-j}\cdot I_{a}+Z_{ar-j}\cdot I_{r}+Z_{as-j}\cdot I_{s}$ [V/m]

19

$\Delta U_{r-j}=Z_{ar-j}\cdot I_{a}+Z_{rr-j}\cdot I_{r}+Z_{rs-j}\cdot I_{s}$ [V/m]

20

$\Delta U_{s-j}=Z_{as-j}\cdot I_{a}+Z_{rs-j}\cdot I_{r}+Z_{ss-j}\cdot I_{s}$ [V/m]

21

hvor

Zaa-j:	impedansen mellom fremleder og jord [$\Omega$/m]
Zas-j, Zar-j, Zrs-j:	gjensidig impedans mellom ledere og jord [$\Omega$/m]
Zss-j:	impedans mellom skinne og jord [$\Omega$/m]

For å beregne den totale impedansen benyttes forutsetningen fra over, $\Delta$U_s-j = 0. I tillegg benyttes at sum strøm i en sløyfe er lik null, I_a+I_r+I_s=0. Skinnestrømmen kan da finnes ut fra likning 21:

$\Delta U_{s-j}=Z_{as-j}\cdot (-I_{r}-I_{s})+Z_{rs-j}\cdot I_{r}+Z_{ss-j}\cdot I_{s}$ [V/m]

22

$I_{s}={\frac {Z_{as-j}-Z_{rs-j}}{Z_{ss-j}-Z_{as-j}}}\cdot I_{r}=b\cdot I_{r}$ [A]

23

Ved å sette inn likning 23 i likning 20, elimineres I_s og en vil da ha:

$\Delta U_{r-j}=Z_{ar-j}\cdot (-I_{r}-b\cdot I_{r})+Z_{rr-j}\cdot I_{r}+Z_{rs-j}\cdot b\cdot I_{r}$ [V/m]

24

Den totale serieimpedansen for kontaktledningsanlegget finnes så ved å dele spenningen på strømmen.

$Z_{tot.m.rl}={\frac {\Delta U_{r-j}}{I_{r}}}=Z_{rr-j}-Z_{ar-j}+(Z_{rs-j}-Z_{ar-j})\cdot b$	[$\Omega$/m]	25
$=Z_{rr-j}-Z_{ar-j}+(Z_{rs-j}-Z_{ar-j})\cdot {\frac {Z_{as-j}-Z_{rs-j}}{Z_{ss-j}-Z_{as-j}}}$

Beregning av serieimpedansene med avledning til jord

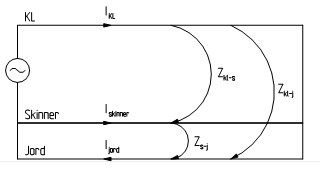
I kapittel 3.2.1 beregnes den totale serieimpedansen for kontaktledningsanlegget på bakgrunn av målinger. Dersom det blir antatt at en har avledning av skinnestrøm til jord, kan en dele den totale impedansen opp i flere delimpedanser, se figur 7. Disse delimpedansene er:

• serieimpedans kontaktledning-jord, Z_kl-j
• serieimpedans skinne-jord, Z_s-j
• serieimpedans kontaktledning-skinne mot jord, Z_kl-s-j

Figur 7 De forskjellige serieimpedansene

Fra Carsons tilnærmede formler har en følgende generelle uttrykket for den totale serieimpedansen, likning 26:

$Z_{l}={\frac {\Delta U_{a-j}}{I_{a}}}=Z_{aa-j}\cdot {\frac {Z_{as-j}^{2}}{Z_{ss-j}}}$[$\Omega$/km]

26

hvor

Zl:	den målte impedansen [$\Omega$/km]
Zaa-j:	fremlederens impedans. Zkl-j [$\Omega$/km]
Zas-j:	gjensidig impedans mellom fremleder og returleder i forhold til jord, Zkl-s-j [$\Omega$/km]
Zss-j:	returlederens impedans, Zs-j [$\Omega$/km]

De generelle uttrykkene for Z_kl-j , Z_kl-s-j , Z_s-j er også behandlet i kapittel 2, henholdsvis likning 4 og likning 8. Ved å innføre de generelle uttrykkene for impedansene i likning 18, blir likningen:

$Z_{l}=(r_{indre,kl}+r_{e}+j\mu _{0}f\cdot ln{\frac {D_{j}}{g_{kl}}})-{\frac {(r_{e}+j\mu _{0}f\cdot ln{\frac {D_{j}}{D_{kl-s}}})^{2}}{(r_{indre,skinne}+r_{e}+j\mu _{0}f\cdot ln{\frac {D_{j}}{g_{s}}})}}$ [$\Omega$/km]

27

hvor

rindre,kl:	indre motstand i kontaktledningen [$\Omega$/km]
rindre,skinne:	indre motstand i skinnene [$\Omega$/km]
re:	tap i jorden [$\Omega$/km]
Dj:	strømmens inntrengningsdybde [m]
gkl:	geometrisk middelavstand for kontaktledning med hensyn på seg selv [m]
gs:	geometrisk middelavstand for skinner med hensyn på seg selv [m]
Dkl-s:	middelavstand mellom kontaktledning og skinner [m]

Dersom det ikke er avledning til jord vil kretsen kunne forenkles. Forsøk som er gjort viser veldig liten avledning til jord. Dersom man ønsker å regne med avledning til jord, henvises det til ref. [1], vedlegg H.

Beregning av serieimpedans uten avledning til jord

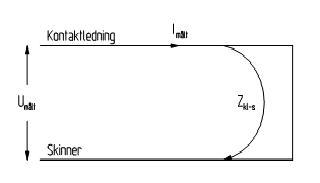
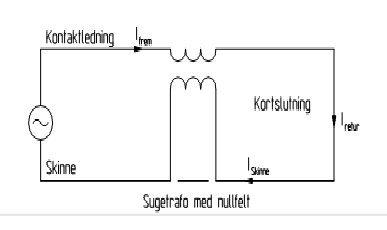
Forutsetninger som er gjort i over er at en del av strømmen går i skinnen, og resten i jord. Siden det ikke ble målt noen avledning til jord, kan målekretsen forenkles. Figur 8 viser hvordan målekretsen blir når det ikke er noen avledning til jord. Kretsen består av kontaktledning, kortslutning og retur i skinner.

Figur 8 Prinsippskisse av forenklet krets

Serieimpedansen for denne kretsen blir enklere enn den som er vist i figur 7, siden det ikke er noen avledning til jord.

$\Delta U=(Z_{kl}+Z_{skinn})\cdot I$

28

hvor

$\Delta U$:	spenningsfall i kretsen
Zkl:	impedans i kontaktledningen
Zskinne:	impedans i skinne
I:	strøm i kretsen

Den totale impedansen i den forenklede kretsen består bare av en impedans, Z_kl-s som er summen av de to delimpedansene Z_kl og Z_skinne i likningen over. Impedansen Z_kl-s er gitt i likning 30 ,med utgangspunkt i likningen under:

$Z_{kl}=r_{kl}+j\mu _{0}f\cdot ln{\frac {g_{kl-s}}{g_{kl}}}$

29

Tilsvarende for Zskinne som vist for Z_kl.

$Z_{kl-s}=r_{kl}+r_{skinne}+j\mu _{0}f\cdot ln{\frac {g_{kl-s}}{g_{kl}}}+j\mu _{0}f\cdot ln{\frac {g_{kl-s}}{g_{skinne}}}$	[$\Omega$/km]	30
$=r_{kl}+r_{skinne}+j\mu _{0}f\cdot ln{\frac {g_{kl-s}^{2}}{g_{kl}\cdot g_{skinne}}}$

hvor

Zkl-s:	total impedans i målekretsen [$\Omega$/km]
rkl:	indre motstand i kontaktledning [$\Omega$/km]
rskinne:	indre motstand i skinnen [$\Omega$/km]
gkl-s:	geometrisk middelavstand mellom kontaktledning og skinner [m]
gkl:	geometrisk middelavstand for kontaktledning med hensyn på seg selv [m]
gskinne:	geometrisk middelavstand for skinne med hensyn på seg selv [m]

Ved hjelp av likning 30 kan serieimpedansen beregnes.

Fra ref [1], vedlegg H, er det hentet en del verdier. Disse er beregnet på bakgrunn av tidligere utførte målinger.

• r_kl=0,124 $\Omega$/km
• r_skinne: frekvensavhengig
• g_kl-s : regnes ut med bakgrunn i figur 5.
• g_kl-s er lik for strøm i enkel eller dobbel skinne, pga. like avstander.
• g_kl=5,3897 mm
• g_skinne er frekvensavhengig, og avhengig av enkel og dobbel skinne.
• $\mu _{0}=4\pi 10^{-7}$H/m

Tabell 1 Verdier for å beregne serieimpedans i forenklet krets

f [Hz]	rkl[$\Omega$/km]	rskinne[$\Omega$/km]	gkl-s [m]	gkl [m]	gsk-enkel [m]	gsk-dobbel [m]
16 2/3	0,124	0,0964	5,65	5,3897	0,000138	0,01438
58,5	0,124	0,1806	5,65	5,3897	0,04126	0,2488
85	0,124	0,2177	5,65	5,3897	0,08377	0,3545

Satt inn i likning 30, blir verdiene for enkel skinne og f=16 2/3 Hz:

$Z_{kl-s}=0,124+0,0964+j4\pi 10^{-7}\cdot 1000\cdot 16,67\cdot ln{\frac {5,65^{2}}{0,0053897\cdot 0,000138}}$	$\Omega$/km	31
$=0,2204+j0,368=0,429\cdot e^{j59}$

Tabell 2 Serieimpedans for forenklet krets, beregnet for 16 2/3 Hz, 58,5 Hz og 85 Hz

f [Hz]	rI[$\Omega$/km]	Xenkel[$\Omega$/km]	Xdobbel [$\Omega$/km]	Zenkel [$\Omega$/km]	Zdobbel [$\Omega$/km]
16 2/3	0,2204	0,368	0,270	0,429	0,348
58,5	0,3046	0,873	0,7408	0,925	0,801
85	0,3417	1,19	1,04	1,24	1,09

Måling for å finne impedans

For å kunne beregne impedansen på bakgrunn av målingene, er det viktig at avledningen på strekningen er klarlagt. Denne kan klarlegges under målingen av impedansen.

Oppkobling på strekning

Impedansmåling

For å måle impedans på en strekning av kontaktledningsanlegget isoleres denne strekningen.

• Skinnene isoleres ved å koble vekk filterimpedansene ved isoleringene i hver ende av strekningen. Skinneisoleringen utgjør en motstand med størrelsesorden 1 k$\Omega$. Dersom det er filterimpedanser innkoblet på strekningen er det viktig at disse frakobles og at eventuelle skinneisolasjoner forbikobles. eventuelle overdragstransformatorer kortsluttes. Vegsikringsanlegg og sporfelter må kobles bort under målingen.
• Kontaktledningen isoleres ved å koble ut kontaktledningsbryterne. Dette gjør at strømmen ikke vil spre seg over til resten av anlegget. Dersom det er sugetransformator på strekningen vil impedansen som måles inneholde totalimpedansen inkludert sugetransformatorens impedans.

Inkludert i impedansen blir også den overgangsmotstand som gjenstander jordet til skinnegangen utgjør. Dette gir forskjell på strekninger med tremaster og master med støpte fundamenter.

Kobling av kretsen med kortslutning i den ene enden og strøm-innmating i den andre er vist i figur 9. Strøm-innmatingen kan enten skje fra transportabelt aggregat eller fra matestasjon. Ved bruk av matestasjon ligger strekningen det måles på, i tilknytning til denne. Det er ta nødvendig å ta hensyn til leder fra matestasjonen til kontaktledningen.

Figur 9 Skisse over målesløyfe med sugetransformator

Måling av avledning

Denne målingen inngår ikke i impedansmålingen. Måling av avledning benyttes for å se spesifikt hvor mye strøm som vil gå i jorden på den målte strekningen.

For å måle avledning fra skinnegangen til jord benyttes ofte en rogowski-spole som klemmes rundt skinnegangen med jevne mellom rom. Ved hjelp av denne og et amperemeter kan strømmen måles. Dersom strømmen avtar mot midten av strekningen er det avledning på strekningen.

Det er innført bruk av isolasjon mellom skinner og sviller, såkalt ”flesk”, for å redusere avledningen. På strekninger med tremaster og ”flesk” er det liten avledning. Strekninger med betongfundamenter og stålmaster kan ha større avledningen fordi mastene og fundamentene er koblet til skinnegangen i forbindelse med jording av mastene.

Målerutiner og bearbeidelse av måledata

Ved måling måles strøm, I, spenning, U, effekt, P og S, eventuelt kan effektmålingene erstattes med måling av cos $\varphi$. Utifra disse måleresultatene beregnes så impedansen for strekningen med kortslutning. Ved beregning må det tas hensyn til størrelsen på avledning fra skinner til jord. Er det liten avledning kan det for beregning av impedans brukes en forenklet krets. Dersom avledningen har en viss størrelse bør det tas hensyn til denne ved beregning av del-impedansene.

Beregning av total serieimpedans

Ut fra de målingene som utføres er det mulig å finne en total serieimpedans for sløyfen kontaktledning-kortslutning-skinne/jord. Det gjøres på følgende måte:

$Z_{tot}={\frac {U_{tot}}{I_{tot}}}$ $\Omega$

32

hvor

U_tot: målt spenning, effektivverdi

I_tot: målt strøm, effektivverdi

For å kunne sammenlikne resultatene fra kort strekning med resultatene fra lang strekning må serieimpedansen deles på strekningens lengde. En vil da finne en tallverdi for den totale serieimpedansen pr. kilometer (likning 33).

$Z_{l}={\frac {Z_{tot}}{antallkilometer}}$ $\Omega$/km

33

For å finne den reelle og imaginære del av den totale serieimpedansen er det først nødvendig å finne vinkelen cos$\varphi$ Cos$\varphi$ finnes ved hjelp av ytelsen og effekten (likning 34).

$cos\varphi ={\frac {P}{S}}$

34

hvor

P: aktiv effekt [kW]

S: tilsynelatende effekt [kVA]

Regneeksempel total serieimpedans

Tabell 3 Data fra en måling, strekningens lengde 1752 m

	58,5 Hz	85 Hz
	Enkel	Dobbel	Enkel	Dobbel
Strøm [A]	38,8	41	12,14	13,06
Spenning [V]	57,5	48,4	24,7	20,8
Frekvens [Hz]	58,4	58,5	84,5	83,6
Ytelse [kVA]	2,23	1,87	0,29	0,26
Effekt [kW]	0,71	0,66	0,072	0,065

I denne tabellen referer enkel og dobbel til om det er målt med enkel skinne eller parallellkobling av skinnene som retur for strømmen.

Under vises beregninger gjort for måling med 58,5 Hz og enkel skinnestreng. Ved å gjøre tilsvarende for de andre målingene fåes de verdiene som står i tabell 4.

Utfra likning 32 kan den totale impedansen for de forskjellige målingene beregnes:

$Z_{tot}={\frac {57,5}{38,8}}=1,48$ $\Omega$

35

Impedansen pr km blir:

$Z_{k}m=z={\frac {Z_{tot}}{antallkm}}={\frac {1,48}{1,752}}=0,846$ $\Omega$/km

36

For å finne r og x pr. km ut fra impedansen, z, må cos  beregnes. Det gjøres utfra likning 34.

$cos\varphi ={\frac {0,71}{2,23}}=0,32$

37

Utfra dette beregnes r og x under:

$r=z\cdot cos\varphi =0,846\cdot 0,32=0,27$ $\Omega$/km

38

$x={\sqrt {Z^{2}-r^{2}}}={\sqrt {0,846^{2}-0,27^{2}}}=0,80$ $\Omega$/km

39

Tabell 4 Serieimpedans, cos$\varphi$, reell og imaginær del for målingene

	58,5 Hz	85 Hz
	Enkel	Dobbel	Enkel	Dobbel
Ztot ($\Omega$)	1,48	1,18	2,03	1,59
Zl ($\Omega$/km)	0,846	0,67	1,16	0,91
cos$\varphi$	0,32	0,33	0,24	0,24
r ($\Omega$/km)	0,27	0,22	0,28	0,22
x ($\Omega$/km)	0,81	0,63	1,13	0,88

I tabell 4 ses det at impedansen med enkel skinne er høyere enn impedansen ved dobbel skinne. Dette kommer av at når strømmen går i en skinne består kretsen av en impedans i skinnen og en i kontaktledningen. Når strømmen går i begge skinnene består kretsen av en parallellkopling av impedansene i skinnene seriekoblet med impedansen i kontaktledningen. Det er parallellkoplingen av skinneimpedansene som gjør at impedansen for dobbel-skinne blir mindre enn impedansen for enkelskinne.

Sammenligning av målte og beregnede verdier

Ved å sammenligne verdiene for Z i tabell 2 og 4, se tabell 5 kommer det klart frem at verdiene ved beregning er litt høyere enn de målte verdiene.

Tabell 5 Impedans ved måling og beregning

	58,5 Hz	85 Hz
	Enkel	Dobbel	Enkel	Dobbel
Målt	0,923	0,801	1,24	1,09
Beregnet	0,846	0,67	1,16	0,91

Forskjellen kan komme av de tilnærmelsene som er gjort ved beregningene.

De viktigste tilnærmelser som er gjort er:

• kontaktledningen og bærelinen blir ekvivalert med en leder med areal lik summen av kontaktledningens og bærelinens
• skinnene blir ekvivalert med en sirkulær massiv leder med samme omkrets som skinnen
• skinnens indre motstand blir beregnet ut fra en gitt strøm
• den indre motstanden i kontaktledningen regnes konstant
• flere av parametrene er frekvensavhengige
• beregningen medfører mange usikkerhetsfaktorer.

Litteraturhenvisninger

1. Bente Langeland – Serieimpedans og avledning i returdelen av Jernbaneverkets kontaktledningsanlegg, NTNU, Hovedoppgave ved Institutt for elkraftteknikk (1997)

2. Birgitte Storøy – Serieimpedans for kontaktledningsanlegget i norske elektriske jernbanesystem, NTNU, Hovedoppgave ved Institutt for elkraftteknikk (1999)

3. Anna Sofie Mørland – Returkrets og jordingssystem på Gardermobanen, NTNU, Hovedoppgave ved Institutt for elkraftteknikk (1996)

4. Arnesen, Faanes, Klevjer og Olsen – Elektriske Kraftsystemer, del 2, NTH, (1994)