Sporets trasé/Sporgeometri
TRASÉFØRING / TEKNISK LINJEFØRING
De eldre jernbanesporene i Norge ble formet etter terrenget på en tid da hensynet til massebalansen ble vektlagt. Krutt var dyrt, og det kostet også mye å flytte på massene. Men med en hastighet på 30 km/h og kurveradier på 250 m, lot bygging av nyanlegg seg gjøre uten de helt store inngrepene. I dag gjelder fortsatt denne utformingen for de fleste strekningene i landet, men kravet til hastighet har naturlig nok økt i takt med teknisk utvikling og moderne transporttilbud. Den avgjørende størrelsen i dag blir derfor dimensjonerende hastighet, som blant annet setter høye krav til sporets geometri.
Når en løsning er valgt for en togtrasé, vil ulike hensyn avsette en del tekniske fastpunkter, det vil si punkter traséen må passere. Med trasering/ teknisk linjeføring menes den geometriske utformingen av linjen mellom de tekniske fastpunktene, og krav til utformingen settes av sporets geometri, hastighetsbetraktninger og de enkelte traseringsparametrene, foruten hensyn til det rullende materiell, som aksellast, trekkraft og kjøremotstand.
For å beskrive traséen teknisk sett, skiller vi mellom horisontal- og vertikal-geometri. De fleste geometriske størrelser betraktes i planet, selv om den faktiske traséen på alle måter ligger i rommet. Her beskrives krumning, overganger, ulik kurvatur og helning på tvers av sporet. Vertikalkurvaturen betraktes som et langsliggende profil, hvor traséen litt forenklet sagt endrer seg mellom stigning og fall. Uansett er denne geometrien mye enklere enn hos horisontalkurvaturen og betraktes separat. Der komplisert horisontalkurvatur forekommer er det også viktig at vertikalkurvaturen ikke innebærer store endringer.
HORISONTALKURVATUR
Kurver i horisontalplanet
I en alminnelig trasé har vi kort fortalt tre elementer: rettlinjer, sirkelkurver og overgangskurver. Sirkelkurvene angis ved radius R som er radius for spormidt. Eldre linjer i Norge har radius helt ned til R = 180 m, som utgjør en svært krapp sirkelkurve. Med dette forstår vi at kurvatur er en av de viktigste faktorene når hastigheten skal imøtekomme dagens krav til effektiv transport. Tabell .1 viser en kurvefordeling for ulike eksisterende baner i Norge:
| R <= 300 m | 300 m < R <= 500 m | 500 m < R <= 1100 m | R > 1100 m | Rettstrekning | Minste radius | |
|---|---|---|---|---|---|---|
| Østfoldbanen, vestre linje (prosentfeil) | 3 % | 13 % | 12 % | 19 % | 58 % | 200 m |
| Østfoldbanen, østre linje | 2 % | 18 % | 17 % | 20 % | 43 % | 250 m |
| Dovrebanen | 7 % | 11 % | 17 % | 25 % | 39 % | 238 m |
| Kongsvingerbanen | 0 % | 3 % | 20 % | 20 % | 56 % | 257 m |
| Rørosbanen | 6 % | 12 % | 15 % | 15 % | 52 % | 189 m |
| Nordlandsbanen | 3 % | 19 % | 16 % | 21 % | 40 % | 225 m |
| Gjøvikbanen | 20 % | 16 % | 16 % | 23 % | 25 % | 200 m |
| Bergensbanen | 12 % | 12 % | 15 % | 19 % | 42 % | 183 m |
| Sørlandsbanen | 11 % | 18 % | 14 % | 17 % | 40 % | 243 m |
| Vestfoldbanen | 12 % | 11 % | 14 % | 21 % | 42 % | 180 m |
| Solørbanen | 1 % | 3 % | 7 % | 28 % | 61 % | 245 m |
| Roa - Hønefoss | 15 % | 21 % | 17 % | 22 % | 25 % | 238 m |
| Raumabanen | 7 % | 6 % | 20 % | 23 % | 43 % | 259 m |
| Hell - Storlien | 9 % | 15 % | 18 % | 16 % | 42 % | 275 m |
| Grong - Namsos | 4 % | 14 % | 13 % | 24 % | 45 % | 250 m |
| Randsfjordbanen (prosentfeil) | 5 % | 21 % | 23 % | 18 % | 35 % | 240 m |
| Flåmsbanen | 52 % | 5 % | 9 % | 1 % | 33 % | 130 m |
| Asker - Spikkestad | 9 % | 11 % | 12 % | 19 % | 50 % | 263 m |
| Arendalslinjen | 33 % | 13 % | 7 % | 21 % | 27 % | 210 m |
| Ofotbanen | 30 % | 20 % | 12 % | 9 % | 29 % | 250 m |
| Øvrige strekninger | 14 % | 9 % | 12 % | 14 % | 52 % | - |
| Totalt | % | % | % | % | % | 130 m |
Sporvidde
Sporvidden er den vinkelrette, horisontale avstanden mellom kjørekanten til de to skinnestrengene, målt 14 mm under skinnehodets topp. I Norge er sporvidden satt lik 1435 mm. Der denne sporvidden er anordnet betegnes sporet normalspor.
Fra gammelt av ble akkurat denne sporvidden anordnet fordi det da ble nok plass for to hester i bredden mellom skinnene. Men opprinnelig ble jernbanen i Norge bygget med smalspor, altså med sporvidder under 1435 mm. En del av disse er i dag museumsbaner, som for eksempel Setesdalsbanen (1067 mm) og Hølandsbanen (750 mm). Såkalt bredspor, dvs. over 1435 mm, finnes også ved flere forvaltninger: En av grunnene til dette var blant annet frykten for at Napoleon skulle bruke jernbanen til transport av soldater ved en eventuell invasjon. Bredspor finnes blant annet i Russland (1520 mm), Finland (1524 mm) og Spania (1667 mm).
Rettlinjer
Rettlinjer er i utgangspunktet relativt uproblematiske med hensyn til traseringsparametre. Som traseringselement er en rettlinje en sirkelkurve med radius lik uendelig. Rettlinjen tilstøter både overgangskurven og sirkelkurven på sporet, sistnevnte ofte på stasjoner og i sidespor.
Traseringsparametre i rettlinjen
Rettlinjens lengde er sjelden bestemmende på hovedspor og derfor som regel ikke omtalt som traseringsparameter. Derimot finnes en rekke tilfeller hvor rettlinje av en viss lengde er påkrevd innlagt for å bedre kjøreforholdene.
Generelt for alle traseringselementer med konstant krumning gjelder lengdekravet følgende tabell:
| Normale krav [m] | Minste krav [m] |
|---|---|
| 0,5 V | 0,25 V |
Dette kravet sørger for at gjennomkjøringstiden for hvert element blir minimum 0.9 sekunder.
I hovedspor finnes ingen hastighetsbegrensninger pga. rettlinjen. Det er de andre traseringselementene som evt. gir dimensjonerende hastighet.
Sirkelkurver
definisjonEn sirkelkurve skal her bety en kurve som i horisontalplanet har konstant krumming, dvs. konstant radius, langs hele kurven.
Traseringsparametre i sirkelkurven
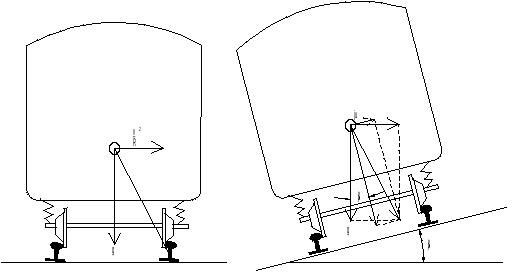
For å beskrive sirkelkurvens egenskaper må vi først ta en del fysiske størrelser i betraktning. Med utgangspunkt i figur 1, og gitt at vi befinner oss i en sirkelkurve, har vi to konstante akselerasjoner: Tyngdens akselerasjon vertikalt nedover g og sentripetalakselerasjonen a rettet innover mot kurvens sentrum. For en passasjer føles det imidlertid som om akselerasjonen er rettet ut av kurven. Kraften på grunn av denne akselerasjonen omtales gjerne som sentrifugalkraft - en størrelse som i fysikken regnes som en fiktivkraft. Vi skal imidlertid i det følgende bruke sideakselerasjon j om nettopp denne størrelsen, som dermed er rettet motsatt vei av den virkelige sentripetalakselerasjonen.
Fra fysikken har vi:
| (1) |
Figur 1 viser situasjonen for sirkelkurve både med og uten overhøyde. Overhøyden, som betyr to skinnestrengers høydeforskjell i forhold til horisontalplanet, anordnes for å kompensere for sideakselerasjonen, og det er den totale akselerasjonens (g + j) komponenter langs vogngulvet som betraktes i det følgende.
Utfra samme figur ser vi at gravitasjonens komponent langs vogngulvet er:
| (2) |
der s er sporvidden som normalt settes lik 1500 mm i disse betraktningene.
På samme måte har vi:
| (3) |
men fordi er liten, kan vi sette , det vil i praksis si at vi regner sideakselerasjonen for å virke parallelt med vogngulvet.
Akselerasjonenes komponenter langs vogngulvet, j’ og g’, er ved en gitt hastighet like store, og vognen er da ikke utsatt for ubalanserte sideakselerasjoner. Vognen har i dette tilfellet såkalt likevektshastighet, og for å oppnå denne situasjonen må den ene skinnen ha en bestemt overhøyde. Denne kalles for teoretisk overhøyde:
| (4) |
Sporvidden, hastigheten og kurveradien bestemmer altså overhøyden. Dersom overhøyden allerede er gitt, kan vi bestemme likevektshastigheten:
| (5) |
At sideakselerasjonen er kompensert ved gravitasjonens komponent i sporplanet under likevektshastigheten kan tydeliggjøres ved:
| (6) |
Men for persontrafikken er som oftest hastigheten større enn likevektshastigheten, og da vil gravitasjonens komponent parallell med sporplanet bare kompensere for deler av sideakselerasjonen - vi får en ukompensert sideakselerasjon ju:
| (7) |
Den ukompenserte sideakselerasjonen ju har grenseverdier. Blir den for stor, vil det føles ubehagelig for passasjerer. Vi setter derfor ofte ju = ju,maks i uttrykket over.
En annen vinkling på den ukompenserte sideakselerasjonen er at overhøyden ikke er stor nok for den aktuelle hastigheten. Vi har dermed et underskudd på overhøyden, eller en manglende overhøyde:
| (8) |
Multipliserer vi ut uttrykket i 7, med s/g, får vi et utrykk for manglende overhøyde som funksjon av den ukompenserte sideakselerasjonen:
| (9) |
I motsatt tilfelle, hvis hastigheten er mindre enn likevektshastigheten, blir ju negativ, det vil si at den er rettet innover i kurven. Vi kan likeledes snakke om en overkompensering, eller overskuddssideakselerasjon, og dette er eksempelvis tilfellet med godstog som trafikkerer spor beregnet på blandet trafikk. Vanligvis betegnes fenomenet overskuddsoverhøyde E. Ved full stans, som på stasjoner, virker kun gravitasjonens komponent, og dette setter grenser for hvor stor overhøyden kan være. I Norge er maksimal overhøyde satt til hmaks = 150 mm, i tråd med det som er mest vanlig hos de fleste forvaltningene i Europa.
Med utgangspunkt i ju,maks / Imaks, er det særlig fire hensyn som skal ivaretas:
- passasjerenes komfort
- sideforskyvning av sporet
- avsporing
- velting
En tommelfingerregel er at så lenge passasjerkomforten er ivaretatt, er de tre sikkerhetshensynene også godt innenfor kravet. En cirka tallfesting av sikkerhetskravene kan gis utfra verdier for manglende overhøyde:
- sideforskyvning: I > 200 mm
- avsporing: I > 300 mm
- velting: I > 400 mm
Med dette utgangspunktet skulle en tro at sikkerheten alltid var ivaretatt og brudd på kravene aldri forekom. Men sideforskyvninger og avsporinger skjer, og som regel skyldes dette at I/ju har vært altfor høy i et kort tidsintervall. Sporfeil og ulike egenskaper hos det rullende materiell medvirker derfor til å overskride de teoretiske grenseverdiene.
Komfortbegrepet vil bli nøye gjennomgått i kapitlet Krengetogstilpasning utfra komfort, men det kan nevnes at grenseverdiene som er diskutert her må variere med hvorvidt en passasjer sitter, står eller går i vogna.
Settes maksimal, ukompensert sideakselerasjon ju, maks inn for ju, får vi en maksimalverdi for overhøyde underskudd Imaks, som igjen kan gi grenseverdi-uttrykk for henholdsvis hastigheten og overhøyden, avhengig av hvilken størrelse som er kjent:
| (10) | |
Begrepet manglende overhøyde er innført hovedsakelig for å lempe på den praktiske gjennomføringen. Tradisjonelt har ligningene .10 også blitt skrevet om med innsetting av kjente størrelser for ytterligere å lette beregningsarbeidet. De ser da slik ut:
| (11) | |
der V er hastighet i km/h, R i m og I og h i mm.
Med gitt hastighet kan vi finne en minsteverdi for overhøyden. Setter vi overhøyden høyere enn hmin, vil den ukompenserte sideakselerasjonen også bli mindre enn ju,maks . I tillegg til det absolutte taket for overhøyder på 150 mm, skal overhøyden aldri overstige den teoretiske overhøyden (ukompensert sideakselerasjon lik null) for det raskeste toget på sporet. Gitt lengden på overgangskurven, må heller ikke overhøyden være så stor at rampestigningshastigheten blir for høy. I siste omgang innebærer lav hastighet i krappe kurver en fare for avsporing når overhøyden blir stor. Oppsummert med formler har vi følgende grenseverdier for overhøyden:
| 1) | ||
| 2) | ||
| 3) | (12) | |
| 4)* | a) b) | |
| 5) |
*) Formlene 4 a) og b) gjelder for hhv. nye baner og eksisterende baner.
Ligning 1) i 12 er skrevet med tanke på de raskeste togene, hvor vi kjører med manglende overhøyde. Ligningen er den samme for godstog, bortsett fra at vi legger til overskuddsoverhøyden i stedet for å trekke fra den manglende overhøyden. For VG = 80 km/h får vi:
| (13)* | |
*)De tre verdiene for overskuddsoverhøyden (i klammeparentes) gjelder for hhv. normale og minstekrav for nye baner og krav for eksisterende baner.
Konstanten k i ligning 5) i 12 får etter gjeldende grenseverdier for traséparametre verdier som angitt i tabell 3.
Tabell 2.3Beregningsgrunnlag for overhøyden pga. rampestignings-hastighet
| Krav/bane | dh/dt | k |
|---|---|---|
| normale krav, nye baner | 28 | 100 |
| minstekrav, nye baner - V > 120 km/h | 35 | 126 |
| minstekrav, nye baner - V ≤ 120 km/h | 46 | 166 |
| eksisterende baner - konvensjonelt materiell | 55 | 198 |
| eksisterende baner - krengemateriell | 75 | 270 |
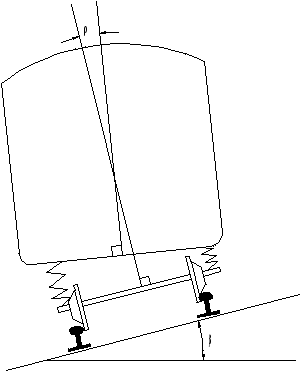
Utover de fysiske grunnbetraktningene ovenfor, må en se nærmere på egenskapene til det rullende materiellet i samspill med sirkelen som traseringselement. To viktige begrep i denne sammenhengen er effektiv sideakselerasjon J og rullvinkelkoeffisienten ρ. På grunn av fjæring og høye hastigheter, vil en togvogn lene seg utover i kurver, noe som vil oppheve noe av den tilsiktede overhøyden i kurven. Denne leningen utover er en målbar vinkel og kalles rullvinkelen ρ, vist på figur 2.
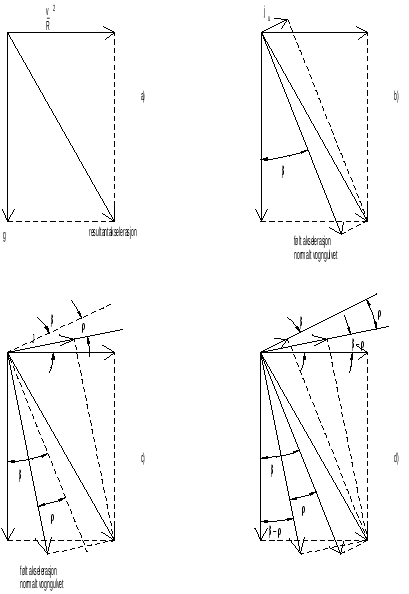
En rullvinkel vil dermed også øke den følte sideakselerasjonen for passasjerene, så den teoretiske, ukompenserte sideakselerasjonen ovenfor vil alltid være for liten. Den reelle følte sideakselerasjoenen kalles effektiv sideakselerasjon. Figur 3 viser sammenhengen mellom de dekomponerte akselerasjonene som virker på vogna når alle de ulike betraktningene over innlemmes. Akselerasjonenes angrepspunkt skal bety tyngdepunktet til det objektet (ideelt sett passasjeren) som betraktes.
På figuren ser vi at resultantakselerasjonen er den samme i alle tilfeller, både i retning og størrelse. Dette kommer av at uansett hvilken referanseramme vi legger til grunn, er det kun hastigheten, kurveradien og tyngdeakselerasjonen som bestemmer resultanten. Vi ser tydelig at den effektive sideakselerasjonen er svært avhengig av hvor mye vogna krenger innover i kurven. I tillegg kan det nevnes at økt krenging vil gi økt normalkraft fra vogngulv på passasjer, slik at passasjeren vil føle seg tyngre.
Forholdet mellom effektiv sideakselerasjon, ukompensert sideakselerasjon og rullvinkelkoeffisient er gitt av følgende ligning:
| (14) |
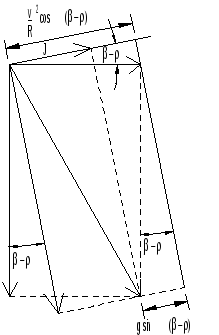
Ved å betrakte figur 4, kan vi utlede sammenhengen mellom rullvinkelkoeffisienten r og rullvinkelen ρ fra ligning 14:
| (15) |
Jf. tidligere tilnærminger, kan vi sette cosβ ≈ cosρ ≈ 1. Med sinβ = h/s kan vi med litt regning komme fram til følgende uttrykk for rullvinkelkoeffisienten:
| (16) |
Uttrykket kan imidlertid forenkles gjennom tilnærming. På grunn av at rullvinkelen er liten, kan vi tilnærme sinρ med ρ . Dessuten er de to første leddene i parentesen i 16 så små at vi kan utelate dem for deretter å oppveie dem ved å sette tyngdeakselerasjonen g = 10. Dermed får vi et svært enkelt uttrykk for rullvinkelkoeffisienten:
| (17) |
der ρ er i radianer.
Likning 17 innsatt i utgangslikningen gir effektiv sideakselerasjon som funksjon av rullvinkelen:
| (18) |
Når denne forenklede formelen tas i bruk, må det nevnes at dynamiske bidrag er utelatt. Disse vil i praksis øke den effektive sideakselerasjonen J ytterligere, men beregningsmessig er det alltid ju som er traseringselementet. Det kan allikevel nevnes at J til en viss grad er tatt hensyn til gjennom regelverket, i det det skilles mellom normal- og plusshastighet.
Uten å gå inn på beviset her, kan det vises at rullvinkelen i stor grad er proporsjonal med sideakselerasjonen, slik at det finnes en konstant c som gir ρ = c ju . I ligning 17 får vi da eliminert hele sideakselerasjonen ju , og rullvinkelkoeffisienten blir en konstant for hvert enkelt rullende materiell. De avgjørende elementer blir da lastens masse og plassering, egenskaper og plassering til vognas fjæringssystem.
For normale person- og godsvogner ligger gjerne rullvinkelkoeffisienten mellom 0.1 og 0.6, der de nyere vogntypene har den laveste verdiene. For krengetog derimot blir situasjonen motsatt, i og med at vogna lener seg innover i stedet for utover i kurven. Vi får dermed negativ koeffisient, og eksempelvis kan vi regne r for det svenske X2000-toget til å ligge rundt
r = -0.7. For NSBs krengetog, som vil være i drift fra midten av 1999, vil r = -0.55.
En annen måte å angi rullvinkelkoeffisienten for krengetog på er størrelsen fr = 1+r. Denne kalles effektiv rullfaktor, og r blir hetende kompensasjonsgrad og angis i prosent.
I alle tilfelle er det viktig å huske at vi i prosjekteringssammenheng som regel betrakter de størrelser som virker i sporplanet mhp. sporgeometrien. For å betrakte størrelsene langs vogngulvet må vi nettopp trekke inn de sistnevnte parametrene, og da blir som regel passasjerenes subjektive opplevelse av fremføringen avgjørende for bestemmelsen av de enkelte parametrene.
Overgangskurver
definisjon
En overgangskurve er definert ved at den har krumning lik tilstøtende kurver i endene og samtidig har kontinuerlig endring av krumning/krumningsradius gjennom hele kurven. Summert er en overgangskurve et traséelement som forbinder to traséelementer med ulik radius. Det mest elementære eksemplet er derfor en overgangskurve som begynner med en krumningsradius lik uendelig, i punktet der den tilstøter en rettlinje, og ender med en krumningsradius lik den tilstøtende sirkelkurven i andre enden.
Den praktiske betydningen av overgangskurven er en smidig overgang fra en akselerert tilstand til en annen, med henblikk først og fremst på passasjerkomfort, men også sikkerhet og slitasje på spor og materiell. Det knytter seg derfor mange problemstillinger til innlemmingen av overgangs-kurver i sporet, hvor de tekniske aspektene rundt traseringsparametrene blir behandlet i det følgende.
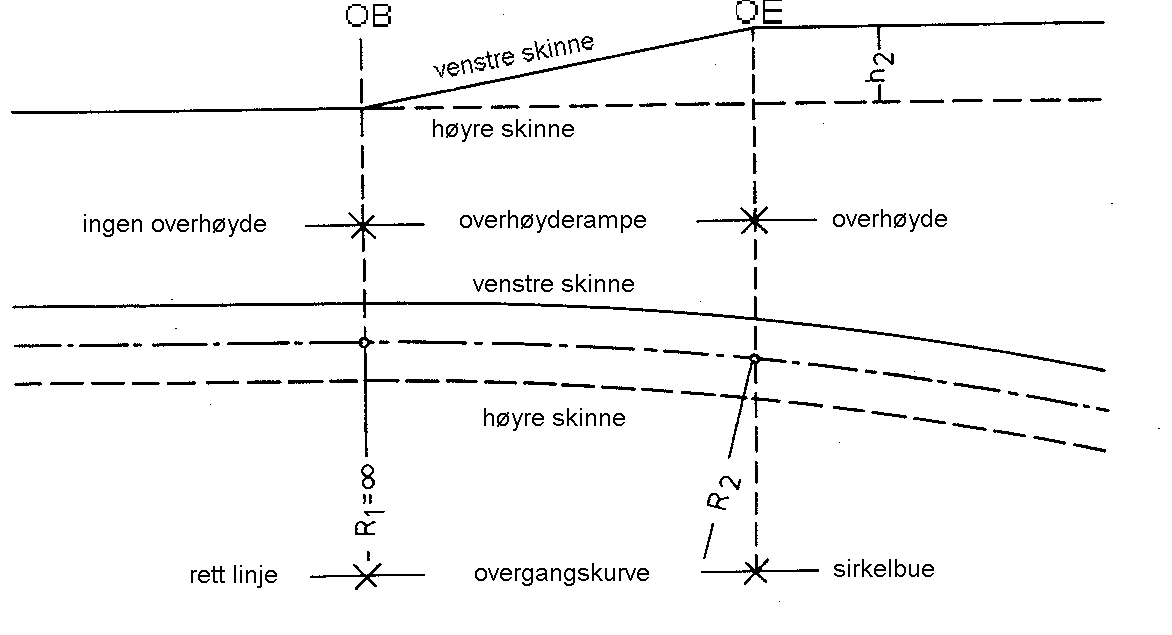
Overhøyderamper
For å oppnå overhøyde på sporet anvendes såkalte overhøyderamper. Disse har den egenskapen at de bygger opp overhøyde kontinuerlig for ytterste skinnestreng. I alminnelighet er overhøyderampene sammenfallende med overgangskurvene. Som vi kan tenke oss, innebærer innlemming av overhøyderamper at en vogn blir liggende skjevt på sporet gjennom hele rampen. Forenklet kan vi si at dersom vogna var konstruert helt stiv, ville kun tre av fire hjul være på sporet samtidig. Rampen må derfor ikke være brattere enn at alle hjul har sikker føring gjennom hele overgangskurven.
Overhøyderamper forekommer dermed mellom rettlinje og sirkelkurve og mellom sirkelkurver. Punktet i overgangen fra rettlinje til overgangskurve betegnes overgangskurvens begynnelse OB, mens punktet i motsatt ende betegnes overgangskurvens ende OE. For overgangskurven fra en sirkelkurve til en annen angir betegnelsene OB og OE kurvens tilstøtende punkter mot hhv. den slakeste og den krappeste av sirklene.
For det første tilfellet kan vi enkelt se for oss oppbygningen av rampen, der dens oppgave er å bygge opp overhøyden til en kommende sirkelkurve, jf. figur .5.
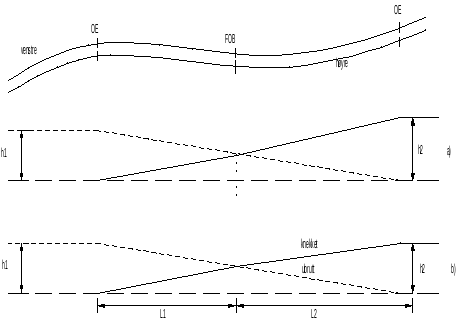
Mer komplisert blir derimot situasjonen hvis vi har to motsatt rettede sirkelkurver uten rettlinje i mellom. Rampene går da rett i hverandre med det kravet at vendepunktet må ha overhøyde lik null. Denne rampeutformingen kalles en sakset overhøyderampe, og vendepunktet betegnes FOB (Felles OB). Tilstøtende overgangskurver med et slikt felles utspring har alltid et punkt OE i motsatt ende. Videre vil en sakset overhøyderampe oppføre seg ulikt for ulike kontrakurver. Hvis de to rampene i saksen har lik stigning, blir situasjonen enkel, jf. fig. .6, mens har de ulik stigning, vil minst en av skinnestrengene få en knekk i FOB. Dette løses ved at den ene strengen løftes ubrutt gjennom hele sakserampen fra OE til OE, for så å bestemme FOBs beliggenhet hvor kravet om null overhøyde skal være oppfylt. Den siste strengen løftes til slutt mellom FOB og endepunktene.
Mange steder er overgangskurvene for korte til at store hastighetsøkninger kan tillates. En kunne ideelt sett ønske seg kurvekorrigeringer som omfattet forlengelse av overgangskurvene, men dette blir fort altfor omfattende og vil medføre store kostnader. Den alternative løsningen på problemet blir derfor å beholde lengden til overgangskurven og samtidig senke rampestigningen.
Tidligere ble denne oppgaven i praksis utført ved å strekke overhøyderampen et stykke inn i sirkelkurven. Enden av rampen ble da ikke sammenfallende med OE og ble benevnt RE - rampens ende. Metoden tillates derimot overhodet ikke i dag, i og med at overhøyden først er bygget helt opp et stykke inne i sirkelkurven. Når hastigheten er høy vil dette gi kritiske utslag på komfort såvel som slitasje.
Dagens løsning består i å redusere overhøyden gjennom hele sirkelkurven, i praksis ved å løfte sporets indre streng.
Ulike typer overgangskurver
Utfra definisjonen av en overgangskurve kan denne utformes på ulikt, matematisk grunnlag. I Norge benyttes kun kurver der den kontinuerlige variasjonen i overhøyde og krumning foregår lineært. Derfor skal vi i det følgende først kort nevne to ikke-lineære typer som finnes før vi i neste omgang tar grundigere for oss den kurvetypen som er anvendt i Norge - klotoiden og dens tilnærminger.
En 4.gradsparabel har krumningsforløp tilsvarende to 2.gradsparabler. Derfor gjelder ulike matematiske uttrykk for henholdsvis første og siste halvdel og kurvens utstrekning:
| (19) | |
der l = lengden langs tangenten, og m det såkalte innrykket, eller innflyttingen, som beskrives nærmere i avsnitt 2.5.4.
En annen kurve med s-formet krumning er sinuskurven, gitt som:
| (20) | |
Den generelle formelen for en klotoide er
| (21) |
der R er den tilstøtende sirkelkurvens radius, eller minste krumningsradius i overgangskurven, L er overgangskurvens lengde langs buen, og A er den såkalte klotoideparameteren.
Alle omskrivinger av 21 vil også gjelde et vilkårlig punkt på kurven, for eksempel når en kjenner r eller l. Ellers vil det være naturlig å velge A i forhold til en bestemt lengde på kurven.
Ved å sette opp et uttrykk for krumningen til overgangskurven, ser vi at den er proporsjonal med kurvens lengde:
| (22) |
Rettvinklede koordinater på klotoiden er ved rekkeutvikling gitt ved:
| (23) | |
(Se utledning i 6.1 (vedlegg).)
Traseringsparametre i overgangskurven
Forholdet mellom endring av overhøyde og posisjon langs rampen kalles rampestigning og er gitt ved følgende uttrykk, som gjerne oppgis i promille:
| (24) |
På grunn av de skjevheter en overhøyderampe innebærer, kalles rampestigningen også for vindskjevhet. Men dette begrepet forekommer i mer utstrakt grad når det er snakk om sporfeil i vertikalretningen. Vi kan derfor tilnærmet si at rampestigning er den tilsiktede endringen av overhøyde i lengderetningen, mens vindskjevhet er den faktiske situasjonen på sporet. Ved store hastigheter er ofte rampestigningen en begrensende parameter, men den er sjelden bestemmende for overgangskurvens lengde. Grenseverdien for rampestigningen er som oftest en betraktning utfra avsporingsfare, og ved nyanlegg eller større utbedringsarbeider skal rampestigningen under ingen omstendighet overstige 1:400.
Avsporing er en av sikkerhetsfaktorene for sirkelkurver, men det er særlig ved rampestigning at risikoen for avsporing er reell. I den anledning skal kort nevnes et avgjørende, fysisk begrep avhengig av flere faktorer.
Det såkalte Y/Q-forholdet - forholdet mellom føringskraft og vertikalkraft på det førende hjulet i en kurve - skal alltid ligge under en maksverdi. Foruten sporets geometri, som er tilsiktet, avhenger forholdet av vogna som benytter sporet og de friksjonsforhold som oppstår.
Hvis en tenker seg en 2-akslet vogn som kjører med lav fart nedover en overhøyderampe fra sirkelkurve til rett spor, vil kreftene mellom skinner og hjul avhenge av overhøyden, rampestigningen og horisontalradius: Helningen gir belastning på indre hjul og avlastning på ytre. Ytre, førende hjul på første aksel avlastes, mens indre belastes. Føringskraften på indre, førende hjul øker med avtagende radius.
Skjevheter i vognens egenskaper og dens last er også medbestemmende.
Når grenseverdier for rampestigning er satt, skal det bety den totale rampestigningen - summen av tilsiktet rampestigning og vindskjevheter som følge av sporfeil. Kravet nevnt tidligere på rampestigning under 1:400 tar høyde for den totale rampestigningen.
Rampestigningshastigheten er overhøydens endring over tid og kan uttrykkes ved:
| (25) |
For krengetog reduseres sideakselerasjonens effekt på passasjerene ved krenging innover i kurven. Dette kan imidlertid betraktes som en økning i oppbyggingen av overhøyde og innebærer derfor også en kraftig økning i rampestigningshastigheten.
En parameter enda nærmere et mål på passasjerkomforten er rykket ψ. Dette er som nevnt et uttrykk for hvor fort den ukompenserte sideakselerasjonen endres over tid:
| (26) |
I og med at ukompensert sideakselerasjon også kan uttrykkes som manglende overhøyde, er rykket også definert som endring av den manglende overhøyden. Jf. .9 får vi:
| (27) |
En annen størrelse som føyer seg inn når lengden av overgangskurven skal bestemmes, og som følger av rampestigning, er rullvinkelhastigheten, eller vridningshastigheten. Denne benyttes først og fremst som et alternativ til rampestigningshastigheten når passasjerkomforten skal ivaretas. Tradisjonelt settes størrelsen opp som følgende forhold: 1 : nV, der V er hastigheten i km/h og n gjerne ligger mellom 4 og 12. Eksempelvis gir n = 4 en vinkelhastighet på 2.7 grader/s, mens undersøkelser har vist at stående passasjerer har akseptert opptil 4 grader/s. Viktig å huske er at rullvinkelen utover i kurven vil oppheve noe av vinkelhastighetens effekt for konvensjonelle tog.
Med utgangspunkt i den alminnelige formelen for klotoiden, uttrykt ved klotoideparameteren A, og krumning som den inverse av radius R, får vi at
| (28) |
for et vilkårlig punkt der lengden fra overgangskurvens begynnelse (OB) er l.
Skal vi utlede krumningen med dynamiske parametre, kan det vises at
| (29) | |
Sammenlikner vi likn. 29 med 28 ser vi at klotoideparameteren A, kan skrives som
| (30) |
Den minste klotoideparameteren (Amin) vi kan ha for en gitt hastighet, v, får vi når vi setter inn de aktuelle grenseverdiene for både rampestigningshastigheten og rykket: dh/dt = dh/dtmaks, ψ = ψmaks.
Formelen ovenfor vil kunne være nyttig for et nyanlegg dersom man har bestemt seg for en viss hastighet og ut fra det ønsker å bestemme minste klotoideparameter. Hvis en hovedpunktsberegning skulle vise at klotoideparameteren er mindre enn denne minste verdien, må man beregne på nytt for øke L og/eller R, evt. senke hastighetskravet.
Ved Jernbaneverket brukes ikke klotoideparameteren for å karakterisere overgangskurvene, men lengden L. På alle sportegninger skal derfor lengden angis. Det kan derfor være nyttig å finne minste klotoidelengde som samsvarer med Amin. Denne blir av uttrykkene over lik
| (31) |
Vi merker oss spesielt hvor sterkt minste klotoidelengde er avhengig av hastigheten; en økning i hastigheten på 25% vil nesten fordoble Lmin!
Det er kanskje noe overraskende at minste klotoidelengde verken er avhengig av overhøyden eller den ukompenserte sideakselerasjonen. Dette virker tilsynelatende i konflikt med andre betraktninger der nettopp h og ju står sentralt for å kunne bestemme minste nødvendige klotoidelengde. Forklaringen er den at vi nå betrakter overhøyden som en variabel som er avhengig av maksimal rampestigningshastighet, minste klotoidelengde og valgt hastighet. Vi kan nå skrive den ideelle overhøyden som samsvarer med uttrykket i .31 som
| (32) |
Som kjent er den ukompenserte sideakselerasjonen avhengig av denne overhøyden og valgt hastighet. Det eneste vi må kontrollere er at h og ju ikke overskrider sine respektive maksimalverdier, dessuten at overhøyden ikke fører til for stor vindskjevhet.
I mange sammenhenger er overhøyden ikke avhengig av de samme størrelsene som nevnt ovenfor (dh/dtmaks, Lmin og v). Da er overhøyden ansett å være “diktatorisk” fastsatt uten hensyn til andre parametre (enn at h < hmaks). I uttrykk for den ukompenserte sideakselerasjonen ju er det selvsagt denne fastsatte overhøyden vi setter inn.
Tilnærming til 3.gradsparabelen
Klotoiden har en svært enkel utgangsformel, men å konstruere en klotoidekurve i praksis innebærer et behov for elektronisk regnekraft. Derfor har overgangskurver tradisjonelt blitt utformet som en god tilnærming gjennom 3.gradsparabelen:
| (33) |
Her ser vi at det refereres til abscisse og ordinat (x og y), og L skal her bety kurvens lengde langs tangenten til kurven i OB.
Men uttrykket er utledet av beregninger på klotoiden og kurver med tilsvarende egenskaper, og i første omgang skal vi derfor gjennomgå en slik utledning:
Med rampestigning 1:n kan vi finne vilkårlig overhøyde ved hx = x/n. Setter vi dette sammen med uttrykket for den teoretiske overhøyden gitt i ligning .4, og snur litt på uttrykket, kan vi få følgende uttrykk for krumningsradius:
| (34) |
Et teoretisk uttrykk for krumningsradius er samtidig gitt ved:
| (35) |
Dette er differensiallikningen for en radioide, der krumningsradien er omvendt proporsjonal med kurvens lengde. Avhengig av om en innfører abscissen, korden eller buen for variabelen x, fremkommer abscisseradioiden, korderadioiden eller bueradioiden. Sistnevnte er kurven som har fått navnet klotoiden.
Ved å forenkle lengdeuttrykkene x og y med og , kan vi rekkeutvikle formelen 35 til følgende uttrykk for bueradioiden:
| (36) |
Uttrykkene for de to andre radioidetypene har noe ulike ledd fra og med andre ledd i parentesen og utover, men i praksis er det bare kurven nær origo som benyttes, og her er egentlig alle radioidene like anvendelige som overgangskurve.
Den tilnærming som tradisjonelt har vært utført, er å kun benytte aller første ledd fra ligning .36, slik at vi får:
| (37) |
Uttrykket til høyre i 37 er nettopp ligningen for en kubisk parabel, eller 3.gradsparabel. Samme uttrykk kan finnes ved å tilnærme kurvens stigning dy/dx med null, siden det kun er en liten del av kurven som benyttes, for så å dobbeltintegrere uttrykket for krumningen.
Som regel ønsker vi å involvere lengden på overgangskurven. Med sistnevnte tilnærming, og gitt x = L, har vi av .35 at C = RL. Dermed ender vi opp med den alminnelig brukte formelen gitt i .33.
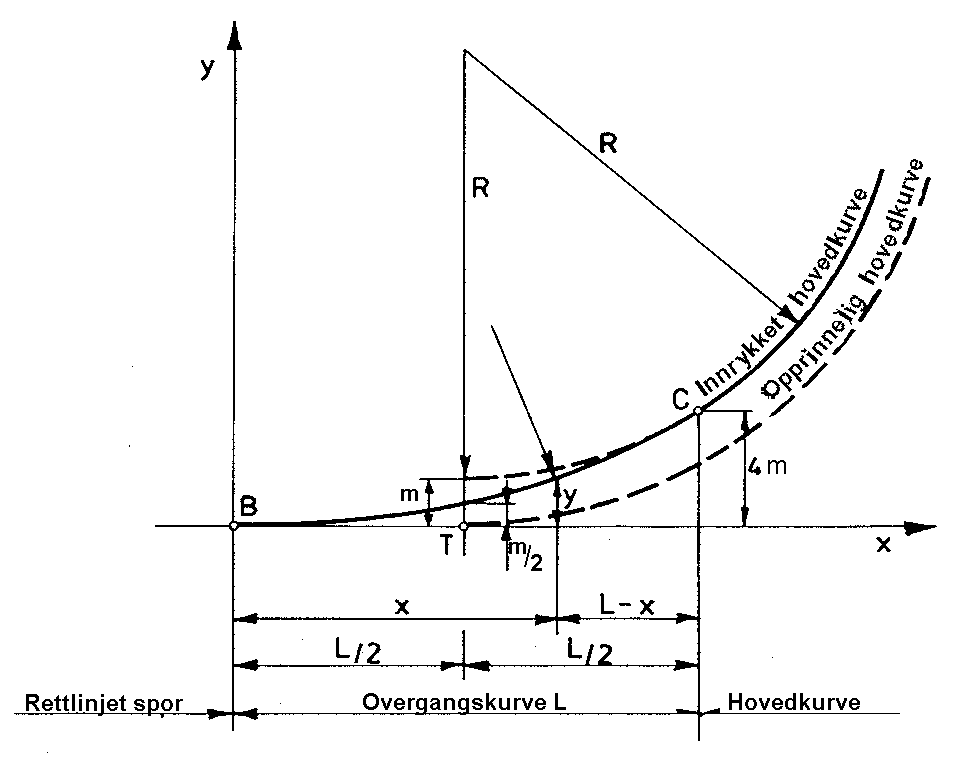
Et tilleggsmoment ved bruk av 3.gradsparabel ligger i dens praktiske utforming, det vil si å bestemme dens beliggenhet. I forhold til et rettvinklet koordinatsystem, er ordinaten y gitt for alle verdier av x langs tangenten. Det vanligste har imidlertid vært å betrakte utgangssituasjonen der en ikke har noen overgang mellom rettlinje og sirkelkurve, som illustrert i fig. .7. En kan da tenke seg en sirkelkurve med radius lik R+m. Størrelsen m kalles innflytting og består av avstanden mellom tangentene til sirkelkurvene med radier R+m og R. 3.gradsparabelen har en slik form at ved halve overgangskurvens lengde, dvs. langs tangenten, er ordinaten lik halve innflyttingen, l/2, mens ved kurvens ende (OE) er den hele 4m. Størrelsen m er gitt ved:
| (38) |
I avsnitt 2.5.2 så vi uttrykkene rettvinklede koordinater (x,y) for klotoiden, som kan benyttes for utsett av en overgangskurve. For 3.gradsparabelen er y gitt som funksjon av x, og vi regner ut innflyttingen m fra en teoretisk sirkelkurve.
Tilnærming til klotoiden gjennom 3.gradsparabelen er tradisjonelt gjort pga. forenklet regnearbeide, men når overgangskurven blir uforholdsmessig lang for radien i sirkelkurven, vil tilnærmingen påvirke beliggenheten til kurven.
Tabell 4 illustrerer dette for ulike overgangskurvelengder og sirkelradier. Lengden L er buelengden til klotoiden, og tallene i tabellen er differansen mellom y-koordinaten til klotoiden, ykloto, og y-koordinaten til 3.gradsparabelen innsatt xkloto i 33:
| (39) |
Tabell 2.4Avvik i mm mellom y-koordinat for klotoide og 3.gradsparabel.
| Radius R | |||||
|---|---|---|---|---|---|
| Lengde L | 250 | 300 | 500 | 800 | 1100 |
| 30 | 0,3 | 0,2 | 0,0 | 0,0 | 0,0 |
| 50 | 2,1 | 1,2 | 0,3 | 0,1 | 0,0 |
| 70 | 8,2 | 4,8 | 1,0 | 0,3 | 0,1 |
| 80 | 14,0 | 8,1 | 1,8 | 0,4 | 0,2 |
| 90 | 22,4 | 13,0 | 2,8 | 0,7 | 0,3 |
| 100 | 34,1 | 19.8 | 4,3 | 1,0 | 0,4 |
| 110 | - | 28,9 | 6,3 | 1,5 | 0,6 |
| 120 | - | 40,9 | 8,9 | 2,2 | 0,8 |
Matematisk er 3.gradsparabelen gitt ved kun å benytte første ledd i rekkeutviklingen som beskriver klotoiden. Som tabellen over viser blir tilnærmingen i noen situasjoner grovere enn i andre, men hvis vi betrakter en enkelt vogn gjennom overgangskurven, vil ikke ethvert punkt i vogna bevege seg lik kurven. Det vil kun de(t) tverrsnitt som faller sammen med den førende hjulgangen. Kurveforløpet varierer altså med ethvert vilkårlig punkt i vogna. Sett fra denne vinkelen vil ethvert eksakt matematisk begrep uansett være forlatt, og på den måten har 3.gradsparabelen blitt stående som en enkel og grei løsning på overgangskurvens form.
Men når det kommer til mer moderne former for prosjektering, er som regel klotoiden lagt til grunn. Praktiske oppgaver på sporet, som justering, etter klotoidebaserte data, kan dermed skape konflikter på kurver opprinnelig utfestet som 3.gradsparabler. På samme måte som tabell .4 viser koordinatavvik mellom de to kurvene, vil den endrede retningen langs overgangskurven også avvike mellom de to, i det klotoiden alltid krummer noe mer enn 3.gradsparabelen.
Konsistens mellom rampens og kurvens parametre
Parametre i overhøyderampen (h, dh/dt) og i overgangskurven (ju, ψ) henger nøye sammen, noe som vil illustreres i det følgende.
Vi tar først utgangspunkt i overhøyderampen. Overhøyden bygges opp til verdien h på tiden trampe (= Lrampe/v), altså tiden det tar å kjøre gjennom overhøyderampen, dvs.
| (40) |
For overgangskurven vil den ukompenserte sideakselerasjonen bygges opp til verdien ju på tiden tkloto (= Lkloto/v), altså tiden det tar å kjøre gjennom overgangskurven, dvs.
| (41) |
Selv om det finnes mange unntak ute i sporet, så skal i følge Teknisk regelverk overhøyderampen og overgangskurven falle sammen. Dette impliserer at de har samme lengde; Lrampe = Lkloto, og at det tar like lang tid å kjøre gjennom dem:
| (42) |
Dersom vi kjenner tre av de fire størrelsene som inngår i uttrykket til høyre i ligning 42 kan vi enkelt regne ut den fjerde. I dette uttrykket må alle størrelsene betraktes som faktisk opptredende størrelser i ett bestemt punkt på overgangskurven (f.eks. i OE). Formulert på denne måten har de neppe noen praktisk anvendelse, kanskje bortsett fra når tre av størrelsene er målte størrelser. Av kanskje større interesse er det derfor å kunne bruke maksimalverdier i ligning 42. Dersom vi velger maksimalverdier for tre av størrelsene vil vi kunne regne ut tillatt verdi for den fjerde.
Kurvekombinasjoner
I horisontalgeometrien finnes noen få hovedtyper av kurvekombinasjoner. Ved prosjektering av nye linjer er som regel alltid alle tre traseringselementene involvert, men for en del eksisterende baner er overgangskurven utelatt. I det følgende skal vi ta for oss hovedtypene, som vil bli fremstilt både som plantegning og ved pilhøydediagram, dvs. krumningsforløp gjennom kurven.
Enkel kurvekombinasjon
Det enkleste kurveforløpet vi har består av overgangen fra rettlinje til sirkelkurve og tilbake igjen vha. overgangskurver. Fig. .8 illustrerer dette.
[[Image:]]
Figur 2.8Enkel kurvekombinasjon: rettlinje - sirkel - rettlinje via overgangskurver.
Sammensatte kurver
Vi skiller tradisjonelt mellom ulike kurvesammensetninger der sirkelkurver alltid inngår. En mye benyttet type er sammensatte kurver, eller kombinasjonskurver, som skal bety flere tilstøtende, ensrettede sirkelkurver med ulik radius.
Figur 2.9Sammensatt kurve
Traseringskravene for sammensatte kurver, eller kombinasjonskurver, er de samme som for vanlige, enkle kurver, jf. til nå gjennomgåtte begrensninger pga. de ulike traseringsparametrene.
Ved prosjektering av nye baner/større linjeomlegginger bør sammensatte kurver imidlertid unngås og andre løsninger velges der det er mulig.
Sammensatte kurver uten overgangskurve
Dersom kurveradius er stor eller hastigheten er liten, kan overgangskurver utelates. Dette gjøres av konstruktive årsaker, og særlig på stasjoner i kontrakurver og i sporveksler. Punkter der rettlinje går direkte over i sirkelkurve betegnes kurvepunkt KP, mens punkter med en momentan overgang fra en sirkelkradius til en annen betegnes felles kurvepunkt FKP.
Figur 2.10Sammensatt kurve uten overgangskurver
uendelig rykkFor sirkelkurver uten overhøyde er som regel også overgangskurver utelatt. Endring i krumning og dermed sideakselerasjon skjer i dette tilfellet momentant. Utfra teoretiske betraktninger tilsier dette at rykket, den tidsderiverte av sideakselerasjonen, blir uendelig stort. Allikevel skjer det en utjevning i praksis, siden materiellet som trafikkerer linjen ikke er stivt, men utstyrt med fjæringsmekanismer. Fig. .11 illustrerer hvordan vognas faktiske akselerasjon arter seg ved inn- og utgang av en sirkelkurve med rettlinjer i endene.
Figur 2.11Sideakselerasjon ved kjøring fra rett spor til sirkelkurve uten overgangskurve.
Betraktningene rundt rulling som følge av fjæring hos materiellet, er gjeldende i perfekte kurver med jevn overgang. I praksis, for tilfellet uten overgangskurver, vil vi få svingninger i vogna som overstiger den teoretiske, ukompenserte sideakselerasjonen.
Det interessante punktet blir imidlertid å fastsette noen grenser for i hvilken utstrekning kurver uten overgangskurver kan benyttes. Her varierer innfallsvinkelen noe for de ulike forvaltninger. Én måte er å angi at endring til en manglende overhøyde I ikke skal overstige 100 mm. Videre kan denne begrenses ved å sette tak på hastigheten v som inngår i uttrykket.
fiktiv overgangskurveEn annen metode er å operere med en såkalt fiktiv overgangskurve. Som overgangskurve brukes da avstanden mellom vognas boggiesentra. Denne kan så settes inn i de vanlige formlene sammen med en akseptabel verdi for den ukompenserte sideakselerasjonen for å finne et utrykk for hvilken hastighet en kan benytte til hvilken kurveradius. Kravene til ukompensert sideakselerasjon er her som regel en senket maksverdi i forhold til vanlig.
Men hastigheten i kurver uten overgangskurver er også avhengig av hva slags kurve som benyttes, det vil si hvilken sammensetning den totale kurven har. De enkleste formene er direkte overgang fra rettlinje til sirkelkurve og direkte overgang mellom to ensrettede sirkelkurver. For disse gjelder vanlig hastighetsberegning utfra en ju,maks.
Motsatt rettede kurver
kontrakurverEn annen vanlig kurvesammensetning er motsatt rettede kurver, eller kontrakurver, som betyr tilstøtende kurver med krumning med ulikt fortegn. I sin alminnelighet har disse kurvene to motsatt rettede, tilstøtende overgangskurver imellom. Ved alle større linjeomlegginger og nyanlegg skal denne formen benyttes.
Figur 2.12Motsatt rettede kurver med overgangskurver
innlagt rettlinjeDer det er anledning til det, legges en rettlinje mellom overgangkurvene fremfor å la dem tilstøte hverandre i en felles OB. Men denne rettlinjen må være av en slik lengde, utfra maksimal tillatt hastighet på strekningen, at kjøring gjennom rettlinjen har en varighet på 0.9 sekunder eller mer.
Motsatt rettede kurver uten overgangskurver
Et siste tilfelle er to motsatt rettede sirkelkurver uten mellomliggende kurve. Denne kurveformen betegnes S-kurve og er foruten på eldre eksisterende spor anvendt bl.a. ved små linjeomlegginger for et begrenset tidsrom. For denne typen kurver gjelder følgende betingelse:
| (43) |
Tradisjonell bruk av formler fra tidligere, med innsatte verdier, gir følgende uttrykk når ju, maks = 0.7 m/s2 og V = 3.6 v (i km/h):
| (44) |
For å sikre ønsket bufferoverdekning (samt utjevne rykket) i kurver som krummer i forskjellig retning, skal det enten velges tilstrekkelig store radier eller det skal anlegges en rettlinje mellom kurvene. For ugunstigste vognkombinasjon gjelder følgende:
Hvis anlegges ingen rettlinje.
Hvis anlegges en rettlinje = 7 m i spor som skal trafikkeres av personvogner og ingen rettlinje i spor som bare skal trafikkeres med godsvogner.
Hvis anlegges en rettlinje = 10 m i spor som skal trafikkeres av personvogner og 7m i spor som bare skal trafikkeres med godsvogner.
Begge radiene skal være ≥ 140 m.
Klotoiden i kurvekombinasjoner
Dersom overgangskurven benyttes mellom to ensrettede sirkelkurver, har vi at:
| (45) |
For kontrakurver, eller motsatt rettede kurver, gjelder:
| (46) |
Jf. avsnitt 2.5.1 om overhøyderamper, gjelder uttrykkene i 46 bare dersom de to overgangskurvene har samme stigning, slik at vi har en rettlinjet, sakset overhøyderampe mellom sirkelkurvene. I motsatt fall må klotoideparameteren være forskjellig for de to kurvene.
VERTIKALKURVATUR
Kurver i vertikalplanet
Geometrien for vertikalkurvaturen er langt enklere enn den for horisontalkurvaturen. Isolert sett består den vertikale traséen av kun to traseringselementer: Stigninger (rettlinjer) og stigningskurver (sirkelkurver) i vertikalplanet. Tilsammen utgjør disse kurvene vertikalkurvaturen.
Linjens vertikalføring fremgår av lengdeprofilet for en gitt banestrekning, som angir størrelsen på stigning og fall på de forskjellige stedene på linjen. Stigning og fall angis i promille.
Tabell 5 angir fordelingen av stigning/fall i vertikalplanet for ulike eksisterende baner i Norge, der stigningene gjelder for alle rettlinjene i vertikalkurvaturen:
| > 25 ‰ | 20,1-25 ‰ | 15,1-20 ‰ | 10,1-15 ‰ | 5,1-10 ‰ | 0,1-5 ‰ | horisontalt | Største stigning | |
|---|---|---|---|---|---|---|---|---|
| Østfoldbanen, vestre linje | 0 % | 2 % | 0 % | 25 % | 35 % | 27 % | 11 % | 25 ‰ |
| Østfoldbanen, østre linje | 0 % | 0 % | 0 % | 41 % | 33 % | 18 % | 8 % | 13 ‰ |
| Dovrebanen | 0 % | 0 % | 16 % | 18 % | 16 % | 31 % | 19 % | 18 ‰ |
| Kongsvingerbanen | 0 % | 0 % | 0 % | 0 % | 5 % | 75 % | 19 % | 5 ‰ |
| Rørosbanen | 0 % | 0 % | 0 % | 14 % | 30 % | 37 % | 19 % | 15 ‰ |
| Nordlandsbanen | 0 % | 0 % | 13 % | 14 % | 24 % | 25 % | 25 % | 19 ‰ |
| Gjøvikbanen | 1 % | 4 % | 40 % | 32 % | 10 % | 7 % | 7 % | 22 ‰ |
| Bergensbanen | 0 % | 9 % | 18 % | 14 % | 18 % | 33 % | 8 % | 21 ‰ |
| Sørlandsbanen | 0 % | 7 % | 17 % | 18 % | 20 % | 20 % | 17 % | 25 ‰ |
| Vestfoldbanen | 0 % | 0 % | 7 % | 27 % | 33 % | 21 % | 11 % | 14 ‰ |
| Solørbanen | 0 % | 0 % | 0 % | 0 % | 20 % | 53 % | 28 % | 8 ‰ |
| Roa - Hønefoss | 0 % | 5 % | 69 % | 18 % | 2 % | 3 % | 3 % | 20 ‰ |
| Raumabanen | 0 % | 1 % | 23 % | 10 % | 16 % | 27 % | 24 % | 20 ‰ |
| Hell - Storlien | 0 % | 0 % | 32 % | 8 % | 16 % | 26 % | 18 % | 19 ‰ |
| Grong - Namsos | 0 % | 0 % | 0 % | 8 % | 33 % | 16 % | 43 % | 11 ‰ |
| Randsfjordbanen | 0 % | 0 % | 0 % | 13 % | 42 % | 32 % | 13 % | 11 ‰ |
| Flåmsbanen | 83 % | 0 % | 0 % | 0 % | 4 % | 9 % | 3 % | 55 ‰ |
| Asker - Spikkestad | 0 % | 0 % | 0 % | 10 % | 31 % | 37 % | 23 % | 11 ‰ |
| Arendalslinjen | 0 % | 0 % | 4 % | 24 % | 9 % | 23 % | 39 % | 22 ‰ |
| Ofotbanen | 0 % | 1 % | 26 % | 58 % | 3 % | 6 % | 6 % | 17 ‰ |
| Øvrige baner | 0 % | 1 % | 17 % | 22 % | 36 % | 18 % | 5 % | - |
| Totalt | 1 % | 2 % | 13 % | 17 % | 22 % | 28 % | 18 % | 55 ‰ |
Stigninger
Med stigning menes her en rettlinje i vertikalplanet som avviker i retning fra en horisontal referanseflate. Kjøreretningen bestemmer om stigningen har positivt (reell stigning) eller negativt (fall) fortegn.
Stigning og motstand
De viktigste avveiningene for å optimalisere stigning og fall er anleggsomkostningene, som kan begrenses ved større stigninger (kortere kjørevei), og driftskostnadene, som raskt vokser ettersom behovet for kraftigere trekkraft gjør seg gjeldende. Likeledes kreves bremsekraft i forhold til fall.
For alt rullende materiell gjelder en felles kjøremotstand under fremføringen. Denne består hovedsaklig av tre ledd: Grunnmotstanden, som utgjøres av friksjon etc., kurvemotstanden i horisontalkurver, og stigningsmotstanden. I vertikalgeometrien fokuserer vi på sistnevnte og dens samspill med den totale kjøremotstanden. Fenomenet består av tyngdekraftens komponent parallelt sporets lengderetning og er helt analogt med tyngdens komponent på tvers av kjøreretningen i kurver med overhøyde.
Figur 2.13Stigningsmotstand
Som regel er ikke stigningen større enn at vi kan tilnærme stigningen (lik tangens til v) med vinkelen v selv.
En uskadelig stigning er en stigning som innebærer mindre motstand enn grunnmotstanden og som derfor ikke gir større trafikkostnader enn på en flat strekning. I motsatt fall har vi en skadelig stigning.
På en del av våre eldre eksisterende baner, vil vertikalkurvaturen vise tegn på tidligere begrensninger hos det rullende materiell. Materiellet hadde ofte ikke kraft nok til å forsere en ideell stigning, dvs. helt jevn stigning fra et punkt til et annet, men måtte ha gjentatte intervaller av varierende stigning, og til og med fall, når den totale kjøremotstanden ble for høy. Disse intervallene fremkom ved å redusere stigningen med kurvemotstanden, slik at lengdeprofilet ble brukket i de horisontale kurvepunktene. Uskadelig stigning er/var sjelden mulig å få til, men en hovedutfordring bestod i å unngå såkalt tapt stigning, dvs. at avvikene fra jevn stigning medførte økt energiforbruk.
Bestemmende fall og stigning
Bestemmende fall/stigning er det fall i promille som beregnes ved å forbinde to punkter i strekningens lengdeprofil med innbyrdes avstand lik 1000 m med en rett linje. For en lengre strekning er det bestemmende fall/stigning den største verdien som fremkommer på en vilkårlig kilometer langs strekningen med denne beregningen.
Linjens stigning og fall angis med fall- og stigningsvisere. Disse settes opp ved begynnelsen av fall- eller stigningsstrekningen, og på steder der det bestemmende fall endres med mer enn 5 ‰. Ved bestemmende fall/stigning under 5 ‰ anvendes ikke visere.
Figur 2.14Eksempel på beregning av bestemmende fall/stigning med anvisere.
I fig. .14 er det bestemmende fall fra km 0 til km 2.1 mindre enn 5 ‰ og anvises derfor ikke. Fra km 2.1 til km 4.1 er det bestemmende fall lik 14.6 ‰ og anvises derfor avrundet til 15. Største fall er 17.2 ‰.
Bestemmende fall/stigning vil naturlig nok stille ulike krav til ulik trafikk og materiell. Derfor er det satt krav om største bestemmende fall/stigning:
Tabell 2.6Største bestemmende fall/stigning på fri linje
| Største bestemmende stigning/fall (‰) | |||
|---|---|---|---|
| Baner med blandet trafikk | Persontrafikkbaner | Sidespor | |
| Normale krav | 12,5 | 20 | 12,5 |
| Minste krav | 20 | 25 | 30 |
I enkelte tilfeller kan sporets absolutte fall/stigning angis i stedet for det bestemmende. Dette gjelder når det forekommer store fall/stigninger over en kort strekning på stasjoner eller sidespor, hvor det f.eks. foregår skifting.
Prosjektering av vertikalkurvaturen er i stor grad avhengig av hastigheten til det materiellet som skal trafikkere den aktuelle strekningen. Største tillatte kjørehastighet for tog på strekninger med fall er ikke bare avhengig av den oppsatte hastigheten i sporavsnittet, men også av togets bremseutstyr og det bestemmende fall på strekningen. Tabell .7 gir en normal sammenstilling av bestemmende fall og hastigheter:
Tabell 2.7Forholdet mellom bestemmende fall og tillatt hastighet
| Bestemmende fall (‰) | Tillatt hastighet (km/h) |
|---|---|
| 12,5 | 200 |
| 15 | 180 |
| 17,5 | 160 |
| 20 | 140 |
| 22,5 | 120 |
| 25 | 100 |
Høyere hastighet enn angitt i tabell 7 kan tillempes hvis signalsystem og rullende materiell tilsier det. Eksempelvis er kravet på Gardermobanen satt til 27 ‰.
Når en ny linje driftsmessig er å betrakte som en forlengelse av en eksisterende bane, eller når det gjelder linjeomlegging, skal det bestemmende fall ikke være større enn for den eksisterende banen. I motsatt fall bør det bestemmende fall velges slik at de forutsatte togslag kan kjøre i stigning og fall i overensstemmelse med hastighetsbetraktningene fra forrige avsnitt.
For rettlinjer i vertikalplanet gjelder at linjer med konstant eller uten stigning mellom sirkelkurver skal ha en lengde på minst 20 m.
Stasjonsområder
På stasjoner og ved hensetting av tog gjelder egne bestemmelser. I første omgang skal det bestemmende fall/stigning ikke overstige 20 ‰ mellom innkjørs- og utkjørshovedsignal.
For hovedspor såvel som sidespor og oppstillingsspor gjelder at sporet bør anlegges horisontalt. Største stigning/fall er 2 ‰/5 ‰ (normal-/minstekrav). Sidespor må i tillegg sikres med avledende sporveksel eller sporsperre. Utfra erfaring med ulike typer materiell må stigning/fall i tillegg avpasses i forhold til igangsetting fra stopp.
Spor mot plattformer har samme krav som ved hensetting.
Stigningskurven
I forrige avsnitt ble det vist et lengdeprofil fra vertikalkurvaturen, der stigning og fall endres i brukne rettlinjer. Men for å få jevn vertikalkurvatur, må hvert slikt brytningspunkt, eller brekkpunkt, rundes av med en sirkelkurve i vertikalplanet, en såkalt stigningskurve.
Stigningskurven fungerer som overgang mellom de ulike stigninger. I teoretisk prosjekteringssammenheng benyttes imidlertid ikke stigningskurver der stigningsforskjellen ikke overstiger 1 ‰.
Figur .15 viser utgangspunktet for innlegging av en stigningskurve. Brytningspunktet (BP) angir hvor kurven skal ligge - enten over eller under knekken i det eksisterende terrenget. Nødvendig utstrekning angis ved stigningskurvens ender (SE). Ved overgang til større stigning, eller til lavere fall, har vi såkalt lavbrekk. I motsatt fall har vi høybrekk.
[[Image:]]
Figur 2.15Vertikalkurver.
Radius
Vertikalkurvens radius fastsettes normalt ved å ta hensyn til reduksjon av aksellasten i vertikalkurver i høybrekk, eller konvekse kurver, som vist i fig. .15. Videre må det tas hensyn til klaringen mellom spor og rullende materiell, som blir dimensjonerende størrelse for spor som trafikkeres med lave hastigheter. Komfort er sjelden dimensjonerende faktor for å bestemme vertikalradius.
Tidligere ble vertikalkurvens radius regnet ut som kvadratet av hastigheten i km/h. Med dagens hastigheter gir det altfor store radier som er vanskelige å tilpasse horisontalgeometrien. Følgende to formler gir henholdsvis normalkravet og minstekravet til radius i vertikalkurver. Hastigheten V inngår i km/h:
| (47) |
| (48) |
Men der det er plass til å benytte større radius enn det som kreves etter .48, bør dette gjøres. Dersom vertikalkurver faller sammen med kurver i horisontalplanet, vil sporets geometri bli komplisert, og overhøyde- og vindskjevhetsfeil kan oppstå. Derfor bør stigningskurvene så langt det er mulig ligge i horisontale rettlinjer.
Vertikalkurven skal ikke falle sammen med overgangskurver eller sporveksler. Opptil nylig var dette tillatt så lenge radius var så stor som 10 000 m, så en rekke slike tilfeller finnes ute på sporet i dag. Et konkret eksempel på dette er hele den østre delen av Oslo Sentralstasjon, som inneholder et stort antall sporveksler og derfor har vertikalkurvatur med nettopp denne radien. I sin alminnelighet skal vertikalkurver aldri ha radius mindre enn 2000 m.
Stigningskurver i horisontal rettlinje skal videre avsluttes minst 15 m foran nærmeste OB og i horisontalkurve minst 15 m foran nærmeste OE.
På sidespor er kravene til minste radius hhv. 1500 m (normalt) og 500 m (minste), og det kan dispenseres for radier helt ned til 250 m under helt bestemte betingelser.
Lengde på kurven
Ser vi igjen på fig. .15 fra avsnitt 3.3, kan vi finne et uttrykk for lengdene t. Vi forutsetter i første omgang at sirkelkurven legges inn slik at disse kan betraktes som tangenter til kurven. Figur .16 illustrerer situasjonen for to vilkårlige kryssende tangenter til en sirkelkurve:
[[Image:]]
Figur 2.16Beregning av lengde, heving og senking i vertikalkurve.
De to tangentene har samme lengde og som uttrykkes ved:
| (49) |
Siden stigning og fall utgjør svært små vinkler, kan en tilnærme størrelsene, som egentlig er forholdstall og dermed tangens til vinklene, med vinklene selv. Dermed kan vi skrive:
| (50) |
Ved å betrakte figur 16 i forhold til horisontalplanet, kan det gjennom en del vinkelbetraktninger vises at vinkelen α/2 er halve forskjellen mellom stigningene. Dermed ender vi opp med et uttrykk for t som funksjon av stigning og kurveradius:
| (51) |
der t er lengden til “tangentene” til de to halvpartene av kurven som utgjør henholdsvis de ulike stigningene s1 og s2, gitt som forholdstall. Her er det viktig å bruke riktig fortegn, slik at fall inngår som “negativ stigning”.
Som for stigninger gjelder det at stigningskurvens lengde ikke skal være kortere enn 20 m.
Heving og senking
I høybrekk foretar vi en senking av brytningspunktet BP ned til punktet P, mens i lavbrekk foretar vi en såkalt heving, jf. figur 15. Betrakter vi figur 16, ønsker vi å finne heving/senking som lengden BP,P. Utfra de påtegnede vinkler fås følgende sammenheng:
| (52) |
Igjen kan vi tilnærme tangens til vinkelen med vinkelen selv, som dermed gir:
| (53) |
Uttrykket helt til høyre i 53 er det vanlige uttrykket for heving og senking, som funksjon av tangentlenden t og kurveradius.
Sporvekslers geometri
Noen definisjoner
En sporveksel er en skinnedel med bevegelige deler for å kunne foreta skifte av spor. Et sporkryss er isolert sett en fast konstruksjon for å krysse to spor.
Videre kan vi sondere mellom tre konstruksjoner der sporveksler inngår: sporsløyfer - forbindelser mellom flere spor, innfart til parallelle møtespor og linjeskillende veksler. Blant førstnevnte inngår også ofte sporkryss.
sporavstandSporavstanden, målt som den vinkelrette avstanden mellom senterlinjen til to nabospor, har en minsteverdi på 4,40 m for nye baner og 4,25 m for eksisterende baner. Men sporavstanden økes i kurver pga. ekstra plassbehov, helt opp til 4,70 m.
teoretisk krysningspunkt og stigningsvinkelFig. .17 viser den enkleste formen for sporveksel, der det såkalte avvikesporet er kurvet og avviker fra et rettlinjet spor. Tangenten til hovedsporet før vekselens begynnelse og tangenten til avvikesporets bueende, begge senterlinjer, danner et krysningspunkt og en vinkel mellom seg. Disse benevnes henholdsvis det teoretiske krysningspunkt og stigningen eller stigningsvinkelen (). Stigningen angis gjerne som en brøk 1 : n, det vil si tangens til kryssingsvinkelen.
Figur 2.17Grunnleggende elementer hos en enkel sporveksel
Figur .17 viser det geometriske bildet av en enkel sporveksel i horisontalplanet, som en plantegning. Men for best mulig å angi geometrien, benyttes som regel en mer teoretisk tegning som figur .18 med såkalte hovedmål påført.
Tegnforklaring:
SS: stokkskinneskjøt
TK:teoretisk kryss
R2:sirkelkurvens endepunkt i avvik
BK:bakkant sporveksel
A:tangentlengde/lengde i X-retning før TK
C:tangentlengde til sirkelkurven etter TK
D:rettlinjet parti i avvik
B:lengde i X-retning av C + D
L:byggelengde; A + B
E:lengde av parti med langsviller utenfor BK
Figur 2.18Hovedmål for enkel sporveksel
Enkle sporveksler
En enkel sporveksel har kun ett avvik - enten til høyre eller venstre. Kurvaturen i avvikesporet er avhengig av stigningen til vekselen, men det er også en sammenheng mellom radien og lengden av kurven i avvikesporet.
kort kurveVi kan skille mellom to hovedtyper av enkle sporveksler. Den første kalles for sporveksel med kort kurve og er gjerne blant de eldre sporvekslene som finnes. Fig. .19 illustrerer hva som menes med kort kurve. Den krumme delen av avvikesporet er ikke lenger enn at den ender før avvikesporet krysser hovedsporet. Dermed er skinnekrysset rettlinjet i begge spor, og krysspissen har samme stigning som sporvekselen. Følgelig er radien i avvikesporet relativt liten.
Figur 2.19Enkel sporveksel med kort kurve
“overskjærende” kurve
For noen eldre veksler med kort kurve består også avvikesporet av to etterfølgende sirkelkurver, avhengig av hvilket element i vekselen det er snakk om. Men en langt mer ustabil geometri har vi for såkalt “overskjærende” kurve. Det vil si at avvikesporet ikke tangerer rettlinjen, men skjærer over dette, jf. figur .20.
[[Image:]]
Figur 2.20Sporveksel med overskjærende kurve
Har vi to overskjærende, motsatt rettede sporveksler på rad, og skal kjøre gjennom begge avvikekurver, er geometrien udefinert. I denne situasjonen er det fare for at buffere vil gå om hverandre.
Figur 2.21Udefinert geometri og bufferkræsj
lang kurveDen andre typen av enkle sporveksler er som regel av nyere dato og har såkalt lang kurve. Det vil si den motsatte situasjonen av den over: Avvikekurven er så lang at den ender etter at den har krysset rettlinjen, som vist på figur .22. Her er skinnekrysset krummet, og krysspissen har en noe lavere stigning enn sporvekselen.
[[Image:|thumb|
]]
Figur 2.22Enkel sporveksel med lang kurve
Sammenlikner en eksisterende sporveksler i rett spor med henholdsvis kort og lang kurve, vil en oppdage at de med lang kurve har en mye slakere kurvatur. Disse er derfor langt mer gunstige når gode kjøreforhold er ønskelig. Tabellene .8 og .9 viser eksisterende, enkle sporveksler med kort og lang kurve. Verdt å merke seg er at der hovedmålene B og C er like store, slik som for de fleste sporveksler med lang kurve, betyr det at sirkelkurven er strukket helt ut til vekselens bakkant (BK).
Tabell 2.8Hovedmål for enkel veksel med kort kurve.
| Profil | Stigning/
Radius |
||||||
| S49 | 1:7 R140 | 9949 | 13224 | 13224 | 3275 | 23174 | 2400 |
| 1:9 R190 | 10519 | 16611 | 10519 | 6092 | 27130 | 3900 | |
| S54 | 1:9 R190 | 10523 | 16616 | 10523 | 27139 | 3000 |
Alle mål er i mm.
Tabell 2.9Hovedmål for enkel sporveksel med lang kurve.
| Profil | Stigning/
Radius |
||||||
| 1:7,5 R190 | 12607
|
17428
|
12607
|
482
|
30035
|
0
| |
| 1:7 R190 | 13502
|
13502
|
13502
|
-
|
27002
|
3000
| |
| 1:6,6 R190 | 14310
|
17425
|
17284
|
141
|
30035
|
0
| |
| S49 | 1:6,28 R190 | 15018
|
15018
|
15018
|
-
|
30035
|
0
|
| 1:9 R300 | 16616
|
16616
|
16616
|
-
|
33232
|
4447
| |
| 1:12 R500 | 20797
|
20797
|
20797
|
-
|
41587
|
6500
| |
| 1:9 R300 | 16616
|
16616
|
16616
|
-
|
33231
|
3000
| |
| S54 | 1:12 R500 | 20797
|
20797
|
20797
|
-
|
41594
|
5835
|
| 1:14 R760 | 27108
|
27108
|
27108
|
-
|
54216
|
3900
| |
| 1:9 R300 | 16615
|
16615
|
16615
|
-
|
33230
|
5400
| |
| 1:12 R500 | 20797
|
21985
|
20797
|
1188
|
42783
|
7200
| |
| UIC60 | 1:14 R760 | 27108
|
27108
|
27108
|
-
|
54216
|
7200
|
| 1:18,4 R1200 1) | 32829
|
32610
|
32610
|
-
|
65438
|
12600
| |
| 1:26,1 R2500 1) | 48109
|
46491
|
46491
|
-
|
94600
|
17400
|
Alle mål er i mm.
1) Klotoideveksel
Kurveveksler
Geometrisk sett er en kurveveksel en bøyd enkel veksel med lang kurve. Det opprinnelige rettsporet blir krummet, slik at vekselens hovedspor har lik krumning med sporet der den skal legges inn.
Kurveveksler benevnes ettersom hvilken vei hovedsporet og deretter avvikesporet krummer. Fig. .23 viser de fire ulike kombinasjonene av høyre- og venstrekrumning som kan forekomme:
[[Image:|thumb|
]]
Figur 2.23Benevnelser av kurveveksler
Beregningsgrunnlag og utgangsmål
Figur .24 gir grunnlaget for en metode å beregne radius og skinnekryssets beliggenhet på. Vi har følgende utgangsmål:
r0:radius til kurvevekselen før bøying (enkel veksel med lang kurve)
t:tangentlenden
s:sporvidden = 1435 mm
:stigningsvinkelen
:spissvinkelen til skinnekrysset K
, :hjelperetninger til skinnekryss og vekselbakkant fra de ulike sirkelsentra
Spissvinkelen til skinnekrysset og tangentlengdene er gitt ved:
(2.54)
Formlene .54 gjelder for både innover- og utoverbøyde kurveveksler. På tilsvarende måte som i figur .24, kan situasjonen illustreres for den utoverbøyde vekselen. Formlene i det følgende vil kun variere med hensyn på fortegn utfra hvilken vei vekselen bøyes. Den utoverbøyde kurvevekselen er imidlertid langt mindre vanlig enn den innoverbøyde, og den forekommer ikke på hovedspor. Dette følger naturlig av at eventuell overhøyde i kurven vil opptre som falsk overhøyde i avvikesporet og dermed begrenser hastigheten gjennom vekselen drastisk.
Figur 2.24Beregningsgrunnlag for innoverbøyd veksel (HH).
Overhøyde i kurveveksler
Dersom en kurve har overhøyde og det skal anlegges veksel i sporet, må vekselen legges inn i eksisterende sporplan. Dette innebærer at overhøydeforholdet mellom skinnene i avvikesporet blir som for hovedsporet, mens det i tillegg finnes en langt større høydeforskjell mellom de to sporene. Denne situasjonen setter også krav til avvikesporets utvikling etter sporvekselen, som blir nærmere utdypet i avsnitt 4.8 om profilberegninger.
Beregning av kurveradius
Både hoved- og avvikespor består av en gjennomgående sirkelkurve. Kurveradiene er utformet i et slikt forhold til hverandre at stigningen er uforandret i forhold til grunnformen. Mens vanlige, rette veksler som regel velges utfra ønsket hastighet gjennom vekselen, er radien den dimensjonerende størrelsen ved kurveveksler, og da særlig for innoverbøyde veksler hvor det allerede krumme avvikesporet skal krummes ytterligere.
Forholdene mellom kurveradiene er gitt ved:
innoverbøyd kurveveksel(2.55)
der t er tangentlengden til halve vekselen, r0 er radius for den ikke bøyde sporveksel, og R og r er radier for henholdsvis hovedkurven og avvikekurven i den bøyde sporvekselen.
På samme måte får vi:
utoverbøyd kurveveksel(2.56)
Siden formlene .55 og .56 er tilnærmingsformler, utelates ofte også tangentlengden t, som alltid er langt mindre enn de ulike radiene. Formlene benyttes når en av radiene R og r er kjent.
Veksler generelt er søkt lagt til rette spor, men dersom dette ikke er mulig, skal kurveveksler utformes etter følgende grenseverdier for manglende overhøyde i kurven:
Imaks = 100 mm
Imaks = 80 mm ved håndbetjent sporveksel til sidespor
På grunnlag av kravene til manglende overhøyde må vi derfor i første omgang kjenne avvikesporets radius som om vekselen ikke var krummet i hovedsporet, r0. For den manglende overhøyden har vi dermed at:
(2.57)
Normalt ved prosjektering av kurveveksler kjenner vi forholdene i kurven der vekselen skal legges inn, ved R, h og v. Av formlene .55 - .57 får vi dermed et uttrykk for minste tillatte utgangsradius r0, det vil si hvilken enkel sporveksel som skal benyttes og så bøyes for å passe inn i det krumme hovedsporet:
(2.58)
for henholdsvis innover- og utoverbøyde kurveveksler.
Radius r i avvikesporet kan også beregnes eksakt ved:
(2.59)
Beregning av lokale koordinater
Vekselprosjektering er koordinatbasert, det vil si at spor og veksler, samt ulike hindringer, skal være målt inn geodetisk. Men den totale prosjekteringen er en integrert prosess: Innmålte punkt i eksisterende hovedspor ligger til grunn for prosjekteringen av hovedsporet gjennom vekselen. Deretter plasseres vekselen med tilhørende avvikespor relativt hovedsporet.
En veksels positive X-akse utgjøres av tangenten til hovedsporets høyre skinne ved stokkskinneskjøten, hvor origo også befinner seg, jf. figur .24. Skinnekrysset Ks X-koordinat er tegnet inn som XN. Den rettvinklede Y-koordinaten i formelen .62 uttrykker dermed beliggenheten til skinnekrysset K i forhold til stokkskinneskjøten (origo):
(2.60)
(2.61)
(2.62)
For alle ovenstående formler med varierende fortegn gjelder at øverste fortegn skal benyttes for innoverbøyde kurveveksler.
Vekselsammensetninger
Konstruksjonene i dette avsnittet eksisterer i relativt stor utstrekning på banenettet i dag, men er ikke lenger regnet blant de gunstigste løsningene for sporskifte og sporforgreining. Vekselsammensetningene i de etterfølgende to avsnittene har en svært komplisert konstruksjon og representerer derfor som regel høye vedlikeholdskostnader.
Enkle og doble kryssveksler
En kryssveksel er en sammensatt sporveksel som kan legges inn der to spor krysser hverandre. En enkel kryssveksel har mulighet for avvik til en side mens en dobbel kryssveksel har mulighet for avvik til begge sider, som vist på figur .25. Kryssveksler har to endekryss og to sidekryss. Tungepartiene ligger vanligvis innenfor endekryssene, det vil si at kryssveksler bare finnes med kort kurve. Innlemming av lange kurver blir straks langt mer komplisert.
[[Image:|thumb|
]]
Figur 2.25Dobbel kryssveksel
Konstruksjonen benyttes fortsatt, men der andre løsninger kan tillempes, benyttes disse.
Usymmetrisk dobbeltveksel
Skal to spor avvike til hver sin side av hovedsporet kreves normalt to enkle sporveksler etter hverandre. For å spare plass har en ofte benyttet en usymmetrisk dobbeltveksel som består av to enkle sporveksler hvor tungepartiene til de to vekslene er plassert rett etter hverandre. En usymmetrisk dobbeltveksel har tre skinnekryss og har samme radius i begge avvik.
[[Image:|thumb|]]Figur 2.26Usymmetrisk dobbeltveksel
Konstruksjonen tas ikke lenger inn ved prosjektering/bygging.
Hastighet i sporveksler - veksler for høye hastigheter
Alminnelig hastighetsbetraktning
med og uten overhøyde
Normalt har vi ikke overhøyde i sporveksler, og den maksimale hastigheten som kan holdes i vekselen er da gitt som for en sirkelkurve uten overhøyde:
(2.63)
Det må dog tilføyes at ju,maks som regel settes lavere enn vanlig siden det mangler overgangskurve og på grunn av ekstra støt ved kjøring gjennom vekselen.
I tilfellet der vi har overhøyde i sporvekselen, regnes tillatt hastighet på vanlig måte som for sirkelkurver med overhøyde. Men også her tillates normalt bare en lavere ju,maks.
Av og til forekommer falsk overhøyde i sporvekselen, overhøyden har negativ verdi. Da benyttes samme formler som for vmaks ellers, men overhøyden må inngå med riktig fortegn.
Se for øvrig L531 Kap. 3 – Hastighetsberegninger.
Overgangskurveveksler / klotoideveksler
Utover de til nå nevnte vekseltyper, er det utviklet en del nyere sporveksler for bruk på strekninger beregnet på høy hastigheter. Målet med disse er å kunne holde høye hastigheter gjennom avvikesporet.
Pr. definisjon er en overgangskurveveksel en enkel sporveksel der avvikesporet ligger helt eller delvis i en overgangskurve. I noen tilfeller varer overgangskurven også lenger enn selve vekselen, slik at OB (R=) kommer etter vekselens bakkant.
Omfanget til klotoidevekslene er langt mindre enn for vanlige veksler, i den betydning at de er ment for hovedspor og ikke finnes i et utall veksel-sammensetninger. Klotoideveksler bøyes heller ikke, så beregningene fra avsnitt 4.3 gjelder ikke her. Vekslene leveres derimot ferdig utformet for montering, ettersom hvilken type som er egnet for den aktuelle strekningen.
Som det fremgår av tabell .9, benyttes to typer klotoideveksler i Norge. Disse er begge av en type der avvikesporet først antar en sirkelkurve med veldig slak krumning for så å etterfølges av en overgangskurve, jf. figur .27:
Figur 2.27Klotoideveksel
Klotoidevekslene vil etterhvert benyttes på hele banenettet, men i første omgang er de to benyttet i alle sporsløyfer på Gardermobanen. Vekslene har imidlertid den forutsetning at sporavstanden er 4.7 m og ikke 4.5 m som normalt på parallelle hovedspor. Innlegging av disse vekslene i sløyfer mellom eksisterende hovedspor forutsetter dermed en utvidelse på 0.2 m av sporavstanden for det aktuelle sporstrekket.
Figurene .28 og .29 på de neste sidene viser hovedmålene for de to klotoidevekslene vi benytter i Norge. Noe som er spesielt for klotoidevekslene, er at klotoiden / overgangskurven ender først etter vekselens bakkant. Først dersom vekslene hadde blitt utviklet som veksler med kort kurve, det vil si rett skinnekryss, hadde disse punktene sammenfalt.
[[Image:]]
Figur 2.28Klotoideveksel - UIC60-60D 1:18,4/1200 m
[[Image:]]
Figur 2.29Klotoideveksel - UIC 60- 60D 1:26,1/2400
Tabell .10 viser noen praktiske eksempler fra ulike eksisterende høyhastighetsbaner i Europa med tillatt hastighet i avvikesporet:
Tabell 2.10Hastighet i sporveksler ved SCNF (TGV-Frankrike), DB (Danmark) og SBB (Sveits).
| Forvaltning | Begynnelsesradius | Stigning | Byggelengde | Tillatt hastighet |
| SNCF | 3000 m | 1:46 | 137 m | 160 km/h |
| SNCF | 6700 m | 1:65 | 193 m | 220 km/h |
| DB 1) | 6000/7000 m | 1:42 | 154 m | 200 km/h |
| SBB 2) | 2200/3800 m | 1:28 | 140 km/h |
1) For komfortabel linjeavgreining består vekselen av to etterfølgende kurveradier på henholdsvis 7000 og 6000 m. Radien på 6000 setter hastighetsbegrensningen i vekselen, og utjevningen til 7000 m er ment å lempe på rykket.
2) Utformet som klotoideveksel, det vil si to tilstøtende klotoider, slik at start- og sluttradius er stor (3800 m) og punktet midt på avvikesporet har en mindre radius (2200 m).
1)2) Den største radien kunne vært benyttet gjennom hele vekselen, men dette ville medført større byggelengde.
Sporkryss
Som oftest forekommer sporkryss som en del av en større konstruksjon der også sporveksler inngår, som neste avsnitt går nærmere inn på.
hovedmålEt sporkryss har i alminnelighet to hovedmål: Stigning og lengde. Det enkleste sporkryss finnes som den faste konstruksjonen som tillater to rette spor å krysse hverandre.
kurvede sporkryssMen sporkryss opptrer også når sirkelkurver krysser hverandre. Da oppstår en situasjon helt analog med den for enkle veksler og kurveveksler: Sporkrysset bøyes, mens stigningen (mellom kurvenes tangenter i krysningspunktet), lengden til hvert enkelt vinkelben, samt byggelengden forblir uendrede størrelser.
Sporsløyfer og -forgreninger
Sporsløyfer, eller sporforbindelser, kan forekomme i en rekke ulike former, og figur .30 viser en skjematisk inndeling av alle grunntypene. (Figuren viser en oversikt over typer av sporsløyfer som har vært bygget. Alle typer behøver ikke nødvendigvis å finnes på det norske jernbanenettet):
[[Image:]]
Figur 2.30Skjematisk oversikt over typer av sporsløyfer
Rette sporsløyfer
De enkleste sporsløyfene får vi når vi skal skifte fra et rettspor til et annet. Er sporene i tillegg parallelle, vil det være naturlig å legge inn to motstående, enkle veksler, med eller uten et rettstykke imellom, avhengig av hastigheten i avvikesporet og krav til byggelengde.
Tegnforklaring
ls:Sporsløyfens totale byggelengde
m:Mellomliggende rettlinje
s, b:Andre hovedmål
SP:Sporavstand
Resterende symboler angår vekslene jf. figur .31.
Figur 2.31Rett, enkel sporsløyfe med mellomliggende rettspor.
Enkle sporveksler med lang kurve.
De ulike hovedmålene finnes som:
(2.64)
(2.65)
(2.66)
(2.67)
forlenget kurve i avvikesporetI de fleste tilfeller benyttes i dag enkle veksler med lang kurve, slik at vekselen ender med et krumt avvikespor. Som regel er det da i tillegg et visst rom for å forlenge buen i avvikesporet også i området med langsviller bak vekselens bakkant (BK). Dette medfører at forbindelsessporets største skjæringsvinkel med rettsporene blir større enn stigningsvinkelen til selve vekslene. Følgelig forskyves de teoretiske krysningspunktene (TK) til vekslene nærmere hverandre og sporsløyfens totale byggelengde kan gjøres mindre. Hvis vi kaller den økte skjæringsvinkelen for , slik at > , og innfører forlenget kurve for avvikesporet i begge veksler, får vi følgende hovedmål:
Figur 2.32Rett, enkel sporsløyfe mellom parallelle spor, med mellomliggende rettlinje og forlenget bue i begge veksler.
Hovedmål:
(2.68)
(2.69)
(2.70)
(2.71)
Tangentlengden t1 er forlengelsen av de opprinnelige tangentlengdene i sporvekslene benevnt A og C (som oftest like lange), slik at tangentene går utfra TK til henholdvis vekselens begynnelse (SS) og enden av den forlengede avvikekurven.
Men rette sporsløyfer forekommer også mellom ikke-parallelle spor. Da er det naturlig å tilpasse vekslene slik at kun én av dem har forlenget bue i avvikesporet. Mer eksakt forlenges det ene avvikesporet slik at stigningsforskjellen blir lik vinkelen mellom hovedsporene: = + . Det geometriske bildet blir en kombinasjon av det i figurene .31 og .32, med disse hovedmålene:
(2.72)
(2.73)
(2.74)
(2.75)
der A er tangentlengden til første halvdel av vekselen.
Kurvesporsløyfer
En sporsløyfe mellom to konsenstriske sirkelkurver er i teorien en rett sporsløyfe mellom parallelle spor som er bøyd, slik at tangentlengdene og stigningen i sporvekslene er uendret. Det tidligere mellomliggende rettstykket m blir en mellomliggende kurve med radius Rz basert på middelet Rm av de to konsentriske kurvene. Figur .33 viser en såkalt likevendende kurvesløyfe mellom to konsentriske spor, der begge sporvekslene som inngår er innoverbøyd. For det ytre sporet må naturlig nok alltid dette gjelde, men for det indre sporet vil ofte utoverbøyde veksler benyttes, for ikke å få altfor lang byggelengde på sløyfen. Da kalles sløyfen for en motsatt vendende kurvesløyfe. Sporvekslene blir bøyd som beskrevet i avsnitt 4.3, og riktige radier mm. må derfor inngå i hovedmålene nedenfor.
Figur 2.33Hovedmål for bøyd, konsentrisk sporsløyfe
(2.76)
(2.77)
(2.78)
(2.79)
Sporsløyfer i kurver på hovedspor må ha overhøyde ettersom de konsentriske kurvene har det. For prosjektering av kurvesløyfer er det spesielt viktig å huske at manglende overhøyde I aldri får overstige 100 mm. I den sammenheng er det formålstjenlig å fremstille et diagram som viser krumning, anvendt overhøyde og manglende overhøyde gjennom hele sløyfen. Som regel må en prøve seg frem med de rammene som er stilt utover den manglende overhøyden, som evt. eksisterende overhøyde, krav til byggelengde og sporavstand. Til slutt finnes en kombinasjon som gir valg av riktige veksler, evt. forlengelse av kurver og optimalt mellomstykke (kurvet forbindelsesspor) mht. både krumning og lengde.
Som prinsippskissen nedenfor viser, skal den ukompenserte sideakselerasjonen i mellomstykket være 0, det tillates ikke manglende overhøyde mellom kontrakurvene.
[[Image:]]
Figur 2.34Prinsippskisse for kurvaturen i en kurvesløyfe[1]
Sporforgreninger og doble sporsløyfer
Doble sporsløyfer kan beskrives som enkle sporsløyfer som blir speilet om midtpunktet på forbindelsessporet. Dette punktet må dermed utgjøres av et sporkryss. Om sporkrysset blir rett eller bøyd avhenger av hvilken type sløyfe det er snakk om. Figur .35 viser et eksempel på hovedmålene til en eksisterende dobbel, rett sporsløyfe mellom parallelle spor:
Figur 2.35UIC60 dobbel sporsløyfe med sporkryss 1:15 og 4 stk. enkle veksler 1:14.
Sporforgreninger kan for såvidt deles inn like kategorisk som sporsløyfer, men i hovedsak sonderes det mellom forgreninger av én eller flere spor og mellom rette og bøyde spor. Det enkleste tilfellet er når et spor skilles med en enkel veksel, mens dersom flere spor avgrenes, vil de som regel krysse hverandre. Avhengig av om sporene er rette eller bøyde, vil vi da få henholdsvis rette og bøyde sporkryss mellom sporene. Beregning av forgreninger foregår i alminnelighet som for veksler og sløyfer ellers.
Sporplaner/sporavstand
Når sporforbindelser og -forgreninger skal konstrueres og formålstjenlige sporveksler skal velges, finnes alltid noen geometriske begrensninger. Regelverket setter krav til sporavstand utfra kurvatur og hastighet, og lengden på sporsløyfer er ofte begrenset av horisontalkurvaturen.
middelpunkt
Middelpunktet er det nærmeste punkt på et forgrenet spor et tog kan komme uten å sperre for tog i det andre sporet. For beregning av sporets middel vises det til kapittel 5, avsnitt 5.10.
effektiv sporlengdeDen effektive sporlengden er den lengden av et spor det kan settes materiell på uten å sperre nabosporet. Denne lengden blir derfor lengden mellom middelpunktene.
[[Image:]]
Figur 2.36Middelpunkt og effektiv sporlengde.
Oppsummert inngår gjerne veksler og dermed sporforbindelser og -forgreninger i et nokså komplekst system i trafikkerte områder som for eksempel rundt en større stasjon. For å presentere sporforholdene grafisk benyttes som regel en geografisk sporplan. Dette er vanligvis en plantegning på et kart i målestokk 1:1000 eller 1:500, der alle spor er korrekt inntegnet med ulike geometriske mål påført. Men siden dette fort kan bli uoversiktlig ved mer komplekse sporforhold, benyttes ofte en såkalt skjematisk sporplan. Denne tar ikke hensyn til horisontalkurvatur, men fremstiller hovedsporene som rettlinjer og sporvekslene med enkle symbol som når hovedmål angis.
Utfra hvilke størrelser som er dimensjonerende i hvert enkelt tilfelle, kan det ofte være aktuelt å skulle finne minste (matematisk) tillatte sporavstand SP for sporsløyfer med andre gitte størrelser. I så fall må formlene i avsnittene 4.7.1 og 4.7.2 skrives om slik at sporavstanden blir frigjort som variabel.
Sporvekslers vertikalkurvatur
Ideelt sett bør veksler på hovedspor bare forekomme på rettlinjede partier, men i praksis legges veksler også inn i kurver. På hovedspor forekommer da også overhøyde, som igjen gjør at vekselen også må prosjekteres i profil. Det samme gjelder i sporsløyfer og -forgreninger der sporene har ulik høyde.
For veksler generelt gjelder at hoved- og avvikesporet er låst til hverandre helt ut til siste langsville. Geometrisk innebærer dette at sporene ligger i samme plan. Først etter siste langsville kan avvikesporets profil utformes fritt.
Figur .37 illustrerer sammenhengen mellom geometrien i plan og profil når sporvekselen ligger i kurve med overhøyde h. Størrelsene y og Z er henholdsvis sporavstand ved siste langsville, som oppgis blant andre hovedmål for veksler, og den høydeforskjellen som utgjøres av h og y.
[[Image:]]
Figur 2.37Plan- og vertikalgeometri for innoverbøyd kurveveksel
Høydeforskjellen Z ved siste langsville er gitt som:
(2.80)
Utover beregninger rundt overhøyde, som normalt behandles under planberegningene, vil også tradisjonell vertikalkurvatur måtte behandles når bøyde veksler med overhøyde forekommer. Siden hovedsporet allerede ligger i helning, og avvikesporet skal utgå i dette helningsplanet, vil avvikseporet ende høyere eller lavere enn hovedsporet avhengig av om det bøyer utover eller innover. I tillegg vil stigning/fall endre seg i forhold til hovedsporet fordi avvikesporet krummes i det samme planet. Stigningsforskjellen p er gitt som:
stigningsforskjell
(2.81)
- i ‰ for henholdsvis utover- og innoverbøyd veksel. Stigningsforskjellen gjelder mellom innerste skinne i hovedsporet og den skinnen i avvikesporet som tilsluttes denne.
[[Image:]]
Figur 2.38Profil av forgrening til parallelle kurver med innoverbøyd kurveveksel.
Figur .38 viser et eksempel på hvordan en sporforgrening i en kurve utvikler seg til to parallelle kurver med samme overhøyde og samme absolutte høyde. Inntil siste langsville (sls) mister avvikesporet høyde (ikke overhøyde), siden begge spor befinner seg i samme hellende plan. Derfor legges det inn en vertikalkurve med en stor radius Rv, slik at avvikesporet på et visst punkt oppnår å komme på samme absolutte høyde som hovedsporet, men uten overhøyde. Deretter opparbeides en tilsvarende overhøyde i avvikesporet som tidligere ved å legge inn en overhøyderampe umiddelbart etter at de to sporene er blitt plangeometrisk parallelle.
Geometriske feil - vedlikehold
Til nå i dette kapitlet har vi først og fremst konsentrert oss om en rekke teoretiske aspekter ved sporgeometrien, dvs. geometrisk utforming etter ideelle ønsker. Sporet er imidlertid gjenstand for stadige justeringer, og i det følgende skal vi belyse en del geometriske feil som oppstår. Feil i sporet er forøvrig grundigere beskrevet i kapitlene L534 – Sporjustering og L535 – Tilstandskontroll.
For geometriens, eller kurvaturens del, er det særlig fire geometriske feil vi ønsker å minimalisere: Vindskjevheter, avvik i side og høyde og uriktig overhøyde. En skulle umiddelbart regne med at de ulike geometriske feilene hadde samme karakter og utbedring for nær identiske spor- og trafikkforhold, men grundige undersøkelser over tid har ikke kunnet bekrefte dette. Hverken trafikkmengde/-type eller sporkonstruksjon kan på statistisk grunnlag vise til noe entydig forringelse av geometrien eller vedlikeholdsbehov.
Derimot kan det vises at høyde- og sidefeil øker lineært både med aksellast og tiden mellom vedlikehold, utenom den initielle justeringen av sporet.
Vindskjevhet
Definisjon og årsak
Fenomenet forekommer i to former: tilsiktet og utilsiktet vindskjevhet. Den tilsiktede vindskjevheten finnes i overhøyderamper og kalles rampestigning. Utilsiktet vindskjevhet er som regel langt større, og den kan oppstå som en geometrisk feil i spor med telefarlige masser, ustabiliserte spor og etter eller under gravearbeider. Den vanligste definisjonen av vindskjevhet er forskjell i overhøyde, målt over en gitt basis. Dette innebærer at skinnestrengene ikke er parallelle i vertikalplanet, men har ulik stigning. En annen definisjon av vindskjevhet er hvis vi tenker oss en helt stiv vogn med fire hjul: Ved vindskjevt spor vil kun tre av hjulene berøre sporet. Avstanden fra det fjerde og ned på skinnestrengen blir dermed sporets vindskjevhet.
Figur 2.39Vindskjevhet som forskjell i overhøyde h2-h1 over en basis B.
Konsekvens
For å se på følgene av vindskjevt spor, er den stive vogna uten fjæring et godt utgangspunkt. Når denne går inn i en overgangskurve og opp en overhøyderampe fra en rettlinje, vil det fremre, ytre hjulet påvirkes av en økt kraft, mens det bakre, ytre hjulet vil avlastes - i det svært teoretiske tilfellet totalt. Ut av sirkelkurven igjen og ned en overhøyderampe skjer det motsatte - det fremre, ytre hjulet avlastes.
For eksisterende rullende materiell er situasjonen den samme, bare mer komplisert på grunn av materiellets dynamiske egenskaper og avhengig av hvor bratt den aktuelle rampa er. Som oftest finnes lokale, utilsiktede vindskjevheter innenfor rampa, som dermed må legges til den tilsiktede vindskjevheten. Hvis denne summen blir stor nok får det ytre hjulet avlasting nok til å klatre over skinnekanten og vi får avsporing. Det er altså i ramper med minkende overhøyde faren for avsporing er aller størst.
Side- og høydefeil
Definisjon og årsak
Side- og høydefeil er kort og godt avvik fra horisontal- og vertikalkurvatur og måles i stor grad ved de samme prinsipper. Ved justering av sidebeliggenheten, eller baksing, justeres alltid høydebeliggenheten samtidig.
Vi skiller mellom tre nivåer av feil: farlige, skadelige og uskadelige feil. Førstnevnte er en fare for sikkerheten og må rettes omgående når de oppdages. Skadelige feil rettes så snart som mulig, etter at alle farlige feil for et strekke er rettet. De uskadelige feilene må holdes under observasjon slik at vedlikeholdet er tilstrekkelig til at de ikke utvikler seg til skadelige feil.
Konsekvens
Slike feil forårsaker en slingrende toggang, som igjen vil forårsake ujevn slitasje på skinnene og befestigelsen. Dessuten kan feil i sidebeliggenheten forårsake solslyng på skinnene.
Overhøydefeil
Årsak
Hvis den tilsiktede overhøyden i en kurve ikke er oppnådd ved en justering, vil belastning av sporet lett kunne påføre kurven ytterligere avvik fra ideell overhøyde. Dermed går vi inn i en ond sirkel hvor feilen bare vokser.
Konsekvens
Dersom følgen av dårlig justering er for stor overhøyde, får vi et større overhøyde overskudd enn vi har regnet med for godstogene. Følgelig kan disse forskyve sporet så hardt innover i kurven at det ødelegger sporet. I motsatt fall blir den manglende overhøyden I så stor for det raskeste materiellet at vi får avsporing.
Brå feil i overhøyden kan også gi feil i baksen. Når disse blir store, oppstår ofte også en sporutvidelse samme sted.
Registrering av kurvatur - løfteskjema
I avsnitt 2.6 om horisontalkurvatur ble de mest anvendte kurvekombinasjonene vist i figurer. Figurene .8 og .12 viser henholdsvis den alminnelige overgangen mellom rettlinje og sirkelkurve, ved hjelp av overgangskurve, og bruk av tilstøtende overgangskurver for kontrakurver (FOB). Begge typer forekommer både med og uten mellomliggende rettlinje. Disse kurvekombinasjonene kan vi betegne som lovlige kombinasjoner. Direkte overgang fra rettlinje til sirkelkurve skal derimot ikke forekomme på hovedspor. Da har vi i så fall en ulovlig kombinasjon. Det som derimot forekommer en del er såkalte felles kurvepunkt (FKP). Disse utgjør gjerne en liten endring i krumning fra en sirkelkurve til en annen.
Alle punkt som innebærer endret situasjon på sporet, har blitt registrert i den såkalte Banedatabanken (BDB), sammen med en rekke andre data som berører tekniske anlegg utover traséen, som VUL-punkt, kontaktledning og signaler. På grunnlag av spordataene fra BDB, kan vi fremstille såkalte løfteskjema. Dette skjemaet inneholder de nødvendige data for justering av sporet med maskin. I tillegg til talldata fra BDB, inneholder det også en grafisk fremstilling av horisontalkurvaturen ved å illustrere krumningen som negativ og positiv i henholdsvis venstre- og høyrekurver i kilometerretningen. På grunn av fortløpende informasjon om punkter uten direkte sammenheng, rangert etter kilometer, er den grafiske fremstillingen til stor hjelp for å tolke sporets horisontale gang.
Vertikalkurvaturen er også fremstilt med tall i løfteskjemaet, men er ikke presentert grafisk. Dette ville ikke gitt merkbare utslag med den målestokken kilometreringen innebærer i hht. til horisontalkurvaturen.
Figur .40 viser et eksempel på en side fra et løfteskjema fra en delstrekning på Sørlandsbanen, etterfulgt av en forklaring på de ulike elementene som er listet.
Figur 2.40Eksempel på løfteskjema: delstrekningen fra banenr. 2000; Nordagutu – Nelaug på Sørlandsbanen
1. kolonnetraseringspunkt, evt. skilt, mast
2. kolonnekm, 3 desimaler (m-nivå)
3-4. kolonneevt. VUL-koordinater
5-7. kolonnehorisontalkurvatur: radius (sirkelkurven), overhøyde og lengde på overgangskurve
8. kolonnegrafisk krumningsdiagram
9-11. kolonnevertikalkurvatur: h.o.h., radius eller stigning og tangentlengde
12-13.kolonne hastighetsskilter
Vedlegg
Utledning av rettvinklede koordinater på klotoiden
I ligning .23, viste vi en rekkeutvikling av klotoiden til et uttrykk der ordinaten y var en funksjon av buelengden l, etterhvert tilnærmet med x. En mer direkte utledning vil være å rekkeutvikle rettvinklede koordinater x og y hver for seg. Dermed kan vi få uttrykk for koordinatene som funksjoner av enten overgangskurvens lengde eller retning for et vilkårlig punkt.
Vi kan starte med å betrakte enhetsklotoiden:rl = 1
Følgende differensialer gjelder:
Integrasjon gir:
der er den tangentielle retningen i et punkt
For rettvinklede koordinater til punkt på enhetsklotoiden har vi:
Med dette utgangspunktet får vi følgende kjerner:
Dermed får vi følgende differensialer:
- som gir disse integralene:
For en vilkårlig klotoide gitt med parameter A, får vi:
Men disse integralene lar seg ikke løse direkte, og må derfor løses gjennom rekkeutvikling.
Cosinus- og sinusfunksjonen er gitt ved:
Dermed kan integralene over løses:
Ønskes stigningsvinkelen i stedet for buelengden l som parameter i ligningene, kan vi sette inn for :
Ønskes summenotasjon, kan formlene over skrives som:
Feil i matematikken (Konverteringsfeil. Tjeneren («cli») rapporterte: «SyntaxError: Illegal TeX function
Found \yenin 1:74»): {\displaystyle \begin{array}{c}x\mathrm{=}\mathrm{\sum }_{n\mathrm{=}1}^{\yen }(\mathrm{-}1{)}^{n+1}\mathrm{\cdot }\frac{{l}^{\mathrm{4n}\mathrm{-}3}}{\left(\mathrm{4n}\mathrm{-}3\left)\mathrm{\cdot }\right(\mathrm{2n}\mathrm{-}2\right)!{2}^{\mathrm{2n}\mathrm{-}2}\mathrm{\cdot }{A}^{\mathrm{4n}\mathrm{-}4}}\\ x\mathrm{=}\sqrt{\mathrm{2t}}\mathrm{\sum }_{n\mathrm{=}1}^{\yen }(\mathrm{-}1{)}^{n+1}\mathrm{\cdot }\frac{{t}^{\mathrm{2n}\mathrm{-}2}}{\left(\mathrm{4n}\mathrm{-}3\left)\mathrm{\cdot }\right(\mathrm{2n}\mathrm{-}2\right)!{A}^{\mathrm{4n}\mathrm{-}4}}\\ \\ y\mathrm{=}\mathrm{\sum }_{n\mathrm{=}1}^{\yen }(\mathrm{-}1{)}^{n+1}\mathrm{\cdot }\frac{{l}^{\mathrm{4n}\mathrm{-}1}}{\left(\mathrm{4n}\mathrm{-}1\left)\mathrm{\cdot }\right(\mathrm{2n}\mathrm{-}1\right)!{2}^{\mathrm{2n}\mathrm{-}2}\mathrm{\cdot }{A}^{\mathrm{4n}\mathrm{-}2}}\\ y\mathrm{=}\sqrt{\mathrm{2t}}\mathrm{\sum }_{n\mathrm{=}1}^{\yen }(\mathrm{-}1{)}^{n+1}\mathrm{\cdot }\frac{{t}^{\mathrm{2n}\mathrm{-}1}}{\left(\mathrm{4n}\mathrm{-}1\left)\mathrm{\cdot }\right(\mathrm{2n}\mathrm{-}1\right)!{A}^{\mathrm{4n}\mathrm{-}2}}\end{array}}
LITTERATURHENVISNINGER
- Berg & Henker - Weichen, Eisenbahnbau, Transpress 259s. (1986)
- Banverket - Spårgeometrihandboken, BVH 586.40 ((01.12.96)
- Banverket - Växelprojekteringshandboken, BVH 586.45 (01.04.95)
- DB - Sporregler, tillæg 2A-2F (1987)
- Esveld, Coenraad, Dr. - Modern Railway Track, (1989)
- Haacke, W. et al. - Matematik für Bauingeniuere (1968)
- Heje, Kolbjørn - Vei og jernbanebygging, Håndbok for undervisning og praksis, H. Aschehaug & CO, 837s. (1941)
- Holme, Jan - Sporveksler, Fag 34045 Jernbaneteknikk VK, NTNU, notat nr. 856 (1993)
- Holom, Finn - Kurs i baneteknikk; Sporets geometri, NSB Bane, Region Øst (1992)
- Jernbaneverket - Overbygning-Prosjektering, Teknisk regelverk JD 530 (01.01.98)
- Jernbaneverket - Overbygning-Bygging, Teknisk regelverk JD 531 (01.01.98)
- Jernbaneverket - Overbygning-Vedlikehold, Teknisk regelverk JD 532 (01.01.98)
- Mathisen, Olav - Kurvestikking, ILM-Ås (1987)
- NBS Rekommendation R26 - Växlar för höga hastigheter, Nordiskt Bantekniskt samarbete (21.10.94)
- NSB - Lærebok for linjepersonalet, Trykk 383, Tjenesteskrifter NSB Hovedadministrasjonen, NSB Jernbaneskolen (1987)
- NSB - Overbygningsnormaler, Trykk 380
- NSB - Banetekniske forutsetninger for togfremføringen, Trykk 302.1 (01.09.85)
- Skoglund, Kjell Arne & Våge, John - Traseringsparametre og kjørekomfort, Fag 34045 Jernbaneteknikk VK, NTNU, notat nr. 1027 (jan. 1997)
- Skoglund, Kjell Arne - Sporgeometri og kjøredynamikk, Fag 34045 Jernbaneteknikk VK, NTNU, notat nr. 955 (mars 1996)
- ↑ Prosjekteringen som vist i denne figuren er ikke forenlig med gjeldende Teknisk regelverk, som forutsetter innlagt en rettlinje mellom vekslene i sløyfa.