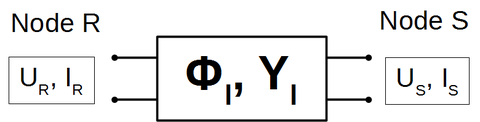Elektrisk systembeskrivelse av kontaktledningsanlegg ver01

__NUMBEREDHEADINGS__

Generelt

Kontaktledningsanlegget overfører effekt mellom matestasjonen og traksjonsmateriell og andre belastninger tilknyttet kontaktledningen. I eldre anlegg skjer overføringen i kontaktledning ved 15 kV nominell spenning, med retur i kjøreskinner ved 0 kV. I nyere anlegg er det innført returledere eller AT-system med positivleder og negativleder. Følgende ledere er vanlige i et kontaktledningsanlegg. Det kan finnes ytterligere ledere parallelt med jernbanetraseen som påvirker eller påvirkes av kontaktledningsanlegget.

<figtable id="tab:Ledere_oversikt">

Ledere oversikt

Leder	Forklaring	Nominell spenning
KL	Kontaktledningsanlegg, omfatter kontakttråd og bæreline	15 kV
RR	Kjøreskinner	0 kV
RL	Returleder	0 kV
FSL	Forsterkningsleder	15 kV
PL	Positivleder (for AT-system)	normalt + 15 kV
NL	Negativleder (for AT-system)	normalt - 15 kV

</figtable>

I dette kapittelet vil det bli beskrevet en matematisk modell som beregner hvordan strøm og spenning fordeler seg mellom ulike ledere i et slikt flerledersystem som et kontaktledningsanlegg utgjør. Denne modellen er det teoretiske grunnlaget for beregning av:

• impedansen mellom matestasjon og belastning i kontaktledningssystemet,
• potensial i returkretsen,
• indusert spenning i ledere som går parallelt med jernbanetraseen,
• belastning på enkeltledere og komponenter i kontaktledningsnettet.

I praktisk bruk er regnemodellen programmert inn i et regneprogram der numeriske parametre for beregningen angis og resultatet presenteres i form av grafer og tabeller.

Enkel transmisjonslinje

Introduksjon

Den enkleste formen for problemet er ei enkelt linjesløyfe. Det finnes mye teori som beskriver problemet, og problemet har kjent analytisk løsning. Det tas i de følgende avsnitt likevel en rask gjennomgang av den grunnleggende teorien, fordi den samme framgangsmåten benyttes for analyse av et flerledersystem.

Telegraflikningene

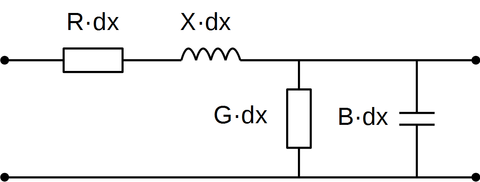
En kontaktledning med retur i kjøreskinner kan forenklet betraktes på denne måten, hvis man ser bort fra lekkasje til jordsmonn. Telegraflikningen tar utgangspunkt i et svært kort linjesegment $\mathrm {d} x$ av linjesløyfa. Linjesegmentet har en seriell resistans $R_{l}\cdot \mathrm {d} x$ og reaktans $X_{l}\cdot \mathrm {d} x=\omega \cdot L\cdot \mathrm {d} x$, og en parallell konduktans $G_{l}\cdot \mathrm {d} x$ og susceptans $B_{l}\cdot \mathrm {d} x=\omega \cdot C\cdot \mathrm {d} x$. Her er L, C og $\omega$ henholdsvis linjens induktans, kapasitans og vinkelfrekvens.

<figure id="fig:Telegraflikningene">

Telegraflikningene: Kretsskjema for et linjesegment dx </figure> Parametrene kan skrives om om slik at impedansen blir $Z_{l}=R_{l}+jX_{l}$ og admittansen blir $Y_{l}=G_{l}+jB_{l}$ Det serielle spenningsfallet dU over dette linjesegmentet er gitt av Ohms lov: (i) ${\frac {\mathrm {d} U}{\mathrm {d} x}}=-Z_{l}\cdot I$ Strømmen som lekker gjennom admittansen $Y$ utgjør forskjellen i strøm over linjesegmentet. Denne strømmen er proporsjonal med spenningen: (ii) ${\frac {\mathrm {d} I}{\mathrm {d} x}}=-Y_{l}\cdot U$ Likningene (i) og (ii) danner et koplet likningssett som i litteraturen kalles for telegraflikningene. Likningssettet kan ordnes med matriserepresentasjon på følgende måte: ${\frac {\mathrm {d} }{\mathrm {d} x}}{\begin{pmatrix}U\\I\end{pmatrix}}={\begin{pmatrix}0&-Z_{l}\\-Y_{l}&0\end{pmatrix}}\cdot {\begin{pmatrix}U\\I\end{pmatrix}}=\mathbf {A} \cdot {\begin{pmatrix}U\\I\end{pmatrix}}$ Her har systemmatrisen A dimensjonene (2 x 2). Løsningen på et slikt likningssett er beskrivet i flere lærebøker i lineæralgebra, for eksempel i Referanse [1]. En rask innføring er gitt i Wikipedia. Egenverdiene $\lambda$ til systemet er: $\lambda _{1}=+{\sqrt {Z_{l}\cdot Y_{l}}}=\gamma$ $\lambda _{2}=-{\sqrt {Z_{l}\cdot Y_{l}}}=-\gamma$ der $\gamma ={\sqrt {Z_{l}\cdot Y_{l}}}$ er linjens forplantningskonstant. De tilhørende egenvektorene kan finnes til å være: $\mathbf {v_{1}} ={\begin{pmatrix}1\\-{\sqrt {\tfrac {Y_{l}}{Z_{l}}}}\end{pmatrix}}={\begin{pmatrix}1\\-{\tfrac {1}{Z_{0}}}\end{pmatrix}}$ $\mathbf {v_{2}} ={\begin{pmatrix}1\\{\sqrt {\tfrac {Y_{l}}{Z_{l}}}}\end{pmatrix}}={\begin{pmatrix}1\\{\tfrac {1}{Z_{0}}}\end{pmatrix}}$ der $Z_{0}={\sqrt {\tfrac {Z_{l}}{Y_{l}}}}$ er linjens karakteristiske impedans. Forplantningskonstanten $\gamma$ er en kompleks størrelse og et mål på hvordan en strøm/spenning dempes og forandrer fase langs en transmisjonslinje. Den karakteristiske impedansen $Z_{0}$ er et mål på sammenhengen mellom strøm og spenning i en transmisjonslinje. Løsningen er gitt av følgende uttrykk: ${\begin{pmatrix}U\\I\end{pmatrix}}(x)=u^{-}\cdot \mathbf {v_{1}} \cdot e^{\lambda _{1}x}+u^{+}\cdot \mathbf {v_{2}} \cdot e^{\lambda _{2}x}$ $U(x)=u^{-}\cdot e^{\gamma x}+u^{+}\cdot e^{-\gamma x}$ $I(x)=-u^{-}\cdot {\tfrac {1}{Z_{0}}}\cdot e^{\gamma x}+u^{+}\cdot {\tfrac {1}{Z_{0}}}\cdot e^{-\gamma x}$ Tallverdiene for konstantene $u^{+}$ og $u^{-}$ er gitt av randverdibetingelser og er avhengig av hvilken strøm/spenning som påtrykkes endene av linjen.

Randverdibetingelser: Beregning av admittanser og impedanser

Løsningen fra forrige avsnitt benyttes for å beskrive en transmisjonslinje med lengde L som en admittansmatrise Y. Vi setter posisjonene $x_{1}=0$ og $x_{2}=L$ for linjeende 1 og 2. Strømretningen for begge linjeendene defineres som positiv inn i linja.

<figure id="fig:Admittansbeskrivelse_2porter">

Et linjesegment med lengde L har lineære karakteristikker og kan beskrives komplett ved en 2x2 admittansmatrise Y </figure> Matrisebeskrivelsen av dette uttrykket blir: ${\begin{pmatrix}I_{1}\\I_{2}\end{pmatrix}}={\begin{pmatrix}Y_{11}&Y_{12}\\Y_{21}&Y_{22}\end{pmatrix}}\cdot {\begin{pmatrix}U_{1}\\U_{2}\end{pmatrix}}$ Innsatt for løsningen i forrige avsnitt finner vi: ${\begin{aligned}U_{1}&=u^{-}+u^{+}\\U_{2}&=u^{-}\cdot e^{\gamma L}+u^{+}\cdot e^{-\gamma L}\\I_{1}&=-u^{-}\cdot {\tfrac {1}{Z_{0}}}+u^{+}\cdot {\tfrac {1}{Z_{0}}}\\-I_{2}&=-u^{-}\cdot {\tfrac {1}{Z_{0}}}\cdot e^{\gamma L}+u^{+}\cdot {\tfrac {1}{Z_{0}}}\cdot e^{-\gamma L}\end{aligned}}$ Man finner $Z_{11}$ og $Z_{21}$ ved først å sette $U_{1}=1$ og $U_{2}=0$ og løse likningene for denne situasjonen. Deretter endrer man situasjon til $U_{1}=0$ og $U_{2}=1$ og bruker dette til å finne $Z_{12}$ og $Z_{22}$. Resultatet fra disse beregningene blir: ${\begin{aligned}Y_{11}&={\frac {1}{Z_{0}}}\\Y_{21}&={\frac {-1}{Z_{0}\cdot \sinh {(\gamma L)}}}\\Y_{12}&={\frac {-1}{Z_{0}\cdot \sinh {(\gamma L)}}}\\Y_{22}&={\frac {1}{Z_{0}}}\end{aligned}}$ Denne admittansmatrisen for en transmisjonslinje av lengde L utgjør en komplett beskrivelse av transmisjonslinjens lineære elektriske egenskaper.

Transmisjonslinje med flere parallelle ledere

Ved flere parallelle ledere vil det i tillegg til resistans og selvinduktans for hver enkelt leder også være en gjensidig induktans mellom hver enkelt leder. Den gjensidige induktansen gir et tillegg til spenningen over en leder som følge av strømmen i hver av de andre lederne. For et system med n (a, b, ... n) ledere kan dette beskrives med matriser på følgende måte:

${\frac {\mathrm {d} }{\mathrm {d} x}}{\begin{pmatrix}U_{a}\\\vdots \\U_{n}\end{pmatrix}}=-\left[{\begin{pmatrix}R_{l,aa}&\cdots &R_{l,an}\\\vdots &\ddots &\vdots \\R_{l,na}&\cdots &R_{l,nn}\end{pmatrix}}+j\cdot {\begin{pmatrix}X_{l,aa}&\cdots &X_{l,an}\\\vdots &\ddots &\vdots \\X_{l,na}&\cdots &X_{l,nn}\end{pmatrix}}\right]\cdot {\begin{pmatrix}I_{a}\\\vdots \\I_{n}\end{pmatrix}}=-{\begin{pmatrix}Z_{l,aa}&\cdots &Z_{l,an}\\\vdots &\ddots &\vdots \\Z_{l,na}&\cdots &Z_{l,nn}\end{pmatrix}}\cdot {\begin{pmatrix}I_{a}\\\vdots \\I_{n}\end{pmatrix}}$

På tilsvarende måte kan det være en konduktiv eller kapasitiv lekkasje mellom hver leder i et ledningssystem. Dette kan beskrives på matriseform på følgende måte for de samme lederne:

${\frac {\mathrm {d} }{\mathrm {d} x}}{\begin{pmatrix}I_{a}\\\vdots \\I_{n}\end{pmatrix}}=-\left[{\begin{pmatrix}G_{l,aa}&\cdots &G_{l,an}\\\vdots &\ddots &\vdots \\G_{l,na}&\cdots &G_{l,nn}\end{pmatrix}}+j\cdot {\begin{pmatrix}B_{l,aa}&\cdots &B_{l,an}\\\vdots &\ddots &\vdots \\B_{l,na}&\cdots &B_{l,nn}\end{pmatrix}}\right]\cdot {\begin{pmatrix}U_{a}\\\vdots \\U_{n}\end{pmatrix}}=-{\begin{pmatrix}Y_{l,aa}&\cdots &Y_{l,an}\\\vdots &\ddots &\vdots \\Y_{l,na}&\cdots &Y_{l,nn}\end{pmatrix}}\cdot {\begin{pmatrix}U_{a}\\\vdots \\U_{n}\end{pmatrix}}$

På kompakt matriseform kan dette skrives:

${\frac {\mathrm {d} }{\mathrm {d} x}}{\begin{pmatrix}\mathbf {U} \\\mathbf {I} \end{pmatrix}}={\begin{pmatrix}0_{n,n}&\mathbf {-Z_{l}} \\\mathbf {-Y_{l}} &0_{n,n}\end{pmatrix}}\cdot {\begin{pmatrix}\mathbf {U} \\\mathbf {I} \end{pmatrix}}=\mathbf {A} \cdot {\begin{pmatrix}\mathbf {U} \\\mathbf {I} \end{pmatrix}}$

Her er systemmatrisen A en matrise med dimensjoner (2n x 2n).

Systemet har 2n egenverdier med 2n tilhørende egenvektorer.

Referanser

[1] Edwards, Penney: Elementary Linear Algebra, Pearson, 1987. ISBN 9780132582605.