Sandkasse/Frank/Dimensjonering-AT: Forskjell mellom sideversjoner
(Redigering.) |
(Redigering.) |
||
| Linje 9: | Linje 9: | ||
== Strømflyt i AT-system på kort matestrekning med tog i alle AT-vinduer == | == Strømflyt i AT-system på kort matestrekning med tog i alle AT-vinduer == | ||
For tilfelle med en last i hvert AT-vindu kan ikke beregningene utført av Varju gi noe direkte svar på strømfordelingen. Tilfellet vil være interessant fordi det kan fortelle om strømfordelingen med stor togtrafikk og jevn fordeling av togene på hele matestrekningen. En tar her utgangspunkt i beregningene utført av Varju for en last som suksessivt flyttes fra midten av hvert AT-vindu, se appendiks. Alle bildene her kan gjennfinnes i appendiks. | For tilfelle med en last i hvert AT-vindu kan ikke beregningene utført av Varju gi noe direkte svar på strømfordelingen. Tilfellet vil være interessant fordi det kan fortelle om strømfordelingen med stor togtrafikk og jevn fordeling av togene på hele matestrekningen. Ut fra det kan en finne korrigeringsfaktorer for å bestemme strømfordelingen. En tar her utgangspunkt i beregningene utført av Varju for en last som suksessivt flyttes fra midten av hvert AT-vindu, se appendiks. Alle bildene her kan gjennfinnes i appendiks. | ||
=== Strømflyt i AT-system med tre AT-vinduer === | === Strømflyt i AT-system med tre AT-vinduer === | ||
For å finne strømmen som flyter i AT-lederne på en matestrekning med tre AT-vinduer undersøkes benyttes figuren under og en metodikk basert på superposisjonsteoremet. Først hentes det ut figurer for togplassering og strøm i midt i hvert AT-vindu fra appendiks. Togene byttes ut med strømkilder som trekker strøm tilsvarende togene. Summen av strømmene til de tre lastene finnes av superposisjonsteoremet som sier at: Den totale strømmen i en hvilken som helst del av en lineær krets tilsvarer den algebraiske summen av strømmer gitt av strømkilde hver for seg. For å bestemme summen av separate strømmer, erstattes alle andre spenningskilder med en kortslutning og alle andre strømkilder med åpne kretser. Dermed fås summen som er vist i det nederste linjediagrammet. | For å finne strømmen som flyter i AT-lederne på en matestrekning med tre AT-vinduer undersøkes benyttes figuren under og en metodikk basert på superposisjonsteoremet. Først hentes det ut figurer for togplassering og strøm i midt i hvert AT-vindu fra appendiks. Togene byttes ut med strømkilder som trekker strøm tilsvarende togene. Summen av strømmene til de tre lastene finnes av superposisjonsteoremet som sier at: Den totale strømmen i en hvilken som helst del av en lineær krets tilsvarer den algebraiske summen av strømmer gitt av strømkilde hver for seg. For å bestemme summen av separate strømmer, erstattes alle andre spenningskilder med en kortslutning og alle andre strømkilder med åpne kretser. Dermed fås summen som er vist i det nederste linjediagrammet. Som en kan se er strømfordelingen for AT-lederne ved spenningskildene 66 % i PL og 34 % i NL. | ||
[[Fil:Tre tog på strekning med tre AT-vinduer.png|thumb|senter|900px|Strømflyt med tre tog midt i hvert AT-vindu. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå og blå er strømkomponent på 30 kV-nivå. Over autotransformatorene er belastningen vist. Her er superposisjonsteoremet anvendt i steg for å finne resulterende strøm.]] | [[Fil:Tre tog på strekning med tre AT-vinduer.png|thumb|senter|900px|Strømflyt med tre tog midt i hvert AT-vindu. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå og blå er strømkomponent på 30 kV-nivå. Over autotransformatorene er belastningen vist. Her er superposisjonsteoremet anvendt i steg for å finne resulterende strøm.]] | ||
=== Strømflyt i AT-system med to AT-vinduer === | === Strømflyt i AT-system med to AT-vinduer === | ||
For anslag av strømfordelingen med last midt på hvert av AT-vinduene, tas det utgangspunkt i tilfellet med én last midt mellom AT-en på en strekning med to AT-vinduene (se appendiks). Det forventes at på en så kort strekning som dette vil begge spenningskildene bidra nokså mye, anslagsvis med fordelingen ⅔ og ⅓ fra spenningskildene henholdsvis til venstre og høyre. I det nederste linjediagrammet er strømmene summert algebraisk. | For anslag av strømfordelingen med last midt på hvert av AT-vinduene, tas det utgangspunkt i tilfellet med én last midt mellom AT-en på en strekning med to AT-vinduene (se appendiks). Det forventes at på en så kort strekning som dette vil begge spenningskildene bidra nokså mye, anslagsvis med fordelingen ⅔ og ⅓ fra spenningskildene henholdsvis til venstre og høyre. I det nederste linjediagrammet er strømmene summert algebraisk. Strømfordelingen for AT-lederne ved spenningskildene er 74 % i PL og 26 % i NL. | ||
[[Fil:To tog på strekning med to AT-vinduer.png|thumb|senter|900px|Strømflyt med to tog midt i hvert AT-vindu. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå og blå er strømkomponent på 30 kV-nivå. Over autotransformatorene er belastningen vist. Her er superposisjonsteoremet anvendt i steg for å finne resulterende strøm.]] | [[Fil:To tog på strekning med to AT-vinduer.png|thumb|senter|900px|Strømflyt med to tog midt i hvert AT-vindu. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå og blå er strømkomponent på 30 kV-nivå. Over autotransformatorene er belastningen vist. Her er superposisjonsteoremet anvendt i steg for å finne resulterende strøm.]] | ||
=== Strømflyt i AT-system med ett AT-vindu === | === Strømflyt i AT-system med ett AT-vindu === | ||
I figuren er det vsit strømfordelingen for en matestrekning bestående kun av ett AT-vindu, se appendiks for forklaring. | I figuren er det vsit strømfordelingen for en matestrekning bestående kun av ett AT-vindu, se appendiks for forklaring. Strømfordelingen for AT-lederne ved spenningskildene er 100 % i PL og 0 % i NL. | ||
[[Fil:Tog midt på strekning med ett AT-vindu.png|thumb|senter|900px|Strømflyt i AT-ledere med en last som trekker 1000 A rett ved autotransformatoren midt på matestrekningen. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå.]] | [[Fil:Tog midt på strekning med ett AT-vindu.png|thumb|senter|900px|Strømflyt i AT-ledere med en last som trekker 1000 A rett ved autotransformatoren midt på matestrekningen. Sorte tall viser resulterende strøm, røde tall er strømkomponenten på 15 kV-nivå.]] | ||
== Beregning av strøm i AT-ledere og autotransformatorer i trafikksimuleringer == | == Beregning av strøm i AT-ledere og autotransformatorer i trafikksimuleringer == | ||
For tog som trekker 1000 A og beveger seg mellom to spenningskilder på en matestrekning med tre, to eller ett AT-vindu, vil strømmen fordele seg nokså ulikt mellom AT-lederne, se appendiks. Dette i motsetning til en matestrekning med mange AT-vinduer der strømmen blir jevnere. Tre ting gjør at representasjonen i | For tog som trekker 1000 A og beveger seg mellom to spenningskilder på en matestrekning med tre, to eller ett AT-vindu, vil strømmen fordele seg nokså ulikt mellom AT-lederne, se appendiks. Dette i motsetning til en matestrekning med mange AT-vinduer der strømmen blir jevnere. Tre ting gjør at representasjonen i kapitlet over er en sterk forenkling: | ||
* Spenningskildene er ingen realistisk representasjon av | * Spenningskildene er ingen realistisk representasjon av virkelige omformerstasjoner. I virkeligheten vil blant annet antall omformere i drift, indre impedans og spenningsregulatorer spiller inn. | ||
* Togene trekke stor strøm visse steder (hastighetsøkning), mens de andre steder trekker de moderat (jevn hastighet, liten stigning og rulling) | * Togene trekke stor strøm visse steder (hastighetsøkning), mens de andre steder trekker de moderat (jevn hastighet, liten stigning og rulling), ingen strøm (rulling med liten fall) eller mater inn strøm (regenerativ bremsing i fall). | ||
* Strømfordeling for effekt i transitt er ikke undersøkt, men en del effekt vil overføres på en matestrekning til den neste. Denne effekten fordeler seg likt mellom AT-lederne. | * Strømfordeling for effekt i transitt er ikke undersøkt, men en del effekt vil overføres på en matestrekning til den neste. Denne effekten fordeler seg likt mellom AT-lederne. | ||
| Linje 36: | Linje 36: | ||
=== Strøm gjennom autotransformatorene i trafikksimuleringer === | === Strøm gjennom autotransformatorene i trafikksimuleringer === | ||
Tabellen under viser korreksjonsfaktorer | Tabellen under viser korreksjonsfaktorer k<sub>PL</sub> for å ta hensyn til usymmetrisk belastning av AT-ledere med en matestrekning bestående av ett, to eller tre AT-vinduer, basert på undersøkelsene i kapittelet over: | ||
{| class="wikitable" style="margin-left:1em; text-align:center" | {| class="wikitable" style="margin-left:1em; text-align:center" | ||
| Linje 47: | Linje 47: | ||
|} | |} | ||
Tabellen viser en interessant tendens, nemmlig at strømmen i NL og PL blir stadige mer jevnt fordelt med økende antall AT-vinduer. Med anslagsvis fem eller flere AT-vinduer ville sannsynligvis strømfordelingen blitt lik mellom de to lederne, og k<sub>PL</sub>=0,5. | |||
En skal her utlede formler og sette opp en metodikk for belastning av AT-ledere på en strekning vist med en grå boks i hver av illustrasjonene nedenfor. Generelt betraktes en kort matestrekning mellom to omformerstasjoner, som i det øverste bilde nedenfor, eller på en strekning med delvis AT-system og BT-system, og et antall tog som trekker tilfeldig effekt, se det nederste bildet nedenfor. | |||
Generelt | |||
[[Fil:Strømmer i et mindre avsnitt med AT-system med to korte matestrekninger.png|thumb|senter|900px|Skisse for problemet med å finne strømmer i et lite avsnitt med AT-system på to etterfølgende matestrekninger.]] | [[Fil:Strømmer i et mindre avsnitt med AT-system med to korte matestrekninger.png|thumb|senter|900px|Skisse for problemet med å finne strømmer i et lite avsnitt med AT-system på to etterfølgende matestrekninger.]] | ||
[[Fil:Strømmer i et mindre avsnitt med AT-system på en lang matestrekning.png|thumb|senter|900px|Skisse for problemet med å finne strømmer i et lite avsnitt med AT-system på en lang matestrekning.]] | [[Fil:Strømmer i et mindre avsnitt med AT-system på en lang matestrekning.png|thumb|senter|900px|Skisse for problemet med å finne strømmer i et lite avsnitt med AT-system på en lang matestrekning.]] | ||
Det vil for hver av disse boksene være en strøm- og effektkomponent som går rett gjennom, kalt transittstrøm. En annen del går inn i boksen og brukes av togene, kalt togstrøm. Pilene viser fortegnkonvensjonen som benyttes, slik at strøm og effekt inn til boksen er togstrøm. Fra simuleringsprogrammene μPAS eller TPSS kan en kun få verdiene for aktiv- og reaktiv effekt som går over en linje (med fortegn), samt spenning og strøm. Alle verdiene som fås fra μPAS eller TPSS vil være referert 15 kV-nivå. Strømmen som går forbi det grå feltet i figurene er gitt av sammenhengen: | |||
Fra simuleringsprogrammene μPAS eller TPSS kan en kun få verdiene for aktiv- og reaktiv effekt som går over en linje (med fortegn), samt spenning og strøm. Alle verdiene som fås fra μPAS | |||
::<math> I_{PLT} = I_{NLT}= \frac {1}{2} \cdot \frac {1}{2} \cdot |\mathbf{I_1}–\mathbf{I_2}| </math> | ::<math> I_{PLT} = I_{NLT}= \frac {1}{2} \cdot \frac {1}{2} \cdot |\mathbf{I_1}–\mathbf{I_2}| </math> | ||
med positive verdier i pilenes retning i figuren. Uthevede symboler betyr fasevektorer (komplekse tall) og alle strømmer er referert 15 kV-nivå. En multipliserer med ½ for å ta hensyn til at strømmen halveres på grunn av doblet spenningsnivå og for at summen av strøm inn på strekningen fordeles på lederne. | med positive verdier i pilenes retning i figuren. Uthevede symboler betyr fasevektorer (komplekse tall) og alle strømmer er referert 15 kV-nivå. En multipliserer med ½ for å ta hensyn til at strømmen halveres på grunn av doblet spenningsnivå og for at summen av strøm inn på strekningen fordeles på lederne. En kan betrakte figuren nedenfor for å forsikre seg om at det stemmer. Der går 360 A i hver av faselederne i AT-vinduet til høyre uten tog referert 15 kV-nivå. Strøm (referert 30 kV) for PL og NL er 180 A og med de retningene på pilene og fortegnene som er brukt, vil differansen bli 720 A, altså fire ganger større strøm enn det som går i PL og NL (180 A), dermed må en mulitplisere med ¼. | ||
Strømmen i PL som tog komsumerer på strekningen: | Strømmen i PL som tog komsumerer på strekningen er gitt av: | ||
::<math> I_{PLtog} = \frac {1}{2} \cdot k_{PL} \cdot |\mathbf{I_1}+\mathbf{I_2}| </math> | ::<math> I_{PLtog} = \frac {1}{2} \cdot k_{PL} \cdot |\mathbf{I_1}+\mathbf{I_2}| </math> | ||
Der en multipliserer med ½ for at summen av strøm inn på strekningen fordeles på lederne. Se igjen på figuen | Der en multipliserer med ½ for at summen av strøm inn på strekningen fordeles på lederne. Se igjen på figuen nedenfor der strøm referert 15 kV-nivå i PL for strøm til toget i venstre AT-vindu er henholdsvis 600 A og 400 A. Med retningen på piler og fortegnsvalg som er gjort må altså summen halveres for at det skal bli riktig strøm i hver av lederne. I tillegg må korrigeringsfaktorene k<sub>PL</sub> anvendes for å ta hensyn til asymmetrisk strømfordeling med få AT-vinduer. | ||
[[Fil:Tog ved første seksjonsskille på strekning med to AT-vinduer.png|thumb|senter|900px|I AT-vinduet til høyre går det en strøm på 360 A i hver av NL og PL om denne refereres til 15 kV-nivå]] | [[Fil:Tog ved første seksjonsskille på strekning med to AT-vinduer.png|thumb|senter|900px|I AT-vinduet til høyre går det en strøm på 360 A i hver av NL og PL om denne refereres til 15 kV-nivå]] | ||
| Linje 77: | Linje 76: | ||
::<math> \mathbf{I_1} = \frac {\mathbf{P_1}-j\mathbf{Q_1}}{\mathbf{U_1}} \land \mathbf{I_2} = \frac {\mathbf{P_2}-j\mathbf{Q_2}}{\mathbf{U_2}} </math> | ::<math> \mathbf{I_1} = \frac {\mathbf{P_1}-j\mathbf{Q_1}}{\mathbf{U_1}} \land \mathbf{I_2} = \frac {\mathbf{P_2}-j\mathbf{Q_2}}{\mathbf{U_2}} </math> | ||
Dermed kan en finne strømmen som går i PL ved 1 ved å sette inn for togstrøm | Dermed kan en finne strømmen som går i PL ved 1 ved å sette inn for summen av togstrøm ('''''I<sub>PLtog</sub>''''') og transittstrøm ('''''I<sub>PLT</sub>'''''): | ||
::<math> I_{1PL} = \left | \mathbf{I_{PLT}}+\mathbf{I_{PLtog}} \right \vert = \left | \frac{1}{4} (\mathbf{I_{1}}-\mathbf{I_{2}}) + \frac{1}{2} k_{PL}(\mathbf{I_{1}}+\mathbf{I_{2}}) \right \vert </math> | ::<math> I_{1PL} = \left | \mathbf{I_{PLT}}+\mathbf{I_{PLtog}} \right \vert = \left | \frac{1}{4} (\mathbf{I_{1}}-\mathbf{I_{2}}) + \frac{1}{2} k_{PL}(\mathbf{I_{1}}+\mathbf{I_{2}}) \right \vert </math> | ||
Sideversjonen fra 24. jul. 2023 kl. 13:01
Innledning
Beregning av strømflyt, termisk belastning og dimensjonering av seriekomponenter i autotransformatorsystem (AT-system) med svært stor belastning kan være utfordrende, fordi strømflyten i lederne ikke er symetrisk. For eksempel vil det på en bane med AT-system (elektrisk utforming E) og stor togtrafikk gå mer strøm i positivleder (PL) enn i negativleder (NL). Om en har elektrisk utforming F vil det gå mer størm i kontaktledningen (KL). Artikkelen her fokuserer på elektrisk utforming E.
Med stor togtrafikk menes at det på en matestrekning går så mange tog at det for det meste av tiden vil være ett eller flere tog mellom hver autotransformator (AT), eller AT-vindu. Da vil det være mye strøm som overføres enfaset (eller 15 kV-nivå) og mindre tofaset (eller på 30 kV-nivå). Desto større trafikk desto større blir denne tendensen. Motsatt vil større effekt i transitt, altså effekt som overføres fra en matestrekning til en annen eller forbi ett eller flere AT-vinduer, medføre lik strøm i PL og NL. Det vil være det samm som å si at det overføres effekt tofset.
I praksis vil problemet være størst i Oslo-området der trafikken i deler av døgnet er svært stor. Det som også kompliserer forholdene er stor effekt i transitt, altså effekt som overføres mellom matestrekninger og forbi koblingshus og matestasjoner. Metoden som det her bygges på forutsetter at det foreligger en trafikksimulering der aktiv og reaktiv effekt, samt spenning, er kjent for innmatepunktene til strekningen som skal analyseres. Det fokuseres på korte strekninger, da det først og fremst vil være korte strekninger i Oslo-området der stor trafikk og stor strømbelastning kan kreve egne analyser.
Første del av artikkelen handler om strømflyten i AT-system med få AT-vinduer. Dette brukes for å finne spesielle korreksjonsfaktorer. Deretter utledes formler for å beregne strømflyt, blant annet basert på korreksjonsfaktorer.
Strømflyt i AT-system på kort matestrekning med tog i alle AT-vinduer
For tilfelle med en last i hvert AT-vindu kan ikke beregningene utført av Varju gi noe direkte svar på strømfordelingen. Tilfellet vil være interessant fordi det kan fortelle om strømfordelingen med stor togtrafikk og jevn fordeling av togene på hele matestrekningen. Ut fra det kan en finne korrigeringsfaktorer for å bestemme strømfordelingen. En tar her utgangspunkt i beregningene utført av Varju for en last som suksessivt flyttes fra midten av hvert AT-vindu, se appendiks. Alle bildene her kan gjennfinnes i appendiks.
Strømflyt i AT-system med tre AT-vinduer
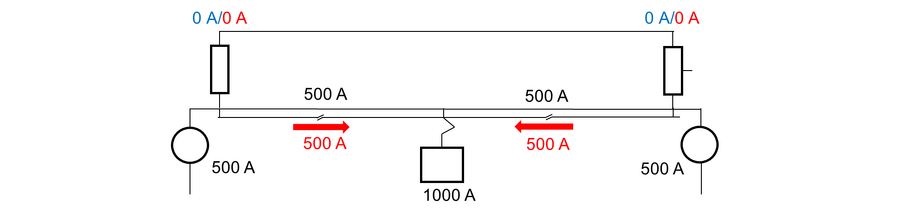
For å finne strømmen som flyter i AT-lederne på en matestrekning med tre AT-vinduer undersøkes benyttes figuren under og en metodikk basert på superposisjonsteoremet. Først hentes det ut figurer for togplassering og strøm i midt i hvert AT-vindu fra appendiks. Togene byttes ut med strømkilder som trekker strøm tilsvarende togene. Summen av strømmene til de tre lastene finnes av superposisjonsteoremet som sier at: Den totale strømmen i en hvilken som helst del av en lineær krets tilsvarer den algebraiske summen av strømmer gitt av strømkilde hver for seg. For å bestemme summen av separate strømmer, erstattes alle andre spenningskilder med en kortslutning og alle andre strømkilder med åpne kretser. Dermed fås summen som er vist i det nederste linjediagrammet. Som en kan se er strømfordelingen for AT-lederne ved spenningskildene 66 % i PL og 34 % i NL.
Strømflyt i AT-system med to AT-vinduer
For anslag av strømfordelingen med last midt på hvert av AT-vinduene, tas det utgangspunkt i tilfellet med én last midt mellom AT-en på en strekning med to AT-vinduene (se appendiks). Det forventes at på en så kort strekning som dette vil begge spenningskildene bidra nokså mye, anslagsvis med fordelingen ⅔ og ⅓ fra spenningskildene henholdsvis til venstre og høyre. I det nederste linjediagrammet er strømmene summert algebraisk. Strømfordelingen for AT-lederne ved spenningskildene er 74 % i PL og 26 % i NL.
Strømflyt i AT-system med ett AT-vindu
I figuren er det vsit strømfordelingen for en matestrekning bestående kun av ett AT-vindu, se appendiks for forklaring. Strømfordelingen for AT-lederne ved spenningskildene er 100 % i PL og 0 % i NL.
Beregning av strøm i AT-ledere og autotransformatorer i trafikksimuleringer
For tog som trekker 1000 A og beveger seg mellom to spenningskilder på en matestrekning med tre, to eller ett AT-vindu, vil strømmen fordele seg nokså ulikt mellom AT-lederne, se appendiks. Dette i motsetning til en matestrekning med mange AT-vinduer der strømmen blir jevnere. Tre ting gjør at representasjonen i kapitlet over er en sterk forenkling:
- Spenningskildene er ingen realistisk representasjon av virkelige omformerstasjoner. I virkeligheten vil blant annet antall omformere i drift, indre impedans og spenningsregulatorer spiller inn.
- Togene trekke stor strøm visse steder (hastighetsøkning), mens de andre steder trekker de moderat (jevn hastighet, liten stigning og rulling), ingen strøm (rulling med liten fall) eller mater inn strøm (regenerativ bremsing i fall).
- Strømfordeling for effekt i transitt er ikke undersøkt, men en del effekt vil overføres på en matestrekning til den neste. Denne effekten fordeler seg likt mellom AT-lederne.
For de aktuelle strekningene som en ser på her vil det være stasjoner ved hver av autotransformatorene. Togene kjører ut av stasjonene og akselererer opp i hastighet rett utenfor stasjonene. Det kan derfor godt tenkes stort strømforbruk før togene kommer midt mellom autotransformatorene. Effektfordeling mellom omformerstasjonene som har sammenheng med første kulepunkt blir inkludert i modellene for trafikksimuleringene og vil være gitt i resultatene.
Strøm gjennom autotransformatorene i trafikksimuleringer
Tabellen under viser korreksjonsfaktorer kPL for å ta hensyn til usymmetrisk belastning av AT-ledere med en matestrekning bestående av ett, to eller tre AT-vinduer, basert på undersøkelsene i kapittelet over:
| Leder | Tre AT-vinduer | To AT-vinduer | Ett AT-vindu |
|---|---|---|---|
| Strøm i NL | 515/1500 → 0,34 | 260/1000 → 0,26 | 0/500 →0,0 |
| Strøm i PL (kPL) | 985/1500 → 0,66 | 740/1000 → 0,74 | 500/500 →1,0 |
Tabellen viser en interessant tendens, nemmlig at strømmen i NL og PL blir stadige mer jevnt fordelt med økende antall AT-vinduer. Med anslagsvis fem eller flere AT-vinduer ville sannsynligvis strømfordelingen blitt lik mellom de to lederne, og kPL=0,5.
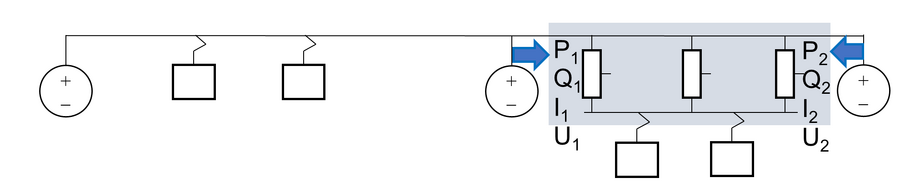
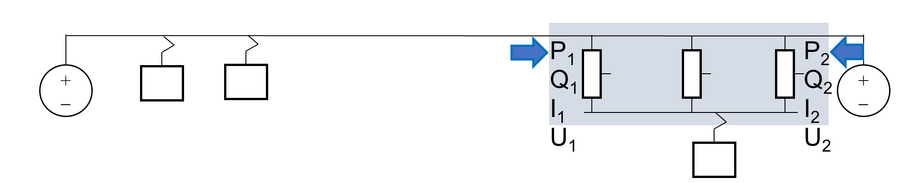
En skal her utlede formler og sette opp en metodikk for belastning av AT-ledere på en strekning vist med en grå boks i hver av illustrasjonene nedenfor. Generelt betraktes en kort matestrekning mellom to omformerstasjoner, som i det øverste bilde nedenfor, eller på en strekning med delvis AT-system og BT-system, og et antall tog som trekker tilfeldig effekt, se det nederste bildet nedenfor.
Det vil for hver av disse boksene være en strøm- og effektkomponent som går rett gjennom, kalt transittstrøm. En annen del går inn i boksen og brukes av togene, kalt togstrøm. Pilene viser fortegnkonvensjonen som benyttes, slik at strøm og effekt inn til boksen er togstrøm. Fra simuleringsprogrammene μPAS eller TPSS kan en kun få verdiene for aktiv- og reaktiv effekt som går over en linje (med fortegn), samt spenning og strøm. Alle verdiene som fås fra μPAS eller TPSS vil være referert 15 kV-nivå. Strømmen som går forbi det grå feltet i figurene er gitt av sammenhengen:
- Feil i matematikken (Konverteringsfeil. Tjeneren («cli») rapporterte: «SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "–" found.in 1:87»): {\displaystyle I_{PLT} = I_{NLT}= \frac {1}{2} \cdot \frac {1}{2} \cdot |\mathbf{I_1}–\mathbf{I_2}| }
med positive verdier i pilenes retning i figuren. Uthevede symboler betyr fasevektorer (komplekse tall) og alle strømmer er referert 15 kV-nivå. En multipliserer med ½ for å ta hensyn til at strømmen halveres på grunn av doblet spenningsnivå og for at summen av strøm inn på strekningen fordeles på lederne. En kan betrakte figuren nedenfor for å forsikre seg om at det stemmer. Der går 360 A i hver av faselederne i AT-vinduet til høyre uten tog referert 15 kV-nivå. Strøm (referert 30 kV) for PL og NL er 180 A og med de retningene på pilene og fortegnene som er brukt, vil differansen bli 720 A, altså fire ganger større strøm enn det som går i PL og NL (180 A), dermed må en mulitplisere med ¼.
Strømmen i PL som tog komsumerer på strekningen er gitt av:
Der en multipliserer med ½ for at summen av strøm inn på strekningen fordeles på lederne. Se igjen på figuen nedenfor der strøm referert 15 kV-nivå i PL for strøm til toget i venstre AT-vindu er henholdsvis 600 A og 400 A. Med retningen på piler og fortegnsvalg som er gjort må altså summen halveres for at det skal bli riktig strøm i hver av lederne. I tillegg må korrigeringsfaktorene kPL anvendes for å ta hensyn til asymmetrisk strømfordeling med få AT-vinduer.
For å finne strømmene I1 og I2 benyttes sammenhengen:
Her defineres fasevinkelen til spenningen som referanse og settes til 0°. Det innebærer at fasevinkelforskjellen for spenningen over denne korte strekningen tilnærmes til å være 0. Videre kan en sette for hver av strømmene I1 og I2:
Dermed kan en finne strømmen som går i PL ved 1 ved å sette inn for summen av togstrøm (IPLtog) og transittstrøm (IPLT):
og ved 2:
Her er det første leddet (differansen) strømkomponenten som overføres forbi AT-vinduet(ene), altså transittstrøm, og det andre leddet er strøm som togene på strekningen forbruker, kalt togstrøm.
Betingelsen for sammenhengen er at matestrekningen er kort, anslagsvis mindre enn fem AT-vinduer.
Strøm gjennom autotransformatorene i trafikksimuleringer
Ut fra det en har sett over angående belastning av autotransformatorene vil de belastes lavt på grunn av den store andelen effektoverføring kun 15 kV-nivå og få AT-vinduer. Imidlertid vil ikke autotransformatorene bli ubelastet om det bare er ett AT-vindu, for selv da er det effekt på 30 kV-nivå som skal overføres (i transitt).
Strømfordelingen vist i figur 84 benyttes, der strømmen inn til autotransformatoren til høyre er gitt direkte av strømmen som mates inn på strekningen. For å finne denne strømmen brukes leddet overfor for strøm i transitt. Derimot er ikke dette tilfelle for belastningen av autotransformatoren til venstre, den belastes ikke for strøm til toget, men for strøm til autotransformatoren i midten. Imidlertid skal det her forutsettes flere tog jevnt fordelt på matestrekingen. Dermed er det strømfordelingen i tilfellene vist i figur 82, figur 87 og figur 88 som er interessant. Belastningen av autotransformatorer ved overgangen til det grå området i figur 92 kan skrives slik:
Der en tar hensyn til antall AT-vinduer ved å ta med faktoren kAT som har verdier gitt av tabellen nedenfor. Verdiene i tabellen er hentet fra figur 82, figur 87 og figur 88 som viser belastningen av autotransformatorene med tog jevnt fordelt på matestrekningen
| Tre AT-vinduer | To AT-vinduer | Ett AT-vindu | |
|---|---|---|---|
| Strøm i AT (kAT) | 1030/1500 → 0,69 | 520/1000 → 0,52 | 0/500 →0,0 |
Belastningen av hver autotransformator ute på matestrekningen finnes som summen av strømmen inn på matestrekningen dividert på antall steder med autotransformator. Da kan en regne med at autotransformatoren på midten gjennomsnittlig belastes minst med så stor strøm.
| Tre AT-vinduer | To AT-vinduer | Ett AT-vindu | |
|---|---|---|---|
| Strøm i midt AT (kmidt AT) | 1030/3000 → 0,3433 | 520/1000 → 0,52 | – |
En formel for strømmen som fordeler seg på autotransformatorene midt på strekningen kan settes opp slik:
Der kmidt AT er korrigeringsfaktoren autotransformatorer på matestrekningen gitt av verdiene i tabell 3 og de andre symbolene er de samme som lengre opp. I et tilfelle med flere enn tre AT-vinduer antas det at korrigeringsfaktoren kmidt AT kan erstattes slik, der n er antall autotransformatorer:
For strøm gjennom autotransformatorer tilknyttet et topolet samleskinneanlegg (koblingshus), må en finne strømmen som mates ut på 15 kV-nivå til tilstøtende matestrekninger. Om matestrekningene tilknyttet samleskinneanlegget er lange, autotransformatorene plassert med lik avstand og med jevnt fordelt effektuttak, kan en anta lik belastning for alle auto-transformatorene. Men om disse forutsetningene ikke er til stede kan bruk av tommel-fingerregler gi feil, for eksempel ved at mer effekt enn vanlig omsettes på 15 kV-nivå og belaster autotransformatorene tilknyttet samleskinnen mye.
Om en kan finne strømmen som går inn til samleskinneanleggets forsyningsområde, markert med gråt i figur 93, vil den delen som er togstrømmen belaste autotransformatoren tilknyttet samleskinneanlegget:
Det grå området kan ha en utstrekning til nærmeste autotransformator i hver retning ut fra koblingshuset, og denne utstrekningen vil påvirke korrigeringsfaktoren kkhAT.
Problemet her er at en ikke har noen sikre beregninger for hvor stor korrigeringsfaktoren kkhAT egentlig skal være. En annen utfordring er å finne strømmer inn mot forsyningsområde til et koblingshus. For Drammen eller Asker koblingshus har en ikke definert linjer i simuleringsmodellene der P, Q, I og U kan avleses der nærmeste autotransformator i hver retning skal stå (det grå arealet i figur 93).
En annen tilnærming er å si at all effekt inn til mateområdet fra omformerstasjonene til koblingsanlegget fordeler seg likt på alle autotransformatorene. Altså at det grå området i figuren over strekes ut mot alle de tre omformerne. Da forutsettes autotransformatoren i koblingshuset å bli belastet likt som alle de andre enhetene.