Elektrisk systembeskrivelse av kontaktledningsanlegg ver01

__NUMBEREDHEADINGS__

Generelt

Kontaktledningsanlegget overfører effekt mellom matestasjonen og traksjonsmateriell og andre belastninger tilknyttet kontaktledningen. I eldre anlegg skjer overføringen i kontaktledning ved 15 kV nominell spenning, med retur i kjøreskinner ved 0 kV. I nyere anlegg er det innført returledere eller AT-system med positivleder og negativleder. Følgende ledere vil bli omtalt videre i dette kapittelet:

<figtable id="tab:Ledere_oversikt">

Ledere oversikt

Leder	Forklaring	Nominell spenning
KL	Kontaktledningsanlegg, omfatter kontakttråd og bæreline	15 kV
RR	Kjøreskinner	0 kV
RL	Returleder	0 kV
FSL	Forsterkningsleder	15 kV
PL	Positivleder (for AT-system)	normalt + 15 kV
NL	Negativleder (for AT-system)	normalt - 15 kV

</figtable>

I dette kapittelet vil det bli beskrevet en matematisk modell som beskriver hvordan strøm og spenning fordeler seg mellom ulike ledere i et slikt flerledersystem som et kontaktledningsanlegg utgjør. En slik modell kan brukes til å beregne:

• impedansen mellom matestasjon og belastning i kontaktledningssystemet,
• potensial i returkretsen,
• indusert spenning i ledere som går parallelt med jernbanetraseen,
• belastning på enkeltledere og komponenter i kontaktledningsnettet.

Introduksjon: Enkel transmisjonslinje

Telegraflikningene

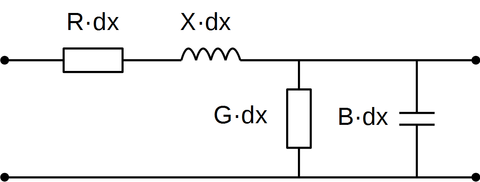
Den enkleste formen for problemet er ei enkelt linjesløyfe. En kontaktledning med retur i kjøreskinner kan forenklet betraktes på denne måten, hvis man ser bort fra lekkasje til jordsmonn. Telegraflikningen tar utgangspunkt i et svært kort linjesegment dx av linjesløyfa. Linjesegmentet har en seriell resistans R · dx og reaktans X · dx, og en parallell konduktans G · dx og susceptans B · dx.

<figure id="fig:Telegraflikningene">

Telegraflikningene: Kretsskjema for et linjesegment dx </figure> Parametrene kan skrives om om slik at impedansen blir $Z=R+jX$ og admittansen blir $Y=G+jB$ Det serielle spenningsfallet dU over dette linjesegmentet er gitt av Ohms lov: (i) ${\frac {\mathrm {d} U}{\mathrm {d} x}}=-Z\cdot I$ Strømmen som lekker gjennom admittansen $Y$ utgjør forskjellen i strøm over linjesegmentet. Denne strømmen er proporsjonal med spenningen: (ii) ${\frac {\mathrm {d} I}{\mathrm {d} x}}=-Y\cdot U$ Likningene (i) og (ii) danner et koplet likningssett som i litteraturen kalles for telegraflikningene. Likningssettet kan ordnes med matriserepresentasjon på følgende måte: ${\frac {\mathrm {d} }{\mathrm {d} x}}{\begin{pmatrix}U\\I\end{pmatrix}}={\begin{pmatrix}0&-Z\\-Y&0\end{pmatrix}}\cdot {\begin{pmatrix}U\\I\end{pmatrix}}$ Løsningen på et slikt likningssett er beskrivet i flere lærebøker i lineæralgebra, for eksempel i Referanse [1]. En rask innføring er gitt i Wikipedia. Egenverdiene $\gamma$ til systemet er: $\lambda _{1}=+{\sqrt {Z\cdot Y}}=\gamma$ $\lambda _{2}=-{\sqrt {Z\cdot Y}}=-\gamma$ der $\gamma ={\sqrt {Z\cdot Y}}$ er linjens transmisjonskonstant. De tilhørende egenvektorene kan finnes til å være: $v_{1}={\begin{pmatrix}1\\-{\sqrt {\tfrac {Y}{Z}}}\end{pmatrix}}={\begin{pmatrix}1\\-{\tfrac {1}{Z_{0}}}\end{pmatrix}}$ $v_{2}={\begin{pmatrix}1\\{\sqrt {\tfrac {Y}{Z}}}\end{pmatrix}}={\begin{pmatrix}1\\{\tfrac {1}{Z_{0}}}\end{pmatrix}}$ der $Z_{0}={\sqrt {\tfrac {Z}{Y}}}$ er linjens karakteristiske impedans. Transmisjonskonstanten $\gamma$ er en kompleks størrelse og et mål på hvordan en strøm/spenning dempes og forandrer fase langs en transmisjonslinje. Den karakteristiske impedansen $Z_{0}$ er et mål på sammenhengen mellom strøm og spenning i en transmisjonslinje. Løsningen er gitt av følgende uttrykk: ${\begin{pmatrix}U\\I\end{pmatrix}}=A\cdot \mathbf {v_{1}} \cdot e^{\lambda _{1}x}+B\cdot \mathbf {v_{2}} \cdot e^{\lambda _{2}x}$ $U=A\cdot e^{\gamma x}+B\cdot e^{-\gamma x}$ $I=-A\cdot {\tfrac {1}{Z_{0}}}\cdot e^{\gamma x}+B\cdot {\tfrac {1}{Z_{0}}}\cdot e^{-\gamma x}$ Tallverdiene for konstantene A og B er gitt av grenseverdibetingelser.

Referanser

[1] Edwards, Penney: Elementary Linear Algebra, Pearson, 1987. ISBN 9780132582605.

Admittanser

Admittansen