Sporets trasé/Minste tverrsnitt og profiler: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
(rettet feil i formel) |
||
| (101 mellomliggende versjoner av 5 brukere er ikke vist) | |||
| Linje 7: | Linje 7: | ||
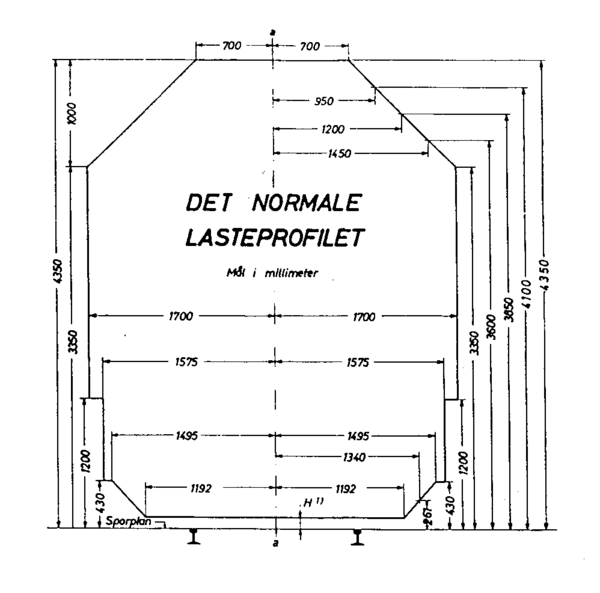
I Norge definerte man tidlig et lasteprofil som anga maskimale lastgrense ved pålasting av godsvogner. Dette lasteprofilet lå et stykke innenfor spilleromslinjen og man fastsatte derfor at heller ingen vogner eller lokomotiver skulle ha større mål enn lasteprofilet, og man opprettet dermed laste- og konstruksjonsprofilet. Denne benevnelsen ble avskaffet ved revisjon av Trykk 402 i 1964 fordi personvogner på den tiden fikk fjærsystemer og bolsterspillrom som tillot langt større sidebevegelser enn hva tilfellet var for godsvogner. | I Norge definerte man tidlig et lasteprofil som anga maskimale lastgrense ved pålasting av godsvogner. Dette lasteprofilet lå et stykke innenfor spilleromslinjen og man fastsatte derfor at heller ingen vogner eller lokomotiver skulle ha større mål enn lasteprofilet, og man opprettet dermed laste- og konstruksjonsprofilet. Denne benevnelsen ble avskaffet ved revisjon av Trykk 402 i 1964 fordi personvogner på den tiden fikk fjærsystemer og bolsterspillrom som tillot langt større sidebevegelser enn hva tilfellet var for godsvogner. | ||
== Beregningsgrunnlag – UIC fiche 505== | == Beregningsgrunnlag – UIC fiche 505== | ||
| Linje 385: | Linje 384: | ||
| + nedfjæring || 0,030 m | | + nedfjæring || 0,030 m | ||
|- | |- | ||
| + hjulslitasje || 0,040 | | + hjulslitasje || 0,040 m<sup>1</sup> | ||
|- | |- | ||
| + diverse bevegelser || 0,020 | | + diverse bevegelser || 0,020 m<sup>1</sup> | ||
|- | |- | ||
| = nødvendig fri høyde over sporplan || 0,170 m | | = nødvendig fri høyde over sporplan || 0,170 m | ||
|} | |} | ||
1) Varierer med materielltype | |||
=== Forskyvning i side=== | === Forskyvning i side=== | ||
| Linje 554: | Linje 554: | ||
- | - | ||
| <math>\frac {n+a} {a}</math> | | <math>\frac {n+a} {a}</math> | ||
| <math>\frac {n}{a}</math> | | align="center" | <math>\frac {n}{a}</math> | ||
|- | |- | ||
| <math>\frac {2n + a}{a}</math> || || || || || || || | | <math>\frac {2n + a}{a}</math> || <math>\frac {2n + a}{a}</math> || align="center" | <math>\frac {n}{a}</math> || align="center" | - | ||
| align="center" | - || <math>\frac {n + a}{a}</math> || align="center" | <math>\frac {n}{a}</math>|| <math>\frac {n + a}{a}</math> | |||
|- | |- | ||
| width="50" |4 || 2 boggier som betraktes som | | width="50" |4 || 2 boggier som betraktes som | ||
løpeboggier | løpeboggier | ||
| align="center" | <math>\frac {n + a}{a}</math> || <math>\frac {2n + a}{a}</math> || colspan=2 align="center" | <math>\frac {n}{a}</math> | |||
| colspan=2 align="center" | <math>\frac {n - a}{a}</math> || colspan=2 align="center" | 1 | |||
|} | |} | ||
| Linje 566: | Linje 569: | ||
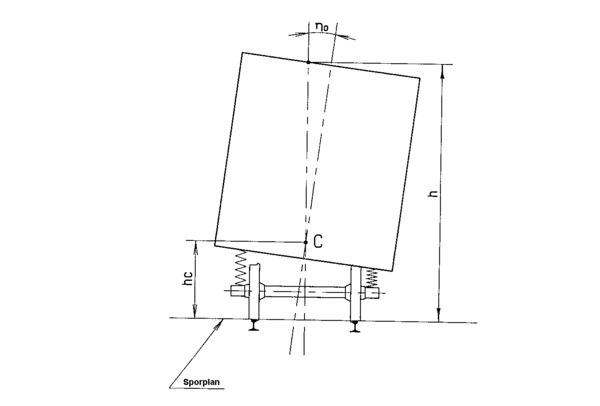
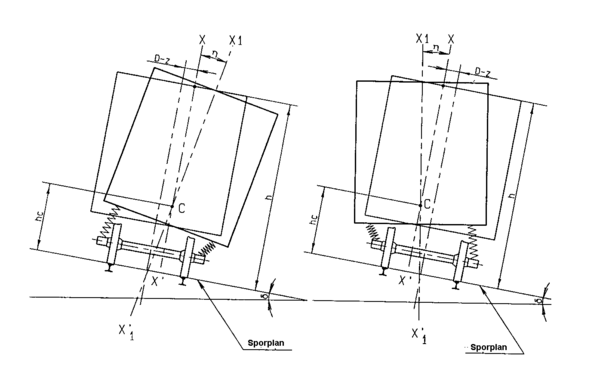
==== Semistatisk forskyvning==== | ==== Semistatisk forskyvning==== | ||
Den semistatiske forskyvningen som benyttes ved beregning av | Den semistatiske forskyvningen som benyttes ved beregning av E<sub>i</sub> og E<sub>a</sub> er avhengig av rullvinkelkoeffisienten s, det betraktede punkts høyde over sporplan og rullsenterets høyde over sporplan hc. Forskyvningen deles mellom materiellets konstruksjonsmål og de faste anlegg (frittromsprofiler) etter følgende prinsipper: | ||
Ved beregning av konstruksjonsmål for materiellet skal i | Ved beregning av konstruksjonsmål for materiellet skal i E<sub>i</sub> og E<sub>a</sub> inngå: | ||
*en manglende overhøyde hhv. overhøyde på opp til 0,050 m | |||
en manglende overhøyde hhv. overhøyde på opp til 0,050 m | *en manglende overhøyde hhv. overhøyde på 0,200 m dersom s > 0,4 og hc > 0,5 | ||
en manglende overhøyde hhv. overhøyde på 0,200 m dersom s > 0,4 og hc > 0,5 | *en manglende overhøyde hhv. overhøyde på 0,200 m dersom det benyttes en større verdi av s, h og h<sub>c</sub> enn det som ble benyttet ved beregning av avstand til faste gjenstander | ||
en manglende overhøyde hhv. overhøyde på 0,200 m dersom det benyttes en større verdi av s, h og | *skjevstilling over 1º som skyldes konstruksjons- og innstillingstoleranser eller skjevlasting | ||
skjevstilling over 1º som skyldes konstruksjons- og innstillingstoleranser eller skjevlasting | |||
Skjevstilling under 1º samt sidesvingninger som følge av kjøring i sporet inngår ved beregning av frittromsprofiler. | Skjevstilling under 1º samt sidesvingninger som følge av kjøring i sporet inngår ved beregning av frittromsprofiler. | ||
| Linje 583: | Linje 585: | ||
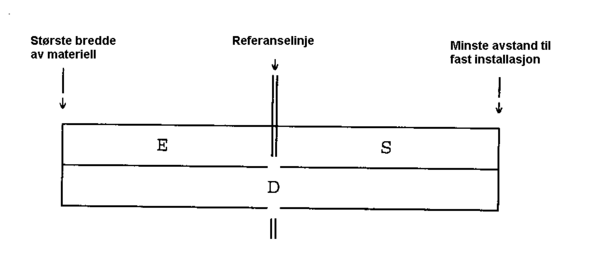
Ved beregning av innskrenkningen E mellom akslene/boggisentrene gjelder: | Ved beregning av innskrenkningen E mellom akslene/boggisentrene gjelder: | ||
Innskrenkningen | ''Innskrenkningen E<sub>i</sub> = Forskyvningen D<sub>i</sub> – Utslaget S<sub>0</sub>'' | ||
Ved beregning av innskrenkningen E mellom akslene/boggisentrene gjelder: | Ved beregning av innskrenkningen E mellom akslene/boggisentrene gjelder: | ||
Innskrenkningen | ''Innskrenkningen E<sub>a</sub> = Forskyvningen D<sub>a</sub> – Utslaget S<sub>0</sub>'' | ||
For alle beregninger av spillrom i sideretning har hjulenes stilling i sporet en betydning ved beregningen. Dette uttrykkes ved innskrenkningskoeffisienten A som korrigerer visse parametre i formlene. | For alle beregninger av spillrom i sideretning har hjulenes stilling i sporet en betydning ved beregningen. Dette uttrykkes ved innskrenkningskoeffisienten A som korrigerer visse parametre i formlene. | ||
| Linje 593: | Linje 595: | ||
Formlene for E ser ut som følger: | Formlene for E ser ut som følger: | ||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i={an_i-n_i^2 +{p^2 \over 4} (A) \over 2R} +{1,465-d \over2}(A)+q+w(A)+z+x_i-S_0 | |||
</math></center> || align="right" | (5.1) | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i={an_a-n_a^2 -{p^2 \over 4} (A) \over 2R} +{1,465-d \over2}(A)+q(A)+w(A)+z+x_a-S_0 | |||
</math></center> || align="right" | (5.2) | |||
|} | |||
De enkelte ledd i formlene kan inndeles i to grupper: | De enkelte ledd i formlene kan inndeles i to grupper: | ||
| Linje 614: | Linje 639: | ||
Det geometriske utslag for et betraktet tverrsnitt på vognkassen i en kurve uttrykkes ved | Det geometriske utslag for et betraktet tverrsnitt på vognkassen i en kurve uttrykkes ved | ||
{|width="100%" | |||
|- | |||
|<center><math> | |||
an-n^2+{p^2 \over 4}(A) \over 2R | |||
</math></center> || align="right" | (5.3) | |||
|} | |||
a er boggisenteravstand eller akselavstand | a er boggisenteravstand eller akselavstand | ||
| Linje 626: | Linje 664: | ||
Med utgangspunkt i fastsettelse av største tillatte sporvidde på 1,465 m, fastsettes spillrommet i sporet til | Med utgangspunkt i fastsettelse av største tillatte sporvidde på 1,465 m, fastsettes spillrommet i sporet til | ||
{|width="100%" | |||
|- | |||
|<center><math> | |||
{1,465-d \over2}(A) | |||
</math></center> || align="right" | (5.4) | |||
|} | |||
der: | |||
*1,465 er største tillatte sporvidde | |||
*d er minimumsavstand mellom flenser | |||
*A er innskrenkningskoeffisienten | |||
Forskyvningen av materiellets midtlinje i forhold til spomidt som følge av spillrom mellom hjulsett og boggiramme uttrykkes med q. Hjulenes stilling i sporet påvirker q gjennom innskrenkningskoeffisienten A. | |||
For | Forskyvningen i sideretning i forhold til midtstillingen av materiellets dreietapp og/eller svingbjelke uttrykkes med w. For materiell uten dreietapp den mulige forskyvningen av boggien i forhold til vognkassen. Denne sideforskyvningen er avhengig av kurveradius og den retning forskyvningen går i. Hjulenes stilling i sporet påvirker w gjennom innskrenkningskoeffisienten A. | ||
Varierer størrelsen av w med kurveradius benyttes: | |||
*w<sub>i</sub>(R) for kurvens innerside ved kurveradius R | |||
*w<sub>a</sub>(R) for kurvens ytterside ved kurveradius R | |||
*w<sub>∞</sub> for rettlinje | |||
==== Rulling av vognkassen==== | |||
Rulling av materiellet med mer enn 1º som følge av materiellets fjærer eller skjevlasting, resulterer i sidebevegelsen z som settes sammen av to ledd. | |||
Det første leddet kan føres tilbake til fjærenes elastisitet og skyldes overhøyde eller manglende overhøyde på 0,050 m. | |||
= | {|width="100%" | ||
|- | |||
|<center><math> | |||
{s \over 30} \left\vert h-h_c \right\vert | |||
</math></center> || align="right" | (5.5) | |||
|} | |||
Det andre leddet kan føres tilbake til skjevlasting mer enn 1º. | |||
= | {|width="100%" | ||
|- | |||
|<center><math> | |||
tan[ \eta - 1^ \circ ]_{>0}* \left\vert h-h_c \right\vert | |||
</math></center> || align="right" | (5.6) | |||
|} | |||
For å ta hensyn til en overhøyde eller manglende overhøyde på 0,200 m fås | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\left[ {s \over 10} \left\vert h-h_c \right\vert - 0,04[h-0,5]_{>0} \right]_{>0} | |||
</math></center> || align="right" | (5.7) | |||
|} | |||
Dermed kan følgende uttrykk for z settes opp: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
z=\left[{s \over 30} +tan \left\vert \eta - 1^\circ \right\vert_{>0} \right]*\left\vert h-h_c \right\vert + \left[ {s \over 10} \left\vert h-h_c \right\vert - 0,04[h-0,5]_{>0} \right]_{>0} | |||
</math></center> || align="right" | (5.8) | |||
|} | |||
Formel 5.8 kan benyttes i redusert form dersom h > h<sub>c</sub>, h > 0,5 m, s ≤ 0,4 og η ≤ 1º kan z settes lik | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
z={s\over 30}(h-h_c) | |||
</math></center> || align="right" | (5.9) | |||
|} | |||
og dersom h < 0,5 m, η ≤ 1º og er uavhengig av h<sub>c</sub> og s kan z settes lik | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
z={4s\over 30}(h_c-h) | |||
</math></center> || align="right" | (5.10) | |||
|} | |||
og dersom h = h<sub>c</sub> kan z settes lik 0 (gjelder også hvis det er snakk om ikke avfjærede deler). | |||
==== Små kurveradier==== | |||
Selv om det ved beregning av frittromsprofilene tas hensyn til vognendens utslag i kurve med leddet S, kan meget lange vogner ha så stort utslag midt på vognen og i enden av overhenget at det kan være nødvendig å begrense vognens breddde for å oppnå sikker kjøring i kurveradier mellom 150 m og 250 m. | |||
For tverrsnitt mellom boggisentrene benyttes x<sub>i</sub> som kun er aktuelt ved boggisenteravstander på 20 m og større. Verdien av x<sub>i</sub> tas kun med dersom | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
{a^2+p^2\over 4}>100 | |||
</math></center> || align="right" | (5.11) | |||
|} | |||
For tverrsnitt i overheng benyttes x<sub>a</sub> dersom | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
an+n^2-{p^2\over a}>120 | |||
</math></center> || align="right" | (5.12) | |||
|} | |||
==== Innflytelse av overhøyderamper==== | |||
Kjøringer gjennom overhøyderamper fører til dynamiske bevegelser av vognkassen. Størrelsen av utslaget avhenger av rampestigning og vognkassens stivhet. Utslaget beregnes som | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\beta *{a+2n\over 3000}*s_r\left\vert h-h_c\right\vert | |||
</math></center> || align="right" | (5.13) | |||
|} | |||
der: | |||
β er vognkassens stivhetskoeffisient (β =1 for stive vogner) | |||
s<sub>r</sub> er rampestigningen | |||
Innflytelsen av overhøyderamper ignoreres av UIC, men den inngår i beregningsemetoden som anvendes i Norge, jf. avsnitt 4.3. | |||
=== Beregning av innskrenkningen E=== | |||
Innskrenkningen E for et materiell beregnes for | |||
*tverrsnitt mellom materiellets ytterakser/boggisentre = E<sub>i</sub> | |||
*tverrsnitt utenfor materiellets ytterakser/boggisentre = E<sub>a</sub> | |||
Materiellets geometriske oppbygning avgjør om det er utslag i kurve eller på rettlinje som er størst. | |||
Ledd i formlene markert med <sup>*</sup> benyttes for høyder opp til og med 0,400 m. | |||
0, | |||
Ledd i formlene markert med <sup>**</sup> benyttes for høyder over 0,400 m. | |||
==== Innskrenkning for lokomotiver==== | |||
Som lokomotiv regnes et materiell som kun er trekkraft, og dermed ikke kan ta med personer eller gods. | |||
'''Beregning av E<sub>i</sub>:''' | |||
Beregn verdien av uttrykket | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
an-n^2+{p^2\over 4}-500(w_\infty-w_{i(250)}) | |||
</math></center> || align="right" | (5.14) | |||
|} | |||
Hvis 5.14 er mindre eller lik 7,5 er det lokomotivets utslag på rettlinje som er dimensjonerende og E<sub>i</sub> beregnes som | |||
= | {|width="100%" | ||
|- | |||
|<center><math> | |||
E_i={1,465-d\over2}+q+w_\infty+z-0.015 | |||
</math></center> || align="right" | (5.15) | |||
|} | |||
Hvis 5.14 er større enn 7,5 er det lokomotivets utslag i kurver som er | |||
dimensjonerende og E<sub>i</sub> beregnes som | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i={an-n^2+{p^2\over4}\over500}+{1,465-d\over2}+q+w_{i(250)}+z+[x_i]_{>0}-0,025^*/0,030^{**} | |||
</math></center> || align="right" | (5.16) | |||
|} | |||
I | I 5.16 inngår x<sub>i</sub> som beregnes som | ||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_i={1\over750}(an-n^2+{p^2\over 4}-100)+w_{i(150)}-w_{i(250)} | |||
</math></center> || align="right" | (5.17) | |||
|} | |||
'''Beregning av E<sub>a</sub>:''' | |||
Beregn verdien av uttrykket | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
an+n^2-{p^2\over 4}-500[(w_\infty-w_{i(250)}){n\over a}+(w_\infty-w_{a(250)}){n+a\over a}] | |||
</math></center> || align="right" | (5.18) | |||
|} | |||
Hvis 5.18 er mindre eller lik 7,5 er det lokomotivets utslag på rettlinje som er dimensjonerende og E<sub>a</sub> beregnes som | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a=({1,465-d\over2}+q+w_\infty){2n+a\over a}+z-0,015 | |||
</math></center> || align="right" | (5.19) | |||
|} | |||
Hvis 5.18 er større enn 7,5 er det lokomotivets utslag i kurver som er | |||
dimensjonerende og E<sub>a</sub> beregnes som | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a={an+n^2-{p^2\over 4}\over 500}+({1,465-d\over 2})({n+a\over a})+q({2n+a\over a})+w_{i(250)}{n\over a}+w_{a(250)}{n+a\over a}+z+[x_a]_{>a}-0,024^*/0,030^{**} | |||
</math></center> || align="right" | (5.20) | |||
|} | |||
I 5.20 inngår x<sub>a</sub> som beregnes som | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_a={1\over750}(an+n^2-{p^2\over 4}-120)+(w_{i(150)}-w_{i(250)}){n\over a}+(w_{a(150)}-w_{a(250)}){n+a\over a} | |||
</math></center> || align="right" | (5.21) | |||
|} | |||
'''Regneeksempel:''' | |||
Alle beregninger utføres på høyder over 0,400 m. | |||
Det er valgt følgende parametre: | |||
a = 9,700 m, d = 1,410 m, p = 2,800 m, q = 0,006, s = 0,1, | |||
ni = a/2 = 4,850 m, na = 3,250 m, hc = 0,500 m, η0 = 1˚, | |||
wi(R) = Wa(R) = 0,060 og uavhengig av radius | |||
'''<big>Konstruksjonsbredden på midten av lokomotivet</big>''' | |||
Det undersøkes om det er lokomotivets utslag på rettlinje eller i kurve som er dimensjonerende. Det skjer ved å sette inn verdier i formel 5.14: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
9,700*4,850-4,850^2+{2,800^2\over 4}-500(0,060-0,060)=25,483 | |||
</math></center> || align="right" | | |||
|} | |||
Verdien av uttrykket er større enn 7,5 som betyr at lokomotivets utslag i kurve blir dimensjonerende og det beregnes etter formel 5.16 og 5.17. | |||
Først kontrolleres det om x<sub>i</sub> > 0. Det skjer ved å sette inn verdier i formel 5.17. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_i={1\over 750}(9,700*4,850-4,850^2+{2,800^2\over 4}-100)+0,060-0,060=-0,0994 | |||
</math></center> || align="right" | | |||
|} | |||
Da verdien av x<sub>i</sub> er negativ inngår den med verdi 0 i formel 5.16. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i={9,700*4,850-4,850^2+{2,800^2\over 4}\over 500}+{1,465-1,410\over 2}+0,006+0,006+z+0-0300=0,1145+z | |||
</math></center> || align="right" | | |||
|} | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 8 Konstruksjonsbredden på midten av lokomotivet | |||
|- | |||
!style="width:200px" | Høyde over sporplan | |||
!style="width:200px" | Halv bredde av referanselinje | |||
! style="width:200px" | E<sub>i</sub> - z | |||
! style="width:200px" | z | |||
! style="width:200px" | Mulig halv bredde for lokomotiv | |||
|- | |||
|0,500|| 1,620|| 0,1145|| 0,0000|| 1,5055 | |||
|- | |||
|1,170 ||1,620|| 0,1145|| 0,0022|| 1,5033 | |||
|- | |||
|1,170|| 1,645 ||0,1145|| 0,0022|| 1,5283 | |||
|- | |||
|3,250|| 1,645|| 0,1145|| 0,0092|| 1,5213 | |||
|- | |||
|3,700|| 1,425|| 0,1145|| 0,0107|| 1,2998 | |||
|- | |||
|4,010|| 1,120|| 0,1145|| 0,0117|| 0,9938 | |||
|- | |||
|4,310|| 0,525|| 0,1145|| 0,0127|| 0,3978 | |||
|} | |||
'''<big>Konstruksjonsbredden i enden av lokomotivet</big>''' | |||
Det undersøkes om det er lokomotivets utslag på rettlinje eller i kurve som er dimensjonerende. Det skjer ved å sette inn verdier i formel: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
9,700*3,250+3,350^2-{2,800^2\over4}-500[(0,060-0,060){3,250\over 9,700}+(0,060-0,060){3,250+9,700\over 9,700}]=40,128 | |||
</math></center> || align="right" | | |||
|} | |||
Verdien av uttrykket er større enn 7,5 som betyr at lokomotivets utslag i kurve blir dimensjonerende og det beregnes etter formel | |||
Først kontrolleres det om x<sub>a</sub> > 0. Det skjer ved å sette inn verdier i formel | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_a={1 \over 750}(9,700*3,250+3,250^2{2,800^2\over 4}-120)+(0,060-0,060){3,250\over 9,700}+(0,060-0,060){3,250+9,700\over ??? }9,700=-0,107 | |||
</math></center> || align="right" | | |||
|} | |||
Da verdien av x<sub>a</sub> er negativ inngår den med verdi 0 i formel | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a={9,700*3,250+3,250^2-{2,800^2\over 4} \over 500}+{1,465-1,410\over 2}{3,250+9,700\over 9,700}+0,006({2*3,250+9,700\over 9,700})+0,060{3,250\over 9,700}+0,060{3,250+9,700\over 9,700}+z+0+0,030=0,1972+z | |||
</math></center> || align="right" | | |||
|} | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 9 Konstruksjonsbredden i enden av lokomotivet | |||
|- | |||
!style="width:200px" | Høyde over sporplan | |||
!style="width:200px" | Halv bredde av referanselinje | |||
! style="width:200px" | E<sub>i</sub> - z | |||
! style="width:200px" | z | |||
! style="width:200px" | Mulig halv bredde for lokomotiv | |||
|- | |||
|0,500|| 1,620 ||0,1972|| 0,0000|| 1,4228 | |||
|- | |||
|1,170|| 1,620|| 0,1972|| 0,0022|| 1,4206 | |||
|- | |||
|1,170 ||1,645|| 0,1972|| 0,0022|| 1,4456 | |||
|- | |||
|3,250|| 1,645|| 0,1972|| 0,0092|| 1,4386 | |||
|- | |||
|3,700|| 1,425|| 0,1972|| 0,0107|| 1,2171 | |||
|- | |||
|4,010|| 1,120|| 0,1972|| 0,0117|| 0,9111 | |||
|- | |||
|4,310|| 0,525|| 0,1972|| 0,0127|| 0,3151 | |||
|} | |||
Konstruksjonsbredden på | '''<big>Konstruksjonsbredden i et valgt punkt på lokomotivet</big>''' | ||
Det skal beregnes de tillatte konstruksjonsmål for et loddrett håndtak på siden av vognkassen. Håndtaket begynner 1,300 m og slutter 2,600 m over sporplan. Håndtaket sitter mellom boggisenterne i en avstand fra nærmeste boggisenter på 2,450 m. | |||
Det ble i eksemplet over fastlagt at lokomotivets utslag i kurve blir dimensjonerende og det beregnes etter formel 5.16 og 5.17. | |||
Først kontrolleres det om x<sub>i</sub> > 0. Det skjer ved å sette inn verdier i formel 5.17. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_i={1\over 750}(9,700*2,450-2.450^2+{2,800^2 \over 4}-100)+0,060-0,060=-0,1070 | |||
</math></center> || align="right" | | |||
|} | |||
Da verdien av x<sub>i</sub> er negativ inngår den med verdi 0 i formel 5.16. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i={9,700*2,450-2,450^2+{2,800^2 \over 4} \over 500} +{1,465-1,410\over 2}+0,006+0,006+z+0-0,030=0,1029+z | |||
</math></center> || align="right" | | |||
|} | |||
Deretter beregnes z for høyden 1,300 m og 2,600 m over sporplan. | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 10 Konstruksjonsbredde for håndtak | |||
|- | |||
!style="width:200px" | Høyde over sporplan | |||
!style="width:200px" | Halv bredde av referanselinje | |||
! style="width:200px" | E<sub>i</sub> - z | |||
! style="width:200px" | z | |||
! style="width:200px" | Mulig halv bredde for lokomotiv | |||
|- | |||
|1,300|| 1,645 ||0,1029|| 0,0027|| 1,5394 | |||
|- | |||
|2,600 ||1,645|| 0,1029 ||0,0070|| 1,5351 | |||
|} | |||
Håndtaket kan dermed plasseres 1,535 m fra spormidt. | |||
1, | |||
==== Innskrenkning for | ==== Innskrenkning for motorvogner==== | ||
Ved beregning av innskrenkningene E<sub>i</sub> og E<sub>a</sub> for motorvogner, inngår en avhengighet mellom spillrommet w og kurveradius. Formlene kan dermed benyttes uansett om det er lineær eller ikke-lineær endring av spillrommet w. | |||
Derimot skjelnes det mellom drivboggi og løpeboggi. Drivboggi er en boggi med påbygget motor/trekkraft på en eller fler av akslene. Løpeboggi er alle andre former for boggi. | |||
Ved beregning av innskrenkningen E for motorvogner anvendes ulike formler avhengig av boggitype, adhesjon og boggiens stilling i sporet, jf. tabell .4 - .7. Beregningsmetode framgår av tabell 11. | |||
{| class="wikitable" | |||
|+Tabell 11 Beregningsmetode som benyttes ved beregning av E for motorvogner | |||
|- | |||
!style="width:200px" |Motorvogn med | |||
!style="width:200px" |Adhesjonstall | |||
!style="width:200px" |Stilling i sporet | |||
!style="width:200px" | Beregnes som | |||
|- | |||
|to drivboggier | |||
|| μ ≥ 0,2 ||Tabell .4 - .7, tilfelle 2|| lokomotiv | |||
|- | |||
|to boggier som betraktes som løpeboggier|| 0 < μ < 0,2|| rowspan=2 |Tabell .4 og .6, tilfelle 2, og tabell .5 og .7, tilfelle 4||rowspan=2 | personvogn | |||
|- | |||
|en boggi som betraktes som løpeboggi og en løpeboggi || 0 < μ < 0,2 | |||
μ = 0 | |||
|- | |||
|en motorboggi og en løpeboggi eller en boggi som betraktes som løpeboggi || μ = 0,2 | |||
μ = 0 | |||
0 < μ < 0,2 | |||
| Tabell .4 - .7, tilfelle 3 | |||
| lokomotiv eller motorvogn<sup>2</sup> | |||
|} | |||
I formlene inngår adhesjonstallet μ. Avstanden fra det betraktede tverrsnitt til boggisentret i den drivende boggi betegnes n<sub>μ</sub>. | |||
'''Beregning av E<sub>i</sub>:''' | |||
Det benyttes den største innskrenkning beregnet ved hjelp av formel 5.22 og 5.23. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i={1,465-d\over 2}+q+w_\infty{a-n_\mu\over a}+w'_\infty{n_\mu\over a}+z-0,015 | |||
</math></center> || align="right" | (5.22) | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i=({an_\mu-n_\mu^2+{p^2\over 4} \ {a-n_\mu\over a}+{p'^2\over4} \ {n_\mu\over a}\over 500})+({1,465-d\over 2} \ {a-n_\mu\over a})+q+w_{i(250)}{a-n_\mu\over a}+w'_{i(250)}{n_\mu\over a}+z+[x_i]_{>0}-0,010^*/0,015^{**}-0,015{a-n_\mu\over a} | |||
</math></center> || align="right" | (5.23) | |||
|} | |||
I formel 5.23 inngår x<sub>i</sub> som beregnes som | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_i={1\over 750}(an_\mu-n_\mu^2+{p^2\over 4} \ {a-n_\mu\over a} + {p'^2\over 4} \ {n_\mu\over a}-100)+(w_{i(150)}-w_{i(250)}){a-n_\mu\over a}+(w'_{i(250)}-w'_{i(150)}){n_\mu\over a} | |||
</math></center> || align="right" | (5.24) | |||
|} | |||
'''Beregning av Ea:''' | |||
For tverrsnitt utenfor boggisentrene skjelnes det mellom om motorvogna kjørerer med drivboggien eller med løpeboggien forrest. Det benyttes ulike formler i de to tilfeller. | |||
Dersom motorvogna kjører med drivboggien forrest i kjøreretningen, anvendes den av formel .25 og .26 som gir størst verdi. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a=({1,465-d\over 2}+q){2n+a\over a}+w_\infty{n+a\over a}+w'_\infty{n\over a}+z-0,015 | |||
</math></center> || align="right" | (5.25) | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a=({an+n^2-{p^2\over 4} \ {n+a\over a}+{p'^2\over4} \ {n\over a}\over500})+({1,465-d\over 2} \ {n+a\over a})+q{2n+a\over a}+w'_{i(250)}{n\over a}+w_{a(250)}{n+a\over a} +z+[x_a]_{>0}-0,025^*70,030^{**} | |||
</math></center> || align="right" | (5.26) | |||
|} | |||
I formel 5.26 inngår x<sub>a</sub> som beregnes som | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_a={1\over 750}(an+n^2-{p^2\over 4} \ {n+a\over a}+{p'^2\over 4} \ {n\over a}-120)+(w'_{i(150)}-w'_{i(250)}){n\over a}+(w_{a(150)}-w_{a(250)}){n+a\over a} | |||
</math></center> || align="right" | (5.27) | |||
|} | |||
Dersom motorvogna kjører med løpeboggien forrest i kjøreretningen, anvendes den av formel og som gir størst verdi. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a=({1,465-d\over 2}+q){2n+a\over a}+w_\infty{n\over a}+w'_\infty{n+a\over a}+z-0,015 | |||
</math></center> || align="right" | (5.28) | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a=({an+n^2-{p^2\over 4} \ {n\over a}+{p'^2\over4} \ {n+a\over a}\over500})+({1,465-d\over 2} +q){2n+a\over a}+w_{i(250)}{n\over a}+w'_{a(250)}{n+a\over a} +z+[x_a]_{>0}-0,025^*70,030^{**} | |||
</math></center> || align="right" | (5.29) | |||
|} | |||
I formel 5.29 inngår x<sub>a</sub> som beregnes som | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_a={1\over 750}(an+n^2-{p^2\over 4} \ {n\over a}+{p'^2\over 4} \ {n+a\over a}-120)+(w_{i(150)}-w_{i(250)}){n\over a}+(w'_{a(150)}-w'_{a(250)}){n+a\over a} | |||
</math></center> || align="right" | (5.30) | |||
|} | |||
'''Regneeksempel:''' | |||
Alle beregninger utføres for høyder over 0,400 m. | |||
Motorvognas parametre: | |||
a = 15,400 m, d = 1,420 m, q = 0,002, s = 0,35, n<sub>i</sub> = 7,700 m, n<sub>a</sub> = 2,750 m, | |||
h<sub>c</sub> = 0,500 m, p = 2,400 m, p’ = 2,200 m, | |||
w<sub>∞</sub> = 0,060, wi(250) = 0,022, wa(250) = 0,046, | |||
w’<sub>∞</sub> = 0,050, w’<sub>i(250)</sub> = 0,020, w’<sub>a(250)</sub> = 0,050, | |||
η<sub>0</sub> < 1˚, μ > 0,2 for drivboggi, μ = 0 for løpeboggi | |||
Med de verdier av μ som er angitt skal motorvogna beregnes som lokomotiv med mindre det er spesielt viktig å utnytte profilet maksimalt, jf. tabell 11. For å eksemplifisere beregningsmetoden for motorvogner tas det utgangspunkt i et slikt tilfelle. | |||
'''<big>Konstruksjonsbredden på midten av motorvogna:</big>''' | |||
Det benyttes ved beregningene n = n<sub>i</sub> = n<sub>μ</sub> = a/2 = 7,700 m. | |||
Først bergnes E<sub>i</sub> etter formel .22. | |||
= | {|width="100%" | ||
|- | |||
|<center><math> | |||
E_i={1,465-1,420\over 2}+0,002+0,060{15,400-7,700\over 15,400}+0,050{7,700\over 15,400}+z-0,015=0,0645+z | |||
= | </math></center> || align="right" | | ||
|} | |||
For å regne ut E<sub>i</sub> etter formel 5.23 må først x<sub>i</sub> beregnes etter formel .24. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_i={1\over 750}(15,400*7,700-7,700^2+{2,400^2\over 4} \ {15,400-7,700\over 15,400}+{2.200^2\over 4} \ {7,700\over 15,400}-100)+(0,022-0,022){15,400-7,700\over 14,400}+(0,020-0,020){7,700\over 15,400}=-0,0524 | |||
= | </math></center> || align="right" | | ||
|} | |||
Merk at siden verdien av w<sub>i(150)</sub> og w’<sub>i(150)</sub> ikke er kjent, settes de til samme verdi som for radius 250. Dette gir en noe større verdi for E og man er på ”sikker side”. | |||
Verdien av x<sub>i</sub> er negativ og inngår dermed med verdien 0 i formel 5.23. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i=({15,400*7,700-7,700^2+({2,400^2\over 4} \ {15,400-7,700\over 15,400})+{(2,200^2\over 4} \ {7,700\over 15,400}\over 500})+({1,465-1,420\over 2} \ {15,400-7,700\over 15,400})+0,002+0,002{15,400-7,700\over 15,400}+0,020{7,700\over 15,400}+z-0-0,015-0,015{15,400-7,700\over15,400}=0,1330+z | |||
</math></center> || align="right" | | |||
|} | |||
Det skal benyttes den største av de beregnede innskrenkninger, dvs. 0,1330 + z. | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 12 Konstruksjonsbredden på midten av motorvogna | |||
|- | |||
!style="width:200px" | Høyde over sporplan | |||
!style="width:200px" | Halv bredde av referanselinje | |||
! style="width:200px" | E<sub>i</sub> - z | |||
! style="width:200px" | z | |||
! style="width:200px" | Mulig halv bredde for lokomotiv | |||
|- | |||
|0,500|| 1,620 ||0,1330|| 0,0000|| 1,4870 | |||
|- | |||
|1,170 ||1,620|| 0,1330 ||0,0078|| 1,4792 | |||
|- | |||
|1,170 ||1,645|| 0,1330|| 0,0078|| 1,5042 | |||
|- | |||
|3,250 ||1,645|| 0,1330|| 0,0321|| 1,4799 | |||
|- | |||
|3,700|| 1,425|| 0,1330|| 0,0373|| 1,2547 | |||
|- | |||
|4,010|| 1,120|| 0,1330|| 0,0410|| 0,9460 | |||
|- | |||
|4,310|| 0,525|| 0,1330|| 0,0445|| 0,3475 | |||
|} | |||
| Linje 1 808: | Linje 1 550: | ||
'''<big>Konstruksjonsbredde i den enden de drivboggien befinner seg</big>''' | |||
Det kontrolleres vha. formel 5.27 om x<sub>a</sub> skal benyttes. | |||
= | {|width="100%" | ||
|- | |||
|<center><math> | |||
x_a={1\over 750} \left( 15,400*2,750+2,750^2-{2,400^2\over 4}*{2,750+15,400\over 15,400}+{2,200^2\over 4}*{2,750\over 15,400}-120\right)+(0,020-0,020)*{2,750\over 15,400}+(0,046-0,046)*{2,750+15,400\over 15,400} | |||
</math></center> || align="right" | | |||
|} | |||
Verdien av x<sub>a</sub> blir negativ og x<sub>a</sub> settes lik null i de videre beregninger. | |||
Deretter beregnes utslaget i enden av vognkassen. Det benyttes n = n<sub>a</sub> = 2,750. Først utføres beregning etter formel 5.25. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a=\left({1,465-1,420\over 2}+0,002\right)*{2*2,750+15,400\over 15,400} +0,060*{2,750+15,400\over 15,400}+0,050*{2,750\over 15,400}+z-0,015=0,0997+z | |||
</math></center> || align="right" | | |||
|} | |||
Deretter utføres beregning etter formel 5.26. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a=\left({15,400*2,750+2,750^2-\left({2,400^2\over4}*{2,750+15,400\over 15,400}\right)+{2,200^2\over 4}*{2,750\over 15,400}\over 500}\right)+\left({1,465-1,420\over 2}*{2,750+15,400\over 15,400}\right)+0,002*{2*2,750+15,400\over 15,400}+0,020*{2,750\over15,400}+0,046*{2,750+15,400\over 15,400}+z+0-0,030=0,1541+z | |||
1, | |||
0, | |||
0, | |||
0, | |||
0, | |||
</math></center> || align="right" | | |||
|} | |||
= | Det skal benyttes den største verdi for E<sub>a</sub>, dvs. E<sub>a</sub> = 0,1541 + z. | ||
Tabell | {| class="wikitable" style="text-align:center" | ||
|+Tabell 5.13 Konstruksjonsbredden i den enden som drivboggien befinner seg | |||
|- | |||
!style="width:200px" | Høyde over sporplan | |||
!style="width:200px" | Halv bredde av referanselinje | |||
! style="width:200px" | E<sub>i</sub> - z | |||
! style="width:200px" | z | |||
! style="width:200px" | Mulig halv bredde for lokomotiv | |||
|- | |||
|0,500|| 1,620|| 0,1541|| 0,0000 ||1,4659 | |||
|- | |||
|1,170|| 1,620|| 0,1541|| 0,0078 ||1,4581 | |||
|- | |||
|1,170|| 1,645|| 0,1541|| 0,0078|| 1,4831 | |||
|- | |||
|3,250|| 1,645|| 0,1541|| 0,0321|| 1,4588 | |||
|- | |||
|3,700|| 1,425|| 0,1541|| 0,0373|| 1,2336 | |||
|- | |||
|4,010|| 1,120|| 0,1541|| 0,0410|| 0,9249 | |||
|- | |||
|4,310|| 0,525|| 0,1541|| 0,0445|| 0,3264 | |||
|} | |||
'''<big>Konstruksjonsbredde i den enden de løpeboggien befinner seg</big>''' | |||
Også ved denne beregningen inngår x<sub>a</sub>, men den er tidligere beregnet til negativ og inngår i formlene med verdi 0. | |||
Deretter beregnes utslaget i enden av vognkassen. Det benyttes n = n<sub>a</sub> = 2,750. Først utføres beregning etter formel 5.28. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a=\left({1,465-1,420\over 2}+0,002\right)*{2*2,750+15,400\over 15,400} +0,060*{2,750\over 15,400}+0,050*{2,750+15,400\over 15,400}+z-0,015=0,0912+z | |||
</math></center> || align="right" | | |||
|} | |||
Deretter utføres beregning etter formel 5.29. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a=\left({15,400*2,750+2,750^2-{2,400^2\over4}*{2,750\over 15,400}-{2,200^2\over 4}*{2,750+15,400\over 15,400}\over 500}\right)+\left({1,465-1,420\over 2}+0,002\right)*{2*2,750+15,400\over 15,400}+0,022*{2,750\over 15,400}+0,050*{2,750+15,400\over 15,400}+z+0-0,030=0,1669+z | |||
</math></center> || align="right" | | |||
|} | |||
Det skal benyttes den største verdi for E<sub>a</sub>, dvs. E<sub>a</sub> = 0,1669 + z. | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 5.14 Konstruksjonsbredden i den enden løpeboggien befinner seg | |||
|- | |||
!style="width:200px" | Høyde over sporplan | |||
!style="width:200px" | Halv bredde av referanselinje | |||
! style="width:200px" | E<sub>i</sub> - z | |||
! style="width:200px" | z | |||
! style="width:200px" | Mulig halv bredde for lokomotiv | |||
|- | |||
|0,500|| 1,620|| 0,1669|| 0,0000 |||1,4531 | |||
|- | |||
|1,170 ||1,620 ||0,1669|| 0,0078|| 1,4453 | |||
|- | |||
|1,170|| 1,645|| 0,1669|| 0,0078|| 1,4703 | |||
|- | |||
|3,250|| 1,645|| 0,1669|| 0,0321|| 1,4460 | |||
|- | |||
|3,700|| 1,425|| 0,1669|| 0,0373|| 1,2208 | |||
|- | |||
|4,010|| 1,120|| 0,1669|| 0,0410|| 0,9121 | |||
|- | |||
|4,310|| 0,525|| 0,1669|| 0,0445|| 0,3136 | |||
|} | |||
==== Innskrenkning for personvogner==== | |||
Ved beregninger av innskrenkningene E<sub>i</sub> og E<sub>a</sub> for personvogner inngår en sammenheng mellom spillrommet w og kurveradius. | |||
Som personvogner regnes materiell til befordring av personer, reisegods og post samt mellomvogner og i visse tilfeller styrevogner i motorvognsett. | |||
'''Beregning av E<sub>i</sub>:''' | |||
Først beregnes uttrykkene | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
an-n^2+{p^2\over 4}-500(w_\infty-w_{i(250)}) | |||
</math></center> || align="right" | (5.31) | |||
|} | |||
og | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
250(1,465-d)-0 | |||
</math></center> || align="right" | (5.32) | |||
|} | |||
der 0 erstattes av 2,5 for høyder t.o.m. 0,400 m. | |||
Hvis uttrykket beregnet etter formel 5.31 er mindre enn eller lik uttrykket beregnet etter formel 5.32, er det personvognas utslag på rettlinje som er dimensjonerende. Det benyttes da følgende formel: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i={1,465-d\over 2}+q+w_\infty+z-0,015 | |||
</math></center> || align="right" | (5.33) | |||
|} | |||
Dersom det er personvognas utslag i kurve som er dimensjonerende, benyttes følgende formel: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i={an-n^2+{p^2\over 4}\over 500}+q+w_{i(250)}+z+[x_i]_{>0}-0,010^*/0,015^{**} | |||
</math></center> || align="right" | (5.34) | |||
|} | |||
I formel 5.34 inngår x<sub>i</sub> som beregnes etter følgende formel: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_i={1\over 750}(an-n^2+{p^2\over 4}-100)+w_{i(150)}-w_{i(250)} | |||
</math></center> || align="right" | (5.35) | |||
|} | |||
'''Beregning av E<sub>a</sub>:''' | |||
Først beregnes uttrykkene | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
an+n^2-{p^2\over 4}- 500[(w_\infty-w_{i(250)}){n\over a}+(w_\infty-w_{a(250)}){n+a\over a}] | |||
</math></center> || align="right" | (5.36) | |||
|} | |||
og | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
250(1,465-d){n\over a}+7,5 | |||
</math></center> || align="right" | (5.37) | |||
|} | |||
der 7,5 erstattes med 5,0 i høyder t.o.m. 0,400 m. | |||
Hvis uttrykket beregnet etter formel 5.36 er mindre enn eller lik uttrykket beregnet etter formel 5.37, er det personvognas utslag på rettlinje som er dimensjonerende. Det benyttes da følgende formel: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a=({1,465-d\over 2}+q+w_\infty){2n+a\over a}+z-0,015 | |||
</math></center> || align="right" | (5.38) | |||
|} | |||
Dersom det er personvognas utslag i kurve som er dimensjonerende, benyttes følgende formel: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a={an+n^2-{p^2\over 4}\over 500}+{1,465-d\over 2} \ {n+a\over a}+q{2n+a\over a}+w_{i(250)}{n\over a}+w_{a(250)}{n+a\over a}+z+[x_a]_{>0}-0,025^*/0,030^{**} | |||
</math></center> || align="right" | (5.39) | |||
|} | |||
I formel 5.39 inngår x<sub>a</sub> som beregnes etter følgende formel: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_a={1\over 750}(an+n^2-{p^2\over 4}-120)+(w_{i(150)}-w_{i(250)}){n\over a}+(w_{a(150)}-w_{a(250)}){n+a\over a} | |||
</math></center> || align="right" | (5.40) | |||
|} | |||
'''Regneeksempel:''' | |||
Alle beregninger utføres for høyder over 0,400 m. | |||
Personvognas parametre: | |||
a = 18,400 m, d = 1,410 m, q = 0,002, s = 0,3, | |||
n<sub>i</sub> = a/2 = 9,200 m, n<sub>a</sub> = 3,253 m, h<sub>c</sub> = 0,500 m, p = 2,560 m, | |||
0 | |||
w = 0,082, w<sub>i(250</sub>) = 0,040, w<sub>a(250)</sub> = 0,028, | |||
η0 < 1˚, μ > 0,2 for drivboggi, μ = 0 for løpeboggi | |||
'''<big>Konstruksjonsbredden på midten av personvogna</big>''' | |||
Først kontrolleres det om det er personvognas utslag på rettlinje eller i kurve som er dimensjonerende. Dette skjer ved beregning etter formlene 5.31 og 5.32. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
18,400*9,200-9,200^2+{2,560^2\over 4} -500(0,082-0,040)=65,28 | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
250(1465-1,410)-0=13,75 | |||
</math></center> || align="right" | | |||
|} | |||
Dette betyr at det er vognas utslag i kurve som er dimensjonerende og det beregnes etter formel 5.34. Her inngår x<sub>i</sub> dersom x<sub>i</sub> > 0. Derfor beregnes først x<sub>i</sub> etter formel 5.35. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_i={1\over 750}\left(18,400*9,200-9,200^2+{2,560^2\over 4}-100\right)+0,040-0,040 | |||
</math></center> || align="right" | | |||
|} | |||
Verdien av x<sub>i</sub> blir negativ og x<sub>i</sub> inngår med verdi lik 0 i de videre beregninger. | |||
Det beregnes etter formel 5.34. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i={18,400*9,200-9,200^2+{2,560^2\over 4}\over 500}+0,002+0,040+z+0-0,015=0,1996+z | |||
</math></center> || align="right" | | |||
|} | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 15 Konstruksjonsbredden på midten av personvogna | |||
|- | |||
!style="width:200px" | Høyde over sporplan | |||
!style="width:200px" | Halv bredde av referanselinje | |||
! style="width:200px" | E<sub>i</sub> - z | |||
! style="width:200px" | z | |||
! style="width:200px" | Mulig halv bredde for lokomotiv | |||
|- | |||
|0,500|| 1,620|| 0,1996|| 0,0000|| 1,4204 | |||
|- | |||
|1,170|| 1,620|| 0,1996|| 0,0067 ||1,4137 | |||
|- | |||
|1,170|| 1,645 ||0,1996|| 0,0067|| 1,4387 | |||
|- | |||
|3,250|| 1,645|| 0,1996|| 0,0275|| 1,4179 | |||
|- | |||
|3,700|| 1,425|| 0,1996|| 0,0320|| 1,1934 | |||
|- | |||
|4,010|| 1,120|| 0,1996|| 0,0351|| 0,8853 | |||
|- | |||
|4,310|| 0,525|| 0,1996|| 0,0381|| 0,2873 | |||
|} | |||
'''<big>Konstruksjonsbredden i enden av personvogna</big>''' | |||
Først kontrolleres det om det er personvognas utslag på rettlinje eller i kurve som er dimensjonerende. Dette skjer ved beregning etter formlene 5.36 og 5.37. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
18,400*3,253+3,253^2-{2,560^2\over 4}-500\left((0,082-0,040){3,253\over 18,400}+(0,082-0,028){3.353+18,400\over 18,400}\right)=33,31 | |||
0 | |||
0 | |||
0 | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
250(1,465-1,410)*{3,253\over 18,400} +4,5=9,93 | |||
</math></center> || align="right" | | |||
|} | |||
Dette betyr at det er vognas utslag i kurve som er dimensjonerende og det beregnes etter formel 5.39. Her inngår x<sub>i</sub> dersom x<sub>i</sub> > 0. Derfor beregnes først x<sub>i</sub> etter formel 5.40. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_a={1\over 750} \left(18,400*3,253+2,253^2-{2,560^2\over 4} -120 \right)+(0,040-0,040){3,253\over 18,400}+(0,028-0,028){3,253+18,400\over 18,400} | |||
</math></center> || align="right" | | |||
|} | |||
Verdien av x<sub>i</sub> blir negativ og x<sub>i</sub> inngår med verdi lik 0 i de videre beregninger | |||
Verdien av innskrenkningen ved vognenden 3,253 m fra boggisenter blir da: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a={18,400*3,253+3,253^2-{2,560^2\over 4}\over 500}+\left({1,465-1,410\over 2}\right)\left({3,253+18,400\over 18,400}\right)+0,002\left({2*3,253+18,400\over 18,400} \right)+0,040{3,253\over 18400}+0,028{3,253+18,400\over 18,400}+z+0-0,030=0,1827+z | |||
</math></center> || align="right" | | |||
|} | |||
==== | {| class="wikitable" style="text-align:center" | ||
|+Tabell 16 Konstruksjonsbredden i enden av personvogna | |||
|- | |||
!style="width:200px" | Høyde over sporplan | |||
!style="width:200px" | Halv bredde av referanselinje | |||
! style="width:200px" | E<sub>i</sub> - z | |||
! style="width:200px" | z | |||
! style="width:200px" | Mulig halv bredde for lokomotiv | |||
|- | |||
|0,500|| 1,620|| 0,1827|| 0,0000|| 1,4373 | |||
|- | |||
|1,170|| 1,620|| 0,1827|| 0,0067|| 1,4306 | |||
|- | |||
|1,170|| 1,645|| 0,1827|| 0,0067|| 1,4556 | |||
|- | |||
|3,250|| 1,645|| 0,1827|| 0,0275|| 1,4348 | |||
|- | |||
|3,700|| 1,425|| 0,1827|| 0,0320|| 1,2103 | |||
|- | |||
|4,010|| 1,120|| 0,1827|| 0,0351|| 0,9022 | |||
|- | |||
|4,310|| 0,525|| 0,1827|| 0,0381|| 0,3042 | |||
|} | |||
==== Innskrenkning for to-akslede vogner==== | |||
For beregning av E<sub>i</sub> og E<sub>a</sub> for to-akslede godsvogner er det ikke avhengig av spillrommet w og kurveradius. Hvis godsvogna har 3 aksler regnes alle mål og beregninger fra ytterakslene. | |||
'''Beregning av E<sub>i</sub>:''' | |||
Først beregnes verdien av uttrykket | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
an-n^2 | |||
= | </math></center> || align="right" | (5.41) | ||
|} | |||
Dersom verdien av uttrykket beregnet etter formel .41 er mindre eller lik 7,5 (5,0 for punkter med høyde t.o.m. 0,400 m), er det godsvognas utslag på rettlinje som er dimensjonerende. Det beregnes etter følgende formel: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i={1,465-d\over 2}+q+z-0,015 | |||
</math></center> || align="right" | (5.42) | |||
|} | |||
Dersom godsvognas utslag i kurve er dimensjonerende beregnes det etter følgende formel: | |||
= | {|width="100%" | ||
|- | |||
|<center><math> | |||
E_i={an-n^2\over 500}+{1,465-d\over 2}+q+z-0,025^*/0,030^{**} | |||
</math></center> || align="right" | (5.43) | |||
|} | |||
'''Beregning av E<sub>a</sub>:''' | |||
Først beregnes verdien av uttrykket | |||
= | {|width="100%" | ||
|- | |||
|<center><math> | |||
an+n^2 | |||
</math></center> || align="right" | (5.44) | |||
|} | |||
Dersom verdien av uttrykket beregnet etter .44 er mindre eller lik 7,5 (5,0 for punkter med høyde t.o.m. 0,400 m), er det godsvognas utslag på rettlinje som er dimensjonerende. Det beregnes etter følgende formel: | |||
= | {|width="100%" | ||
|- | |||
|<center><math> | |||
E_a=({1,465-d\over 2}+q){2n+a\over a}+z-0.015 | |||
</math></center> || align="right" | (5.45) | |||
|} | |||
Dersom godsvognas utslag i kurve er dimensjonerende beregnes det etter følgende formel: | |||
= | {|width="100%" | ||
|- | |||
|<center><math> | |||
E_a={an-n^2\over 500}+({1,465-d\over 2} +q){2n+a\over a}+z-0,025^*/0,030^{**} | |||
</math></center> || align="right" | (5.46) | |||
|} | |||
'''Regneeksempel:''' | |||
Alle beregninger utføres for høyder over 0,400 m. | |||
Godsvognas parametre: | |||
a = 8,000 m, d = 1,410 m, q = 0,023, s = 0,1, | |||
ni = a/2 = 4,000 m, na = 2,390 m, hc = 0,500 m, | |||
η0 < 1˚, w = 0 (ingen boggi) | |||
'''<big>Konstruksjonsbredden på midten av godsvogna</big>''' | |||
Beregning etter formel .41 gir | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
8,000*4,000-4,000^2=16,000 | |||
</math></center> || align="right" | | |||
|} | |||
Verdien er større enn 7,5 og det er vognas stilling i kurve som er dimensjonerende. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i={8,000*4,000-4,000^2\over 500}+{1,465-1,410\over 2}+0,023+z-0,030=0,0525+z | |||
</math></center> || align="right" | | |||
|} | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 17 Konstruksjonsbredden på midten av godsvogna | |||
|- | |||
!style="width:200px" | Høyde over sporplan | |||
!style="width:200px" | Halv bredde av referanselinje | |||
! style="width:200px" | E<sub>i</sub> - z | |||
! style="width:200px" | z | |||
! style="width:200px" | Mulig halv bredde for lokomotiv | |||
|- | |||
|0,500|| 1,620|| 0,0525|| 0,0000|| 1,5675 | |||
|- | |||
|1,170|| 1,620|| 0,0525|| 0,0022|| 1,5653 | |||
|- | |||
|1,170|| 1,645|| 0,0525|| 0,0022|| 1,5903 | |||
|- | |||
|3,250|| 1,645|| 0,0525|| 0,0092|| 1,5833 | |||
|- | |||
|3,700|| 1,425|| 0,0525|| 0,0107|| 1,3618 | |||
|- | |||
|4,010|| 1,120|| 0,0525|| 0,0117|| 1,0558 | |||
|- | |||
|4,310|| 0,525|| 0,0525|| 0,0127|| 0,4598 | |||
|} | |||
'''<big>Konstruksjonsbredden i enden av godsvogna</big>''' | |||
Beregning etter formel 5.44 gir: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
8,000*2,390+2,390^2=24,832 | |||
</math></center> || align="right" | | |||
|} | |||
Verdien er større enn 7,5 og det er vognas stilling i kurve som er dimensjonerende. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a={8,000*2,390-2,390^2\over 500}+({1,465-1,410\over 2}+0,023){2*2,390+8,00\over 8000}+z-0,030=0,0775+z | |||
+ | |||
+ | |||
+ | |||
= | |||
</math></center> || align="right" | | |||
|} | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 18 Konstruksjonsbredden i enden av godsvogna | |||
|- | |||
!style="width:200px" | Høyde over sporplan | |||
!style="width:200px" | Halv bredde av referanselinje | |||
! style="width:200px" | E<sub>i</sub> - z | |||
! style="width:200px" | z | |||
! style="width:200px" | Mulig halv bredde for lokomotiv | |||
|- | |||
|0,500|| 1,620|| 0,0775|| 0,0000|| 1,5425 | |||
|- | |||
|1,170|| 1,620|| 0,0775|| 0,0022|| 1,5403 | |||
|- | |||
|1,170|| 1,645|| 0,0775|| 0,0022|| 1,5653 | |||
|- | |||
|3,250|| 1,645|| 0,0775|| 0,0092|| 1,5583 | |||
|- | |||
|3,700|| 1,425|| 0,0775|| 0,0107|| 1,3368 | |||
|- | |||
|4,010|| 1,120|| 0,0775|| 0,0117|| 1,0308 | |||
|- | |||
|4,310|| 0,525|| 0,0775|| 0,0127|| 0,4348 | |||
|} | |||
==== Innskrenkning for godsvogner med boggier==== | |||
For selve boggien og deler i fast forbindelse med denne, benyttes formlene for 2-akslede vogner. | |||
'''Beregning av E<sub>i</sub>:''' | |||
Først beregnes uttrykkene | |||
= | {|width="100%" | ||
|- | |||
|<center><math> | |||
an-n^2+{p^2\over 4} | |||
</math></center> || align="right" | (5.47) | |||
|} | |||
og | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
250(1,454-d)-0 | |||
</math></center> || align="right" | (5.48) | |||
|} | |||
der 0 erstattes av 2,5 for høyder t.o.m. 0,400 m. | |||
Hvis uttrykket beregnet etter formel .47 er mindre enn eller lik uttrykket beregnet etter formel .48, er det godsvognas utslag på rettlinje som er dimensjonerende. Det benyttes da følgende formel: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i={1,465-d\over 2} +q+w+z-0,015 | |||
</math></center> || align="right" | (5.49) | |||
|} | |||
Dersom det er personvognens utslag i kurve som er dimensjonerende, benyttes følgende formel: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_i={an-n^2+{p^2\over 4}\over 500}+q+w+z+[x_i]_{>0}-0,010^*/0,015^{**} | |||
</math></center> || align="right" | (5.50) | |||
|} | |||
I formel .50 inngår x<sub>i</sub> som beregnes etter følgende formel: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_i={1\over 750}(an-n^2+{p^2\over 4}-100) | |||
</math></center> || align="right" | (5.51) | |||
|} | |||
'''Beregning av E<sub>a</sub>:''' | |||
Først beregnes uttrykkene | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
an+n^2-{p^2\over 4} | |||
</math></center> || align="right" | (5.52) | |||
|} | |||
og | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
250(1,465-d){n\over a}+7,5 | |||
</math></center> || align="right" | (5.53) | |||
|} | |||
der 7,5 erstattes med 5,0 i høyder t.o.m. 0,400 m. | |||
Hvis uttrykket beregnet etter formel .52 er mindre enn eller lik uttrykket beregnet etter formel .53, er det godsvognas utslag på rettlinje som er dimensjonerende. Det benyttes da følgende formel: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E_a=({1,465-d\over 2}+q+w){2n+a\over a}+z-0,015 | |||
</math></center> || align="right" | (5.54) | |||
|} | |||
Dersom det er godsvognas utslag i kurve som er dimensjonerende, benyttes følgende formel: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
[ | E_a={an+n^2-{p^2\over 4}\over 500}+{1,465-d\over 2} \ {n+a\over a}+(q+w){2n+a\over a}+z+[x_a]_{>0}-0.025^*/0,030^{**} | ||
</math></center> || align="right" | (5.55) | |||
|} | |||
I formel .55 inngår x<sub>a</sub> som beregnes etter følgende formel: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
x_a={1\over 750}(an+n^2-{p^2\over 4}-120) | |||
</math></center> || align="right" | (5.56) | |||
|} | |||
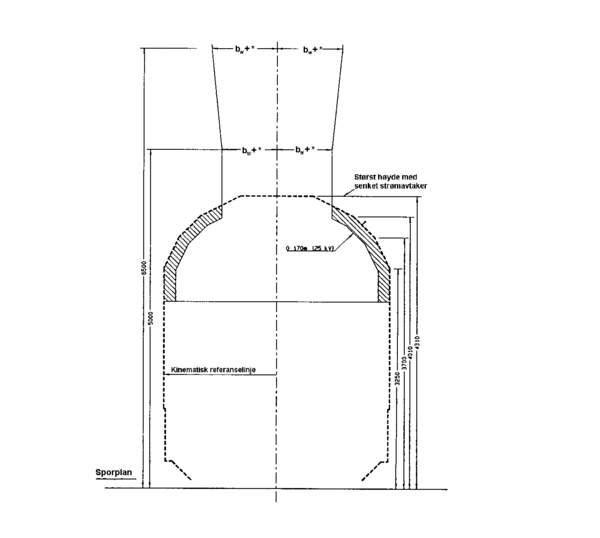
==== Gjenstander på taket av elektrisk materiell==== | |||
For | For gjenstander på taket av elektrisk materiell gjelder en egen referanselinje, jf. figur 7. Denne referanselinjen er tenkt benyttet til gjenstander i forbindelse med strømavtakeren og øvrige spenningsførende komponenter samt alle ikke-spenningsførende komponenter. | ||
Beregning av ytterstilling for strømavtakere på elektriske motorvogner med en drivboggi og en løpeboggi, skal utføres som om motorvognen har to boggier av samme type som den strømavtakeren sitter over. | |||
For å sikre at strømavtakeren alltid holder seg innenfor referanselinjen for spenningsførende deler, må det utføres en beregning av innskrenkningen E. Det beregnes innskrenkning med strømavtakeren hevet til høyde 6,50 m over sporplan (E’<sub>i</sub> og E’<sub>a</sub>) og til høyde 5,00 m over sporplan (E’’<sub>i</sub> og E’’<sub>a</sub>). Dersom beregningene viser at den relevante innskrenkning E’ hhv. E’’ er negativ eller 0 er referanselinjen overholdt. Dette vil alltid være tilfelle når strømavtakeren strømavtakeren er plassert over boggisenteret. | |||
6, | |||
'''Innledende beregninger:''' | |||
Først beregnes j’, dvs. differansen mellom den beregnede og den virkelige forskyvning som følge av spillrom. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
j'_i=q+w_i-0,0375 | |||
</math></center> || align="right" | (5.57) | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
j'_a=q{2n+a\over a}+w_a{n+a\over a}+w_i{n\over a}-0,0375 | |||
</math></center> || align="right" | (5.58) | |||
|} | |||
Deretter beregnes z’, dvs. differansen mellom den beregnede rulling og den virkelige forskyvning som følge av rulling av det øverste punktet på strømavtakeren. | |||
Hvis rullvinkelkoeffisienten s ≤ 0,225 benyttes formelen: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
z'={8\over30}(s-0,225)+(t-0,03)+(\tau-0,01)+6(\Theta -0,05) | |||
</math></center> || align="right" | (5.59) | |||
|} | |||
[[Fil:Fig531-535.png|600px|thumb||center|<caption>Figur 35 Frittromsprofil for PXXX</caption>]] | |||
Hvis s > 0,225 benyttes formelen: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
z'={8\over10}(s-0,225)+(t-0,03)+(\tau-0,01)+6(\Theta -0,05) | |||
</math></center> || align="right" | (5.60) | |||
|} | |||
Deretter beregnes z’’, dvs. differansen mellom den beregnede rulling og den virkelige forskyvning som følge av rulling av den øverste delen av strømavtakeren. | |||
Hvis rullvinkelkoeffisienten s ≤ 0,225 benyttes formelen: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
z''={6\over30}s+\sqrt{t\left({h-h_t\over6,5-h_t}\right)^2+\tau^2+\left\vert\Theta(h-h_c)\right\vert^2-0,0925} | |||
</math></center> || align="right" | (5.61) | |||
|} | |||
Hvis s > 0,225 benyttes formelen: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
z''={6\over10}s+\sqrt{t\left({h-h_t\over6,5-h_t}\right)^2+\tau^2+\left\vert\Theta(h-h_c)\right\vert^2-0,1825} | |||
</math></center> || align="right" | (5.62) | |||
|} | |||
'''Beregning av innskrenkningen E mellom boggisentrene:''' | |||
Ved beregningen av E må det først finnes ut om det er innstillingen av materiellet i kurve eller på rettlinje som er dimensjonerende. Det beregnes E’<sub>i</sub> og E”<sub>i</sub> med n = n<sub>i</sub>. | |||
Dersom an – n² + (p²/4) ≤ 5 er det innstillingen på rettlinje som er dimensjonerende. Det anvendes følgende formler: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E'_i=j'_i+z' \ \ \ for \ h=6,5m | |||
</math></center> || align="right" | (5.63) | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E''_i=j'_i+z'' \ \ \ for \ h=5,0m | |||
</math></center> || align="right" | (5.64) | |||
|} | |||
Dersom an – n² + (p²/4) > 5 er det innstillingen i kurve som er dimensjonerende. Det anvendes følgende formler: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E'_i={an-n^2+{p^2\over4}-5\over300}+j'_i+z' \ \ \ for \ \ h=6,5m | |||
</math></center> || align="right" | (5.65) | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E''_i={an-n^2+{p^2\over4}-5\over300}+j'_i+z'' \ \ \ for \ \ h=5,0m | |||
</math></center> || align="right" | (5.66) | |||
|} | |||
'''Beregning av innskrenkningen E utenfor boggisentrene:''' | |||
Ved beregningen av E må det først finnes ut om det er innstillingen av materiellet i kurve eller på rettlinje som er dimensjonerende. Det beregnes E’<sub>i</sub> og E”<sub>i</sub> med n = n<sub>a</sub>. | |||
Dersom an + n² - (p²/4) ≤ 5 er det innstillingen på rettlinje som er dimensjonerende. Det anvendes følgende formler: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E'_a=j'_a+z'+{1,465-d\over 2} \ {2n\over a} \ \ \ for \ \ h=6,5m | |||
</math></center> || align="right" | (5.67) | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E''_a=j'_a+z''+{1,465-d\over 2} \ {2n\over a} \ \ \ for \ \ h=5,0m | |||
</math></center> || align="right" | (5.68) | |||
|} | |||
Dersom an + n² - (p²/4) > 5 er det innstillingen i kurve som er dimensjonerende. Det anvendes følgende formler: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E'_a={an+n^2-{p^2\over4}-5\over300}j'_a+z'+{1,465-d\over 2} \ {2n\over a} \ \ \ for \ \ h=6,5m | |||
</math></center> || align="right" | (5.69) | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
E'_a={an+n^2-{p^2\over4}-5\over300}j'_a+z''+{1,465-d\over 2} \ {2n\over a} \ \ \ for \ \ h=5,0m | |||
</math></center> || align="right" | (5.70) | |||
|} | |||
Når strømavtakeren er senket, skal referanselinjen for strømavtakere også være overholdt. Dersom materiellet skal framføres på ikke-elektrifiserte, skal den gjeldende referanselinjen for strekningen overholdes. | |||
Alle de deler på taket av materiellet som ikke er isolert og som kan være strømførende, skal være plassert slik at de ligger 0,170 m fra referanselinjen. | |||
== Frittromsprofiler== | |||
Frittromsprofiler angir hvor nær et objekt (bru, signal, fjell, plattform, skilt osv.) kan være sporet. | |||
=== Tillegg til referanselinjens horisontale mål=== | |||
I dette avsnittet beskrives de beregningsmetoder som beskrives i UIC fiche 505-4. | |||
==== Geometrisk utslag==== | |||
Det geometriske utslag beregnes som de ekstra bevegelser som opptrer når toget kjører gjennom kurver pga. materiellets gangegenskaper . Utslaget vil dermed bestå av et radiusavhengig og et sporviddeavhengig ledd. | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 5.19 Økning av frittromsprofilets breddemål i kurver | |||
|- | |||
!style="width:400px" | Høyde over sporplan | |||
!style="width:400px" | Utslag [mm] | |||
|- | |||
|∞ - 1500|| 0 | |||
|- | |||
|1499 – 500 ||5 | |||
|- | |||
|499 – 300|| 10 | |||
|- | |||
|299 – 250|| 15 | |||
|- | |||
|249 – 240|| 25 | |||
|- | |||
|239 – 230 ||35 | |||
|- | |||
|229 – 220|| 50 | |||
|- | |||
|219 – 210|| 60 | |||
|- | |||
|209 – 200|| 75 | |||
|- | |||
|199 – 190|| 90 | |||
|- | |||
|189 – 180|| 110 | |||
|- | |||
|179 – 170|| 130 | |||
|- | |||
|169 – 160|| 150 | |||
|- | |||
|159 – 150|| 175 | |||
|- | |||
|149 – 140|| 205 | |||
|- | |||
|139 – 130 ||235 | |||
|- | |||
|129 – 120|| 275 | |||
|} | |||
Følgende mål skal ikke økes: | |||
*målene m og n rundt skinnehodet | |||
*alle mål i el-profiler da strømavtakeren er plassert over boggien | |||
==== Semistatisk forskyvning==== | |||
Den semistatiske forskyvningen avhenger av overhøydeoverskuddet E eller manglende overhøyde I og som derfor ikke kan innberegnes i innskrenkningen E til materiellet. Da forskyvningen I egentlig er en dreining, inngår det betraktede punkts høyde (h) over sporplan i formelen. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
{0,4\over1,5}*[E \ eller \ I-0,05]_{>0}*[h-0,5]_{>0} | |||
</math></center> || align="right" | (5.71) | |||
|} | |||
Ved beregning av materiell etter UIC fiche 505-1 inngår E hhv. I = 0,05 m i beregningen av materiellet. Det må derfor regnes med et ytterligere tillegg dersom E hhv. I er > 0,05 m. | |||
==== Feil i sporets beliggenhet==== | |||
Feil i sporets beliggenhet skyldes forskyvning av sporet i sideretning pga. driftsmessige forhold og måles som hvor langt ut spormidt kan bevege seg i forhold til skal-beliggenheten. Maksimal grense for en slik forskyvning er anbefalt av UIC å være ± 0,025 m. | |||
==== Virkning av overhøydefeil==== | |||
Dersom det skjer en fullstendig avbalansering av sentrifugalkraften gjennom overhøyden, snakker man om likevektsoverhøyde. Ved alle andre tilfeller har man overhøydeoverskudd E eller manglende overhøyde I (”overhøydefeil”). | |||
Overhøydeoverskudd har man når den aktuelle overhøyden er større enn den avbalanserte overhøyden. Materiellet vil krenge innover i kurven. | |||
Manglende overhøyde har man når den aktuelle overhøyden er mindre enn den avbalanserte overhøyden. Materiellet vil krenge utover i kurven. | |||
For spor med hastigheter > 80 km/h, regnes en dynamisk virkning av ”overhøydefeilen” på 0,015 m. Den tilsvarende geometriske virkning kan uttrykkes med | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
0,015{h\over1,5}=0,01h | |||
</math></center> || align="right" | (5.72) | |||
|} | |||
For spor med hastigheter ≤ 80 km/h, regnes en dynamisk virkning av ”overhøydefeilen” på 0,020 m. Den tilsvarende geometriske virkning kan uttrykkes med | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
0,020{h\over1,5}=0,0133h | |||
</math></center> || align="right" | (5.73) | |||
|} | |||
==== Dynamisk rulling==== | |||
Dynamisk rulling følger av den dynamiske vekselvirkning mellom spor og materiell. Denne rullingen er avhengig av sporets vedlikeholdsstandard. Hvert land fastsetter egne toleranser, men dersom de ikke foreligger har UIC gitt følgende tabell. | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 20 Utslag pga. dynamisk rulling grunnet sporets vedlikeholdsstandard | |||
|- | |||
!style="width:300px" | | |||
!style="width:300px"| Kurvens ytterside eller rettlinje | |||
!style="width:300px" | Kurvens innerside | |||
|- | |||
|Godt vedlikeholdt spor|| 0,039 m|| 0,007 m | |||
|- | |||
|Øvrige spor|| 0,065|| m 0,065 m | |||
|} | |||
==== Virkningen av materiellets skjevstilling==== | |||
Virkningen av materiellets skjevstilling som følge av konstruksjons- og innstillingstoleranser eller ujevn lastfordeling, skal innregnes i frittromsprofilene med 1˚. Skjevstillingen settes sammen av to ledd der eksentrisk nyttelast inngår med 0,050 m og unøyaktig fjærjustering inngår med 0,015 m. Summen av verdiene = 0,065 m, tilsvarer 1˚ skjevstilling. | |||
==== Nasjonelt tillegg==== | |||
Tillegget fastsettes av hver enkelt forvaltning bl.a. av hensyn til | |||
*spesialtransporter, konteinere, dobbeldekkere osv. | |||
*utseende av eksisterende frittromsprofiler | |||
*sikkerhetstillegg pga. økt hastighet | |||
*sikkerhetstillegg pga. sterk vind | |||
*utligningstillegg for å oppnå loddrette linjer i frittromsprofiler | |||
Det foreligger ingen standardisering for disse verdiene. | |||
==== Reduksjon av tillegg==== | |||
Tillegg pga. feil i sporets beliggenhet, virkning av overhøydefeil, dynamisk rulling og virkning av materiellets skjevstilling opptrer tilfeldig og behandles av den grunn statistisk. Summen av disse tilleggene betegnes Σ og beregnes som den kvadratiske middelverdi av summen med tillegg av 20 %, jf. UIC fiche 505, bilag F). På denne måten oppnår man en reduksjon av tilleggene. Denne reduksjonen gjelder bare punkter på referanselinjen over 0,500 m over sporplan. | |||
Regneeksempel: | |||
Tilfeldige bevegelser gir: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\sum=1,2\sqrt{(0,025)^2+\left[0,01h+{0,4\over 1,5}*0,015(h-0,5)\right]^2+\left({0,4\over1,5}\right)^2(0,039^2+0,065^2)(h-0,5)^2} | |||
</math></center> || align="right" | (5.72) | |||
|} | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 21 Tilfeldige bevegelser i høyde h over sporplan | |||
|- | |||
!style="width:300px"| h | |||
!style="width:300px" | Tilfeldige | |||
bevegelser | |||
|- | |||
|1,170|| 0,037 | |||
|- | |||
|3,530|| 0,090 | |||
|- | |||
|3,835|| 0,098 | |||
|- | |||
|4,680|| 0,120 | |||
|} | |||
=== Tillegg til referanselinjens vertikale mål=== | |||
Infrastrukturen korrigerer alle vertikale mål på referanselinjen med et spillrom som tar hensyn til vertikalkurvaturen. Dette gjøres ved at vertikale mål over 1,200 m over sporplan økes med 50000/R der R er vertikalradien. Vertikale mål under 1,200 m reduseres tilsvarende. I praksis beregnes det kun tillegg ved R < 10000 m. | |||
=== Beregning av konstruksjonsmål ut fra frittromsprofil - norsk beregningsmodell=== | |||
I dette avsnittet er det beskrevet hvordan beregningen av konstruksjonsmålene for rullende materiell er beregnet i Norge. Denne metoden ble beskrevet i forbindelse med anskaffelsen av B3-materiell og tok utgangspunkt i frittromsprofilet, jf, avsnitt 2.2.4. Konstruksjonsmålene fremkommer ved å beregne summen av innskrenkningen E og Σ. | |||
I E inngår også utslag som følge av kjøring gjennom overhøyderampen, jf. avsnitt 3.5.5. | |||
Den norske beregningsmodellen ble senere utviklet som et edb-program med navn PROFIL. Bestillinger av profilberegninger gjøres ved å fylle ut skjemaet som vist i tabell 22 . | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 22 Skjema for bestilling av profilberegninger | |||
|- | |||
!style="width:900px" colspan=7 | Til: ___________________________________ Fra: _______________________________ Dato: | |||
|- | |||
!style="width:900px" style="text-align:left"|Bestilling av profilberegning for | |||
|} | |||
{| class="wikitable" style="text-align:center" | |||
|- | |||
!style="width:100px"| | |||
!style="width:300px" | | |||
!style="width:100px"| | |||
!style="width:100px"|Alt 1 | |||
!style="width:100px" | Alt 2 | |||
!style="width:100px"| Alt 3 | |||
!style="width:100px" | Alt 4 | |||
|- | |||
|a|| Boggisenteravstand|| [m] || || || || | |||
|- | |||
|p ||Akselavstand i boggi|| [m]|| || || || | |||
|- | |||
|d|| Hjulsatsens min. sporvidde|| [mm]|| 1410|| 1410|| 1410|| 1410 | |||
|- | |||
|q|| Maks. fjærspill i primærfjæring ||[m]|| || || || | |||
|- | |||
|w ||Maks. fjærspill i sekundærfjæring|| [m]|| || || || | |||
|- | |||
|? x|| Avstand boggisenter til sidefjæring|| [m]|| || || || | |||
|- | |||
|k|| Kurvefaktor (k = ½ · a· ? x)|| [m<sup>2</sup>] || || || || | |||
|- | |||
|s ||Rullvinkelkoeffisient ||[-]|| || || || | |||
|- | |||
|h<sub>c</sub>|| Høyde til rullsenterover sporplan|| [m]|| || || || | |||
|- | |||
|ß ||Vognkassens stivhetskoeffisient ||[-] ||1|| 1|| 1|| 1 | |||
|- | |||
|?<sub>hA</sub>|| Vognkassens skjevstillingpga. eksentrisk nyttelast ||[rad]|| 0,009|| 0,009|| 0,009|| 0,009 | |||
|- | |||
|?<sub>HB</sub>|| Vognkassens skjevstillingpga. unøyaktig | |||
fjærjustering | |||
||[rad]|| 0,009|| 0,009 ||0,009|| 0,009 | |||
|- | |||
|R<sub>min</sub>|| Minste beregnede kurveradius|| [m]|| || || || | |||
|- | |||
|n<sub>i</sub> ||Snitt fra boggisenter mot vognmidte|| [m]|| || || || | |||
|- | |||
|n<sub>a</sub>|| Snitt fra boggisenter mot vognende|| [m]|| || || || | |||
|- | |||
|?|| y Beregningens vertikale trinnlengde|| [m]|| || || || | |||
|- | |||
|Y ||Beregningens vertikale område|| [m]|| || || || | |||
|- | |||
|colspan=7 | | |||
|- | |||
|style="text-align:left" colspan=7 |'''Beregningstilfeller:''' | |||
|- | |||
|A|| Toakslede vogner/lokomotiver|| || || || || | |||
|- | |||
|B|| Boggivogner uten motor|| || || || || | |||
|- | |||
|M<sub>2</sub>|| Boggimotorvogner og –lok med 2 motorboggier|| || || || || | |||
|- | |||
|style="text-align:left" colspan=7 |'''For boggimotorvogner og –lok med drift på bare en boggi gjelder:''' | |||
|- | |||
|M<sub>1L</sub>|| Snitt fra vognmidte mot løpeboggi|| [m] || || || || | |||
|- | |||
|M<sub>2L</sub>|| Snitt fra vognmidte mot drivboggi|| [m]|| || || || | |||
|- | |||
|style="text-align:left" colspan=7 | '''Krenging:''' | |||
|- | |||
|?<sub>k</sub> ||Maksimal krengevinkel|| [grd]|| || || || | |||
|- | |||
|h<sub>k</sub>|| Krengesenterhøyde over sporplan ||[m]|| || || || | |||
|- | |||
|} | |||
{| class="wikitable" style="text-align:center" | |||
|- | |||
!style="width:900px" colspan=7 style="text-align:left"|'''Radius-, overhøyde- og hastighetsdata:''' | |||
|- | |||
|style="width:50px"|R ||style="width:50px"|h||style="width:50px"| v1 + 5||style="width:50px"| I1||style="width:50px"| v2 ||style="width:50px"|I2||style="width:150px"| | |||
|- | |||
|[m]|| [m]|| [km/h]|| [m]|| [km/h]|| [m]|| | |||
|- | |||
|180|| 0,150|| 60|| 0,086|| || || | |||
|- | |||
|250|| 0,150|| 75 ||0,115|| || || | |||
|- | |||
|350|| 0,145 ||90 ||0,128|| || || | |||
|- | |||
|450|| 0,135|| 100|| 0,127|| || || | |||
|- | |||
|700|| 0,110|| 115|| 0,113|| || || | |||
|- | |||
|1000|| 0,080|| 125|| 0,104|| || || | |||
|- | |||
|8|| 0|| 125|| 0|| || || | |||
|} | |||
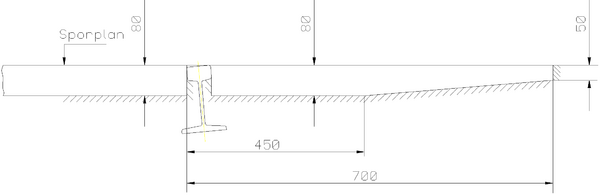
== Minste tverrsnitt== | |||
Utenfor frittromsprofilene er det definert et ytterligere profil som kalles minste tverrsnitt. Dette profilet kan i prinsippet ha innskrenkninger som befinner seg mellom minste tverrsnitt og frittromsprofilene. Minste tverrsnitt kan defineres som følger: | |||
Til hver side av sporet, over sporet og også mellom skinnene skal et visst rom være fritt for hindringer slik at man har den forutsatte klaring for fremføring av tog. Tverrsnittet av dette rom benevnes minste tverrsnitt. | |||
Måleaksen for minste tverrsnitt står vinkelrett på sporplanet i spormidt. | |||
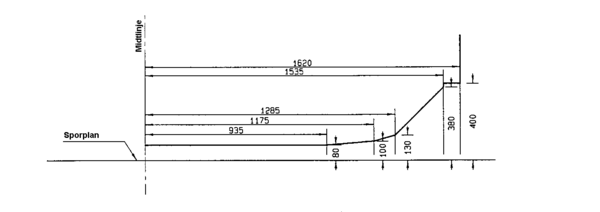
=== Fastsatte minste tverrsnitt for eksisterende baner=== | |||
De ulike banestrekningene har i sin tid blitt bygget med ulike tverrsnitt. Dette har ført til at man gjennom tiden har operert med en rekke forskjellige minste tverrsnitt. Ved fornyelsen av NSBs regelverk i 1993 ble det bestemt at man for eksisterende baner kun skulle operere med ett tverrsnitt, A-85. For nye baner valgte man å basere seg på et UIC-tverrsnitt benevnt UIC GC som samsvarte med tverrsnitt som ble anvendt hos enkelte andre forvaltninger. | |||
Fra og med 1998 ble to nye minste tverrsnitt innført:: A-96 og A-C. | |||
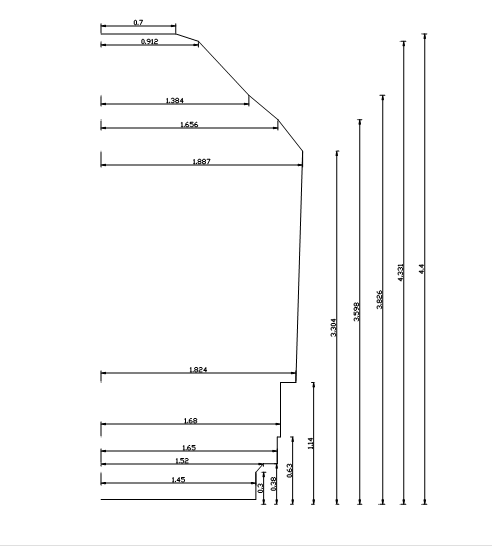
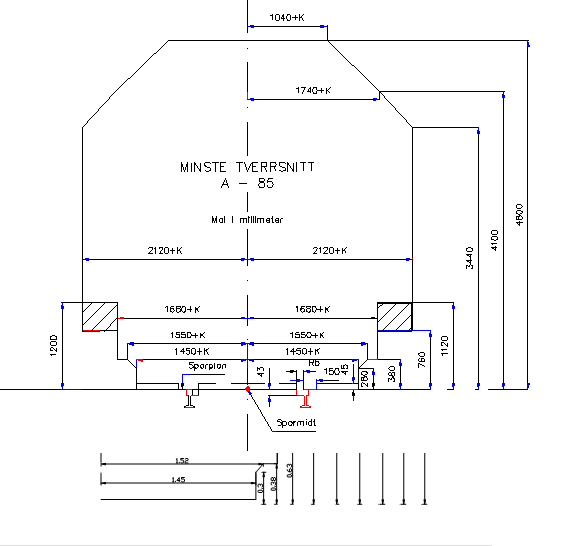
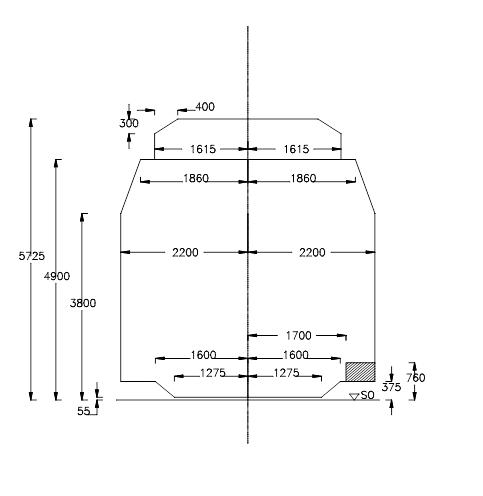
==== Minste tverrsnitt A-85==== | |||
Minste tverrsnitt A-85 ble innført 1985 og var den gang det største minste tverrsnitt. I tillegg ble det benyttet 3 mindre minste tverrsnitt for enkelte banestrekninger. I 1993 ble disse tverrsnittene fjernet og man A-85 ble innført på hele det norske jernbanenettet. Dermed fikk man langt flere innskrenkninger å forholde seg til. | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 23 Øvrige minste tverrsnitt fram til 1993 | |||
|- | |||
!style="width:300px"| Minste tverrsnitt | |||
!style="width:300px" | Strekning | |||
|- | |||
|RA-85 (redusert A-85)|| Myrdal – Bergen | |||
|- | |||
|B|| Nelaug – Arendal | |||
|- | |||
|C|| Sira – Flekkefjord | |||
|- | |||
|} | |||
I tillegg til minste tverrsnitt gjelder for elektrifiserte spor følgende profiler | |||
*fritt profil for strømavtaker | |||
*minste tverrsnitt E | |||
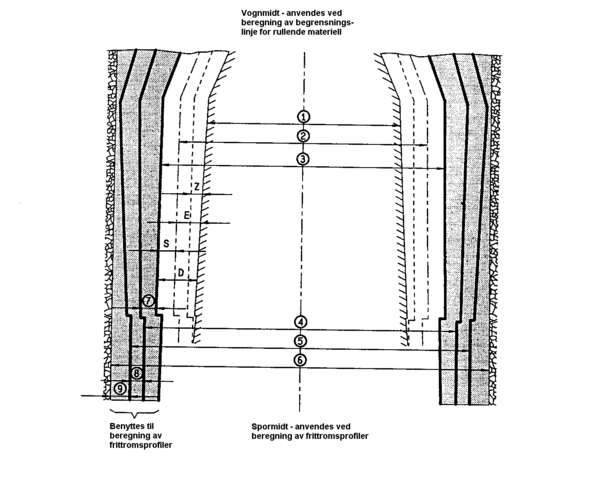
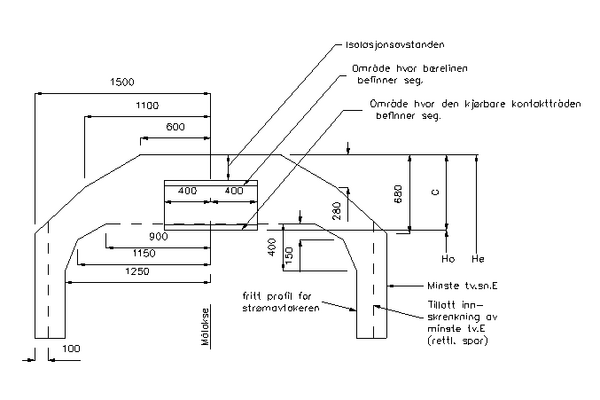
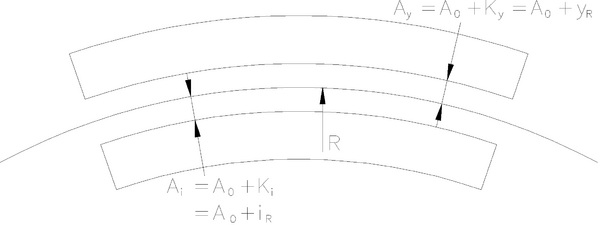
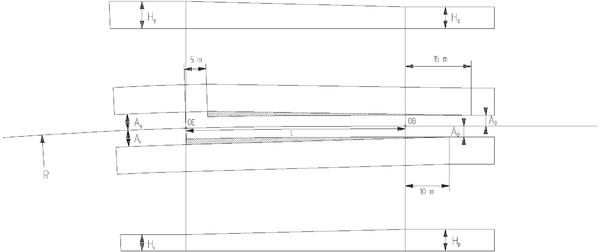
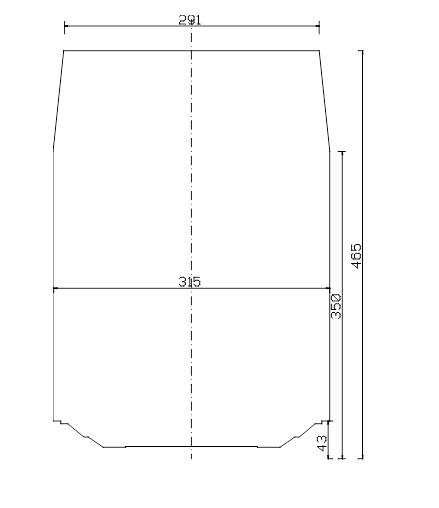
[[Fil:Fig531-514.png|600px|thumb||center|<caption>Figur 14 Minste tverrsnitt A-85</caption>]] | |||
K<sub>i</sub>= kurveutslag mot den indre siden av en kurve | |||
K<sub>y</sub> = kurveutslag mot den ytre siden av en kurve | |||
Det skraverte feltet er beskrevet i avsnitt 5.4. | |||
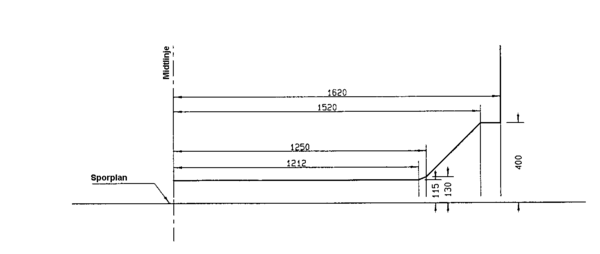
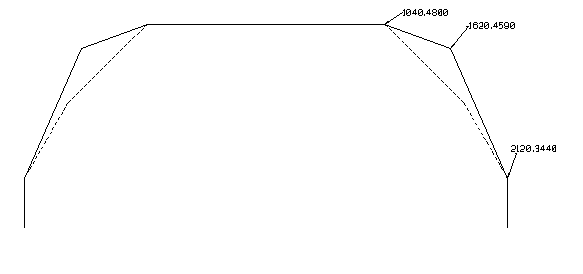
==== Minste tverrsnitt A-96==== | |||
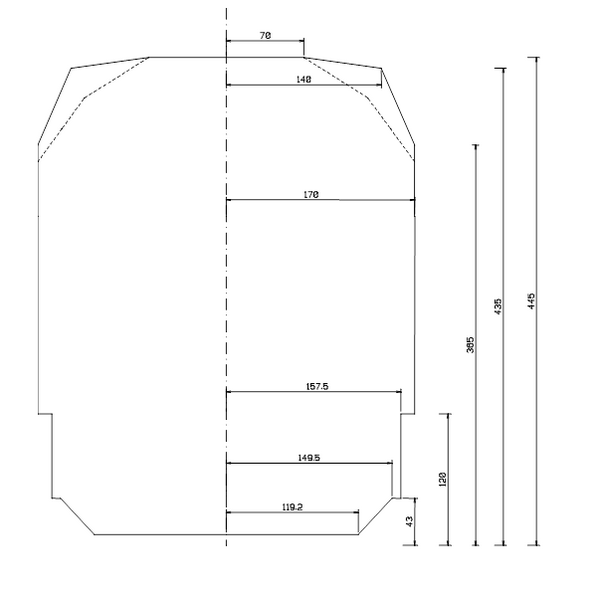
Minste tverrsnitt A-96 er definert som det minimumstverrsnitt som tillater framføring av transporter i henhold til lasteprofil K. Da lasteprofil K har samme bredde som utvidet lasteprofil for 2-akslede vogner under 3500 mm og samme høyde, kan A-96 stort sett sammenfalle med A-85. Kun punktet (1740,4100) må erstattes. A-96 får i stedet punktet (1620,4590) som er basert på at klaringen mellom A-96 og lasteprofil K ikke noe sted skal være mindre enn 300 mm. | |||
[[Fil:Fig531-515.png|600px|thumb||center|<caption>Figur 15 Minste tverrsnitt A-96, øvre del</caption>]] | |||
I tillegg kommer kurveutslag, jf. tabell 25 og tabell 26. | |||
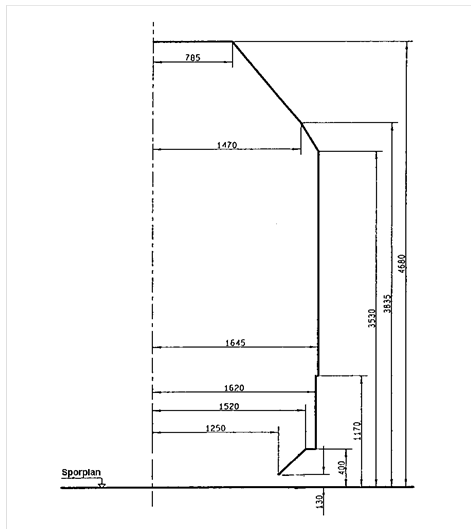
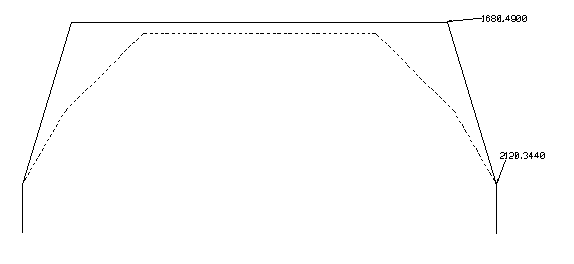
==== Minste tverrsnitt A-C==== | |||
Minste tverrsnitt A-C er tenkt som det minimumstverrsnitt som tillater framføring av transporter i henhold til lasteprofil UIC GC. Tverrsnittet sammenfaller med A-85 lavere enn 3440 mm over skinnetopp. | |||
[[Fil:Fig531-516.png|600px|thumb||center|<caption>Figur 16 Minste tverrsnitt A-C, øvre del</caption>]] | |||
I tillegg kommer kurveutslag, jf. tabell 25. | |||
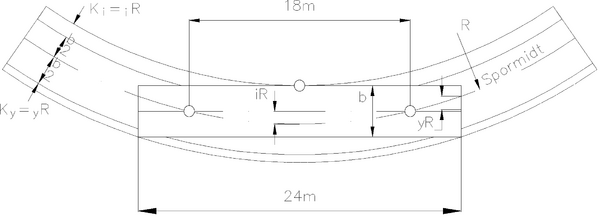
=== Kurveutslag === | |||
Minste tverrsnitts bredde varierer med sporets kurvatur på grunn av det ekstra plassbehov som oppstår når lange vogner befinner seg i kurver samt dynamiske bevegelser som krenging og rulling av vognkassen. | |||
For eksisterende baner beregnes kun statisk kurveutslag. Alle breddemål økes med kurveutslaget i sirkelkurver, overgangskurver og på rettlinje i nærheten av kurver. Kurveutslagene er forskjellige for kurvens indre og ytre side. Størrelsen av kurveutslagene er fastlagt på grunnlag av en teoretisk vogn med lengde 24 m og akselavstand 18 m. De samme verdiene for kurveutslag legges i utgangspunktet til grunn for A-96 og A-C. | |||
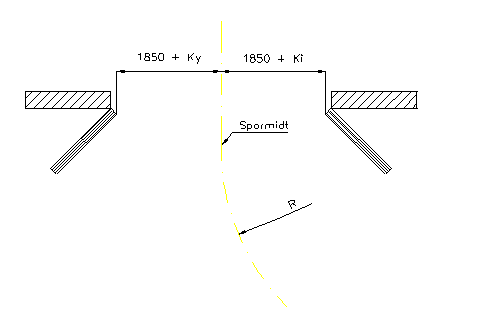
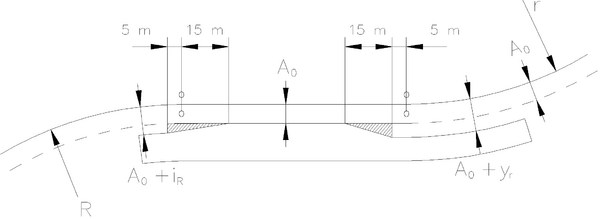
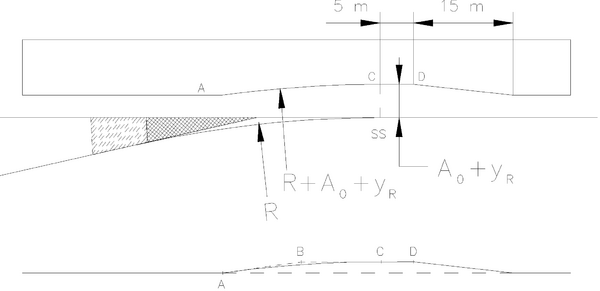
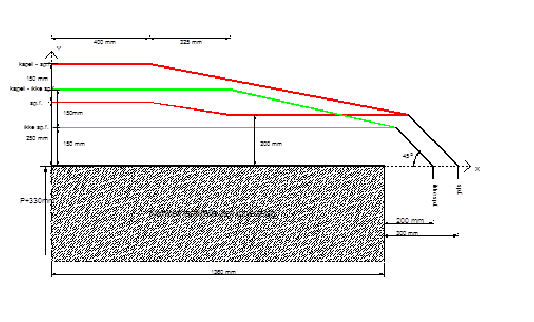
[[Fil:Fig522-203.png|600px|thumb||center|<caption>Figur 17 Kurveutslag</caption>]] | |||
Kurveutslag mot plattformer og lasteramper beregnes som vist i avsnitt 5.12.2. | |||
==== Breddeutvidelse i sirkelkurver for nye baner==== | |||
For nye baner utenom stasjonsområder økes alle breddemål i sirkelkurver, overgangskurver og på rettlinje i nærheten av kurver iht. tabell 24. Breddeutvidelsen tar hensyn til kurveutslag samt plass til dynamiske bevegelser. | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 24 Breddeutvidelse utenom stasjonsområder for nye baner | |||
|- | |||
!style="width:300px"| R [m] | |||
!style="width:300px" | k [mm] | |||
|- | |||
|Rettlinje|| 0 | |||
|- | |||
|20000|| 0 | |||
|- | |||
|10000|| 0 | |||
|- | |||
|5000|| 80 | |||
|- | |||
|4000|| 100 | |||
|- | |||
|3000|| 120 | |||
|- | |||
|1000|| 120 | |||
|- | |||
|600|| 130 | |||
|- | |||
|500|| 140 | |||
|- | |||
|300|| 150 | |||
|} | |||
Mellomverdier interpoleres lineært og avrundes opp til nærmeste hele cm. | |||
For nye baner innenfor stasjonsområder beregnes kurveutslag iht. tabell 25 med fradrag av 80 mm. Dog skal avstand fra spormidt aldri være mindre enn 2,20 m (gjelder 0,375/0,76 - 3,8 m over sporplan). | |||
For eksisterende baner beregnes kurveutslag i sirkelkurver etter følgende formler: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
K_i= {81000 \over 2 R} \ \ [mm], \ \ \ K_y= {63000 \over 2 R} \ \ [mm] | |||
</math></center> || align="right" | (5.74) | |||
|} | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 5.25 Verdier av kurveutslag for A-85, A-96 og A-C | |||
|- | |||
!style="width:150px" | R [m] | |||
!style="width:150px" | K<sub>i</sub> [mm] | |||
!style="width:150px" | K<sub>y</sub> [mm] | |||
!style="width:150px" | R [m] | |||
!style="width:150px" | K<sub>i</sub> [m] | |||
!style="width:150px" | K<sub>y</sub> [mm] | |||
|- | |||
|180|| 225 ||175|| 600|| 68 ||53 | |||
|- | |||
|190 ||214|| 166 ||650|| 63|| 49 | |||
|- | |||
|200|| 203|| 158|| 700|| 58|| 45 | |||
|- | |||
|210|| 193|| 150|| 750|| 54|| 42 | |||
|- | |||
|220|| 184|| 144|| 800|| 51|| 40 | |||
|- | |||
|230|| 176|| 137|| 850|| 48|| 38 | |||
|- | |||
|240|| 169|| 132 ||900|| 45|| 35 | |||
|- | |||
|250|| 162|| 126|| 950|| 43|| 34 | |||
|- | |||
|260|| 156|| 122|| 1000|| 41|| 32 | |||
|- | |||
|270|| 150|| 117|| 1100 ||37|| 29 | |||
|- | |||
|280|| 145|| 113|| 1200|| 34|| 27 | |||
|- | |||
|290|| 140|| 109|| 1300|| 32|| 25 | |||
|- | |||
|300|| 135|| 105|| 1400|| 29|| 23 | |||
|- | |||
|325|| 125|| 97|| 1500|| 27|| 21 | |||
|- | |||
|350|| 116|| 90|| 2000|| 21|| 16 | |||
|- | |||
|375|| 108|| 84|| 3000|| 14|| 11 | |||
|- | |||
|400|| 102|| 79|| 4000|| 10|| 8 | |||
|- | |||
|425|| 96|| 75|| 5000|| 8|| 6 | |||
|- | |||
|450|| 90|| 70|| 6000|| 7|| 5 | |||
|- | |||
|475 ||86|| 67|| 7000|| 6 ||4 | |||
|- | |||
|500|| 81|| 63|| 8000|| 5|| 4 | |||
|- | |||
|550|| 74|| 58|| > 8000|| 0|| 0 | |||
|} | |||
R = kurvens radius | |||
==== Redusert kurveutslag==== | |||
For å begrense omfanget av kostnadsutløsende tiltak, er det som minstekrav for korte vogner spesielt beregnet for kombitrafikkk, etablert et "redusert kurveutslag" som dispensasjonskriterium. | |||
Redusert kurveutslag er tilpasset ulike vogntyper med flg. parametre: | |||
1) akselavstand = 13,5 m og overheng = 2,0 m | |||
2) akselavstand = 10,0 m og overheng = 3,0 m | |||
Det betyr at for området høyere enn 3440 mm kan man regne med redusert kurveutslag for A-96 ved hjelp av formel .3. | |||
Indre kurveutslag: | |||
Tilfelle 1 med a = 13,5 m er dimensjonerende. Settes a = 13,5 m og n = a/2 = 6,75 m inn i formel .3 får man: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
K_i={an-n^2\over2R}={a\cdot{a\over2}-\left({a\over2}\right)^2\over2R}={a^2\over 8R}={13,5\cdot13,5\over 8R}={22781\over R}[mm] | |||
</math></center> || align="right" | (5.75) | |||
|} | |||
Ytre kurveutslag: | |||
Tilfelle 2 med a = 10,0 m og overheng = 3,0 m er dimensjonerende. Settes a = 10,0 m og n = 13,0 m inn i formel .3 får man: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
K_y={an-n^2\over 2R}={10\cdot13-13^2\over 2R}={19500\over R}[mm] | |||
</math></center> || align="right" | (5.76) | |||
|} | |||
Følgende tabell for kurveutslag framkommer: | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 26 Redusert kurveutslag | |||
|- | |||
!style="width:300px"| Radius [m] | |||
!style="width:300px"| K<sub>i</sub> [mm] | |||
!style="width:300px"| K<sub>y</sub> [mm] | |||
|- | |||
|200|| 114(203)|| 98(158) | |||
|- | |||
|250|| 91 (162)|| 78 (126) | |||
|- | |||
|300|| 76 (135)|| 65 (105) | |||
|- | |||
|400|| 57 (102)|| 49 (79) | |||
|- | |||
|500|| 46 (81)|| 39 (63) | |||
|- | |||
|600|| 38 (68)|| 33 (53) | |||
|- | |||
|700|| 33 (58)|| 28 (45) | |||
|- | |||
|800|| 28 (51)|| 24 (40) | |||
|- | |||
|900|| 25 (45)|| 22 (35) | |||
|- | |||
|1000|| 23 (41)|| 20 (32) | |||
|- | |||
|1200|| 19 (34)|| 16 (27) | |||
|- | |||
|1500|| 15 (27)|| 13 (21) | |||
|- | |||
|2000|| 11 (21)|| 10 (16) | |||
|- | |||
|5000|| 5 (8)|| 4 (6) | |||
|- | |||
|8000|| 3 (5)|| 2 (4) | |||
|} | |||
=== Minste tverrsnitt for nye baner=== | |||
Minste tverrsnitt for nye baner bygger på minste tverrsnitt UIC GC. UIC-tverrsnittet opererer imidlertid kun med kurveutslag for helt krappe radier (R < 250 m) og har ulike profiler for stasjonsspor og fri linje. | |||
[[Fil:Fig531-518.png|600px|thumb||center|<caption>Figur 18 Minste tverrsnitt for nye baner</caption>]] | |||
Det skraverte området på figuren angir innskrenkninger i profilet for plattformkanter og signaltekniske anlegg innenfor stasjonsområder. | |||
==== Tillegg i kurver==== | |||
For nye baner beregnes det et tillegg i kurver på fri linje ut fra både en statisk og en dynamisk betraktning. Det dynamiske tillegget øker med økende kurvehastighet. | |||
Alle breddemål økes i sirkelkurver, overgangskurver og på rettlinje i nærheten av kurver i henhold til tabell 27: | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 27 Tillegg i kurver for nye baner | |||
|- | |||
!style="width:300px"| R [m] | |||
!style="width:300px"| k [mm] | |||
|- | |||
|Rettlinje || 0 | |||
|- | |||
|20000|| 0 | |||
|- | |||
|10000|| 0 | |||
|- | |||
|5000|| 80 | |||
|- | |||
|4000|| 100 | |||
|- | |||
|3000|| 120 | |||
|- | |||
|1000|| 120 | |||
|- | |||
|600|| 130 | |||
|- | |||
|500|| 140 | |||
|- | |||
|300|| 150 | |||
|} | |||
Mellomverdier interpoleres lineært og avrundes opp til nærmeste hele cm. | |||
=== Minste tverrsnitt på stasjonsspor=== | |||
Det skraverte området av minste tverrsnitt for nye baner angir innskrenkninger i profilet for plattformkanter og signaltekniske anlegg innenfor stasjonsområder. | |||
Det skraverte området av minste tverrsnitt A-85 angir tillatt innskrenkning på spor innenfor stasjonsområder. Med henblikk på framføring av spesialtransporter bør det på alle stasjoner være minst en togvei - fortrinnsvis hovedtogsporet - hvor dette skraverte feltet holdes fritt for konstruksjoner. Denne togveien benevnes transportsporet. | |||
Mot transportsporet skal det ikke forekomme lasteramper, dvergsignaler og andre faste konstruksjoner som befinner seg nærmere sporet enn 2120 mm + kurveutslaget fra spormidt og som er høyere enn 760 mm over sporplanet. | |||
Sporforbindelser til frilasteplasser og sidespor til anlegg som skal kunne ta imot spesialtransporter, bør tilfredsstille de samme krav som transportsporet. | |||
=== Den nederste begrensning av minste tverrsnitt=== | |||
==== Sporrennen==== | |||
[[Fil:Fig531-519.png|600px|thumb||center|<caption>Figur 19 Sporrennen</caption>]] | |||
Bredden av sporrennen skal være minst: | |||
R<sub>b</sub> = 70 mm når sporvidden (spv) 1445 med mer | |||
R<sub>b</sub> = spv - 1375 mm for spv > 1445 mm | |||
R<sub>b</sub> = 100 mm i planovergang med trelemmer | |||
Konstruksjonsdeler som danner sporrennens indre begrensning (f.eks. planovergangslemmer), skal sikres mot skinnene slik at sporrennens bredde ikke kan reduseres. | |||
For enkelte konstruksjonsdeler reduseres kravet til R<sub>b</sub>. Dette gjelder: | |||
*ledeskinner/vingeskinner i sporveksler | |||
*sporkryss | |||
*sporbremser | |||
*gummilister i planoverganger | |||
==== Faste konstruksjoner mellom og utenfor skinnene==== | |||
Bortsett fra sporrennen ligger den nederste begrensningslinjen i sporplanet. Følgende unntak gjelder: | |||
*Planovergangslemmer på elektrifiserte strekninger eller i isolerte sporfelt skal ligge minst 5 mm over sporplanet, men ikke mer enn 20 mm (a). | |||
*Toppen av ledeskinnene i sporveksel kan ha en høyde inntil 20 mm over sporplan (a). | |||
*På spor innenfor stasjonsområder kan faste konstruksjoner ha en høyde inntil 45 mm over sporplan (b). | |||
*Toppen av ledeskinnene i sidekryssene for kryssveksler kan ha en høyde inntil 60 mm over sporplan (c). | |||
[[Fil:Fig531-520.png|600px|thumb||center|<caption>Figur 20 Begrensninger mellom og utenfor skinnene</caption>]] | |||
Mellom skinnene gjelder unntakene lenger enn R<sub>b</sub> fra kjørekanten. Utenfor skinnene gjelder unntakene lenger enn 150 mm fra kjørekanten. Unntakene gjelder ikke på steder hvor det forekommer vertikalkurver med R<sub>v</sub> 1500 m. | |||
==== Hensyn til bruk av sporrenser==== | |||
I spor hvor det forutsettes bruk av sporrenser skal det om vinteren holdes fritt et rom inntil 700 mm utenfor kjørekanten av skinnene. | |||
[[Fil:Fig531-521.png|600px|thumb||center|<caption>Figur 21 Fritt rom for bruk av sporrenser</caption>]] | |||
Der faste konstruksjoner betinger løft av sporrenseren, skal det på fri linje merkes med anvisere for sporrenserkjøring. | |||
=== Fritt profil for strømavtaker=== | |||
Fritt profil for strømavtaker angir plassbehovet for passasje av materiellets strømavtaker. I dette profilet skal kun kontakttråden være. Profilet får ikke kurveutslag. Profilet er vist på figur 22. | |||
=== Minste tverrsnitt E=== | |||
[[Fil:Fig531-522.png|600px|thumb||center|<caption>Figur 22 Fritt profil for strømavtaker og minste tverrsnitt E</caption>]] | |||
Minste tverrsnitt E er det tverrsnittet som trengs til fri passasje av strømavtakeren samt kontakttråden, bærelinen og andre konstruksjonsbestanddeler som tilhører kontaktledningsanlegget. Tverrsnittet er dimensjonert slik at det mellom begrensningslinjene og de spennings-førende deler er tilstrekkelig isolasjonsavstand. Målaksen for minste tverrsnitt E står vinkelrett på sporplanet i spormidt. Minste tverrsnitt E får ikke kurveutslag. På rettlinjet spor og mer enn 30 m fra nærmeste OB, KP eller SS (sporvekselkurve) tillates at minste tverrsnitt E sideveis blir innskrenket med 100 mm. Høyden for minste tverrsnitt E (H<sub>E</sub>) er avhengig av kontakttrådhøyden ved opphengningspunktet (H<sub>0</sub>) og av kontaktledningens konstruksjonshøyde (C): | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
H_E=H_0+C | |||
</math></center> || align="right" | (5.77) | |||
|} | |||
Verdier for H<sub>0</sub> og C er gitt i JD530, kap. 5. | |||
For nye baner er minste tverrsnitt E tegnet inn sammen med minste tverrsnitt. | |||
=== Master og andre gjenstander ved siden av sporet=== | |||
Master og andre gjenstander med stor høyde (bukker for lastekraner, skilter, signaler, barduner, vannstendere o.l.) skal på områder hvor det forekommer skifting, plasseres slik at avstanden til minste tverrsnitt blir minst 400 mm i en høyde mellom 1500 mm og 3500 mm over nærmeste skinne, jf. figur .23. | |||
[[Fil:Fig531-523.png|600px|thumb||center|<caption>Figur 23 Avstand til master og andre gjenstander for A-85/96/C</caption>]] | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
a_i=2520+K_i+2,3h \ \ \ \ \ a_y=2520+K_y-h | |||
</math></center> || align="right" | (5.78) | |||
|} | |||
=== Portåpninger=== | |||
Minste bredde (= normalbredde) for portåpninger i rettlinjet spor er 3700 mm. Ligger sporet gjennom porten i eller i nærheten av kurve, økes bredden med kurveutslagene. | |||
[[Fil:Fig531-524.png|600px|thumb||center|<caption>Figur 24 Portåpning i kurve</caption>]] | |||
I bestemte tilfeller kreves minste tverrsnitt i portåpninger: | |||
*Når sporet gjennom bygningen danner den eneste forbindelse til sporanlegg på den andre siden av bygningen. | |||
*I bygninger hvor det skal kunne mottas transporter med overskridelse av lasteprofilet. | |||
Høyden for porter skal være minst 5600 mm. Høyden kan reduseres til 4800 mm i bygninger der elektrifisering ikke er aktuelt. | |||
=== Sporets middel === | |||
{| class="wikitable" | |||
|- | |||
|<small>Fra Teknisk Regelverk: https://trv.banenor.no/wiki/Underbygning/Prosjektering_og_bygging/Profiler_og_minste_tverrsnitt#Sporets_middel</small> | |||
Med sporets middel menes det punkt hvor avstanden mellom to spor er tilstrekkelig stor til at rullende materiell farefritt kan passere hverandre. | |||
a) Sporavstanden ved middel skal være så stor at det mellom lasteprofilet anbrakt på det ene spor og minste tverrsnitt på det andre spor skal være 100 mm klaring. | |||
# Utførelse: Sporets middel skal markeres med Skilt/Plassering_av_skilt_langs_sporet/Skiltoversikt#Middelmerke. | |||
# Utførelse: Hele middelmerket skal være innenfor middel, slik at langs hele middelmerket skal sporavstanden tilfredsstille kravet i punkt a). | |||
# Utførelse: Sporets middel skal beregnes ut fra et lasteprofil med bredde 3400 mm, og som minste tverrsnitt skal A-85, A-96 og A-C benyttes, også for nye baner. | |||
# Utførelse: Både for lasteprofilet og for minste tverrsnitt skal det regnes med kurveutslag og tillegg for eventuell overhøyde i sporene. | |||
# Unntak: Dersom ingen av sporene er togspor, kan det tillates at de ovennevnte profiler går inntil 100 mm inn i hverandre. | |||
# Unntak: For nye baner skal sporavstanden ved middel, beregnet etter ovennevnte regler, ikke understige 4000 mm. | |||
|} | |||
Da beregning av sporets middel er basert på godkjent UIC-materiell, kan man ikke uten videre plassere spesialtransporter helt fram til middelmerket. | |||
{| class="wikitable" | |||
|- | |||
! | |||
! Beregning av middel | |||
|- | |||
| [[File:Middel-tilfelle1.svg|130px]] | |||
| S | |||
|- | |||
| [[File:Middel-tilfelle2.svg|130px]] | |||
| S + K<sub>y</sub> | |||
|- | |||
| [[File:Middel-tilfelle3.svg|130px]] | |||
| S + K<sub>i</sub> + 2,3*h | |||
|- | |||
| [[File:Middel-tilfelle4.svg|130px]] | |||
| S + K<sub>i</sub> + K<sub>y</sub> + 2,3*abs(h<sub>2</sub>-h<sub>1</sub>) | |||
|- | |||
| [[File:Middel-tilfelle5.svg|130px]] | |||
| S + 2*K<sub>y</sub> | |||
|} | |||
<font color="red"> | |||
S = 2120 mm + 1700 mm + 100 mm = 3920 mm (dersom ingen av sporene er togspor er S = 3720 mm) | |||
</font> | |||
'''Eksempel på beregning av sporets middel:''' | |||
R<sub>1</sub> = 300 m, h = 0 mm, R<sub>2</sub> = ∞, A-85 | |||
:A-85 2120 mm | |||
+ Ytre kurveutslag 105 mm | |||
+ Lasteprofil 1700 mm | |||
+ Klaring 100 mm | |||
---------------- | |||
= Sporavstand ved middel 4025 mm | |||
=== Sporavstand=== | |||
Avstanden mellom to nabospor skal alltid være så stor at rullende materiell ikke berører hverandre. Utover denne minimumsavstanden ønskes ytterligere avstand for å ta hensyn til | |||
*plassering av master og signaler | |||
*plass til personale under skifting og | |||
*aerodynamiske påvirkninger ved høye hastigheter | |||
Sporavstanden måles fra spormidt til spormidt | |||
Den minste sporavstanden på dobbeltsporede eller flersporede strekninger framgår av tabell .28 og tabell .29. | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 28 Minste sporavstander på linjen, nye baner | |||
|- | |||
!style="width:300px"| Radius [m] | |||
!style="width:300px"| Sp [m] | |||
|- | |||
|R < 350|| 4,70 | |||
|- | |||
|350 < R < 500|| 4,68 | |||
|- | |||
|500 < R < 600|| 4,66 | |||
|- | |||
|600 < R < 1000|| 4,64 | |||
|- | |||
|1000 < R < 4000|| 4,60 | |||
|- | |||
|4000 < R < 5000|| 4,56 | |||
|- | |||
|R > 5000|| 4,40 | |||
|} | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 29 Minste sporavstander på linjen, eksisterende baner | |||
|- | |||
!style="width:300px"| Radius [m] | |||
!style="width:300px"| Sp [m] | |||
|- | |||
|- | |||
|R < 250 ||3,95+75/R | |||
|- | |||
|R ≥250|| 4,25 | |||
|} | |||
Den normale sporavstanden der rullende materiell hensettes og der driftsoppgaver i forbindelse med det rullende materiell utføres, er 4,70 m. | |||
=== Plattformer=== | |||
Ved bygging av personvogner og plattformer forsøker man å skape de beste inn- og utstigningsforhold for passasjerene. Dette betyr gode trinn, liten høydeforskjell og kort avstand mellom vogn og plattform. Plattformtypene betegnes etter høyde over sporplan. | |||
==== Plattformhøyder==== | |||
Opprinnelig ble plattformene i Norge bygget relativt lavt og en rekke av disse lave plattformer er fortsatt i bruk i dag. Nye plattformer bygges i dag enten med 570 mm høyde eller med 700 mm høyde over sporplan. | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 30 Plattformhøyder | |||
|- | |||
!style="width:300px"| Plattformtype | |||
!style="width:300px"| Plattformhøyde | |||
|- | |||
|- | |||
|Lav ||350 mm | |||
|- | |||
|Normal|| 570 mm | |||
|- | |||
|Høy ||700 mm | |||
|} | |||
Høy plattformer har hos oss i hovedsak blitt bygget i nærtrafikkområdet rundt Oslo. | |||
==== Plattform mot spor uten overhøyde ==== | |||
Avstand fra spormidt regnes ut etter følgende formler: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
A_i=A_0+K_i \ \ og \ \ A_y=A_0+K_y | |||
</math></center> || align="right" | (5.79) | |||
|} | |||
Hvor A<sub>0</sub> = 1700 eller 2240 mm. Størrelsene A<sub>i</sub> og A<sub>y</sub> er konstante når plattformen eller rampen over hele lengden ligger mot en sirkelkurve. | |||
[[Fil:Fig531-525.png|600px|thumb||center|<caption>Figur 25 Plattform mot spor i kurve</caption>]] | |||
Når sporet delvis ligger i en kurve, eller når det er et kurvepunkt i nærheten av enden av plattformen/rampen, varierer A<sub>i</sub> og A<sub>y</sub> som vist i figur 26. | |||
[[Fil:Fig531-526.png|600px|thumb||center|<caption>Figur 26 Plattform mot spor som delvis ligger i kurve</caption>]] | |||
Skravering viser områdene hvor kurveutslagene forandres lineært. | |||
Som hovedregel gjelder verdiene gitt i tabell 31 (retning fra største kurve til minste kurve). | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 31 Avstand til plattform når sporet delvis ligger i kurve | |||
|- | |||
!style="width:300px"| Ved plattform/rampe i innerkurve | |||
!style="width:300px"| Ved plattform/rampe i ytterkurve | |||
|- | |||
|- | |||
|Minste Ai til 15 m før Kp||Minste Ay til 20 m før Kp | |||
|- | |||
|Største Ai fra 5 m etter Kp|| Største Ay fra 5 m før Kp | |||
|} | |||
Ligger det en sporveksel i sporet mot plattformen/rampen, må det tas hensyn til kurveutslagene for det avvikende spor, jf. figur 27. I slike tilfeller kan det være hensiktsmessig å skjematisere forløpet av rampens kant, dvs. den stiplede linjen A-B-C istedenfor sirkelsegmentet. På den måten oppnås en forenkling av målføringen under byggingen. | |||
[[Fil:Fig531-527.png|600px|thumb||center|<caption>Figur 27 Plattform mot spor med sporveksel</caption>]] | |||
Rampens/plattformens høyde er konstant. | |||
==== Plattform mot spor med overhøyde==== | |||
I spor med overhøyde må kurveutslagene og plattformhøydene bestemmes etter følgende formler, jf. figur 28: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
A_i=1680+K_i+{h\over1500}*H_p \ \ \ [mm] | |||
</math></center> || align="right" | (5.80) | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
H_i=H_p \ \ \ 0,63*h{h\over1500}*K_i \ \ \ [mm] | |||
</math></center> || align="right" | (5.81) | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
A_y=1680+K_y+{h\over1500}*(H_p \ \ 375) \ \ \ [mm] | |||
</math></center> || align="right" | (5.82) | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
H_y=H_p +1,63 *h+{h\over1500}*K_y \ \ \ [mm] | |||
</math></center> || align="right" | (5.83) | |||
|} | |||
(5.83) | |||
[[Fil:Fig531-528.png|600px|thumb||center|<caption>Figur 28 Høyde til plattform når sporet ligger med overhøyde</caption>]] | |||
På grunn av overhøyderampen får plattformene varierende avstander og høyder mellom OB og OE, jf. figur 29. | |||
[[Fil:Fig531-529.png|600px|thumb||center|<caption>Figur 29 Avstand til plattform når sporet ligger med overhøyde</caption>]] | |||
Som hovedregel gjelder verdiene gitt i tabell 32 (retning fra største kurve til minste kurve). | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 32 Område som får kurveutslag | |||
|- | |||
!style="width:300px"| Ved plattform/rampe i innerkurve | |||
!style="width:300px"| Ved plattform/rampe i ytterkurve | |||
|- | |||
|- | |||
|Minste Ai til 10 m før OB||Minste Ay til 15 m før OB | |||
|- | |||
|Største Ai fra OE|| Største Ay fra 5 m før OE | |||
|} | |||
Endringer i plattformens høyde over skinnetopp utføres lineært mellom OB og OE. | |||
=== Innskrenkninger i minste tverrsnitt=== | |||
Som følge av trafikken og justeringsarbeidene kan sporets beliggenhet og overhøyde forandre seg med tiden. Faste gjenstander og konstruksjoner som plasseres mot begrensningslinjene for minste tverrsnitt kan etter hvert danne innskrenkninger i minste tverrsnitt, | |||
==== Registreringer av innskrenkninger i minste tverrsnitt==== | |||
Ved jevne mellomrom blir det foretatt en kontroll av minste tverrsnitt. Dette skjer vha. målevogn. Fram til 1985 ble minste tverrsnitt kontrollert vha. maler. Dette var en tungvinn og lite nøyaktig registreringsmetode. I perioden 1986 -1995 ble det anvendt en fotogrammetrisk metode som bestod i at man fotograferte to delvis overlappende fotografier ved hver innskrenkning. Deretter ble bildene behandlet i en modell og koordinater ble beregnet. F.o.m. 1996 er det blitt anvendt en målevogn med roterende laser. Her blir profilet målt kontinuerlig og det avdekkes på stedet hvor stor innskrenkningen er. | |||
[[Fil:Fig531-530.png|600px|thumb||center|<caption>Figur 30 Målevogn med roterende laser</caption>]] | |||
Alle innskrenkningene i minste tverrsnitt legges inn i en edb-basert simuleringsmodell. Her kan man simulere spesialtransporter og nye vognkonsepter på de ulike norske jernbanestrekninger. | |||
[[Fil:Fig531-531.png|600px|thumb||center|<caption>Figur 31 Simulering av A-96</caption>]] | |||
== Lasteprofiler== | |||
=== Det normale lasteprofil=== | |||
Lasteprofilene angir begrensningen i høyde- og sideretning for last på godsvogner. | |||
[[Fil:Fig531-532.png|600px|thumb||center|<caption>Figur 32 Det normale lasteprofil</caption>]] | |||
1) | |||
:H = 100 mm, unntatt for vogner som skal bremses i sporbremsene ved Alnabru. | |||
:For disse vognene gjelder: | |||
:H = 140 mm når a = 6 - 10 m | |||
:H = 180 mm når a = 10 - 16 m | |||
:H = 200 mm når a = 16 - 20 m | |||
Lasteprofilet kan utnyttes fullt ut over en lengde L = a + 2n. | |||
*a er for 2- og 3-akslede vogner avstanden mellom vognens ytterste aksler og for boggivogner avstanden mellom boggisentrene. | |||
*n er lastens overheng. | |||
Lengden L er i tillegg avhengig av avstanden P mellom de ytterste aksler i boggien for boggivogner. | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 33 Verdier for p, a og n for godsvogner | |||
|- | |||
! colspan=2 |For vogner hvor samtidig: | |||
! | |||
|- | |||
!style="width:300px"| p | |||
er mindre eller lik: | |||
!style="width:300px"| A | |||
Er: | |||
!style="width:300px"| n | |||
kan maksimalt være | |||
|- | |||
|2,5 m|| 17,0 -18,0 m ||3,00 m | |||
|- | |||
|6,0 m|| 16,0 - 17,0 m|| 3,30 m | |||
|- | |||
|6,0 m|| 14,5 - 16,0 m|| 3,40 m | |||
|- | |||
|6,0 m|| 13,0 - 14,5 m|| 3,65 m | |||
|- | |||
|6,0 m|| 12,0 - 13,0 m|| 3,85 m | |||
|- | |||
|6,0 m ||11,0 -12,0 m|| 4,00 m | |||
|- | |||
|6,0 m|| 10,0 - 11,0 m|| 4,20 m | |||
|- | |||
|6,0 m ||8,0 – 10,0 m|| 4,30 m | |||
|- | |||
|6,0 m ||7,0 - 8,0 m|| 4,00 m | |||
|- | |||
|-|| 6,0 - 7,0 m|| 3,70 m | |||
|- | |||
|-|| 5,0 - 6,0 m|| 3,25 m | |||
|- | |||
|-|| 4,0 - 5,0 m|| 2,60 m | |||
|- | |||
|- ||3,0 - 4,0 m|| 2,00 m | |||
|} | |||
=== Det utvidede lasteprofil === | |||
Utvidet lasteprofil for last på 2-akslede vogner kan nyttes når lasten ikke rager utover vognenes endebjelker. | |||
=== Lasteprofil K=== | |||
Lasteprofil K bygger på det utvidede lasteprofil, men avviker i øvre hjørne: | |||
1200 - 3650 mm høyde er halv bredde 1700 mm | |||
et knekkpunkt i 4350 mm høyde og halv bredde 1400 mm | |||
et knekkkpunt i 4450 mm høyde og halv bredde 700 mm | |||
[[Fil:Fig531-533.png|600px|thumb||center|<caption>Figur 33 Lasteprofil K og det utvidede lastreprofil (stiplet)</caption>]] | |||
=== Internasjonale lasteprofiler=== | |||
==== UIC GC==== | |||
Lasteprofilet UIC GC er, med sin bredde 1,455 m i høyden 4,650 m over skinnetopp, så stort at ingen land har ønsket å innføre det generelt. Det er dermed heller ikke opptatt i RIV. En rekke land forsøker å innføre det på utvalgte strekninger. | |||
[[Fil:Fig531-534.png|600px|thumb||center|<caption>Figur 34 Lasteprofil UIC GC</caption>]] | |||
På de nye høyhastighetsstrekningene gjennom Europa innføres dette profilet, selv om det ikke er planlagt framføring av gods på disse strekningene. Innføringen skyldes primært at profilet kommer av seg selv pga. det anvendte kontaktledningsssystem. | |||
UIC GC er interessant både i Sverige og i Danmark fordi de nødvendige lasteprofiler i disse land for kjøring av containere og dobbeltdekkere (DSB) ligner mye på UIC GC. | |||
Som det framgår av figuren er lasteprofilet UIC GC betydelig større enn lasteprofil K i øvre del av profilet. | |||
=== Konteiner- og semitrailerprofiler=== | |||
Konteiner- og semitrailerprofiler betegnes internasjonalt vha. et UIF-nr. som angir den maksimale størrelsen på konteineren/semitrailerene som kan fremføres på de ulike strekningene. Et UIF-nr. består av en bokstav (C for konteiner/P for semitrailer) og et tresifret tall som angir høyden i cm for konteineren/semitraileren. Denne høyden er basert på en standardisert vogn med lastehøyde 33 cm. De viktigste lasttilfellene er listet opp i tabell .34. | |||
{| class="wikitable" style="text-align:center" | |||
|+Tabell 34 Lasttilfeller | |||
|- | |||
!style="width:300px"|UIF-nr. | |||
!style="width:300px"|Lasttilfelle | |||
!style="width:300px"|Høyde over | |||
Skinnetopp | |||
!style="width:300px"|Avstand fra | |||
Spormidt | |||
|- | |||
|C400|| Vekselbeholder 3150|| 4330|| 1300 | |||
|- | |||
|C405|| Vekselbeholder 3200|| 4380|| 1300 | |||
|- | |||
|P400|| EU-semi (4000) i brønn|| 4330|| 1360 | |||
|- | |||
|P407|| Semi 4070 i brønn|| 4400|| 1360 | |||
|- | |||
|P410|| Semi 4010 i brønn ||4430|| 1360 | |||
|} | |||
Frittromsprofilet for lasttilfellene PXXX er vist i figur 35. | |||
EMBED Sketch | |||
[[Fil:Fig531-535.png|600px|thumb||center|<caption>Figur 35 Frittromsprofil for PXXX</caption>]] | |||
| Linje 2 995: | Linje 4 059: | ||
Tabell 35 Toleranser mellom lasttilfellene PXXX og frittromsprofilet | {| class="wikitable" style="text-align:center" | ||
|+Tabell 35 Toleranser mellom lasttilfellene PXXX og frittromsprofilet | |||
|- | |||
!style="width:150px"| | |||
!Ikke spenningsførende (ikke sp.f.) | |||
!colspan=2 |Spenningsførende (sp.f.) | |||
|- | |||
|ΔX ||200 mm ||colspan=2|300mm | |||
|- | |||
| rowspan=2 |ΔY|| ||ledning||fester | |||
|- | |||
|150 mm ||250 mm|| 200 mm | |||
|} | |||
{| class="wikitable" style="text-align:center" | |||
|- | |||
|style="width:150px"| ΔY - kapell ||style="width:150px"| +150 mm | |||
|} | |||
| Linje 3 021: | Linje 4 107: | ||
----------------------------- | |||
LITTERATURHENVISNINGER | '''''LITTERATURHENVISNINGER''''' | ||
1. DSB - Registersektoren - Profilmål, Konstruktionsmål, læsseprofiler og fritrumsprofiler (1994) | 1. '''DSB - Registersektoren - Profilmål''', Konstruktionsmål, læsseprofiler og fritrumsprofiler (1994) | ||
2. Jacobus Meulman: Bpk 38 – Konstruksjonsprofiler for rullende materiell (1977) | 2. '''Jacobus Meulman''': Bpk 38 – Konstruksjonsprofiler for rullende materiell (1977) | ||
3. Jacobus Meulman: Grunnlag for beregning av de ”dynamiske profiler” (udatert) | 3. '''Jacobus Meulman''': Grunnlag for beregning av de ”dynamiske profiler” (udatert) | ||
4. Jacobus Meulman: Oversikt over metoden for beregning av konstruksjonsprofiler (1988) | 4. '''Jacobus Meulman''': Oversikt over metoden for beregning av konstruksjonsprofiler (1988) | ||
5. Jernbaneverket, JD530 Overbygning – regler for prosjektering | 5. '''Jernbaneverket''', JD530 Overbygning – regler for prosjektering | ||
Siste sideversjon per 16. jan. 2023 kl. 11:25
__NUMBEREDHEADINGS__
Innledning
De første tog i Norge ble levert fra England og naturlig nok bygget etter engelske tegninger. Det samme var forholdet i andre europeiske land. Disse bindingene til de engelske mål og tradisjoner med til dels korte sporavstander og lave tunneler preger fremdeles mye av eksisterende europeisk infrastruktur.
Grunnlaget for felles konstruksjons- og frittromsprofiler ble utarbeidet av de europeiske jernbaner omkring 1900, men først i 1913 kunne man ta i bruk ” Technische Einheit im Eisenbahnwesen (TE) / Unité Technique des Chemins de Fer (UT)”.
I Norge definerte man tidlig et lasteprofil som anga maskimale lastgrense ved pålasting av godsvogner. Dette lasteprofilet lå et stykke innenfor spilleromslinjen og man fastsatte derfor at heller ingen vogner eller lokomotiver skulle ha større mål enn lasteprofilet, og man opprettet dermed laste- og konstruksjonsprofilet. Denne benevnelsen ble avskaffet ved revisjon av Trykk 402 i 1964 fordi personvogner på den tiden fikk fjærsystemer og bolsterspillrom som tillot langt større sidebevegelser enn hva tilfellet var for godsvogner.
Beregningsgrunnlag – UIC fiche 505
Begrensningslinjer
Utviklingen av nytt materiell viste at de gamle beregningsmetoder ikke var tilstrekkelig. UIC ble av den grunn bedt om å utarbeide nye begrensningslinjer for lokomotiver og vogner. Resultatet ble UIC fiche 505, bind 1–4.
Hovedprinsippet i oppbyggingen av profillinjer er for UIC anvendelsen av en referanselinje.
Referanselinjen er en teoretisk linje som danner grense mellom det rullende materiell og de faste gjenstander i sporet.
Forholdet mellom konstruksjonsbredde og referanselinje kan uttrykkes slik:
Konstruksjonsbredde ≤ referanselinje – innskrenkningen Ei eller Ea.
I det etterfølgende er det beskrevet grunnlaget for de forskjellige begrensningslinjer som oppstår ved bruk av UIC 505. Betegnelser og innbyrdes plassering fremgår av figur 1.
- 1 grenselinje for rullende materiell (konstruksjonsmål)
- 2 referanselinje
- 3 ytterstilling for rullende materiell i stillstand beregnet på grunnlag av formlene for innskrenkning
- 4 grenselinje for det kinematiske plassbehov (kinematisk begrensningslinje)
- 5 grenselinje for faste gjenstander
- 6 frittromsprofil (minste tverrsnitt)
- 7 semistatisk forskyvning med den del av overhøyden som overstiger 50 mm
- 8 de verdier som av sportekniske grunner må fastesettes for sideforskyvning
- 9 hver enkelte forvaltnings egne tillegg mht. lokale forhold
Koordinatsystemet
Ved beskrivelse av høyde- og breddemål i forbindelse med profiler danner X-aksen sporplanet og Y-aksen normalen på sporplanet i spormidt.
Begrensningslinjen for gods
Ved plassering av gods på åpne vogner kan man ikke hver gang foreta beregninger etter UIC fiche 505. Her anvender man i stedet lasteprofiler. Gods som er lastet i henhold til lasteprofilet overholder referanselinjen.
Oppdeling av referanselinjen
Referanselinjen deles opp i følgende høydeintervaller:
- området under 0,130 m over sporplan avhengig av type rullende materiell
- området mellom 0,130 m og 0,400 m over sporplan for alle typer rullende materiell
- området over 0,400 m over sporplan for alle typer rullende materiell med unntak av ikke-isolerte, strømførende ledninger på taket
- området for strømavtaker inkludert ikke-isolerte, strømførende ledninger på taket
Det skal alltid tas hensyn til nedsenkning av rullende materiell ved bruk av de viste referanselinjer. Slik nedsenkning forårsakes av hjulslitasje og nedfjæring.
UIC-referanselinje
Når UIC fiche 505 ble tatt i bruk ble det innført en referanselinje som gjaldt normalsporede jernbanestrekninger på det europeiske kontinent. For at UIC-referanselinjen skulle kunne aksepteres i alle land, måtte man basere seg på eksisterende, internasjonalt rullende materiell samt de minste europeiske frittromsprofiler. Det ble av den grunn valgt det franske profil, selv om det engelske faktisk var enda mindre.
UIC-referanselinjen fremkommer som de minste omriss av alle de referanselinjer som anvendes innenfor UIC (unntatt England).
Alle UIC-medlemslandene har akseptert uansett evt. lokale forhold å anvende UIC-referanselinjen med dertil hørende beregningsmetode og formler overalt på deres strekninger. Dette betyr at rullende materiell til bruk i internasjonal samtrafikk skal konstrueres slik at UIC-referanselinjen ikke overskrides.
UIC-referanselinje under 0,130 m
For intervallet fra sporplan til høyden 0,130 m over skinnetopp, gjelder spesielle referanselinjer:
- referanselinje rundt skinnehode og spormidt
- referanselinje for lokomotiver og motorvogner (inkl. styre- og mellomvogner)
- referanselinje for person- og godsvogner
Referanselinjen rundt skinnehodet og spormidt framgår av figur 4.
Følgende kommentarer er knyttet til figur 4:
- 1 Størst forekommende bredde av hjulflensen mhp. eventuell skjevstilling av hjulet.
- 2 Absolutt ytterstilling av hjulets innerside når hjulsettet er skjøvet helt over på motsatt skinne. Dette målet er avhengig av sporvidden.
- 3 Absolutt nærmeste plassering av ledeskinne.
- 4 Absolutt nærmeste plassering av deler av rullende materiell over skinnen.
- 5 Absolutt ytterste stilling av hjulets utvendige side og av de deler av rullende materiell som er i forbindelse med hjulet.
- 6 Område for plassering av ”krokodiller” (børster under lokomotivet som skaper elektrisk kontakt ved at de berører skinnene – inngår i sikringsanlegg hos enkelte forvaltninger).
Referanselinjen for lokomotiver og motorvogner (inkl. styre- og mellomvogner) framgår av figur 5.
Referanselinjen for person- og godsvogner framgår av figur .6.
UIC-referanselinje for strømavtaker
For strømavtakere gjelder referanselinjen som vist på figur 7.
bw = halve bredden av strømavtakerens bøyle iht. UIC fiche 608.
= tillatt forskyvning av vognkassen samt ytterligere forskyvning av strømavtakeren ved plassering utenfor boggisenter. Denne forskyvningen beregnes etter UIC fiche 505-1 som følger:
- for høyden h = 6,500 m over skinnetopp anvendes UIC-formlene 111, 112, 113 og 114
- for høyden h = 5,000 m over skinnetopp anvendes UIC-formlene 115, 116 og 117
Det skraverte området på figuren markerer der det ikke skal forekomme uisolerte spenningsførende deler.
Utvidet UIC-referanselinje
Allerede under utarbeidelsen av UIC-referanselinjen var man klar over at det måtte tas hensyn til de nord- og østeuropeiske land som hadde et høyere profil. Det ble derfor i fiche 505-4, bilag 3, gitt mulighet til å benytte en ”utvidet UIC-referanselinje”. Målene på denne framgår av figur 8.
For de land som benytter ”utvidet UIC-referanselinje” (bl.a. Tyskland og Danmark) betyr det at
- det rullende materiell skal konstrueres slik at det ikke overskrider ”utvidet UIC-referanselinje
- det ikke forekommer innskrenkninger i ”utvidet UIC-referanselinje”
Referanselinje ved Jernbaneverket
I Norge ble jernbanen bygget ut med kurveutslag slik at det ikke var logisk å ta utgangspunkt i UICs referanselinje. Man valgte i stedet å ta utgangspunkt i frittromsprofilet for beregninger av konstruksjonsmål for det rullende materiell. Dette betyr at man opererer med flere sett referanselinjer. I praktiske beregninger anvendes referanselinjer for R = 130 m, 180 m, 250 m, 350 m, 450 m, 700 m, 1000 m og rettlinje. Referanselinjene for de ulike radier framkommer ved at kurveutslag for hhv. indre og ytre side legges til alle horisontale mål for referanselinjen for rettlinje. Kurveutslagets størrelse er iht. tabell 25.
Konstruksjonsmål for rullende materiell
Beregning av mål for lokomotiver, motorvogner, person- og godsvogner foregår etter UIC fiche 505.
Reglene i TE var i mange år det europeiske grunnlag for konstruksjon av norsk rullende materiell og helt til slutten av 70-tallet ble norsk materiell bygget på dette grunnlaget.
På 60-tallet arbeidet UIC med å systematisere og modernisere beregningsmetodene. Dette arbeidet resulterte i:
- UIC fiche 505-1, konstruksjonsmål for trekkraft
- UIC fiche 505-2, konstruksjonsmål for personvogner
- UIC fiche 505-3, konstruksjonsmål for godsvogner
- UIC fiche 505-4, oppstilling av frittromsprofiler
- UIC fiche 505-5, grunnlag for UIC 505 samt utviklingshistorie
I 1992 ble UIC fiche 505-1, 505-2 og 505-3 samlet til ett bind. Dette kunne skje fordi prinsippene var de samme for alle tre materielltyper. Den nye fiche fikk betegnelsen UIC fiche 505-1, VI, Eisenbahnfahrzeuge, Fahrzeugbegrenzungslienen.
Beregningsmetoder
Som det framgikk av avsnitt 2.2 skal alt rullende materiell holde seg innenfor referanselinjen. Ut fra det aktuelle materiellets parametre kan derfor de maksimale konstruksjonsmål beregnes ved å benytte UICs beregningsmetode. Disse maskimale konstruksjonsmål kalles materiellets begrensningslinje.
Normalt beregnes begrensningslinjen i midten og i enden av vognkassen. Beregning av punkter i andre tverrsnitt kan være nødvendig dersom slike punkter stikker ut over vognkassen.
Grunnbegreper i UIC fiche 505
I dette avsnittet gjennomgås de grunnleggende begreper som anvendes i UIC fiche 505.
Referanselinje
Med utgangspunkt i referanselinjen fastsettes den begrensingslinje som ikke må overskrides ved bygging av materiellet.
Kurveutslag
Kurveutslag er den del av materiellets utslag som kun stammer fra kurvens radius. Kurveutslaget mellom materiellets akser betegnes dgi og i overheng dga. Alle punkter i samme avsnitt får samme verdi for kurveutslag uavhengig av høyde over skinnetopp.
Kurveutslaget i et punkt i et tverrsnitt uttrykkes som differansen mellom avstanden fra punktet til spormidt når materiellet står i kurve og avstanden fra punktet til spormidt når materiellet står på rettlinje. Det forutsettes at
- hjulsettene i begge tilfeller står midt i sporet
- spill er likt fordelt
- materiellet er symmetrisk
- materiellet ikke henger skjevt i fjærene
Skjevstilling
Med et materiells skjevstilling forstås den vinkel som vognkassens midtlinje danner med loddlinjen når materiellet står i vannrett spor og det ikke forekommer friksjon.
Skjevstillingsvinkelen betegnes η0. Linjenes skjæringspunkt kalles rullsenter.
Skjevstilling kan komme av feil i konstruksjonen, unøyaktig fjærjustering eller eksentrisk nyttelast.
Rullsenter
Hvis en vognkasse utsettes for en tversgående kraft som er parallell med sporplanet, vil vognkassen rulle. Den tversgående kraft kan være en komponent av tyngdekraften eller sentrifugalkraften.
Hvis de tversgående spillrom og bevegelsen i støtdemperne er fullt utnyttet, inntar vognkassens midtlinje (markert med XX’) en skrå stilling (markert med X1X’1, se figur 11. Linjenes skjæringspunkt kalles materiellets rullsenter. Punktet betegnes C og høyden av rullsenter over sporplan betegnes hc.
Rullvinkelkoeffisient
Hvis materiellet står stille i et spor med overhøyde vil vognkassen helle i bærefjærene og danne en vinkel η med normalen på sporplanet. Rullvinkelkoeffisienten betegnes s og kan beregnes eller måles i praksis, da den avhenger av materiellets belastning. Ved beregninger har rullvinkelkoeffisienten i mange år vært satt til 0,4 for personvogner og 0,2 for godsvogner. For nyere passasjertog settes rullvinkelkoeffisienten normalt til 0,3 hhv. 0,32. Årsaken til at rullvinkelkoeffisienten for godsvogner kan settes til 0,2 henger sammen med de stivere fjærer samt kravet om at forholdet 1:1,25 for belastning av en aksels to hjul overholdes.
Begrensningslinje for rullende materiell
Begrensningslinjen for en type rullende materiell er den største omrisslinje som de enkelte deler av materiellet ikke må overskride. Denne linjen framkommer ved å benytte reglene for innskrenkninger i forhold til referanselinjen. Innskrenkningene for den enkelte type rullende materiell er avhengig av:
- materiellets geometriske parametre
- det betraktede tverrsnittets plassering i forhold til boggisenter hhv. aksel
- høyde over skinnetopp for det betraktede punkt
- konstruksjonsmessige toleranser
- den forutsatte største tillate slitasje
- fjærparametre
Begrensningslinjen inneholder dermed alle aktuelle parametre når materiellet står stille.
Det mulige omriss for materiellet tilsvarer det ikke-skraverte området på figur 12, men i praksis bygges materiellet etter det skraverte området med unntak av stigtrinn, håndtak etc. legges i det ikke-skraverte området.
For ikke å bygge materiellet altfor smalt foretar man normalt en avfasing i endene.
Begrensningslinje for det kinematiske plassbehov
Et materiell som er bygget opp etter begrensningslinjen for rullende materiell vil når det kjører på sporet, innta en stilling som er avhengig av:
- hjulsettenes stilling i sporet
- spillrom i sideretning
- skjevlasting
- semistatisk forskyvning
Semistatisk forskyvning
Som semistatisk forskyvning medregnes den del av sideforskyvningen som skyldes
- bevegelse i materiellets fjærer (rullvinkelkoeffisienten s) som følge av en sentrifugalkraft som ikke er kompensert av overhøyden, evt. et overhøydeoverskudd
- skjevstilling
Verdien er avhengig av høyden h til det betraktede punkt.
Utslag
Med utslag forstås det utslag ut over referanselinjen som er tillatt for et materiell når det befinner seg i spor med større sporvidde enn 1435 mm. Utslag kan forekomme både i kurve og på rettlinje.
Utslaget S i en bestemt høyde fås slik: Til materiellets halve bredde legges forskyvningen D og deretter trekkes referanselinjens halve bredde fra i samme høyde.
Utslaget inngår ved beregning av frittromsprofiler (minste tverrsnitt).
Ytterstilling
Med ytterstilling forstås plassering av materiellet når utslaget S har den maksimale verdien av S0.
Innskrenkning Ei og Ea
For å sikre at materiellet ikke overskrider ytterstillingen, når alle forskyvninger som inngår i D medregnes, må kjøretøyets halve breddemål innskrenkes i forhold til referanselinjen med verdien E. Dette betyr at Ei eller Ea ≥ D – S0.
Ei: Størrelse av innskrenkningen av referanselinjens halve breddemål for tverrsnitt mellom ytterakslene for materiell uten boggier og breddemål for tverrsnitt mellom boggisentrene for materiell med boggier.
Ea: Størrelse av innskrenkningen av referanselinjens halve breddemål for tverrsnitt utenfor ytterste aksel for materiell uten boggier og breddemål for tverrsnitt utenfor boggisentrene for materiell med boggier.
Den halve bredden av materiellets vognkasse må ikke i noe tilfelle være større enn den halve bredden av referanselinjen med fradrag av innskrenkningen E.
Forskyvning i høyde
Den dynamiske påvirkning av materiellet gjør det nødvendig å ta hensyn til en loddrett forskyvning, da materiellet både oppover og nedover skal holde seg innenfor referanselinjens mål. Som utgangspunkt for beregningen betraktes et tomt materiell uten slitasje. Det tas ikke hensyn til semistatisk forskyvning for punkter over 0,400 m over sporplan.
Fastleggelse av minste høyde over sporplan
Ved fastleggelse av minste høyde over sporplan skal det for alle punkter lavere enn 1,170 m over sporplan, tas hensyn til den nedadgående loddrette forskyvning.
Nedsenkning uavhengig av belastning og fjæring
Følgende forhold er uavhengig av vognkassens belastning og av fjærenes tilstand:
- største tillatte hjulslitasje
- slitasje på materielldeler som glidestykke, bremsestenger mv.
- største tillatte slitasje i akselleie
- nedsenkning av boggirammen i forhold til konstruksjonsmålene ved full utnyttelse av tillatte byggetoleranser
- nedsenkning av vognkassen i forhold til konstruksjonsmålene ved full utnyttelse av tillatte byggetoleranser
Nedsenkning på grunn av deformasjon
Følgende forhold medfører nedsenkning på grunn av deformasjon som avhenger av materiellets belastning og fjæring:
- største tillatte nedbøyning av aksel
- største tillatte nedbøyning av boggiramme
- største tillatte nedbøyning i vognkassen som følge av tversgående nedbøyning, langsgående nedbøyning og vridning
Dette gjelder alle typer materiell med unntak av godsvogner, der det av hensyn til den dynamiske påvirkning ved beregning av nedbøyning i langsgående retning anvendes en last tilsvarende vognens største lasteevne med 30 % tillegg.
Nedsenkning på grunn av fjærer
På jernbanemateriell anvendes i hovedsak et kombinert fjærsystem med primær- og sekundærfærer. For de enkelte fjærtyper må det tas hensyn til følgende nedfjæring:
| Fjærtype | Nedfjæring pga. |
|---|---|
| Stålfjærer og gummifjærer | Statisk last |
| Dynamiske påvirkninger | |
| Fjærtoleranser | |
| Luftfjær | Fullstendig nedfjæring, dvs. tom luftbelg (inkl. evt. nødfjæring) |
For de ulike materielltyper gjelder følgende nedsenkning pga. nedfjæring:
| Materielltype | Nedfjæring med |
|---|---|
| Lokomotiver | Overbelastning på 30 % av den avfjærede vekt |
| Motorvogner | 30 % av den avfjærede vekt |
| Personvogner uten passasjerer | 0,030 m |
| Personvogner, pakk- og postvogner med største belastning | Overbelastning på 30 % av den avfjærede vekt eller fullstendig nedfjæring |
| Ordinære godsvogner | Fullstendig nedfjæring |
| Spesielle godsvogner | Overbelastning på 30 % av den avfjærede vekt eller fullstendig nedfjæring |
Det finnes ingen regler for nedfjæring i forbindelse i forbindelse med hjul og aksel.
I henhold til UIC 505-1, bilag 5 kan det ved kjøring i vertikalkurver forekomme nedfjæring utenfor materiellets understøtningsfirkant (ved vognender og på sidene). Spesielt for godsvogner anbefales det å ta hensyn til en ytterligere forskyvning fz som følge av vognkassens ”urolige gange”. En slik bevegelse kan skyldes tømming av luftbelgene eller skjevlast. Det henvises til formler i UIC 505-1, bilag 5.
Fastleggelse av største høyde over sporplan
Hvis den loddrette forskyvning ikke er kjent eller ikke kan beregnes, anbefaler UIC at det benyttes en fast verdi 0,015 m for hvert fjærtrinn i materiellet. Da de fleste materielltyper har to fjærsystemer, regnes både opp- og nedfjæring til 0,030 m.
| Regneeksempel: | |
|---|---|
| Referanselinje | 0,080 m |
| + nedfjæring | 0,030 m |
| + hjulslitasje | 0,040 m1 |
| + diverse bevegelser | 0,020 m1 |
| = nødvendig fri høyde over sporplan | 0,170 m |
1) Varierer med materielltype
Forskyvning i side
For å kunne benytte referanselinjen til beregning av begrensningslinjen må det tas hensyn til forskyvning i sideretning.
Tillatte utslag
Utslaget S må ikke overskride den maksimale verdi av S, kalt S0. Størrelsen av S0 framgår av tabell 3.
| Materielltype | Spor | Beregning av Ei (mellom aksler/boggier) | Beregning av Ea (utenfor aksler/boggier) | ||
|---|---|---|---|---|---|
| h ≤ 0,400 | h > 0,400 | h ≤ 0,400 | h > 0,400 | ||
| Alle | Rettlinje | 0,015 | 0,015 | 0,015 | 0,015 |
| To-akslede
vogner |
R = 250 | 0,025 | 0,030 | 0,025 | 0,030 |
| R = 150 | 0,158 | 0,163 | 0,185 | 0,190 | |
| Boggivogner | R = 250 | 0,010 | 0,015 | 0,025 | 0,030 |
| R = 150 | 0,143 | 0,148 | 0,185 | 0,190 | |
Stilling i kurve
Materiellets stilling i kurver avhenger av sidespillet i de konstruksjonsdeler som danner forbindelse mellom vognkasse og spor samt om det er enkeltaksel, drivboggi eller løpeboggi.
Alt etter materiellets plassering i sporet kan det avledes en innskrenknings-koeffisient A som anvendes i formlene for beregning av Ei og Ea.
Størrelsen av innskrenkningskoeffisienten A framgår av tabellene 4, 5, 6 og 7.
For motorvogner og styrevogner gjelder det spesielle forhold at de inndeles etter adhesjonstallet μ slik at:
- hvis μ ≥ 0,2 betraktes boggien som drivboggi
- hvis 0 < μ < 0,2 betraktes boggien som løpeboggi
- hvis μ = 0 er boggien en løpeboggi
| Materielltype | W∞ | |||
| 1 | 2-akslet, enkeltboggi
samt deler i forbindelse med aksler og boggier |
1 | - | |
| 2 | 2 boggier med unntak
av de i punkt 3 |
1 | - | |
| 3 | En boggi betraktet som
drivboggi og en som løpeboggi |
1 | W∞
|
W∞
|
| Materielltype | Wi (R) | |||||
| 1 | 2-akslet, enkeltboggi
samt deler i forbindelse med aksler og boggier |
1 | - | - | ||
| 2 | 2 boggier med unntak
av de i punkt 3 |
1 | 1 | 1 | ||
| 3 | En boggi betraktet som
drivboggi og en som løpeboggi |
1 | Wi
|
Wi'
|
||
| 4 | 2 boggier som betraktes
som løpeboggier |
1 | 1 | 1 | ||
| Materielltype | q | W∞ | |||
| 1 | 2-akslet, enkeltboggi
samt deler i forbindelse med aksler og boggier |
- | |||
| 2 | 2 boggier med unntak
av de i punkt 3 |
||||
| 3 | En boggi betraktet som
drivboggi og en som løpeboggi |
W∞
|
W∞'
| ||
| Materielltype | q | Wi(R) | Wa(R) | ||||||
| 1 | 2-akslet, enkeltboggi
samt deler i forbindelse med aksler og boggier |
- | - | - | |||||
| 2 | 2 boggier som betraktes som
drivboggier |
1 | |||||||
| 3 | En boggi betraktet som
drivboggi og en som løpeboggi |
Wi
- |
Wi'
|
Wa
|
Wa'
- |
||||
| - | - | ||||||||
| 4 | 2 boggier som betraktes som
løpeboggier |
1 | |||||||
Semistatisk forskyvning
Den semistatiske forskyvningen som benyttes ved beregning av Ei og Ea er avhengig av rullvinkelkoeffisienten s, det betraktede punkts høyde over sporplan og rullsenterets høyde over sporplan hc. Forskyvningen deles mellom materiellets konstruksjonsmål og de faste anlegg (frittromsprofiler) etter følgende prinsipper:
Ved beregning av konstruksjonsmål for materiellet skal i Ei og Ea inngå:
- en manglende overhøyde hhv. overhøyde på opp til 0,050 m
- en manglende overhøyde hhv. overhøyde på 0,200 m dersom s > 0,4 og hc > 0,5
- en manglende overhøyde hhv. overhøyde på 0,200 m dersom det benyttes en større verdi av s, h og hc enn det som ble benyttet ved beregning av avstand til faste gjenstander
- skjevstilling over 1º som skyldes konstruksjons- og innstillingstoleranser eller skjevlasting
Skjevstilling under 1º samt sidesvingninger som følge av kjøring i sporet inngår ved beregning av frittromsprofiler.
Innskrenkningen E
Ved beregning av innskrenkningen E mellom akslene/boggisentrene gjelder:
Innskrenkningen Ei = Forskyvningen Di – Utslaget S0
Ved beregning av innskrenkningen E mellom akslene/boggisentrene gjelder:
Innskrenkningen Ea = Forskyvningen Da – Utslaget S0
For alle beregninger av spillrom i sideretning har hjulenes stilling i sporet en betydning ved beregningen. Dette uttrykkes ved innskrenkningskoeffisienten A som korrigerer visse parametre i formlene.
Formlene for E ser ut som følger:
| (5.1) |
| (5.2) |
De enkelte ledd i formlene kan inndeles i to grupper:
Geometrisk betingede (som også oppstår når vognen står stille)
kurveutslag spillrom i sideretning spillrom i glidestykker særlige tillegg for små radier
og semistatisk betingede (som følge av bevegelse)
rulling
Kurveutslag
Det geometriske utslag for et betraktet tverrsnitt på vognkassen i en kurve uttrykkes ved
| (5.3) |
a er boggisenteravstand eller akselavstand
p er akselavstand i boggi
R er kurveradius
A er innskrenkningskoeffisienten
n er avstand fra det betraktede tverrsnitt til aksel/boggisenter
Stilling i sporet
Med utgangspunkt i fastsettelse av største tillatte sporvidde på 1,465 m, fastsettes spillrommet i sporet til
| (5.4) |
der:
- 1,465 er største tillatte sporvidde
- d er minimumsavstand mellom flenser
- A er innskrenkningskoeffisienten
Forskyvningen av materiellets midtlinje i forhold til spomidt som følge av spillrom mellom hjulsett og boggiramme uttrykkes med q. Hjulenes stilling i sporet påvirker q gjennom innskrenkningskoeffisienten A.
Forskyvningen i sideretning i forhold til midtstillingen av materiellets dreietapp og/eller svingbjelke uttrykkes med w. For materiell uten dreietapp den mulige forskyvningen av boggien i forhold til vognkassen. Denne sideforskyvningen er avhengig av kurveradius og den retning forskyvningen går i. Hjulenes stilling i sporet påvirker w gjennom innskrenkningskoeffisienten A.
Varierer størrelsen av w med kurveradius benyttes:
- wi(R) for kurvens innerside ved kurveradius R
- wa(R) for kurvens ytterside ved kurveradius R
- w∞ for rettlinje
Rulling av vognkassen
Rulling av materiellet med mer enn 1º som følge av materiellets fjærer eller skjevlasting, resulterer i sidebevegelsen z som settes sammen av to ledd.
Det første leddet kan føres tilbake til fjærenes elastisitet og skyldes overhøyde eller manglende overhøyde på 0,050 m.
| (5.5) |
Det andre leddet kan føres tilbake til skjevlasting mer enn 1º.
| (5.6) |
For å ta hensyn til en overhøyde eller manglende overhøyde på 0,200 m fås
| (5.7) |
Dermed kan følgende uttrykk for z settes opp:
| (5.8) |
Formel 5.8 kan benyttes i redusert form dersom h > hc, h > 0,5 m, s ≤ 0,4 og η ≤ 1º kan z settes lik
| (5.9) |
og dersom h < 0,5 m, η ≤ 1º og er uavhengig av hc og s kan z settes lik
| (5.10) |
og dersom h = hc kan z settes lik 0 (gjelder også hvis det er snakk om ikke avfjærede deler).
Små kurveradier
Selv om det ved beregning av frittromsprofilene tas hensyn til vognendens utslag i kurve med leddet S, kan meget lange vogner ha så stort utslag midt på vognen og i enden av overhenget at det kan være nødvendig å begrense vognens breddde for å oppnå sikker kjøring i kurveradier mellom 150 m og 250 m.
For tverrsnitt mellom boggisentrene benyttes xi som kun er aktuelt ved boggisenteravstander på 20 m og større. Verdien av xi tas kun med dersom
| (5.11) |
For tverrsnitt i overheng benyttes xa dersom
| (5.12) |
Innflytelse av overhøyderamper
Kjøringer gjennom overhøyderamper fører til dynamiske bevegelser av vognkassen. Størrelsen av utslaget avhenger av rampestigning og vognkassens stivhet. Utslaget beregnes som
| (5.13) |
der:
β er vognkassens stivhetskoeffisient (β =1 for stive vogner)
sr er rampestigningen
Innflytelsen av overhøyderamper ignoreres av UIC, men den inngår i beregningsemetoden som anvendes i Norge, jf. avsnitt 4.3.
Beregning av innskrenkningen E
Innskrenkningen E for et materiell beregnes for
- tverrsnitt mellom materiellets ytterakser/boggisentre = Ei
- tverrsnitt utenfor materiellets ytterakser/boggisentre = Ea
Materiellets geometriske oppbygning avgjør om det er utslag i kurve eller på rettlinje som er størst.
Ledd i formlene markert med * benyttes for høyder opp til og med 0,400 m.
Ledd i formlene markert med ** benyttes for høyder over 0,400 m.
Innskrenkning for lokomotiver
Som lokomotiv regnes et materiell som kun er trekkraft, og dermed ikke kan ta med personer eller gods.
Beregning av Ei:
Beregn verdien av uttrykket
| (5.14) |
Hvis 5.14 er mindre eller lik 7,5 er det lokomotivets utslag på rettlinje som er dimensjonerende og Ei beregnes som
| (5.15) |
Hvis 5.14 er større enn 7,5 er det lokomotivets utslag i kurver som er
dimensjonerende og Ei beregnes som
| (5.16) |
I 5.16 inngår xi som beregnes som
| (5.17) |
Beregning av Ea:
Beregn verdien av uttrykket
| (5.18) |
Hvis 5.18 er mindre eller lik 7,5 er det lokomotivets utslag på rettlinje som er dimensjonerende og Ea beregnes som
| (5.19) |
Hvis 5.18 er større enn 7,5 er det lokomotivets utslag i kurver som er
dimensjonerende og Ea beregnes som
| (5.20) |
I 5.20 inngår xa som beregnes som
| (5.21) |
Regneeksempel:
Alle beregninger utføres på høyder over 0,400 m.
Det er valgt følgende parametre:
a = 9,700 m, d = 1,410 m, p = 2,800 m, q = 0,006, s = 0,1,
ni = a/2 = 4,850 m, na = 3,250 m, hc = 0,500 m, η0 = 1˚,
wi(R) = Wa(R) = 0,060 og uavhengig av radius
Konstruksjonsbredden på midten av lokomotivet
Det undersøkes om det er lokomotivets utslag på rettlinje eller i kurve som er dimensjonerende. Det skjer ved å sette inn verdier i formel 5.14:
Verdien av uttrykket er større enn 7,5 som betyr at lokomotivets utslag i kurve blir dimensjonerende og det beregnes etter formel 5.16 og 5.17.
Først kontrolleres det om xi > 0. Det skjer ved å sette inn verdier i formel 5.17.
Da verdien av xi er negativ inngår den med verdi 0 i formel 5.16.
| Høyde over sporplan | Halv bredde av referanselinje | Ei - z | z | Mulig halv bredde for lokomotiv |
|---|---|---|---|---|
| 0,500 | 1,620 | 0,1145 | 0,0000 | 1,5055 |
| 1,170 | 1,620 | 0,1145 | 0,0022 | 1,5033 |
| 1,170 | 1,645 | 0,1145 | 0,0022 | 1,5283 |
| 3,250 | 1,645 | 0,1145 | 0,0092 | 1,5213 |
| 3,700 | 1,425 | 0,1145 | 0,0107 | 1,2998 |
| 4,010 | 1,120 | 0,1145 | 0,0117 | 0,9938 |
| 4,310 | 0,525 | 0,1145 | 0,0127 | 0,3978 |
Konstruksjonsbredden i enden av lokomotivet
Det undersøkes om det er lokomotivets utslag på rettlinje eller i kurve som er dimensjonerende. Det skjer ved å sette inn verdier i formel:
Verdien av uttrykket er større enn 7,5 som betyr at lokomotivets utslag i kurve blir dimensjonerende og det beregnes etter formel
Først kontrolleres det om xa > 0. Det skjer ved å sette inn verdier i formel
Da verdien av xa er negativ inngår den med verdi 0 i formel
| Høyde over sporplan | Halv bredde av referanselinje | Ei - z | z | Mulig halv bredde for lokomotiv |
|---|---|---|---|---|
| 0,500 | 1,620 | 0,1972 | 0,0000 | 1,4228 |
| 1,170 | 1,620 | 0,1972 | 0,0022 | 1,4206 |
| 1,170 | 1,645 | 0,1972 | 0,0022 | 1,4456 |
| 3,250 | 1,645 | 0,1972 | 0,0092 | 1,4386 |
| 3,700 | 1,425 | 0,1972 | 0,0107 | 1,2171 |
| 4,010 | 1,120 | 0,1972 | 0,0117 | 0,9111 |
| 4,310 | 0,525 | 0,1972 | 0,0127 | 0,3151 |
Konstruksjonsbredden i et valgt punkt på lokomotivet
Det skal beregnes de tillatte konstruksjonsmål for et loddrett håndtak på siden av vognkassen. Håndtaket begynner 1,300 m og slutter 2,600 m over sporplan. Håndtaket sitter mellom boggisenterne i en avstand fra nærmeste boggisenter på 2,450 m.
Det ble i eksemplet over fastlagt at lokomotivets utslag i kurve blir dimensjonerende og det beregnes etter formel 5.16 og 5.17.
Først kontrolleres det om xi > 0. Det skjer ved å sette inn verdier i formel 5.17.
Da verdien av xi er negativ inngår den med verdi 0 i formel 5.16.
Deretter beregnes z for høyden 1,300 m og 2,600 m over sporplan.
| Høyde over sporplan | Halv bredde av referanselinje | Ei - z | z | Mulig halv bredde for lokomotiv |
|---|---|---|---|---|
| 1,300 | 1,645 | 0,1029 | 0,0027 | 1,5394 |
| 2,600 | 1,645 | 0,1029 | 0,0070 | 1,5351 |
Håndtaket kan dermed plasseres 1,535 m fra spormidt.
Innskrenkning for motorvogner
Ved beregning av innskrenkningene Ei og Ea for motorvogner, inngår en avhengighet mellom spillrommet w og kurveradius. Formlene kan dermed benyttes uansett om det er lineær eller ikke-lineær endring av spillrommet w.
Derimot skjelnes det mellom drivboggi og løpeboggi. Drivboggi er en boggi med påbygget motor/trekkraft på en eller fler av akslene. Løpeboggi er alle andre former for boggi.
Ved beregning av innskrenkningen E for motorvogner anvendes ulike formler avhengig av boggitype, adhesjon og boggiens stilling i sporet, jf. tabell .4 - .7. Beregningsmetode framgår av tabell 11.
| Motorvogn med | Adhesjonstall | Stilling i sporet | Beregnes som
|
|---|---|---|---|
| to drivboggier | μ ≥ 0,2 | Tabell .4 - .7, tilfelle 2 | lokomotiv |
| to boggier som betraktes som løpeboggier | 0 < μ < 0,2 | Tabell .4 og .6, tilfelle 2, og tabell .5 og .7, tilfelle 4 | personvogn |
| en boggi som betraktes som løpeboggi og en løpeboggi | 0 < μ < 0,2
μ = 0 | ||
| en motorboggi og en løpeboggi eller en boggi som betraktes som løpeboggi | μ = 0,2
μ = 0 0 < μ < 0,2 |
Tabell .4 - .7, tilfelle 3 | lokomotiv eller motorvogn2 |
I formlene inngår adhesjonstallet μ. Avstanden fra det betraktede tverrsnitt til boggisentret i den drivende boggi betegnes nμ.
Beregning av Ei:
Det benyttes den største innskrenkning beregnet ved hjelp av formel 5.22 og 5.23.
| (5.22) |
| (5.23) |
I formel 5.23 inngår xi som beregnes som
| (5.24) |
Beregning av Ea:
For tverrsnitt utenfor boggisentrene skjelnes det mellom om motorvogna kjørerer med drivboggien eller med løpeboggien forrest. Det benyttes ulike formler i de to tilfeller.
Dersom motorvogna kjører med drivboggien forrest i kjøreretningen, anvendes den av formel .25 og .26 som gir størst verdi.
| (5.25) |
| (5.26) |
I formel 5.26 inngår xa som beregnes som
| (5.27) |
Dersom motorvogna kjører med løpeboggien forrest i kjøreretningen, anvendes den av formel og som gir størst verdi.
| (5.28) |
| (5.29) |
I formel 5.29 inngår xa som beregnes som
| (5.30) |
Regneeksempel:
Alle beregninger utføres for høyder over 0,400 m.
Motorvognas parametre:
a = 15,400 m, d = 1,420 m, q = 0,002, s = 0,35, ni = 7,700 m, na = 2,750 m,
hc = 0,500 m, p = 2,400 m, p’ = 2,200 m,
w∞ = 0,060, wi(250) = 0,022, wa(250) = 0,046,
w’∞ = 0,050, w’i(250) = 0,020, w’a(250) = 0,050,
η0 < 1˚, μ > 0,2 for drivboggi, μ = 0 for løpeboggi
Med de verdier av μ som er angitt skal motorvogna beregnes som lokomotiv med mindre det er spesielt viktig å utnytte profilet maksimalt, jf. tabell 11. For å eksemplifisere beregningsmetoden for motorvogner tas det utgangspunkt i et slikt tilfelle.
Konstruksjonsbredden på midten av motorvogna:
Det benyttes ved beregningene n = ni = nμ = a/2 = 7,700 m.
Først bergnes Ei etter formel .22.
For å regne ut Ei etter formel 5.23 må først xi beregnes etter formel .24.
Merk at siden verdien av wi(150) og w’i(150) ikke er kjent, settes de til samme verdi som for radius 250. Dette gir en noe større verdi for E og man er på ”sikker side”.
Verdien av xi er negativ og inngår dermed med verdien 0 i formel 5.23.
Det skal benyttes den største av de beregnede innskrenkninger, dvs. 0,1330 + z.
| Høyde over sporplan | Halv bredde av referanselinje | Ei - z | z | Mulig halv bredde for lokomotiv |
|---|---|---|---|---|
| 0,500 | 1,620 | 0,1330 | 0,0000 | 1,4870 |
| 1,170 | 1,620 | 0,1330 | 0,0078 | 1,4792 |
| 1,170 | 1,645 | 0,1330 | 0,0078 | 1,5042 |
| 3,250 | 1,645 | 0,1330 | 0,0321 | 1,4799 |
| 3,700 | 1,425 | 0,1330 | 0,0373 | 1,2547 |
| 4,010 | 1,120 | 0,1330 | 0,0410 | 0,9460 |
| 4,310 | 0,525 | 0,1330 | 0,0445 | 0,3475 |
Konstruksjonsbredde i den enden de drivboggien befinner seg
Det kontrolleres vha. formel 5.27 om xa skal benyttes.
Verdien av xa blir negativ og xa settes lik null i de videre beregninger.
Deretter beregnes utslaget i enden av vognkassen. Det benyttes n = na = 2,750. Først utføres beregning etter formel 5.25.
Deretter utføres beregning etter formel 5.26.
Det skal benyttes den største verdi for Ea, dvs. Ea = 0,1541 + z.
| Høyde over sporplan | Halv bredde av referanselinje | Ei - z | z | Mulig halv bredde for lokomotiv |
|---|---|---|---|---|
| 0,500 | 1,620 | 0,1541 | 0,0000 | 1,4659 |
| 1,170 | 1,620 | 0,1541 | 0,0078 | 1,4581 |
| 1,170 | 1,645 | 0,1541 | 0,0078 | 1,4831 |
| 3,250 | 1,645 | 0,1541 | 0,0321 | 1,4588 |
| 3,700 | 1,425 | 0,1541 | 0,0373 | 1,2336 |
| 4,010 | 1,120 | 0,1541 | 0,0410 | 0,9249 |
| 4,310 | 0,525 | 0,1541 | 0,0445 | 0,3264 |
Konstruksjonsbredde i den enden de løpeboggien befinner seg
Også ved denne beregningen inngår xa, men den er tidligere beregnet til negativ og inngår i formlene med verdi 0.
Deretter beregnes utslaget i enden av vognkassen. Det benyttes n = na = 2,750. Først utføres beregning etter formel 5.28.
Deretter utføres beregning etter formel 5.29.
Det skal benyttes den største verdi for Ea, dvs. Ea = 0,1669 + z.
| Høyde over sporplan | Halv bredde av referanselinje | Ei - z | z | Mulig halv bredde for lokomotiv |
|---|---|---|---|---|
| 0,500 | 1,620 | 0,1669 | 0,0000 | 1,4531 |
| 1,170 | 1,620 | 0,1669 | 0,0078 | 1,4453 |
| 1,170 | 1,645 | 0,1669 | 0,0078 | 1,4703 |
| 3,250 | 1,645 | 0,1669 | 0,0321 | 1,4460 |
| 3,700 | 1,425 | 0,1669 | 0,0373 | 1,2208 |
| 4,010 | 1,120 | 0,1669 | 0,0410 | 0,9121 |
| 4,310 | 0,525 | 0,1669 | 0,0445 | 0,3136 |
Innskrenkning for personvogner
Ved beregninger av innskrenkningene Ei og Ea for personvogner inngår en sammenheng mellom spillrommet w og kurveradius.
Som personvogner regnes materiell til befordring av personer, reisegods og post samt mellomvogner og i visse tilfeller styrevogner i motorvognsett.
Beregning av Ei:
Først beregnes uttrykkene
| (5.31) |
og
| (5.32) |
der 0 erstattes av 2,5 for høyder t.o.m. 0,400 m.
Hvis uttrykket beregnet etter formel 5.31 er mindre enn eller lik uttrykket beregnet etter formel 5.32, er det personvognas utslag på rettlinje som er dimensjonerende. Det benyttes da følgende formel:
| (5.33) |
Dersom det er personvognas utslag i kurve som er dimensjonerende, benyttes følgende formel:
| (5.34) |
I formel 5.34 inngår xi som beregnes etter følgende formel:
| (5.35) |
Beregning av Ea:
Først beregnes uttrykkene
| (5.36) |
og
| (5.37) |
der 7,5 erstattes med 5,0 i høyder t.o.m. 0,400 m.
Hvis uttrykket beregnet etter formel 5.36 er mindre enn eller lik uttrykket beregnet etter formel 5.37, er det personvognas utslag på rettlinje som er dimensjonerende. Det benyttes da følgende formel:
| (5.38) |
Dersom det er personvognas utslag i kurve som er dimensjonerende, benyttes følgende formel:
| (5.39) |
I formel 5.39 inngår xa som beregnes etter følgende formel:
| (5.40) |
Regneeksempel:
Alle beregninger utføres for høyder over 0,400 m.
Personvognas parametre:
a = 18,400 m, d = 1,410 m, q = 0,002, s = 0,3,
ni = a/2 = 9,200 m, na = 3,253 m, hc = 0,500 m, p = 2,560 m,
w = 0,082, wi(250) = 0,040, wa(250) = 0,028,
η0 < 1˚, μ > 0,2 for drivboggi, μ = 0 for løpeboggi
Konstruksjonsbredden på midten av personvogna
Først kontrolleres det om det er personvognas utslag på rettlinje eller i kurve som er dimensjonerende. Dette skjer ved beregning etter formlene 5.31 og 5.32.
Dette betyr at det er vognas utslag i kurve som er dimensjonerende og det beregnes etter formel 5.34. Her inngår xi dersom xi > 0. Derfor beregnes først xi etter formel 5.35.
Verdien av xi blir negativ og xi inngår med verdi lik 0 i de videre beregninger. Det beregnes etter formel 5.34.
| Høyde over sporplan | Halv bredde av referanselinje | Ei - z | z | Mulig halv bredde for lokomotiv |
|---|---|---|---|---|
| 0,500 | 1,620 | 0,1996 | 0,0000 | 1,4204 |
| 1,170 | 1,620 | 0,1996 | 0,0067 | 1,4137 |
| 1,170 | 1,645 | 0,1996 | 0,0067 | 1,4387 |
| 3,250 | 1,645 | 0,1996 | 0,0275 | 1,4179 |
| 3,700 | 1,425 | 0,1996 | 0,0320 | 1,1934 |
| 4,010 | 1,120 | 0,1996 | 0,0351 | 0,8853 |
| 4,310 | 0,525 | 0,1996 | 0,0381 | 0,2873 |
Konstruksjonsbredden i enden av personvogna
Først kontrolleres det om det er personvognas utslag på rettlinje eller i kurve som er dimensjonerende. Dette skjer ved beregning etter formlene 5.36 og 5.37.
Dette betyr at det er vognas utslag i kurve som er dimensjonerende og det beregnes etter formel 5.39. Her inngår xi dersom xi > 0. Derfor beregnes først xi etter formel 5.40.
Verdien av xi blir negativ og xi inngår med verdi lik 0 i de videre beregninger
Verdien av innskrenkningen ved vognenden 3,253 m fra boggisenter blir da:
| Høyde over sporplan | Halv bredde av referanselinje | Ei - z | z | Mulig halv bredde for lokomotiv |
|---|---|---|---|---|
| 0,500 | 1,620 | 0,1827 | 0,0000 | 1,4373 |
| 1,170 | 1,620 | 0,1827 | 0,0067 | 1,4306 |
| 1,170 | 1,645 | 0,1827 | 0,0067 | 1,4556 |
| 3,250 | 1,645 | 0,1827 | 0,0275 | 1,4348 |
| 3,700 | 1,425 | 0,1827 | 0,0320 | 1,2103 |
| 4,010 | 1,120 | 0,1827 | 0,0351 | 0,9022 |
| 4,310 | 0,525 | 0,1827 | 0,0381 | 0,3042 |
Innskrenkning for to-akslede vogner
For beregning av Ei og Ea for to-akslede godsvogner er det ikke avhengig av spillrommet w og kurveradius. Hvis godsvogna har 3 aksler regnes alle mål og beregninger fra ytterakslene.
Beregning av Ei:
Først beregnes verdien av uttrykket
| (5.41) |
Dersom verdien av uttrykket beregnet etter formel .41 er mindre eller lik 7,5 (5,0 for punkter med høyde t.o.m. 0,400 m), er det godsvognas utslag på rettlinje som er dimensjonerende. Det beregnes etter følgende formel:
| (5.42) |
Dersom godsvognas utslag i kurve er dimensjonerende beregnes det etter følgende formel:
| (5.43) |
Beregning av Ea:
Først beregnes verdien av uttrykket
| (5.44) |
Dersom verdien av uttrykket beregnet etter .44 er mindre eller lik 7,5 (5,0 for punkter med høyde t.o.m. 0,400 m), er det godsvognas utslag på rettlinje som er dimensjonerende. Det beregnes etter følgende formel:
| (5.45) |
Dersom godsvognas utslag i kurve er dimensjonerende beregnes det etter følgende formel:
| (5.46) |
Regneeksempel:
Alle beregninger utføres for høyder over 0,400 m.
Godsvognas parametre:
a = 8,000 m, d = 1,410 m, q = 0,023, s = 0,1,
ni = a/2 = 4,000 m, na = 2,390 m, hc = 0,500 m,
η0 < 1˚, w = 0 (ingen boggi)
Konstruksjonsbredden på midten av godsvogna
Beregning etter formel .41 gir
Verdien er større enn 7,5 og det er vognas stilling i kurve som er dimensjonerende.
| Høyde over sporplan | Halv bredde av referanselinje | Ei - z | z | Mulig halv bredde for lokomotiv |
|---|---|---|---|---|
| 0,500 | 1,620 | 0,0525 | 0,0000 | 1,5675 |
| 1,170 | 1,620 | 0,0525 | 0,0022 | 1,5653 |
| 1,170 | 1,645 | 0,0525 | 0,0022 | 1,5903 |
| 3,250 | 1,645 | 0,0525 | 0,0092 | 1,5833 |
| 3,700 | 1,425 | 0,0525 | 0,0107 | 1,3618 |
| 4,010 | 1,120 | 0,0525 | 0,0117 | 1,0558 |
| 4,310 | 0,525 | 0,0525 | 0,0127 | 0,4598 |
Konstruksjonsbredden i enden av godsvogna
Beregning etter formel 5.44 gir:
Verdien er større enn 7,5 og det er vognas stilling i kurve som er dimensjonerende.
| Høyde over sporplan | Halv bredde av referanselinje | Ei - z | z | Mulig halv bredde for lokomotiv |
|---|---|---|---|---|
| 0,500 | 1,620 | 0,0775 | 0,0000 | 1,5425 |
| 1,170 | 1,620 | 0,0775 | 0,0022 | 1,5403 |
| 1,170 | 1,645 | 0,0775 | 0,0022 | 1,5653 |
| 3,250 | 1,645 | 0,0775 | 0,0092 | 1,5583 |
| 3,700 | 1,425 | 0,0775 | 0,0107 | 1,3368 |
| 4,010 | 1,120 | 0,0775 | 0,0117 | 1,0308 |
| 4,310 | 0,525 | 0,0775 | 0,0127 | 0,4348 |
Innskrenkning for godsvogner med boggier
For selve boggien og deler i fast forbindelse med denne, benyttes formlene for 2-akslede vogner.
Beregning av Ei:
Først beregnes uttrykkene
| (5.47) |
og
| (5.48) |
der 0 erstattes av 2,5 for høyder t.o.m. 0,400 m.
Hvis uttrykket beregnet etter formel .47 er mindre enn eller lik uttrykket beregnet etter formel .48, er det godsvognas utslag på rettlinje som er dimensjonerende. Det benyttes da følgende formel:
| (5.49) |
Dersom det er personvognens utslag i kurve som er dimensjonerende, benyttes følgende formel:
| (5.50) |
I formel .50 inngår xi som beregnes etter følgende formel:
| (5.51) |
Beregning av Ea:
Først beregnes uttrykkene
| (5.52) |
og
| (5.53) |
der 7,5 erstattes med 5,0 i høyder t.o.m. 0,400 m.
Hvis uttrykket beregnet etter formel .52 er mindre enn eller lik uttrykket beregnet etter formel .53, er det godsvognas utslag på rettlinje som er dimensjonerende. Det benyttes da følgende formel:
| (5.54) |
Dersom det er godsvognas utslag i kurve som er dimensjonerende, benyttes følgende formel:
| (5.55) |
I formel .55 inngår xa som beregnes etter følgende formel:
| (5.56) |
Gjenstander på taket av elektrisk materiell
For gjenstander på taket av elektrisk materiell gjelder en egen referanselinje, jf. figur 7. Denne referanselinjen er tenkt benyttet til gjenstander i forbindelse med strømavtakeren og øvrige spenningsførende komponenter samt alle ikke-spenningsførende komponenter.
Beregning av ytterstilling for strømavtakere på elektriske motorvogner med en drivboggi og en løpeboggi, skal utføres som om motorvognen har to boggier av samme type som den strømavtakeren sitter over.
For å sikre at strømavtakeren alltid holder seg innenfor referanselinjen for spenningsførende deler, må det utføres en beregning av innskrenkningen E. Det beregnes innskrenkning med strømavtakeren hevet til høyde 6,50 m over sporplan (E’i og E’a) og til høyde 5,00 m over sporplan (E’’i og E’’a). Dersom beregningene viser at den relevante innskrenkning E’ hhv. E’’ er negativ eller 0 er referanselinjen overholdt. Dette vil alltid være tilfelle når strømavtakeren strømavtakeren er plassert over boggisenteret.
Innledende beregninger:
Først beregnes j’, dvs. differansen mellom den beregnede og den virkelige forskyvning som følge av spillrom.
| (5.57) |
| (5.58) |
Deretter beregnes z’, dvs. differansen mellom den beregnede rulling og den virkelige forskyvning som følge av rulling av det øverste punktet på strømavtakeren.
Hvis rullvinkelkoeffisienten s ≤ 0,225 benyttes formelen:
| (5.59) |
Hvis s > 0,225 benyttes formelen:
| (5.60) |
Deretter beregnes z’’, dvs. differansen mellom den beregnede rulling og den virkelige forskyvning som følge av rulling av den øverste delen av strømavtakeren.
Hvis rullvinkelkoeffisienten s ≤ 0,225 benyttes formelen:
| (5.61) |
Hvis s > 0,225 benyttes formelen:
| (5.62) |
Beregning av innskrenkningen E mellom boggisentrene:
Ved beregningen av E må det først finnes ut om det er innstillingen av materiellet i kurve eller på rettlinje som er dimensjonerende. Det beregnes E’i og E”i med n = ni.
Dersom an – n² + (p²/4) ≤ 5 er det innstillingen på rettlinje som er dimensjonerende. Det anvendes følgende formler:
| (5.63) |
| (5.64) |
Dersom an – n² + (p²/4) > 5 er det innstillingen i kurve som er dimensjonerende. Det anvendes følgende formler:
| (5.65) |
| (5.66) |
Beregning av innskrenkningen E utenfor boggisentrene:
Ved beregningen av E må det først finnes ut om det er innstillingen av materiellet i kurve eller på rettlinje som er dimensjonerende. Det beregnes E’i og E”i med n = na.
Dersom an + n² - (p²/4) ≤ 5 er det innstillingen på rettlinje som er dimensjonerende. Det anvendes følgende formler:
| (5.67) |
| (5.68) |
Dersom an + n² - (p²/4) > 5 er det innstillingen i kurve som er dimensjonerende. Det anvendes følgende formler:
| (5.69) |
| (5.70) |
Når strømavtakeren er senket, skal referanselinjen for strømavtakere også være overholdt. Dersom materiellet skal framføres på ikke-elektrifiserte, skal den gjeldende referanselinjen for strekningen overholdes.
Alle de deler på taket av materiellet som ikke er isolert og som kan være strømførende, skal være plassert slik at de ligger 0,170 m fra referanselinjen.
Frittromsprofiler
Frittromsprofiler angir hvor nær et objekt (bru, signal, fjell, plattform, skilt osv.) kan være sporet.
Tillegg til referanselinjens horisontale mål
I dette avsnittet beskrives de beregningsmetoder som beskrives i UIC fiche 505-4.
Geometrisk utslag
Det geometriske utslag beregnes som de ekstra bevegelser som opptrer når toget kjører gjennom kurver pga. materiellets gangegenskaper . Utslaget vil dermed bestå av et radiusavhengig og et sporviddeavhengig ledd.
| Høyde over sporplan | Utslag [mm] |
|---|---|
| ∞ - 1500 | 0 |
| 1499 – 500 | 5 |
| 499 – 300 | 10 |
| 299 – 250 | 15 |
| 249 – 240 | 25 |
| 239 – 230 | 35 |
| 229 – 220 | 50 |
| 219 – 210 | 60 |
| 209 – 200 | 75 |
| 199 – 190 | 90 |
| 189 – 180 | 110 |
| 179 – 170 | 130 |
| 169 – 160 | 150 |
| 159 – 150 | 175 |
| 149 – 140 | 205 |
| 139 – 130 | 235 |
| 129 – 120 | 275 |
Følgende mål skal ikke økes:
- målene m og n rundt skinnehodet
- alle mål i el-profiler da strømavtakeren er plassert over boggien
Semistatisk forskyvning
Den semistatiske forskyvningen avhenger av overhøydeoverskuddet E eller manglende overhøyde I og som derfor ikke kan innberegnes i innskrenkningen E til materiellet. Da forskyvningen I egentlig er en dreining, inngår det betraktede punkts høyde (h) over sporplan i formelen.
| (5.71) |
Ved beregning av materiell etter UIC fiche 505-1 inngår E hhv. I = 0,05 m i beregningen av materiellet. Det må derfor regnes med et ytterligere tillegg dersom E hhv. I er > 0,05 m.
Feil i sporets beliggenhet
Feil i sporets beliggenhet skyldes forskyvning av sporet i sideretning pga. driftsmessige forhold og måles som hvor langt ut spormidt kan bevege seg i forhold til skal-beliggenheten. Maksimal grense for en slik forskyvning er anbefalt av UIC å være ± 0,025 m.
Virkning av overhøydefeil
Dersom det skjer en fullstendig avbalansering av sentrifugalkraften gjennom overhøyden, snakker man om likevektsoverhøyde. Ved alle andre tilfeller har man overhøydeoverskudd E eller manglende overhøyde I (”overhøydefeil”).
Overhøydeoverskudd har man når den aktuelle overhøyden er større enn den avbalanserte overhøyden. Materiellet vil krenge innover i kurven.
Manglende overhøyde har man når den aktuelle overhøyden er mindre enn den avbalanserte overhøyden. Materiellet vil krenge utover i kurven.
For spor med hastigheter > 80 km/h, regnes en dynamisk virkning av ”overhøydefeilen” på 0,015 m. Den tilsvarende geometriske virkning kan uttrykkes med
| (5.72) |
For spor med hastigheter ≤ 80 km/h, regnes en dynamisk virkning av ”overhøydefeilen” på 0,020 m. Den tilsvarende geometriske virkning kan uttrykkes med
| (5.73) |
Dynamisk rulling
Dynamisk rulling følger av den dynamiske vekselvirkning mellom spor og materiell. Denne rullingen er avhengig av sporets vedlikeholdsstandard. Hvert land fastsetter egne toleranser, men dersom de ikke foreligger har UIC gitt følgende tabell.
| Kurvens ytterside eller rettlinje | Kurvens innerside | |
|---|---|---|
| Godt vedlikeholdt spor | 0,039 m | 0,007 m |
| Øvrige spor | 0,065 | m 0,065 m |
Virkningen av materiellets skjevstilling
Virkningen av materiellets skjevstilling som følge av konstruksjons- og innstillingstoleranser eller ujevn lastfordeling, skal innregnes i frittromsprofilene med 1˚. Skjevstillingen settes sammen av to ledd der eksentrisk nyttelast inngår med 0,050 m og unøyaktig fjærjustering inngår med 0,015 m. Summen av verdiene = 0,065 m, tilsvarer 1˚ skjevstilling.
Nasjonelt tillegg
Tillegget fastsettes av hver enkelt forvaltning bl.a. av hensyn til
- spesialtransporter, konteinere, dobbeldekkere osv.
- utseende av eksisterende frittromsprofiler
- sikkerhetstillegg pga. økt hastighet
- sikkerhetstillegg pga. sterk vind
- utligningstillegg for å oppnå loddrette linjer i frittromsprofiler
Det foreligger ingen standardisering for disse verdiene.
Reduksjon av tillegg
Tillegg pga. feil i sporets beliggenhet, virkning av overhøydefeil, dynamisk rulling og virkning av materiellets skjevstilling opptrer tilfeldig og behandles av den grunn statistisk. Summen av disse tilleggene betegnes Σ og beregnes som den kvadratiske middelverdi av summen med tillegg av 20 %, jf. UIC fiche 505, bilag F). På denne måten oppnår man en reduksjon av tilleggene. Denne reduksjonen gjelder bare punkter på referanselinjen over 0,500 m over sporplan.
Regneeksempel:
Tilfeldige bevegelser gir:
| (5.72) |
| h | Tilfeldige
bevegelser |
|---|---|
| 1,170 | 0,037 |
| 3,530 | 0,090 |
| 3,835 | 0,098 |
| 4,680 | 0,120 |
Tillegg til referanselinjens vertikale mål
Infrastrukturen korrigerer alle vertikale mål på referanselinjen med et spillrom som tar hensyn til vertikalkurvaturen. Dette gjøres ved at vertikale mål over 1,200 m over sporplan økes med 50000/R der R er vertikalradien. Vertikale mål under 1,200 m reduseres tilsvarende. I praksis beregnes det kun tillegg ved R < 10000 m.
Beregning av konstruksjonsmål ut fra frittromsprofil - norsk beregningsmodell
I dette avsnittet er det beskrevet hvordan beregningen av konstruksjonsmålene for rullende materiell er beregnet i Norge. Denne metoden ble beskrevet i forbindelse med anskaffelsen av B3-materiell og tok utgangspunkt i frittromsprofilet, jf, avsnitt 2.2.4. Konstruksjonsmålene fremkommer ved å beregne summen av innskrenkningen E og Σ.
I E inngår også utslag som følge av kjøring gjennom overhøyderampen, jf. avsnitt 3.5.5.
Den norske beregningsmodellen ble senere utviklet som et edb-program med navn PROFIL. Bestillinger av profilberegninger gjøres ved å fylle ut skjemaet som vist i tabell 22 .
| Til: ___________________________________ Fra: _______________________________ Dato: | ||||||
|---|---|---|---|---|---|---|
| Bestilling av profilberegning for | ||||||
| Alt 1 | Alt 2 | Alt 3 | Alt 4 | |||
|---|---|---|---|---|---|---|
| a | Boggisenteravstand | [m] | ||||
| p | Akselavstand i boggi | [m] | ||||
| d | Hjulsatsens min. sporvidde | [mm] | 1410 | 1410 | 1410 | 1410 |
| q | Maks. fjærspill i primærfjæring | [m] | ||||
| w | Maks. fjærspill i sekundærfjæring | [m] | ||||
| ? x | Avstand boggisenter til sidefjæring | [m] | ||||
| k | Kurvefaktor (k = ½ · a· ? x) | [m2] | ||||
| s | Rullvinkelkoeffisient | [-] | ||||
| hc | Høyde til rullsenterover sporplan | [m] | ||||
| ß | Vognkassens stivhetskoeffisient | [-] | 1 | 1 | 1 | 1 |
| ?hA | Vognkassens skjevstillingpga. eksentrisk nyttelast | [rad] | 0,009 | 0,009 | 0,009 | 0,009 |
| ?HB | Vognkassens skjevstillingpga. unøyaktig
fjærjustering |
[rad] | 0,009 | 0,009 | 0,009 | 0,009 |
| Rmin | Minste beregnede kurveradius | [m] | ||||
| ni | Snitt fra boggisenter mot vognmidte | [m] | ||||
| na | Snitt fra boggisenter mot vognende | [m] | ||||
| ? | y Beregningens vertikale trinnlengde | [m] | ||||
| Y | Beregningens vertikale område | [m] | ||||
| Beregningstilfeller: | ||||||
| A | Toakslede vogner/lokomotiver | |||||
| B | Boggivogner uten motor | |||||
| M2 | Boggimotorvogner og –lok med 2 motorboggier | |||||
| For boggimotorvogner og –lok med drift på bare en boggi gjelder: | ||||||
| M1L | Snitt fra vognmidte mot løpeboggi | [m] | ||||
| M2L | Snitt fra vognmidte mot drivboggi | [m] | ||||
| Krenging: | ||||||
| ?k | Maksimal krengevinkel | [grd] | ||||
| hk | Krengesenterhøyde over sporplan | [m] | ||||
| Radius-, overhøyde- og hastighetsdata: | ||||||
|---|---|---|---|---|---|---|
| R | h | v1 + 5 | I1 | v2 | I2 | |
| [m] | [m] | [km/h] | [m] | [km/h] | [m] | |
| 180 | 0,150 | 60 | 0,086 | |||
| 250 | 0,150 | 75 | 0,115 | |||
| 350 | 0,145 | 90 | 0,128 | |||
| 450 | 0,135 | 100 | 0,127 | |||
| 700 | 0,110 | 115 | 0,113 | |||
| 1000 | 0,080 | 125 | 0,104 | |||
| 8 | 0 | 125 | 0 | |||
Minste tverrsnitt
Utenfor frittromsprofilene er det definert et ytterligere profil som kalles minste tverrsnitt. Dette profilet kan i prinsippet ha innskrenkninger som befinner seg mellom minste tverrsnitt og frittromsprofilene. Minste tverrsnitt kan defineres som følger:
Til hver side av sporet, over sporet og også mellom skinnene skal et visst rom være fritt for hindringer slik at man har den forutsatte klaring for fremføring av tog. Tverrsnittet av dette rom benevnes minste tverrsnitt.
Måleaksen for minste tverrsnitt står vinkelrett på sporplanet i spormidt.
Fastsatte minste tverrsnitt for eksisterende baner
De ulike banestrekningene har i sin tid blitt bygget med ulike tverrsnitt. Dette har ført til at man gjennom tiden har operert med en rekke forskjellige minste tverrsnitt. Ved fornyelsen av NSBs regelverk i 1993 ble det bestemt at man for eksisterende baner kun skulle operere med ett tverrsnitt, A-85. For nye baner valgte man å basere seg på et UIC-tverrsnitt benevnt UIC GC som samsvarte med tverrsnitt som ble anvendt hos enkelte andre forvaltninger.
Fra og med 1998 ble to nye minste tverrsnitt innført:: A-96 og A-C.
Minste tverrsnitt A-85
Minste tverrsnitt A-85 ble innført 1985 og var den gang det største minste tverrsnitt. I tillegg ble det benyttet 3 mindre minste tverrsnitt for enkelte banestrekninger. I 1993 ble disse tverrsnittene fjernet og man A-85 ble innført på hele det norske jernbanenettet. Dermed fikk man langt flere innskrenkninger å forholde seg til.
| Minste tverrsnitt | Strekning
|
|---|---|
| RA-85 (redusert A-85) | Myrdal – Bergen |
| B | Nelaug – Arendal |
| C | Sira – Flekkefjord |
I tillegg til minste tverrsnitt gjelder for elektrifiserte spor følgende profiler
- fritt profil for strømavtaker
- minste tverrsnitt E
Ki= kurveutslag mot den indre siden av en kurve
Ky = kurveutslag mot den ytre siden av en kurve
Det skraverte feltet er beskrevet i avsnitt 5.4.
Minste tverrsnitt A-96
Minste tverrsnitt A-96 er definert som det minimumstverrsnitt som tillater framføring av transporter i henhold til lasteprofil K. Da lasteprofil K har samme bredde som utvidet lasteprofil for 2-akslede vogner under 3500 mm og samme høyde, kan A-96 stort sett sammenfalle med A-85. Kun punktet (1740,4100) må erstattes. A-96 får i stedet punktet (1620,4590) som er basert på at klaringen mellom A-96 og lasteprofil K ikke noe sted skal være mindre enn 300 mm.
I tillegg kommer kurveutslag, jf. tabell 25 og tabell 26.
Minste tverrsnitt A-C
Minste tverrsnitt A-C er tenkt som det minimumstverrsnitt som tillater framføring av transporter i henhold til lasteprofil UIC GC. Tverrsnittet sammenfaller med A-85 lavere enn 3440 mm over skinnetopp.
I tillegg kommer kurveutslag, jf. tabell 25.
Kurveutslag
Minste tverrsnitts bredde varierer med sporets kurvatur på grunn av det ekstra plassbehov som oppstår når lange vogner befinner seg i kurver samt dynamiske bevegelser som krenging og rulling av vognkassen.
For eksisterende baner beregnes kun statisk kurveutslag. Alle breddemål økes med kurveutslaget i sirkelkurver, overgangskurver og på rettlinje i nærheten av kurver. Kurveutslagene er forskjellige for kurvens indre og ytre side. Størrelsen av kurveutslagene er fastlagt på grunnlag av en teoretisk vogn med lengde 24 m og akselavstand 18 m. De samme verdiene for kurveutslag legges i utgangspunktet til grunn for A-96 og A-C.
Kurveutslag mot plattformer og lasteramper beregnes som vist i avsnitt 5.12.2.
Breddeutvidelse i sirkelkurver for nye baner
For nye baner utenom stasjonsområder økes alle breddemål i sirkelkurver, overgangskurver og på rettlinje i nærheten av kurver iht. tabell 24. Breddeutvidelsen tar hensyn til kurveutslag samt plass til dynamiske bevegelser.
| R [m] | k [mm]
|
|---|---|
| Rettlinje | 0 |
| 20000 | 0 |
| 10000 | 0 |
| 5000 | 80 |
| 4000 | 100 |
| 3000 | 120 |
| 1000 | 120 |
| 600 | 130 |
| 500 | 140 |
| 300 | 150 |
Mellomverdier interpoleres lineært og avrundes opp til nærmeste hele cm.
For nye baner innenfor stasjonsområder beregnes kurveutslag iht. tabell 25 med fradrag av 80 mm. Dog skal avstand fra spormidt aldri være mindre enn 2,20 m (gjelder 0,375/0,76 - 3,8 m over sporplan).
For eksisterende baner beregnes kurveutslag i sirkelkurver etter følgende formler:
| (5.74) |
| R [m] | Ki [mm] | Ky [mm] | R [m] | Ki [m] | Ky [mm] |
|---|---|---|---|---|---|
| 180 | 225 | 175 | 600 | 68 | 53 |
| 190 | 214 | 166 | 650 | 63 | 49 |
| 200 | 203 | 158 | 700 | 58 | 45 |
| 210 | 193 | 150 | 750 | 54 | 42 |
| 220 | 184 | 144 | 800 | 51 | 40 |
| 230 | 176 | 137 | 850 | 48 | 38 |
| 240 | 169 | 132 | 900 | 45 | 35 |
| 250 | 162 | 126 | 950 | 43 | 34 |
| 260 | 156 | 122 | 1000 | 41 | 32 |
| 270 | 150 | 117 | 1100 | 37 | 29 |
| 280 | 145 | 113 | 1200 | 34 | 27 |
| 290 | 140 | 109 | 1300 | 32 | 25 |
| 300 | 135 | 105 | 1400 | 29 | 23 |
| 325 | 125 | 97 | 1500 | 27 | 21 |
| 350 | 116 | 90 | 2000 | 21 | 16 |
| 375 | 108 | 84 | 3000 | 14 | 11 |
| 400 | 102 | 79 | 4000 | 10 | 8 |
| 425 | 96 | 75 | 5000 | 8 | 6 |
| 450 | 90 | 70 | 6000 | 7 | 5 |
| 475 | 86 | 67 | 7000 | 6 | 4 |
| 500 | 81 | 63 | 8000 | 5 | 4 |
| 550 | 74 | 58 | > 8000 | 0 | 0 |
R = kurvens radius
Redusert kurveutslag
For å begrense omfanget av kostnadsutløsende tiltak, er det som minstekrav for korte vogner spesielt beregnet for kombitrafikkk, etablert et "redusert kurveutslag" som dispensasjonskriterium.
Redusert kurveutslag er tilpasset ulike vogntyper med flg. parametre:
1) akselavstand = 13,5 m og overheng = 2,0 m
2) akselavstand = 10,0 m og overheng = 3,0 m
Det betyr at for området høyere enn 3440 mm kan man regne med redusert kurveutslag for A-96 ved hjelp av formel .3.
Indre kurveutslag:
Tilfelle 1 med a = 13,5 m er dimensjonerende. Settes a = 13,5 m og n = a/2 = 6,75 m inn i formel .3 får man:
| (5.75) |
Ytre kurveutslag:
Tilfelle 2 med a = 10,0 m og overheng = 3,0 m er dimensjonerende. Settes a = 10,0 m og n = 13,0 m inn i formel .3 får man:
| (5.76) |
Følgende tabell for kurveutslag framkommer:
| Radius [m] | Ki [mm] | Ky [mm]
|
|---|---|---|
| 200 | 114(203) | 98(158) |
| 250 | 91 (162) | 78 (126) |
| 300 | 76 (135) | 65 (105) |
| 400 | 57 (102) | 49 (79) |
| 500 | 46 (81) | 39 (63) |
| 600 | 38 (68) | 33 (53) |
| 700 | 33 (58) | 28 (45) |
| 800 | 28 (51) | 24 (40) |
| 900 | 25 (45) | 22 (35) |
| 1000 | 23 (41) | 20 (32) |
| 1200 | 19 (34) | 16 (27) |
| 1500 | 15 (27) | 13 (21) |
| 2000 | 11 (21) | 10 (16) |
| 5000 | 5 (8) | 4 (6) |
| 8000 | 3 (5) | 2 (4) |
Minste tverrsnitt for nye baner
Minste tverrsnitt for nye baner bygger på minste tverrsnitt UIC GC. UIC-tverrsnittet opererer imidlertid kun med kurveutslag for helt krappe radier (R < 250 m) og har ulike profiler for stasjonsspor og fri linje.
Det skraverte området på figuren angir innskrenkninger i profilet for plattformkanter og signaltekniske anlegg innenfor stasjonsområder.
Tillegg i kurver
For nye baner beregnes det et tillegg i kurver på fri linje ut fra både en statisk og en dynamisk betraktning. Det dynamiske tillegget øker med økende kurvehastighet.
Alle breddemål økes i sirkelkurver, overgangskurver og på rettlinje i nærheten av kurver i henhold til tabell 27:
| R [m] | k [mm]
|
|---|---|
| Rettlinje | 0 |
| 20000 | 0 |
| 10000 | 0 |
| 5000 | 80 |
| 4000 | 100 |
| 3000 | 120 |
| 1000 | 120 |
| 600 | 130 |
| 500 | 140 |
| 300 | 150 |
Mellomverdier interpoleres lineært og avrundes opp til nærmeste hele cm.
Minste tverrsnitt på stasjonsspor
Det skraverte området av minste tverrsnitt for nye baner angir innskrenkninger i profilet for plattformkanter og signaltekniske anlegg innenfor stasjonsområder.
Det skraverte området av minste tverrsnitt A-85 angir tillatt innskrenkning på spor innenfor stasjonsområder. Med henblikk på framføring av spesialtransporter bør det på alle stasjoner være minst en togvei - fortrinnsvis hovedtogsporet - hvor dette skraverte feltet holdes fritt for konstruksjoner. Denne togveien benevnes transportsporet.
Mot transportsporet skal det ikke forekomme lasteramper, dvergsignaler og andre faste konstruksjoner som befinner seg nærmere sporet enn 2120 mm + kurveutslaget fra spormidt og som er høyere enn 760 mm over sporplanet.
Sporforbindelser til frilasteplasser og sidespor til anlegg som skal kunne ta imot spesialtransporter, bør tilfredsstille de samme krav som transportsporet.
Den nederste begrensning av minste tverrsnitt
Sporrennen
Bredden av sporrennen skal være minst:
Rb = 70 mm når sporvidden (spv) 1445 med mer
Rb = spv - 1375 mm for spv > 1445 mm
Rb = 100 mm i planovergang med trelemmer
Konstruksjonsdeler som danner sporrennens indre begrensning (f.eks. planovergangslemmer), skal sikres mot skinnene slik at sporrennens bredde ikke kan reduseres.
For enkelte konstruksjonsdeler reduseres kravet til Rb. Dette gjelder:
- ledeskinner/vingeskinner i sporveksler
- sporkryss
- sporbremser
- gummilister i planoverganger
Faste konstruksjoner mellom og utenfor skinnene
Bortsett fra sporrennen ligger den nederste begrensningslinjen i sporplanet. Følgende unntak gjelder:
- Planovergangslemmer på elektrifiserte strekninger eller i isolerte sporfelt skal ligge minst 5 mm over sporplanet, men ikke mer enn 20 mm (a).
- Toppen av ledeskinnene i sporveksel kan ha en høyde inntil 20 mm over sporplan (a).
- På spor innenfor stasjonsområder kan faste konstruksjoner ha en høyde inntil 45 mm over sporplan (b).
- Toppen av ledeskinnene i sidekryssene for kryssveksler kan ha en høyde inntil 60 mm over sporplan (c).
Mellom skinnene gjelder unntakene lenger enn Rb fra kjørekanten. Utenfor skinnene gjelder unntakene lenger enn 150 mm fra kjørekanten. Unntakene gjelder ikke på steder hvor det forekommer vertikalkurver med Rv 1500 m.
Hensyn til bruk av sporrenser
I spor hvor det forutsettes bruk av sporrenser skal det om vinteren holdes fritt et rom inntil 700 mm utenfor kjørekanten av skinnene.
Der faste konstruksjoner betinger løft av sporrenseren, skal det på fri linje merkes med anvisere for sporrenserkjøring.
Fritt profil for strømavtaker
Fritt profil for strømavtaker angir plassbehovet for passasje av materiellets strømavtaker. I dette profilet skal kun kontakttråden være. Profilet får ikke kurveutslag. Profilet er vist på figur 22.
Minste tverrsnitt E
Minste tverrsnitt E er det tverrsnittet som trengs til fri passasje av strømavtakeren samt kontakttråden, bærelinen og andre konstruksjonsbestanddeler som tilhører kontaktledningsanlegget. Tverrsnittet er dimensjonert slik at det mellom begrensningslinjene og de spennings-førende deler er tilstrekkelig isolasjonsavstand. Målaksen for minste tverrsnitt E står vinkelrett på sporplanet i spormidt. Minste tverrsnitt E får ikke kurveutslag. På rettlinjet spor og mer enn 30 m fra nærmeste OB, KP eller SS (sporvekselkurve) tillates at minste tverrsnitt E sideveis blir innskrenket med 100 mm. Høyden for minste tverrsnitt E (HE) er avhengig av kontakttrådhøyden ved opphengningspunktet (H0) og av kontaktledningens konstruksjonshøyde (C):
| (5.77) |
Verdier for H0 og C er gitt i JD530, kap. 5.
For nye baner er minste tverrsnitt E tegnet inn sammen med minste tverrsnitt.
Master og andre gjenstander ved siden av sporet
Master og andre gjenstander med stor høyde (bukker for lastekraner, skilter, signaler, barduner, vannstendere o.l.) skal på områder hvor det forekommer skifting, plasseres slik at avstanden til minste tverrsnitt blir minst 400 mm i en høyde mellom 1500 mm og 3500 mm over nærmeste skinne, jf. figur .23.
| (5.78) |
Portåpninger
Minste bredde (= normalbredde) for portåpninger i rettlinjet spor er 3700 mm. Ligger sporet gjennom porten i eller i nærheten av kurve, økes bredden med kurveutslagene.
I bestemte tilfeller kreves minste tverrsnitt i portåpninger:
- Når sporet gjennom bygningen danner den eneste forbindelse til sporanlegg på den andre siden av bygningen.
- I bygninger hvor det skal kunne mottas transporter med overskridelse av lasteprofilet.
Høyden for porter skal være minst 5600 mm. Høyden kan reduseres til 4800 mm i bygninger der elektrifisering ikke er aktuelt.
Sporets middel
| Fra Teknisk Regelverk: https://trv.banenor.no/wiki/Underbygning/Prosjektering_og_bygging/Profiler_og_minste_tverrsnitt#Sporets_middel
Med sporets middel menes det punkt hvor avstanden mellom to spor er tilstrekkelig stor til at rullende materiell farefritt kan passere hverandre. a) Sporavstanden ved middel skal være så stor at det mellom lasteprofilet anbrakt på det ene spor og minste tverrsnitt på det andre spor skal være 100 mm klaring.
|
Da beregning av sporets middel er basert på godkjent UIC-materiell, kan man ikke uten videre plassere spesialtransporter helt fram til middelmerket.
| Beregning av middel | |
|---|---|
|
S |
|
S + Ky |
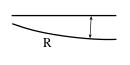
|
S + Ki + 2,3*h |
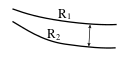
|
S + Ki + Ky + 2,3*abs(h2-h1) |
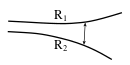
|
S + 2*Ky |
S = 2120 mm + 1700 mm + 100 mm = 3920 mm (dersom ingen av sporene er togspor er S = 3720 mm)
Eksempel på beregning av sporets middel:
R1 = 300 m, h = 0 mm, R2 = ∞, A-85
- A-85 2120 mm
+ Ytre kurveutslag 105 mm
+ Lasteprofil 1700 mm
+ Klaring 100 mm
= Sporavstand ved middel 4025 mm
Sporavstand
Avstanden mellom to nabospor skal alltid være så stor at rullende materiell ikke berører hverandre. Utover denne minimumsavstanden ønskes ytterligere avstand for å ta hensyn til
- plassering av master og signaler
- plass til personale under skifting og
- aerodynamiske påvirkninger ved høye hastigheter
Sporavstanden måles fra spormidt til spormidt
Den minste sporavstanden på dobbeltsporede eller flersporede strekninger framgår av tabell .28 og tabell .29.
| Radius [m] | Sp [m] |
|---|---|
| R < 350 | 4,70 |
| 350 < R < 500 | 4,68 |
| 500 < R < 600 | 4,66 |
| 600 < R < 1000 | 4,64 |
| 1000 < R < 4000 | 4,60 |
| 4000 < R < 5000 | 4,56 |
| R > 5000 | 4,40 |
| Radius [m] | Sp [m] |
|---|---|
| R < 250 | 3,95+75/R |
| R ≥250 | 4,25 |
Den normale sporavstanden der rullende materiell hensettes og der driftsoppgaver i forbindelse med det rullende materiell utføres, er 4,70 m.
Plattformer
Ved bygging av personvogner og plattformer forsøker man å skape de beste inn- og utstigningsforhold for passasjerene. Dette betyr gode trinn, liten høydeforskjell og kort avstand mellom vogn og plattform. Plattformtypene betegnes etter høyde over sporplan.
Plattformhøyder
Opprinnelig ble plattformene i Norge bygget relativt lavt og en rekke av disse lave plattformer er fortsatt i bruk i dag. Nye plattformer bygges i dag enten med 570 mm høyde eller med 700 mm høyde over sporplan.
| Plattformtype | Plattformhøyde |
|---|---|
| Lav | 350 mm |
| Normal | 570 mm |
| Høy | 700 mm |
Høy plattformer har hos oss i hovedsak blitt bygget i nærtrafikkområdet rundt Oslo.
Plattform mot spor uten overhøyde
Avstand fra spormidt regnes ut etter følgende formler:
| (5.79) |
Hvor A0 = 1700 eller 2240 mm. Størrelsene Ai og Ay er konstante når plattformen eller rampen over hele lengden ligger mot en sirkelkurve.
Når sporet delvis ligger i en kurve, eller når det er et kurvepunkt i nærheten av enden av plattformen/rampen, varierer Ai og Ay som vist i figur 26.
Skravering viser områdene hvor kurveutslagene forandres lineært.
Som hovedregel gjelder verdiene gitt i tabell 31 (retning fra største kurve til minste kurve).
| Ved plattform/rampe i innerkurve | Ved plattform/rampe i ytterkurve |
|---|---|
| Minste Ai til 15 m før Kp | Minste Ay til 20 m før Kp |
| Største Ai fra 5 m etter Kp | Største Ay fra 5 m før Kp |
Ligger det en sporveksel i sporet mot plattformen/rampen, må det tas hensyn til kurveutslagene for det avvikende spor, jf. figur 27. I slike tilfeller kan det være hensiktsmessig å skjematisere forløpet av rampens kant, dvs. den stiplede linjen A-B-C istedenfor sirkelsegmentet. På den måten oppnås en forenkling av målføringen under byggingen.
Rampens/plattformens høyde er konstant.
Plattform mot spor med overhøyde
I spor med overhøyde må kurveutslagene og plattformhøydene bestemmes etter følgende formler, jf. figur 28:
| (5.80) |
| (5.81) |
| (5.82) |
| (5.83) |
(5.83)
På grunn av overhøyderampen får plattformene varierende avstander og høyder mellom OB og OE, jf. figur 29.
Som hovedregel gjelder verdiene gitt i tabell 32 (retning fra største kurve til minste kurve).
| Ved plattform/rampe i innerkurve | Ved plattform/rampe i ytterkurve |
|---|---|
| Minste Ai til 10 m før OB | Minste Ay til 15 m før OB |
| Største Ai fra OE | Største Ay fra 5 m før OE |
Endringer i plattformens høyde over skinnetopp utføres lineært mellom OB og OE.
Innskrenkninger i minste tverrsnitt
Som følge av trafikken og justeringsarbeidene kan sporets beliggenhet og overhøyde forandre seg med tiden. Faste gjenstander og konstruksjoner som plasseres mot begrensningslinjene for minste tverrsnitt kan etter hvert danne innskrenkninger i minste tverrsnitt,
Registreringer av innskrenkninger i minste tverrsnitt
Ved jevne mellomrom blir det foretatt en kontroll av minste tverrsnitt. Dette skjer vha. målevogn. Fram til 1985 ble minste tverrsnitt kontrollert vha. maler. Dette var en tungvinn og lite nøyaktig registreringsmetode. I perioden 1986 -1995 ble det anvendt en fotogrammetrisk metode som bestod i at man fotograferte to delvis overlappende fotografier ved hver innskrenkning. Deretter ble bildene behandlet i en modell og koordinater ble beregnet. F.o.m. 1996 er det blitt anvendt en målevogn med roterende laser. Her blir profilet målt kontinuerlig og det avdekkes på stedet hvor stor innskrenkningen er.
Alle innskrenkningene i minste tverrsnitt legges inn i en edb-basert simuleringsmodell. Her kan man simulere spesialtransporter og nye vognkonsepter på de ulike norske jernbanestrekninger.
Lasteprofiler
Det normale lasteprofil
Lasteprofilene angir begrensningen i høyde- og sideretning for last på godsvogner.
1)
- H = 100 mm, unntatt for vogner som skal bremses i sporbremsene ved Alnabru.
- For disse vognene gjelder:
- H = 140 mm når a = 6 - 10 m
- H = 180 mm når a = 10 - 16 m
- H = 200 mm når a = 16 - 20 m
Lasteprofilet kan utnyttes fullt ut over en lengde L = a + 2n.
- a er for 2- og 3-akslede vogner avstanden mellom vognens ytterste aksler og for boggivogner avstanden mellom boggisentrene.
- n er lastens overheng.
Lengden L er i tillegg avhengig av avstanden P mellom de ytterste aksler i boggien for boggivogner.
| For vogner hvor samtidig: | ||
|---|---|---|
| p
er mindre eller lik: |
A
Er: |
n
kan maksimalt være |
| 2,5 m | 17,0 -18,0 m | 3,00 m |
| 6,0 m | 16,0 - 17,0 m | 3,30 m |
| 6,0 m | 14,5 - 16,0 m | 3,40 m |
| 6,0 m | 13,0 - 14,5 m | 3,65 m |
| 6,0 m | 12,0 - 13,0 m | 3,85 m |
| 6,0 m | 11,0 -12,0 m | 4,00 m |
| 6,0 m | 10,0 - 11,0 m | 4,20 m |
| 6,0 m | 8,0 – 10,0 m | 4,30 m |
| 6,0 m | 7,0 - 8,0 m | 4,00 m |
Det utvidede lasteprofil
Utvidet lasteprofil for last på 2-akslede vogner kan nyttes når lasten ikke rager utover vognenes endebjelker.
Lasteprofil K
Lasteprofil K bygger på det utvidede lasteprofil, men avviker i øvre hjørne:
1200 - 3650 mm høyde er halv bredde 1700 mm et knekkpunkt i 4350 mm høyde og halv bredde 1400 mm et knekkkpunt i 4450 mm høyde og halv bredde 700 mm
Internasjonale lasteprofiler
UIC GC
Lasteprofilet UIC GC er, med sin bredde 1,455 m i høyden 4,650 m over skinnetopp, så stort at ingen land har ønsket å innføre det generelt. Det er dermed heller ikke opptatt i RIV. En rekke land forsøker å innføre det på utvalgte strekninger.
På de nye høyhastighetsstrekningene gjennom Europa innføres dette profilet, selv om det ikke er planlagt framføring av gods på disse strekningene. Innføringen skyldes primært at profilet kommer av seg selv pga. det anvendte kontaktledningsssystem.
UIC GC er interessant både i Sverige og i Danmark fordi de nødvendige lasteprofiler i disse land for kjøring av containere og dobbeltdekkere (DSB) ligner mye på UIC GC.
Som det framgår av figuren er lasteprofilet UIC GC betydelig større enn lasteprofil K i øvre del av profilet.
Konteiner- og semitrailerprofiler
Konteiner- og semitrailerprofiler betegnes internasjonalt vha. et UIF-nr. som angir den maksimale størrelsen på konteineren/semitrailerene som kan fremføres på de ulike strekningene. Et UIF-nr. består av en bokstav (C for konteiner/P for semitrailer) og et tresifret tall som angir høyden i cm for konteineren/semitraileren. Denne høyden er basert på en standardisert vogn med lastehøyde 33 cm. De viktigste lasttilfellene er listet opp i tabell .34.
| UIF-nr. | Lasttilfelle | Høyde over
Skinnetopp |
Avstand fra
Spormidt |
|---|---|---|---|
| C400 | Vekselbeholder 3150 | 4330 | 1300 |
| C405 | Vekselbeholder 3200 | 4380 | 1300 |
| P400 | EU-semi (4000) i brønn | 4330 | 1360 |
| P407 | Semi 4070 i brønn | 4400 | 1360 |
| P410 | Semi 4010 i brønn | 4430 | 1360 |
Frittromsprofilet for lasttilfellene PXXX er vist i figur 35.
EMBED Sketch
Frittromsprofilet vil avhenge av hvorvidt det grenser til spenningsførende eller ikke-spenningsførende deler. I tillegg er det beregnet et tillegg for plass til kapell. Toleransene er gitt i tabell .35.
| Ikke spenningsførende (ikke sp.f.) | Spenningsførende (sp.f.)
| ||
|---|---|---|---|
| ΔX | 200 mm | 300mm | |
| ΔY | ledning | fester | |
| 150 mm | 250 mm | 200 mm | |
| ΔY - kapell | +150 mm |
LITTERATURHENVISNINGER
1. DSB - Registersektoren - Profilmål, Konstruktionsmål, læsseprofiler og fritrumsprofiler (1994)
2. Jacobus Meulman: Bpk 38 – Konstruksjonsprofiler for rullende materiell (1977)
3. Jacobus Meulman: Grunnlag for beregning av de ”dynamiske profiler” (udatert)
4. Jacobus Meulman: Oversikt over metoden for beregning av konstruksjonsprofiler (1988)
5. Jernbaneverket, JD530 Overbygning – regler for prosjektering