Sporets sidemotstand: Forskjell mellom sideversjoner
| (46 mellomliggende revisjoner av samme bruker vises ikke) | |||
| Linje 18: | Linje 18: | ||
===Sideforskyvningsmotstand=== | ===Sideforskyvningsmotstand=== | ||
[[Fil:Sideforskyvningsmotstand.PNG|thumb|300px|Figur 6.1: Sideforskyvningsmotstand avhengig av vei]] | |||
Sideforskyvningsmotstanden kan defineres som den motstand en sville møter | Sideforskyvningsmotstanden kan defineres som den motstand en sville møter | ||
når den beveger seg eller prøver å bevege seg sideveis. Den totale sideforskyvningsmotstand | når den beveger seg eller prøver å bevege seg sideveis. Den totale sideforskyvningsmotstand | ||
| Linje 27: | Linje 28: | ||
|- | |- | ||
|F<sub>e</sub>= motstand fra ballastskulder/svilleender | |F<sub>e</sub>= motstand fra ballastskulder/svilleender | ||
|} | |||
{| | |||
|<math> F=F_{b}+F_{s}+F_{e} </math> | |||
| | |||
| | |||
|(6.1) | |||
|} | |} | ||
Vi kan regne med følgende bidrag fra de 3 komponentene til den totale | Vi kan regne med følgende bidrag fra de 3 komponentene til den totale | ||
sideforskyvningsmotstanden: | sideforskyvningsmotstanden: | ||
{| | |||
|<math> F_{b}: 30-50 % </math> | |||
|- | |||
||<math> F_{s}: 40-60 % </math> | |||
|- | |||
||<math> F_{e}: 10-30 % </math> | |||
|} | |||
Praktiske forsøk har vist at sideforskyvningsmotstanden er avhengig av veien | Praktiske forsøk har vist at sideforskyvningsmotstanden er avhengig av veien | ||
svillene forflytter seg (figur 6.1). | svillene forflytter seg (figur 6.1). | ||
| Linje 55: | Linje 65: | ||
====Ballastprofilet==== | ====Ballastprofilet==== | ||
[[Fil:Sideforskyvningsmotstand avhengig av ballastskulder.PNG|thumb|150px|Figur 6.2: Sideforskyvningsmotstand avhengig av ballastskulder]] | |||
[[Fil:Sidemotstand avhengig av ballast i svillemellomrom.PNG|thumb|150px|Figur 6.3 Sidemotstand avhengig av ballast i svillemellomrom]] | |||
Ballastskulderen har en avgjørende innflytelse på sporets sideforskyvningsmotstand. | Ballastskulderen har en avgjørende innflytelse på sporets sideforskyvningsmotstand. | ||
Figur 6.2 viser hvordan sideforskyvningsmotstanden endrer seg | Figur 6.2 viser hvordan sideforskyvningsmotstanden endrer seg | ||
når skulderbredde og høyde endrer seg. Resultatene bygger på praktiske | når skulderbredde og høyde endrer seg. Resultatene bygger på praktiske | ||
forsøk utført av European Rail Research Institute (ERRI). | forsøk utført av European Rail Research Institute (ERRI). | ||
Figur 6.2 viser f.eks, at sideforskyvningsmotstanden øker med ca. 10% | Figur 6.2 viser f.eks, at sideforskyvningsmotstanden øker med ca. 10% | ||
| Linje 72: | Linje 82: | ||
sideveis forskyvning. Figur 6.3 viser hvordan sideforskyvningsmotstanden | sideveis forskyvning. Figur 6.3 viser hvordan sideforskyvningsmotstanden | ||
reduseres når vi fjerner ballast fra svillemellomrommet. | reduseres når vi fjerner ballast fra svillemellomrommet. | ||
'''Ballastprofiler''' | '''Ballastprofiler''' | ||
[[Fil:Ballastprofiler for helsveist spor.PNG|thumb|150px|Figur 6.4 Ballastprofiler for helsveist spor]] | |||
For å sikre tilstrekkelig sidemotstand er det satt krav til ballastprofilet for spor | For å sikre tilstrekkelig sidemotstand er det satt krav til ballastprofilet for spor | ||
som skal helsveises (Figur 6.4) [JD 530, kap 10]. Tabell 6.1 viser hvilke | som skal helsveises (Figur 6.4) [JD 530, kap 10]. Tabell 6.1 viser hvilke | ||
profiler som skal anvendes ved forskjellige kombinasjoner av kurveradier og | profiler som skal anvendes ved forskjellige kombinasjoner av kurveradier og | ||
svilletyper. | svilletyper. | ||
{| class="wikitable" | {| class="wikitable" | ||
| Linje 133: | Linje 139: | ||
Etter sporjustering skal det iverksettes hastighetsreduksjon i kurver med | Etter sporjustering skal det iverksettes hastighetsreduksjon i kurver med | ||
radius £ 400 m dersom det kan forventes skinnetemperaturer over + | radius £ 400 m dersom det kan forventes skinnetemperaturer over +30˚C [JD | ||
532, kap.13]. Full sidemotstand oppnås etter ca. 150 000 brt togpassering. | 532, kap.13]. Full sidemotstand oppnås etter ca. 150 000 brt togpassering. | ||
Dette tilsvarer 3 - 6 dager ved hovedspor i Norge. Bruk av dynamisk | Dette tilsvarer 3 - 6 dager ved hovedspor i Norge. Bruk av dynamisk | ||
| Linje 144: | Linje 150: | ||
og svillebytte. Etter ballastrensing kan vi regne med at motstanden er | og svillebytte. Etter ballastrensing kan vi regne med at motstanden er | ||
redusert til 20 - 30 % av full motstand. | redusert til 20 - 30 % av full motstand. | ||
[[Fil:Sideforskyvningsmotstand etter sporjustering.PNG|thumb|center|300px|Figur 6.5 Sideforskyvningsmotstand etter sporjustering]] | |||
Det må utvises meget stor aktsomhet ved slike sporarbeider i varmt vær. | Det må utvises meget stor aktsomhet ved slike sporarbeider i varmt vær. | ||
Regler for vedlikehold av helsveist spor [JD 532, kap. 10] gir temperaturbegrensninger | Regler for vedlikehold av helsveist spor [JD 532, kap. 10] gir temperaturbegrensninger | ||
for slike arbeider. Arbeid som svekker sporets stabilitet skal | for slike arbeider. Arbeid som svekker sporets stabilitet skal | ||
bare utføres i skinnetemperaturområdet 0 - + | bare utføres i skinnetemperaturområdet 0 - +30˚C. | ||
====Svilletype==== | ====Svilletype==== | ||
| Linje 156: | Linje 162: | ||
6.6 viser resultatet av praktiske forsøk med sideforskyvning av sporavsnitt | 6.6 viser resultatet av praktiske forsøk med sideforskyvning av sporavsnitt | ||
med forskjellige svilletyper. Forsøkene er utført av ERRI. | med forskjellige svilletyper. Forsøkene er utført av ERRI. | ||
I figuren er forskyvningsmotstanden for tresviller brukt som referanse. Vi ser | I figuren er forskyvningsmotstanden for tresviller brukt som referanse. Vi ser | ||
| Linje 166: | Linje 169: | ||
tresville veier fra 50-80 kg. | tresville veier fra 50-80 kg. | ||
[[Fil:Svilletyper.PNG|thumb|300px|Figur 6.7: Svilletyper]] | |||
[[Fil:Sideforskyvningsmotstand med forskjellige svilletyper.PNG|thumb|center|300px|Figur 6.6: Sideforskyvningsmotstand med forskjellige svilletyper]] | |||
Formen på svillene har også betydning for sideforskyvningsmotstanden. | Formen på svillene har også betydning for sideforskyvningsmotstanden. | ||
Figur 6.7 viser skjematisk tresville, monoblokk betongsville og toblokk | Figur 6.7 viser skjematisk tresville, monoblokk betongsville og toblokk | ||
| Linje 176: | Linje 181: | ||
svillene. Dette pga. at friksjonen mellom underkant av sville og ballasten | svillene. Dette pga. at friksjonen mellom underkant av sville og ballasten | ||
utgjør en stor del av den totale sideforskyvningsmotstanden. | utgjør en stor del av den totale sideforskyvningsmotstanden. | ||
Sideforskyvningsmotstand uttrykkes gjerne som motstand pr. lengdeenhet. | Sideforskyvningsmotstand uttrykkes gjerne som motstand pr. lengdeenhet. | ||
| Linje 183: | Linje 186: | ||
ved å dividere med svilleavstanden. | ved å dividere med svilleavstanden. | ||
{| | |||
|<math> Sporets sideforskyvnigsmotstand = {motstand pr. sville \over svilleavstand} </math> | |||
| | |||
| | |||
| | |||
|(6.2) | |||
|} | |||
Sporets sideforskyvningsmotstand er altså omvendt proporsjonal med | Sporets sideforskyvningsmotstand er altså omvendt proporsjonal med | ||
| Linje 198: | Linje 208: | ||
nypakket spor, mens figur 6.10 viser verdier fra målinger på tresvillespor i | nypakket spor, mens figur 6.10 viser verdier fra målinger på tresvillespor i | ||
USA. | USA. | ||
[[Fil:Måling av sideforskyvningsmotstand.PNG|thumb|left|300px|Figur 6.8 Måling av sideforskyvningsmotstand]] | |||
Figur 6.8 Måling av sideforskyvningsmotstand | [[Fil:Sideforskyvningsmotstand for tresviller.PNG|thumb|200px|Figur 6.10 Sideforskyvningsmotstand for tresviller ved varierende ballaststyrke]] | ||
[[Fil:Sideforskyvningsmotstand i nypakket spor.PNG|thumb|center|300px|Figur 6.9 Sideforskyvningsmotstand i nypakket spor]] | |||
Figur 6. | |||
Figur 6. | |||
===Vridningsmotstand=== | ===Vridningsmotstand=== | ||
For at en utknekking av sporet i horisontalplanet skal kunne oppstå, må | For at en utknekking av sporet i horisontalplanet skal kunne oppstå, må | ||
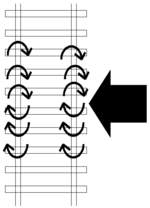
skinnene rotere i forhold til svillene (figur 6.11). | skinnene rotere i forhold til svillene (figur 6.11). | ||
Når vi betrakter sporet som en ramme bestående av skinner og sviller vil | Når vi betrakter sporet som en ramme bestående av skinner og sviller vil | ||
| Linje 225: | Linje 230: | ||
sideisolator som har betydelig lengre anleggsflate mot skinnefotsiden enn | sideisolator som har betydelig lengre anleggsflate mot skinnefotsiden enn | ||
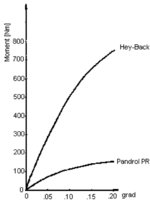
Pandrol PR/e-clip-systemene og vil derfor ha en større vridningsmotstand. | Pandrol PR/e-clip-systemene og vil derfor ha en større vridningsmotstand. | ||
[[Fil:Hey-Back og Pandrol PR.PNG|thumb|150px|Figur 6.12 Vridningsmotstand for Hey-Back og Pandrol PR]] | |||
[[Fil:Vridningsmotstand.PNG|thumb|center|150px|Figur 6.11 Vridningsmotstand]] | |||
'''Slitasje på isolator og mellomlegg''' | '''Slitasje på isolator og mellomlegg''' | ||
| Linje 234: | Linje 241: | ||
solslyng. Det er derfor god grunn til å holde isolatorenes tilstand under | solslyng. Det er derfor god grunn til å holde isolatorenes tilstand under | ||
oppsyn i krappe kurver. | oppsyn i krappe kurver. | ||
===Skinneprofilets betydning for sidestabiliteten=== | ===Skinneprofilets betydning for sidestabiliteten=== | ||
[[Fil:Sikkerhet mot utknekking.PNG|thumb|300px|Figur 6.13 Skinneprofilets innflytelse på sikkerhet mot utknekking]] | |||
Skinneprofilets treghetsmoment om skinnens vertikale akse har innflytelse på | Skinneprofilets treghetsmoment om skinnens vertikale akse har innflytelse på | ||
hvor stivt hele sporet blir mot sideveis forskyvning. Samtidig øker | hvor stivt hele sporet blir mot sideveis forskyvning. Samtidig øker | ||
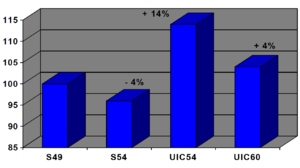
| Linje 248: | Linje 254: | ||
4% i forhold til S49. | 4% i forhold til S49. | ||
Figur 6. | ==Solslyng== | ||
===Utknekkingsmekanismer=== | |||
[[Fil:Knekkformer.PNG|thumb|300px|Figur 6.14 Knekkformer]] | |||
[[Fil:Figur6.15.PNG|thumb|300px|Figur 6.15]] | |||
[[Fil:Likevektstilstander ved utknekking.PNG|thumb|300px|Figur 6.16 Likevektstilstander ved utknekking]] | |||
Solslyng er utknekking av sporet i horisontalplanet som oppstår pga. store | |||
trykkrefter i skinnene ved høye skinnetemperaturer der sporets sidestabilitet | |||
er for liten til å fastholde sporet. Ved JBV er definisjonen på solslyng at | |||
pilhøydefeilen er på min. 25 mm målt med 10 m korde. Prinsipielt kan | |||
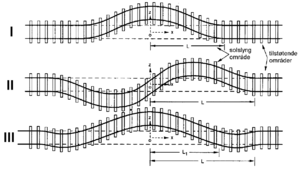
utknekking skje i 3 forskjellige former (figur 6.14). Sporet kan knekke ut i en | |||
enkel halv-sinusbølge (modus 1) eller flere halvsinusbølger (modus 2 og 3). | |||
Ved en utknekking vil det alltid skje en langsgående bevegelse av skinnene i | |||
de tilstøtende områder på begge sider av solslyngen. Vi kan si at skinnene | |||
”mates” inn i solslyngområdet. Dette fører til at aksialkreftene i skinnene | |||
påvirkes i de tilstøtende områder. | |||
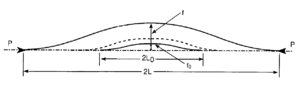
Figur 6.15 viser et helsveist spor på rettlinje med en liten sinusformet sporfeil | |||
med pilhøyde f<sub>0</sub> og lengde 2L<sub>0</sub>. Når aksialtrykkreftene i sporet øker som følge | |||
av en temperaturøkning, vil sporforskyvningen kunne øke noe inntil en kritisk | |||
temperaturøkning Tk nås. Når skinnetemperaturen overstiger den kritiske | |||
temperaturen, vil det skje en plutselig utknekking til en stor pilhøyde f over | |||
lengde 2L. En ytterligere temperaturøkning vil gradvis øke sporforskyvningen. | |||
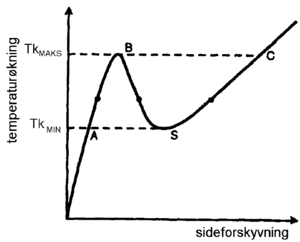
Figur 6.16 viser sideforskyvning som funksjon av temperaturøkning ved | |||
solslyng. Fra A til B foregår det en liten sideforskyvning som følge av at | |||
aksialtrykkreftene øker. Ved B har vi en ustabil situasjon hvor sporet plutselig | |||
knekker ut. Utknekkingen medfører en avlasting av trykkreftene inntil sporet | |||
er stabilt ved S. Skinnetemperaturen ved pkt. S defineres som den lavere | |||
kritiske knekktemperatur, Tk<sub>MIN</sub>. Skinnetemperaturen ved pkt. B defineres | |||
som den høyere kritiske knekktemperatur, Tk<sub>MAKS</sub>. | |||
Tk<sub>MIN</sub> er den laveste skinnetemperaturen hvor sporet kan knekke ut fra pkt. A | |||
dersom sporet blir tilført ekstra energi utenfra. Ved Tk<sub>MAKS</sub> derimot vil sporet | |||
knekke ut uten tilførsel av ekstra energi. Sporets likevekt ved Tk<sub>MAKS</sub> kan | |||
sammenlignes med den likevekt et kronestykke har når vi balanserer det på | |||
en skarp kant. | |||
I figur 6.16 er det forutsatt at solslyng opptrer som en plutselig | |||
sporforskyvning. Dette er ikke alltid tilfelle. Ved en kombinasjon av store | |||
initielle sporfeil og liten sideforskyvningsmotstand kan sporet sideforskyves | |||
gradvis uten noen ”eksplosiv” fase. | |||
===Solslyng under togpassering=== | |||
[[Fil:Dynamisk avlastning.PNG|thumb|300px|Figur 6.17: Dynamisk avlastning]] | |||
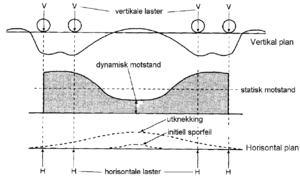
Under togpassering vil sporet bevege seg i vertikalplanet i bølgebevegelser. | |||
Under hver aksel og boggi får vi en nedbøyning, mens vi foran, mellom og | |||
bak aksler og boggier får en heving av sporet (figur 6.17). | |||
'''Dynamisk avlastning''' | |||
Denne dynamiske avlastningen resulterer i at sideforskyvningsmotstanden | |||
reduseres. Tapet av sideforskyvningsmotstand er sporets egenvekt | |||
multiplisert med friksjonskoeffisienten mellom sville og ballast. | |||
Sideforskyvningsmotstanden under dynamisk avlastning blir da: | |||
{| | |||
|<math>F_{D}=F_{S}-\mu \cdot Q</math> | |||
| | |||
| | |||
| | |||
|(6.3) | |||
|} | |||
{| | |||
|F<sub>D</sub>=sideforskyvningsmotst under avlastning | |||
|- | |||
| F<sub>S</sub>=statisk sideforskyvningsmots. | |||
|- | |||
|μ = friksjonskoeffisient sville ballast | |||
|- | |||
|Q= sporets egenvekt | |||
|} | |||
'''Friksjon mellom sville og ballast''' | |||
Friksjonskoeffisienten mellom sville og ballast kan bestemmes gjennom | |||
praktiske forsøk. For betongsviller kan den variere mellom 0,4 og 0,9 | |||
avhengig av ruhet av svillenes underside, ballastkvalitet og | |||
konsolideringsgrad. For tresviller kan vi ha langt større variasjoner fordi | |||
ballastmateriale i noen tilfeller kan grave seg inn i svilleoverflaten og øke | |||
friksjonen betraktelig. | |||
Reduksjonen i sideforskyvningsmotstand fører til en reduksjon i kritisk | |||
knekktemperatur og dermed økt fare for solslyng under togpassering. En stor | |||
del av solslyngtilfellene skjer derfor under togpassering. Sammen med sporets egenvekt og friksjon sville/ballast vil størrelse og karakteristikk av den | |||
dynamiske avlastningen avgjøre hvor mye den kritiske knekktemperaturen | |||
reduseres i forhold til ubelastet spor. Følgende faktorer har innflytelse på den | |||
dynamiske avlastingen: | |||
*aksellast | |||
*akselavstand | |||
*boggiavstand | |||
*sporets vertikale stivhet (ballastsiffer) | |||
===Beregning av kritisk knekktemperatur=== | |||
Kritisk knekktemperatur kan finnes ved å betrakte sporet som en uendelig | |||
lang stav som hviler på et underlag som yter motstand mot forskyvning ved | |||
friksjon. Matematisk eksakte løsninger kan bare finnes ved hjelp av | |||
differensialligninger. Imidlertid kan tilnærmede løsninger finnes gjennom | |||
energibetraktninger. | |||
====Meiers metode==== | |||
[[Fil:Knekkformer - Meier.PNG|thumb|300px|Figur 6.18: Knekkformer - Meier]] | |||
[[Fil:Betongsviller etter Meier.PNG|thumb|300px|Figur 6.19 Kritisk temperaturøkning S49/betongsviller etter Meier]] | |||
[[Fil:Tresviller etter Meier.PNG|thumb|300px|Figur 6.20 Kritisk temperaturøkning S49/tresviller etter Meier]] | |||
[[Fil:Betongsviller etter Meier S49.PNG|thumb|300px|Figur 6.21 Kritisk temperaturøkning S49/betongsviller etter Meier]] | |||
Meier lanserte en metode for beregning av kritisk knekktemperatur i Tyskland | |||
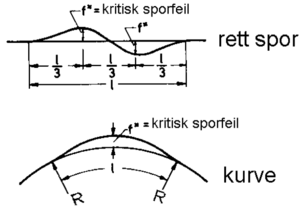
i 1937. Metoden antar knekkformer som vist i figur 6.18. I modellen inngår en | |||
faktor som kalles ”sporets ekvivalente treghetsmoment”, altså skinnestigens | |||
stivhet sideveis. Denne faktoren bestemmes ut fra praktiske forsøk for hver | |||
aktuelle sporkonstruksjon. | |||
Ved hjelp av energibetraktninger kan man finne empiriske formler for kritisk | |||
sporfeil og kritisk knekktemperatur. Formel 6.4 gir kritisk sporfeil og formel | |||
6.5 gir kritisk knekktemperatur for rettlinjet spor. | |||
{| | |||
|<math>f*=8,7 \cdot F \cdot {E \cdot J \over P \cdot k^2} </math> | |||
| | |||
| | |||
| | |||
|(6.4) | |||
|} | |||
{| | |||
|<math> T_k = \sqrt {8,7 \cdot J \cdot F \over \alpha \cdot A^2 \cdot E \cdot f} </math> | |||
| | |||
| | |||
| | |||
||(6.5) | |||
|} | |||
Formel 6.6 gir kritisk sporfeil og formel 6.7 gir kritisk knekktemperatur for | |||
kurver. | |||
{| | |||
|<math> f*=(F-{Pk \over R} ) \cdot {16 \cdot E \cdot J \over Pk} </math> | |||
| | |||
| | |||
|(6.6) | |||
|} | |||
{| | |||
<math> T_k = -{8 \cdot J \over \alpha \cdot A \cdot R \cdot f}+ \sqrt { ({8 \cdot J \over \alpha \cdot A \cdot R \cdot f})^2 +{16 \cdot J \cdot F \over \alpha^2 \cdot A^2 \cdot E \cdot f}} </math> | |||
|(6.7) | |||
|} | |||
{| | |||
T<sub>k</sub> = kritisk temperaturøkning [°C] | |||
|- | |||
|E = elastisitets modulen = 2,07* 10<sup>5</sup> [N/mm^2] | |||
|- | |||
|α = strålets utvidelseskoeff.= 1,15*10<sub>5</sub> | |||
|- | |||
|A= skinnenes samlede tverrsnittflate [mm^2] | |||
|- | |||
| J=sporets ekvivalente treghetsmoment [mm^4] | |||
|- | |||
| R= kurveradius [mm] | |||
|- | |||
| F= sideforskyvningsmotstand [N/mm] | |||
|- | |||
|f*=kritisk sporfeil | |||
|- | |||
|f= antatt sporfeil [mm] | |||
|- | |||
|Pk=kritisk trykkraft i sporet | |||
|} | |||
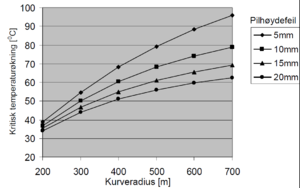
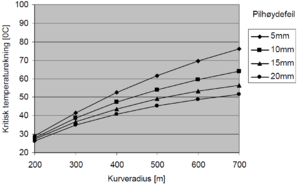
Figur 6.19 og 6.20 viser beregninger som er foretatt på S49 - spor med treog | |||
betongsviller med Meiers metode. Kritisk temperaturøkning er økning av | |||
skinnetemperaturen i forhold til nøytraltemperaturen. | |||
Det er brukt følgende forutsetninger i beregningene: | |||
*svilleavstand = 65 cm | |||
*ballastskulder = 40 cm | |||
*koeffisient for konsolideringsgrad = 0,7 | |||
*koeffisient for løfting mellom boggier = 0,7 | |||
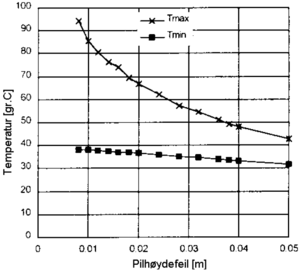
Vi ser at kritisk temperaturøkning for en kurve med radius = 300 m er 50˚C | |||
for betongsvillesporet med pilhøydefeil = 10 mm. Dette gir oss en sikkerhetsmargin | |||
mot solslyng på ca. 15˚C (forutsatt maks skinnetemperatur +55˚C og | |||
nøytraltemperatur +20˚C). Dette er for lite og viser tydelig behovet for større | |||
sidemotstand i krappe kurver. | |||
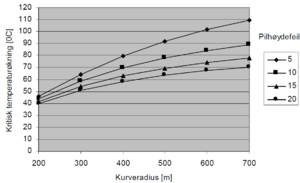
Større sidemotstand kan oppnås ved å øke skulderbredden på ballastprofilet | |||
som vist i figur 6.21. Her er skulderbredden økt til 55 cm som foreskrevet i JD | |||
530 for spor med liten kurveradius (< 300 m for betongsviller / < 400 m for | |||
tresviller). Sporet vil nå teoretisk knekke ut ved skinnetemperatur på 80˚C i | |||
en 300 m radius kurve med pilhøydefeil på 10 mm (forutsatt maks | |||
skinnetemperatur +55˚C og nøytraltemperatur +20˚C). Dette gir oss en | |||
sikkerhetsmargin på ca. 25˚C. | |||
Forutsetninger i beregningene: | |||
*svilleavstand = 65 cm | |||
*ballastskulder = 55 cm | |||
*ballast over svilleplan: 10 cm | |||
*koeffisient for konsolideringsgrad = 0,7 | |||
*koeffisient for løfting mellom boggier = 0,7 | |||
====Nyere beregningsprogrammer==== | |||
{| class="wikitable floatright" | |||
|+Tabell 6.2 Grunnparametere i sensitivitetsanalyse | |||
|Kurveradius | |||
|400 m | |||
|- | |||
|Sideforskyvningsmotstand maksverdi | |||
|17,5 kN/m spor | |||
|- | |||
|Sideforskyvningsmotstand grenseverdi | |||
|9,6 kN/m spor | |||
|- | |||
|Sporets langsgående stivhet | |||
|1,378E+06 N/m/m spor | |||
|- | |||
|Sporets vridningsstivhet | |||
|1,113E+05 Nm/rad/m spor | |||
|- | |||
|Sporfeilens amplitude 38,1 mm | |||
|Sporfeilens halve bølgelengde 4,57 m | |||
|} | |||
Det er i de senere årene utarbeidet flere PC-baserte beregningsprogrammer | |||
for å analysere sikkerheten mot utknekking av helsveist spor. To av | |||
programmene er CWR-BUCKLE som er utarbeidet av US Departement of | |||
Transportation (DOT) og CWERRI som er utviklet av European Rail | |||
Research Institute (ERRI). | |||
Disse programmene kan beregne kritiske knekktemperaturer med grunnlag i | |||
følgende parametere: | |||
*kurveradius | |||
*sideforskyvningsmotstand | |||
*lengdeforskyvningsmotstand | |||
*vridningsmotstand | |||
*horisontal sporfeil (amplitude og lengde) | |||
*evt. vertikale laster fra togpasseringer | |||
I tillegg kan CWERRI brukes til å beregne aksialkrefter og kritisk | |||
knekktemperatur for kompliserte forhold med spor på bruer, for eksempel | |||
dobbeltsporede bruer med flere spenn. | |||
Eksemplet som følger viser hvordan kritisk knekktemperatur endres når vi | |||
endrer de forskjellige parametere som har innflytelse på knekktemperaturene. | |||
Beregningene er utført ved hjelp av CWERRI. Tabell 6.2 viser grunnverdien | |||
som er valgt for de forskjellige parametere. | |||
I beregningene ble det anvendt vertikale laster som vist i figur 6.22. | |||
Figur 6.23 til 6.28 viser hvordan kritisk knekktemperaturer endres når vi | |||
endrer de forskjellige parametere. Kritisk knekktemperatur er her | |||
temperaturøkning i forhold til nøytraltemperaturen. | |||
[[Fil:Vertikale laster.PNG|thumb|center|600px|Figur 6.22 Vertikale laster i modellen]] | |||
[[Fil:Innflytelse fra sideforsk.motstand på kritisk knekktemperatur.PNG|thumb|300px|Figur 6.24 Innflytelse fra sideforsk.motstand på kritisk knekktemperatur]] | |||
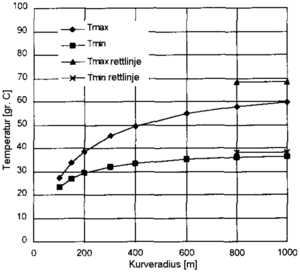
[[Fil:Innflytelse fra kurveradius på kritisk knekktemperatur.PNG|thumb|center|300px|Figur 6.23 Innflytelse fra kurveradius på kritisk knekktemperatur]] | |||
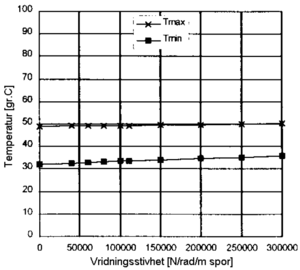
[[Fil:Innflytelse fra vridningsstivhet på kritisk knekktemperatur.PNG|thumb|300px|Figur 6.26 Innflytelse fra vridningsstivhet på kritisk knekktemperatur]] | |||
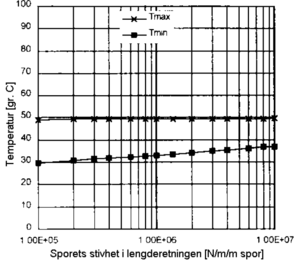
[[Fil:Innflytelse fra stivhet i lengderetn. på kritisk knekktemperatur.PNG|thumb|center|300px|Figur 6.25 Innflytelse fra stivhet i lengderetn. på kritisk knekktemperatur]] | |||
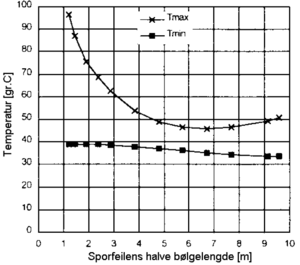
[[Fil:Innflytelse fra sporfeilens lengde på kritisk knekktemperatur.PNG|thumb|300px|Figur 6.28 Innflytelse fra sporfeilens lengde på kritisk knekktemperatur]] | |||
[[Fil:Innflytelse fra pilhøydefeil på kritisk knekktemperatur.PNG|thumb|center|300px|Figur 6.27 Innflytelse fra pilhøydefeil på kritisk knekktemperatur]] | |||
===Sikkerhet mot solslyng=== | |||
'''UIC 720''' | |||
Solslyng utgjør en betydelig avsporingsrisiko som kan medføre både | |||
menneskelig og materiell skade, og i verste fall føre til tap av liv. Det er derfor | |||
viktig å ha en tilstrekkelig sikkerhetsmargin mot solslyng. UIC 720 angir | |||
sikkerhetskriterier basert på de kritiske knekktemperaturer Tk<sub>MIN</sub> og Tk<sub>MAKS</sub>. | |||
Premissene for sikkerhetskriteriene er at et helsveist spor skal kunne motstå | |||
utknekking under alle belastninger som kan forventes. Vi definerer T<sub>TILLATT</sub> | |||
som den maksimale temperaturøkningen i skinnene relativt til | |||
nøytraltemperaturen som vi kan tillate når tilfredsstillende sikkerhet mot | |||
solslyng skal opprettholdes. | |||
Utgangspunkt for bestemming av T<sub>TILLATT</sub> er fastsetting av kritiske | |||
knekktemperaturer, enten ved hjelp av analytiske metoder (som for eksempel | |||
CWERRI) eller utledet med bakgrunn i praktiske forsøk. T<sub>TILLATT</sub> kan baseres | |||
på den lavere kritiske knekktemperatur Tk<sub>MIN</sub>, eller en temperatur over Tk<sub>MIN</sub> | |||
(men lavere enn Tk<sub>MAKS</sub>), avhengig av hvilket sikkerhetsnivå man ønsker: | |||
*Nivå 1: T<sub>TILLATT</sub>= Tk<sub>MIN</sub> | |||
*Nivå 2: T<sub>TILLATT</sub> = Tk<sub>MIN</sub>+ Δt | |||
'''Nivå 1''' | |||
Nivå 1 er basert på det faktum at sporet bare kan knekke ut ved | |||
skinnetemperaturer over Tk<sub>MIN</sub>. Ved denne skinnetemperaturen må sporet | |||
tilføres betydelig energi for at solslyng skal oppstå. Sikkerhetskriterie basert | |||
på nivå 1 gir en buffer mot faktorer som ikke er med i modellen som er | |||
anvendt for bestemmelse av kritisk knekktemperatur. Dette kan for eksempel | |||
være bremse / traksjonskrefter og dynamiske impulslaster. | |||
'''Nivå 2''' | |||
Nivå 2 er et mindre konservativt sikkerhetskriterie som tillater at | |||
skinnetemperaturen kan ligge mellom Tk<sub>MIN</sub>. og Tk<sub>MAKS</sub>. Dette krever at man er | |||
i stand til hele tiden å vedlikeholde sporet innenfor fastsatte toleranser mhp. | |||
sporets sidestabilitet og beliggenhet, samt at dynamiske laster fra trafikken | |||
holdes innenfor fastlagte grenser. | |||
Jernbaneverkets nett er rikt på kurver med liten kurveradius. Mange steder | |||
har vi dessuten problemer med å vedlikeholde et riktig ballastprofil pga. | |||
manglende fyllingsbredder. Med bakgrunn i ovennevnte må vi ha et | |||
sikkerhetskriterie basert på nivå 1 i Norge. | |||
==Sporforskyvning== | |||
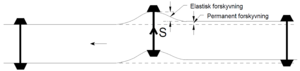
Sporforskyvning kan defineres som en permanent lateral forskyvning av et | |||
sporsegment som er forårsaket av laterale sporkrefter fra passerende tog. | |||
Sporforskyvningen kan utvikle seg kumulativt gjennom mange togpasseringer, | |||
eller opptre mer plutselig. Dersom sideforskyvningen blir for | |||
stor, kan det medføre fare for avsporing. | |||
===Sporforskyvningsmekanismer=== | |||
Når toget styres gjennom en kurve virker det en lateral kraft fra hver aksel | |||
utover mot sporet. Mot denne kraften virker friksjonskrefter mellom sville og | |||
ballast, samt skinnestigens treghetsmoment i horisontalplanet. | |||
Sporforskyvningen kan anta et elastisk forløp, dvs. at sporet beveger seg | |||
tilbake til utgangsposisjonen etter passering av akslene. Men dersom de | |||
laterale sporkreftene blir store nok vil sporet få en varig deformasjon. Ved | |||
gjentatte belastninger vil forskyvningen enten stabilisere seg, eller fortsette å | |||
vokse progressivt. | |||
Det er altså friksjon mellom ballast og sville som i hovedsak motvirker | |||
sporforskyvning. Friksjonen er avhengig av normalkraften, dvs. aksellasten. | |||
På samme måte som den dynamiske avlastningen mellom aksler og boggier | |||
reduserer friksjonen, vil friksjonen mellom sville og ballast øke med økende | |||
aksellast under togets aksler. Forholdet mellom laterale og vertikale | |||
sporkrefter vil dermed ha stor betydning for sporforskyvningen. Rullende | |||
materiell som genererer høye laterale sporkrefter i forhold til aksellasten vil | |||
altså ha en ugunstig innvirkning på sporforskyvningen. | |||
Vi så i avsnitt 2.1 at sporets sideforskyvningsmotstand blir betydelig nedsatt | |||
etter sporjustering og andre arbeider som reduserer ballastens | |||
konsolideringsgrad. Dette har stor innvirkning på sporforskyvning av belastet | |||
spor. Vi kan regne med opptil 50 % mindre sporforskyvning i et konsolidert | |||
betongsvillespor enn i et nyjustert betongsvillespor. | |||
Både sporets kurveradius og aksialkraften i skinnene påvirker | |||
sporforskyvningen. Beregninger utført av US Departement of Transportation | |||
(DOT) viser at sporforskyvningen øker med 40 % i en kurve med radius 291 | |||
m i forhold til rettlinje når skinnetemperaturen er 50˚C høyere enn | |||
nøytraltemperaturen. Avhengig av kurveradius viser beregninger videre at | |||
sporforskyvningen øker med 20 – 40% når skinnetemperaturen øker med | |||
50˚C. Forutsetninger for beregningene er 20 akselpasseringer med et | |||
forhold mellom lateral og horisontal sporkraft på 0,4. | |||
===Prud`hommes forsøk=== | |||
'''sporets dynamiske forskyvningsmotstand''' | |||
[[Fil:Sideforskyvning av belastet spor.PNG|thumb|300px|Figur 6.29 Sideforskyvning av belastet spor]] | |||
[[Fil:Sideforskyvning som funksjon.PNG|thumb|300px|Figur 6.30 Sideforskyvning som funksjon av antall belastninger]] | |||
I Frankrike ble det i begynnelsen av 1960-årene utført forsøk for å finne | |||
sammenhengen mellom den sidekraft S som forårsaker en permanent | |||
sideforskyvning, og aksellasten P. Figur 6.29 viser i prinsipp hvordan | |||
forsøkene ble utført. En lateral kraft blir overført til sporet gjennom en aksel | |||
med en gitt statisk aksellast. Etter at belastningsvognen har passert, blir den | |||
permanente deformasjonen målt. Belastningen blir så gjentatt med stadig | |||
økende lateral kraft. En sammenheng mellom påført lateral kraft og | |||
permanent sideforskyvning kunne dermed fastlegges. Den laterale kraften | |||
som var nødvendig for å frembringe en signifikant permanent forskyvning ble | |||
betegnet som sporets dynamiske forskyvningsmotstand. | |||
Det ble senere utført tester hvor den laterale kraften ble holdt konstant i | |||
serier av belastninger. Figur 6.30 viser at forskyvninger forårsaket av laterale | |||
krefter under en grense stabiliserer seg på et konstant nivå etter et antall | |||
belastninger. Dersom sporet belastes med krefter ut over denne grensen får | |||
vi derimot en progressiv sideforskyvning. Denne grensen blir her betegnet | |||
som sporets dynamiske forskyvningsmotstand. | |||
Basert på testene som ble utført på et helsveist tresvillespor med U33 (46 | |||
kg/m) skinner utviklet Prud`homme en empirisk formel som uttrykker sporets | |||
motstand mot sideforskyvning avhengig av aksellasten (formel 6.8). | |||
{| | |||
|<math> S_{LIM}= 10 +{P \over 3} </math> | |||
| | |||
| | |||
| | |||
|(6.8) | |||
|} | |||
{| | |||
|S<sub>LIM</sub>= dynamisk motstand mot sporforskyvning [N] | |||
|- | |||
|P= aksellast [N] | |||
|} | |||
Prud`hommes formel er blitt brukt i mange land som retningslinje for hvor | |||
store laterale krefter som kan tillates fra det rullende materiell. Formelen tar | |||
ikke hensyn til aksialkrefter i skinnene og forskjellige kurveradier. | |||
Prud`homme anbefalte senere å multiplisere med en faktor = 0,85 for å ta | |||
hensyn til aksialkrefter og kurvatur. I Jernbaneverkets spor tillates følgende | |||
laterale krefter fra det rullende materiell: | |||
*Personvogner og lokomotiver: S<sub>maks</sub> = 10 + P/3 | |||
*Godsvogner: S<sub>maks</sub> = 0,85*(10+P/3) | |||
===Måling av sidemotstand i Norge=== | |||
I forbindelse med forberedelsene til å sette inn krengetog i kommersiell drift, | |||
ble det i 1996 utført målinger av sporets motstand mot sideforskyvning på | |||
Sørlandsbanen. Målingene ble utført av Banverkets ”belastningsmätvagn”. | |||
Under målingene ble sporet belastet med vertikale laster på 40, 70 og 100 | |||
kN. Under disse lastene ble sporet flyttet sideveis henholdsvis 0.4, 0.7 og 1.0 | |||
mm samtidig som man målte den laterale kraften som var nødvendig for | |||
sideforskyvningen. | |||
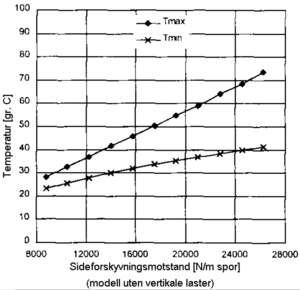
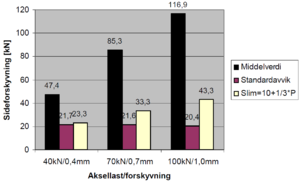
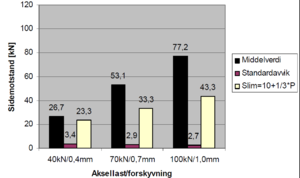
Det ble utført målinger både på tresvillespor og betongsvillespor. Figur 6.31 | |||
og 6.32 viser resultatet fra målingene. I diagrammene er også grenseverdier | |||
beregnet med Prud`hommes formel angitt. Som vi ser av figurene har | |||
betongsvillesporet betydelig høyere motstand mot forskyvning enn | |||
tresvillesporet. | |||
Målingene viser videre at både tresvillesporet og betongsvillesporet har | |||
betydelig høyere motstand mot sporforskyvning enn grenseverdiene som er | |||
fastsatt for tillatte sporkrefter. Det vil med andre ord si at sikkerhetsmarginen | |||
mot sporforskyvning er relativt god. | |||
[[Fil:Pandrol e 1877.PNG|thumb|300px|Figur 6.32 Sidemotstand S49/betongssviller/Pandrol e 1877]] | |||
[[Fil:Hey-Back.PNG|thumb|center|300px|Figur 6.31 Sidemotstand S49/tresviller/Hey-Back]] | |||
==Litteraturhenvisninger== | |||
*1. Sørlie, Per Hermann. ''Krefter i helsveist spor'',1992 | |||
*2. ''Einfluss verschiedener Massnahmen auf den Querversschiebewiderstand des unbelasteten Gleises'',ORE Q D117 Report 8, 1976 | |||
*3. European Rail Research Institute. ''Improved knowledge of forces in CWR Track'',ERRI D202 Report 3, 1995 | |||
*4. ''Lateral stability of rails, especially of long welded rails'', ORE Q D14, 1965 | |||
*5. Esveld, Conraed. ''Improved knowledge of CWR track'', Cost effectiveness and safety aspects of railway track Conference, desember 98, Paris | |||
*6. Stjern, Kåre. ''Sporets sidestabilitet i kurver med små radier ved høye skinnetemperaturer'', Rapport nr.3 fra studieopphold ved TU München, 1985 | |||
*7. Kish, Andrew , Samavedam, Gopal & Wormley, David. ''Fundamentals of track lateral shift for high-speed rail applications'', Cost effectiveness and safety aspects of railway track Conference,desember 98, Paris | |||
*8. Banverket. ''Mätning av spårets sidomotstånd för NSB - Mätrapport'', Banverket / Banlaboratoriet, 1996 | |||
Siste sideversjon per 19. feb. 2015 kl. 12:03
__NUMBEREDHEADINGS__
Innledning
For å unngå at sporet knekker ut ved store trykkspenninger i skinnene, må vi ha tilstrekkelig sidestabilitet i sporet. En rekke faktorer er med på å bestemme hvor stabilt sporet er mot sideveis forskyvning. De viktigste er
- ballastprofil
- ballastkvalitet
- ballastens komprimeringsgrad
- svilletype
- befestigelsestype
- skinneprofil
Sportekniske krav til et helsveist spor er gitt i [JD 530].
Faktorer som påvirker sidestabiliteten
Sporets stabilitet mot sideveis utknekking er avhengig av
- sporets sideforskyvningsmotstand
- sporets vridningsmotstand
Sideforskyvningsmotstand
Sideforskyvningsmotstanden kan defineres som den motstand en sville møter når den beveger seg eller prøver å bevege seg sideveis. Den totale sideforskyvningsmotstand kan vi dele opp i 3 komponenter:
| Fb = motstand fra svillebunn |
| Fs = motstand fra svillesider/svillemellomrom |
| Fe= motstand fra ballastskulder/svilleender |
| (6.1) |
Vi kan regne med følgende bidrag fra de 3 komponentene til den totale
sideforskyvningsmotstanden:
Praktiske forsøk har vist at sideforskyvningsmotstanden er avhengig av veien svillene forflytter seg (figur 6.1).
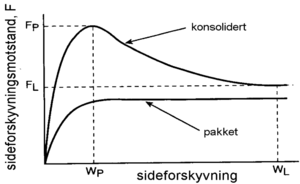
For nylig pakket spor antar forskyvningsmotstanden en konstant verdi etter noen få millimeter forskyvningsvei. For et konsolidert spor når forskyvningsmotstanden en maksverdi (FP) før den avtar til en konstant verdi (FL). Praktiske forsøk har vist at maksverdien for konsolidert spor opptrer ved en sideforskyvning på 5 mm eller mindre, mens forskyvningsmotstanden når en konstant verdi etter 100 - 150 mm forskyvningsvei.
Følgende faktorer har innflytelse på motstanden som sporet møter ved sideforskyvning:
- ballastprofil
- ballastkvalitet
- ballastens konsolideringsgrad
- svilletype
- svilleavstand
Ballastprofilet
Ballastskulderen har en avgjørende innflytelse på sporets sideforskyvningsmotstand. Figur 6.2 viser hvordan sideforskyvningsmotstanden endrer seg når skulderbredde og høyde endrer seg. Resultatene bygger på praktiske forsøk utført av European Rail Research Institute (ERRI).
Figur 6.2 viser f.eks, at sideforskyvningsmotstanden øker med ca. 10% dersom skulderbredden øker fra 40 til 55 cm utenfor svilleende. En opphoping av ballastskulderen på 10 cm medfører videre ca. 20% økning i side-forskyvningsmotstanden.
Ballastmengde i svillemellomrommet
Også ballastmengden i svillemellomrommet bidrar til sporets motstand mot sideveis forskyvning. Figur 6.3 viser hvordan sideforskyvningsmotstanden reduseres når vi fjerner ballast fra svillemellomrommet.
Ballastprofiler
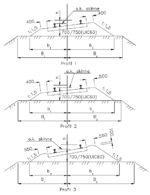
For å sikre tilstrekkelig sidemotstand er det satt krav til ballastprofilet for spor som skal helsveises (Figur 6.4) [JD 530, kap 10]. Tabell 6.1 viser hvilke profiler som skal anvendes ved forskjellige kombinasjoner av kurveradier og svilletyper.
| spor med tresviller | spor med betongsviller | skinnelengder > 30 m. | skinnelengder < 30 m. |
|---|---|---|---|
| Rettlinje og radier > 500 m | Rettlinje og radier > 400 m | Profil 1 | Profil 1 |
| Radier 499-400 m | Radier 399-300 m | Profil 2 | Profil 1 |
| Radier 399-300 m | Radier 299-250 m | Profil 3 | Profil 1 |
| Radier < 300 m | Radier < 250 m | ikke tillatt | Profil 1 |
Ballastkvalitet
Ballastmaterialets kornform og fraksjonering har innflytelse på hvor stor motstand ballasten yter mot sideveis forskyvning av svillene. Det er et krav om at ballasten i et helsveist spor skal bestå av fullverdi pukk med kornstørrelse 25-63 mm. (tidl. 25-50 mm).
Forurensninger og vann i ballasten vil nedsette forskyvningsmotstanden betraktelig. Dårlig drenering vil altså være med på å redusere sikkerheten mot solslyng.
Ballastens konsolideringssgrad
Sporjustering
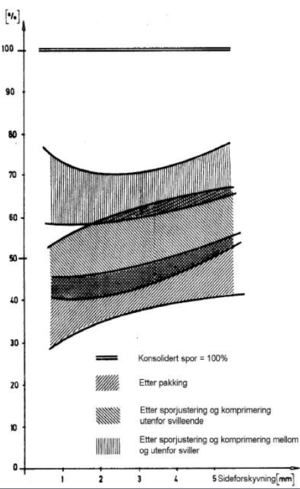
Alle arbeider som reduserer ballastens konsolideringsgrad medfører en reduksjon i sideforskyvningsmotstanden. Figur 6.5 viser resultater av forsøk med å sideforskyve sporet etter sporjustering. Vi ser at forskyvningsmotstanden rett etter sporjustering faller til 30-50 % av full motstand. Dersom vi bruker kantvibrator øker motstanden noe, mens bruk av dynamisk sporstabilisator som vibrerer hele sporet øker forskyvningsmotstanden til mellom 60 og 75 % av full motstand.
Etter sporjustering skal det iverksettes hastighetsreduksjon i kurver med radius £ 400 m dersom det kan forventes skinnetemperaturer over +30˚C [JD 532, kap.13]. Full sidemotstand oppnås etter ca. 150 000 brt togpassering. Dette tilsvarer 3 - 6 dager ved hovedspor i Norge. Bruk av dynamisk sporstabilisator vil øke sidemotstanden tilsvarende ca. 80 000 brt umiddelbart.
Ballastrensing
Andre sporarbeider som reduserer forskyvningsmotstanden er ballastrensing og svillebytte. Etter ballastrensing kan vi regne med at motstanden er redusert til 20 - 30 % av full motstand.
Det må utvises meget stor aktsomhet ved slike sporarbeider i varmt vær. Regler for vedlikehold av helsveist spor [JD 532, kap. 10] gir temperaturbegrensninger for slike arbeider. Arbeid som svekker sporets stabilitet skal bare utføres i skinnetemperaturområdet 0 - +30˚C.
Svilletype
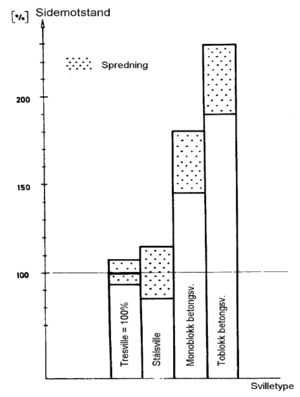
Svillenes form og tyngde er med på å bestemme sporets sidestabilitet. Figur 6.6 viser resultatet av praktiske forsøk med sideforskyvning av sporavsnitt med forskjellige svilletyper. Forsøkene er utført av ERRI.
I figuren er forskyvningsmotstanden for tresviller brukt som referanse. Vi ser at betongsviller har vesentlig bedre sideforskyvningsmotstand enn tresviller og stålsviller. Det er fremfor alt tyngden til betongsvillene som gjør at disse yter større motstand. Vekten til en betongsville er 250 - 300 kg mens en tresville veier fra 50-80 kg.
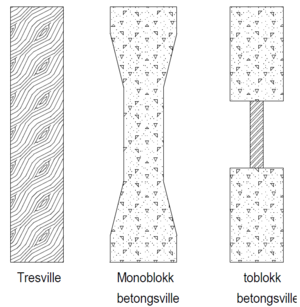
Formen på svillene har også betydning for sideforskyvningsmotstanden. Figur 6.7 viser skjematisk tresville, monoblokk betongsville og toblokk betongsville sett ovenfra. Vi ser at monoblokk betongsvillens “innsving” på midten bidrar til større friksjon mot ballasten ved sideveis forskyvning enn den rektangulære tresvillen. Toblokk betongsviller har to endeflater som yter motstand mot bevegelse sideveis og er således den svilletypen med suverent best sideforskyvningsmotstand. Det er også verdt å merke seg at betongsvillenes underkant har betydelig større flate enn overkanten på svillene. Dette pga. at friksjonen mellom underkant av sville og ballasten utgjør en stor del av den totale sideforskyvningsmotstanden.
Sideforskyvningsmotstand uttrykkes gjerne som motstand pr. lengdeenhet. Dersom vi kjenner motstanden for en sville finner vi sideforskyvningsmotstanden ved å dividere med svilleavstanden.
| (6.2) |
Sporets sideforskyvningsmotstand er altså omvendt proporsjonal med
svilleavstanden. For å opprettholde tilstrekkelig sideforskyvningsmotstand i et
helsveist spor er det derfor viktig at ikke svilleavstanden blir for stor. Ved JBV
tillates det maks 65 cm svilleavstand i helsveist spor dersom sporet har
kurveradius større enn 500 m. For kurver med mindre radius skal
svilleavstanden ikke overstige 60 cm.
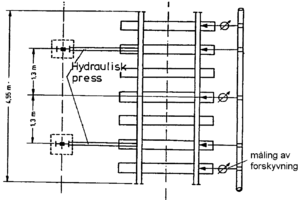
Målinger av sideforskyvningsmotstand
Sideforskyvningsmotstanden måles ved å skyve/dytte enten enkeltsviller eller flere sviller sammen. Figur 6.8 viser et oppsett for å måle sideforskyvningsmotstanden. Figur 6.9 viser typiske verdier for sideforskyvningsmotstand i nypakket spor, mens figur 6.10 viser verdier fra målinger på tresvillespor i USA.
Vridningsmotstand
For at en utknekking av sporet i horisontalplanet skal kunne oppstå, må skinnene rotere i forhold til svillene (figur 6.11).
Når vi betrakter sporet som en ramme bestående av skinner og sviller vil vridningsmotstanden i rammens ledd ha innflytelse på sidestabiliteten til sporet. Vridningsmotstanden, eller rammestivheten er avhengig av befestigelsen. Fjærens klemkraft og friksjonen mellom skinne og mellomlegg/isolator er av stor betydning.
Lengden av skinnefotsidens anleggsflate mot underlagsplate eller isolator er avgjørende. Dersom vi sammenligner Hey-Back befestigelsessystem med Pandrol PR og e–systemer ser vi at Hey-Back platens ribbekant har betydelig lengre anleggsflate mot skinnefotsiden enn Pandrol-isolatoren har. Figur 6.12 viser tydelig hvor stor betydning denne forskjellen har på vridningsmotstanden. Det nye befestigelsessystemet Pandrol Fastclip har en sideisolator som har betydelig lengre anleggsflate mot skinnefotsiden enn Pandrol PR/e-clip-systemene og vil derfor ha en større vridningsmotstand.
Slitasje på isolator og mellomlegg
På et betongsvillespor vil slitasje på isolator og mellomlegg kunne redusere vridningsmotstanden betraktelig ved at det oppstår "slark" i befestigelsen. Slitasje på isolatorer opptrer først og fremst i krappe kurver hvor de laterale sporkreftene er størst. Nettopp i krappe kurver har vi den største risiko for solslyng. Det er derfor god grunn til å holde isolatorenes tilstand under oppsyn i krappe kurver.
Skinneprofilets betydning for sidestabiliteten
Skinneprofilets treghetsmoment om skinnens vertikale akse har innflytelse på hvor stivt hele sporet blir mot sideveis forskyvning. Samtidig øker aksialkraften i skinnene når tverrsnittsarealet øker. Det er dermed ikke gitt at et større skinneprofil medfører større sikkerhet mot solslyng. Figur 6.13 viser hvilken innflytelse forskjellige skinneprofil har for sikkerhet mot utknekking, hvor det er tatt utgangspunkt i S49. Beregningene gjelder for rett linje og er utført etter Meiers metode (se avsnitt 3.3.1). Vi ser for eksempel at S54 medfører en reduksjon i sikkerhet mot solslyng på 4% i forhold til S49.
Solslyng
Utknekkingsmekanismer
Solslyng er utknekking av sporet i horisontalplanet som oppstår pga. store trykkrefter i skinnene ved høye skinnetemperaturer der sporets sidestabilitet er for liten til å fastholde sporet. Ved JBV er definisjonen på solslyng at pilhøydefeilen er på min. 25 mm målt med 10 m korde. Prinsipielt kan utknekking skje i 3 forskjellige former (figur 6.14). Sporet kan knekke ut i en enkel halv-sinusbølge (modus 1) eller flere halvsinusbølger (modus 2 og 3). Ved en utknekking vil det alltid skje en langsgående bevegelse av skinnene i de tilstøtende områder på begge sider av solslyngen. Vi kan si at skinnene ”mates” inn i solslyngområdet. Dette fører til at aksialkreftene i skinnene påvirkes i de tilstøtende områder.
Figur 6.15 viser et helsveist spor på rettlinje med en liten sinusformet sporfeil med pilhøyde f0 og lengde 2L0. Når aksialtrykkreftene i sporet øker som følge av en temperaturøkning, vil sporforskyvningen kunne øke noe inntil en kritisk temperaturøkning Tk nås. Når skinnetemperaturen overstiger den kritiske temperaturen, vil det skje en plutselig utknekking til en stor pilhøyde f over lengde 2L. En ytterligere temperaturøkning vil gradvis øke sporforskyvningen.
Figur 6.16 viser sideforskyvning som funksjon av temperaturøkning ved solslyng. Fra A til B foregår det en liten sideforskyvning som følge av at aksialtrykkreftene øker. Ved B har vi en ustabil situasjon hvor sporet plutselig knekker ut. Utknekkingen medfører en avlasting av trykkreftene inntil sporet er stabilt ved S. Skinnetemperaturen ved pkt. S defineres som den lavere kritiske knekktemperatur, TkMIN. Skinnetemperaturen ved pkt. B defineres som den høyere kritiske knekktemperatur, TkMAKS.
TkMIN er den laveste skinnetemperaturen hvor sporet kan knekke ut fra pkt. A dersom sporet blir tilført ekstra energi utenfra. Ved TkMAKS derimot vil sporet knekke ut uten tilførsel av ekstra energi. Sporets likevekt ved TkMAKS kan sammenlignes med den likevekt et kronestykke har når vi balanserer det på en skarp kant.
I figur 6.16 er det forutsatt at solslyng opptrer som en plutselig sporforskyvning. Dette er ikke alltid tilfelle. Ved en kombinasjon av store initielle sporfeil og liten sideforskyvningsmotstand kan sporet sideforskyves gradvis uten noen ”eksplosiv” fase.
Solslyng under togpassering
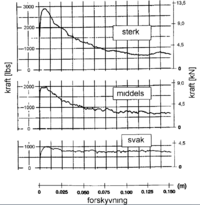
Under togpassering vil sporet bevege seg i vertikalplanet i bølgebevegelser. Under hver aksel og boggi får vi en nedbøyning, mens vi foran, mellom og bak aksler og boggier får en heving av sporet (figur 6.17).
Dynamisk avlastning
Denne dynamiske avlastningen resulterer i at sideforskyvningsmotstanden reduseres. Tapet av sideforskyvningsmotstand er sporets egenvekt multiplisert med friksjonskoeffisienten mellom sville og ballast. Sideforskyvningsmotstanden under dynamisk avlastning blir da:
| (6.3) |
| FD=sideforskyvningsmotst under avlastning |
| FS=statisk sideforskyvningsmots. |
| μ = friksjonskoeffisient sville ballast |
| Q= sporets egenvekt |
Friksjon mellom sville og ballast
Friksjonskoeffisienten mellom sville og ballast kan bestemmes gjennom praktiske forsøk. For betongsviller kan den variere mellom 0,4 og 0,9 avhengig av ruhet av svillenes underside, ballastkvalitet og konsolideringsgrad. For tresviller kan vi ha langt større variasjoner fordi ballastmateriale i noen tilfeller kan grave seg inn i svilleoverflaten og øke friksjonen betraktelig. Reduksjonen i sideforskyvningsmotstand fører til en reduksjon i kritisk knekktemperatur og dermed økt fare for solslyng under togpassering. En stor del av solslyngtilfellene skjer derfor under togpassering. Sammen med sporets egenvekt og friksjon sville/ballast vil størrelse og karakteristikk av den dynamiske avlastningen avgjøre hvor mye den kritiske knekktemperaturen reduseres i forhold til ubelastet spor. Følgende faktorer har innflytelse på den dynamiske avlastingen:
- aksellast
- akselavstand
- boggiavstand
- sporets vertikale stivhet (ballastsiffer)
Beregning av kritisk knekktemperatur
Kritisk knekktemperatur kan finnes ved å betrakte sporet som en uendelig lang stav som hviler på et underlag som yter motstand mot forskyvning ved friksjon. Matematisk eksakte løsninger kan bare finnes ved hjelp av differensialligninger. Imidlertid kan tilnærmede løsninger finnes gjennom energibetraktninger.
Meiers metode
Meier lanserte en metode for beregning av kritisk knekktemperatur i Tyskland i 1937. Metoden antar knekkformer som vist i figur 6.18. I modellen inngår en faktor som kalles ”sporets ekvivalente treghetsmoment”, altså skinnestigens stivhet sideveis. Denne faktoren bestemmes ut fra praktiske forsøk for hver aktuelle sporkonstruksjon.
Ved hjelp av energibetraktninger kan man finne empiriske formler for kritisk sporfeil og kritisk knekktemperatur. Formel 6.4 gir kritisk sporfeil og formel 6.5 gir kritisk knekktemperatur for rettlinjet spor.
| (6.4) |
| (6.5) |
Formel 6.6 gir kritisk sporfeil og formel 6.7 gir kritisk knekktemperatur for
kurver.
| (6.6) |
| (6.7) |
| E = elastisitets modulen = 2,07* 105 [N/mm^2] |
| α = strålets utvidelseskoeff.= 1,15*105 |
| A= skinnenes samlede tverrsnittflate [mm^2] |
| J=sporets ekvivalente treghetsmoment [mm^4] |
| R= kurveradius [mm] |
| F= sideforskyvningsmotstand [N/mm] |
| f*=kritisk sporfeil |
| f= antatt sporfeil [mm] |
| Pk=kritisk trykkraft i sporet |
Figur 6.19 og 6.20 viser beregninger som er foretatt på S49 - spor med treog betongsviller med Meiers metode. Kritisk temperaturøkning er økning av skinnetemperaturen i forhold til nøytraltemperaturen.
Det er brukt følgende forutsetninger i beregningene:
- svilleavstand = 65 cm
- ballastskulder = 40 cm
- koeffisient for konsolideringsgrad = 0,7
- koeffisient for løfting mellom boggier = 0,7
Vi ser at kritisk temperaturøkning for en kurve med radius = 300 m er 50˚C for betongsvillesporet med pilhøydefeil = 10 mm. Dette gir oss en sikkerhetsmargin mot solslyng på ca. 15˚C (forutsatt maks skinnetemperatur +55˚C og nøytraltemperatur +20˚C). Dette er for lite og viser tydelig behovet for større sidemotstand i krappe kurver. Større sidemotstand kan oppnås ved å øke skulderbredden på ballastprofilet som vist i figur 6.21. Her er skulderbredden økt til 55 cm som foreskrevet i JD 530 for spor med liten kurveradius (< 300 m for betongsviller / < 400 m for tresviller). Sporet vil nå teoretisk knekke ut ved skinnetemperatur på 80˚C i en 300 m radius kurve med pilhøydefeil på 10 mm (forutsatt maks skinnetemperatur +55˚C og nøytraltemperatur +20˚C). Dette gir oss en sikkerhetsmargin på ca. 25˚C.
Forutsetninger i beregningene:
- svilleavstand = 65 cm
- ballastskulder = 55 cm
- ballast over svilleplan: 10 cm
- koeffisient for konsolideringsgrad = 0,7
- koeffisient for løfting mellom boggier = 0,7
Nyere beregningsprogrammer
| Kurveradius | 400 m |
| Sideforskyvningsmotstand maksverdi | 17,5 kN/m spor |
| Sideforskyvningsmotstand grenseverdi | 9,6 kN/m spor |
| Sporets langsgående stivhet | 1,378E+06 N/m/m spor |
| Sporets vridningsstivhet | 1,113E+05 Nm/rad/m spor |
| Sporfeilens amplitude 38,1 mm | Sporfeilens halve bølgelengde 4,57 m |
Det er i de senere årene utarbeidet flere PC-baserte beregningsprogrammer for å analysere sikkerheten mot utknekking av helsveist spor. To av programmene er CWR-BUCKLE som er utarbeidet av US Departement of Transportation (DOT) og CWERRI som er utviklet av European Rail Research Institute (ERRI). Disse programmene kan beregne kritiske knekktemperaturer med grunnlag i følgende parametere:
- kurveradius
- sideforskyvningsmotstand
- lengdeforskyvningsmotstand
- vridningsmotstand
- horisontal sporfeil (amplitude og lengde)
- evt. vertikale laster fra togpasseringer
I tillegg kan CWERRI brukes til å beregne aksialkrefter og kritisk knekktemperatur for kompliserte forhold med spor på bruer, for eksempel dobbeltsporede bruer med flere spenn. Eksemplet som følger viser hvordan kritisk knekktemperatur endres når vi endrer de forskjellige parametere som har innflytelse på knekktemperaturene. Beregningene er utført ved hjelp av CWERRI. Tabell 6.2 viser grunnverdien som er valgt for de forskjellige parametere.
I beregningene ble det anvendt vertikale laster som vist i figur 6.22.
Figur 6.23 til 6.28 viser hvordan kritisk knekktemperaturer endres når vi endrer de forskjellige parametere. Kritisk knekktemperatur er her temperaturøkning i forhold til nøytraltemperaturen.
Sikkerhet mot solslyng
UIC 720
Solslyng utgjør en betydelig avsporingsrisiko som kan medføre både menneskelig og materiell skade, og i verste fall føre til tap av liv. Det er derfor viktig å ha en tilstrekkelig sikkerhetsmargin mot solslyng. UIC 720 angir sikkerhetskriterier basert på de kritiske knekktemperaturer TkMIN og TkMAKS. Premissene for sikkerhetskriteriene er at et helsveist spor skal kunne motstå utknekking under alle belastninger som kan forventes. Vi definerer TTILLATT som den maksimale temperaturøkningen i skinnene relativt til nøytraltemperaturen som vi kan tillate når tilfredsstillende sikkerhet mot solslyng skal opprettholdes. Utgangspunkt for bestemming av TTILLATT er fastsetting av kritiske knekktemperaturer, enten ved hjelp av analytiske metoder (som for eksempel CWERRI) eller utledet med bakgrunn i praktiske forsøk. TTILLATT kan baseres på den lavere kritiske knekktemperatur TkMIN, eller en temperatur over TkMIN (men lavere enn TkMAKS), avhengig av hvilket sikkerhetsnivå man ønsker:
- Nivå 1: TTILLATT= TkMIN
- Nivå 2: TTILLATT = TkMIN+ Δt
Nivå 1
Nivå 1 er basert på det faktum at sporet bare kan knekke ut ved skinnetemperaturer over TkMIN. Ved denne skinnetemperaturen må sporet tilføres betydelig energi for at solslyng skal oppstå. Sikkerhetskriterie basert på nivå 1 gir en buffer mot faktorer som ikke er med i modellen som er anvendt for bestemmelse av kritisk knekktemperatur. Dette kan for eksempel være bremse / traksjonskrefter og dynamiske impulslaster.
Nivå 2
Nivå 2 er et mindre konservativt sikkerhetskriterie som tillater at skinnetemperaturen kan ligge mellom TkMIN. og TkMAKS. Dette krever at man er i stand til hele tiden å vedlikeholde sporet innenfor fastsatte toleranser mhp. sporets sidestabilitet og beliggenhet, samt at dynamiske laster fra trafikken holdes innenfor fastlagte grenser.
Jernbaneverkets nett er rikt på kurver med liten kurveradius. Mange steder har vi dessuten problemer med å vedlikeholde et riktig ballastprofil pga. manglende fyllingsbredder. Med bakgrunn i ovennevnte må vi ha et sikkerhetskriterie basert på nivå 1 i Norge.
Sporforskyvning
Sporforskyvning kan defineres som en permanent lateral forskyvning av et sporsegment som er forårsaket av laterale sporkrefter fra passerende tog. Sporforskyvningen kan utvikle seg kumulativt gjennom mange togpasseringer, eller opptre mer plutselig. Dersom sideforskyvningen blir for stor, kan det medføre fare for avsporing.
Sporforskyvningsmekanismer
Når toget styres gjennom en kurve virker det en lateral kraft fra hver aksel utover mot sporet. Mot denne kraften virker friksjonskrefter mellom sville og ballast, samt skinnestigens treghetsmoment i horisontalplanet. Sporforskyvningen kan anta et elastisk forløp, dvs. at sporet beveger seg tilbake til utgangsposisjonen etter passering av akslene. Men dersom de laterale sporkreftene blir store nok vil sporet få en varig deformasjon. Ved gjentatte belastninger vil forskyvningen enten stabilisere seg, eller fortsette å vokse progressivt.
Det er altså friksjon mellom ballast og sville som i hovedsak motvirker sporforskyvning. Friksjonen er avhengig av normalkraften, dvs. aksellasten. På samme måte som den dynamiske avlastningen mellom aksler og boggier reduserer friksjonen, vil friksjonen mellom sville og ballast øke med økende aksellast under togets aksler. Forholdet mellom laterale og vertikale sporkrefter vil dermed ha stor betydning for sporforskyvningen. Rullende materiell som genererer høye laterale sporkrefter i forhold til aksellasten vil altså ha en ugunstig innvirkning på sporforskyvningen.
Vi så i avsnitt 2.1 at sporets sideforskyvningsmotstand blir betydelig nedsatt etter sporjustering og andre arbeider som reduserer ballastens konsolideringsgrad. Dette har stor innvirkning på sporforskyvning av belastet spor. Vi kan regne med opptil 50 % mindre sporforskyvning i et konsolidert betongsvillespor enn i et nyjustert betongsvillespor.
Både sporets kurveradius og aksialkraften i skinnene påvirker sporforskyvningen. Beregninger utført av US Departement of Transportation (DOT) viser at sporforskyvningen øker med 40 % i en kurve med radius 291 m i forhold til rettlinje når skinnetemperaturen er 50˚C høyere enn nøytraltemperaturen. Avhengig av kurveradius viser beregninger videre at sporforskyvningen øker med 20 – 40% når skinnetemperaturen øker med 50˚C. Forutsetninger for beregningene er 20 akselpasseringer med et forhold mellom lateral og horisontal sporkraft på 0,4.
Prud`hommes forsøk
sporets dynamiske forskyvningsmotstand
I Frankrike ble det i begynnelsen av 1960-årene utført forsøk for å finne sammenhengen mellom den sidekraft S som forårsaker en permanent sideforskyvning, og aksellasten P. Figur 6.29 viser i prinsipp hvordan forsøkene ble utført. En lateral kraft blir overført til sporet gjennom en aksel med en gitt statisk aksellast. Etter at belastningsvognen har passert, blir den permanente deformasjonen målt. Belastningen blir så gjentatt med stadig økende lateral kraft. En sammenheng mellom påført lateral kraft og permanent sideforskyvning kunne dermed fastlegges. Den laterale kraften som var nødvendig for å frembringe en signifikant permanent forskyvning ble betegnet som sporets dynamiske forskyvningsmotstand.
Det ble senere utført tester hvor den laterale kraften ble holdt konstant i serier av belastninger. Figur 6.30 viser at forskyvninger forårsaket av laterale krefter under en grense stabiliserer seg på et konstant nivå etter et antall belastninger. Dersom sporet belastes med krefter ut over denne grensen får vi derimot en progressiv sideforskyvning. Denne grensen blir her betegnet som sporets dynamiske forskyvningsmotstand.
Basert på testene som ble utført på et helsveist tresvillespor med U33 (46 kg/m) skinner utviklet Prud`homme en empirisk formel som uttrykker sporets motstand mot sideforskyvning avhengig av aksellasten (formel 6.8).
| (6.8) |
| SLIM= dynamisk motstand mot sporforskyvning [N] |
| P= aksellast [N] |
Prud`hommes formel er blitt brukt i mange land som retningslinje for hvor store laterale krefter som kan tillates fra det rullende materiell. Formelen tar ikke hensyn til aksialkrefter i skinnene og forskjellige kurveradier. Prud`homme anbefalte senere å multiplisere med en faktor = 0,85 for å ta hensyn til aksialkrefter og kurvatur. I Jernbaneverkets spor tillates følgende laterale krefter fra det rullende materiell:
- Personvogner og lokomotiver: Smaks = 10 + P/3
- Godsvogner: Smaks = 0,85*(10+P/3)
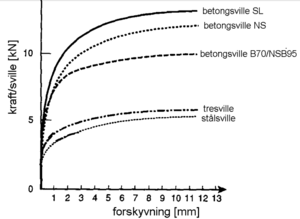
Måling av sidemotstand i Norge
I forbindelse med forberedelsene til å sette inn krengetog i kommersiell drift, ble det i 1996 utført målinger av sporets motstand mot sideforskyvning på Sørlandsbanen. Målingene ble utført av Banverkets ”belastningsmätvagn”. Under målingene ble sporet belastet med vertikale laster på 40, 70 og 100 kN. Under disse lastene ble sporet flyttet sideveis henholdsvis 0.4, 0.7 og 1.0 mm samtidig som man målte den laterale kraften som var nødvendig for sideforskyvningen. Det ble utført målinger både på tresvillespor og betongsvillespor. Figur 6.31 og 6.32 viser resultatet fra målingene. I diagrammene er også grenseverdier beregnet med Prud`hommes formel angitt. Som vi ser av figurene har betongsvillesporet betydelig høyere motstand mot forskyvning enn tresvillesporet. Målingene viser videre at både tresvillesporet og betongsvillesporet har betydelig høyere motstand mot sporforskyvning enn grenseverdiene som er fastsatt for tillatte sporkrefter. Det vil med andre ord si at sikkerhetsmarginen mot sporforskyvning er relativt god.
Litteraturhenvisninger
- 1. Sørlie, Per Hermann. Krefter i helsveist spor,1992
- 2. Einfluss verschiedener Massnahmen auf den Querversschiebewiderstand des unbelasteten Gleises,ORE Q D117 Report 8, 1976
- 3. European Rail Research Institute. Improved knowledge of forces in CWR Track,ERRI D202 Report 3, 1995
- 4. Lateral stability of rails, especially of long welded rails, ORE Q D14, 1965
- 5. Esveld, Conraed. Improved knowledge of CWR track, Cost effectiveness and safety aspects of railway track Conference, desember 98, Paris
- 6. Stjern, Kåre. Sporets sidestabilitet i kurver med små radier ved høye skinnetemperaturer, Rapport nr.3 fra studieopphold ved TU München, 1985
- 7. Kish, Andrew , Samavedam, Gopal & Wormley, David. Fundamentals of track lateral shift for high-speed rail applications, Cost effectiveness and safety aspects of railway track Conference,desember 98, Paris
- 8. Banverket. Mätning av spårets sidomotstånd för NSB - Mätrapport, Banverket / Banlaboratoriet, 1996