Stabilitet i kraftsystemet: Forskjell mellom sideversjoner
(fjernet numberheadings) |
|||
| (22 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
== Innledning== | == Innledning== | ||
| Linje 48: | Linje 47: | ||
=== Ulike dynamiske fenomener=== | === Ulike dynamiske fenomener=== | ||
[[Fil:Fig542-1401.png|thumb|600px|''Figur 1: Oversikt over dynamiske fenomener i et kraftsystem samt innenfor hvilke tidskonstanter de opererer'']] | |||
De ulike dynamiske fenomenene i kraftsystemet kan deles inn i 5 forskjellige grupper etter deres fysikalske karakter. Fenomenene er gruppert etter typisk tidskonstant og vist i figur 1. De ulike fenomenene kan påvirke hverandre når tidskonstantene ligger i samme område. Slik påvirkning kan dersom en ikke tar hensyn til den føre til ekstra utfordringer for å sikre kompatibilitet og stabilitet. | De ulike dynamiske fenomenene i kraftsystemet kan deles inn i 5 forskjellige grupper etter deres fysikalske karakter. Fenomenene er gruppert etter typisk tidskonstant og vist i figur 1. De ulike fenomenene kan påvirke hverandre når tidskonstantene ligger i samme område. Slik påvirkning kan dersom en ikke tar hensyn til den føre til ekstra utfordringer for å sikre kompatibilitet og stabilitet. | ||
De raskeste dynamiske fenomenene er bølgeeffektene med tidskonstanter fra mikrosekunder for lynimpulser til millisekunder for RLC-kretser. Siden de er gitt av de elektriske parameterne i systemet kalles fenomenen også for elektriske. Disse effektene oppstår oftere i systemer med høyere spenning og tilhører normalt nettdelen av systemet. Resonanser i RLC-kretser har vist seg å kunne oppstå i kraftsystemer for jernbane med liten demping, for eksempel i fjernlednings og autotransformatorsystemer hvor kapasitansen er høy. Dette blir videre behandlet under elektrisk resonansustabilitet i kapittel 5. | De raskeste dynamiske fenomenene er bølgeeffektene med tidskonstanter fra mikrosekunder for lynimpulser til millisekunder for RLC-kretser. Siden de er gitt av de elektriske parameterne i systemet kalles fenomenen også for elektriske. Disse effektene oppstår oftere i systemer med høyere spenning og tilhører normalt nettdelen av systemet. Resonanser i RLC-kretser har vist seg å kunne oppstå i kraftsystemer for jernbane med liten demping, for eksempel i fjernlednings og autotransformatorsystemer hvor kapasitansen er høy. Dette blir videre behandlet under elektrisk resonansustabilitet i kapittel 5. | ||
| Linje 67: | Linje 61: | ||
=== Svingninger og resonanser=== | === Svingninger og resonanser=== | ||
[[Fil:Fig542-1402.png|thumb|600px|''Figur 2: Til venstre eksempel på frekvensrespons både i amplitude og fase for en RCL-serieresonanskrets med høy og lav demping. Til høyre eksempel på sprangresponsen for samme kretsen.'']] | |||
Alle komponentene i kraftsystemet har sin måte å respondere på endringer og forstyrrelser på, gitt av sin fysikalske natur eller regulering. Dynamisk uttrykkes denne responsen gjerne ved hjelp av en frekvensresponskarakteristikk. Slik karakteristikk kan utarbeides både for kontaktledningen, lokomotivene og omformerne som vist i de neste kapitlene. Et eksempel på en frekvensresponskarakteristikk er vist i figur 2 sammen med sprangresponsen i tidsplanet. | Alle komponentene i kraftsystemet har sin måte å respondere på endringer og forstyrrelser på, gitt av sin fysikalske natur eller regulering. Dynamisk uttrykkes denne responsen gjerne ved hjelp av en frekvensresponskarakteristikk. Slik karakteristikk kan utarbeides både for kontaktledningen, lokomotivene og omformerne som vist i de neste kapitlene. Et eksempel på en frekvensresponskarakteristikk er vist i figur 2 sammen med sprangresponsen i tidsplanet. | ||
Ved noen frekvenser kan responsen være dempet slik at komponenten helt eller nesten er upåvirket av forstyrrelsen. Forstyrrelser ved andre frekvenser kan gjøre at komponenten påvirkes til å gi et signal tilbake til systemet med en gitt amplitude og tidsforskyvning i forhold til forstyrrelsen. Den nye forstyrrelsen på systemet kan i sin tur påvirke andre komponenter med sin respons. Frekvenser av forstyrrelser og påvirkninger som gjør at komponenter eller systemer blir stående å svinge mot hverandre med liten demping kalles resonansfrekvenser. Ved liten eller ingen demping kan disse pendlingene bare fortsette å vokse helt til en komponent går i stykker eller et vern løser ut. Systemet er da ustabilt. | Ved noen frekvenser kan responsen være dempet slik at komponenten helt eller nesten er upåvirket av forstyrrelsen. Forstyrrelser ved andre frekvenser kan gjøre at komponenten påvirkes til å gi et signal tilbake til systemet med en gitt amplitude og tidsforskyvning i forhold til forstyrrelsen. Den nye forstyrrelsen på systemet kan i sin tur påvirke andre komponenter med sin respons. Frekvenser av forstyrrelser og påvirkninger som gjør at komponenter eller systemer blir stående å svinge mot hverandre med liten demping kalles resonansfrekvenser. Ved liten eller ingen demping kan disse pendlingene bare fortsette å vokse helt til en komponent går i stykker eller et vern løser ut. Systemet er da ustabilt. | ||
| Linje 84: | Linje 74: | ||
Tidsforsinkelse er ofte en del av karakteristikken og egenskapene til komponentene i reguleringssløyfen og er gjerne ikke til å unngå. Stor tidsforsinkelse kan gjøre at et system blir ustabilt. Samtidig kan en tidsforsinkelse være med på å dempe et system slik at signaler med høy frekvens ikke får innvirkning på systemet og dermed også virker stabiliserende. | Tidsforsinkelse er ofte en del av karakteristikken og egenskapene til komponentene i reguleringssløyfen og er gjerne ikke til å unngå. Stor tidsforsinkelse kan gjøre at et system blir ustabilt. Samtidig kan en tidsforsinkelse være med på å dempe et system slik at signaler med høy frekvens ikke får innvirkning på systemet og dermed også virker stabiliserende. | ||
==== Illustrerende eksempel og generelt stabilitetskriterium==== | ==== Illustrerende eksempel og generelt stabilitetskriterium==== | ||
[[Fil:Fig542-1403.png|thumb|1100px|''Figur 3: Illustrasjon av et system med én komponent'']] | |||
Problemstillingen er illustrert i figur 3 med en komponent, for eksempel et lokomotiv, som en del av et system, for eksempel banestrømforsyningen. Ved en endring eller forstyrrelse i innsignalet til lokomotivet (for eksempel spenningen på lokomotivets strømavtaker) reagerer lokomotivet ved å endre på utsignalet sitt (strømmen) slik at ønsket virkning (hastigheten til toget) opprettholdes/oppnåes. Systemet (banestrømforsyningen) reagerer på dette signalet (lokomotivets endrede strøm) med et endret innsignal til komponenten (spenningsfall over kontaktledningsimpedansen gir lavere spenning for toget). Slik påvirker komponenten og systemet hverandre til de finner en likevekt. | Problemstillingen er illustrert i figur 3 med en komponent, for eksempel et lokomotiv, som en del av et system, for eksempel banestrømforsyningen. Ved en endring eller forstyrrelse i innsignalet til lokomotivet (for eksempel spenningen på lokomotivets strømavtaker) reagerer lokomotivet ved å endre på utsignalet sitt (strømmen) slik at ønsket virkning (hastigheten til toget) opprettholdes/oppnåes. Systemet (banestrømforsyningen) reagerer på dette signalet (lokomotivets endrede strøm) med et endret innsignal til komponenten (spenningsfall over kontaktledningsimpedansen gir lavere spenning for toget). Slik påvirker komponenten og systemet hverandre til de finner en likevekt. | ||
Dersom komponenten eller systemet har en resonansfrekvens som er dårlig dempet, vil den forhåpentligvis likevel svinge til en likevektstilstand. | Dersom komponenten eller systemet har en resonansfrekvens som er dårlig dempet, vil den forhåpentligvis likevel svinge til en likevektstilstand. | ||
Dersom det er tidsforsinkelser i komponenten og systemet, kan en oppleve at den tiden signalet bruker fra endringen gjøres til det er kommet gjennom komponenten og systemet sammenfaller med halve periodetiden til resonansfrekvensen. Da vil tilbakekoblingen gjennom systemet føre til at signalet bare går rundt og rundt mellom komponent og system. Komponenten eller systemet må således passe på å svekke dette signalet slik at det ikke adderes for hver gang det går rundt. Energien i signalet må ledes ut av systemet gjennom demping. Hvis ikke vil svingningene i systemet vokse ettersom tiden går. Et kjent eksempel på en slik tilbakekoblingseffekt er en mikrofon som kommer for nær høyttaleren og hvor resultatet er en raskt voksende pipetone. | Dersom det er tidsforsinkelser i komponenten og systemet, kan en oppleve at den tiden signalet bruker fra endringen gjøres til det er kommet gjennom komponenten og systemet sammenfaller med halve periodetiden til resonansfrekvensen. Da vil tilbakekoblingen gjennom systemet føre til at signalet bare går rundt og rundt mellom komponent og system. Komponenten eller systemet må således passe på å svekke dette signalet slik at det ikke adderes for hver gang det går rundt. Energien i signalet må ledes ut av systemet gjennom demping. Hvis ikke vil svingningene i systemet vokse ettersom tiden går. Et kjent eksempel på en slik tilbakekoblingseffekt er en mikrofon som kommer for nær høyttaleren og hvor resultatet er en raskt voksende pipetone. | ||
Et generelt stabilitetskriterium er derfor at tidsforsinkelsen gjennom komponent og system ikke er slik at tilbakekoblingen er halve periodetiden av resonansfrekvensen. Det vil si at tilbakekoblingen ikke må komme i motfase med innsignalet. Samtidig må komponent og system ikke forsterke signalet slik at det vokser, det vil si at forsterkningen må være mindre enn 1. | Et generelt stabilitetskriterium er derfor at tidsforsinkelsen gjennom komponent og system ikke er slik at tilbakekoblingen er halve periodetiden av resonansfrekvensen. Det vil si at tilbakekoblingen ikke må komme i motfase med innsignalet. Samtidig må komponent og system ikke forsterke signalet slik at det vokser, det vil si at forsterkningen må være mindre enn 1. | ||
| Linje 114: | Linje 99: | ||
=== Lastflytproblem og spenningskollaps=== | === Lastflytproblem og spenningskollaps=== | ||
[[Fil:Fig542-1404.png|thumb|600px|''Figur 4: Nesekurve (PU-kurve)'']] | |||
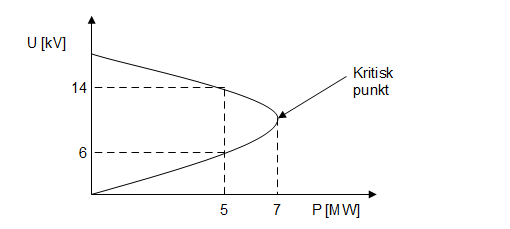
En matematisk løsning av et lastflytproblem i et kraftsystem har to likevektspunkter, det ene er stabilt og det andre gjerne er ustabilt. Karakteristikken til hvordan et kraftsystem påvirkes av økt belastning beskrives ofte ved hjelp av nesekurver som viser spenningen som funksjon av aktiv eller reaktiv effekt i et punkt. Disse er også kalt PU- eller QU-kurver avhengig av om det er aktiv eller reaktiv effekt som er den uavhengige variabelen. Et eksempel på en slik nesekurve er vist i figur 4 | En matematisk løsning av et lastflytproblem i et kraftsystem har to likevektspunkter, det ene er stabilt og det andre gjerne er ustabilt. Karakteristikken til hvordan et kraftsystem påvirkes av økt belastning beskrives ofte ved hjelp av nesekurver som viser spenningen som funksjon av aktiv eller reaktiv effekt i et punkt. Disse er også kalt PU- eller QU-kurver avhengig av om det er aktiv eller reaktiv effekt som er den uavhengige variabelen. Et eksempel på en slik nesekurve er vist i figur 4 | ||
Vi ser at dersom en skal kunne ta ut 5 MW, så kan dette skje enten ved 14 kV spenning eller 6 kV. La oss ta utganspunkt i løsningen som ligger på oppsiden av kurven ved 14 kV. Ved økende belastning ser en at spenningen synker. Maksimal overførbar effekt er 7 MW. Ved dette punktet, som kalles for det kritiske punktet, er impedansen i lasten lik impedansen i overføringen. | Vi ser at dersom en skal kunne ta ut 5 MW, så kan dette skje enten ved 14 kV spenning eller 6 kV. La oss ta utganspunkt i løsningen som ligger på oppsiden av kurven ved 14 kV. Ved økende belastning ser en at spenningen synker. Maksimal overførbar effekt er 7 MW. Ved dette punktet, som kalles for det kritiske punktet, er impedansen i lasten lik impedansen i overføringen. | ||
| Linje 130: | Linje 113: | ||
=== Lastens spenningsavhengighet=== | === Lastens spenningsavhengighet=== | ||
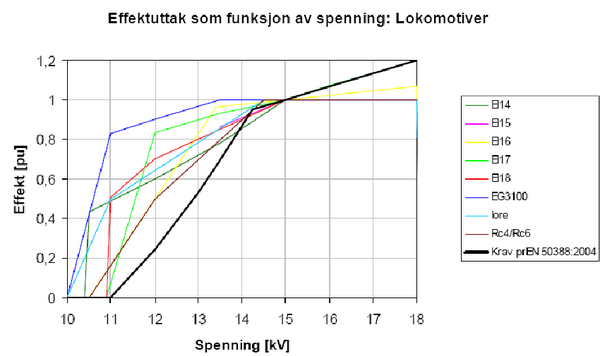
[[Fil:Fig542-1405.png|thumb|600px|''Figur 5: Effekt/spenningskarakteristikk for ulike typer norske lokomotiver sammenlignet med EN 50388. Hentet fra [6].'']] | |||
Et lokomotiv er i utgangspunktet hastighetsstyrt av lokomotivføreren. Nyere lokomotiver har da selv en reguleringssløyfe som setter en referanseverdi for trekkraften. For eldre lokomotiver må lokomotivføreren også være den som bestemmer denne. Det vil si at dersom spenningen på kontaktledningen synker, vil lokomotivet øke pådraget slik at effekten og dermed hastigheten holdes konstant. Slik regulering kan føre til spenningskollaps i kraftsystemet og blant annet derfor er ofte lokomotivene utstyrt med en effekt- eller strømbegrensning som funksjon av spenningen. Eksempel på slike karakteristikker er gitt i figur 5 for ulike typer norsk materiell. Når spenningen synker under et vist nivå, reduserer lokomotivet sitt maksimale effektuttak fra kontaktledningen. Dersom lokomotivet ikke ligger på grensen til maksimal effekt eller maksimal strøm, vil lokomotivet virke som en konstant effektlast helt til spenningen eventuelt er blitt så lav at lokomotivet er ved sin maksimale effekt ved den aktuelle spenningen i henhold til karakteristikken. | Et lokomotiv er i utgangspunktet hastighetsstyrt av lokomotivføreren. Nyere lokomotiver har da selv en reguleringssløyfe som setter en referanseverdi for trekkraften. For eldre lokomotiver må lokomotivføreren også være den som bestemmer denne. Det vil si at dersom spenningen på kontaktledningen synker, vil lokomotivet øke pådraget slik at effekten og dermed hastigheten holdes konstant. Slik regulering kan føre til spenningskollaps i kraftsystemet og blant annet derfor er ofte lokomotivene utstyrt med en effekt- eller strømbegrensning som funksjon av spenningen. Eksempel på slike karakteristikker er gitt i figur 5 for ulike typer norsk materiell. Når spenningen synker under et vist nivå, reduserer lokomotivet sitt maksimale effektuttak fra kontaktledningen. Dersom lokomotivet ikke ligger på grensen til maksimal effekt eller maksimal strøm, vil lokomotivet virke som en konstant effektlast helt til spenningen eventuelt er blitt så lav at lokomotivet er ved sin maksimale effekt ved den aktuelle spenningen i henhold til karakteristikken. | ||
Figuren viser til sammenligning kravet til slik effektbegrensning som funksjon av spenningen gitt i normen EN 50388 (omregnet fra strøm til effekt – sort kurve). Stigningen på kurven under knekkpunktet er en avveining mellom ønsket om å unngå spenningskollaps og at lokomotivet skal kunne finne et stabilt arbeidspunkt der effekten ikke forandrer seg for mye som funksjon av spenningen. Dersom lokomotivet ikke finner et stabilt arbeidspunkt kan en få lavfrekvente pendlinger som beskrevet i kapittel 4. | Figuren viser til sammenligning kravet til slik effektbegrensning som funksjon av spenningen gitt i normen EN 50388 (omregnet fra strøm til effekt – sort kurve). Stigningen på kurven under knekkpunktet er en avveining mellom ønsket om å unngå spenningskollaps og at lokomotivet skal kunne finne et stabilt arbeidspunkt der effekten ikke forandrer seg for mye som funksjon av spenningen. Dersom lokomotivet ikke finner et stabilt arbeidspunkt kan en få lavfrekvente pendlinger som beskrevet i kapittel 4. | ||
| Linje 147: | Linje 126: | ||
hvor: | hvor: | ||
*P = effekten til lasten ved aktuell spenning | *P = effekten til lasten ved aktuell spenning | ||
*P<sub>0</sub> = effekten til lasten ved nominell spenning | *P<sub>0</sub> = effekten til lasten ved nominell spenning | ||
| Linje 159: | Linje 137: | ||
=== Reaktiv kompensering=== | === Reaktiv kompensering=== | ||
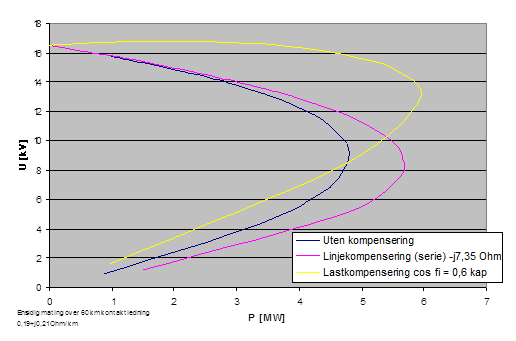
[[Fil:Fig542-1406.png|thumb|600px|''Figur 6: Eksempel på nesekurver (PU-kurver) ved ulike typer av kompensering '']] | |||
Ettersom lokomotivets effektuttak, og dermed også evnen til å holde ønsket hastighet, kan være avhengig av kontaktledningsspenningen, er det ønskelig at spenningen er så god som mulig. Akseptabel spenning på togets strømavtaker er gitt i Teknisk regelverk for prosjektering av banestrømforsyning | Ettersom lokomotivets effektuttak, og dermed også evnen til å holde ønsket hastighet, kan være avhengig av kontaktledningsspenningen, er det ønskelig at spenningen er så god som mulig. Akseptabel spenning på togets strømavtaker er gitt i [https://trv.jbv.no/wiki/Banestr%C3%B8mforsyning/Prosjektering_og_bygging/Kraftsystem#Kvalitet Teknisk regelverk for prosjektering av banestrømforsyning]. | ||
For å heve spenningen kan en kompensere for en del av spenningsfallet eller det reaktive tapet i kontaktledningen. Dette kan gjøres ved hjelp av kondensatorbatterier som beskrevet i lærebokens kapittel [[Kondensatorbatterier]], eller ved kapasitiv kompensering i togene. El 16 er for eksempel utstyrt med telefilterkondensatorer på 0,6 MVAr for blant annet bedring av effektfaktor. Lokomotiver med firekvadrants nettstrømrettere har mulighet for å styre reaktiv effekt etter ønske. | For å heve spenningen kan en kompensere for en del av spenningsfallet eller det reaktive tapet i kontaktledningen. Dette kan gjøres ved hjelp av kondensatorbatterier som beskrevet i lærebokens kapittel [[Kondensatorbatterier]], eller ved kapasitiv kompensering i togene. El 16 er for eksempel utstyrt med telefilterkondensatorer på 0,6 MVAr for blant annet bedring av effektfaktor. Lokomotiver med firekvadrants nettstrømrettere har mulighet for å styre reaktiv effekt etter ønske. | ||
| Linje 171: | Linje 149: | ||
Ved lastkompensering virker kontaktledningsspenningen som toget ser god veldig lenge, helt til den plutselig kollapser uten forvarsel ved en spenning som er å regne som en vanlig spenning på strømavtaker (13 kV). Dette i motsetning til uten kompensering og med seriekompensering hvor spenningskollapsen skjer ved så lav spenning at lasten fått har redusert pådraget sitt eller koblet ut. | Ved lastkompensering virker kontaktledningsspenningen som toget ser god veldig lenge, helt til den plutselig kollapser uten forvarsel ved en spenning som er å regne som en vanlig spenning på strømavtaker (13 kV). Dette i motsetning til uten kompensering og med seriekompensering hvor spenningskollapsen skjer ved så lav spenning at lasten fått har redusert pådraget sitt eller koblet ut. | ||
Mer om kapasitiv kompensering fra lokomotivene kan finnes i [6]. | Mer om kapasitiv kompensering fra lokomotivene kan finnes i [6]. | ||
| Linje 194: | Linje 167: | ||
==== Roterende omformere==== | ==== Roterende omformere==== | ||
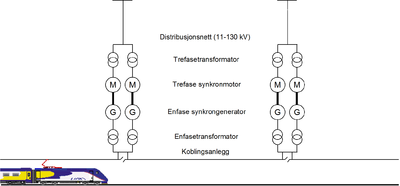
[[Fil:Fig542-1407.png|thumb|400px|''Figur 7: Illustrasjon av typisk matesituasjon i den norske banestrømforsyningen.'']] | |||
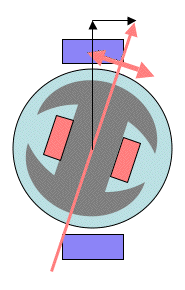
[[Fil:Fig542-1408.png|thumb|200px|''Figur 8: Prinspippskisse av synkronmaskinrotor i forhold til stator samt polhjulsvinkelen β. Figur laget av emkamatik til JD 590 hentet fra [6].'']] | |||
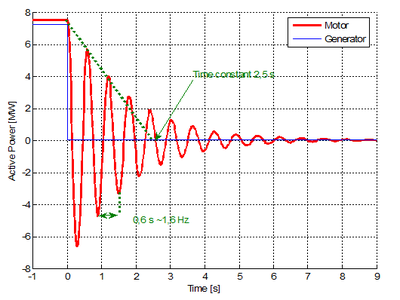
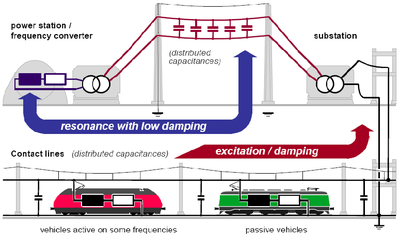
[[Fil:Fig542-1409.png|thumb|400px|''Figur 9: Simulert sprangrespons (lastavslag på 7,5 MW) for et roterende omformeraggregat'']] | |||
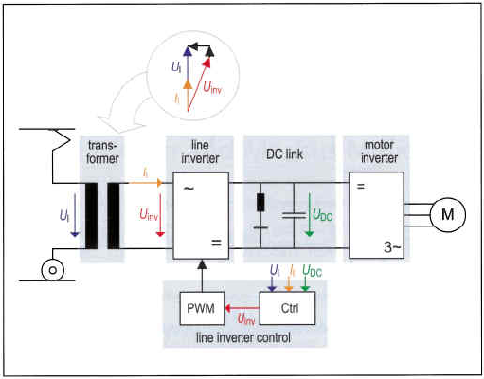
Banestrømforsyningen i Norge domineres av roterende omformeraggregater bestående av en synkronmotor og en synkrongenerator koplet på samme aksel. En forskjell i antall faser og antall poler lik 3:1 gjør at elektrisk energi ved trefase 50 Hz omformes til 16 2/3 Hz enfase. En skisse av typisk matesituasjon i den norske banestrømforsyningen er vist i figur 7. De roterende omformeraggregatene finnes i størrelser av 3,1, 5,8, 7,0, og 10,0 MVA kontinuerlig ytelse. 5,8 MVA og 7,0 MVA aggregatene er vanligst. En omformerstasjon består av ett til tre aggregater, men to er typisk. Antall aggregater i drift tilpasses variasjonene i effektetterspørsel gitt av togtrafikken. | Banestrømforsyningen i Norge domineres av roterende omformeraggregater bestående av en synkronmotor og en synkrongenerator koplet på samme aksel. En forskjell i antall faser og antall poler lik 3:1 gjør at elektrisk energi ved trefase 50 Hz omformes til 16 2/3 Hz enfase. En skisse av typisk matesituasjon i den norske banestrømforsyningen er vist i figur 7. De roterende omformeraggregatene finnes i størrelser av 3,1, 5,8, 7,0, og 10,0 MVA kontinuerlig ytelse. 5,8 MVA og 7,0 MVA aggregatene er vanligst. En omformerstasjon består av ett til tre aggregater, men to er typisk. Antall aggregater i drift tilpasses variasjonene i effektetterspørsel gitt av togtrafikken. | ||
Alle elektriske maskiner har en elektromekanisk resonansfrekvens i området 1-2 Hz. Dette er implisitt gitt av den klassiske svingelikningen | Alle elektriske maskiner har en elektromekanisk resonansfrekvens i området 1-2 Hz. Dette er implisitt gitt av den klassiske svingelikningen | ||
{|width="35%" | {|width="35%" | ||
| Linje 217: | Linje 188: | ||
Polhjulsvinkelen for en synkronmaskin er skissert sammen med rotor og stator i figur 8. Når rotor pendler går den vekselvis fortere og senere enn synkron hastighet. Polhjulsvinkelen vil da øke og minke faseforskjøvet (tidsforsinket) etter hastighetsendringene. | Polhjulsvinkelen for en synkronmaskin er skissert sammen med rotor og stator i figur 8. Når rotor pendler går den vekselvis fortere og senere enn synkron hastighet. Polhjulsvinkelen vil da øke og minke faseforskjøvet (tidsforsinket) etter hastighetsendringene. | ||
Resonansfrekvensen f<sub>res</sub> , også kalt egenfrekvensen, er i stor grad bestemt av tre hovedparametere; hvor stor endringen i aktiv effekt er ved en gitt endring av maskinenens polhjulsvinkel (K<sub>Sm</sub> –typisk litt over 1), omformeraggregatets totale H-konstant (typisk rundt 2,5 til 3,2) og nettfrekvensen ω<sub>N</sub> slik som formel 3 (hentet fra [6]) viser. Det er motoren som dominerer det totale aggregatets oppførsel blant annet på grunn av at nettfrekvensen i trefasenettet er tre ganger større enn i jernbanenettet. Typisk egenfrekvens er i området 1,6 til 1,9 Hz. | Resonansfrekvensen f<sub>res</sub> , også kalt egenfrekvensen, er i stor grad bestemt av tre hovedparametere; hvor stor endringen i aktiv effekt er ved en gitt endring av maskinenens polhjulsvinkel (K<sub>Sm</sub> –typisk litt over 1), omformeraggregatets totale H-konstant (typisk rundt 2,5 til 3,2) og nettfrekvensen ω<sub>N</sub> slik som formel 3 (hentet fra [6]) viser. Det er motoren som dominerer det totale aggregatets oppførsel blant annet på grunn av at nettfrekvensen i trefasenettet er tre ganger større enn i jernbanenettet. Typisk egenfrekvens er i området 1,6 til 1,9 Hz. | ||
| Linje 238: | Linje 205: | ||
Magnetiseringssystemet med likestrøms feltmaskin for motor og generator er ikke raskt nok til kunne ha noen innvirkning på rotorpendlingene. | Magnetiseringssystemet med likestrøms feltmaskin for motor og generator er ikke raskt nok til kunne ha noen innvirkning på rotorpendlingene. | ||
==== Statiske omformere==== | ==== Statiske omformere==== | ||
| Linje 255: | Linje 218: | ||
==== Beskrivelse av lokomotivene==== | ==== Beskrivelse av lokomotivene==== | ||
[[Fil:Fig542-1410.png|thumb|600px|''Figur 10: Hovedstrømkrets med de viktigste reguleringsparameterne i et moderne lokomotiv med fire kvadrants nettstrømretter. Hentet fra [6].'']] | |||
For enklest mulig hastighetsregulering av togene ble det i Norge og Sverige valgt elektrifisering med lav frekvens. På den måten kunne en benytte såkalte serie vekselstrømsmotorer som i utgangspunktet er en likestrømsmotor med anker og felt i serie og hvor hastigheten er proporsjonal med spenningen over motoren. Denne motortypen kjennes f. eks. fra alminnelig håndverktøy. Spenningsreguleringen ble utført ved hjelp av trinnkopling på lokomotivets hovedtransformator, først på lavspentsiden og senere på høyspentsiden for å redusere strømmen som måtte brytes. Eksempel på slike trinnkoplerlokomotiver fremdeles er i bruk er NSB/CargoNet El 14. | For enklest mulig hastighetsregulering av togene ble det i Norge og Sverige valgt elektrifisering med lav frekvens. På den måten kunne en benytte såkalte serie vekselstrømsmotorer som i utgangspunktet er en likestrømsmotor med anker og felt i serie og hvor hastigheten er proporsjonal med spenningen over motoren. Denne motortypen kjennes f. eks. fra alminnelig håndverktøy. Spenningsreguleringen ble utført ved hjelp av trinnkopling på lokomotivets hovedtransformator, først på lavspentsiden og senere på høyspentsiden for å redusere strømmen som måtte brytes. Eksempel på slike trinnkoplerlokomotiver fremdeles er i bruk er NSB/CargoNet El 14. | ||
| Linje 263: | Linje 226: | ||
Utviklingen av kraftelektronikk og styringsmuligheter for denne gjorde at det på 80-tallet var mulig å ta i bruk den enkle og robuste asynkronmotoren. Togets hastighet gis da av frekvensen til spenningen over motoren gitt av motorstrømretteren. Likespenningen inn på motorstrømretteren gis av en nettstrømretter, og i DC-linken mellom disse sitter et lite filter for glatting og energilagring siden effekten overføres i enfasesystemet med en frekvens på 33 1/3 Hz. Operasjon av strømretterne i alle fire kvadranter gir mulighet for både tilbakemating av bremseenergi og styring av reaktiv effekt. Slike lokomotiver kalles gjerne nettstrømretterlokomotiver eller asynkronlokomotiv . Utviklingen av halvlederteknologien har gått fra tyristorer med slukkekretser (NSB El17) til GTO-tyristorer (Gate Turn Of) (NSB El18 og type 73) til IGBT (Insulated Gate Bipolar Transistor) (NSB type 72). Eksempel på hovedstrømskrets med de viktigste reguleringsparameterne i et slikt lokomotiv er vist i figur 14.10. | Utviklingen av kraftelektronikk og styringsmuligheter for denne gjorde at det på 80-tallet var mulig å ta i bruk den enkle og robuste asynkronmotoren. Togets hastighet gis da av frekvensen til spenningen over motoren gitt av motorstrømretteren. Likespenningen inn på motorstrømretteren gis av en nettstrømretter, og i DC-linken mellom disse sitter et lite filter for glatting og energilagring siden effekten overføres i enfasesystemet med en frekvens på 33 1/3 Hz. Operasjon av strømretterne i alle fire kvadranter gir mulighet for både tilbakemating av bremseenergi og styring av reaktiv effekt. Slike lokomotiver kalles gjerne nettstrømretterlokomotiver eller asynkronlokomotiv . Utviklingen av halvlederteknologien har gått fra tyristorer med slukkekretser (NSB El17) til GTO-tyristorer (Gate Turn Of) (NSB El18 og type 73) til IGBT (Insulated Gate Bipolar Transistor) (NSB type 72). Eksempel på hovedstrømskrets med de viktigste reguleringsparameterne i et slikt lokomotiv er vist i figur 14.10. | ||
Mer detaljer informasjon om lokomotiver og deres elektriske oppbygning og virkemåte kan finnes i [6]. | Mer detaljer informasjon om lokomotiver og deres elektriske oppbygning og virkemåte kan finnes i [6]. | ||
==== Repeterende lastendringer==== | ==== Repeterende lastendringer==== | ||
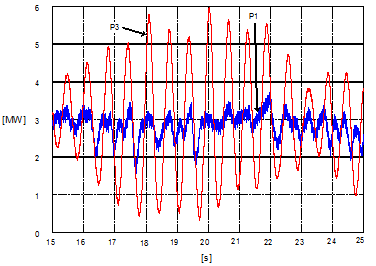
[[Fil:Fig542-1411.png|thumb|600px|''Figur 11: Målt effekt på enfase- (P1) og trefasesiden (P3) på Oppdal omformer under sliring ved El18 i 1999. Figuren her hentet fra måling nummer 25 i [6].'']] | |||
I nyere lokomotiver, både tyristor- og asynkronlokomotiver, finnes det ulike styringer som regulerer effekten diskontinuerlig, for eksempel | I nyere lokomotiver, både tyristor- og asynkronlokomotiver, finnes det ulike styringer som regulerer effekten diskontinuerlig, for eksempel | ||
*adhesjonskontrollen gjennom plutselig nedregulering av motormoment for å hindre at hjul slipper og | *adhesjonskontrollen gjennom plutselig nedregulering av motormoment for å hindre at hjul slipper og | ||
| Linje 280: | Linje 238: | ||
Det var adhesjonskontrollen som var årsaken til de lavfrekvente pendlingene som ble observert ved bruk av El 18 ved Oppdal omformer i 1996-1997. Figur 14.11 viser målt enfaseeffekt ved sliring sammen med tilsvarende forsterket trefaseeffekt. Problemene ble løst ved en endring av reguleringen på lokomotivene i 1999. Etter dette har det vært vanlig at alt nytt materiell blir testet for å avdekke uheldig regulering, for eksempel NSB type 72 [6], NSB type 73 [6] og MTAB IORE [6]. Testene utføres ved dårlig adhesjon (glatte skinner) og ved svak energiforsyning (lav installert ytelse i matestasjonen og med stor avstand til toget). | Det var adhesjonskontrollen som var årsaken til de lavfrekvente pendlingene som ble observert ved bruk av El 18 ved Oppdal omformer i 1996-1997. Figur 14.11 viser målt enfaseeffekt ved sliring sammen med tilsvarende forsterket trefaseeffekt. Problemene ble løst ved en endring av reguleringen på lokomotivene i 1999. Etter dette har det vært vanlig at alt nytt materiell blir testet for å avdekke uheldig regulering, for eksempel NSB type 72 [6], NSB type 73 [6] og MTAB IORE [6]. Testene utføres ved dårlig adhesjon (glatte skinner) og ved svak energiforsyning (lav installert ytelse i matestasjonen og med stor avstand til toget). | ||
==== Tilbakekoblingseffekter (feedback loop effects)==== | ==== Tilbakekoblingseffekter (feedback loop effects)==== | ||
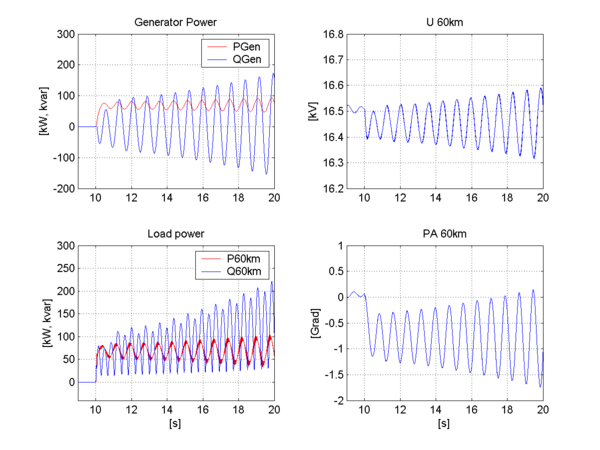
[[Fil:Fig542-1412.png|thumb|600px|''Figur 12: Ustabilitet på grunn av tilbakekoblingseffekter. Simulering utført i [6]. P og Q er henholdsvis aktiv og reaktiv effekt. Gen betyr generator og P60km/Q60km er ved lokomotivet. U er spenningens amplitude og PA er spenningens fasevinkel.'']] | |||
I enfasesystemer kan en forenklet si at effekten leveres til lokomotivet i pakker hver halvperiode av nettfrekvensen (i 16 2/3 Hz nett er perioden 30 ms). Innen hvert slik periode (eller tidsvindu) bør både spenning og strøm ha mest mulig sinusform. Dersom lokomotivet endrer effektopptaket sitt, må trege ytre reguleringssløyfer styre de raske indre reguleringssløyfene som prøver å lage sinusformen til strømmen som toget trekker. Det betyr at effektreguleringen i lokomotivet må være tregere enn nettfrekvensen. På grunn av denne nødvendige tidsforsinkelsen har alle asynkronlokomotiver med nettstrømrettere en dynamisk oppførsel med tilbakekoblingseffekter slik som omtalt i avsnitt 2.3.2. | I enfasesystemer kan en forenklet si at effekten leveres til lokomotivet i pakker hver halvperiode av nettfrekvensen (i 16 2/3 Hz nett er perioden 30 ms). Innen hvert slik periode (eller tidsvindu) bør både spenning og strøm ha mest mulig sinusform. Dersom lokomotivet endrer effektopptaket sitt, må trege ytre reguleringssløyfer styre de raske indre reguleringssløyfene som prøver å lage sinusformen til strømmen som toget trekker. Det betyr at effektreguleringen i lokomotivet må være tregere enn nettfrekvensen. På grunn av denne nødvendige tidsforsinkelsen har alle asynkronlokomotiver med nettstrømrettere en dynamisk oppførsel med tilbakekoblingseffekter slik som omtalt i avsnitt 2.3.2. | ||
| Linje 294: | Linje 249: | ||
Høy linjeimpedans (ved nettfrekvens) øker faren for tilbakekoblingseffekter siden denne virker som en forsterkning i reguleringssløyfene siden den er med på å bestemme spenningsfallet mellom matepunkt og lokomotiv. Samtidig gjør linjeimpedansen at vinkelen til spenningen på lokomotivets strømavtaker endres. | Høy linjeimpedans (ved nettfrekvens) øker faren for tilbakekoblingseffekter siden denne virker som en forsterkning i reguleringssløyfene siden den er med på å bestemme spenningsfallet mellom matepunkt og lokomotiv. Samtidig gjør linjeimpedansen at vinkelen til spenningen på lokomotivets strømavtaker endres. | ||
I lokomotivets nettstrømretter er det en egen reguleringssløyfe kalt faselåst sløyfe (phase locked loop – PLL | I lokomotivets nettstrømretter er det en egen reguleringssløyfe kalt faselåst sløyfe (phase locked loop – PLL) som justerer strømretterens frekvens og fase riktig i forhold til nettfrekvensen. Endring av spenningens vinkel kan oppfattes som en (midlertidig) endring av nettfrekvensen og kan ved gjentatte endringer være vanskelig å forholde seg til for PLL. Roterende omformeraggregater som pendler (roterer vekselvis fortere og senere enn synkront turtall) kan forverre situasjonen. Riktig innstilling av en PLL kan være vanskelig fordi overharmoniske i linjespenningen gjør det nødvendig med filtrering og som dermed gir en tidsforsinkelse på målingen. | ||
Problemet kjennes ofte igjen ved at bare moderat økning av effekten fører til stort spenningsfall og at en får inntrykk av at spenningen hopper opp og ned. Lokomotivet kan begynne å rykke/riste og eller ikke virke i det hele tatt slik som NSB type 72 før forbedringene i 2004. Stort spenningsfall på grunn av høy linjeimpedans fører også gjerne til lav tilgjengelig effekt på grunn av strømbegrensningen ved synkende spenning gitt i EN 50388 (se avsnitt 3.3) selv uten uheldig design av reguleringen, men situasjonen er da også stabil. Problemene blir gjerne større ved flere tog på en strekning samtidig ettersom alles effekttrekk virker inn på spenningen. | Problemet kjennes ofte igjen ved at bare moderat økning av effekten fører til stort spenningsfall og at en får inntrykk av at spenningen hopper opp og ned. Lokomotivet kan begynne å rykke/riste og eller ikke virke i det hele tatt slik som NSB type 72 før forbedringene i 2004. Stort spenningsfall på grunn av høy linjeimpedans fører også gjerne til lav tilgjengelig effekt på grunn av strømbegrensningen ved synkende spenning gitt i EN 50388 (se avsnitt 3.3) selv uten uheldig design av reguleringen, men situasjonen er da også stabil. Problemene blir gjerne større ved flere tog på en strekning samtidig ettersom alles effekttrekk virker inn på spenningen. | ||
| Linje 301: | Linje 256: | ||
Figur 12 viser et eksempel på hvordan ustabilitet ved tilbakekoblingseffekter kan oppstå sammen med en dårlig dempet roterende omformer over 60 km kontaktledning. Etter en økning i togets aktive effekt på ca 75 kW dempes ikke pendlingene ut, men forsterkes og systemet er blir ustabilt. Tilsvarende ustabilitet er også observert i Zürich i Sveits uten dårlige dempede roterende omformere. | Figur 12 viser et eksempel på hvordan ustabilitet ved tilbakekoblingseffekter kan oppstå sammen med en dårlig dempet roterende omformer over 60 km kontaktledning. Etter en økning i togets aktive effekt på ca 75 kW dempes ikke pendlingene ut, men forsterkes og systemet er blir ustabilt. Tilsvarende ustabilitet er også observert i Zürich i Sveits uten dårlige dempede roterende omformere. | ||
== Elektrisk Resonansustabilitet== | == Elektrisk Resonansustabilitet== | ||
| Linje 314: | Linje 265: | ||
I september samme år opplevde en en tilsvarende totalstopp i andre og større deler av Sveits. Re 460-lokomotivene var dominerende i trafikk på det tidspunktet og alle sammen stoppet samtidig på grunn av for høy 100 Hz-komponent i linjestrømmen. Samtidig observerte en spenningsvariasjoner med frekvens på 165 Hz og spenning på over 2 kV. En så at problemene gjerne oppsto ved gitte situasjoner i trafikken – lørdag formiddag: Liten trafikk, mange nye Re 460 lokomotiver og få gamle trinnkoplerlokomotiver. | I september samme år opplevde en en tilsvarende totalstopp i andre og større deler av Sveits. Re 460-lokomotivene var dominerende i trafikk på det tidspunktet og alle sammen stoppet samtidig på grunn av for høy 100 Hz-komponent i linjestrømmen. Samtidig observerte en spenningsvariasjoner med frekvens på 165 Hz og spenning på over 2 kV. En så at problemene gjerne oppsto ved gitte situasjoner i trafikken – lørdag formiddag: Liten trafikk, mange nye Re 460 lokomotiver og få gamle trinnkoplerlokomotiver. | ||
En fant tidlig ut at disse fenomenene hadde å gjøre med samspillet mellom kraftsystemet og lokomotivene. Problemet ble etter hvert løst ved å endre på programvaren som styrer nettstrømretterne i Re 460. Mer om hendelsene i Sveits kan finnes i [6] og [ | En fant tidlig ut at disse fenomenene hadde å gjøre med samspillet mellom kraftsystemet og lokomotivene. Problemet ble etter hvert løst ved å endre på programvaren som styrer nettstrømretterne i Re 460. Mer om hendelsene i Sveits kan finnes i [6] og [7]. | ||
Dette kapittelet gir en innføring i de fysiske fenomenene i forbindelse med elektrisk resonansustabilitet, eller lineær stabilitet som det også har blitt kalt. Kapittelet forteller også hvordan og hvorfor disse fenomenene oppstår i kraftsystem for jernbane og hvordan de påvirkes. Fenomenene som beskrives her oppstår normalt i frekvensområdet 3-5 ganger nominell frekvens og høyere. | Dette kapittelet gir en innføring i de fysiske fenomenene i forbindelse med elektrisk resonansustabilitet, eller lineær stabilitet som det også har blitt kalt. Kapittelet forteller også hvordan og hvorfor disse fenomenene oppstår i kraftsystem for jernbane og hvordan de påvirkes. Fenomenene som beskrives her oppstår normalt i frekvensområdet 3-5 ganger nominell frekvens og høyere. | ||
=== Elektriske resonanser i kraftsystemet=== | === Elektriske resonanser i kraftsystemet=== | ||
[[Fil:Fig542-1413.png|thumb|400px|''Figur 13: Representasjon av resistanser, induktanser og kapasitanser i et kraftsystem for jernbane. Hentet fra [6].'']] | |||
[[Fil:Fig542-1414.png|thumb|600px|''Figur 14: Ekvivalent elektrisk krets'']] | |||
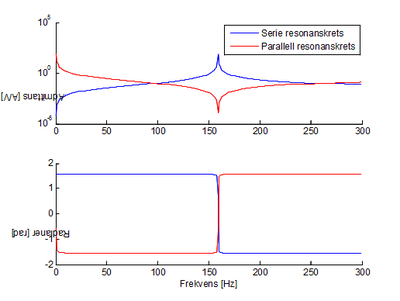
[[Fil:Fig542-1415.png|thumb|400px|''Figur 15: Admittans i absoluttverdi øverst og fase nederst for serie resonanskrets og parallell resonanskrets (R=0,01 Ohm, L=0,01H og C=0,0001F). Resonansfrekvens for begge kretsene er 159,1549 Hz.'']] | |||
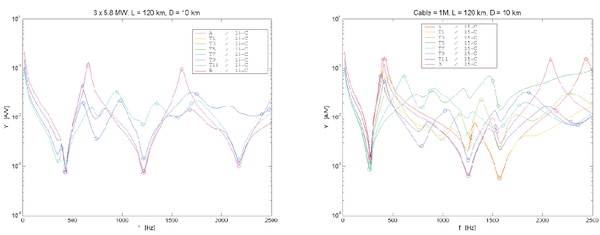
[[Fil:Fig542-1416.png|thumb|600px|''Figur 16: Admittans (absoluttverdi) som funksjon av frekvensen for et autotransformatorsystem. A, T1, T3 osv angir ulike steder i nettet hvor A og B er omformerstasjoner og T angir autotransformatorstasjoner. Hentet fra [6]'']] | |||
Kraftsystemet består av ulike komponenter som elektrisk kan representeres ved hjelp av resistanser R, induktanser L, kapasitanser C eller kombinasjoner av disse. Fenomenene omtalt i dette avsnittet sogner til ”elektriske fenomener” vist i figur 1. Figur 13 er hentet fra [6] og viser hvordan disse kan fordele seg i et kraftsystem for jernbane: | Kraftsystemet består av ulike komponenter som elektrisk kan representeres ved hjelp av resistanser R, induktanser L, kapasitanser C eller kombinasjoner av disse. Fenomenene omtalt i dette avsnittet sogner til ”elektriske fenomener” vist i figur 1. Figur 13 er hentet fra [6] og viser hvordan disse kan fordele seg i et kraftsystem for jernbane: | ||
*Linjer består av en resistans og en induktans, men har også en strøkapasitans mot jord | *Linjer består av en resistans og en induktans, men har også en strøkapasitans mot jord | ||
| Linje 326: | Linje 281: | ||
Sett inn i nettet vil en fra et punkt kunne se en ekvivalent elektrisk krets der induktanser og kapasitanser står i både serie og parallell mot jord. I et nett med en roterende omformer og en lang linje vil en fra 15 kV samleskinne i omformerstasjonen kunne se en ekvivalentkrets som vist i figur 14: En kapasitans (linjens strøkapasitans) i parallell med synkronmaskinen og transformatorens resistans og reaktans. Dette kalles for en praktisk resonanskrets og er egentlig en parallellresonanskrets. Sett fra toget, eller nærmere bestemt togets nettstrømretter, vil en i tillegg se togets transformatorimpedans i serie. | Sett inn i nettet vil en fra et punkt kunne se en ekvivalent elektrisk krets der induktanser og kapasitanser står i både serie og parallell mot jord. I et nett med en roterende omformer og en lang linje vil en fra 15 kV samleskinne i omformerstasjonen kunne se en ekvivalentkrets som vist i figur 14: En kapasitans (linjens strøkapasitans) i parallell med synkronmaskinen og transformatorens resistans og reaktans. Dette kalles for en praktisk resonanskrets og er egentlig en parallellresonanskrets. Sett fra toget, eller nærmere bestemt togets nettstrømretter, vil en i tillegg se togets transformatorimpedans i serie. | ||
For signaler påtrykt mellom kontaktledning og jord fra for eksempel en omformer eller et lokomotiv, vil en se forskjellig impedans i ekvivalentkretsen avhengig av signalets frekvens. Det er vanlig i disse betraktningene å benytte begrepet admittans som er den inverse av impedansen og måles i Siemens eller Mho framfor impedans. Ved å kikke inn i en elektrisk krets, det være seg eksempelet over eller for eksempel et lokomotiv, vil en altså kunne se en frekvensavhengig admittans som kalles inputadmittansen. Alle tre komponentene, R, L og C, er frekvensavhengige. For en gitt frekvens kan admittansen akkurat som impedansen Z=R+jX uttrykkes som en kompleks størrelse som Y=G+jB der G kalles konduktans og B kalles suceptans. | For signaler påtrykt mellom kontaktledning og jord fra for eksempel en omformer eller et lokomotiv, vil en se forskjellig impedans i ekvivalentkretsen avhengig av signalets frekvens. Det er vanlig i disse betraktningene å benytte begrepet admittans som er den inverse av impedansen og måles i Siemens eller Mho framfor impedans. Ved å kikke inn i en elektrisk krets, det være seg eksempelet over eller for eksempel et lokomotiv, vil en altså kunne se en frekvensavhengig admittans som kalles inputadmittansen. Alle tre komponentene, R, L og C, er frekvensavhengige. For en gitt frekvens kan admittansen akkurat som impedansen Z=R+jX uttrykkes som en kompleks størrelse som Y=G+jB der G kalles konduktans og B kalles suceptans. | ||
| Linje 347: | Linje 294: | ||
I figur 15 er vist admittansen i amplitude og fase for en serie resonanskrets og en parallell resonanskrets (også kalt en praktisk resonanskrets) som funksjon av frekvensen. Ved resonans er admittansens fase lik 0 slik som forklart over. I begge disse tilfellene går kretsene fra å være induktive til kapasitive eller motsatt ved resonansen, men å krysse 0-linjen er ikke noen betingelse for at resonans skal oppstå. Vi ser også at ved serieresonans er admittansens absoluttverdi høy (lik lav impedans) og ved parallellresonans vil admittansens størrelse være lav (lik høy impedans). | I figur 15 er vist admittansen i amplitude og fase for en serie resonanskrets og en parallell resonanskrets (også kalt en praktisk resonanskrets) som funksjon av frekvensen. Ved resonans er admittansens fase lik 0 slik som forklart over. I begge disse tilfellene går kretsene fra å være induktive til kapasitive eller motsatt ved resonansen, men å krysse 0-linjen er ikke noen betingelse for at resonans skal oppstå. Vi ser også at ved serieresonans er admittansens absoluttverdi høy (lik lav impedans) og ved parallellresonans vil admittansens størrelse være lav (lik høy impedans). | ||
Resistansen R i kretsen virker i tillegg som en demping av energipendlingene mellom L og C i og med at den kan lede energi ut av systemet gjennom varme. Uten dempingen vil eventuelle pendlinger bare bli stående og aldri dø ut. Naturlig demping i systemet er virvelstrømmer (eng.:”eddy currents”) i synkronmaskiner og transformatorer som er frekvensavhengig og blir mindre ved lavere frekvens. Demping i form av parallellresistanser er veldig liten i kraftsystemer for jernbane, men eksisterer for eksempel gjennom togvarme og gjennom lekkstrømmer over isolatorene for høyspenningskomponenter/-linjer, spesielt i fuktig vær. | Resistansen R i kretsen virker i tillegg som en demping av energipendlingene mellom L og C i og med at den kan lede energi ut av systemet gjennom varme. Uten dempingen vil eventuelle pendlinger bare bli stående og aldri dø ut. Naturlig demping i systemet er virvelstrømmer (eng.:”eddy currents”) i synkronmaskiner og transformatorer som er frekvensavhengig og blir mindre ved lavere frekvens. Demping i form av parallellresistanser er veldig liten i kraftsystemer for jernbane, men eksisterer for eksempel gjennom togvarme og gjennom lekkstrømmer over isolatorene for høyspenningskomponenter/-linjer, spesielt i fuktig vær. | ||
| Linje 357: | Linje 300: | ||
Figur 16 viser hvordan absoluttverdien av admittansen sett inn i et autotransformatorsystem på forskjellige steder i nettet (A, T1, T3 osv) varierer som funksjon av frekvensen. Resonanser er merket av med ringer på kurvene. Figurene er hentet fra [6] og beregningene er utført for to omformerstasjoner med 120 km kontaktledning og AT-ledninger (positiv- og negativleder) mellom. I høyre figur er det introdusert 10 km med kabler for AT-ledningene i forhold til venstre figur. Dette øker kapasitansen i systemet og reduserer laveste resonansfrekvens fra 430 Hz til 275 Hz. | Figur 16 viser hvordan absoluttverdien av admittansen sett inn i et autotransformatorsystem på forskjellige steder i nettet (A, T1, T3 osv) varierer som funksjon av frekvensen. Resonanser er merket av med ringer på kurvene. Figurene er hentet fra [6] og beregningene er utført for to omformerstasjoner med 120 km kontaktledning og AT-ledninger (positiv- og negativleder) mellom. I høyre figur er det introdusert 10 km med kabler for AT-ledningene i forhold til venstre figur. Dette øker kapasitansen i systemet og reduserer laveste resonansfrekvens fra 430 Hz til 275 Hz. | ||
På figur 16 til høyre ser vi at for alle stedene i systemet finnes en felles resonans like under 500 Hz. Dette kalles en global resonans. Ved litt lavere frekvens ser en at det kun er punktene midt mellom omformerstasjonene som har resonansfrekvenser, dette kalles en lokal resonans. Vi ser at dempingen er lavere ved den globale resonansen enn ved den lokale rett til høyre. | På figur 16 til høyre ser vi at for alle stedene i systemet finnes en felles resonans like under 500 Hz. Dette kalles en global resonans. Ved litt lavere frekvens ser en at det kun er punktene midt mellom omformerstasjonene som har resonansfrekvenser, dette kalles en lokal resonans. Vi ser at dempingen er lavere ved den globale resonansen enn ved den lokale rett til høyre. | ||
| Linje 369: | Linje 308: | ||
=== Lokomotiver som eksiterer resonansene=== | === Lokomotiver som eksiterer resonansene=== | ||
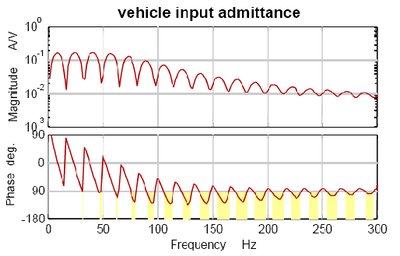
[[Fil:Fig542-1417.png|thumb|400px|''Figur 17: Frekvensrespons/inputadmittans for Re460 hentet fra [6].'']] | |||
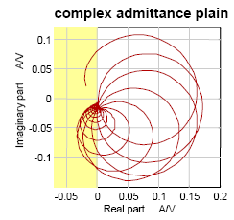
[[Fil:Fig542-1418.png|thumb|400px|''Figur 18: Inputadmittansen for Re460 vist i det komplekse admittansplanet hentet fra [6].'']] | |||
Moderne lokomotiver med nettstrømrettere (fire kvadrant kraftelektronikkomformere) kan være eksitasjonskilder for de elektriske resonansene i et kraftsystem. Styringen av nettstrømretteren reagerer på endringer i linjespenningen med små uungåelige tidsforsinkelser, for eksempel for å forme strømmen som en sinuskurve uten overharmoniske uavhengig av spenningen. Forsinkelsene er uunngåelige på grunn av mikroprosessortid og puls/bredde-moduleringen. Disse fenomenene faller inn under betegnelsen ”elektroniske fenomener” i figur 1. | |||
På samme måte som for kraftsystemet kan en plotte frekvensresponsen for et slikt lokomotiv i form av inputadmittansen. Et eksempel på en slik er vist i figur 17. Dersom lokomotivet ved en frekvens har en admittans som har fasevinkel over/under ±π/2 (90˚) mottar det ikke lenger energi ved denne frekvensen, men produserer isteden energi. Dette kalles at lokomotivet er aktivt ved denne frekvensen og er markert med gult på figuren. Av eksempelet i figur 17 ser vi at lokomotivet blant annet er aktivt ved ca. 30 Hz, og ved flere andre intervaller oppover. | |||
På samme måte som for kraftsystemet kan en plotte frekvensresponsen for et slikt lokomotiv i form av inputadmittansen. Et eksempel på en slik er vist i figur 17. Dersom lokomotivet ved en frekvens har en admittans som har fasevinkel over/under ±π/2 (90˚) mottar det ikke lenger energi ved denne frekvensen, men produserer isteden energi. Dette kalles at lokomotivet er aktivt ved denne frekvensen og er markert med gult på figuren. Av eksempelet i figur 17 ser vi at lokomotivet blant annet er aktivt ved ca | |||
Den samme frekvensresponsen er vist i figur 18 for det komplekse admittansplanet. I gult område er lokomotivet aktivt. De fire hovedretningene i det komplekse admittansplanet er: | Den samme frekvensresponsen er vist i figur 18 for det komplekse admittansplanet. I gult område er lokomotivet aktivt. De fire hovedretningene i det komplekse admittansplanet er: | ||
| Linje 384: | Linje 320: | ||
*90 grader: lokomotivet virker som en kapasitans | *90 grader: lokomotivet virker som en kapasitans | ||
*-180 grader: lokomotivet er ”negativ ohmsk” eller aktivt og produserer energi ved den gitte frekvensen med en gang en spenning er påtrykt. | *-180 grader: lokomotivet er ”negativ ohmsk” eller aktivt og produserer energi ved den gitte frekvensen med en gang en spenning er påtrykt. | ||
Frekvensresponsen for nettstrømretterlokomotiver er uavhengig av driftstilfellet (belastning, hastighet, traksjon/bremsing osv.). Det er i hovedsak nettstrømretteren som er av betydning i forhold til lokomotivets oppførsel. Grunnen er at motorstrømretteren i lokomotivet ligger ”skjult” bak DC-linken. Andre typer lokomotiver enn nettstrømretterlokmotiver er som regel passive for alle frekvenser, men det finnes unntak. | Frekvensresponsen for nettstrømretterlokomotiver er uavhengig av driftstilfellet (belastning, hastighet, traksjon/bremsing osv.). Det er i hovedsak nettstrømretteren som er av betydning i forhold til lokomotivets oppførsel. Grunnen er at motorstrømretteren i lokomotivet ligger ”skjult” bak DC-linken. Andre typer lokomotiver enn nettstrømretterlokmotiver er som regel passive for alle frekvenser, men det finnes unntak. | ||
| Linje 395: | Linje 325: | ||
Ofte er det ikke ønskelig at et lokomotiv produserer strømmer med gitte frekvenser, for eksempel rundt 95 og 105 Hz som er de frekvensene tradisjonelle norske sporfelt arbeider ved. Dette kan unngås i lokomotivet ved hjelp av såkalt anticontrol og medfører at en får et aktivt område i frekvens rett under det frekvensområdet en prøver å undertrykke. | Ofte er det ikke ønskelig at et lokomotiv produserer strømmer med gitte frekvenser, for eksempel rundt 95 og 105 Hz som er de frekvensene tradisjonelle norske sporfelt arbeider ved. Dette kan unngås i lokomotivet ved hjelp av såkalt anticontrol og medfører at en får et aktivt område i frekvens rett under det frekvensområdet en prøver å undertrykke. | ||
I Norge og Sverige er det innført et krav til nye lokomotiver at de ikke skal være aktive over | I Norge og Sverige er det innført et krav til nye lokomotiver at de ikke skal være aktive over 87 Hz. | ||
Inputadmittansen for et lokomotiv kan beregnes og måles. Beregningene krever at en har tilgang til særdeles detaljert informasjon om styringen av lokomotivet. Ved høyere frekvenser spiller selv mindre tidsforsinkelser i f. eks. elektronikkortene som styrer krafthalvlederne en rolle, så i praksis er det neppe mulig å oppnå presise resultater på bakgrunn av beregninger alene. Ved måling derimot kan en ved å injisere spenninger med ulike frekvenser overlagret grunnfrekvensen registrerer lokomotivets respons på disse, det vil si inputadmittansen. Denne ”sveipen” over det aktuelle frekvensområdet kan for eksempel gjøres av et vanlig lokomotiv med en programvare for nettstrømretteren spesielt programmert for dette. En tredje mulighet er simulering i en realtidssimulator med ”hardware-in-the-loop”, d. v. s. at det virkelige styrings- og reguleringssystem fra lokomotivet kombineres med en signalprosessor som kjører et program som simulerer effektkretsene (forsyning, transformator, DC-mellemkress, etc.). | Inputadmittansen for et lokomotiv kan beregnes og måles. Beregningene krever at en har tilgang til særdeles detaljert informasjon om styringen av lokomotivet. Ved høyere frekvenser spiller selv mindre tidsforsinkelser i f. eks. elektronikkortene som styrer krafthalvlederne en rolle, så i praksis er det neppe mulig å oppnå presise resultater på bakgrunn av beregninger alene. Ved måling derimot kan en ved å injisere spenninger med ulike frekvenser overlagret grunnfrekvensen registrerer lokomotivets respons på disse, det vil si inputadmittansen. Denne ”sveipen” over det aktuelle frekvensområdet kan for eksempel gjøres av et vanlig lokomotiv med en programvare for nettstrømretteren spesielt programmert for dette. En tredje mulighet er simulering i en realtidssimulator med ”hardware-in-the-loop”, d. v. s. at det virkelige styrings- og reguleringssystem fra lokomotivet kombineres med en signalprosessor som kjører et program som simulerer effektkretsene (forsyning, transformator, DC-mellemkress, etc.). | ||
Informasjon om eksisterende kjøretøys aktive egenskaper er gitt i [https://trv.jbv.no/wiki/Banestr%C3%B8mforsyning/Prosjektering_og_bygging/Kraftsystem/Vedlegg/Kompatibilitetsstudie_steg_1-7_(Informativt)#Characterisation_of_existing_rolling_stock Teknisk regelverk/Banestrømforsyning/Prosjektering_og_bygging/Kraftsystem/Vedlegg/Kompatibilitetsstudie steg 1-7 (Informativt)#Characterisation of existing rolling stock]. | |||
=== Lokomotiver med passive filter=== | === Lokomotiver med passive filter=== | ||
| Linje 414: | Linje 346: | ||
=== Resonansustabilitet=== | === Resonansustabilitet=== | ||
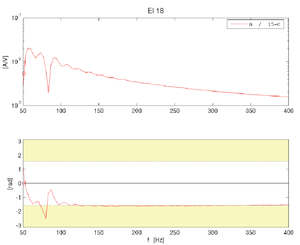
[[Fil:Fig542-1420.png|thumb|300px|''Figur 20: Inputadmittans for NSB El18'']] | |||
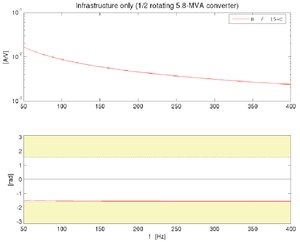
[[Fil:Fig542-1419.png|thumb|center|300px|''Figur 19: Frekvensrespons for en halv roterende omformer Q38 (5,8 MVA)'']] | |||
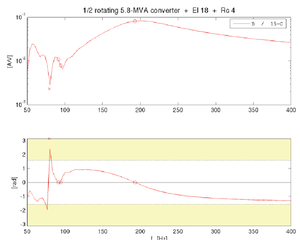
[[Fil:Fig542-1422.png|thumb|300px|''Figur 22: Resonans og ustabilitet ved 80 Hz'']] | |||
[[Fil:Fig542-1421.png|thumb|center|300px|''Figur 21: En roterende omformer og et El18 lokomotiv sammen'']] | |||
I dette avsnittet skal vi se hvordan et kraftsystem kan eksiteres til elektrisk resonans på grunn av et aktivt lokomotiv og et lokomotiv med passivt filter. I dette tilfellet er det elektriske og elektroniske fenomener som virker ved samme frekvens og som gir ustabiliteten. Alle figurene er hentet fra [6]. | I dette avsnittet skal vi se hvordan et kraftsystem kan eksiteres til elektrisk resonans på grunn av et aktivt lokomotiv og et lokomotiv med passivt filter. I dette tilfellet er det elektriske og elektroniske fenomener som virker ved samme frekvens og som gir ustabiliteten. Alle figurene er hentet fra [6]. | ||
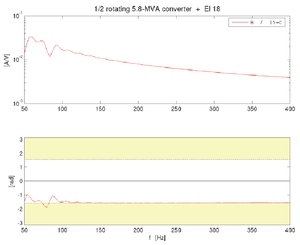
Figur 19 viser frekvensresponsen for en halv roterende omformer Q38 (5,8 MVA). En ser at den er uten resonanser og nesten helt induktiv i hele frekvensområdet. Ettersom frekvensen øker ser vi at admittansen blir stadig mindre og fasevinkelen kryper nærmere –π/2 (-90˚). Den elektriske ekvivalenten av omformeren er tidligere vist i figur 14. Med en halv menes at ytelsen til aggregatet er halvert ved at impedansen er doblet. Det er ikke noen kontaktledning med strøkapasitanser i dette viste eksempelet. | Figur 19 viser frekvensresponsen for en halv roterende omformer Q38 (5,8 MVA). En ser at den er uten resonanser og nesten helt induktiv i hele frekvensområdet. Ettersom frekvensen øker ser vi at admittansen blir stadig mindre og fasevinkelen kryper nærmere –π/2 (-90˚). Den elektriske ekvivalenten av omformeren er tidligere vist i figur 14. Med en halv menes at ytelsen til aggregatet er halvert ved at impedansen er doblet. Det er ikke noen kontaktledning med strøkapasitanser i dette viste eksempelet. | ||
Rett ved omformeren plasseres så et lokomotiv type NSB El18 som har en inputadmittans som vist i figur 20. Vi ser at lokomotivet er aktivt i frekvensområdet 75-84 Hz. Systemet er likevel stabilt siden det ikke er noen resonansfrekvenser som kan eksiteres, dette er vist i figur 21. | Rett ved omformeren plasseres så et lokomotiv type NSB El18 som har en inputadmittans som vist i figur 20. Vi ser at lokomotivet er aktivt i frekvensområdet 75-84 Hz. Systemet er likevel stabilt siden det ikke er noen resonansfrekvenser som kan eksiteres, dette er vist i figur 21. | ||
Sammen med den roterende omformeren og El 18-lokomotivet plasseres så et lokomotiv type Rc 4 som på samme måte som El 16 har telefilterkondensatorer på 0,6 MVAr. Det introduserer en resonans i systemet rundt 80 Hz. Denne resonansen eksiteres av at El 18 er aktiv ved denne frekvensen og resultatet blir ustabilt som vist i figur 22 hvor faseresponsen passerer ±π/2. Vi ser at admittansen er lav ved denne frekvensen, hvilket tyder på en parallellresonans. | Sammen med den roterende omformeren og El 18-lokomotivet plasseres så et lokomotiv type Rc 4 som på samme måte som El 16 har telefilterkondensatorer på 0,6 MVAr. Det introduserer en resonans i systemet rundt 80 Hz. Denne resonansen eksiteres av at El 18 er aktiv ved denne frekvensen og resultatet blir ustabilt som vist i figur 22 hvor faseresponsen passerer ±π/2. Vi ser at admittansen er lav ved denne frekvensen, hvilket tyder på en parallellresonans. | ||
Telefilterkondensatorene introduserer også flere andre resonansfrekvenser i systemet, rett under 100 Hz og rett under 200 Hz. Ved sistenevnte resonansfrekvens er admittansen høy, noe som tyder på en serieresonans. | Telefilterkondensatorene introduserer også flere andre resonansfrekvenser i systemet, rett under 100 Hz og rett under 200 Hz. Ved sistenevnte resonansfrekvens er admittansen høy, noe som tyder på en serieresonans. | ||
Ustabiliteten, det vil si energipendlingene mellom de elektriske komponentene gir overspenninger som enten løser eller ødelegger overspenningsvern. I lokomotiver og statiske omformerstasjoner vil en kunne merke ustabiliteten ved at vern, for eksempel 100 Hz-vern, løser. Pendlingene kan også føre til overoppheting av dempemotstander i forbindelse med passive filter. En kan også oppleve at signal og sikringsanlegget påvirkes. Det er innlysende at dette kan føre til problemer for togtrafikken. | Ustabiliteten, det vil si energipendlingene mellom de elektriske komponentene gir overspenninger som enten løser eller ødelegger overspenningsvern. I lokomotiver og statiske omformerstasjoner vil en kunne merke ustabiliteten ved at vern, for eksempel 100 Hz-vern, løser. Pendlingene kan også føre til overoppheting av dempemotstander i forbindelse med passive filter. En kan også oppleve at signal og sikringsanlegget påvirkes. Det er innlysende at dette kan føre til problemer for togtrafikken. | ||
=== Hvordan undersøke stabiliteten=== | === Hvordan undersøke stabiliteten=== | ||
[[Fil:Fig542-1423.png|thumb|600px|''Figur 23: Eksempel på "complete approach" hentet fra [6]'']] | |||
Studie av stabiliteten i forhold til elektriske resonanser kan i hovedsak deles inn i to typer. Den enkleste er kalt ”separation approach” og innebærer en undersøkelse av resonansfrekvensene i kraftsystemet som vist i avsnitt 5.2 og inputadmittansen til lokomotivene som skal trafikkere i systemet som vist i avsnitt 5.3. Dersom laveste resonansfrekvens i systemet (inkludert eventuelle passive filter i lokomotiver osv) er høyere enn den høyeste frekvensen som lokomotivene som skal trafikkere i systemet er aktiv, vil ikke resonanser kunne eksiteres og ustabilitet ikke være noe problem. I eksempelet i avsnitt 5.7 er en slik undersøkelse tilstrekkelig for å finne ut at ustabilitet kan oppstå. | Studie av stabiliteten i forhold til elektriske resonanser kan i hovedsak deles inn i to typer. Den enkleste er kalt ”separation approach” og innebærer en undersøkelse av resonansfrekvensene i kraftsystemet som vist i avsnitt 5.2 og inputadmittansen til lokomotivene som skal trafikkere i systemet som vist i avsnitt 5.3. Dersom laveste resonansfrekvens i systemet (inkludert eventuelle passive filter i lokomotiver osv) er høyere enn den høyeste frekvensen som lokomotivene som skal trafikkere i systemet er aktiv, vil ikke resonanser kunne eksiteres og ustabilitet ikke være noe problem. I eksempelet i avsnitt 5.7 er en slik undersøkelse tilstrekkelig for å finne ut at ustabilitet kan oppstå. | ||
Dersom en ikke er sikker på at laveste resonansfrekvens i systemet er høyere enn den høyeste frekvensen hvor et lokomotiv er aktivt må en bruke en mer arbeidskrevende metode kalt ”complete approach”. Fremdeles må en kjenne inputadmittansen for både kraftsystemet og lokomotivene som skal trafikkere banen. Men en må nå beregne eller simulere den endelige admittansen i hele systemet inkludert lokomotivene for alle situasjoner som kan oppstå. Det vil si at en må plassere lokomotivene i kraftsystemet på relevante plasser. Dette er arbeidsomt fordi en kan forvente nærmest uendelig mange kombinasjoner av lokomotiver, plasseringer, koblingssituasjoner i nettet, omformeraggregater i drift osv. Ved undersøkelse av stabiliteten ved leveransen av flytogene til NSB Gardermobanen ble det utført beregning av stabiliteten i 450 000 ulike driftsituasjoner. | Dersom en ikke er sikker på at laveste resonansfrekvens i systemet er høyere enn den høyeste frekvensen hvor et lokomotiv er aktivt må en bruke en mer arbeidskrevende metode kalt ”complete approach”. Fremdeles må en kjenne inputadmittansen for både kraftsystemet og lokomotivene som skal trafikkere banen. Men en må nå beregne eller simulere den endelige admittansen i hele systemet inkludert lokomotivene for alle situasjoner som kan oppstå. Det vil si at en må plassere lokomotivene i kraftsystemet på relevante plasser. Dette er arbeidsomt fordi en kan forvente nærmest uendelig mange kombinasjoner av lokomotiver, plasseringer, koblingssituasjoner i nettet, omformeraggregater i drift osv. Ved undersøkelse av stabiliteten ved leveransen av flytogene til NSB Gardermobanen ble det utført beregning av stabiliteten i 450 000 ulike driftsituasjoner. Likevel er plasseringen mindre viktig i AT-system ettersom overføringsimpedansen er så lav. | ||
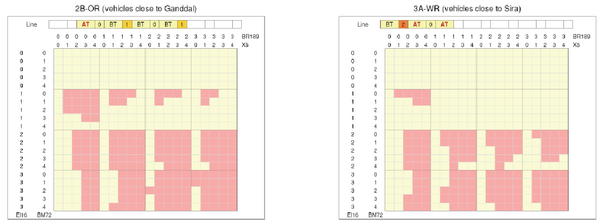
Figur 23 viser et eksempel på ”complete approach” fra studiene som ble utført i forbindelse med pilotutbyggingen av autotransformatorsystemet på Sørlandsbanen mellom Kristiansand og Stavanger. Spesielt her er at det er mange tunneler som krever at en legger positiv- og negativleder i kabel. Øverst i figurene (”line”) vises konfigurasjonen av kraftsystemet med AT- eller BT-system samt antall omformeraggregater i de ulike stasjonene i drift. Antall lokomotiver av hver type (El 16, tp 72, BR 189 og X5) er variert for de ulike simuleringene. Gul rute angir at situasjonen er stabil og rød rute angir at situasjonen er ustabil. | Figur 23 viser et eksempel på ”complete approach” fra studiene som ble utført i forbindelse med pilotutbyggingen av autotransformatorsystemet på Sørlandsbanen mellom Kristiansand og Stavanger. Spesielt her er at det er mange tunneler som krever at en legger positiv- og negativleder i kabel. Øverst i figurene (”line”) vises konfigurasjonen av kraftsystemet med AT- eller BT-system samt antall omformeraggregater i de ulike stasjonene i drift. Antall lokomotiver av hver type (El 16, tp 72, BR 189 og X5) er variert for de ulike simuleringene. Gul rute angir at situasjonen er stabil og rød rute angir at situasjonen er ustabil. | ||
En ser at uten El 16 med sine telefilterkondensatorer er alle kombinasjonene av annet materiell stabilt. Ved økende antall El 16 skal det mindre til for at ustabilitet oppstår. Flere lokomotiver av de andre typene reduserer imidlertid induktansen i systemet (flere tog i parallell), noe som er med på å øke resonansfrekvensene. | |||
Teoretiske beregninger og simuleringer bør alltid verifiseres med målinger. | |||
<!--For mer detaljert informasjon om hvordan modellering og undersøkelse av elektriske resonansustabilitet i banestrømforsyningen, se [6] and [6].--> | |||
For | Oppsummert kan følgende fremgangsmetode benyttes for å undersøke om det kan oppstå elektrisk resonansustabilitet: | ||
# '''Definer grense''': Definer f<sub>l</sub> lik den høyeste frekvensen kraftelektronikkomponenter (kjøretøy eller omformerstasjoner) kan være aktive basert på avsnitt 5.3, minimum 87 Hz som er kravet til nye komponenter. | |||
# '''Forenklet resonansberegning''': Estimer grovt den laveste elektriske resonansfrekvensen f<sub>res</sub> i kraftsystemet basert på formelen i avsnitt 5.2. For enkelthetsskyld kan R settes lik 0. Vedlegg B i NEK TS 50238-2:2010 gir input på hvordan beregne L og C. Dersom f<sub>res</sub> > 2*f<sub>l</sub> kan en konkludere med at det er svært liten fare for ustabilitet. Se nærmere beskrivelse i [[Overslagsberegning for resonansstabilitet]]. | |||
# '''Separate approach''': Dersom f<sub>res</sub> < 2*f<sub>l</sub> bør det etableres en mer nøyaktig modell av kraftsystemet uten tog for beregning av resonansfrekvensene. Dersom f<sub>res</sub> > f<sub>l</sub> er det liten fare for ustabilitet med mindre det forventes trafikk med kjøretøy med særlige kapsitive filter (eks. Rc og El16 med telefilter, eller motorvognsett med høyspentkabler på taket). Da bør denne kapasitansen hensyntas i beregningen, alternativt må det legges til grunn margin. | |||
# '''Complete approach''': Dersom det ikke er mulig å overholde f<sub>res</sub> > f<sub>l</sub> må kraftelektronikkomponentenes karakteristiske frekvensrespons tas med i betraktning. Kraftsystemet har noe naturlig demping gjennom resistanser, og denne dempingen kan være tilstrekkelig til å hindre ustabilitet selv om kraftelektronikkomponenten er aktiv ved en resonansfrekvens. Tilnærmingen kan deles angrepsmåter: | |||
## Full Complete approach hvor det plasseres inn tog i kraftsystemmodellen (for eksempel den som er etablert i punkt 3) | |||
## Mini-Complete approach hvor en med kunnskapen om dempingen i nettet (for eksempel funnet i punkt 3) gjør prinsipielle vurderinger av hvor mange tog av hver type i ulike kombinasjoner som må til for å gjøre nettet ustabilt. Det vil si sammenligne nettets positive demping med togenes eventuelle negative demping ved forventede resonansfrekvenser. | |||
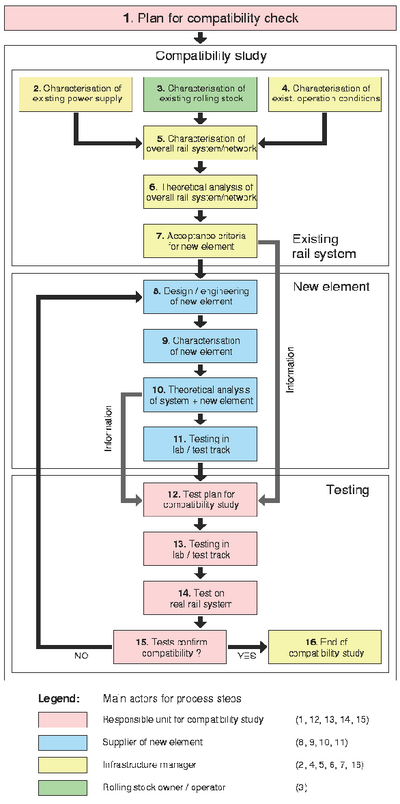
== Hvordan sikre stabilitet og kompatibilitet== | == Hvordan sikre stabilitet og kompatibilitet== | ||
[[Fil:Fig542-1424.png|thumb|400px|''Figur 24: Stabilitetsstudie som anbefalt i EN 50388.'']] | |||
Et optimalt, eller i det minste tilfredsstillende, samspill mellom nye lokomotiver og eksisterende lokomotiver og jernbane infrastruktur er en kompleks oppgave. Lokomotivene blir kontinuerlig utviklet for å bedre ytelsen og redusere kostnadene. Lang levetid for både lokomotiver og infrastrukturinstallasjoner gir at mange forskjellige teknologier må passe sammen. Forskjellig grad av emisjon og immunitet mot uregelmessigheter og forstyrrelser gir ekstra utfordringer. Leverandøren av lokomotivet, togselskapet og infrastrukturforvalter har ofte forskjellige krav med tanke på optimalisering. | Et optimalt, eller i det minste tilfredsstillende, samspill mellom nye lokomotiver og eksisterende lokomotiver og jernbane infrastruktur er en kompleks oppgave. Lokomotivene blir kontinuerlig utviklet for å bedre ytelsen og redusere kostnadene. Lang levetid for både lokomotiver og infrastrukturinstallasjoner gir at mange forskjellige teknologier må passe sammen. Forskjellig grad av emisjon og immunitet mot uregelmessigheter og forstyrrelser gir ekstra utfordringer. Leverandøren av lokomotivet, togselskapet og infrastrukturforvalter har ofte forskjellige krav med tanke på optimalisering. | ||
| Linje 477: | Linje 402: | ||
For å gi hint og tips om hvordan en skal komme i gang med en slik sjekk samt hva en bør være observant på, er det lagd et dokument som beskriver en form for beste praksis for å nå kompatiblitet | For å gi hint og tips om hvordan en skal komme i gang med en slik sjekk samt hva en bør være observant på, er det lagd et dokument som beskriver en form for beste praksis for å nå kompatiblitet | ||
==Litteraturhenvisning == | ==Litteraturhenvisning == | ||
Siste sideversjon per 4. feb. 2025 kl. 08:19
Innledning
Dette kapittelet i læreboka gir en kort introduksjon til emnet stabilitet i kraftsystemet med hovedvekt på den norske banestrømforsyningen.
Bakgrunn
Jernbaneverket har ansvaret for drift av et 15 kV 16 2/3 Hz kraftsystem for elektrisk energiforsyning til tog. Kraftsystemet består av 2500 km elektrifisert jernbane (kontaktledning) og 500 MVA installert ytelse (29 omformerstasjoner med roterende omformeraggregater, 6 omformerstasjoner med statiske omformeraggregater, 5 transformatorstasjoner og 2 vannkraftstasjoner). I tillegg finnes 157 km 55 kV fjernledning og rundt 100 km 15 kV mateledning. Daglig trafikkeres nettet av rundt 1100 elektriske tog, hvilket medfører et årlig energiforbruk på 550-600 GWh.
Enfasenettet på hovedstrekningene er forholdsvis svakt og mates i hovedsak av spredte omformeraggregater med relativt små ytelser. Ytelsene til lokomotiver/tog har generelt økt og kan være større enn ytelsen til et enkelt omformeraggregat. Ved innføring av nytt elektrisk rullende materiell i Norge har det ofte vært problemer i forbindelse med pendlinger/svingninger i nettet, samt problemer med økt spenningsfølsomhet på togene. Dette gir utfordringer blant annet rundt optimalisering av lokomotivenes oppbygning og regulatorinnstilling.
I fremtiden ser en for seg nye utfordringer gjennom reduksjon av overføringsimpedansen (for eksempel ved innføring av autotransformatorsystem eller fjernledning på høyere spenningsnivå), sentralisering i færre og større omformerstasjoner, innføring av flere statiske omformerstasjoner og at rullende materiell i større grad vil bestå av store enheter med kraftelektronikkstyring av asynkronmotorer. Foreløpige erfaringer viser at stabilitetsvurderinger av kraftsystemet blir stadig viktigere.
Hensikt
Hensikten med kapittelet er å gi en kort innføring i fenomenene, begrepene og problemene i forhold til stabilitet i kraftsystem for jernbane slik at Jernbaneverkets ingeniører lettere kan forstå og ta hensyn til dette ved planlegging, prosjektering, bygging, drift og vedlikehold av infrastrukturen.
Annet
Lærebokkapittelet er et resultat og en nedtegning av kompetansen en har tilegnet seg i FOU prosjektet ”Stabilitet i banestrømforsyningen” ved Infrastruktur Premiss og utvikling elkraft i 2005-2006 i samarbeid med Banverket samt konsulentene Markus Meyer (emkamatik GmbH i Sveits) og Lars Buhrkall (Danmark). Omfanget av kapittel 4 om lavfrekvente pendlinger er begrenset siden det fremdeles gjenstår en del undersøkelser og etablering av metodikk innen temaet.
For mer detaljert informasjon om krav til rullende materiell i forhold til samspill mot elektrisk infrastruktur henvises det til [JD 590] kapittel 4 ”Elkraft”.
Terminologi
I boken er det ofte benyttet ordet lokomotiv når en snakker om kjøretøyet eller trekkraftenheten siden dette normalt er enklere å forholde seg til og forstå. Med lokomotiv menes da også motorvognen(e) i et motorvognstog.
Kraftsystemets dynamikk og stabilitet
Et elektrisk kraftsystem består av mange individuelle elementer som kan generere, transportere og forbruke elektrisk energi og er koblet sammen til et stort, komplekst system. Disse elementene er som oftest påvirket av ulike fenomener og begrensninger, og kontrolleres derfor av egne reguleringssløyfer. På grunn av denne sammenkoblingen finnes mange muligheter for dynamisk samspill elementene imellom.
For mer detaljert informasjon om stabilitet og kontroll i kraftsystemer henvises det til [6] som finnes på Jernbaneverkets bibliotek.
Definisjon av stabilitet og kompatiblitet
Stabilitet handler om balanse – balanse mellom krefter. Et system er stabilt dersom en har en likevekt mellom krefter som virker mot hverandre.
Med ustabilitet mener en ofte at en mister kontroll over systemet, det vil si at en ikke har balanse mellom kreftene som virker mot hverandre. Dette gir seg ofte til kjenne ved at en eller flere variable vokser eller minker utover sine normale grenser ved økende tid. Forløpet kan enten være preget av svingninger som vokser og vokser eller uten svingninger i det hele tatt. Men en kan også si at et system er ustabilt dersom oppståtte svinginger ikke dempes ut fort nok. Ustabilitet ender som oftest med at komponenter i systemet går i stykker eller at de blir koblet ut av vern og overvåkning.
Det er i hovedsak viktig å vurdere hvordan kraftsystemet responderer ved mindre lastendringer og forskjellige typer forstyrrelser samt hvordan ulike komponenter i systemet spiller sammen. En sier at et system er stasjonært stabilt dersom det har en iboende egenskap til å forbli i en stabil tilstand. Dersom et system er transient stabilt vil det også etter en større forstyrrelse, for eksempel en kortslutning, finne tilbake til en akseptabel stasjonær stabil tilstand. Noen former for ustabilitet kan bygge seg opp fra nærmest ingenting, bare en liten forstyrrelse er nok. Slike fenomener er dermed selveksiterende og omtales gjerne som småsignalstabilitet.
Stabilitet er i stor grad et spørsmål om demping. Demping vil si at en liten forstyrrelse blir redusert ettersom den brer seg i systemet. Energien som systemet tilføres på grunn av forstyrrelsen må ledes ut av systemet. I motsatt fall er dempingen negativ og systemet tilføres stadig mer energi, noe som fører til at systemet blir ustabilt. En annen formulering av fenomenet demping er tilførsel av noe det er underskudd på og forbruk av noe det er overskudd på.
Dersom komponenter i et system, for eksempel infrastruktur og lokomotiver, påvirker hverandre på en slik måte at systemet blir ustabilt, samspiller de ikke. Samspill mellom komponenter i et system betegnes ofte med ordet kompatibilitet (forenelighet, sameksistens).
Ulike dynamiske fenomener
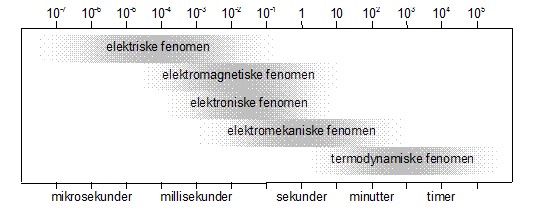
De ulike dynamiske fenomenene i kraftsystemet kan deles inn i 5 forskjellige grupper etter deres fysikalske karakter. Fenomenene er gruppert etter typisk tidskonstant og vist i figur 1. De ulike fenomenene kan påvirke hverandre når tidskonstantene ligger i samme område. Slik påvirkning kan dersom en ikke tar hensyn til den føre til ekstra utfordringer for å sikre kompatibilitet og stabilitet.
De raskeste dynamiske fenomenene er bølgeeffektene med tidskonstanter fra mikrosekunder for lynimpulser til millisekunder for RLC-kretser. Siden de er gitt av de elektriske parameterne i systemet kalles fenomenen også for elektriske. Disse effektene oppstår oftere i systemer med høyere spenning og tilhører normalt nettdelen av systemet. Resonanser i RLC-kretser har vist seg å kunne oppstå i kraftsystemer for jernbane med liten demping, for eksempel i fjernlednings og autotransformatorsystemer hvor kapasitansen er høy. Dette blir videre behandlet under elektrisk resonansustabilitet i kapittel 5.
Elektromagnetiske dynamiske effekter finner ofte sted i viklingene i elektriske maskiner ved forstyrrelser, vernutkobling eller samspill mot nettet. Generatorens anker og dempeviklinger spiller en stor rolle. Typiske tidskonstanter er fra millisekunder til sekunder.
Det nyeste fenomenene er de elektroniske som skyldes tidskonstanter, forsinkelser og tilbakekoblingseffekter i styringselektronikk. Disse er spesielt synlige ved styring av moderne kraftelektronikk (lokomotiver og statiske omformere) og ligger i typisk område fra millisekunder til sekunder. Ofte kalles fenomenene også for reguleringstekniske dersom de skyldes implementering i regulatorer, men elektroniske fenomen kan også skyldes iboende og uunngåelige egenskaper i elektronikk (styringselektronikk eller kraftelektronikk). Elektroniske fenomen kan eksitere både bølgeeffekter og elektromekaniske effekter og vil bli videre behandlet i både kapittel 4 og 5.
Med tidskonstanter fra ett til flere sekunder har en elektromekaniske fenomener som er gitt av svingende roterende masser i generatorer og motorer. De elektriske maskinene kan svinge mot andre elektriske maskiner eller om nettet. Svingningen kan være eksitert av både lastendring, forstyrrelse, vernutkobling eller regulering. Maskinens rotorvikling, dempevikling og treghetsmoment spiller stor rolle. Slike rotorpendlinger har vært observert flere ganger i Jernbaneverkets roterende omformeraggregater og vil bli behandlet videre i kapittel 4.
De langsomste fenomenene er de termodynamiske. Disse er mest knyttet til varmekraftverk og regulering av disse, samt damp- og diesellokomotiver. Men oppvarming av elektriske ledere og maskiner kan også havne i denne kategorien. Disse fenomenene omtales ikke i denne boka.
Svingninger og resonanser
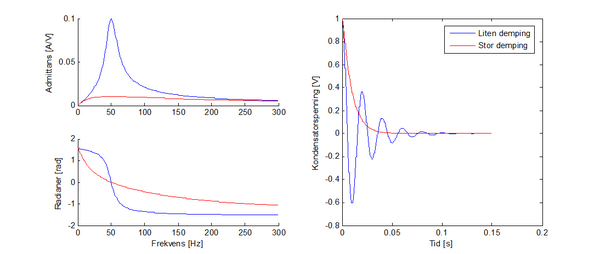
Alle komponentene i kraftsystemet har sin måte å respondere på endringer og forstyrrelser på, gitt av sin fysikalske natur eller regulering. Dynamisk uttrykkes denne responsen gjerne ved hjelp av en frekvensresponskarakteristikk. Slik karakteristikk kan utarbeides både for kontaktledningen, lokomotivene og omformerne som vist i de neste kapitlene. Et eksempel på en frekvensresponskarakteristikk er vist i figur 2 sammen med sprangresponsen i tidsplanet.
Ved noen frekvenser kan responsen være dempet slik at komponenten helt eller nesten er upåvirket av forstyrrelsen. Forstyrrelser ved andre frekvenser kan gjøre at komponenten påvirkes til å gi et signal tilbake til systemet med en gitt amplitude og tidsforskyvning i forhold til forstyrrelsen. Den nye forstyrrelsen på systemet kan i sin tur påvirke andre komponenter med sin respons. Frekvenser av forstyrrelser og påvirkninger som gjør at komponenter eller systemer blir stående å svinge mot hverandre med liten demping kalles resonansfrekvenser. Ved liten eller ingen demping kan disse pendlingene bare fortsette å vokse helt til en komponent går i stykker eller et vern løser ut. Systemet er da ustabilt.
Forsterkninger og tidsforsinkelser
I reguleringsteknikken er begrepene forsterkning og tidsforsinkelse av stor betydning.
Forsterkning av et signal er ofte tillagt av en regulator siden den øker hastigheten og responsen til systemet. Men det kan også hende at den er en del av reguleringssløyfen som en ikke kan unngå, for eksempel kontaktledningsimpedansen i et lokomotivs regulering. For stor forsterkning kan føre til at systemet blir ustabilt.
Tidsforsinkelse er ofte en del av karakteristikken og egenskapene til komponentene i reguleringssløyfen og er gjerne ikke til å unngå. Stor tidsforsinkelse kan gjøre at et system blir ustabilt. Samtidig kan en tidsforsinkelse være med på å dempe et system slik at signaler med høy frekvens ikke får innvirkning på systemet og dermed også virker stabiliserende.
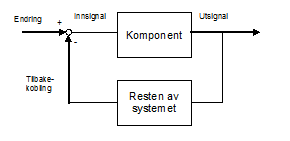
Illustrerende eksempel og generelt stabilitetskriterium
Problemstillingen er illustrert i figur 3 med en komponent, for eksempel et lokomotiv, som en del av et system, for eksempel banestrømforsyningen. Ved en endring eller forstyrrelse i innsignalet til lokomotivet (for eksempel spenningen på lokomotivets strømavtaker) reagerer lokomotivet ved å endre på utsignalet sitt (strømmen) slik at ønsket virkning (hastigheten til toget) opprettholdes/oppnåes. Systemet (banestrømforsyningen) reagerer på dette signalet (lokomotivets endrede strøm) med et endret innsignal til komponenten (spenningsfall over kontaktledningsimpedansen gir lavere spenning for toget). Slik påvirker komponenten og systemet hverandre til de finner en likevekt.
Dersom komponenten eller systemet har en resonansfrekvens som er dårlig dempet, vil den forhåpentligvis likevel svinge til en likevektstilstand. Dersom det er tidsforsinkelser i komponenten og systemet, kan en oppleve at den tiden signalet bruker fra endringen gjøres til det er kommet gjennom komponenten og systemet sammenfaller med halve periodetiden til resonansfrekvensen. Da vil tilbakekoblingen gjennom systemet føre til at signalet bare går rundt og rundt mellom komponent og system. Komponenten eller systemet må således passe på å svekke dette signalet slik at det ikke adderes for hver gang det går rundt. Energien i signalet må ledes ut av systemet gjennom demping. Hvis ikke vil svingningene i systemet vokse ettersom tiden går. Et kjent eksempel på en slik tilbakekoblingseffekt er en mikrofon som kommer for nær høyttaleren og hvor resultatet er en raskt voksende pipetone.
Et generelt stabilitetskriterium er derfor at tidsforsinkelsen gjennom komponent og system ikke er slik at tilbakekoblingen er halve periodetiden av resonansfrekvensen. Det vil si at tilbakekoblingen ikke må komme i motfase med innsignalet. Samtidig må komponent og system ikke forsterke signalet slik at det vokser, det vil si at forsterkningen må være mindre enn 1.
Det er i tillegg vanlig å kreve margin mot slik ustabilitet i både tidsforsinkelse (fase) og forsterkning.
Tidsforsinkelsen og forsterkningen av et signal gjennom komponenten og systemet er avhengig av hvilken frekvens signalet har. Responsen, det vil si forsterkning og tidsforsinkelse/fase for et lokomotiv sammen med en gitt banestrømforsyning som funksjon av signalets frekvens kan ses i figur 2.
Slik ustabilitet som skissert her kalles gjerne småsignalustabilitet ettersom kun en liten endring eller forstyrrelse er nok til å gjøre det ustabilt. Dette medfører avvik fra referanseverdien eller svingninger som bygger seg opp fra nærmest ingenting til å bli så store at utstyr ødelegges eller vern kobler ut. Dette kaller en gjerne også for selveksiterende.
Spenningsustabiliet
Innledning
Spenningsustabilitet omhandler hvorvidt spenningen i et system er innenfor gitte grenser. I svake kraftsystemer (høy impedans eller liten produksjon i forhold til forbruket) vil en gjerne oppleve at spenningen synker under gitte akseptgrenser. Dette er ikke nødvendigvis spenningsustabilt, men dersom lasten øker ytterligere kan en oppleve at spenningen regelrett kollapser (faller til 0). Spenningskollaps har vært tilfelle i energiforsyningen i flere land de siste årene, blant annet Sverige og USA.
Dette avsnittet gir et kort innblikk i spenningsustabilitet generelt og for jernbane spesielt.
Lastflytproblem og spenningskollaps
En matematisk løsning av et lastflytproblem i et kraftsystem har to likevektspunkter, det ene er stabilt og det andre gjerne er ustabilt. Karakteristikken til hvordan et kraftsystem påvirkes av økt belastning beskrives ofte ved hjelp av nesekurver som viser spenningen som funksjon av aktiv eller reaktiv effekt i et punkt. Disse er også kalt PU- eller QU-kurver avhengig av om det er aktiv eller reaktiv effekt som er den uavhengige variabelen. Et eksempel på en slik nesekurve er vist i figur 4
Vi ser at dersom en skal kunne ta ut 5 MW, så kan dette skje enten ved 14 kV spenning eller 6 kV. La oss ta utganspunkt i løsningen som ligger på oppsiden av kurven ved 14 kV. Ved økende belastning ser en at spenningen synker. Maksimal overførbar effekt er 7 MW. Ved dette punktet, som kalles for det kritiske punktet, er impedansen i lasten lik impedansen i overføringen.
Dersom lasten er en ren impedans uten noen form for regulering er alle punktene på nesekurven mulige arbeidspunkt. En vandring langs kurven fra høyeste spenning til laveste spenning tilsvarer en endring i lastens impedans fra uendelig til null (kortslutning).
Dersom lasten har en form for regulering for å sikre for eksempel konstant effekt eller konstant strøm, vil bare punkter på oversiden av kurven være stabile. Det kritiske punktet ytterst til høyre på kurven er også stabilt, men en marginal økning av lasten vil føre til at spenningen synker. Regulatoren vil så regulere impedansen for å holde sin skal-verdi, men kun oppleve at spenningen synker enda mer. Dette kalles et spenningskollaps eller spenningsskred.
Slik spenningsustabilitet har lenge i den vanlige energiforsyningen vært ansett som nærmest et stasjonært fenomen ettersom det ofte er noe som bygger seg opp over lang tid. Økende utnyttelse av kraftnettet og andelen regulerte/styrte laster i nettet har imidlertid gjort at det må oppfattes som et dynamisk fenomen. Ofte er spenningsustabilitet knyttet opp i mot mangel på reaktiv effekt for å dekke det reaktive spenningsfallet i overføringen.
Lastens spenningsavhengighet
Et lokomotiv er i utgangspunktet hastighetsstyrt av lokomotivføreren. Nyere lokomotiver har da selv en reguleringssløyfe som setter en referanseverdi for trekkraften. For eldre lokomotiver må lokomotivføreren også være den som bestemmer denne. Det vil si at dersom spenningen på kontaktledningen synker, vil lokomotivet øke pådraget slik at effekten og dermed hastigheten holdes konstant. Slik regulering kan føre til spenningskollaps i kraftsystemet og blant annet derfor er ofte lokomotivene utstyrt med en effekt- eller strømbegrensning som funksjon av spenningen. Eksempel på slike karakteristikker er gitt i figur 5 for ulike typer norsk materiell. Når spenningen synker under et vist nivå, reduserer lokomotivet sitt maksimale effektuttak fra kontaktledningen. Dersom lokomotivet ikke ligger på grensen til maksimal effekt eller maksimal strøm, vil lokomotivet virke som en konstant effektlast helt til spenningen eventuelt er blitt så lav at lokomotivet er ved sin maksimale effekt ved den aktuelle spenningen i henhold til karakteristikken.
Figuren viser til sammenligning kravet til slik effektbegrensning som funksjon av spenningen gitt i normen EN 50388 (omregnet fra strøm til effekt – sort kurve). Stigningen på kurven under knekkpunktet er en avveining mellom ønsket om å unngå spenningskollaps og at lokomotivet skal kunne finne et stabilt arbeidspunkt der effekten ikke forandrer seg for mye som funksjon av spenningen. Dersom lokomotivet ikke finner et stabilt arbeidspunkt kan en få lavfrekvente pendlinger som beskrevet i kapittel 4.
Spenningsavhengigheten til en last kan uttrykkes på følgende måte:
| 1 |
hvor:
- P = effekten til lasten ved aktuell spenning
- P0 = effekten til lasten ved nominell spenning
- U = aktuell spenning
- U0 = nominell spenning
- MP = spenningsavhengigheten
Når lasten trekker samme effekt uansett spenning er den spenningsuavhengig og MP = 0. Reguleres lasten etter konstant strøm er MP=1. Og dersom lasten oppfører seg som en konstant impedans er MP=2. Tilsvarende gjelder for reaktiv effekt Q.
Transformatorer med trinnkobling kan også føre til en konstant effekt virkning av ellers konstante impedanslaster siden den øker sekundærsspenningen sin når spenningsfallet foran den synker for å holde spenningen over lasten mest mulig konstant.
Reaktiv kompensering
Ettersom lokomotivets effektuttak, og dermed også evnen til å holde ønsket hastighet, kan være avhengig av kontaktledningsspenningen, er det ønskelig at spenningen er så god som mulig. Akseptabel spenning på togets strømavtaker er gitt i Teknisk regelverk for prosjektering av banestrømforsyning.
For å heve spenningen kan en kompensere for en del av spenningsfallet eller det reaktive tapet i kontaktledningen. Dette kan gjøres ved hjelp av kondensatorbatterier som beskrevet i lærebokens kapittel Kondensatorbatterier, eller ved kapasitiv kompensering i togene. El 16 er for eksempel utstyrt med telefilterkondensatorer på 0,6 MVAr for blant annet bedring av effektfaktor. Lokomotiver med firekvadrants nettstrømrettere har mulighet for å styre reaktiv effekt etter ønske.
Figur 6 viser ensammenligning av nesekurver for nett med ulike typer kompensering og uten kompensering. Det er tatt utgangspunkt i en ensidig matet strekning hvor lasten er plassert 60 km fra matepunktet. Matepunktet holder en konstant spenning på 16,5 kV og kontaktlednings impedans er 0,19+j0,21 Ohm/km. Vi ser at maksimal overførbar effekt er ca 4,5 MW ved en spenning på 9 kV over lasten.
Ved å sette inn et kondensatorbatteri på –j7,35 Ohm i serie med kontaktledningen, reduseres overføringsimpedansens reaktive del. Dette tilsvare en kompenseringsgrad på 58 %. På den måten ser vi at maksimal overførbar effekt øker til ca 5,5 MW med samme spenning.
Ved at lasten (lokomotivet) selv kompenserer med effektfaktor 0,6 kapasitiv, ser vi at maksimal overførbar effekt også nå er økt i forhold til uten kompensering. Spenningen på lasten holder seg også konstant en god stund selv om det aktive effektbehovet øker. Men plutselig begynner spenningen å synke raskt og det kritiske punktet er nå nådd allerede ved 13 kV over lasten.
Ved lastkompensering virker kontaktledningsspenningen som toget ser god veldig lenge, helt til den plutselig kollapser uten forvarsel ved en spenning som er å regne som en vanlig spenning på strømavtaker (13 kV). Dette i motsetning til uten kompensering og med seriekompensering hvor spenningskollapsen skjer ved så lav spenning at lasten fått har redusert pådraget sitt eller koblet ut.
Mer om kapasitiv kompensering fra lokomotivene kan finnes i [6].
Kobling til lavfrekvente pendlinger
Den kapasitive kompenseringen har som vist innvirkning på spenningen på togets strømavtaker. Lokomotiv kan også begrense strømmen eller effekten sin ved lave spenninger. Spenningsvariasjoner på grunn av endringer i aktiv og reaktiv effekt kan føre til at lokomotivet har problemer med å finne et stabilt arbeidspunkt og kan resultere i lavfrekvente pendlinger som beskrevet i avsnitt 4.
Lavfrekvente pendlinger
Innledning
I 1996-1997 ble det på Oppdal omformerstasjon oppdaget pendlinger i trefaseeffekten levert til stasjonen når tog ble fremført med nytt lokomotiv type NSB El 18. Typisk frekvens på pendlingene var 1,5 til 2,0 Hz. Det ble også observert tilsvarende pendlinger på Bergensbanen og Sørlandsbanen. Fenomenet var lite kjent og dette var starten på flere forskningsprosjekter, gjerne i samarbeid med eksterne konsulenter.
Dette kapittelet gir en introduksjon i hvordan lavfrekvente pendlinger kan oppstå, hva som er konsekvensen og litt om hvordan en kan redusere eller unngå problemene.
Banestrømsforsyningen
Roterende omformere
Banestrømforsyningen i Norge domineres av roterende omformeraggregater bestående av en synkronmotor og en synkrongenerator koplet på samme aksel. En forskjell i antall faser og antall poler lik 3:1 gjør at elektrisk energi ved trefase 50 Hz omformes til 16 2/3 Hz enfase. En skisse av typisk matesituasjon i den norske banestrømforsyningen er vist i figur 7. De roterende omformeraggregatene finnes i størrelser av 3,1, 5,8, 7,0, og 10,0 MVA kontinuerlig ytelse. 5,8 MVA og 7,0 MVA aggregatene er vanligst. En omformerstasjon består av ett til tre aggregater, men to er typisk. Antall aggregater i drift tilpasses variasjonene i effektetterspørsel gitt av togtrafikken.
Alle elektriske maskiner har en elektromekanisk resonansfrekvens i området 1-2 Hz. Dette er implisitt gitt av den klassiske svingelikningen
| 2 |
hvor :
- H er et uttrykk for den roterende massen
- Ωa er synkronmaskinens aktuelle rotasjonshastighet
- Ωn er rotasjonshastighet for en eventuell synkron referanse i systemet (gjerne lik nettfrekvensen)
- Mm er elektrisk moment på akselen gitt av omformerens motor og er funksjon av polhjulsvinkelen βm
- Mg er elektrisk moment på akselen gitt av omformerens generator og er funksjon av polhjulsvinkelen βg
- D er et uttrykk for dempingen i omformeraggregatet
Polhjulsvinkelen for en synkronmaskin er skissert sammen med rotor og stator i figur 8. Når rotor pendler går den vekselvis fortere og senere enn synkron hastighet. Polhjulsvinkelen vil da øke og minke faseforskjøvet (tidsforsinket) etter hastighetsendringene.
Resonansfrekvensen fres , også kalt egenfrekvensen, er i stor grad bestemt av tre hovedparametere; hvor stor endringen i aktiv effekt er ved en gitt endring av maskinenens polhjulsvinkel (KSm –typisk litt over 1), omformeraggregatets totale H-konstant (typisk rundt 2,5 til 3,2) og nettfrekvensen ωN slik som formel 3 (hentet fra [6]) viser. Det er motoren som dominerer det totale aggregatets oppførsel blant annet på grunn av at nettfrekvensen i trefasenettet er tre ganger større enn i jernbanenettet. Typisk egenfrekvens er i området 1,6 til 1,9 Hz.
| 3 |
Ved et sprang i lasten fra for eksempel et tog, vil omformeraggregatet gå til den nye belastningssituasjonen som et underdempet system med frekvens til innsvingningen lik aggregatets egenfrekvens. Med pendling eller svingning menes at omformerens rotor veksler mellom å rotere fortere og senere enn 500 omdreininger i minuttet som er aggregatets nominelle turtall. Nøyaktig svingefrekvens gis av omformertype, antall aggregater i parallell, enfase og trefasenettets stivhet og spenningsregulatorinnstilling. Pendlingene er lettest å observere i omformerens trefaseeffekt, men kan også observere i enfasespenningen
En simulert sprangrespons til et roterende omformeraggregat er vist i figur 9 i form av motor- (trefase) og generatoreffekt (enfase). En kan se at aggregatet svinger inn til en ny tilstand med en frekvens rundt 1,6 Hz.
Denne underkritisk dempede innsvingningen er i seg selv ikke kritisk ettersom den typisk dempes ut (forsvinner) etter 5-15 sekunder. Dersom lastendringen gjentas med en frekvens rundt aggregatets egenfrekvens vil svingningene ikke dø ut, men opprettholdes.
Av historiske grunner er ikke synkronmotoren utstyrt med eksplisitte dempeviklinger, men har kun en begrenset dempevirkning på grunn av virvelstrømmer i rotorens massive poler som oppstår ved avvik fra synkront turtall. Mangelen på demping som hindrer omformerens rotor å pendle er kjernen i de lavfrekvente pendlingene som til nå har vært tema i den norske banestrømforsyningen. Synkrongeneratoren er utstyrt med kraftige dempeviklinger for å dempe 33 1/3 Hz pendlinger på grunn av den pulserende enfaseffekten. En forutsetning for at dempeviklinger skal kunne bidra med demping av lavfrekvente pendlinger er at synkronmaskinen går i samkjøring med et nett slik at den har en synkron referanse å forholde seg til. Jo stivere nett, jo bedre dempevirkning. Det er derfor viktig at enfasenettet også er samkjørt for å dra nytte av generatorens dempeviklinger.
Magnetiseringssystemet med likestrøms feltmaskin for motor og generator er ikke raskt nok til kunne ha noen innvirkning på rotorpendlingene.
Statiske omformere
Statiske PWM omformere har den samme strukturen som nettstrømretterne i lokomotiver (se kapittel 4.3.3), men siden de oppfører seg på en litt annen måte (spenningskilde framfor strømkilde) er de mindre kritiske med hensyn på tilbakekoblingseffekter og tilhørende ustabiliteter.
Kondensatorbatterier
Ved seriekompensering av kontaktledningen har det vært opplevd store lavfrekvente pendlinger i omformerstasjoner med roterende aggregater, spesielt ved lav ytelse i stasjonen. Ved høy kompenseringsgrad kan kontaktledningens elektriske resonansfrekvens (se avsnitt 5) bli så lav at den er i nærheten av nettfrekvensen. Dersom differansen mellom nettfrekvensen og linjens resonansfrekvens, også kalt komplementærfrekvensen, kommer i nærheten av omformerens egenfrekvens, kan en liten forstyrrelse være nok til at store pendlinger bygger seg opp over tid. Dette kalles selveksitering på grunn av asynkrongeneratoreffekter og er knyttet til forhold bestemt av synkronmaskinens konstruksjon. Fenomenet er ikke ukjent i den vanlige energiforsyningen og er for jernbane studert iMal:Tr.
Rullende materiell
Beskrivelse av lokomotivene
For enklest mulig hastighetsregulering av togene ble det i Norge og Sverige valgt elektrifisering med lav frekvens. På den måten kunne en benytte såkalte serie vekselstrømsmotorer som i utgangspunktet er en likestrømsmotor med anker og felt i serie og hvor hastigheten er proporsjonal med spenningen over motoren. Denne motortypen kjennes f. eks. fra alminnelig håndverktøy. Spenningsreguleringen ble utført ved hjelp av trinnkopling på lokomotivets hovedtransformator, først på lavspentsiden og senere på høyspentsiden for å redusere strømmen som måtte brytes. Eksempel på slike trinnkoplerlokomotiver fremdeles er i bruk er NSB/CargoNet El 14.
Ettersom utviklingen av halvlederkomponenter skred frem ble det utviklet lokomotiver med likestrømsmotorer hvor ankerstrømmen ble likerettet ved hjelp av en diodebro. På grunn av strømmens bølgeform kalles motorene gjerne for bølgestrømsmotorer. Spenningsreguleringen foregikk fremdeles ved hjelp av trinnkopling på hovedtransformatoren. Eksempel på slike diodelokomotiver som fremdeles er i bruk er Hector Rail BR 161 (tidligere NSB El15).
Likeretting av strømmen ved hjelp av tyristorer var et stort fremskritt siden spenningen nå kunne reguleres kontinuerlig ved utstyring av halvlederne. På grunn av stort forbruk av reaktiv effekt og produksjon av overharmoniske strømmer er mange av tyristorlokomotivene utstyrt med et kapasitivt filter. Elektronisk styring av trekkraften gir også muligheter for bedre adhesjonsutnyttelse siden trekkraften ikke må reguleres i trinn. Eksempel på tyristormateriell som fremdeles er i bruk NSB type 69, NSB/CargoNet El16 og svenske Rc-lokomotiver.
Utviklingen av kraftelektronikk og styringsmuligheter for denne gjorde at det på 80-tallet var mulig å ta i bruk den enkle og robuste asynkronmotoren. Togets hastighet gis da av frekvensen til spenningen over motoren gitt av motorstrømretteren. Likespenningen inn på motorstrømretteren gis av en nettstrømretter, og i DC-linken mellom disse sitter et lite filter for glatting og energilagring siden effekten overføres i enfasesystemet med en frekvens på 33 1/3 Hz. Operasjon av strømretterne i alle fire kvadranter gir mulighet for både tilbakemating av bremseenergi og styring av reaktiv effekt. Slike lokomotiver kalles gjerne nettstrømretterlokomotiver eller asynkronlokomotiv . Utviklingen av halvlederteknologien har gått fra tyristorer med slukkekretser (NSB El17) til GTO-tyristorer (Gate Turn Of) (NSB El18 og type 73) til IGBT (Insulated Gate Bipolar Transistor) (NSB type 72). Eksempel på hovedstrømskrets med de viktigste reguleringsparameterne i et slikt lokomotiv er vist i figur 14.10.
Mer detaljer informasjon om lokomotiver og deres elektriske oppbygning og virkemåte kan finnes i [6].
Repeterende lastendringer
I nyere lokomotiver, både tyristor- og asynkronlokomotiver, finnes det ulike styringer som regulerer effekten diskontinuerlig, for eksempel
- adhesjonskontrollen gjennom plutselig nedregulering av motormoment for å hindre at hjul slipper og
- strømbegrensning for å hindre sammenbrudd i kontaktledningsspenningen (se avsnitt 7.2 i [EN 50388]) (se avsnitt 3)
Slik inngripen provoserer energiforsyningen til å svare med en sprangrespons hvilket ikke er kritisk alene. Men dersom lastendringer repeteres med en frekvens som sammenfaller med kraftsystemets resonansfrekvenser for øvrig kan lavfrekvente pendlinger oppstå.
Det var adhesjonskontrollen som var årsaken til de lavfrekvente pendlingene som ble observert ved bruk av El 18 ved Oppdal omformer i 1996-1997. Figur 14.11 viser målt enfaseeffekt ved sliring sammen med tilsvarende forsterket trefaseeffekt. Problemene ble løst ved en endring av reguleringen på lokomotivene i 1999. Etter dette har det vært vanlig at alt nytt materiell blir testet for å avdekke uheldig regulering, for eksempel NSB type 72 [6], NSB type 73 [6] og MTAB IORE [6]. Testene utføres ved dårlig adhesjon (glatte skinner) og ved svak energiforsyning (lav installert ytelse i matestasjonen og med stor avstand til toget).
Tilbakekoblingseffekter (feedback loop effects)
I enfasesystemer kan en forenklet si at effekten leveres til lokomotivet i pakker hver halvperiode av nettfrekvensen (i 16 2/3 Hz nett er perioden 30 ms). Innen hvert slik periode (eller tidsvindu) bør både spenning og strøm ha mest mulig sinusform. Dersom lokomotivet endrer effektopptaket sitt, må trege ytre reguleringssløyfer styre de raske indre reguleringssløyfene som prøver å lage sinusformen til strømmen som toget trekker. Det betyr at effektreguleringen i lokomotivet må være tregere enn nettfrekvensen. På grunn av denne nødvendige tidsforsinkelsen har alle asynkronlokomotiver med nettstrømrettere en dynamisk oppførsel med tilbakekoblingseffekter slik som omtalt i avsnitt 2.3.2.
Slike effekter er naturlig for alle slike reguleringssystemer og kan være småsignalustabilt og dermed selveksiterende. Det er derfor viktig med behørig design og parametrisering av lokomotivet ut i fra hvilket system det skal operere i. Alle slike effekter er ulineære og et elektronisk fenomen. Tilsvarende effekter kan også oppstå mellom roterende og statiske omformerstasjoner.
Symptomer på fenomenet er gjerne amplitude- og/eller fasemodulering av linjestrøm og -spenning, effekt- og momentpendlinger og rotorpendlinger i roterende omformeraggregater. Resultatet er ofte rykk i lokomotivet eller at det ikke vil fungere i det hele tatt slik som erfart med NSB type 72 under spesielle matesituasjoner. Ved design av en traksjonsutrustning er det viktig å ta hensyn til dette sammen med infrastrukturens egenskaper (typisk spenning, overharmoniske, kontaktledningsimpedans) og planlagte driftsbetingelser. Ved idriftsettelse av lokomotivet er det viktig å teste at reguleringsutrustningen fungerer riktig.
Høy linjeimpedans (ved nettfrekvens) øker faren for tilbakekoblingseffekter siden denne virker som en forsterkning i reguleringssløyfene siden den er med på å bestemme spenningsfallet mellom matepunkt og lokomotiv. Samtidig gjør linjeimpedansen at vinkelen til spenningen på lokomotivets strømavtaker endres.
I lokomotivets nettstrømretter er det en egen reguleringssløyfe kalt faselåst sløyfe (phase locked loop – PLL) som justerer strømretterens frekvens og fase riktig i forhold til nettfrekvensen. Endring av spenningens vinkel kan oppfattes som en (midlertidig) endring av nettfrekvensen og kan ved gjentatte endringer være vanskelig å forholde seg til for PLL. Roterende omformeraggregater som pendler (roterer vekselvis fortere og senere enn synkront turtall) kan forverre situasjonen. Riktig innstilling av en PLL kan være vanskelig fordi overharmoniske i linjespenningen gjør det nødvendig med filtrering og som dermed gir en tidsforsinkelse på målingen.
Problemet kjennes ofte igjen ved at bare moderat økning av effekten fører til stort spenningsfall og at en får inntrykk av at spenningen hopper opp og ned. Lokomotivet kan begynne å rykke/riste og eller ikke virke i det hele tatt slik som NSB type 72 før forbedringene i 2004. Stort spenningsfall på grunn av høy linjeimpedans fører også gjerne til lav tilgjengelig effekt på grunn av strømbegrensningen ved synkende spenning gitt i EN 50388 (se avsnitt 3.3) selv uten uheldig design av reguleringen, men situasjonen er da også stabil. Problemene blir gjerne større ved flere tog på en strekning samtidig ettersom alles effekttrekk virker inn på spenningen.
Dette problemet oppleves oftere i Norge og Sverige på grunn av den til tider høye kontaktledningsimpedansen og svake matingen (lav ytelse i omformerstasjoner med dårlig dempede roterende aggregater) i forhold til andre land. Derfor er det viktig at riktig impedans og omformere tas hensyn til i designprosessen sammen med antall tog i trafikk samtidig.
Figur 12 viser et eksempel på hvordan ustabilitet ved tilbakekoblingseffekter kan oppstå sammen med en dårlig dempet roterende omformer over 60 km kontaktledning. Etter en økning i togets aktive effekt på ca 75 kW dempes ikke pendlingene ut, men forsterkes og systemet er blir ustabilt. Tilsvarende ustabilitet er også observert i Zürich i Sveits uten dårlige dempede roterende omformere.
Elektrisk Resonansustabilitet
Innledning
Like før påske i 1995 opplevde en i Sveits gjentatte og på det tidspunktet uforklarlige stopp i all togtrafikk rundt storbyen Zürich. Et stort antall lokomotiver av type Re 450 benyttet i persontrafikk og et antall nye universallokomotiver av type Re 460 (medlem av LOK2000-familien sammen med blant annet NSB sin El 18) stoppet helt opp samtidig. Både Re 450 og Re 460 er utstyrt med firekvadrant nettstrømrettere.
I september samme år opplevde en en tilsvarende totalstopp i andre og større deler av Sveits. Re 460-lokomotivene var dominerende i trafikk på det tidspunktet og alle sammen stoppet samtidig på grunn av for høy 100 Hz-komponent i linjestrømmen. Samtidig observerte en spenningsvariasjoner med frekvens på 165 Hz og spenning på over 2 kV. En så at problemene gjerne oppsto ved gitte situasjoner i trafikken – lørdag formiddag: Liten trafikk, mange nye Re 460 lokomotiver og få gamle trinnkoplerlokomotiver.
En fant tidlig ut at disse fenomenene hadde å gjøre med samspillet mellom kraftsystemet og lokomotivene. Problemet ble etter hvert løst ved å endre på programvaren som styrer nettstrømretterne i Re 460. Mer om hendelsene i Sveits kan finnes i [6] og [7].
Dette kapittelet gir en innføring i de fysiske fenomenene i forbindelse med elektrisk resonansustabilitet, eller lineær stabilitet som det også har blitt kalt. Kapittelet forteller også hvordan og hvorfor disse fenomenene oppstår i kraftsystem for jernbane og hvordan de påvirkes. Fenomenene som beskrives her oppstår normalt i frekvensområdet 3-5 ganger nominell frekvens og høyere.
Elektriske resonanser i kraftsystemet
Kraftsystemet består av ulike komponenter som elektrisk kan representeres ved hjelp av resistanser R, induktanser L, kapasitanser C eller kombinasjoner av disse. Fenomenene omtalt i dette avsnittet sogner til ”elektriske fenomener” vist i figur 1. Figur 13 er hentet fra [6] og viser hvordan disse kan fordele seg i et kraftsystem for jernbane:
- Linjer består av en resistans og en induktans, men har også en strøkapasitans mot jord
- Synkronmaskiner (roterende omformere) med tilhørende transformatorer består i hovedsak av induktanser, men også noe resistans og kapasitans
- Lokomotiver kan se ut som en resistans, induktans eller en kapasitans alt etter utforming og styring
- Statiske omformere kan se ut som en resistans, induktans eller en kapasitans alt etter utforming og styring (ikke vist i figuren)
Sett inn i nettet vil en fra et punkt kunne se en ekvivalent elektrisk krets der induktanser og kapasitanser står i både serie og parallell mot jord. I et nett med en roterende omformer og en lang linje vil en fra 15 kV samleskinne i omformerstasjonen kunne se en ekvivalentkrets som vist i figur 14: En kapasitans (linjens strøkapasitans) i parallell med synkronmaskinen og transformatorens resistans og reaktans. Dette kalles for en praktisk resonanskrets og er egentlig en parallellresonanskrets. Sett fra toget, eller nærmere bestemt togets nettstrømretter, vil en i tillegg se togets transformatorimpedans i serie.
For signaler påtrykt mellom kontaktledning og jord fra for eksempel en omformer eller et lokomotiv, vil en se forskjellig impedans i ekvivalentkretsen avhengig av signalets frekvens. Det er vanlig i disse betraktningene å benytte begrepet admittans som er den inverse av impedansen og måles i Siemens eller Mho framfor impedans. Ved å kikke inn i en elektrisk krets, det være seg eksempelet over eller for eksempel et lokomotiv, vil en altså kunne se en frekvensavhengig admittans som kalles inputadmittansen. Alle tre komponentene, R, L og C, er frekvensavhengige. For en gitt frekvens kan admittansen akkurat som impedansen Z=R+jX uttrykkes som en kompleks størrelse som Y=G+jB der G kalles konduktans og B kalles suceptans.
Induktansen og kapasitansen vil utveksle energi lagret som magnetisk energi som i en spole og elektrisk energi som i en kondensator. For bestemte frekvenser vil suceptansen i spolen og kondensatoren være i et slikt størrelsesforhold at admittansen vil oppleves som rent ohmsk, det vil si at den imaginære delen av admittansen er lik 0. I slike tilfeller har vi resonans og denne frekvensen kalles derfor for resonansfrekvens.
I dette tilfellet, figur 14, kan resonansfrekvensen beregnes ved følgende formel hvor vi ser at jo større R, L, og C blir, jo lavere blir resonansfrekvensen:
I figur 15 er vist admittansen i amplitude og fase for en serie resonanskrets og en parallell resonanskrets (også kalt en praktisk resonanskrets) som funksjon av frekvensen. Ved resonans er admittansens fase lik 0 slik som forklart over. I begge disse tilfellene går kretsene fra å være induktive til kapasitive eller motsatt ved resonansen, men å krysse 0-linjen er ikke noen betingelse for at resonans skal oppstå. Vi ser også at ved serieresonans er admittansens absoluttverdi høy (lik lav impedans) og ved parallellresonans vil admittansens størrelse være lav (lik høy impedans).
Resistansen R i kretsen virker i tillegg som en demping av energipendlingene mellom L og C i og med at den kan lede energi ut av systemet gjennom varme. Uten dempingen vil eventuelle pendlinger bare bli stående og aldri dø ut. Naturlig demping i systemet er virvelstrømmer (eng.:”eddy currents”) i synkronmaskiner og transformatorer som er frekvensavhengig og blir mindre ved lavere frekvens. Demping i form av parallellresistanser er veldig liten i kraftsystemer for jernbane, men eksisterer for eksempel gjennom togvarme og gjennom lekkstrømmer over isolatorene for høyspenningskomponenter/-linjer, spesielt i fuktig vær.
Vanlig kontaktledning (ofte omtalt som konvensjonelt kontaktledningsanlegg) har normalt laveste resonansfrekvens i området 800-1500 Hz. Men lange linjer, svak mating eller bruk av kabler kan redusere laveste resonansfrekvens under dette området.
Figur 16 viser hvordan absoluttverdien av admittansen sett inn i et autotransformatorsystem på forskjellige steder i nettet (A, T1, T3 osv) varierer som funksjon av frekvensen. Resonanser er merket av med ringer på kurvene. Figurene er hentet fra [6] og beregningene er utført for to omformerstasjoner med 120 km kontaktledning og AT-ledninger (positiv- og negativleder) mellom. I høyre figur er det introdusert 10 km med kabler for AT-ledningene i forhold til venstre figur. Dette øker kapasitansen i systemet og reduserer laveste resonansfrekvens fra 430 Hz til 275 Hz.
På figur 16 til høyre ser vi at for alle stedene i systemet finnes en felles resonans like under 500 Hz. Dette kalles en global resonans. Ved litt lavere frekvens ser en at det kun er punktene midt mellom omformerstasjonene som har resonansfrekvenser, dette kalles en lokal resonans. Vi ser at dempingen er lavere ved den globale resonansen enn ved den lokale rett til høyre.
Den spesifikke kapasitansen i et system er nærmest uavhengig av spenningen mens absoluttverdien av generator- og transformatorimpedanser er proporsjonal med kvadratet av spenningsnivået (men konstant i per unit verdier). Derfor er den laveste resonansfrekvensen i et kraftsystem omvent proporsjonal med systemspenningen. Det vil si at fjernlednings- og autotransformatorsystemer derfor er mer kritisk i forhold til elektrisk resonansustabilitet enn konvensjonell kontaktledning. Seksjoner med kabler i slike systemer er svært kritiske.
Kondensatorbatterier er imidlertid mindre kritiske. Seriekondensatorbatterier har så stor kapasitans at den resulterende resonansfrekvensen gjerne kommer under 50 Hz og de virker nesten som en kortslutning for høyere frekvenser. Ved høy kompenseringsgrad kan resonansfrekvensen bli så lav at en kan få problemer med lavfrekvente pendlinger, se avsnitt 4.2.3. Parallellkondensatorbatterier har alltid en induktans i serie og gir typisk resonansfrekvenser under 70 Hz. De virker som en induktans for høyere frekvenser.
Lokomotiver som eksiterer resonansene
Moderne lokomotiver med nettstrømrettere (fire kvadrant kraftelektronikkomformere) kan være eksitasjonskilder for de elektriske resonansene i et kraftsystem. Styringen av nettstrømretteren reagerer på endringer i linjespenningen med små uungåelige tidsforsinkelser, for eksempel for å forme strømmen som en sinuskurve uten overharmoniske uavhengig av spenningen. Forsinkelsene er uunngåelige på grunn av mikroprosessortid og puls/bredde-moduleringen. Disse fenomenene faller inn under betegnelsen ”elektroniske fenomener” i figur 1.
På samme måte som for kraftsystemet kan en plotte frekvensresponsen for et slikt lokomotiv i form av inputadmittansen. Et eksempel på en slik er vist i figur 17. Dersom lokomotivet ved en frekvens har en admittans som har fasevinkel over/under ±π/2 (90˚) mottar det ikke lenger energi ved denne frekvensen, men produserer isteden energi. Dette kalles at lokomotivet er aktivt ved denne frekvensen og er markert med gult på figuren. Av eksempelet i figur 17 ser vi at lokomotivet blant annet er aktivt ved ca. 30 Hz, og ved flere andre intervaller oppover.
Den samme frekvensresponsen er vist i figur 18 for det komplekse admittansplanet. I gult område er lokomotivet aktivt. De fire hovedretningene i det komplekse admittansplanet er:
- 0 grader: lokomotivet virker som en ren resistans og tar energi ut av systemet og oppfører seg som en passiv komponent
- -90 grader: lokomotivet virker som en induktans og utveksler reaktiv energi med linjen
- 90 grader: lokomotivet virker som en kapasitans
- -180 grader: lokomotivet er ”negativ ohmsk” eller aktivt og produserer energi ved den gitte frekvensen med en gang en spenning er påtrykt.
Frekvensresponsen for nettstrømretterlokomotiver er uavhengig av driftstilfellet (belastning, hastighet, traksjon/bremsing osv.). Det er i hovedsak nettstrømretteren som er av betydning i forhold til lokomotivets oppførsel. Grunnen er at motorstrømretteren i lokomotivet ligger ”skjult” bak DC-linken. Andre typer lokomotiver enn nettstrømretterlokmotiver er som regel passive for alle frekvenser, men det finnes unntak.
Ofte er det ikke ønskelig at et lokomotiv produserer strømmer med gitte frekvenser, for eksempel rundt 95 og 105 Hz som er de frekvensene tradisjonelle norske sporfelt arbeider ved. Dette kan unngås i lokomotivet ved hjelp av såkalt anticontrol og medfører at en får et aktivt område i frekvens rett under det frekvensområdet en prøver å undertrykke.
I Norge og Sverige er det innført et krav til nye lokomotiver at de ikke skal være aktive over 87 Hz.
Inputadmittansen for et lokomotiv kan beregnes og måles. Beregningene krever at en har tilgang til særdeles detaljert informasjon om styringen av lokomotivet. Ved høyere frekvenser spiller selv mindre tidsforsinkelser i f. eks. elektronikkortene som styrer krafthalvlederne en rolle, så i praksis er det neppe mulig å oppnå presise resultater på bakgrunn av beregninger alene. Ved måling derimot kan en ved å injisere spenninger med ulike frekvenser overlagret grunnfrekvensen registrerer lokomotivets respons på disse, det vil si inputadmittansen. Denne ”sveipen” over det aktuelle frekvensområdet kan for eksempel gjøres av et vanlig lokomotiv med en programvare for nettstrømretteren spesielt programmert for dette. En tredje mulighet er simulering i en realtidssimulator med ”hardware-in-the-loop”, d. v. s. at det virkelige styrings- og reguleringssystem fra lokomotivet kombineres med en signalprosessor som kjører et program som simulerer effektkretsene (forsyning, transformator, DC-mellemkress, etc.).
Informasjon om eksisterende kjøretøys aktive egenskaper er gitt i Teknisk regelverk/Banestrømforsyning/Prosjektering_og_bygging/Kraftsystem/Vedlegg/Kompatibilitetsstudie steg 1-7 (Informativt)#Characterisation of existing rolling stock.
Lokomotiver med passive filter
Lokomotiver med passive filter, ofte tyristorlokomotiver, har også en innvirkning på den elektriske resonansustabiliteten. De passive filterne representerer en ekstra kapasitans i systemet som reduserer resonansfrekvensen. Mest kritisk er NSB El 16 og de svenske Rc-lokomotivene med et filter på 0,6 MVAr ved 15 kV. Dette filteret er både for filtrering av overharmoniske og forbedring av effektfaktoren (cos phi) og omtales gjerne som telefilter. De eldste versjonene av NSB tp 69 har også noen mindre passive filter for filtrering av overharmoniske. Nettstrømretterlokomotiver kan også ustyres med passive filter (f. eks. NSB El17 og SJ X2000).
Overharmoniske
Dette kapittelet har så langt omhandlet de oscillasjoner som involverer lokomotivets reguleringssystem og som oppstår når inputadmittansen har en kritisk vinkel (lokomotivet er aktivt) og kraftsystemet. Det kan imidlertid også oppstå tilsynelatende lignende resonanser og oscillasjoner uten at reguleringssystemet i lokomotivet er involvert på grunn av nettstrømretterens overharmoniske komponenter. Disse oscillasjonene er ikke ustabilitet i snever reguleringsteknisk forstand med tilbakekobling og forsterkning som bygger seg opp som forklart i avsnitt 2.3.2 (lukket sløyfe), men en eksitasjon av en resonans uten tilbakekobling (åpen sløyfe). Men på grunn av at de overharmoniske spenningene kan anta høye amplituder (flere kV) er konsekvensen minst like stor som ved elektriske resonansustabilitet. Fenomenet er oppleves ofte i 50 Hz strømforsyning til tog.
Statiske omformere
Statiske omformere for jernbane er normalt utstyrt med passive filter på enfasesiden for å redusere produksjonen av overharmoniske strømmer. Disse filterne har også resonanser som kan bli eksitert til svigninger av aktive lokomotiver, men slik resonans er ofte mindre kritisk fordi filterne gjerne inneholder dempemotstander.
På den annen side, statiske PWM-omformere har den samme strukturen som nettstrømretterne i lokomotiver, men siden de oppfører seg på en litt annen måte (spenningskilde framfor strømkilde) er de mindre kritiske med hensyn på raske tilbakekoblingseffekter og tilhørende ustabiliteter.
Resonansustabilitet
I dette avsnittet skal vi se hvordan et kraftsystem kan eksiteres til elektrisk resonans på grunn av et aktivt lokomotiv og et lokomotiv med passivt filter. I dette tilfellet er det elektriske og elektroniske fenomener som virker ved samme frekvens og som gir ustabiliteten. Alle figurene er hentet fra [6].
Figur 19 viser frekvensresponsen for en halv roterende omformer Q38 (5,8 MVA). En ser at den er uten resonanser og nesten helt induktiv i hele frekvensområdet. Ettersom frekvensen øker ser vi at admittansen blir stadig mindre og fasevinkelen kryper nærmere –π/2 (-90˚). Den elektriske ekvivalenten av omformeren er tidligere vist i figur 14. Med en halv menes at ytelsen til aggregatet er halvert ved at impedansen er doblet. Det er ikke noen kontaktledning med strøkapasitanser i dette viste eksempelet.
Rett ved omformeren plasseres så et lokomotiv type NSB El18 som har en inputadmittans som vist i figur 20. Vi ser at lokomotivet er aktivt i frekvensområdet 75-84 Hz. Systemet er likevel stabilt siden det ikke er noen resonansfrekvenser som kan eksiteres, dette er vist i figur 21.
Sammen med den roterende omformeren og El 18-lokomotivet plasseres så et lokomotiv type Rc 4 som på samme måte som El 16 har telefilterkondensatorer på 0,6 MVAr. Det introduserer en resonans i systemet rundt 80 Hz. Denne resonansen eksiteres av at El 18 er aktiv ved denne frekvensen og resultatet blir ustabilt som vist i figur 22 hvor faseresponsen passerer ±π/2. Vi ser at admittansen er lav ved denne frekvensen, hvilket tyder på en parallellresonans.
Telefilterkondensatorene introduserer også flere andre resonansfrekvenser i systemet, rett under 100 Hz og rett under 200 Hz. Ved sistenevnte resonansfrekvens er admittansen høy, noe som tyder på en serieresonans.
Ustabiliteten, det vil si energipendlingene mellom de elektriske komponentene gir overspenninger som enten løser eller ødelegger overspenningsvern. I lokomotiver og statiske omformerstasjoner vil en kunne merke ustabiliteten ved at vern, for eksempel 100 Hz-vern, løser. Pendlingene kan også føre til overoppheting av dempemotstander i forbindelse med passive filter. En kan også oppleve at signal og sikringsanlegget påvirkes. Det er innlysende at dette kan føre til problemer for togtrafikken.
Hvordan undersøke stabiliteten
Studie av stabiliteten i forhold til elektriske resonanser kan i hovedsak deles inn i to typer. Den enkleste er kalt ”separation approach” og innebærer en undersøkelse av resonansfrekvensene i kraftsystemet som vist i avsnitt 5.2 og inputadmittansen til lokomotivene som skal trafikkere i systemet som vist i avsnitt 5.3. Dersom laveste resonansfrekvens i systemet (inkludert eventuelle passive filter i lokomotiver osv) er høyere enn den høyeste frekvensen som lokomotivene som skal trafikkere i systemet er aktiv, vil ikke resonanser kunne eksiteres og ustabilitet ikke være noe problem. I eksempelet i avsnitt 5.7 er en slik undersøkelse tilstrekkelig for å finne ut at ustabilitet kan oppstå.
Dersom en ikke er sikker på at laveste resonansfrekvens i systemet er høyere enn den høyeste frekvensen hvor et lokomotiv er aktivt må en bruke en mer arbeidskrevende metode kalt ”complete approach”. Fremdeles må en kjenne inputadmittansen for både kraftsystemet og lokomotivene som skal trafikkere banen. Men en må nå beregne eller simulere den endelige admittansen i hele systemet inkludert lokomotivene for alle situasjoner som kan oppstå. Det vil si at en må plassere lokomotivene i kraftsystemet på relevante plasser. Dette er arbeidsomt fordi en kan forvente nærmest uendelig mange kombinasjoner av lokomotiver, plasseringer, koblingssituasjoner i nettet, omformeraggregater i drift osv. Ved undersøkelse av stabiliteten ved leveransen av flytogene til NSB Gardermobanen ble det utført beregning av stabiliteten i 450 000 ulike driftsituasjoner. Likevel er plasseringen mindre viktig i AT-system ettersom overføringsimpedansen er så lav.
Figur 23 viser et eksempel på ”complete approach” fra studiene som ble utført i forbindelse med pilotutbyggingen av autotransformatorsystemet på Sørlandsbanen mellom Kristiansand og Stavanger. Spesielt her er at det er mange tunneler som krever at en legger positiv- og negativleder i kabel. Øverst i figurene (”line”) vises konfigurasjonen av kraftsystemet med AT- eller BT-system samt antall omformeraggregater i de ulike stasjonene i drift. Antall lokomotiver av hver type (El 16, tp 72, BR 189 og X5) er variert for de ulike simuleringene. Gul rute angir at situasjonen er stabil og rød rute angir at situasjonen er ustabil.
En ser at uten El 16 med sine telefilterkondensatorer er alle kombinasjonene av annet materiell stabilt. Ved økende antall El 16 skal det mindre til for at ustabilitet oppstår. Flere lokomotiver av de andre typene reduserer imidlertid induktansen i systemet (flere tog i parallell), noe som er med på å øke resonansfrekvensene.
Teoretiske beregninger og simuleringer bør alltid verifiseres med målinger.
Oppsummert kan følgende fremgangsmetode benyttes for å undersøke om det kan oppstå elektrisk resonansustabilitet:
- Definer grense: Definer fl lik den høyeste frekvensen kraftelektronikkomponenter (kjøretøy eller omformerstasjoner) kan være aktive basert på avsnitt 5.3, minimum 87 Hz som er kravet til nye komponenter.
- Forenklet resonansberegning: Estimer grovt den laveste elektriske resonansfrekvensen fres i kraftsystemet basert på formelen i avsnitt 5.2. For enkelthetsskyld kan R settes lik 0. Vedlegg B i NEK TS 50238-2:2010 gir input på hvordan beregne L og C. Dersom fres > 2*fl kan en konkludere med at det er svært liten fare for ustabilitet. Se nærmere beskrivelse i Overslagsberegning for resonansstabilitet.
- Separate approach: Dersom fres < 2*fl bør det etableres en mer nøyaktig modell av kraftsystemet uten tog for beregning av resonansfrekvensene. Dersom fres > fl er det liten fare for ustabilitet med mindre det forventes trafikk med kjøretøy med særlige kapsitive filter (eks. Rc og El16 med telefilter, eller motorvognsett med høyspentkabler på taket). Da bør denne kapasitansen hensyntas i beregningen, alternativt må det legges til grunn margin.
- Complete approach: Dersom det ikke er mulig å overholde fres > fl må kraftelektronikkomponentenes karakteristiske frekvensrespons tas med i betraktning. Kraftsystemet har noe naturlig demping gjennom resistanser, og denne dempingen kan være tilstrekkelig til å hindre ustabilitet selv om kraftelektronikkomponenten er aktiv ved en resonansfrekvens. Tilnærmingen kan deles angrepsmåter:
- Full Complete approach hvor det plasseres inn tog i kraftsystemmodellen (for eksempel den som er etablert i punkt 3)
- Mini-Complete approach hvor en med kunnskapen om dempingen i nettet (for eksempel funnet i punkt 3) gjør prinsipielle vurderinger av hvor mange tog av hver type i ulike kombinasjoner som må til for å gjøre nettet ustabilt. Det vil si sammenligne nettets positive demping med togenes eventuelle negative demping ved forventede resonansfrekvenser.
Hvordan sikre stabilitet og kompatibilitet
Et optimalt, eller i det minste tilfredsstillende, samspill mellom nye lokomotiver og eksisterende lokomotiver og jernbane infrastruktur er en kompleks oppgave. Lokomotivene blir kontinuerlig utviklet for å bedre ytelsen og redusere kostnadene. Lang levetid for både lokomotiver og infrastrukturinstallasjoner gir at mange forskjellige teknologier må passe sammen. Forskjellig grad av emisjon og immunitet mot uregelmessigheter og forstyrrelser gir ekstra utfordringer. Leverandøren av lokomotivet, togselskapet og infrastrukturforvalter har ofte forskjellige krav med tanke på optimalisering.
Manglende kompatibilitet mellom lokomotiver og infrastruktur oppdages ofte ved at ting ikke virker eller oppfører seg som de skal. I verste fall virker de ikke i det hele tatt. Dette fører gjerne først til driftsforstyrrelser og videre til unødvendige ekstrakostnader. I verste konsekvens kan det føre til skader på rullende materiell og infrastruktur. Ny infrastruktur kan påvirke eksisterende lokomotiver og vice versa.
Det er spesielt viktig å være observant på at stabilitetsproblemer lett kan oppstå
- i svak banestrømforsyning (for eksempel høy kontaktledningsimpedans og dårlig dempede roterende omformere)
- der uvanlige tekniske løsninger er benyttet
- der en ikke har dokumentasjon på eksisterende anlegg og lokomotiver og derfor ikke vet nøyaktig oppførsel
- i prosjekter der sluttbruker er ukjent eller ny eller i prosjekter hvor erfaring fra tidligere tilsvarende prosjekter mangler
Som et første skritt er det derfor viktig å få tak i tilstrekkelig informasjon om både infrastruktur og lokomotiver som trafikkerer infrastrukturen. Det er også viktig å ha tydelige krav for aksept av nye lokomotiver. Både leverandøren av lokomotivet, togselskapet og infrastrukturforvalteren bør så tidlig som mulig sette seg ned sammen for å utarbeide en plan for hvordan stabilitet og kompatibilitet skal sikres. Det er viktig at en samarbeider og har en gjensidig forståelse for hverandres ulike krav og begrensninger helt fra starten av et prosjekt. Lavfrekvente pendlinger og tilhørende ustabilitet er et typisk eksempel der felles forståelse er nødvendig ettersom metodikk for undersøkelse av dette samt klare målbare akseptkrav ikke er etablert.
Det har foreløpig ikke vært mulig å definere helt klare og sikre krav mot ustabilitet og inkompatibilitet. En stabilitetsstudie for nye lokomotiver eller endring av infrastruktur er innført i standarden [EN 50388] kapittel 10.2. Stegene i en slik sjekk er vist i figur 24. Det er ikke nødvendigvis slik at alle stegene må gjennomføres. Det viktigste er at mulighetene for ustabilitet og inkompatibilitet kartlegges. Dersom det ikke avdekkes noen risiko for problemer er det en grei konklusjon og avslutning på sjekken. Dersom en ser at problemer kan oppstå må en sette opp en plan for hvordan de ulike punktene skal undersøkes, rettes og sjekkes ut.
For å gi hint og tips om hvordan en skal komme i gang med en slik sjekk samt hva en bør være observant på, er det lagd et dokument som beskriver en form for beste praksis for å nå kompatiblitet
Litteraturhenvisning
1. T. Toftevaag, M. Pálsson, O. Rokseth. Measurements in Oppdal converter station with tests of NSB's Class 72 - Low frequency oscillations during acceleration and regenerative braking on track with bad adhesion, SINTEF Energy Research November 2002
2. T. Toftevaag, M. T. Pálsson. Målinger i Oppdal omformerstasjon i forbindelse med testkjøring av krengetoget (BM 73) – Måleopplegg, resultater og analyser, Notat SINTEF Energy Research, 2000-02-25
3. T. Toftevaag, M. Pálsson, O. Rokseth, B. Gustavsen. Measurements in Rombak converter station in connection with tests of MTAB's new IOre locomotive on Ofotbanen - Low frequency oscillations, regeneration and harmonics, SINTEF Energy Research November 2000
4. R. Lundberg. Lärobok I elektroteknik för Statens Järnvägers personal – Del IV Omformarstationer, Svenska Tryckeriaktiebolaget Stockholm 1959 (581155)
5. P. Sture. Elektrifisering av jernbanen i Norge – Den teknisk-historiske utvikling i tidsrommet 1908=>1992, Nesodden 1996/1998
6. Rätselhafte Lokomotivstörungen im Raum Zürich, Schweizer Eisenbahn-Revue 5/1995
7. M. Meyer, J. Schöning.Netzstabilität in grossen Bahnnetzen, Schweizer Eisenbahn-Revue und Eisenbahn-Revue International 7-8/1999
8. M. Meyer, J. Schöning. Power Supply Stability in Large Railway Networks, Presentasjon på ESCARV 2000-07-07
9. S. Menth. Jernbaneverket AT system model structure and frequency responses, Emkamatik dokument 05-0088
10. M. Meyer. Jernbaneverket: AT system stability analysis, emkamatik document 05-0089
11. M. Meyer. AT system stability analysis for Sørlandsbanen: Resonance and stability calculation, Emkamatik dokument 06-0129
12. S. Danielsen, F. Martinsen. Gjennomgang av redundans- og dimensjoneringskriteriet for banestrømforsyning
13. S. Danielsen. Utredning av stabilitetsgrense ved kapasitiv kompensering – Utredning i forbindelse med gjennomgang av prEN 50 388, BanePartner på oppdrag fra Jernbaneverket Hovedkontoret Elkraft. 2002-12-16. Prosjekt nummer 292254
14. E. Friman et.al. NIM NES R10 Requirements on rolling stock in Norway and Sweden regarding EMC with the electrical infrastructure and coordination with the power supply and other vehicles
15. M. Meyer. AT system stability analysis for Sørlandsbanen: Structure of calculation models, Emkamatik dokument 06
16. M. Meyer. AT system stability analysis for Sørlandsbanen: Resonance and stability calculation, Emkamatik dokument 06-0129 versjon 3 2006-08-23
17. M. Meyer. Jernbaneverket / Banverket: Best practice to reach compatibility between rail vehicles and power supply, Emkamatik dokument 06-0105 versjon 1 2006-02-03
18. S. Menth og M. Meyer. Low frequency power oscillations in electric railway systems, Elektrische Bahnen 104 (2006)
19. S. Østlund. Elektrisk Traktion, KTH 2005
20. P. Kundur. Power System Stability and Control, McGraw Hill 1993
21. S. Menth og M. Meyer. Rotating Converters BV / JBV: Description of Simulation Model,Emkamatik dokument 06-0132 versjon 1 from 18.9.2006
22. Banverket og Jernbaneverket. Requirements on rolling stock in Norway and Sweden regarding EMC with the electrical infrastructure and coordination with the power supply and other vehicles, NIM NES R10
23. F. Johannessen og P. C. Bruu. Stabilitet i NSBs nett, Diplomoppgave ved NTNU desember 1996
24. T. Toftevaag, M. P. Pálsson, O. Rokseth. Målinger under prøveinstallasjon av statiske magnetisering med dempetilsats (PSS) samt analyse av resultater – Oppdal omformerstasjon Mars 1999, Sintef Energiforskning TR F 4986
25. S. Danielsen. Pågående arbeider i PhD-studiet Effekt-/spenningstabilitet i kraftsystem for jernbane, NTNU