El 18 på Flåmsbana: Forskjell mellom sideversjoner
(fjernet numberheadings) |
|||
| (141 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
== Innledning == | == Innledning == | ||
| Linje 176: | Linje 175: | ||
==== | ==== Kraft ved hjulslag på tresviller på elastisk underlag ==== | ||
Målinger av tester i bl. annet. ORE D 161 viser at ved en aksellast på 22,50 tonn så øker slagkraften med 30 kN/mm for tresviller på elastisk underlag ved framføringshastighet på 30 km/h. | Målinger av tester i bl. annet. ORE D 161 viser at ved en aksellast på 22,50 tonn så øker slagkraften med 30 kN/mm for tresviller på elastisk underlag ved framføringshastighet på 30 km/h. | ||
| Linje 186: | Linje 185: | ||
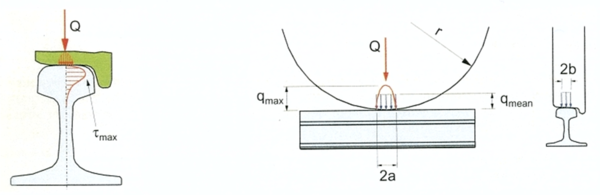
==== | ==== Støtkrefter i skinneskjøter i lasket spor ==== | ||
Overgang fra eksisterende lokomotiv El 17 med aksellast 16 tonn til nytt lokomotiv El 18 med aksellast 21,3 tonn gir en økning i støtkreftene P1 og P2 på om lag en faktor lik 1,15 for hastighet V = 30 km/h. Økningen i lasten har en faktor lik 1,33. | Overgang fra eksisterende lokomotiv El 17 med aksellast 16 tonn til nytt lokomotiv El 18 med aksellast 21,3 tonn gir en økning i støtkreftene P1 og P2 på om lag en faktor lik 1,15 for hastighet V = 30 km/h. Økningen i lasten har en faktor lik 1,33. | ||
| Linje 195: | Linje 194: | ||
==== | ==== Belastning i svevende skjøter i lasket spor ==== | ||
For svevende skjøter opptrer store belastninger i stållaskene vurdert etter en konservativ metode. Det er imidlertid nødvendig å være oppmerksom på at laskene har anlegg mot overkant skinnefot og underkant skinnehode. Stållaskene opptrer dermed ikke som teoretisk virkende fritt bærende bjelker. Store belastninger kan imidlertid føre til utmatting ved skruehullene på grunn av dynamiske belastninger. | For svevende skjøter opptrer store belastninger i stållaskene vurdert etter en konservativ metode. Det er imidlertid nødvendig å være oppmerksom på at laskene har anlegg mot overkant skinnefot og underkant skinnehode. Stållaskene opptrer dermed ikke som teoretisk virkende fritt bærende bjelker. Store belastninger kan imidlertid føre til utmatting ved skruehullene på grunn av dynamiske belastninger. | ||
==== | ==== Belastning i sporveksler (krysspiss og braketter) ==== | ||
En enkel betraktning viser at støtkraft i krysspiss vil øke med en faktor lik 1,15 ved overgang fra El 17 til El 18. Ved ofte passeringer må det forventes hurtigere nedbrytning av krysspiss. | En enkel betraktning viser at støtkraft i krysspiss vil øke med en faktor lik 1,15 ved overgang fra El 17 til El 18. Ved ofte passeringer må det forventes hurtigere nedbrytning av krysspiss. | ||
| Linje 207: | Linje 206: | ||
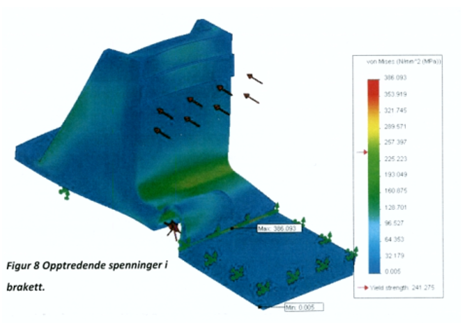
I områder for ledeskinner kan det forekomme at ledeskinnen blir belastet bare på horisontale krefter da de vertikale kreftene fra hjulbane overføres til hovedskinne. Ledeskinnene er festet til underliggende sville og blir dermed utkraget. Ved stor horisontal belastning kan det derfor inntreffe brudd i brakettfot ved små sporveksler. Det er ikke mulig å konkretisere om dette vil skje; sannsynligheten er meget lav. Men brakettene må overvåkes. | I områder for ledeskinner kan det forekomme at ledeskinnen blir belastet bare på horisontale krefter da de vertikale kreftene fra hjulbane overføres til hovedskinne. Ledeskinnene er festet til underliggende sville og blir dermed utkraget. Ved stor horisontal belastning kan det derfor inntreffe brudd i brakettfot ved små sporveksler. Det er ikke mulig å konkretisere om dette vil skje; sannsynligheten er meget lav. Men brakettene må overvåkes. | ||
=== Belastning på skinnehodet === | === Belastning på skinnehodet === | ||
| Linje 325: | Linje 322: | ||
Det vurderes imidlertid at kapasitet mot sideforskyvning er tilstrekkelig god nok. | Det vurderes imidlertid at kapasitet mot sideforskyvning er tilstrekkelig god nok. | ||
mangel av informasjon er beregnet (Y/Q)<sub>j, a, max</sub> i dynamisk tilstand: | |||
=== Vurdering av (Y/Q) ved dynamisk belastning === | |||
I mangel av informasjon er beregnet (Y/Q)<sub>j, a, max</sub> i dynamisk tilstand: | |||
<math> | |||
\left({Y\over Q}\right)_{j,a,max}={96,00 \over 184,00}=0,52<0,80 | |||
</math> | |||
| Linje 334: | Linje 344: | ||
Det er ingen fare for avsporing. | Det er ingen fare for avsporing. | ||
=== Vurdering av (Y/Q) ved statisk belastning ved lav hastighet (hjulavlastning) === | |||
Det legges til grunn at El 18 har et hjulprofil som gir flensvinkel på 68° - 70°. For en friksjonskoeffisient μ = 0,36 blir | |||
<math> | |||
\left({Y\over Q}\right)_{ytre}=1,20 | |||
</math> | |||
| Linje 351: | Linje 367: | ||
Det eksisterer ingen fare for avsporing i kvasistatisk tilstand under forutsetning av at El 18 har foreskrevne verdier mht. torsjonsegenskaper. | Det eksisterer ingen fare for avsporing i kvasistatisk tilstand under forutsetning av at El 18 har foreskrevne verdier mht. torsjonsegenskaper. | ||
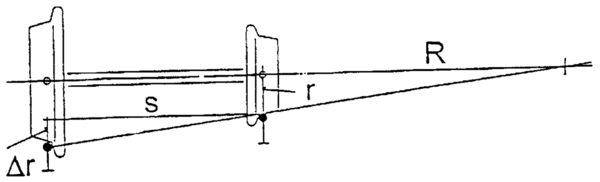
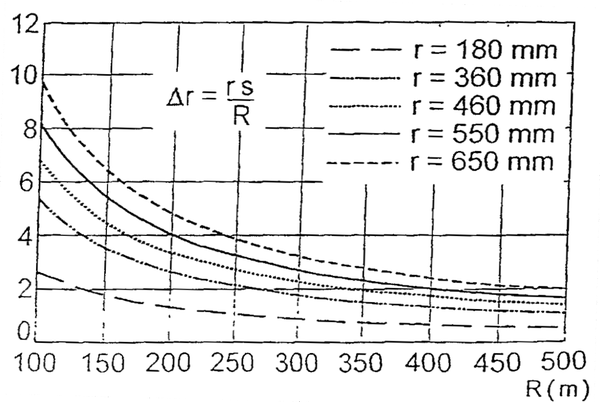
=== Delta r (∆r)-kriteriet === | |||
=== Delta r kriteriet === | |||
| Linje 361: | Linje 375: | ||
Det blir bedt om en redegjørelse om i hvilken grad NSB iverksetter tiltak for best mulig overholdelse av kriteriet. | Det blir bedt om en redegjørelse om i hvilken grad NSB iverksetter tiltak for best mulig overholdelse av kriteriet. | ||
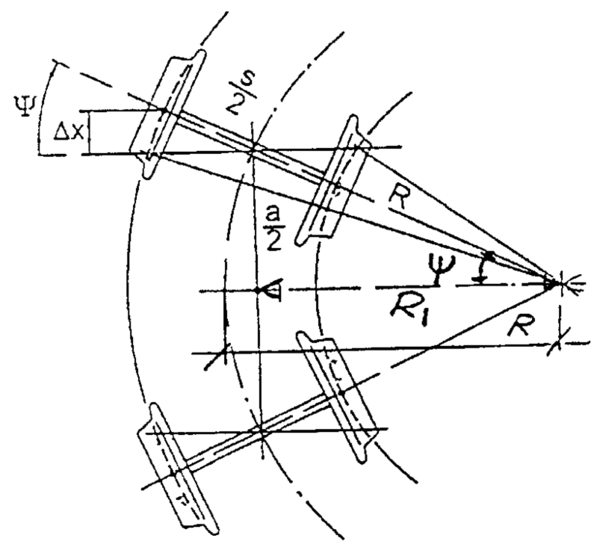
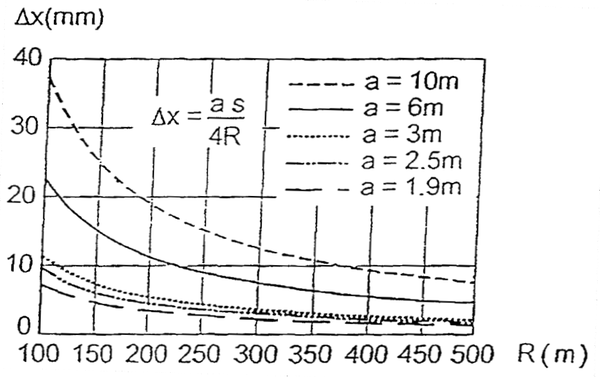
=== Vurdering av radiell styringsindeks === | === Vurdering av radiell styringsindeks === | ||
| Linje 423: | Linje 436: | ||
En togstamme bestående av et lokomotiv av type El 17 og 3 vogner har en samlet vekt: | En togstamme bestående av et lokomotiv av type El 17 og 3 vogner har en samlet vekt: | ||
<math> | |||
m_{LOK \ og \ 3VOGNER}=16000\cdot4+1,10\cdot3\cdot4\cdot11750=219100kg | |||
</math> | |||
En togstamme bestående av et lokomotiv av type El 18 og 3 vogner har en samlet vekt: | En togstamme bestående av et lokomotiv av type El 18 og 3 vogner har en samlet vekt: | ||
<math> | |||
m_{LOK \ og \ 3VOGNER}=21300\cdot4+1,10\cdot3\cdot4\cdot11750=2402300kg | |||
</math> | |||
| Linje 768: | Linje 796: | ||
[[Fil:Figur 0x.x.PNG|600px|thumb||center|<caption> </caption>]] | |||
== Kort beskrivelse av El 18 == | == Kort beskrivelse av El 18 == | ||
| Linje 778: | Linje 810: | ||
[[Fil:Figur_02.PNG|600px|thumb||center|<caption> Figur 6.1 El 18</caption>]] | |||
| Linje 783: | Linje 816: | ||
| Linje 806: | Linje 838: | ||
Det legges til grunn at vognene med passasjerer har en aksellast lik 11.750 kg. | Det legges til grunn at vognene med passasjerer har en aksellast lik 11.750 kg. | ||
== Kapasitet på bruer og fyllinger == | == Kapasitet på bruer og fyllinger == | ||
| Linje 818: | Linje 849: | ||
<math> | |||
{\sum P\over l}={85,20\over18,50}=4,61 \ tonn/m<6,60 \ tonn/m | |||
</math> | |||
| Linje 827: | Linje 862: | ||
<math> | |||
{P\over a}={21,30\over2,80}=7,60 \ tonn/m<11,00 \ tonn/m | |||
</math> | |||
| Linje 836: | Linje 875: | ||
<math> | |||
{P\over a}={21,30\over2,35}=9,06 \ tonn/m<15,00 \ tonn/m | |||
</math> | |||
El 18 tilfredsstiller alle krav til last på bruer. | |||
=== Stabilitet i fyllinger og skjæringer === | === Stabilitet i fyllinger og skjæringer === | ||
| Linje 869: | Linje 910: | ||
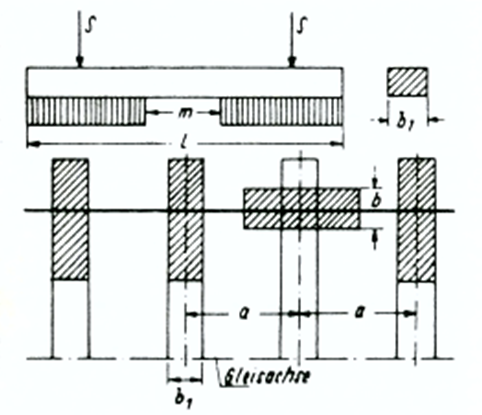
[[Fil:Figur_03.PNG|600px|thumb||center|<caption> Figur 8.1 Prinsipp for oppbygning av tverrsvilleoverbygning</caption>]] | |||
| Linje 919: | Linje 960: | ||
<math> | |||
b={(a-m)\cdot b_1\over 2\cdot l}={F\over 2l} \ (mm) | |||
</math> | |||
Figur 8.2 illustrerer aspektet. | |||
< | <math> | ||
F=(l-m)\cdot b_1=2\cdot b\cdot a | |||
</math> | |||
[[Fil:Figur_08.2ex.PNG|600px|thumb||center|<caption> Figur 8.2 Omvandling av tverrsvilleoverbygning til fiktiv langsvilleoverbygning</caption>]] | |||
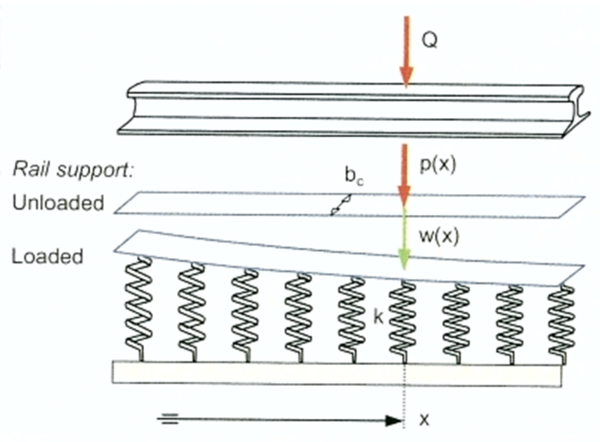
=== Etablering av statisk fjærstivhet (punktstivhet) k, statisk ballaststivhet (linjestivhet) β og statisk ballastsiffer (flatestivhet) C; sammenhenger === | === Etablering av statisk fjærstivhet (punktstivhet) k, statisk ballaststivhet (linjestivhet) β og statisk ballastsiffer (flatestivhet) C; sammenhenger === | ||
| Linje 950: | Linje 997: | ||
<math> | |||
\beta={k\over a} \left( {N\over mm^2}\right) | |||
</math> | |||
Omregning gir: | |||
Ballaststivheten beskriver dermed en linjefjær i vertikalplanet. Termen a er avstanden mellom svillene. | |||
Ballastsifferet defineres: | |||
<math> | |||
C=2\cdot {k\over a} \left( {{N\over mm} \over mm^2}={N\over mm^3}\right) | |||
</math> | |||
Ballastsifferet blir en bladfjær. Termen F er belastet flate av sville mot ballastlaget. | |||
Omregning gir: | |||
<math> | |||
k={F\over2}\cdot C \ \left( mm^2\cdot{N\over mm^3}={N\over mm}\right) | |||
</math> | |||
Ballaststivheten uttrykt ved balastsifferet C: | Ballaststivheten uttrykt ved balastsifferet C: | ||
<math> | |||
\beta={k\over a}=C\cdot {1\over2}\cdot {F\over a} \left( {N\over mm^2}\right) | |||
</math> | |||
| Linje 969: | Linje 1 045: | ||
[[Fil:Figur_08.3.PNG|600px|thumb||center|<caption> Figur 8.3 Definisjon av fjærkarakteristikker i overbygningen</caption>]] | |||
| Linje 985: | Linje 1 062: | ||
[[Fil:Figur_08.4.PNG|600px|thumb||center|<caption> Figur 8.4 Vinkelkoeffisienten α beskriver ballastsifferet C</caption>]] | |||
< | |||
=== Etablering av elastiske sjikt === | === Etablering av elastiske sjikt === | ||
| Linje 1 007: | Linje 1 081: | ||
<math> | |||
{1\over k}={1\over k_{rp}}+{1\over k_b} | |||
</math> | |||
<math> | |||
k={k_{rp}\cdot k_b\over k_{rp}+k_b} \ \left({N\over mm}\right) | |||
</math> | |||
<math> | |||
C_{TOTAL} = {k\over {F\over 2}}=2\cdot {k\over F} \ \left( {N/mm\over mm^2}={N\over mm^3}\right) | |||
</math> | |||
| Linje 1 028: | Linje 1 108: | ||
Termen k<sub>rp</sub> er stivheten til gummielementet i mellomlegget. Videre er kb stivheten i ballastlaget med underbygning. | |||
Ballaststivheten β blir tilsvarende: | |||
<math> | |||
\beta={\beta_{rp}\cdot \beta_b\over \beta_b+\beta_{rp}} \ \left({N\over mm^2}\right) | |||
</math> | |||
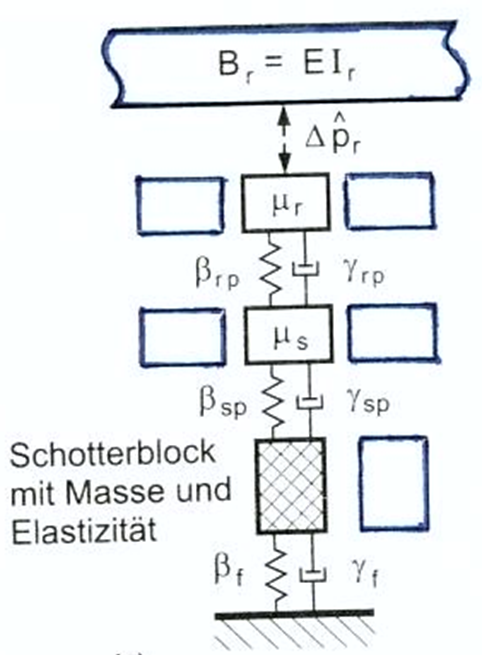
I en avansert overbygningskonstruksjon kan svillene bli påmontert gummimatter i underkant av sville. Dermed eksisterer et 3. elastisk sjikt som er svillematten. Under forutsetning av at ballastlaget med underbygning beskrives som en ballastblokk med masse og elastisitet, blir formelverket tilsvarende (antakelse om seriekobling av fjærelementene): | |||
<math> | |||
{1\over k}={1\over k_{rp}}+{1\over k_{sp}}+{1\over k_{b}} | |||
</math> | |||
| Linje 1 054: | Linje 1 137: | ||
<math> | |||
k={k_{rp}\cdot k_{sp}\cdot k_b\over k_{sp}\cdot k_b+k_{rp}\cdot k{b}+k_{rp}\cdot k_{sp}} | |||
</math> | |||
| Linje 1 062: | Linje 1 147: | ||
Her betyr: | |||
< | Stivhet til mellomlegget i gummi: k<sub>rp</sub> | ||
Stivhet til svillematte: k<sub>sp</sub> | |||
Stivhet til ballastlaget mot underbygning: k<sub>b</sub> | |||
<math> | |||
C = {k\over {F\over 2}}=2\cdot {k\over F} \ \left( {N/mm\over mm^2}={N\over mm^3}\right) | |||
</math> | |||
Ved betraktning med ballaststivheten β blir tilsvarende: | |||
<math> | |||
\beta={\beta_{rp}\cdot \beta_{sp}\cdot \beta_f\over \beta_{sp}\cdot \beta_f+\beta_{rp}\cdot \beta_{f}+\beta_{rp}\cdot \beta_{sp}} | |||
</math> | |||
En variant beskrives ved anvendelse av ballastmatter som legges i formasjonsplanet. Dersom ballastsjiktet mellom en svillematte og ballastmatte betraktes som en blokk uten elastiske egenskaper, etableres også i dette tilfellet et system med 3 elastiske sjikt. Det nederste elastiske sjiktet består da av ballastmatte og undergrunn med stivhet k<sub>f</sub>. Formlene blir tilsvarende som over: | |||
| Linje 1 101: | Linje 1 189: | ||
Termen β<sup>f</sup> er stivheten til ballastmattene lagt i formasjonsplanet; dvs. at undergrunnen også har innflytelse. Figur 8.5 gir en oversikt over aspektet. | |||
[[Fil:Figur_08.5.PNG|600px|thumb||center|<caption> Figur 8.5 Overbygning med 3 elastiske sjikt; termen ϒ er demping av sjiktene</caption>]] | |||
En siste variant beskrives ved mellomlegg i gummi mellom skinne og sville og ballastmatte lagt i formasjonsplanet; dvs. at elastisk svillematte ikke påføres underside av sville. I stedet påføres et relativt hardt underlag i gummi som tjener til å skåne betong og pukk for spissbelastninger. | |||
Da blir ligningene: | |||
<math> | |||
k={k_{rp}\cdot k_{bp}\over k_{rp}+k_{bp}} \ \left({N\over mm}\right) | |||
</math> | |||
<math> | |||
\beta={\beta_{rp}\cdot \beta_{bp}\over \beta_{rp}+\beta_{bp}} \ \left({N\over mm^2}\right) | |||
</math> | |||
=== Beregning av dynamisk ballastsiffer eller dynamisk ballaststivhet === | |||
< | Det statiske ballastsifferet C (N/mm<sup>3</sup>), eventuelt den statiske ballaststivhet β (N/mm<sup>2</sup>) for overbygningen gjelder bare for et materiell som står stille. | ||
Ved framføring av materiellet i sporet med hastighet endrer sporets karakteristikker seg slik at det må benyttes tilsvarende dynamiske parametere C<sub>DYN</sub>, eventuelt β<sub>DYN</sub>. Det er forbundet med omfangsrike algoritmer i en kompleks analyse for å beregne disse parameterne. Aspektet har sammenheng med at også dempingsegenskapene og opptredende frekvenser må bli tatt hensyn til. Imidlertid ved lave hastigheter vil ikke endringene bli så framtredende. | |||
I denne studien vil ved dimensjonering bli benyttet de statiske parametere. Senere vil en beregning for de dynamiske parametere bli fulgt opp. | |||
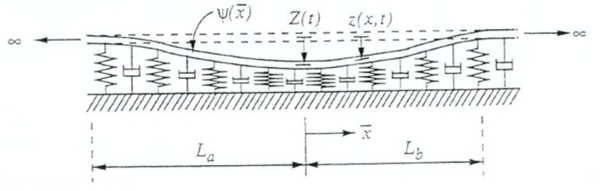
=== Interessante frekvensområder i vekselvirking rullende materiell – spor === | |||
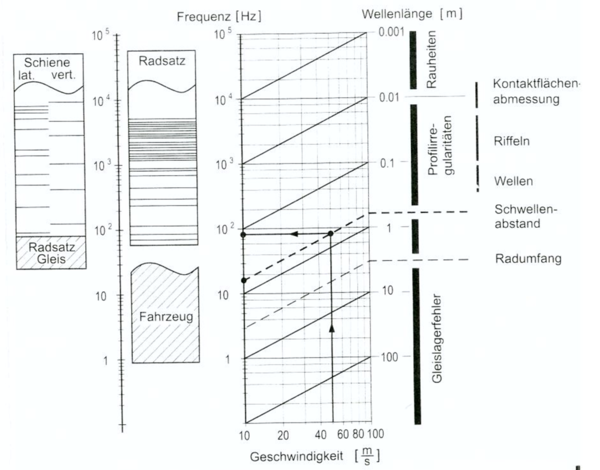
Det skal diskuteres interessante frekvensområder som oppstår i en vekselvirking av rullende materiell og spor for Malmbanen ved tunge aksellaster. Figur 8.6 illustrerer aspektet. | |||
[[Fil:Figur_08.6.PNG|600px|thumb||center|<caption> Figur 8.6 Sammenheng mellom kjørehastighet i (m/s), opptredende frekvenser i (Hz) og bølgelengder i (m) i sporet; noen frekvenser er uten betydning; andre frekvenser gir resonans</caption>]] | |||
Det oppstår en mengde ulike frekvenser med forskjellige bølgelengder som påvirker sporet i samtidighet ved framføring av togmateriell. Aspektet fører til dynamiske belastninger på sporkonstruksjonen: | |||
I | *Tilfelle I: Rifler og bølger på skinnehodet | ||
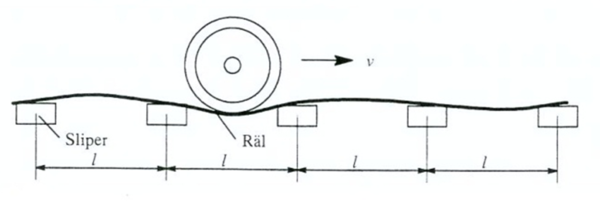
*Tilfelle II: Svilleavstand (sporet har en annen elastisitet over sville enn mellom svillene) | |||
*Tilfelle III: Bøyelinje ved nedsenkning av skinne under belastning på grunn av elastisitet | |||
*Tilfelle IV: Globale bølgelengder i sporet med vertikale amplituder; disse betraktes i området 3 – 25 m | |||
Parametere som bidrar til nedsenkning av sporet og som forårsaker dynamiske belastninger og i særlig grad til tunge akselerasjonsbevegelser av skinnene under påvirkning fra rullende materiell: | |||
*Tilfelle V: Hengende sviller | |||
Tilfellene er illustrert i figurene 8.7, 8.8, 8.9, 8.10 og 8.11. | |||
Det er synlig at algoritmene blir svært omfattende dersom alle tilfellene skal modelleres for samtidighet i opptreden (som skjer i sann tilstand). Det blir vanligvis søkt etter forenklinger. | |||
[[Fil:Figur_08.7.PNG|600px|thumb||center|<caption> Figur 8.7 Tilfelle I: Rifler og bølger på skinnehodet; lengder er ca. 40 – 60 mm, hastighet v = 8,33 m/s (30 km/h) medfører f = ca. 160 Hz; hastighet v = 16,7 m/s (60 km/h) medfører f = ca. 330 Hz</caption>]] | |||
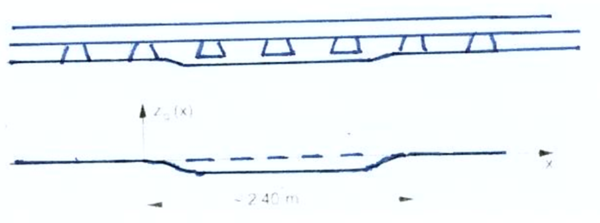
[[Fil:Figur_08.8.PNG|600px|thumb||center|<caption> Figur 8.8 Tilfellet II: Sporets elastisitet er stivere over sville enn mellom svillene; l = 0,64 m; hastighet v = 8,33 m/s (V = 30 km/h); f = ca. 13 Hz (abrupt endring i elastisitet medfører dynamiske krefter) </caption>]] | |||
[[Fil:Figur_08.9.PNG|600px|thumb||center|<caption> Figur 8.9 Tilfellet III: Sporkonstruksjonens elastisitet medfører en bøyelinje beskrevet ved den karakteristiske lengde L gjennom den vertikale belastning; L antas normalt i intervallet 0,60 – 0,80 m for Flåmsbana; samlet lengde er 2,36 · L = 2000 – 2300 mm </caption>]] | |||
[[Fil:Figur_08.10.PNG|600px|thumb||center|<caption> Figur 8.10 Tilfellet IV: Global bølgelengde i sporet; vurderes normalt i området 3 – 25 m </caption>]] | |||
| Linje 1 213: | Linje 1 300: | ||
[[Fil:Figur_08.11.PNG|600px|thumb||center|<caption> Figur 8.11 Tilfellet V: Hengende sviller </caption>]] | |||
| Linje 1 220: | Linje 1 307: | ||
I tillegg vurderes støtkrefter på grunn av hjulslag. På elastisk spor medfører støtet en kraftig kortvarig økning av bøyemomentet på skinnen. I et frosset spor blir slaget teoretisk uendelig stort og aspektet kan føre til skinnebrudd. | |||
Ovennevnte aspekter krever omfattende modelleringer for beregning av resulterende beskatningsparametere. Da ulike bøyelinjer med forskjellige lengder opptrer under tilstandene i samtidighet, må ideelt matematiske Fourier rekker anvendes for nøyaktig modellering. Dette gjennomføres ikke i dette beregningsheftet. Det blir derimot søkt etter forenklinger. | |||
Det skisseres 2 modeller for beregning av belastning på komponenter på sporet med grunnlag i bøyemomenter på skinner: | |||
*DAF for dynamisk belastning basert på Zimmermanns metode | |||
*Dynamisk modell som anvender vognens karakteristikker og irregulariteter i sporet | |||
=== Enkel modell (DAF MODELL basert på Zimmermanns metode) === | |||
Det er utviklet en modell for betraktning av en tilleggsfaktor for beregning av dynamisk vertikalkraft med utgangspunkt i den statiske hjulkraft. Den hastighetsavhengige faktor er forskjellig for passasjervogner og godsvogner. Videre influerer vurdering av sporkvaliteten og hastigheten på relevant faktor. | |||
Beregninger kan gjennomføres uten algebracomputersystemer (lommekalkulator er tilstrekkelig). | |||
Følgende ligning blir benyttet: | |||
<math> | |||
Q_{DYN}=Q_0\cdot (1+DAF) | |||
</math> | |||
Termen Q<sup>0</sup> er statisk kraft fra hjul. I kurvekjøring benyttes kvasistatisk hjulkraft på grunn av omlagring av kreftene: | |||
<math> | |||
Q_{DYN}=Q_{KV.STAT.}\cdot (1+DAF) | |||
</math> | |||
DAF er betegnelse for dynamisk innflytelsesfaktor (Dynamic Amplification Factor). | |||
Det beregnes først en hastighetsavhengig faktor: | |||
<math> | |||
\Phi=1 \ \ V<60 \ km/h | |||
</math> | |||
<math> | |||
\Phi=1+0,50\cdot {(V-60)\over 190} \ \ \ passasjertog \ \ og \ \ lok \ \ 60 \le V \le 200 \ km/h | |||
</math> | |||
<math> | |||
\Phi=1+0,50\cdot {(V-60)\over 80} \ \ \ godsvogner \ \ 60\le V \le 140 \ km/h | |||
</math> | |||
Dernest vurderes sporets standard: | |||
<math> | |||
\phi = 0,10 \ - \ 0,15 \ \ \ meget \ god \ sporkvalitet \ ( krav \ for \ hoyhastighetsbaner) | |||
</math> | |||
<math> | |||
\phi = 0,20 \ \ \ normal \ sporkvalitet \ for \ konvensjonelle baner | |||
</math> | |||
<math> | |||
\phi = 0,25 \ - \ 0,30 \ \ \ for \ baner\ med \ lav \ sporkvalitetsniva | |||
</math> | |||
Produktet av hastighetsavhengig faktor og sporets standard definerer faktor for standardavviket σ. | |||
Alternativt kan faktor for standardavviket beregnes ved kjent vertikalfeil s i sporet: | |||
<math> | |||
\sigma=\left({s\cdot \Phi \over 5}\right) | |||
</math> | |||
Endelig defineres multiplikasjonsfaktor for standardavviket: | |||
<math> | |||
t = 3 \ \ \ for \ komponenter \ i \ kontakt \ med \ hjul \ (skinner; \ befestigelse; \ sviller) | |||
</math> | |||
<math> | |||
t = 1 \ ; \ 2 \ \ \ for \ komponenter \ lengere \ vekk \ hjulet \ (ballast) | |||
</math> | |||
Dynamisk innflytelsesfaktor DAF: | |||
<math> | |||
DAF=t\cdot \sigma =t\cdot\Phi \cdot \phi | |||
</math> | |||
Den resulterende dynamiske kraft blir dermed: | |||
<math> | |||
Q_{DYN}=Q_0\cdot (1+t\cdot\sigma)=Q_0\cdot(1+t\cdot\Phi\cdot\phi) | |||
</math> | |||
<math> | |||
Q_{DYN}=Q_{KV.STAT.}\cdot (1+t\cdot\sigma)=Q_0\cdot(1+t\cdot\Phi\cdot\phi) | |||
</math> | |||
==== Formelverk for beregninger av belastning på overbygningens komponenter ==== | |||
I det etterfølgende er vist formelverket i Zimmermanns metode. | |||
Det | Det må først beregnes en grunnverdi L for langsvilleoverbygningen: | ||
<math> | |||
{ | l=\sqrt[4]{4\cdot E \cdot I_{X-X}\over b\cdot C} \ (mm) | ||
</math> | |||
Her betyr: | |||
L er grunnverdi for langsvilleoverbygning (mm) | |||
E er elastisitetsmodul for skinnestålet (N/mm<sup>2</sup>) | |||
I<sub>X-X</sub> er skinneprofilets treghetsmoment (mm<sup>4</sup>) | |||
b er medvirkende bredde av fiktiv lengdebjelke (mm) | |||
C er sporets statiske ballastsiffer (N/mm<sup>3</sup>) | |||
Anvendelse av sporets statiske ballastsiffer gjelder for togmateriell som ikke er i bevegelse. For tog i bevegelse skal det fortrinnsvis benyttes det dynamiske ballastsiffer. Det dynamiske ballastsifferet er høyere enn det statiske fordi sporet stivner litt ved framføring. Normalt antas at C<sub>DYN</sub> er 10 til 50 % høyere enn C<sub>STAT</sub>. I formelverket beskrevet under benyttes en nøytral betegnelse C. | |||
I formelverket under menes med enkeltlast bare denne lasten eller enkeltlast med et kvasistatisk tillegg ved omlagring av vertikalkrefter på ytre og indre skinnestreng på grunn av sentrifugalkraften ved framføring i kurver. | |||
Direkte under enkeltlast beregnes nedsenkning eller deformasjon av skinnen: | |||
<math> | |||
y_{0I}={Q_{0I}\over2bCL} \ (mm) | |||
</math> | |||
Direkte under enkeltlast beregnes bøyemomentet i statisk og dynamisk tilstand ved DAF: | |||
<math> | |||
M_{0I,STATISK}={Q_{0I}\cdot L\over4} \ kNm | |||
</math> | |||
<math> | |||
M_{0I,DYN}={Q_{0I}\cdot L\over4}\cdot DAF \ kNm | |||
</math> | |||
Spenning i underkant skinnefot i statisk og dynamisk tilstand: | |||
<math> | |||
\sigma_{0I,STATISK} ={M_{0I,STATISK}\over W_U} \ \left({N\over mm^2}\right) | |||
</math> | |||
<math> | |||
\sigma_{0I,DYN} ={M_{0I,DYN}\over W_U} \ \left({N\over mm^2}\right) | |||
</math> | |||
Bøyelinjens halve lengde beregnes: | |||
<math> | |||
{3\over4}\cdot\Pi\cdot L=2,36\cdot L | |||
</math> | |||
Ved lang bøyelinje vil naboaksel få innflytelse på betraktet sted for dimensjonering (vanligvis direkte under betraktet enkeltlast) og dermed på belastningen på skinne. Dette tas hensyn til ved anvendelse av koeffisienter i tabell som er blitt utledet av influenslinjer. | |||
Det etableres forholdet: | |||
<math> | |||
\xi={x\over L} | |||
</math> | |||
Termen x er avstand fra det betraktede stedet hvor hjullasten virker til et sted med avstand x fra dette stedet; x kan for eksempel beskrive avstanden mellom 2 hjulsett. | |||
For nednøyning av skinne gjelder: | |||
<math> | |||
y_{0,II}={Q_{0I}\over2bCL}+{Q_{0II}\over2bCL}\cdot\eta \ (mm) | |||
</math> | |||
For momentberegning gjelder: | |||
<math> | |||
M_{0,STATISK,II}={Q_{0I}\cdot L\over 4}+{Q_{0II}\cdot L\over 4}\cdot\mu \ (kNm) | |||
</math> | |||
Parameterne ƞ og µ kan avleses i tabeller i handbøker. | |||
Dynamiske parametere: | |||
<math> | |||
M_{0,DYN,II}=M_{0,STATISK,II}\cdot DAF \ \ kNm | |||
</math> | |||
<math> | |||
\sigma_{0,STATISK,II}={M_{0,STATISK,II}\over W_U}\ \ \left({N\over mm^2}\right) | |||
</math> | |||
<math> | |||
\sigma_{0,DYN,II}={M_{0,DYN,II}\over W_U}\ \ \left({N\over mm^2}\right) | |||
</math> | |||
Formelverk for beregning av trykk i underkant sville og i befestigelsesområdet for sville iht. Zimmermanns metode og dynamisk faktor iht. Eisenmann: | |||
Trykk mot underkant sville under enkeltlast: | |||
<math> | |||
p_{0I,STATISK} =C\cdot y_{0I} \ \ (N/mm^2) | |||
</math> | |||
<math> | |||
p_{0I,DYN}=p_{0I,STATISK}\cdot DAF \ \ (N/mm^2) | |||
</math> | |||
Dersom nabolast må betraktes, blir formelen: | |||
<math> | |||
p_{0II,STATISK}=C\cdot (y_{0,I}+y_{0,II}) \ \ (N/mm^2) | |||
</math> | |||
<math> | |||
p_{0II,DYN}=p_{0II,STATISK}\cdot(y_{0,I}+y_{0,II}) \cdot DAF \ \ (N/mm^2) | |||
</math> | |||
Belastning på sville i befestigelsesområdet i statisk og dynamisk tilstand: | |||
<math> | |||
S_{0I,STATISK} =b\cdot a\cdot p_{0I,STATISK}=b\cdot a\cdot C_{STATISK} \cdot y_{0I} | |||
</math> | |||
<math> | |||
S_{0I,DYN}=S_{0I,STATISK} \cdot DAF | |||
</math> | |||
Under hensyntagen til nabolast blir formelen: | |||
<math> | |||
S_{0II,STATISK} =b\cdot a\cdot p_{0II,STATISK}=b\cdot a\cdot C_{STATISK} \cdot (y_{0I}+y_{0II}) | |||
</math> | |||
<math> | |||
S_{0II,DYN} =b\cdot a\cdot p_{0II,DYN} | |||
</math> | |||
==== Algoritmer for relative betraktninger med utgangspunkt i referanseparametere ==== | |||
Det eksisterer matematiske avhengigheter med hensyn til bestemmende parametere i sporet i Zimmermanns metode. Utgangspunktet er gitte kjente referanseparametere. | |||
Referanseparametere er: | |||
*Treghetsmoment til skinneprofil: I<sub>REF</sub> (mm<sup>4</sup>) | |||
*Motstandsmoment til skinneprofil: W<sub>REF</sub> (mm<sup>3</sup>) | |||
*Resulterende ballastsiffer: C<sub>REF</sub> (N/mm<sup>3</sup>) | |||
*Svilleavstand: a<sub>REF</sub> (mm) | |||
*Svilleflate: F<sub>REF</sub> (mm<sup>2</sup>) | |||
Det kan påvises sammenhenger for spenning i underkant i skinnefot; i nedsenkning av skinne og trykk mot ballast fra sville som gitt i tabell 8.1. | |||
{| class="wikitable" style="text-align:center" width="900px" | |||
|+Tabell 8.1 Sammenstilling av parametere med referanseparametere | |||
|- | |||
! | |||
!K <sub>σ</sub> | |||
!K <sub>y</sub> | |||
!K <sub>p</sub> | |||
|- | |||
|I; W|| | |||
<math> | |||
\sqrt[4]{I\over I_{REF}}\cdot{W_{REF}\over W} | |||
</math> | |||
|<math> | |||
\sqrt[4]{I_{REF}\over I} | |||
</math> | |||
|<math> | |||
\sqrt[4]{I_{REF}\over I} | |||
</math> | |||
|- | |||
|C | |||
|<math> | |||
\sqrt[4]{C_{REF}\over C} | |||
</math> | |||
|<math> | |||
\sqrt[4]{\left({ C_{REF}\over C}\right)^3} | |||
</math> | |||
|<math> | |||
\sqrt[4]{C\over C_{REF}} | |||
</math> | |||
|- | |||
|a | |||
|<math> | |||
\sqrt[4]{a\over a_{REF}} | |||
</math> | |||
|<math> | |||
\sqrt[4]{\left({ a\over a_{REF}}\right)^3} | |||
</math> | |||
|<math> | |||
\sqrt[4]{\left({ a\over a_{REF}}\right)^3} | |||
</math> | |||
|- | |||
|F | |||
|<math> | |||
\sqrt[4]{F_{REF}\over F } | |||
</math> | |||
|<math> | |||
\sqrt[4]{\left({ F_{REF}\over F }\right)^3} | |||
</math> | |||
|<math> | |||
\sqrt[4]{\left({ F_{REF}\over F }\right)^3} | |||
</math> | |||
|- | |||
| | |||
|<math> | |||
\sigma=K_\sigma\cdot\sigma_{REF} | |||
</math> | |||
|<math> | |||
y=K_y\cdot y_{REF} | |||
</math> | |||
|<math> | |||
p=K_p\cdot p_{REF} | |||
</math> | |||
|} | |||
Dersom referanseverdiene er kjent, kan verdier for dimensjonerende parametere beregnes. | |||
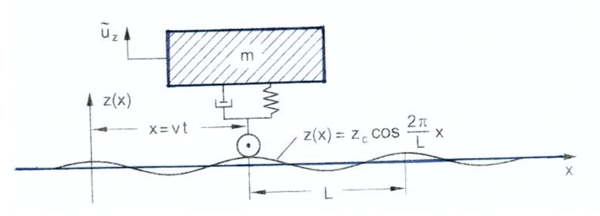
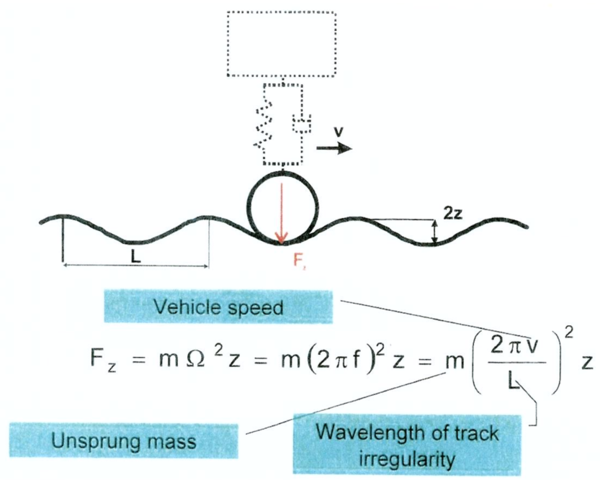
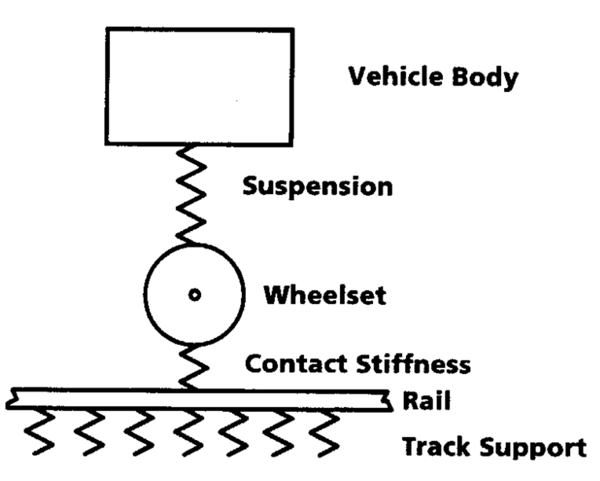
=== En modell for betraktning av frekvensrelatert opptreden av vertikalkrefter; endimensjonal modell med en frihetsgrad === | |||
En relativ enkel modell for beregning av dynamisk vertikalkraft under hensyntagen til irregulariteter definert ved bølgelengder i sporet for konstant hastighet defineres. For vognen legges det til grunn en endimensjonal modell med en frihetsgrad; dvs. en vogn med kun primæroppheng. Dette er en vanlig konstruksjon for godsvogner; dvs. at vognkasse ligger på boggiramme. Dersom det skulle være et sekundæroppheng, så ville bevegelsene til vognkasse bli så lave at det dynamiske bidraget fra vognkasse kan elimineres. Bare den statiske vekt må medtas. | |||
For vurdering av vognens påvirkning benyttes en fiktiv modell. Framgangsmåten forklares i det etterfølgende: | |||
<math> | |||
Q_{DYN}=Q_0+Q_{dLF}+Q_{dHF}=(m_c+m_w)\cdot g +m_c\cdot a_c+m_w\cdot v^2 \cdot z''+{\Delta z \over H_r(i\Omega )+H_w(i\Omega )+{1\over k_h}}+0,10\cdot Q_{HENG} | |||
</math> | |||
Her betyr følgende: | |||
Q<sub>DYN</sub> er resulterende vertikalkraft (kN) | |||
Q<sub>0</sub> er statisk hjulkraft (kN); eventuelt benyttes den kvasistatiske hjulkraft (kN) | |||
Q0 er statisk hjulkraft (kN) | |||
Q<sub>dLF</sub> er lavfrekvent dynamisk kraft forårsaket av vognkasse og boggiramme (kN) | |||
Q<sub>dHF</sub> er høyfrekvent dynamisk kraft forårsaket av uavfjæret masse til hjulsats (kN) | |||
m<sub>c</sub> er masse til vognkasse og boggi (kg) | |||
m<sub>w</sub> er uavfjæret masse til hjulsats (kg) | |||
g er tyngdens akselerasjon (m/s<sup>2</sup>) | |||
a<sub>c</sub> er akselerasjonen til vognkasse; eventuelt sammen med boggiramme (m/s<sup>2</sup>) | |||
v er framføringshastighet til vogn (m/s) | |||
er annen derivert av irregularitet av vertikal sporfeil; dvs. krumning | |||
Brøkuttrykket beskriver belastning på grunn av rifler og bølger i sporet. Det erkjennes bruk av overføringsfunksjoner. | |||
<math> | |||
{\Delta z \over H_r(i\Omega )+H_w(i\Omega )+{1\over k_h}} | |||
</math> | |||
Q<sub>HENG</sub> beskriver belastning på grunn av hengende sviller. | |||
I tillegg kan også kraft fra hjulslag virke. | |||
De enkelte leddene i formelen skal gjennomgås. | |||
==== Beregning av vognkassens akselerasjon ==== | |||
Det er greit å beregne akselerasjonen a<sub>c</sub> til vognkassen gjennom egnet formel idet det tas hensyn til vognkassens oppheng i en modell med en frihetsgrad. | |||
Først beregnes opptredende vinkelfrekvens for framføring på grunn av bølgelengden i sporet: | |||
<math> | |||
\Omega ={2\pi v\over L} \ \ (rad/s) | |||
</math> | |||
ω er vinkelfrekvens for resonans hvor c er karakteristikk for fjærstivhet og m<sub>C</sub> er masse av avfjæret vogn: | |||
<math> | |||
\omega = \sqrt {c\over m_c} \ \ (rad/s) | |||
</math> | |||
Forholdet mellom opptredende frekvens og resonansfrekvens er: | |||
<math> | |||
\eta={\Omega\over \omega} | |||
</math> | |||
| Linje 1 748: | Linje 1 990: | ||
Den relative demping D under hensyntagen til demperkarakteristikk d: | |||
<math> | |||
D={d\over2\sqrt{cm_C}} | |||
</math> | |||
| Linje 1 760: | Linje 2 004: | ||
Akselerasjonen a<sub>c</sub> beregnes under forutsetning av neglisjering av opptredende fasevinkler: | |||
<math> | |||
a_c={\eta^2\cdot \sqrt{1+(2D\eta )^2}\over \sqrt{(1-\eta^2)^2+(2D\eta )^2}}\cdot z\cdot \omega^2 | |||
</math> | |||
==== Parameter for bevegelse av uavfjæret masse ==== | |||
Parameteren kan også uttrykkes ved | |||
<math> | |||
z''=\left({2\pi\over L}\right)^2\cdot z | |||
</math> | |||
Dermed er det mulig å beregne den dynamiske kraft på skinnegangen når irregulariteten i vertikal retning i sporet ved definert bølgelengde er kjent. Termen L er bølgelengde i sporet. | |||
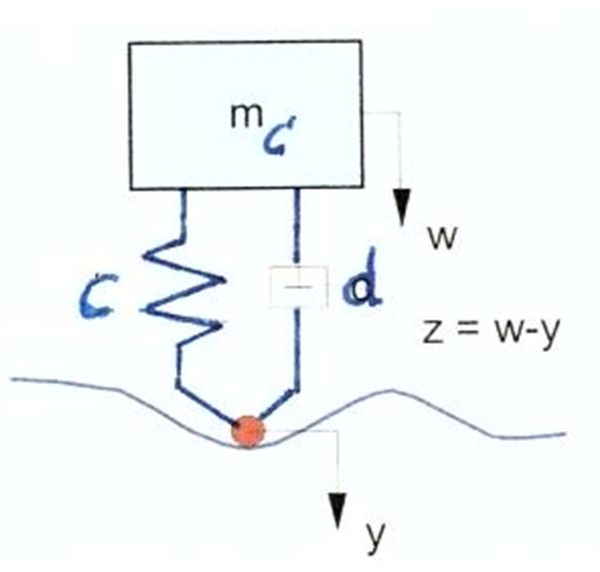
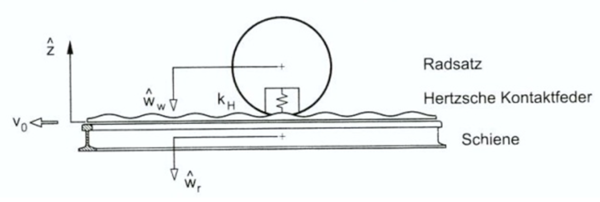
==== Modell for beregning av vertikalkraft ved irregulariteter på skinnehodet ==== | |||
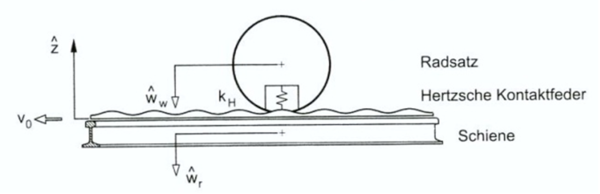
Modellen tar hensyn til sammenknytning mellom hjul og skinne over kontaktbetingelsene. Hertzian fjærstivhet i kombinasjon med sporets irregularitet blir benyttet til å definere kontaktkraften. | |||
En resulterende deformasjon blir uttrykt ved differansen i forskyvningen av hjul, skinne og irregulariteten i skinne: | |||
<math> | |||
\Delta z(t)=\Delta\omega_r(t)-\Delta\omega_\omega(t)+\Delta\delta(t) | |||
</math> | |||
Ligningen formulerer at den resulterende irregularitet kan beregnes ved en forskyvning av skinnen nedover i vertikal retning, ved en bevegelse av hjulsatsen oppover i vertikal retning og ved sammentrykking av kontaktfjæren. | |||
Det er fordelaktig å framskaffe overføringsfunksjonene da bevegelsene uttrykkes i forhold til disse. Variasjonen av kraften Q iht. irregulariteten tas med: | |||
<math> | |||
\Delta\omega_r=H_r(i\Omega )\cdot\Delta Q | |||
</math> | |||
<math> | |||
\Delta\omega_\omega=-H_r(i\Omega )\cdot\Delta Q | |||
</math> | |||
<math> | |||
\Delta\delta={1\over k_h}\cdot\Delta Q | |||
</math> | |||
| Linje 1 839: | Linje 2 095: | ||
Dermed kan den variable kraft ∆Q beregnes: | |||
<math> | |||
\Delta Q={\Delta z\over H_r(i\Omega)+H_w(i\Omega)+{1\over k_h}} | |||
</math> | |||
∆z er den målte irregularitet, H<sub>r</sub> er reseptansen for skinne (m/N), Hw er reseptansen for hjulsatsen (m/N) og k<sub>h</sub> (kN/mm) er reseptansen for Hertz kontakt. | |||
∆Q representerer variasjonen i det dynamiske krafttillegget med frekvensen | |||
<math> | |||
cos\left({2\pi v_0\over l}\right) | |||
</math> | |||
Termen l er lende av bølge på skinnehodet. | |||
Når uttrykket i parentesen er lik 1, får ∆Q sin maksimale verdi. | |||
Det framgår av ovennevnte formel at en kompleks analyse er nødvendig. Med informasjon om verdier på amplitudene, lengde l av riflene og hastigheten kan det dynamiske tillegget beregnes. | |||
Rifler og bølger vil opptre ved framføring med høye aksellaster og det regnes med et dynamisk tillegg på 10 % av aksellasten; dvs. 40 kN: | |||
<math> | |||
\Delta Q=0,10\cdot P=20 \ kN | |||
</math> | |||
Verdien er å betrakte som relativt lav; dette skyldes den lave framføringshastigheten på 60 km/h. | |||
Det vises i denne sammenheng til en artikkel i ZEVS Glaser Annalen: | |||
“Stresses in rails due to static, dynamic and thermal loadings” | |||
Artikkelen er på tysk. | |||
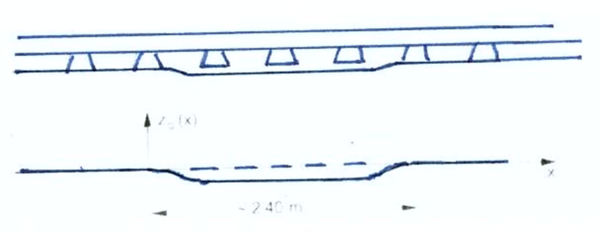
==== Hensyntagen til hengende sviller (vaskesviller) ==== | |||
Effekt av hengende sviller er økt belastning på skinner, sviller og ballast og større krefter i hjul / skinne kontaktflaten relatert til hjul skinne kontaktmekanikken. I IAVSD (International Association of Vehicle Systems Dynamics) i 2009 i Stockholm ble det presentert hva hengende sviller gir i økt belastning. Resultatene er basert på numerisk simulering. | |||
Når det gjelder selve skinnen, kan deformasjonen øke med opp til 60 % (naturlig nok) og økning av belastning i skinnefot kan bli opp til 26 %. Mest ille er imidlertid de store akselerasjonsbevegelsene til skinnene. | |||
Det regnes med et beskjedent tillegg på ca. 10 % av statisk hjulkraft. Det forutsettes at konstruksjonen og byggingen av overbygningen blir utført på en måte som gir nødvendig drenering: | |||
< | <math> | ||
Q_{HENG}=0,10\cdot Q_0 | |||
</math> | |||
==== Endelig formel ==== | |||
Den endelige formel for beregning av dynamisk vertikalkraft uttrykkes ved: | |||
<math> | |||
Q_{DYN}=Q_0+Q_{dLF}+Q_{dHF}=(m_c+m_w)\cdot g+m_c\cdot a_c+m_w\cdot v^2\cdot z''+\Delta Q+Q_{HENG} | |||
</math> | |||
<math> | |||
Q_{DYN}=Q_0+Q_{dLF}+Q_{dHF}=(m_c+m_w)\cdot g+m_c\cdot a_c+m_w\cdot v^2\cdot z''+{\Delta z\over H_r(i\Omega )+H_w(i\Omega )+{1\over k_h}}+0.10\cdot Q_{HENG} | |||
</math> | |||
| Linje 1 926: | Linje 2 203: | ||
Det gjelder: | |||
<math> | |||
z''=\left({2\pi\over L}\right)^2\cdot z | |||
</math> | |||
Dermed blir formelen: | |||
<math> | |||
Q_{DYN}=Q_0+Q_{dLF}+Q_{dHF}=(m_c+m_w)\cdot g+m_c\cdot a_c+m_w\cdot \left({2\pi v\over L}\right)^2\cdot z+{\Delta z\over H_r(i\Omega )+H_w(i\Omega )+{1\over k_h}}+0.10\cdot Q_{HENG} | |||
</math> | |||
| Linje 1 956: | Linje 2 229: | ||
En endimensjonal modell med to frihetsgrader har enda en term. Aspektet gir tilkjenne at det finnes to masser som er avfjæret. Disse er vognkasse og boggiramme. Uavfjæret masse vil være hjulsettet med hjulskivene. Formelen vil da bli: | |||
< | <math> | ||
Q_{DYN}=(m_c+m_b+m_w)\cdot g+m_c\cdot a_c+m_b\cdot a_b +m_w\cdot \left({2\pi v\over L}\right)^2\cdot z+{\Delta z\over H_r(i\Omega )+H_w(i\Omega )+{1\over k_h}}+0.10\cdot Q_{HENG} | |||
</math> | |||
==== Illustrasjon av de enkelte termer i formel ==== | |||
Første term er selvforklarende. Termen viser samlet kraft for vognkasse med boggiramme og hjulsats uttrykt ved deres masser og tyngdens akselerasjon. | |||
Figur 8.12 illustrerer term nummer 2 som beskriver det dynamiske tillegget fra vognkasse under hensyntagen til vognkassens vertikale akselerasjon. Bølgelengde med vertikal amplitude i sporet har betydning. Dette vil framgå av formelverket. | |||
[[Fil:Figur_08.12.PNG|600px|thumb||center|<caption> Figur 8.12 Bevegelse av vognkasse med primæroppheng; vognkassen får en akselerasjonsbevegelse som gir opphav til dynamisk tilleggskraft </caption>]] | |||
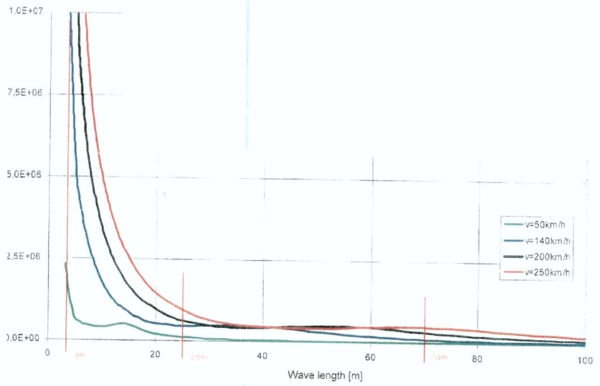
Figur 8.13 illustrerer det dynamiske tillegget fra uavfjæret masse (hjulsats) som beveger seg på et spor med vertikal sporfeil (amplitude) over en bølgelengde L (term nummer 3 i formel). Bølgelengder betraktes i området 3 – 25 m. | |||
[[Fil:Figur_08.13.PNG|600px|thumb||center|<caption> Figur 8.13 Formel for beregning av dynamisk kraft fra uavfjæret masse (hjulsats) | |||
Lengde av bølge er av betydning for størrelsen på det dynamiske tillegget fra uavfjæret masse. </caption>]] | |||
[[Fil:Figur_08.14.PNG|600px|thumb||center|<caption> Figur 8.14 Beskatningsparameter for komponenter på spor og rullende materiell som funksjon av bølgelengde i skinnene i sporet ved ulike hastigheter; for framføring i nedre hastighetsnivå (50 – 60 km/h) vil korte bølgelengder ned mot 3 m gi utslag i økt belastning </caption>]] | |||
| Linje 2 010: | Linje 2 279: | ||
Term nummer 4 beskriver en høyfrekvent bevegelse på grunn av rifler og bølger i skinnehodet. På grunn av det lave hastighetsnivået vil denne kraften uttrykt i prosent av akselkraft ikke bli alt for stor. Men på grunn av den høye aksellasten får kraften allikevel en størrelse. Figur 8.15 illustrerer situasjonen. Beregninger må gjennomføres i en kompleks analyse og dimensjonerende parametere framstilles som funksjon av hastighetsavhengige frekvenser med lengder på riflene og bølgene. | |||
[[Fil:Figur_08.15.PNG|600px|thumb||center|<caption> Figur 8.15 Formulering av den kinematiske betingelse ved kontaktbetingelsene mellom hjul og skinne; det framgår at kontaktfjær ved Hertz inngår </caption>]] | |||
Term nummer 5 er selvforklarende. Hengende sviller eller vaskesviller betyr at det ikke er fast og kontinuerlig kontakt mellom sville og ballast. Under forutsetning av tilfredsstillende dreneringsforhold og i forbindelse med pakking med etterfølgende stabilisering av sporet forventes sjeldent opptreden av hengende sviller. Det er i beregningene allikevel tatt med et lite bidrag til den dynamiske kraft. | |||
[[Fil:Figur_08.16.PNG|600px|thumb||center|<caption> Figur 8.16 Hengende sviller </caption>]] | |||
| Linje 2 038: | Linje 2 305: | ||
I tillegg kan det forekomme hjulslag på hjulbanen. Hjulslaget vil gi et kortvarig høyt spissmoment på elastisk underlag. | |||
På frosset underlag vil det opptre et uelastisk støt som gir meget høye støtkrefter. | |||
==== Formelverk for beregning av dimensjonerende parametere ==== | |||
Modellen tar hensyn til belastning på sporets komponenter som funksjon av longitudinelle bølgelengder i sporet ved beskrivelse av et cosinusspor samt rifler og bølger på skinnehodet i tillegg til opptreden av hengende sviller. | |||
Formelverket benytter ballaststivheten β i dimensjon (N/mm<sup>2</sup>). I Zimmermanns metode inngår tradisjonelt ballastsifferet C i dimensjon (N/mm<sup>3</sup>). Verdier for denne parameteren i overbygningskonstruksjonen er mer kjent for enn verdiene for ballaststivheten. | |||
I de etterfølgende beregninger vil det bli antatt verdier for C. En omregning til β blir nødvendig. Algoritmene beskrives for å anskueliggjøre sammenhengen. | |||
Det gjentas: | |||
<math> | |||
k={F\over 2}\cdot C \ \ \left({N\over mm}\right) | |||
</math> | |||
<math> | |||
\beta={k\over a}=C\cdot {F\over 2\cdot a} \ \ \left({N\over mm^2}\right) | |||
</math> | |||
Det defineres: | |||
<math> | |||
B_r=E\cdot I_{X-X} \ \ (Nmm^2) | |||
</math> | |||
Faktor utrykkes: | |||
<math> | |||
\gamma =\sqrt[4]{\beta\over 4B_r} \ \ \ (\sqrt[4]{{N\over mm^2}\over Nmm^2}=\sqrt[4]{1\over mm^4}={1\over mm}) | |||
</math> | |||
| Linje 2 094: | Linje 2 371: | ||
Termen er den inverse verdi av grunnverdi L for langsvilleoverbygningen i Zimmermanns metode: | |||
<math> | |||
\sqrt[4]{\beta\over 4B_r}=\sqrt[4]{{k\over a}\over 4\cdot E\cdot I_{X-X}}=\sqrt[4]{{F\over 2\cdot a}\cdot C\over 4\cdot E\cdot I_{X-X}}=\sqrt[4]{b\cdot C\over 4\cdot E\cdot I_{X-X}}={1\over L} \ \ \left({1\over mm}\right) | |||
</math> | |||
<math> | |||
L=\sqrt[4]{4\cdot E\cdot I_{X-X}\over b\cdot C} \ \ (mm) | |||
</math> | |||
Bøyelinjens halve lengde beregnes: | |||
<math> | |||
\left\vert x\right\vert ={3\cdot \pi \over 4\cdot \gamma} \ \ \ \left({1\over {1\over mm}}=mm\right) | |||
</math> | |||
Denne formelen sammenlignes med formel i Zimmermanns metode: | |||
<math> | |||
\left\vert x\right\vert={3\over 4}\cdot\pi\cdot{1\over\sqrt[4]{\beta\over 4\cdot B_r}}={3\over 4}\cdot\pi\cdot{1\over\sqrt[4]{b\cdot C\over 4\cdot E\cdot I_{X-X}}}={3\over 4}\cdot\pi\cdot{\sqrt[4]{4\cdot E\cdot I_{X-X}}\over\sqrt[4]{b\cdot C}} | |||
</math> | |||
<math> | |||
== | \left\vert x\right\vert={3\over 4}\cdot\pi\cdot\sqrt[4]{4\cdot E\cdot I_{X-X}\over b\cdot C}={3\over 4}\cdot\pi\cdot L | ||
</math> | |||
Det skal også demonstreres samsvar for nedbøyningsberegning. Utgangspunkt er Zimmermanns formel (på generelt grunnlag): | |||
<math> | |||
y={Q\over 2\cdot b\cdot C\cdot L}={Q\over 2\cdot b\cdot C\cdot\sqrt[4]{4\cdot E\cdot I_{X-X}\over b\cdot C}} ={Q\over\sqrt[4]16\cdot\sqrt[4]{b^4\cdot C^4\cdot 4 \cdot E\cdot I_{X-X}\over b\cdot C}} | |||
</math> | |||
<math> | |||
y= {Q\over \sqrt[4]{64\cdot E\cdot I\cdot b^3\cdot C^3}}={Q\over\sqrt[4]{64\cdot B_r\cdot \beta^3}} | |||
</math> | |||
Relasjonene er dermed bevist. | |||
Det er vist at bøyelinens halve bølgelengde blir beregnet etter samme prosedyre som for Zimmermanns metode. | |||
Dermed etableres forholdet (som for Zimmermann): | |||
<math> | |||
\xi ={x\over L} | |||
</math> | |||
Termen L er grunnverdien for en fiktiv langsvilleoverbygning beregnet etter formel i Zimmermanns metode. Det vises til denne metoden. | |||
Faktorene ƞ og µ avleses i tabell. | |||
Direkte under enkeltlast beregnes nedsenking eller deformasjon av skinnen: | |||
<math> | |||
y_{0,I}={Q_{01}\over\sqrt[4]{64\cdot B_r\cdot \beta^3}} \ \ (mm) | |||
</math> | |||
Dersom nabolast må betraktes, blir formelen: | |||
<math> | |||
y_{0,II}= {Q_{01}\over\sqrt[4]{64\cdot B_r\cdot \beta^3}} + {Q_{II}\over\sqrt[4]{64\cdot B_r\cdot \beta^3}}\cdot\eta \ \ (mm) | |||
</math> | |||
Direkte under enkeltlast beregnes bøyemomentet i statisk og dynamisk tilstand: | |||
<math> | |||
M_{0I,STATISK}=Q_{0I} \cdot\sqrt[4]{B_r\over 64\beta} \ \ \ kNm | |||
</math> | |||
For beregning av det dynamiske momentet skal strengt tatt den dynamiske ballaststivhet β<sup>DYN</sup> benyttes. Den dynamiske stivhet er litt forskjellig fra den statiske stivhet da sporet normalt stivner litt når toget framføres. I formel under er imidlertid benyttet den statiske stivhet β. Feilen er ikke særlig stor på grunn av lav hastighet. | |||
<math> | |||
M_{0I,DYN}=Q_{0I,DYN} \cdot\sqrt[4]{B_r\over 64\beta} \ \ \ kNm | |||
</math> | |||
Dersom nabolast må betraktes, blir formelen: | |||
<math> | |||
M_{0II,STATISK}=Q_{0I} \cdot\sqrt[4]{B_r\over 64\beta}+Q_{0II} \cdot\sqrt[4]{B_r\over 64\beta} \cdot\mu \ \ \ kNm | |||
</math> | |||
<math> | |||
{ | M_{0II,DYN}=Q_{0I,DYN} \cdot\sqrt[4]{B_r\over 64\beta}+Q_{0II,DYN} \cdot\sqrt[4]{B_r\over 64\beta} \cdot\mu \ \ \ kNm | ||
</math> | |||
Spenning i underkant skinnefot i statisk og dynamisk tilstand: | |||
<math> | |||
\sigma_{0I,STATISK}={M_{0I,STATISK}\over W_U} \ \ \ \left({N\over mm^2}\right) | |||
</math> | |||
<math> | |||
\sigma_{0I,DYN}={M_{0I,DYN}\over W_U} \ \ \ \left({N\over mm^2}\right) | |||
</math> | |||
Dersom nabolast må betraktes, blir formelen: | |||
<math> | |||
\sigma_{0II,STATISK}= {M_{0I,STATISK}\over W_U} + {M_{0II,STATISK}\over W_U} \ \ \ \left({N\over mm^2}\right) | |||
</math> | |||
<math> | |||
\sigma_{0II,DYN}= {M_{0I,DYN}\over W_U} + {M_{0II,DYN}\over W_U} \ \ \ \left({N\over mm^2}\right) | |||
</math> | |||
| Linje 2 334: | Linje 2 591: | ||
Den statiske og dynamiske kraft i befestigelsesområdet på sville under enkeltlast uttrykkes ved: | |||
<math> | |||
R_{0I,STATISK}=Q_{0I,STATISK}\cdot a\cdot\sqrt[4]{k\over 64\cdot B_r\cdot a}=Q_{0I,STATISK}\cdot a\cdot\sqrt[4]{k\over 64\cdot E\cdot I_{X-X}\cdot a} | |||
</math> | |||
En beregning i dynamisk tilstand krever dimensjonering i en kompleks analyse. En slik analyse medfører omfangsrike algoritmer. Analysen gjennomføres ikke her. | |||
I stedet benyttes den dynamiske kraft Q<sub>DYN</sub> beregnet ifølge den avanserte metode som tar hensyn til bølgelengder i sporet. Det anvendes kvasistatiske stivhetsparametere til sporet. Aspektet medfører en tilnærmelse. Formelen blir under enkeltlast: | |||
<math> | |||
R_{0I,DYN}=Q_{0I,DYN}\cdot a\cdot\sqrt[4]{k\over 64\cdot B_r\cdot a}=Q_{0I,DYN}\cdot a\cdot\sqrt[4]{k\over 64\cdot E\cdot I_{X-X}\cdot a} | |||
</math> | |||
| Linje 2 369: | Linje 2 621: | ||
Det foretas en dimensjonsanalyse: | |||
<math> | |||
R_{0I,DYN}=kN\cdot m\cdot\sqrt[4]{{N\over mm}\over {N\over mm^2}\cdot mm^4\cdot mm}=kN\cdot m\cdot\sqrt[4]{1\over mm^4}=kN\cdot m\cdot{1\over m}=kN | |||
</math> | |||
Formelen blir mer krevende dersom nabolast må tas med. Imidlertid gjelder uttrykket generelt: | |||
<math> | |||
R=y(0)\cdot\beta\cdot\alpha | |||
</math> | |||
Dermed blir formelen: | |||
<math> | |||
R_{0,II,DYN}= ({Q_{01}\over\sqrt[4]{64\cdot B_r\cdot \beta^3}} + {Q_{0II}\over\sqrt[4]{64\cdot B_r\cdot \beta^3}}\cdot\eta )\cdot\beta\cdot a \ \ (mm) | |||
</math> | |||
Trykket mot svillens underside utledes av R<sub>STATISK</sub> og R<sub>DYN</sub> (tilnærmede formler): | |||
<math> | |||
p_ {0I,STATISK} = {2\cdot R_{0I,STATISK}\over (l-m)\cdot b_1} | |||
</math> | |||
<math> | |||
p_ {0I,DYN} = {2\cdot R_{0I,DYN}\over (l-m)\cdot b_1} | |||
</math> | |||
Dersom nabosville tas med, blir uttrykket tilsvarende: | |||
<math> | |||
p_ {0II,STATISK} = {2\cdot R_{0II,STATISK}\over (l-m)\cdot b_1} | |||
</math> | |||
<math> | |||
p_ {0II,DYN} = {2\cdot R_{0II,DYN}\over (l-m)\cdot b_1} | |||
</math> | |||
=== Sammendrag av belastninger på skinne === | |||
Samtlige belastningsparametere beskrives. | |||
| Linje 2 450: | Linje 2 710: | ||
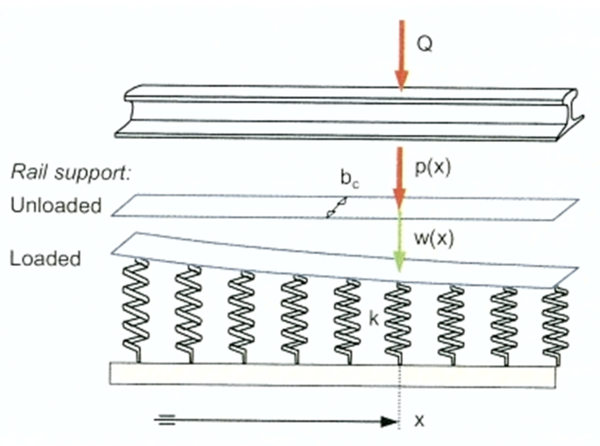
==== Skinnen betraktes som en uendelig lang bjelke på elastisk underlag ==== | |||
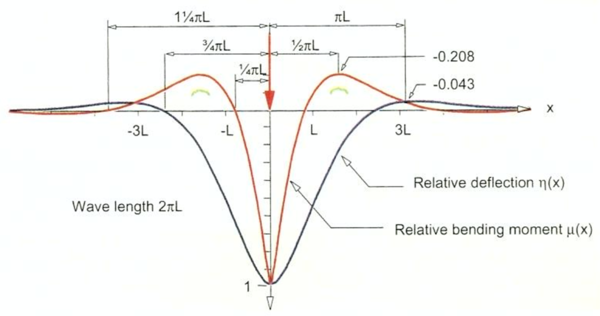
Figur 8.17 beskriver modellen: | |||
[[Fil:Figur_08.17.PNG|600px|thumb||center|<caption> Figur 8.17 Skinne betraktes som uendelig lang bjelke</caption>]] | |||
Figur 8.18 gir en beskrivelse av nedsenknings- og momentkurve til skinnen på elastisk underlag. | |||
[[Fil:Figur_08.18.PNG|600px|thumb||center|<caption> Figur 8.18 Forskyvnings- og momentkurve til skinnen ved belastning fra hjullast</caption>]] | |||
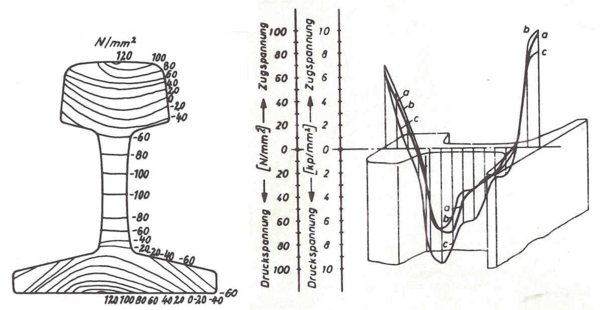
Spenningsbildet i skinnetverrsnittet ved sentrisk belastning av hjulkraft Q er vist i figur 8.19, romertall I. | |||
[[Fil:Figur_08.19.PNG|600px|thumb||center|<caption>Figur 8.19 Spenningsbilde i skinnetverrsnitt; romertall I representerer spennkingsbildet ved sentrisk belastning; romertallene II og III ivaretar også spenningsbilder på skinner i kurver</caption>]] | |||
==== Egenspenninger ==== | |||
Det opptrer egenspenninger som oppstår i forbindelse med retteprosessen ved produksjon av skinner. Figur 8.20 viser fordelingen av egenspenningene i tverrsnittet i skinnen. Variasjonen mht. strekkspenninger og trykkspenninger i tverrsnittet er vist. | |||
[[Fil:Figur_08.20.PNG|600px|thumb||center|<caption>Figur 8.20 Egenspenninger i skinner som oppstår ved produksjonen</caption>]] | |||
==== Temperaturspenninger ==== | |||
Endringer i temperaturen gir opphav til longitudinelle spenninger i tverrsnittet i skinneprofilet. Normalt har skinnen en nøytraltemperatur på 20° - 24 °C. Kraften på | |||
Temperaturspenningene beregnes med følgende formel: | |||
<math> | |||
P=\alpha_{th}\cdot E\cdot\Delta T\cdot A \ \ \ (kN) | |||
</math> | |||
| Linje 2 516: | Linje 2 775: | ||
Her betyr: | |||
P er longitudinell kraft i skinnen (kN) | |||
α<sub>th</sub> er utvidelseskoeffisienten i lengderetningen for stål som settes til 1,15 · 10<sup>-5</sup> · (1/°C) | |||
∆T er temperaturendring (°C) i forhold til skinnens nøytraltemperatur | |||
A er tverrsnittsarealet (mm2) | |||
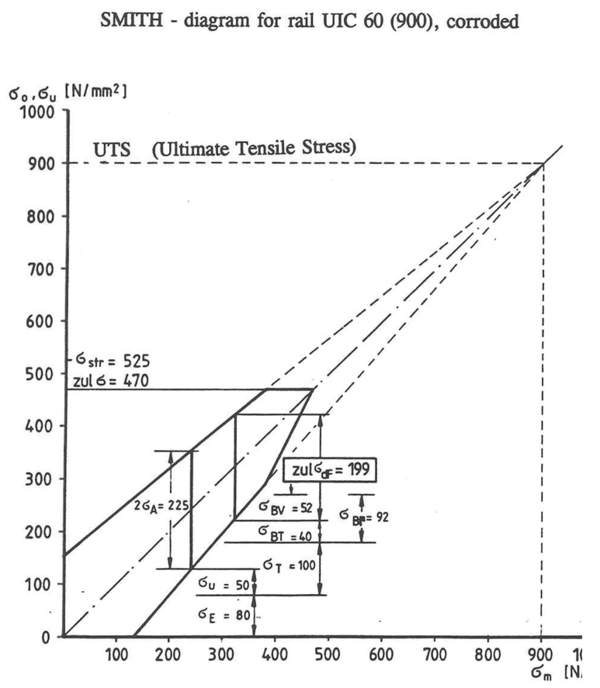
==== Smiths diagram og resulterende spenninger ==== | |||
I figur 8.21 er vist Smiths diagram for vurdering av tillatt spenning i underkant skinnefot i symmetriaksen ved sentrisk vertikal belastning i korrodert tilstand. | |||
Den dynamiske belastning må betraktes sammen med egenspenning i skinnestålet og spenninger på grunn av temperaturvariasjoner. Videre trekkes inn spenning i skinne som opptrer i brukonstruksjoner hvor det ikke er glideskjøter. | |||
Det framkommer følgende ligning: | |||
<math> | |||
zul \ \sigma_{dF}+\sigma_{E}+\sigma_{T}+\sigma_{BT} \le zul \ \sigma \ \ \ \left({N\over mm^2}\right) | |||
</math> | |||
<math> | |||
\gamma \cdot \sigma_{DYN \ FOT}\le zul \ \sigma_{dF} | |||
</math> | |||
Her betyr: | |||
zul σ<sub>d F</sub> er tillatt spenning i underkant av skinnefot i symmetriaksen på utmatting forårsaket av den dynamiske vertikale hjulkraft ved framføring av materiellet. | |||
σ<sub>E</sub> er egenspenning i skinnestålet | |||
σ<sub>T</sub> er temperaturspenning | |||
σ<sub>BT</sub> er spenning i skinne som opptrer i brukonstruksjoner hvor glideskjøter ikke er installert | |||
zul σ er tillatt resulterende spenning i skinnen | |||
σ<sub>DYN FOT</sub> er beregnet dynamisk spenning på grunn av kraft fra hjul ved framføring | |||
γ er sikkerhetsfaktor | |||
I | I Smiths diagram finnes også følgende betegnelser: | ||
σ<sub>BV</sub> er spenning som antas å opptre i skinnen fra bremsing og traksjon fra materiell på bruer | |||
σ<sub>U</sub> er minimumsbelastning ved utmattingstester i benk | |||
σ<sub>A</sub> er maksimalspenning for belastning ved utmattingstester i benk | |||
[[Fil:Figur_08.21.PNG|600px|thumb||center|<caption>Figur 8.21 Smiths diagram for vurdering tillatt spenning forårsaket av trafikkbelastning</caption>]] | |||
Den tillatte trafikkspenning inkludert sikkerhetsfaktor for skinne 60E1 i kvalitet 900 er zul σ<sub>d F</sub> = 200 N/mm<sup>2</sup>. | |||
I beregningene benyttes en sikkerhetsfaktor ϒ = 1,1. Det vil da gjelde for skinnekvalitet R 260 Mn: | |||
<math> | |||
\gamma \cdot \sigma_{DYN \ FOT}=1,10\cdot \sigma_{DYN \ FOT}\le zul \ \sigma_{dF} = 200 \ N/mm^2 | |||
</math> | |||
For skinnekvalitet R 200 Mn gjelder: | |||
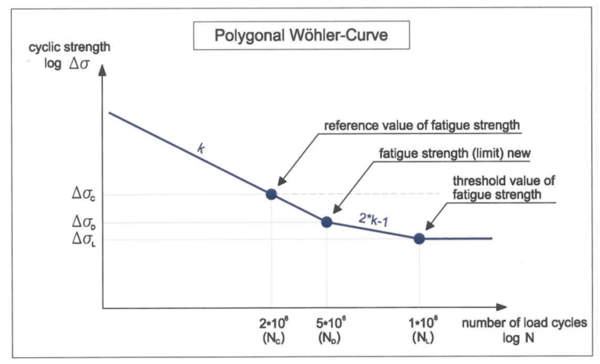
==== Polygonal Wöhler kurve ==== | |||
Dersom den beregnede eller opptredende spenning er mindre eller lik den tillatte trafikkspenning zul σdF , så kan levetiden for skinnen bli tilnærmet uendelig lang relatert til belastning på momentbøyning. Dette er vist i den polygonale Wöhler kurve: | |||
[[Fil:Figur_08.22.PNG|600px|thumb||center|<caption> Figur 8.22 Polygonal Wöhler kurve</caption>]] | |||
En lang levetid i sporet forutsetter normalt vedlikehold som regelmessig sliping av skinner, pakking og justering av sporet. | |||
<big>'''Lasttilfelle I.1: 21,3 tonns aksellast, skinne 49E1, svilleavstand 640 mm, tresviller, vekt 70 kg, svillelengde 2500 mm, bølgelengde 10 m'''</big> | |||
'''I.1.1 Zimmermanns metode med dynamisk tilleggsfaktor DAF; C<sub>b</sub> = 0,15 N/mm<sup>2</sup>''' | |||
Det gjennomføres en beregning med skinne 49E1 og sville med vekt 70 kg og svilleavstand a = 640 mm. | |||
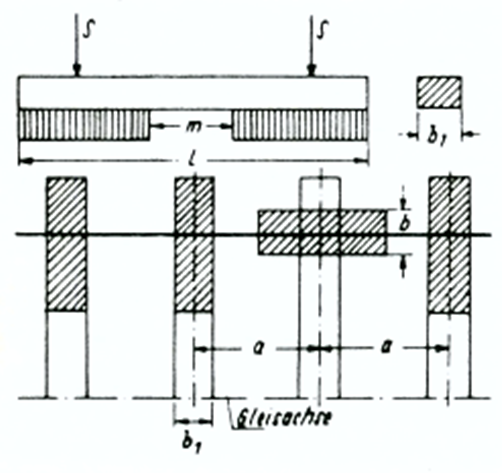
Del 1: Svilleflate | |||
[[Fil:Figur_del1.PNG|600px|thumb||center|<caption> </caption>]] | |||
Belastet svilleflate: | |||
<math> | |||
F=(2500-500)\cdot 250=500000 \ mm^2 | |||
</math> | |||
Fiktiv medvirkende bredde: | |||
<math> | |||
b={500000\over 2\cdot 640}=390 \ \ mm | |||
</math> | |||
Del 2: Elastisitetsegenskaper i overbygning | |||
Elastisitet i ballastsengen og overbygning (antakelse): | |||
<math> | |||
C_b=0,15 \ {N\over mm^3} | |||
</math> | |||
| Linje 2 678: | Linje 2 951: | ||
Det er vekselvis Heyback og Pandrol befestigelse på tresviller med tilhørende underlagsplater. Det legges til grunn at mellomleggene ikke bidrar til elastisitet i befestigelsen og i sporet. Den totale elastisitet er derfor lik ballastens elastisitet. | |||
<math> | |||
C_{TOTAL}=0,15 \ {N\over mm^3} | |||
</math> | |||
| Linje 2 692: | Linje 2 967: | ||
Del 3: Beregning av karakteristisk lengde L ved valg av skinneprofil | |||
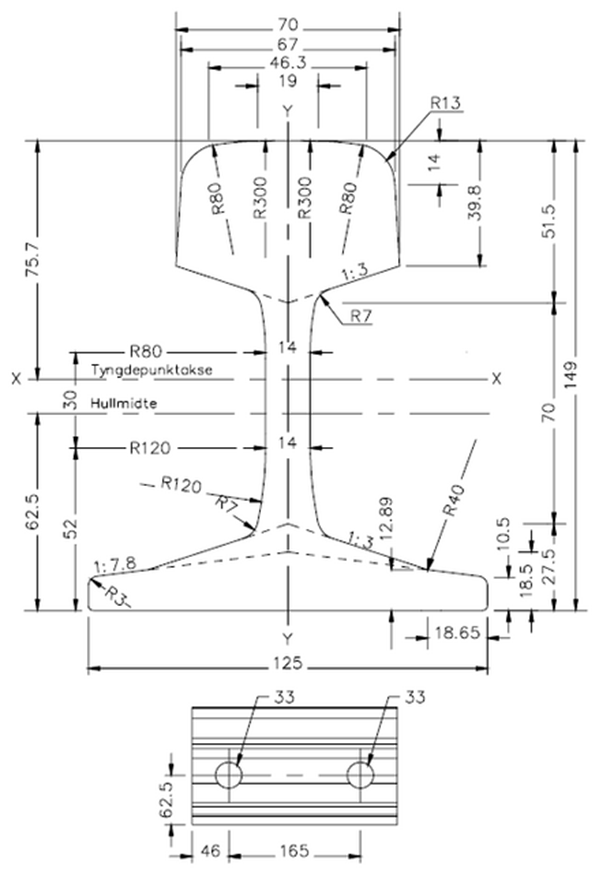
Det velges skinne 49E1: | |||
Treghetsmoment: I<sub>X – X</sub> = 1819 ·104 mm<sup>4</sup> | |||
I<sub>Y – Y</sub> = 320 · 104 mm<sup>4</sup> | |||
Motstandsmoment: W<sub>X – X</sub> = 248 · 103 mm<sup>3</sup> | |||
W<sub>Y – Y</sub> = 51,2 · 103 mm<sup>3</sup> | |||
Vekt: G = 49 kg/m | |||
Elastisitetsmodul: E = 2,15 · 10<sup>5</sup> N/mm<sup>2</sup> | |||
Beregning av karakteristisk lengde ved anvendelse av statisk ballastsiffer: | |||
<math> | |||
L=\sqrt[4]{4\cdot E\cdot I \over b \cdot C} =\sqrt[4]{4\cdot 2,15\cdot 10^5 \cdot 1819 \cdot 10^4\over 390 \cdot 0,15}=720 \ mm | |||
</math> | |||
Halv bølgelengde: | |||
<math> | |||
{3\over 4}\cdot\pi\cdot L=2,36\cdot 772=1822 \ mm \ \ < \ \ 2800 \ mm | |||
</math> | |||
Det er ingen belastning fra naboaksel for den aksel som betraktes. | |||
===== Beregning for rett linje og store kurveradier ===== | |||
Del 4: Lastberegning: | |||
===== Statisk betraktning ===== | |||
Statisk akselkraft: | |||
<math> | |||
P_0=213 \ kN | |||
</math> | |||
Statisk hjulkraft: | |||
<math> | |||
Q_0={1\over 2}\cdot P_0={1\over 2}\cdot 213=106,50 \ kN | |||
</math> | |||
Det legges på et beskjedent kvasistatisk tillegg: | |||
<math> | |||
\Delta Q = 3,50 \ kN | |||
</math> | |||
Kvasistatisk betraktning | |||
Kvasistatisk kraft blir: | |||
<math> | |||
Q_{KV}=Q_0+\Delta Q= 106,50+3,50=110 \ kN | |||
</math> | |||
Nedbøyning beregnet med statisk ballastsiffer: | |||
<math> | |||
y_{KV.STATI}={110\cdot 10^3\over 2\cdot 390\cdot 0,15\cdot 720}=1,27 \ mm | |||
</math> | |||
Moment: | |||
<math> | |||
M_{KV.STATI,II}={110\cdot 10^3\cdot 720\over 4}=19,80 \ kNm | |||
</math> | |||
Spenning i underkant skinnefot, symmetriakse: | |||
<math> | |||
\sigma_{KV.STAT,II}={M_{KV.STAT,II}\over W_U}={19,80\cdot 10^6 \over 248\cdot 10^3}=80,00 \ {N\over mm^2} | |||
</math> | |||
Trykk mot underkant sville under enkeltlast: | |||
<math> | |||
p_{STATISK}=C\cdot y_{KV.STAT:}=0,15\cdot 1,27=0,19 \ {N\over mm^2} | |||
</math> | |||
Belastning på sville i befestigelsen: | |||
<math> | |||
S_{STATISK}=b\cdot a\cdot p_{STATIASK}=390\cdot 640\cdot 0,15\cdot 10^{-3}=37,50 \ kN | |||
</math> | |||
===== Dynamisk betraktning ===== | |||
Dynamisk tilleggsfaktor DAF | |||
<math> | |||
\Phi =1,0+0,50\cdot{(30-60)\over 80}=1,0 | |||
</math> | |||
Antatt sporstandard: | |||
<math> | |||
\phi =0,20 | |||
</math> | |||
Statistisk sikkerhet: | |||
<math> | |||
t=3 | |||
</math> | |||
Dynamisk tilleggsfaktor: | |||
<math> | |||
DAF=t\cdot \phi\cdot \Phi | |||
</math> | |||
<math> | |||
DAF=3\cdot 0,20\cdot 1=0,60 | |||
</math> | |||
Dynamisk vertikalkraft: | |||
<math> | |||
Q_{DYN}=Q_{KV.STAT.}\cdot(1+DAF)=110\cdot (1,00+0,60)=176,00 \ kN | |||
</math> | |||
Dynamisk moment: | |||
<math> | |||
M_{DYNI}=19,80\cdot 1,60=31,60 \ kNm | |||
</math> | |||
Dynamisk spenning i underkant skinnefot i symmetriaksen: | |||
<math> | |||
\sigma_{DYN}={M_{DYN,II}\over W_U}={31,60\cdot 10^6\over 248\cdot 10^3}=128,00{N\over mm^2} | |||
</math> | |||
Sikkerhetsfaktor er bestemt til 1,10: | |||
<math> | |||
\gamma\cdot \sigma_{DYN}=1,10\cdot 128,00=141,00{N\over mm^2} | |||
</math> | |||
Trykk mot underkant sville under enkeltlast | |||
<math> | |||
p_{DYN}=DAF\cdot p_{KV.STAT.}=1,60\cdot 0,19=0,300{N\over mm^2} | |||
</math> | |||
Belastning på sville i befestigelsen: | |||
<math> | |||
S_{DYN}=DAF\cdot S_{KV.STAT}=1,60\cdot 37,50=60,00 \ kN | |||
</math> | |||
| Linje 3 100: | Linje 3 270: | ||
Beregningene er sammenfattet i tabell (se under) | |||
< | {| class="wikitable" style="text-align:center" width="900px" | ||
|- | |||
!Skinneprofil | |||
!49E1 | |||
!49E1 | |||
|- | |||
|Skinnekvalitet for bøyning (N/mm<sup>2</sup>)|| 700|| 900 | |||
|- | |||
|Ballastsiffer C (N/mm<sup>3</sup>)|| 0,15 ||0,15 | |||
|- | |||
|Hastighet (km/h)|| 30|| 30 | |||
|- | |||
|Karakteristisk L (mm)|| 720|| 720 | |||
|- | |||
|(3/4) x Π x L (mm)|| 1822|| 1822 | |||
|- | |||
|Akselkraft (kN)|| 213|| 213 | |||
|- | |||
|Qqst (kN) || 106,50|| 106,50 | |||
|- | |||
|Nedbøying y<sub>KV:ST.</sub> fra betraktet hjul for Q<sub>KV.ST.</sub> (mm)|| 1,27 || 1,27 | |||
|- | |||
|Bøyemoment M<sub>KV.ST.</sub> (kNm)|| 19,80|| 19,80 | |||
|- | |||
|Belastning i skinnefot symmetriakse, σ (N/mm<sup>2</sup>)|| 80,00|| 80,00 | |||
|- | |||
|Trykk mot underkant sville (N/mm<sup>2</sup>)|| 0,19|| 0,19 | |||
|- | |||
|Skinnesetekraft (kN)|| 37,50|| 37,50 | |||
|- | |||
|Dynamisk tilleggsfaktor (-)|| 1,60|| 1,60 | |||
|- | |||
|Q<sub>DYN</sub> (kN)|| 176,00|| 176,00 | |||
|- | |||
|Bøyemoment (kNm)|| 31,60|| 31,60 | |||
|- | |||
|Spenning σ dyn (N/mm<sup>2</sup>)|| 128,00|| 128,00 | |||
|- | |||
|1,1 x σ dyn (N/mm<sup>2</sup>)|| 141,00 ||141,00 | |||
|- | |||
|tillatt σ dyn (N/mm<sup>2</sup>)|| 160,00|| 200,00 | |||
|- | |||
|Egenspenninger (N/mm<sup>2</sup>)|| 80,00 ||80,00 | |||
|- | |||
|Temperaturspenning|| 100,00|| 100,00 | |||
|- | |||
|Svilletrykk p dyn (N/mm<sup>2</sup>) ||0,30|| 0,30 | |||
|- | |||
|Svillesetekraft R dyn (kN)|| 60,00|| 60,00 | |||
|} | |||
Det | På rett strekning og i kurver med store radier oppstår spenninger i dynamisk tilstand i skinnefot i symmetriaksen som er lavere enn tillatt tilrådelig spenningskapasitet for skinner i kvalitet R200Mn og i kvalitet R260Mn. Det skulle derfor ikke være fare for utmatting. | ||
Det påpekes at den kvasistatiske kraft QKV.ST. vurderes i samsvar med tilhørende kvasistatisk kraft i EN 14363 evaluert i et lavpassfilter på 20 Hz. Denne kraften er en 50 % verdi kraft. | |||
Den dynamiske kraft QDYN vurderes i samsvar med tilhørende dynamisk kraft i EN 14363 evaluert i et lavpassfilter på 20 Hz. Denne kraften er en 99,85 % kraft og forekommer dermed meget sjeldent. | |||
<big>'''Beregning i kurver med små radier; R = 150 m; D = 50 mm; V = 30 km/h'''</big> | |||
Det blir antatt en framføringshastighet V = 30 km/h tilsvarende v = 8,33 m/s. For en kurve med R = 150 m og D = 50 mm beregnes en liten ukompensert sideakselerasjon og overskuddshøyde: | |||
<math> | |||
a_q={v^2\over R}-g\cdot{D\over s} | |||
</math> | |||
<math> | |||
a_q={8,33^2\over 150}-9,81\cdot{50\over 1500}=0,14{m\over s^2} | |||
</math> | |||
<math> | |||
I=153\cdot a_q=153\cdot 0,14=22 \ mm | |||
</math> | |||
| Linje 3 171: | Linje 3 370: | ||
Med en aksellast m<sub>LOK AKSEL</sub> = 21300 kg og a<sub>q</sub> = 0,14 m/s<sup>2</sup> blir sentrifugal kraften: | |||
<math> | |||
S=m_{LOK \ AKSEL}=21300\cdot 0,14\cdot 10^{-3}=3,00 \ kN | |||
</math> | |||
Med tyngdepunktshøyde h = 2,00 m og sporvidde s = 1,50 m blir den kvasistatiske tilleggskraft: | |||
<math> | |||
\Delta Q=S\cdot {h\over s}=3,00\cdot {2,0\over 1,5}=4,00 \ kN | |||
</math> | |||
Det regnes med et kvasistatisk tillegg på ΔQ = 8,50 kN > 4,00 kN på grunn av kurvekjøring og beskjeden eksentrisk last på lokomotivet. | |||
Dette gir kvasistatisk kraft: | |||
<math> | |||
Q_{KV.STAT.}=(106,50+8,50)=115,00 \ kN | |||
</math> | |||
'''Vurderinger av spenningstilstand for kombinasjon av vertikale og laterale krefter''' | |||
For beregning av spenninger i fot av skinne for vertikale krefter benyttes den kvasistatiske og dynamiske tilstand. I Zimmermanns metode beregnes den kvasistatiske vertikale kraft og denne gis et tillegg (DAF = dynamic implification factor) for fastsettelse av den dynamiske vertikale kraft. Metoden er meget enkel og har dermed en del svakheter. Zimmermanns metode gir ingen opplysninger om frekvensrelaterte tilstander. | |||
For en kombinasjon av vertikale og laterale krefter blir aspektet meget omfattende. De vertikale kreftene bestemmes normalt i dynamisk tilstand når disse opptrer alene. For de laterale kreftene er det nødvendig med en vurdering. | |||
Det kan antas 3 innfallsvinkler: | |||
*Grenseverdi for Y<sub>KV.STAT</sub>: bestemt i norm | |||
*Anvendelse av EN 13104 for traksjonsaksler for bestemmelse av Y krefter | |||
*Anvendelse av resultat fra tester El 18 | |||
Bestemmelse av dynamisk tilleggsfaktor (DAF) for beregning av YDYN: | |||
*Dimensjonerende Y<sub>KV.STAT.</sub> med tillegg av DAF (dynamic amplification factor) | |||
'''Grenseverdi for Y<sub>KV.STAT.</sub> bestemt i norm for aksellaster ved forsøk''' | |||
<math> | |||
Y_{qst,lim}=60 \ kN | |||
</math> | |||
60 kN er en høy verdi i kvasistatisk tilstand og opptrer trolig for trekkmateriell og ikke for vogner med løpeboggier. Det må legges til at denne verdien sammenlignes med evaluering av målt midlere (50 % verdi) verdi i et lavpassfilter på 20 Hz. | |||
Den kvasistatiske laterale kraft i kombinasjon med den vertikale kraft vil gi store spenninger i dimensjonerende hjørner i skinneprofilet. Plastiske deformasjoner vil kunne forekomme. | |||
'''Anvendelse av EN 13104 for traksjonsaksler for bestemmelse av Y krefter''' | |||
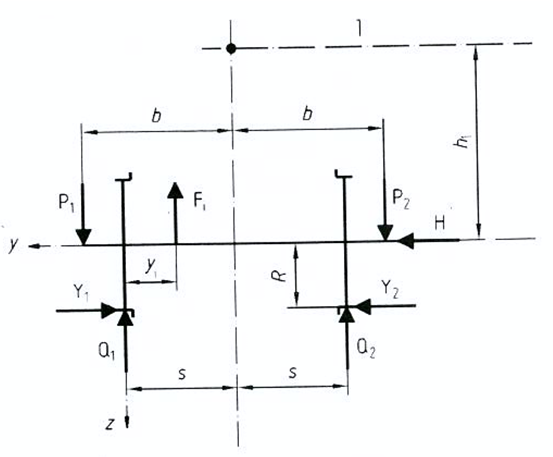
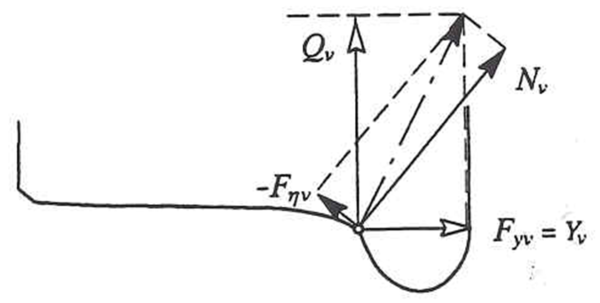
Systemskisse for beregning av lateral kraft Y<sub>1</sub> er vist i figur I1. | |||
[[Fil:Figur_figur1.PNG|600px|thumb||center|<caption> Figur I1 Krefter på en hjulaksel iht. EN 13103 og 13104</caption>]] | |||
Dersom kraften Y<sub>1</sub> er fra førende hjul på førende aksel, angir EN 13104 følgende formel for beregning av denne parameteren for masser i bevegelse (bremsing og traksjon er ikke inkludert): | |||
<math> | |||
Y_1=0,35\cdot m_1\cdot g | |||
</math> | |||
Det kreves en forklaring på hvordan denne kraften er utledet. | |||
Termen Y<sub>2</sub> er friksjonskraft mellom hjul og skinne på indre skinnestreng og har en verdi lik: | |||
<math> | |||
Y_2=0,175\cdot m_1\cdot g | |||
</math> | |||
Denne kraften forutsettes å være i likevekt med føringskraften P på ytre skinnestreng. | |||
Videre legges til grunn en støtfaktor: | |||
<math> | |||
f_q=0,75 | |||
</math> | |||
Endelig gjennomkjører akselen kurver med en ukompensert sideakselerasjon lik 1,0 m/s<sup>2</sup> (i normen): | |||
<math> | |||
a_q=1,00 \ m/s^2 | |||
</math> | |||
Dermed blir den ytre laterale kraft Y<sub>1</sub> | |||
<math> | |||
Y_1=\left( 0,175\cdot m_1\cdot g+m_1\cdot g\cdot {a_q\over g} + m_1\cdot g\cdot {f_q\over g}\right) | |||
</math> | |||
<math> | |||
Y_1=\left( 0,175+ {a_q\over g} + {f_q\over g}\right)\cdot m_1\cdot g | |||
</math> | |||
<math> | |||
Y_1=\left( 0,175+0,100+0,075 \right)\cdot m_1\cdot g | |||
</math> | |||
<math> | |||
Y_1=0,350\cdot m_1\cdot g | |||
</math> | |||
Termen m<sub>1</sub> er vognkassens masse med last på en aksel. Dersom denne settes til 21,30 tonn, blir Y kraften: | |||
<math> | |||
Y_1=0,350\cdot 21300\cdot 10=74,55 \ kN | |||
</math> | |||
Det er i ovennevnte beregning lagt til grunn en ukompensert sideakselerasjon a<sub>q</sub> = 1,00 m/s<sup>2</sup>. El 18 kjører gjennom kurvene med langsommere hastighet på Flåmsbana. For V = 30 km/h opptrer det en beskjeden ukompensert sideakselerasjon a<sub>q</sub> = 0,14 m/s<sup>2</sup>. | |||
Ved en slik forutsetning blir den laterale kraften: | |||
<math> | |||
Y_1=(0,175+0,014+0,075)\cdot m_1\cdot g=(0,175+0,014+0,075)\cdot 21300\cdot 10=56,32 \ kN | |||
</math> | |||
Det er et spørsmål om denne kraften skal vurderes som kvasistatisk eller dynamisk. Normen angir lave verdier for tillatte spenninger som framkommer ved dividering med en sikkerhetsfaktor. | |||
Det bør nevnes at virkning av høy ukompensert sideakselerasjon og dermed høy sentrifugalkraft ifølge utallige målinger ikke fører til tilsvarende høy føringskraft på kanten av skinnehodet sammenlignet med framføring med lav a<sub>q</sub>. Dette skyldes trolig at friksjonen av føringskraften mot skinnehodet er større ved lav ukompensert sideakselerasjon enn ved høy a<sub>q</sub>. Dermed utlignes forskjellen mht. føringskraften og tilhørende lateral spenning. | |||
'''Anvendelse av resultat fra tester for El 18''' | |||
En tredje innfallsvinkel er å benytte rapporter fra gjennomførte tester. | |||
Det vites ikke om slike tester er gjennomført i Norge eller i andre land. Imidlertid har El 18 en boggi med gode radielle styringsegenskaper i kurver. | |||
Grenseverdi for Y <sub>KV.STAT.</sub> bestemt i norm for høyere aksellaster ved forsøk med tillegg av DAF (dynamic amplification factor) | |||
Dynamisk innflytelsesfaktor DAF: | |||
<math> | |||
DAF=t\cdot\sigma=t\cdot \Phi \cdot \phi | |||
</math> | |||
Den statistiske sikkerhet er t = 3. Hastighetsinnflytelse bestemmes til φ = 1 og sporets standard i lateral retning vurderes til å være ϕ = 0,20. | |||
På grunn av kurver med radier R = 150 m opptrer horisontale og vertikale krefter i befestigelsen. Aspektet gir en resulterende kraft rettet mot befestigelsen. Det forventes ikke en økning i helningsvinkelen for virkningslinjen for den resulterende kraft fra det tyngre lokomotivet El 18 sammenlignet med virkningslinjen for de kombinasjonskrefter som oppstår ved framføring av det lettere lokomotivet El 17. Med El 17 eksisterer betydelig erfaring for virkning på befestigelsen. | |||
Dermed blir DAF = 0,60. | |||
Formel for dynamisk lateral kraft er: | |||
<math> | |||
Y_{DYN}=(1+DAF)\cdot Y_{KV.STAT.} | |||
</math> | |||
<math> | |||
Y_{DYN}=1,60\cdot Y_{KV.STAT.} | |||
</math> | |||
Det er nevnt 3 innfallsvinkler for vurdering av den kvasistatiske Y kraft | |||
Kraft i norm: Y<sub>KV.STAT.</sub> = 60,00 kN | |||
Kraft i EN 13104: Y = 56,32 kN | |||
Kraft i test (maks. verdi): mangler opplysninger | |||
Kraften på 60 kN i norm er høy og gjelder i hovedsak for lokomotiv. Vogner med løpeaksler vil gi lavere verdier. I det etterfølgende fastsettes: | |||
<math> | |||
Y_{KV.STAT.}=60,00 \ kN | |||
</math> | |||
<math> | |||
Y_{DYN}=1,60 \cdot 60,00=96,00 \ kN | |||
</math> | |||
Det gjennomføres i det etterfølgende en fullstendig beregning med utgangspunkt i vertikal og lateral kraft i kvasistatisk og dynamisk tilstand. | |||
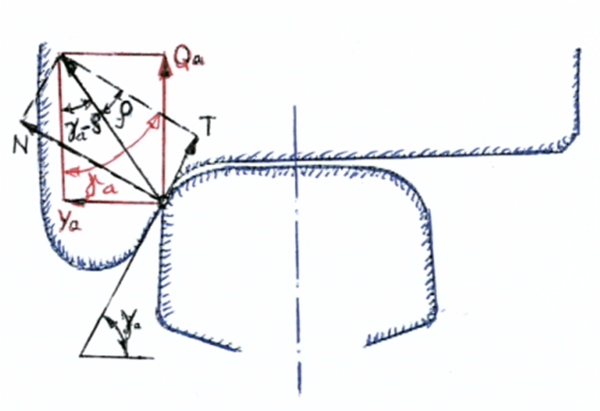
Samvirke av eksentrisk hjulkraft Q og høy lateral kraft Y kan føre til betydelige spenninger på bøyning i kantene på skinnehode og skinnefot. Dette gjelder punktene A, B, C og D som er vist i figur 8.19. Denne tilstanden oppstår i hovedsak i kurver med små radier i sporet og i sporveksler med små radier ved passering av tunge lokomotiv. Ved tunge aksellaster i godsvogner med enkle boggikonstruksjoner (ikke tilstrekkelig gode radielle styringsegenskaper) vil betydelige spenningsnivåer opptre. | |||
I litteraturen diskuteres om beregninger på utmatting i dynamisk tilstand er nødvendig da antallet av slike situasjoner vanligvis er begrenset og har lokal opptreden i en kurve. Imidlertid på Flåmsbana med et stort antall av kurveradier (ned mot R = 150 m) vil lokale spenningsmaksima opptre og det vil alltid være en mulighet for opptreden av plastisk deformasjon dersom ytelsesgrensen for stålet blir overskredet et tilstrekkelig antall ganger. | |||
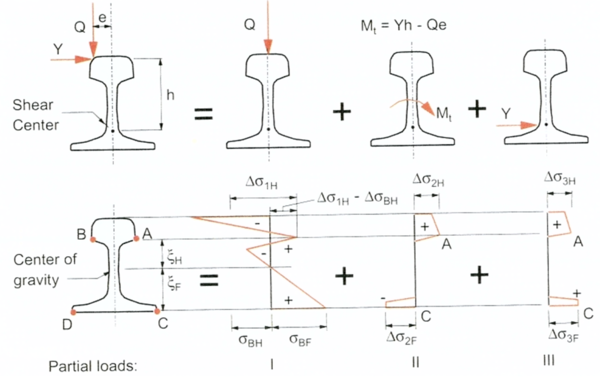
Det er hensiktsmessig å foreta en dekomponering av kraftbildet som vist i figur 8.1. Spenningsbildene i tverrsnittet på profilet er vist. | |||
[[Fil:Figur_figur2.PNG|600px|thumb||center|<caption> Figur I2 Spenningsbilder ved belastning på skinneprofilet i kurver med små radier</caption>]] | |||
Det opptrer ulike momenter. | |||
Bøyemoment på grunn av vertikalkraft Q i senter skinne på skinnehodet (kvasistatisk og dynamisk): | |||
<math> | |||
M_B={Q\cdot L\over 4} \ (kNm) | |||
</math> | |||
Torsjonsmoment på grunn av eksentrisk angrepspunkt for vertikalkraft Q og angrepspunkt for lateral kraft Y (kvasistatisk og dynamisk): | |||
<math> | |||
M_T=Y\cdot h-Q\cdot e | |||
</math> | |||
Hovedspenningene kan beregnes. | |||
Bøyningsspenning i skinnehode: | |||
<math> | |||
\sigma_{BH}=\lambda_{OH}\cdot M_B | |||
</math> | |||
Bøyningsspenning i skinnefot: | |||
<math> | |||
\sigma_{BF}=\lambda_{OF}\cdot M_B | |||
</math> | |||
Delspenning I på grunn av tverrsnittform av skinneprofilet for dynamisk kraft Q: | |||
<math> | |||
\Delta\sigma_{1H}=\lambda_{1H}\cdot Q | |||
</math> | |||
<math> | |||
\Delta\sigma_{1F}=0 | |||
</math> | |||
''Delspenning II på grunn av torsjonsmomentet M<sub>T</sub>:'' | |||
<math> | |||
\Delta\sigma_{2H}=\lambda_{2H}\cdot M_T | |||
</math> | |||
<math> | |||
\Delta\sigma_{2F}=\lambda_{2F}\cdot M_T | |||
</math> | |||
Delspenning III på grunn av lateral kraft Y: | |||
<math> | |||
\Delta\sigma_{3H}=\lambda_{3H}\cdot Y | |||
</math> | |||
<math> | |||
\Delta\sigma_{3F}=\lambda_{3F}\cdot Y | |||
</math> | |||
Den resulterende spenning I hver lokalisering uttrykkes: | |||
<math> | |||
\sigma_{HA}=-\sigma_{BH}+0,9\cdot (\Delta\sigma_{1H}+\Delta\sigma_{2H}+\Delta\sigma_{3H}) | |||
</math> | |||
<math> | |||
\sigma_{HB}=-\sigma_{BH}+0,9\cdot (\Delta\sigma_{1H}-\Delta\sigma_{2H}-\Delta\sigma_{3H}) | |||
</math> | |||
<math> | |||
\sigma_{FC}=-\sigma_{BF}+0,9\cdot ( -\Delta\sigma_{2F}+\Delta\sigma_{3F}) | |||
</math> | |||
<math> | |||
\sigma_{FD}=+\sigma_{BF}+0,9\cdot ( +\Delta\sigma_{2F}-\Delta\sigma_{3F}) | |||
</math> | |||
Faktorene λ med indekser for skinneprofil 49E1, 54E3 og 60E1 er gitt I litteraturen: | |||
{| class="wikitable" style="text-align:center" width="1000px" | |||
|- | |||
!rowspan=2| Skinneprofil | |||
!colspan=9| Koeffisienter for beregning av spenninger i skinneprofil ved kombinerte laster Q og Y | |||
|- | |||
!h (cm)|| e (cm)|| λ<sub>OH</sub>(cm<sup>-3</sup>)|| λ<sub>1H</sub>(cm<sup>-2</sup>)|| λ<sub>2H</sub> (cm<sup>-3</sup>)|| λ<sub>3H</sub> (cm<sup>-2</sup>)|| λ<sub>OF</sub> (cm<sup>-3</sup>)|| λ<sub>2F</sub> (cm <sup>-3</sup>)|| λ<sub>3F</sub>(cm<sup>-2</sup>) | |||
|- | |||
|49E1|| 9,90|| 3,35|| 0,0020|| 0,054|| 0,016|| 0,160|| 0,0040|| 0,0152|| 0,2980 | |||
|- | |||
|54E3|| 10,20 ||3,35|| 0,0017|| 0,049 ||0,014|| 0,140|| 0,0036|| 0,0131|| 0,2610 | |||
|- | |||
|60E1|| 12,90|| 3,60|| 0,0018|| 0,050|| 0,017|| 0,110|| 0,0027|| 0,0126 ||0,2290 | |||
|} | |||
For skinne i kvalitet R 260 Mn gjelder følgende grenseverdier for anbefalte tillatte spenninger: | |||
I punktene A og B: 325 N/mm<sup>2</sup> | |||
I punktene C og D: 250 N/mm<sup>2</sup> | |||
I symmetriakse i fot: 200 N/mm<sup>2</sup> | |||
For skinne i kvalitet R200Mn vurderes for Flåmsbana følgende grenseverdier for anbefalte | |||
tillatte spenninger: | |||
I punktene A og B: 285 N/mm<sup>2</sup> | |||
I punktene C og D: 210 N/mm<sup>2</sup> | |||
I symmetriakse i fot: 160 N/mm<sup>2</sup> | |||
Spenningene gjelder i dynamisk tilstand ved vedvarende opptreden av belastninger. | |||
'''Spenninger i skinneprofil ved bøyning på grunn av kurveradius''' | |||
I kurver med små radier opptrer i tillegg horisontale bøyningsmomenter som må beregnes. Følgende ligninger benyttes: | |||
<math> | |||
\sigma_{A}={E\cdot b_{HODE}\over 2\cdot R} \ \ \left({N\over mm^2}\right) | |||
</math> | |||
<math> | |||
\sigma_{B}=-{E\cdot b_{HODE}\over 2\cdot R} \ \ \left({N\over mm^2}\right) | |||
</math> | |||
<math> | |||
\sigma_{C}={E\cdot b_{FOT}\over 2\cdot R} \ \ \left({N\over mm^2}\right) | |||
</math> | |||
<math> | |||
\sigma_{D}=-{E\cdot b_{FOT}\over 2\cdot R} \ \ \left({N\over mm^2}\right) | |||
</math> | |||
Termene betyr: | |||
E: elastisitetsmodul for stål (N/mm<sup>2</sup>) | |||
b<sub>HODE</sub>: bredde av skinnehode (mm) | |||
b<sub>FOT</sub>: bredde av skinnefot (mm) | |||
R: kurveradius (mm) | |||
'''Kvasistatisk vurdering''' | |||
Iht. foregående beregninger for vertikal last: | |||
<math> | |||
Q_0=106,50 \ kN | |||
</math> | |||
<math> | |||
Q_{KV.STAT}=115,00 \ kN | |||
</math> | |||
<math> | |||
M_{KV.STAT, II}={115\cdot 10^3 \cdot 720\over 4}\cdot 10^{-6}=20,70 \ kNm | |||
</math> | |||
<math> | |||
\sigma_{KV.STATI}={M_{KV.STAT.}\over W_U}={20,70\cdot 10^6\over 248\cdot 10^3}=83,50 \ {N\over mm^2} | |||
</math> | |||
<math> | |||
p_{STATIK}=0,19{N\over mm^2} | |||
</math> | |||
<math> | |||
S_{KV.STAT}=37,50 \ kN | |||
</math> | |||
<math> | |||
Y_{KV.STAT.}=60,00 \ kN | |||
</math> | |||
Torsjonsmoment MT: | |||
<math> | |||
M_T=Y_{KV.STAT.}\cdot h-Q_{KV.STAT.}\cdot e | |||
</math> | |||
<math> | |||
M_{T \ KV.STAT.}=60,00\cdot 0,099-115,00\cdot0,0335=2,09 \ kNm | |||
</math> | |||
Delspenningene beregnes: | |||
<math> | |||
\sigma_{BH}=\lambda_{OH}\cdot M_B=\lambda_{OH}\cdot M_{KV.STAT.}=0,0020\cdot 20,70\cdot 10^6\cdot 10^{-3}=41,40{N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{BF}=\lambda_{OF}\cdot M_B=0,0040\cdot 20,70\cdot 10^6\cdot 10^{-3}=82,80{N\over mm^2} | |||
</math> | |||
<math> | |||
\Delta\sigma_{1H}=\lambda_{1H}\cdot Q_{KV.STAT.}=0,054\cdot 115,00 \cdot 10^{-2}\cdot 10^3=63,10 {N\over mm^2} | |||
</math> | |||
<math> | |||
\Delta\sigma_{2H}=\lambda_{2H}\cdot M_T=0,016\cdot 2,09\cdot 10^6\cdot 10^{-3}=33,50 {N\over mm^2} | |||
</math> | |||
<math> | |||
\Delta\sigma_{3H}=\lambda_{3H}\cdot Y_{KV.STAT.}=0,160\cdot 60,00\cdot 10^3\cdot 10^{-2}=96,00 {N\over mm^2} | |||
</math> | |||
<math> | |||
\Delta\sigma_{1F}=0 | |||
</math> | |||
<math> | |||
\Delta\sigma_{2F}=\lambda_{2F}\cdot M_T=0,0152\cdot 2,09\cdot 10^6\cdot 10^{-3}=31,80 {N\over mm^2} | |||
</math> | |||
<math> | |||
\Delta\sigma_{3F}=\lambda_{3F}\cdot Y_{KV.STAT.}=0,298\cdot 60,00\cdot 10^3\cdot 10^{-2}=179,00 {N\over mm^2} | |||
</math> | |||
De resulterende spenninger blir: | |||
<math> | |||
\sigma_{HA}=-\sigma_{BH} + 0,90\cdot (\Delta\sigma_{1H}+\Delta\sigma_{2H}+\Delta\sigma_{3H}) | |||
</math> | |||
<math> | |||
\sigma_{HA}=-41,40+0,90\cdot(62,10+33,50+96,00)=131,00 {N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{HB}=-\sigma_{BH} + 0,90\cdot (\Delta\sigma_{1H}-\Delta\sigma_{2H}-\Delta\sigma_{3H}) | |||
</math> | |||
<math> | |||
\sigma_{HB}=-41,40+0,90\cdot(62,10-33,50-96,00)=-102,00 {N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{FC}=\sigma_{BF} + 0,90\cdot (-\Delta\sigma_{2F}+\Delta\sigma_{3F}) | |||
</math> | |||
<math> | |||
\sigma_{FC}=82,80+0,90\cdot(-31,80+179,00)=215,30 | |||
</math> | |||
<math> | |||
\sigma_{FD}=\sigma_{BF} + 0,90\cdot (+\Delta\sigma_{2F}-\Delta\sigma_{3F}) | |||
</math> | |||
<math> | |||
\sigma_{FD}=82,80+0,90\cdot(+31,80-179,00)=-49,70{N\over mm^2} | |||
</math> | |||
'''Dynamisk vurdering''' | |||
Iht. foregående beregninger for vertikal kraft: | |||
<math> | |||
Q_{DYN}=184,00 \ kN | |||
</math> | |||
<math> | |||
M_{DYN}=1,6\cdot 20,70= 33,10 \ kNm | |||
</math> | |||
<math> | |||
\gamma\cdot\sigma_{DYN}=147,40{N\over mm^2} | |||
</math> | |||
<math> | |||
p_{DYN}=0,300{N\over mm^2} | |||
</math> | |||
<math> | |||
S_{DYN}=60,00 \ kN | |||
</math> | |||
<math> | |||
Y_{DYN}=1,6\cdot 60,00=96,00 \ kN | |||
</math> | |||
Torsjonsmomentet blir: | |||
<math> | |||
M_{T \ DYN}=Y_{DYN}\cdot h-Q_{DYN}\cdot e | |||
</math> | |||
<math> | |||
M_{T \ DYN }=96,00\cdot 0,099-184,00\cdot 0,0335=3,34 \ kNm | |||
</math> | |||
Delspenningene beregnes: | |||
<math> | |||
\sigma_{BH}=\lambda_{OH}\cdot M_{DYN}=0,0020\cdot 33.10\cdot 10^6\cdot 10^{-3}=66,20{N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{BF}=\lambda_{OF}\cdot M_{DYN}=0,0040\cdot 33,10\cdot 10^6\cdot 10^{-3}=132,40{N\over mm^2} | |||
</math> | |||
<math> | |||
\Delta\sigma_{1H}=\lambda_{1H}\cdot Q_{DYN.}=0,054\cdot 184,00 \cdot 10^{-2}\cdot 10^3=99,40 {N\over mm^2} | |||
</math> | |||
<math> | |||
\Delta\sigma_{2H}=\lambda_{2H}\cdot M_{T \ DYN}=0,016\cdot 3,34\cdot 10^6\cdot 10^{-3}=53,40 {N\over mm^2} | |||
</math> | |||
<math> | |||
\Delta\sigma_{3H}=\lambda_{3H}\cdot Y_{DYN }=0,160\cdot 96,00\cdot 10^3\cdot 10^{-2}=153,60 {N\over mm^2} | |||
</math> | |||
<math> | |||
\Delta\sigma_{1F}=0 | |||
</math> | |||
<math> | |||
\Delta\sigma_{2F}=\lambda_{2F}\cdot M_{T \ DYN}=0,0152\cdot 3,34\cdot 10^6\cdot 10^{-3}=50,80{N\over mm^2} | |||
</math> | |||
<math> | |||
\Delta\sigma_{3F}=\lambda_{3F}\cdot Y_{DYN }=0,298\cdot 96,00\cdot 10^3\cdot 10^{-2}=286,00 {N\over mm^2} | |||
</math> | |||
De resulterende spenninger blir: | |||
<math> | |||
\sigma_{HA}=-\sigma_{BH} + 0,90\cdot (\Delta\sigma_{1H}+\Delta\sigma_{2H}+\Delta\sigma_{3H}) | |||
</math> | |||
<math> | |||
\sigma_{HA}=-66,20+0,90\cdot(99,40+53,40+153,60)=208,70 {N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{HB}=-\sigma_{BH} + 0,90\cdot (\Delta\sigma_{1H}-\Delta\sigma_{2H}-\Delta\sigma_{3H}) | |||
</math> | |||
<math> | |||
\sigma_{HB}=-66,20+0,90\cdot(99,40-53,40-153,60)=-163,00 {N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{FC}=\sigma_{BF} + 0,90\cdot (-\Delta\sigma_{2F}+\Delta\sigma_{3F}) | |||
</math> | |||
<math> | |||
\sigma_{FC}=132,40+0,90\cdot(-50,80+286,00)=344,10{N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{FD}=\sigma_{BF} + 0,90\cdot (+\Delta\sigma_{2F}-\Delta\sigma_{3F}) | |||
</math> | |||
<math> | |||
\sigma_{FD}=132,40+0,90\cdot(+50,80-286,00)=-80,00{N\over mm^2} | |||
</math> | |||
'''Spenninger i bøyning på grunn av kurveradius''' | |||
R =150 m | |||
<math> | |||
\sigma_{A}={E\cdot b_{HODE}\over 2\cdot R}={2,15\cdot 10^5\cdot 67\over 2\cdot 150000}=48,00 {N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{B}=-{E\cdot b_{HODE}\over 2\cdot R}=-48,00 {N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{C}={E\cdot b_{FOT}\over 2\cdot R}={2,15\cdot 10^5\cdot 125\over 2\cdot 150000}=90,00 {N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{C}=-{E\cdot b_{FOT}\over 2\cdot R}=-90,00 {N\over mm^2} | |||
</math> | |||
'''Egenspenninger''' | |||
Egenspenninger bestemmes: | |||
<math> | |||
\sigma_{A}=-40 {N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{B}=-40 {N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{C}=-60 {N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{D}=-60 {N\over mm^2} | |||
</math> | |||
'''Temperaturspenninger''' | |||
Temperaturspenningene kan være trykkspenninger eller strekkspenninger og er konstant over hele tverrsnittet når de opptrer. | |||
<math> | |||
\sigma_{TVERSNITT}=100 {N\over mm^2} | |||
</math> | |||
Eventuelt: | |||
<math> | |||
\sigma_{TVERSNITT}=-100 {N\over mm^2} | |||
</math> | |||
'''Kvasistatisk vurdering''' | |||
Resulterende spenninger blir: | |||
<math> | |||
\sigma_{HA}=-\sigma_{BH} + 0,90\cdot (\Delta\sigma_{1H}+\Delta\sigma_{2H}+\Delta\sigma_{3H}) +\sigma_{A,KURVE}-\sigma_{A,RESIDULAL}+\sigma_{A,TEMP} | |||
</math> | |||
<math> | |||
\sigma_{HA}=-41,40+0,90\cdot(62,10+35,50+96,00)+48,00-40,00+100,00=239,00 {N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{HB}=-\sigma_{BH} + 0,90\cdot (\Delta\sigma_{1H}-\Delta\sigma_{2H}-\Delta\sigma_{3H}) -\sigma_{A,KURVE}-\sigma_{A,RESIDULAL}+\sigma_{A,TEMP} | |||
</math> | |||
<math> | |||
\sigma_{HB}=-41,40+0,90\cdot(62,10-35,50-96,00)-48,00-40,00+100,00=-90,00 {N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{FC}=\sigma_{BF} + 0,90\cdot (-\Delta\sigma_{2F}+\Delta\sigma_{3F}) +\sigma_{A,KURVE}-\sigma_{A,RESIDULAL}+\sigma_{A,TEMP} | |||
</math> | |||
<math> | |||
\sigma_{FC}= 82,80+0,90\cdot(-31,80+179,00)+96,00-60,00+100,00 = 351,30{N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{FD}=\sigma_{BF} + 0,90\cdot (+\Delta\sigma_{2F}-\Delta\sigma_{3F})-\sigma_{A,KURVE}-\sigma_{A,RESIDULAL}+\sigma_{A,TEMP} | |||
</math> | |||
<math> | |||
\sigma_{FD}=82,80+0,90\cdot(+31,80-179,00)-96,00-60,00+100,00 = -105,70{N\over mm^2} | |||
</math> | |||
'''Dynamisk vurdering''' | |||
<math> | |||
\sigma_{HA}=-\sigma_{BH} + 0,90\cdot (\Delta\sigma_{1H}+\Delta\sigma_{2H}+\Delta\sigma_{3H}) +\sigma_{A,KURVE}-\sigma_{A,RESIDULAL}+\sigma_{A,TEMP} | |||
</math> | |||
<math> | |||
\sigma_{HA}=-66,20+0,90\cdot(94,40+53,40+153,60)+48,00-40,00+100,00=316,70 {N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{HB}=-\sigma_{BH} + 0,90\cdot (\Delta\sigma_{1H}-\Delta\sigma_{2H}-\Delta\sigma_{3H}) -\sigma_{A,KURVE}-\sigma_{A,RESIDULAL}+\sigma_{A,TEMP} | |||
</math> | |||
<math> | |||
\sigma_{HB}=-66,20+0,90\cdot(94,40-53,40-153,60)-48,00-40,00+100,00=-151,00 {N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{FC}=\sigma_{BF} + 0,90\cdot (-\Delta\sigma_{2F}+\Delta\sigma_{3F}) +\sigma_{A,KURVE}-\sigma_{A,RESIDULAL}+\sigma_{A,TEMP} | |||
</math> | |||
<math> | |||
\sigma_{FC}= 132,40+0,90\cdot(-50,80+286,00)+96,00-60,00+100,00 = 480,00{N\over mm^2} | |||
</math> | |||
<math> | |||
\sigma_{FD}=\sigma_{BF} + 0,90\cdot (+\Delta\sigma_{2F}-\Delta\sigma_{3F})-\sigma_{A,KURVE}-\sigma_{A,RESIDULAL}+\sigma_{A,TEMP} | |||
</math> | |||
<math> | |||
\sigma_{FD}= 132,40+0,90\cdot(+50,80-286,00)-96,00-60,00+100,00 = -136,00{N\over mm^2} | |||
</math> | |||
Det gjentas følgende vedr. anbefalte tillatte spenninger: | |||
*For skinne i kvalitet R 260 Mn gjelder følgende grenseverdier for anbefalte tillatte spenninger: | |||
I punktene A og B: 325 N/mm<sup>2</sup> | |||
I punktene C og D: 250 N/mm<sup>2</sup> | |||
I symmetriakse i fot: 200 N/mm<sup>2</sup> | |||
*For skinne i kvalitet R200Mn vurderes for Flåmsbana følgende grenseverdier for anbefalte tillatte spenninger: | |||
I punktene A og B: 285 N/mm<sup>2</sup> | |||
I punktene C og D: 210 N/mm<sup>2</sup> | |||
I symmetriakse i fot: 160 N/mm<sup>2</sup> | |||
De anbefalte spenningene gjelder i dynamisk tilstand ved vedvarende opptreden av belastninger. | |||
De beregnede spenningene er å betrakte som 99,85 % verdier og forekommer derfor sjeldent. | |||
Det er dermed ikke overhengende fare for opptreden av plastiske deformasjoner. | |||
Beregningene er sammenfattet i tabeller i det etterfølgende. | |||
Den første tabellen viser de beregnede belastninger i kvasistatisk tilstand. | |||
Den andre tabellen viser de beregnede belastninger i dynamisk tilstand | |||
{| class="wikitable" style="text-align:center" width="900px" | |||
|- | |||
!Kvasistatisk betraktning | |||
!colspan=2|Spor (49E1 og a = 640 mm) | |||
Radius R = 150 m, D = 50 mm, | |||
V = 30 km/h | |||
I = 22 mm (a<sub>q</sub> = 0,14 m/s<sup>2</sup>) | |||
Skinnekvalitet R 200 Mn; 700 N/mm<sup>2</sup> | |||
!colspan=2|Spor (49E1 og a = 640 mm) | |||
Radius R = 150m, D = 50 med mer | |||
V = 30 km/h | |||
I = 22 mm (a<sub>q</sub> = 0,14 m/s<sup>2</sup>) | |||
Skinnekvalitet R 260 Mn; 900 N/mm<sup>2</sup> | |||
|- | |||
!Krefter (kN) ||width="150px"| Målt|| Beregnet||width="150px"| Målt|| Beregnet | |||
|- | |||
|P (kN)|| || 213,00 || ||213,00 | |||
|- | |||
|Q<sub>STATIKK</sub> (kN)|| || 106,50|| || 106,50 | |||
|- | |||
|ΔQ<sub>STATIKK</sub> (kN)|| || 8,50|| || 8,50 | |||
|- | |||
|Q<sub>KV.STATIKK</sub> (kN)|| || 115,00|| || 115,00 | |||
|- | |||
|Q<sub>DYN</sub> (kN) || || || || | |||
|- | |||
|Y<sub>KV.STATIKK</sub> (kN)|| ||60,00|| || 60,00 | |||
|- | |||
|Y<sub>DYN</sub> (kN)|| || || || | |||
|- | |||
|Y/Q)<sub>2m DYN</sub>|| || || || | |||
|- | |||
|C<sub>TOTAL</sub> (N/mm<sup>3</sup>)|| || 0,15|| || 0,15 | |||
|- | |||
|Svilleavstand|| || 640 mm|| || 640 mm | |||
|- | |||
|L || ||720 mm || || 720 mm | |||
|- | |||
|¾ x Π x L || ||1822 mm || ||1822 mm | |||
|- | |||
|colspan=5 |Beregninger av belastninger på skinneprofil | |||
|- | |||
|Kvasistatisk bøyemoment || || 20,70 kNm || || 20,70 kNm | |||
|- | |||
|Hovedspenninger || | |||
| 41,40 N/mm | |||
82,80 N/mm<sup>2</sup> | |||
| | |||
|1282,80 N/mm<sup>2</sup> | |||
82,80 N/mm<sup>2</sup> | |||
|- | |||
|Torsjonsmoment || ||2,09 kNm|| ||2,09 kNm | |||
|- | |||
| rowspan=3| Delspenninger | |||
| | |||
|62,10 N/mm<sup>2</sup> | |||
0 | |||
| | |||
|62,10 N/mm<sup>2</sup> | |||
0 | |||
|- | |||
| | |||
|33,50 N/mm<sup>2</sup> | |||
31,80 N/mm<sup>2</sup> | |||
| | |||
|33,50 N/mm<sup>2</sup> | |||
31,80 N/mm<sup>2</sup> | |||
|- | |||
| | |||
|96,00 N/mm<sup>2</sup> | |||
179,00 N/mm<sup>2</sup> | |||
| | |||
|96,00 N/mm<sup>2</sup> | |||
179,00 N/mm<sup>2</sup> | |||
|- | |||
|rowspan=4|Resulterende | |||
spenninger på bøyepåkjenning | |||
| ||31,00 N/mm<sup>2</sup>||| ||131,00 N/mm<sup>2</sup> | |||
|- | |||
| ||- 102,00 N/mm<sup>2</sup>|| || - 102,00 N/mm<sup>2</sup> | |||
|- | |||
| ||215,30 N/mm<sup>2</sup>|| ||215,30 N/mm<sup>2</sup> | |||
|- | |||
| ||-49,70 N/mm<sup>2</sup>|| ||-49,70 N/mm<sup>2</sup> | |||
|- | |||
|rowspan=2|Grenseverdi for spenning|| ; || || || | |||
|- | |||
| ; || || || | |||
|- | |||
|Egenspenninger | |||
| I | |||
σ<sub>RC, D</sub> | |||
| -40 N/mm<sup>2</sup> | |||
-60 N/mm<sup>2</sup> | |||
| | |||
| -40 N/mm<sup>2</sup> | |||
- 60 N/mm<sup>2</sup> | |||
|- | |||
|Temperatur|| σ<sub>TEMP</sub>||100 N/mm<sup>2</sup>|| ||100 N/mm<sup>2</sup> | |||
|- | |||
| rowspan=2 | Bøyning i kurver|| ||± 48,00 N/mm<sup>2</sup>|| ||± 48,00 N/mm<sup>2</sup> | |||
|- | |||
| ||± 90,00 N/mm<sup>2</sup>|| ||± 90,00 N/mm<sup>2</sup> | |||
|} | |||
{| class="wikitable" style="text-align:center" width="900px" | |||
|- | |||
!Dynamisk betraktning | |||
!colspan=2|Spor (49E1 og a = 640 mm) | |||
Radius R = 150 m, D = 50 mm, | |||
V = 30 km/h | |||
I = 22 mm (a<sub>q</sub> = 0,14 m/s<sup>2</sup>) | |||
Skinnekvalitet R 200 Mn; 700 N/mm<sup>2</sup> | |||
!colspan=2|Spor (49E1 og a = 640 mm) | |||
Radius R = 150m, D = 50 med mer | |||
V = 30 km/h | |||
I = 22 mm (a<sub>q</sub> = 0,14 m/s<sup>2</sup>) | |||
Skinnekvalitet R 260 Mn; 900 N/mm<sup>2</sup> | |||
|- | |||
!Krefter (kN) ||width="150px"| Målt|| Beregnet||width="150px"| Målt|| Beregnet | |||
|- | |||
|P (kN)|| || 213,00 || ||213,00 | |||
|- | |||
|Q<sub>STATIKK</sub> (kN)|| || 106,50|| || 106,50 | |||
|- | |||
|ΔQ<sub>STATIKK</sub> (kN)|| || 8,50|| || 8,50 | |||
|- | |||
|Q<sub>KV.STATIKK</sub> (kN)|| || 115,00|| || 115,00 | |||
|- | |||
|Q<sub>DYN</sub> (kN) || ||184,00 || ||184,00 | |||
|- | |||
|Y<sub>KV.STATIKK</sub> (kN)|| ||60,00|| || 60,00 | |||
|- | |||
|Y<sub>DYN</sub> (kN)|| ||96,00 || ||96,00 | |||
|- | |||
|Y/Q)<sub>2m DYN</sub>|| || || || | |||
|- | |||
|C<sub>TOTAL</sub> (N/mm<sup>3</sup>)|| || 0,15|| || 0,15 | |||
|- | |||
|Svilleavstand|| || 640 mm|| || 640 mm | |||
|- | |||
|L || ||720 mm || || 720 mm | |||
|- | |||
|¾ x Π x L || ||1822 mm || ||1822 mm | |||
|- | |||
|colspan=5 |Beregninger av belastninger på skinneprofil | |||
|- | |||
|Dynamisk bøyemoment || || 33,10 kNm || || 33,10 kNm | |||
|- | |||
|Hovedspenninger || | |||
|66,20 N/mm2 | |||
132,40 N/mm2 | |||
| | |||
|66,20 N/mm2 | |||
132,40 N/mm2 | |||
|- | |||
|Torsjonsmoment || ||3,34 kNm|| ||3,34 kNm | |||
|- | |||
| rowspan=3| Delspenninger | |||
| | |||
|99,40 N/mm<sup>2</sup> | |||
0 | |||
| | |||
|99,40 N/mm<sup>2</sup> | |||
0 | |||
|- | |||
| | |||
|53,40 N/mm<sup>2</sup> | |||
50,80 N/mm<sup>2</sup> | |||
| | |||
|53,40 N/mm<sup>2</sup> | |||
50,80 N/mm<sup>2</sup> | |||
|- | |||
| | |||
|153,60 N/mm<sup>2</sup> | |||
286,00 N/mm<sup>2</sup> | |||
| | |||
|153,60 N/mm<sup>2</sup> | |||
286,00 N/mm<sup>2</sup> | |||
|- | |||
|rowspan=4|Resulterende | |||
spenninger på bøyepåkjenning | |||
| ||208,70 N/mm<sup>2</sup>|| ||208,70 N/mm<sup>2</sup> | |||
|- | |||
| ||- 163,00 N/mm<sup>2</sup>|| || - 163,00 N/mm<sup>2</sup> | |||
|- | |||
| ||344,10 N/mm<sup>2</sup>|| ||344,10 N/mm<sup>2</sup> | |||
|- | |||
| ||-80,00 N/mm<sup>2</sup>|| ||-80,00 N/mm<sup>2</sup> | |||
|- | |||
|rowspan=2|Grenseverdi for spenning|| ; ||± 285 N/mm<sup>2</sup> || ||± 325 N/mm<sup>2</sup> | |||
|- | |||
| ; ||± 210 N/mm<sup>2</sup> || ||± 250 N/mm<sup>2</sup> | |||
|- | |||
|Egenspenninger | |||
| σ<sub>R A, B</sub> | |||
σ<sub>R C, D</sub> | |||
| -40 N/mm<sup>2</sup> | |||
-60 N/mm<sup>2</sup> | |||
| | |||
| -40 N/mm<sup>2</sup> | |||
- 60 N/mm<sup>2</sup> | |||
|- | |||
|Temperatur|| σ<sub>TEMP</sub>||100 N/mm<sup>2</sup>|| ||100 N/mm<sup>2</sup> | |||
|- | |||
| rowspan=2 | Bøyning i kurver|| ||± 48,00 N/mm<sup>2</sup>|| ||± 48,00 N/mm<sup>2</sup> | |||
|- | |||
| ||± 90,00 N/mm<sup>2</sup>|| ||± 90,00 N/mm<sup>2</sup> | |||
|} | |||
Det skal formuleres kommentarer til beregningene. | |||
På rett strekning og i kurver med store radier oppstår spenninger i dynamisk tilstand i skinnefot i symmetriaksen som er lavere enn tillatt tilrådelig spenningskapasitet for skinner i kvalitet R 200Mn og i kvalitet R 260Mn. Det skulle derfor ikke være fare for utmatting. | |||
Det påpekes at den kvasistatiske kraft Q<sub>KV.ST.</sub> vurderes i samsvar med tilhørende kvasistatisk kraft i EN 14363 evaluert i et lavpassfilter på 20 Hz. Denne kraften er en 50 % verdi knyttet til belastningen. | |||
Den dynamiske kraft Q<sub>DYN</sub> vurderes i samsvar med tilhørende dynamisk kraft i EN 14363 evaluert i et lavpassfilter på 20 Hz. Denne kraften er en 99,85 % verdi og forekommer dermed meget sjeldent. | |||
I kurver med små radier opptrer en kombinasjon av eksentrisk virkende vertikalkrefter og horisontale krefter. I en kvasistatisk vurdering er de beregnede spenninger i kant av skinnehode og skinnefot tolererbare og akseptable i skinnekvalitet R 200 Mn og R 260 Mn. De kvasistatiske spenninger er å oppfatte som 50 % verdier i en statistisk vurdering og opptrer dermed ofte. | |||
Dynamisk betraktning for eksentrisk virkende vertikalkrefter og horisontale krefter gir beregningsmessig meget høye spenninger i kantene på skinnehode og i skinnefot. De beregnede spenninger overskrider anbefalte grenseverdier; særlig gjelder dette for skinnekvalitet R 200 Mn. Plastiske deformasjoner vil kunne opptre teoretisk. Imidlertid er det nødvendig å være oppmerksom på de beregnede dynamiske spenningene er å oppfatte som 99,85 % verdier i en vurdering i et lavpassfilter på 20 Hz og at de derfor opptrer meget sjeldent og har lokal opptreden. De største spenningene som opptrer i underkant skinnefot i punkt C har en størrelse på 344,10 N/mm<sup>2</sup>; dvs. ca. 50 % av strekkfastheten for skinnestål R 200 Mn. | |||
I tillegg til belastningen fra rullende materiell opptrer også belastning forårsaket av kurveradius, egenspenninger og temperaturspenninger. I særlige tilfeller kan da resulterende spenning bli opp mot 480 N/mm<sup>2</sup>. Imidlertid er det da nødvendig å være oppmerksom på at temperaturspenningene sjeldent opptrer med maksimale verdier. Aspektet vil ha betydning for sannsynlighet for opptreden av plastisk deformasjon i punkt C. | |||
Det er også å bemerke at skinner i kvalitet R200 Mn har ligget i sporet siden ca. 1965. Ifølge BANADATA Innsyn finnes ca. 10.000 – 11.000 løpemeter skinner i denne kvaliteten. Øvrige skinner har kvalitet R900 Mn og er lagt i sporet på et senere tidspunkt. | |||
Det blir dermed et spørsmål hvorfor skinnene i R 200 Mn ennå ligger i sporet. | |||
<big>'''I.1.2 Beregning i henhold til modell med en frihetsgrad'''</big> | |||
El 18 består av et lokomotiv med avfjæret vognkasse, avfjæret boggiramme og uavfjæret hjulsett. | |||
Det beregnes de dynamiske vertikale krefter med utgangspunkt i nedennevnte formel. Det tas dermed i betrakting den vertikale akselerasjon av lokomotivets vognkasse. | |||
For ikke å gjøre beregningen for omstendelig blir vognen og boggiramme vurdert som en avfjæret masse i samvirke. Med den lave hastighet som eksisterer på Flåmsbana, er dette greit. | |||
EN 14363 setter en grenseverdi for den vertikale akselerasjon til 3 m/s<sup>2</sup> for bevegelse av vognkasser i lokomotiv. Denne verdien benyttes i det etterfølgende. | |||
Det gjennomføres en beregning som tar hensyn til vognkassens karakteristiske parametere og irregulariteter i sporet: | |||
<math> | |||
Q_{DYN}=Q_{NOM}+Q_{d LF}+Q_{d HF} | |||
</math> | |||
<math> | |||
Q_{DYN}=Q_{0}+Q_{d LF}+Q_{d HF}=(m_c +m_w)\cdot g+m_c\cdot a_c+m_w\cdot v^2\cdot z'' +{ \Delta z\over H_r(i\Omega )+H_w(i\Omega)+{1\over k_h}}+0,10\cdot Q_{HENG} | |||
</math> | |||
Termen kan omskrives: | |||
<math> | |||
m_w\cdot v^2\cdot z'' =m_w \cdot\left({2\pi v\over L}\right)^2 \cdot z | |||
</math> | |||
<math> | |||
Q_{DYN}=Q_{0}+Q_{d LF}+Q_{d HF}=(m_c +m_w)\cdot g+m_c\cdot a_c+m_w \cdot\left({2\pi v\over L}\right)^2 \cdot z +{ \Delta z\over H_r(i\Omega )+H_w(i\Omega)+{1\over k_h}}+0,10\cdot Q_{HENG} | |||
</math> | |||
Det regnes med følgende verdier for parametere: | |||
Masse av vogn og delvis boggi på et hjulsett: m<sub>C</sub> = 20300 kg | |||
Masse av hjulsett og delvis boggi (uavfjæret masse): m<sub>W</sub> = 1000 kg | |||
Tyngdens akselerasjon: g = ca. 10 m/s<sup>2</sup> | |||
Vognkassens vertikale akselerasjon med boggiramme: a<sub>C</sub> (skal beregnes); (m/s<sup>2</sup>) | |||
Framføringshastighet: v (m/s) | |||
Vertikal irregularitet i sporet: z (m) | |||
Bølgelengde i sporet (cosinusspor): L (m) | |||
Overføringsfunksjon for rifler og bølger på skinne (se formel) | |||
Statisk hjulkraft av lokomotiv: | |||
<math> | |||
{1\over 2}\cdot(m_W+m_B+m_C)\cdot g=106,50 \ kN | |||
</math> | |||
Kvasistatisk tillegg: | |||
<math> | |||
{1\over 2}\cdot(m_W+m_B+m_C)\cdot g=8,50 \ kN | |||
</math> | |||
Kvasistatisk hjulkraft: | |||
<math> | |||
Q_{KV.STAT.}=115,00 \ kN | |||
</math> | |||
Vognkassens dimensjonerende parametere inkludert boggiramme på et hjulsett: | |||
Demperkarakteristikk (antatt): d = 80 kNs/m | |||
Karakteristikk for fjærstivhet: c = 1080 kN/m | |||
Sporkarakteristikker: | |||
Bølgelengde i cosinusspor (belastet spor): L = 10 m | |||
Vertikal irregularitet i skinne: z = 0,05 m | |||
Framføringshastighet: V = 30 km/h (v = 8,3 m/s) | |||
Omløpshastighet: | |||
<math> | |||
\Omega={2\pi v\over L}={2 \cdot \pi \cdot 8,3\over | |||
10}= 5,2 \ rad/s | |||
</math> | |||
Vognens egenfrekvens inkludert boggiramme relatert til en aksel (antakelse om lik fordeling): | |||
<math> | |||
\omega= \sqrt{c\over m}= \sqrt {1080 \cdot 10^3\over 20300}= 7,3 \ rad/s | |||
</math> | |||
Dimensjonsløs frekvens for bevegelse: | |||
<math> | |||
\eta = {\Omega\over \omega}={5,2\over 7,3}=0,71 | |||
</math> | |||
Dempingsgrad: | |||
<math> | |||
D={d \over 2\sqrt{c\cdot m}}={80\cdot 10^3\over 2\sqrt{1080\cdot 10^3\cdot 10300}}=0,27 | |||
</math> | |||
Vertikale akselerasjonsbevegelser til vognkasse med boggiramme: | |||
<math> | |||
a_C=-\Omega^2\cdot {\sqrt{1+(2D\eta)^2}\over \sqrt{(1-\eta^2)^2+(2D\eta )^2}}\cdot z | |||
</math> | |||
<math> | |||
a_C = -5,2^2\cdot {\sqrt{1+(2 \cdot 0,27 \cdot 0,71)^2} \over \sqrt{(1-0,71^2)^2+(2 \cdot 0,27 \cdot 0,71)^2 } } \cdot 0,05 = -2,30 {m\over s^2} | |||
</math> | |||
Vertikalbevegelse til vognkasse med boggiramme: | |||
<math> | |||
u_Z= {\sqrt{1+(2D\eta)^2}\over \sqrt{(1-\eta^2)^2+(2D\eta )^2}}\cdot z | |||
</math> | |||
<math> | |||
u_Z = {\sqrt{1+(2 \cdot 0,27 \cdot 0,71)^2} \over \sqrt{(1-0,71^2)^2+(2 \cdot 0,27 \cdot 0,71)^2 } } \cdot 0,05 = 85 \ mm | |||
</math> | |||
I det etterfølgende settes vognkassens akselerasjon over boggi lik grenseverdi i EN 14363 til aC = 3,00 m/s<sup>2</sup> > 2,30 m/s<sup>2</sup>. Det gjentas at verdiene for demperkarakteristikk og fjærkarakteristikk er antatt. | |||
Dynamisk kraft fra avfjæret vognkasse med boggiramme på grunn av vertikal akselerasjonsbevegelse: | |||
<math> | |||
{1\over 2}\cdot(m_C+m_B)\cdot a_C={1\over2}\cdot 20300 \cdot 3,00=30,45 \ kN | |||
</math> | |||
Dynamisk kraft fra hjulsett (uavfjæret masse): | |||
<math> | |||
{1\over 2}\cdot m_W\cdot\left({2\pi v\over L}\right)^2\cdot z ={1\over 2}\cdot 1000\cdot\left( {2\cdot\pi\cdot 8,3\over 10}\right)^2\cdot 0,005=0,70 \ kN | |||
</math> | |||
Kraft fra rifler og bølger på skinnehodet: | |||
Overføringsverdi: | |||
<math> | |||
{\Delta\hat z\over H_r(i\Omega )+h_w(i\Omega ) +{1\over k_h}}=30 \ kN | |||
</math> | |||
Kraft på grunn av hengende sviller: | |||
<math> | |||
Q_{HENG}=0,05\cdot P_0=0,05\cdot 400=15 \ kN | |||
</math> | |||
Resulterende dynamisk kraft på skinne: | |||
<math> | |||
Q_{DYN}=106,50+3,50+30,45+0,70+30,00+15,00=186,15 \ kN | |||
</math> | |||
Beregning av belastning i henhold til formler i avansert metode | |||
Resulterende statisk ballastsiffer er beregnet til: | |||
<math> | |||
C=0,15 {N\over mm^3} | |||
</math> | |||
Fjærstivhet k er beregnet til: | |||
<math> | |||
k={k \over a} ={37,50 \cdot 10^3\over 640}=58,60 {N\over mm^2} | |||
</math> | |||
Ballaststivheten beregnes med svilleavstand a = 640 mm: | |||
<math> | |||
\beta ={k\over a}={37,50\cdot 10^3\over 640}=58,60 {N\over mm^2} | |||
</math> | |||
Produkt av elastisitetsmoment og treghetsmoment: | |||
<math> | |||
B_r=E\cdot I_{X-X}=2,15\cdot 10^5 \cdot 1819 \cdot 10^4=3,91\cdot10^12 \ Nmm^2 | |||
</math> | |||
Deformasjon av skinne ved statisk last: | |||
<math> | |||
y_{II}={Q_{KV.STAT.}\over \sqrt[4]{64\cdot 3,91\cdot 10^{12}\cdot 58,60^3}}=1,28 \ mm | |||
</math> | |||
Dynamisk moment: | |||
<math> | |||
M_{DYN}=Q_{DYN} \cdot \sqrt[4]{B_r\over 64\beta} \ kNm | |||
</math> | |||
<math> | |||
M_{DYN}=186,15\cdot 10^3 \cdot \sqrt[4]{3,91 \cdot 10^{12}\over 64\cdot 58,60}=33,45 \ kNm | |||
</math> | |||
Dynamisk spenning i underkant skinne: | |||
<math> | |||
\sigma_{DYN}={33,45\cdot 10^6\over 248 \cdot 10^3}=135,00 \left({N\over mm^2} \right) | |||
</math> | |||
Sikkerhetsfaktor er bestemt til 1,10: | |||
<math> | |||
\gamma \cdot \sigma_{DYN,II}=1,10\cdot 135,00=148,50 {N\over mm^2} < zul \ \sigma_{dF}=160; \ \ 200{N\over mm^2} | |||
</math> | |||
Kraft på sville i befestigelse blir: | |||
<math> | |||
R_{DYN}=({186,50\cdot 10^3\over \sqrt[4]{64\cdot 2,15\cdot 10^5\cdot 1819\cdot 10^4\cdot 58,6^3}})\beta \cdot a=83,00 \ kN | |||
</math> | |||
Trykk mot underside sville: | |||
<math> | |||
p_{DYN}={2\cdot R_{DYN}\over (l-m)\cdot b_1} | |||
</math> | |||
<math> | |||
p_{DYN}={2\cdot 83,00\over 500000}=0,33 \ {N\over mm^2} | |||
</math> | |||
Beregningsmetoden gir en dypere analyse av virkningen av de ulike opptredende laster og krefter og dermed en bedre forståelse av hva som skjer i sporet; i dette tilfellet på rett strekning. | |||
På grunn av den lave hastigheten blir beregningsresultatene omtrent de samme som for Zimmermanns metode med dynamisk tillegg. | |||
Det må imidlertid ikke være tvil om hvilken metode som er den beste; det er den avanserte metode. | |||
== Belastning i befestigelse == | |||
Sporet på Flåmsbana er lagt ut med tresviller. Det finnes overveiende 2 befestigelser: | |||
*Pandrol (trolig PR 341 A) | |||
*Hey – Back (trolig HBFJ49) | |||
Figur 9.1 viser befestigelse av type Hey – Back. | |||
[[Fil:Figur_09.1.PNG|600px|thumb||center|<caption> Figur 9.1 Befestigelse av type Hey – Back på tresviller</caption>]] | |||
På grunn av kurver med radier R = 150 m opptrer horisontale og vertikale krefter i befestigelsen. Aspektet gir en resulterende kraft rettet mot befestigelsen. Det forventes ikke en økning i helningsvinkelen for virkningslinjen for den resulterende kraft fra det tyngre lokomotivet El 18 sammenlignet med virkningslinjen for de kombinasjonskrefter som oppstår ved framføring av det lettere lokomotivet El 17. Med El 17 eksisterer betydelig erfaring for virkning på befestigelsen. | |||
Imidlertid vil det trolig bli en økning i de horisontale krefter fra El 18 på grunn av større tyngde. Aspektet kan føre til hurtigere opptreden av slitasje i skruehullene på tresvillene på grunn av treets mekaniske egenskaper. Det er derfor nødvendig å føre kontroll med skruene ved for eksempel utøvelse av et dreiemoment (som beskrevet i regelverket). | |||
== Belastninger fra hjulslag og belastning på skjøter i lasket spor på elastisk underlag og i sporveksler == | |||
=== Kraft ved hjulslag på tresviller på elastisk underlag === | |||
Selve slagenergien ved hjulslag er ikke særlig stor; den er i første rekke avhengig av størrelsen på det flate partiet på hjulet og av vognmassen. Slagkraften kan imidlertid bli meget stor og forårsake et kortvarig opptredende bøyemoment av betydelig størrelse. | |||
Det dynamiske moment er i det foregående beregnet til M<sub>DYN</sub> = 33,45 kNm. Dette momentet innbefatter også parametere som korte rifler og bølger på skinnehodet samt svevende sviller. | |||
Det blir tatt utgangspunkt i et hjul med radius r = 550 mm (litt benyttet) og en lengde på det flate partiet på 80 mm. Det blir da antatt et tilfelle som er dårligere enn gjeldende verdi i retningslinjene (60 mm). | |||
Beregninger gir: | |||
<math> | |||
a=\sqrt{550^2-(80/2)^2}=\sqrt{302500 - 1600}=548,50 \ mm | |||
</math> | |||
Pilhøyde i det flate partiet beregnes til: | |||
<math> | |||
f=r-a=550,00-548,50=1,50 \ mm | |||
</math> | |||
Målinger av tester i bl. annet. ORE D 161 viser at ved en aksellast på 22,50 tonn så øker slagkraften med 30 kN/mm for tresviller på elastisk underlag ved framføringshastighet på 30 km/h. | |||
Slagkraften skulle dermed anta en verdi på ca. 45,00 kN. Dette er ikke urovekkende. | |||
=== Støtkrefter i skinneskjøter i lasket spor === | |||
På grunn av de små kurveradier på Flåmsbana er det overveiende lasket spor på hele strekningen (det finnes mellomliggende partier med sveiste skjøter). | |||
I skjøtene opptrer støtkrefter P1 og P2. | |||
Ved irregulariteter på skinnehodet og hjulbane vil det ved framføring av materiell oppstå støt- eller slagkrefter. Slike krefter vil særlig oppstå i laskede skjøter, men også i forbindelse med hjulslag og andre defekter på hjulbane, korte bølgelengder på skinnehodet, diskrete irregulariteter samt sveiste skjøter i for eksempel sporveksler og i vilkårlig opptredende ruhet på skinnehodet. | |||
Litteraturen beskriver støtkreftene ved P1 og P2. Eksempler er vist i figurene 10.1 og 10.2. | |||
[[Fil:Figur_10.1.PNG|600px|thumb||center|<caption> Figur 10.1 Helning av skinne i lasket skjøt</caption>]] | |||
[[Fil:Figur_10.2.PNG|600px|thumb||center|<caption> Figur 10.2 Varianter av lasket skjøt</caption>]] | |||
P1 opptrer umiddelbart på skinnehodet og kan forårsake høye frekvenser og har et mønster som gjør at skinne og hjul beveger seg ut av fase. | |||
Følgende formel er vist: | |||
<math> | |||
P1=P_0 + 2\alpha v \sqrt{k_H\cdot m_{T1}\over 1+{m_{T1}\over m_u}} | |||
</math> | |||
Her betyr: | |||
P<sub>0</sub> er statisk hjulkraft; dvs. identisk med Q<sub>0</sub> (kN) | |||
2 α totale vinkel i fordypningen av irregulariteten (rad) | |||
v er hastighet (m/s) | |||
k<sub>H</sub> er lineariteten i Hertz kontaktstivhet (N/m) | |||
m<sub>T1</sub> er effektiv ekvivalent spormasse for beregning av P1 (kg) | |||
m<sub>U</sub> er uavfjæret masse av hjulsats (kg) | |||
Modell for beregning av slagkrefter og støtkrefter er vist i figur 10.3. | |||
[[Fil:Figur_10.3.PNG|600px|thumb||center|<caption> Figur 10.3 Skisse av modell for beregning av støtkrefter og slagkrefter</caption>]] | |||
P2 opptrer litt senere i overbygningskonstruksjonen og forårsaker skade og nedbrytning av denne. | |||
Følgende formel gjelder: | |||
<math> | |||
P2=P_0+2\alpha v\sqrt{m_U\over m_U +m_{T2}}\cdot \left( 1-{c_T\pi\over \sqrt {k_{T2}\cdot(m_U+m_{T2})}}\right)\cdot\sqrt{k_{T2}m_U} | |||
</math> | |||
I tillegg til ovennevnte betegnelser betyr: | |||
m<sub>T2</sub> er ekvivalent medsvingende spormasse for beregning av P2 (kg) | |||
k<sub>T2</sub> er ekvivalent sporstivhet for beregning av P2 (N/m) | |||
c<sub>T</sub> er ekvivalent spordemping for beregning av P2 (Ns/m) | |||
Litteraturen beskriver også en enklere formel: | |||
<math> | |||
P2=P0+\lambda \cdot 2\cdot\alpha\cdot v\cdot\sqrt{k\cdot m_U} | |||
</math> | |||
Her betyr: | |||
λ er dimensjonsløs faktor avhengig av sporpakking (≤ 1) | |||
k er sporets stivhet som er beregnet til 37,50 N/m | |||
Slagkreftene eller støtkreftene blir i det vesentligste en funksjon av hjulkrat og hastighet. | |||
I eksisterende situasjon er hjullasten omtrent 10,65 tonn og hastigheten er 30 km/h. | |||
Tabell under gir oversikt over kilder til opphav av P1 og P2 krefter og tiltak som må iverksettes. | |||
{| class="wikitable" style="text-align:center" width="900px" | |||
|+ Tabell P1 og P2 krefter og vedlikehold | |||
|- | |||
!Type av irregularitet | |||
!Utøvende kraft | |||
!Vedlikeholdstiltak | |||
|- | |||
|Hjulslag og defekter på hjul|| P1; P2 ||hjuldreining | |||
|- | |||
|Korte bølgelengder på skinnehodet|| P1; P2 ||Sliping | |||
(slag- og støtkrefter blir normalt ikke dimensjonerende) | |||
|- | |||
|Diskrete irregulariteter i sveise-skjøter, laskede skjøter, sporveksler|| P1; P2; rullende materiell|| Utretting; sliping, pakking | |||
|- | |||
|Vilkårlig opptredende ruhet på skinnehodet|| P1; P2|| Sliping | |||
|- | |||
|Vilkårlig opptredende feil i ballast|| Rullende materiell ||Pakking | |||
|} | |||
<small>Tabell P1 og P2 krefter og vedlikehold</small> | |||
Det skal gjennomføres en beregning for eksisterende og framtidig situasjon. | |||
Følgende parameterverdier antas for ny situasjon: | |||
Statisk hjulkraft: P<sub>0</sub> = 106,50 kN | |||
2 x vinkel for skjøt: 2 α = 20 mrad = 0,02 radianer | |||
Hertzian kontakt fjærstivhet: k<sub>H</sub> = 1,40 · 109 N/m | |||
Effektiv spormasse: m<sub>T1</sub> = 2000 · 0,60 · 0,30 · 1,20 = 432 kg | |||
Uavfjæret masse av et halvt hjulsett: m<sub>U</sub> = 500 kg | |||
Hastighet er: V = 30 km/h = 8,33 m/s | |||
Kraften beregnes: | |||
<math> | |||
P1=P_0+2\alpha v\sqrt{k_H\cdot m_{T1}\over 1+{m_{T1}\over m_u}} | |||
</math> | |||
<math> | |||
P1=106,50+2\cdot 0,02 \cdot 8,33\cdot\sqrt{1,40\cdot 10^9\cdot 432\over 1 +{432\over 500}}=106,50+190,00=296,50 \ kN | |||
</math> | |||
<math> | |||
P2=P0+\lambda\cdot 2 \cdot\alpha\cdot v\cdot\sqrt{k\cdot m_U} | |||
</math> | |||
<math> | |||
P2=106,50+1\cdot 2\cdot 0,02\cdot 8,33\cdot \sqrt{37,50\cdot 500}=106,50+45,70=152,20 \ kN | |||
</math> | |||
Følgende parameterverdier antas for eksisterende lokomotiv El 17: | |||
Statisk hjulkraft: P0 = 80 kN | |||
2 x vinkel for skjøt: 2 α = 20 mrad = 0,02 radianer | |||
Hertzian kontakt fjærstivhet: k<sub>H</sub> = 1,40 · 10<sup>9</sup> N/m | |||
Effektiv spormasse: m<sub>T1</sub> = 2000 · 0,60 · 0,30 · 1,20 = 432 kg | |||
Uavfjæret masse av et halvt hjulsett: m<sub>U</sub> = 400 kg | |||
Hastighet er: V = 30 km/h = 8,33 m/s | |||
<math> | |||
P1=80,00+2\cdot 0,02\cdot 8,33\cdot \sqrt{1,40\cdot 10^9 \cdot 432\over 1+{432\over 400}}=80,00+180,0=260,00 \ kN | |||
</math> | |||
<math> | |||
P2=80,00+1\cdot 2\cdot 0,02\cdot 8,33\cdot \sqrt{37,50\cdot 400}=80,00+40,80=120,80 \ kN | |||
</math> | |||
Overgang fra eksisterende lokomotiv med aksellast lik 16 tonn og hastighet lik 30 km/h til nytt lokomotiv med aksellast lik 21,3 tonn og hastighet lik 30 km/h gir en økning i P1 og P2 på om lag en faktor lik 1,15. Økningen i last har en faktor lik 1,33. | |||
=== Belastning i svevende skjøter i lasket spor === | |||
En skjøt i et lasket spor kan få opplegg på 3 ulike måter. I tilfellet av svevende skjøt oppstår et moment på bøyning mellom svillene. En slik skjøt er vist i figur 10.4. | |||
[[Fil:Figur_10.4.PNG|600px|thumb||center|<caption> Figur 10.4 Eksempler på opplegg av skjøt i lasket spor; a) svevende skjøt; b) opplegg på 3 sviller; c) opplegg på 2 sviller</caption>]] | |||
Av de 3 mulige oppleggsmetodene er det bare tilfelle a) som er kritisk. Aspektet henger sammen med at treghetsmomentet til laskene samlet er mindre enn treghetsmomentet til skinnen. På grunn av konstruksjonen kan alternativt skinnene betraktes som utkraget fra sville til skjøt. Det vil derfor bli en større nedsenkning av skinnen når tog passerer over skjøten. | |||
Spennvidde regnet mellom de ytre boltene er om lag 430 mm. Den reelle lysåpning er ca. 250 mm. | |||
Overgang fra El 17 til El 18 gir en lastøkning på en faktor lik 1,33. | |||
Den dynamiske hjulkraft er Q<sub>DYN</sub> = 176,00 kN (se beregninger foran). Momentet blir: | |||
<math> | |||
M_{DYN}=0,175\cdot Q_{DYN}\cdot L=0,161\cdot 176,00\cdot 0,720=30,40 \ kNm | |||
</math> | |||
Formelen er hentet fra Modern Railway Track og termen L er den karakteristiske lengde som er beregnet foran. | |||
Det er foran beregnet et moment på bøyning i dynamisk tilstand for skinner på elastisk underlag lik 31,60 kNm. Dette moment gir en spenning i underkant skinnefot i symmetriaksen σ<sub>DYN</sub> = 141,00 N/mm2. Spenningen i dynamisk tilstand oppfattes som moderat; dette gjelder også for kvalitet R 200 Mn (bruddfasthet lik 680 N/mm2). | |||
Momentet over skjøtåpningen er mindre enn i sporet; 20,40 kNm < 31,60 kNm. | |||
Treghetsmomentet for 2 laskede skjøter er: | |||
<math> | |||
I_{X-X}=2\cdot {1\over 12}\cdot b\cdot h^3=2\cdot {1\over 12}\cdot 25\cdot 95^3=3,57\cdot 10^6 \ mm^4 | |||
</math> | |||
Spenningen i laskene blir: | |||
<math> | |||
\sigma_{DYN}={M\over I_{X-X}}\cdot {1\over2}\cdot y={20,40\cdot 10^6\over 3,57\cdot 10^6}\cdot 47=270 \ {N\over mm^2} | |||
</math> | |||
Tilsvarende spenning fra El 17: | |||
<math> | |||
\sigma_{DYN}={1\over 1,33} \cdot 270,00=204 \ {N\over mm^2} | |||
</math> | |||
Spenningene er beregnet konservativt; dvs. etter en metode som har innebygget mye sikkerhet. De beregnede spenningene representerer de absolutt høyeste verdiene som kan aksepteres; dette gjelder for belastning fra El 18. Stållaskene blir forspente med 4 bolter. | |||
Stållaskene støtter seg på konsollene på skinnefot i overkantkant og på skinnehodet i underkant. Stållaskene behøver dermed ikke å overta belastningen tilsvarende en fritt bærende bjelke. Boltehullene er imidlertid et svakt punkt og dynamiske belastninger kan føre til at utmatting kan inntreffe. | |||
=== Krefter i sporveksler === | |||
Støtkrefter i krysspiss i sporveksel forventes å øke med 15 % ved overgang fra El 17 til El 18. Ved ofte passeringer vil aspektet føre til en noe hurtigere slitasje i krysspissen. | |||
I områder for ledeskinner kan det forekomme at ledeskinnen blir belastet bare på horisontale krefter da de vertikale kreftene fra hjulbane overføres til hovedskinne. Ledeskinnene er festet til underliggende sville og blir dermed utkraget. Ved stor horisontal belastning kan det derfor inntreffe brudd i brakettfot ved små sporveksler. Det er ikke mulig å konkretisere om dette vil skje; sannsynligheten er meget lav. Men brakettene må overvåkes. De nedenstående bilder er hentet fra Ofotbanen og tjener til kunnskapsoverføring. | |||
[[Fil:Figur_10.5.PNG|600px|thumb||center|<caption> Figur 10.5 Illustrasjonsbilde av parti med ledeskinne på indre streng; bildet er hentet fra Ofotbanen</caption>]] | |||
[[Fil:Figur_10.6.PNG|600px|thumb||center|<caption> Figur 10.7 Brudd i brakett i sporveksel (kurverveksel); bilde er hentet fra Ofotbanen</caption>]] | |||
[[Fil:Figur_10.7.PNG|600px|thumb||center|<caption> Figur 10.7 Modellering av belastning på horisontal kraft på brakett</caption>]] | |||
== Belastning på skinnehodet == | |||
Kapitlet inneholder beregner av kontaktspenningene relatert til hjul/skinne kontaktmekanikken. Beregningene er utført i henhold til en forenklet metode og til en mer detaljert metode. | |||
For den forenklede metode antas en rektangulær kontaktflate med et gjennomsnittlig flatetrykk. | |||
For den mer detaljerte metode legges til grunn en elliptisk kontaktflate med en ellipsoide trykkfordeling. | |||
Det er kjent at kontaktflaten i mange operative forhold er ikke – elliptisk. Ikke elliptiske kontaktflater oppstår for eksempel for skinne 60E1 i kombinasjon med hjul S1002 for nominelle tverrprofil. Ikke elliptiske kontaktmodeller krever anvendelse av sofistiske beregningsmetoder iht. Kalkers teorier som ikke blir vurdert her. | |||
=== Forenklet studie === | |||
Denne metoden tar utgangspunkt i et jevnt fordelt trykk i kontaktflaten mellom hjul og skinne. Litteraturen bekrefter at for hjul med diameter mellom 600 mm og 1200 mm kan en simplifisert todimensjonal metode anvendes for beregninger av spenninger i skinnehodet. Alle radier som inngår i beregningene, blir antatt å være uendelige. Unntaket er radius til hjulet som må benyttes. Kontaktarealet blir dermed rektangulært og kontaktbelastningene har form som en semi elliptisk sylinder. Det vises til figur 11.1. | |||
[[Fil:Figur_11.1.PNG|600px|thumb||center|<caption> Figur 11.1 Belastning i kontaktflaten mellom hjul og skinne samt skjærspenninger i en dybde av 2 – 4 mm under skinnehodets overflate</caption>]] | |||
[[Fil:Figur_11.2.PNG|600px|thumb||center|<caption> Figur 11.2 Flatetrykk ved todimensjonal metode i samsvar med bildene i figur 11.1; lengden av den rektangulære flate er 2 b</caption>]] | |||
I denne forenklede metode benyttes det midlere trykket q<sub>mean</sub> i kontaktflaten. Det er foreslått følgende formel: | |||
<math> | |||
q_{mean}=\sqrt{{\pi\cdot E\over 64\cdot (1-v^2)} \cdot{Q\over r\cdot b}} | |||
</math> | |||
Her betyr: | |||
Q er statisk eller kvasistatisk hjulkraft (kN) | |||
r er hjulradius (mm) | |||
2 b er lengde av kontaktflate mellom hjul og skinne (mm) | |||
E er stålets elastisitetsmodul (N/mm<sup>2</sup>) | |||
v er Poissons ratio eller tverrkontraksjonen for stålet | |||
For E = 2,15 · 10<sup>5</sup> N/mm2, v = 0,3 og b = 6 mm (2 b = 12 mm) oppnås en praktisk formel: | |||
<math> | |||
q_{mean}=1374\cdot \sqrt {Q\over r} \ \ \left({N\over mm^2}\right) | |||
</math> | |||
Den maksimale skjærspenning opptrer på tvers av skinnehodet. I lengderetningen vil skjærspenningen avta litt på grunn av belastning fra bøyemomenter. | |||
Uttrykt ved q<sub>mean</sub> beregnes skjærspenning: | |||
<math> | |||
\tau=412\cdot \sqrt {Q\over r} \ \ \left({N\over mm^2}\right) | |||
</math> | |||
For en skinne med stålkvalitet 900 N/mm<sup>2</sup> er den anbefalte maksimale skjærspenning ved gjentatt belastning: | |||
<math> | |||
\tau_{max}=260 \ {N\over mm^2} | |||
</math> | |||
Dvs. at skjærkapasiteten kan utrykkes ved den klassisk kjente tilnærming | |||
<math> | |||
\tau_{max}\approx {\sigma_{BRUDD}\cdot 0,50\over \sqrt3}={900\cdot 0,50\over 1,71}=260 \ {N\over mm^2} | |||
</math> | |||
Forholdet mellom flytespenning og tillatt skjærspenning blir dermed: | |||
<math> | |||
n={900\over 260}=3,46 | |||
</math> | |||
Dersom dette forholdstallet overføres for andre stålkvaliteter, kan tilsvarende anbefalte maksimale skjærspenninger for slike stålkvaliteter angis. For hodeherdede skinner i kvalitet 1100 N/mm<sup>2</sup> kan den tillatte anbefalte maksimale skjærspenning settes høyere: | |||
<math> | |||
\tau_{max}=320 \ {N\over mm^2} | |||
</math> | |||
For bløtere skinner i kvalitet 700 N/mm<sup>2</sup> kan den tillatte anbefalte maksimale skjærspenning vurderes til: | |||
<math> | |||
\tau_{max}=205 \ {N\over mm^2} | |||
</math> | |||
Med ovenfor angitte formler kan den nødvendige hjulradius beregnes for å unngå for store kontaktspenninger og skjærspenninger i skinnehodet. Spørsmålet er hvilken hjulradius som skal legges til grunn; et helt nytt hjul levert fra leverandør eller et hjul som er halvt eller delvis utnyttet, dvs. midlere eller delvis utnyttet hjuldiameter før hjulet må skrotes. | |||
Den største tillatte hjulkraft eller kvasistatisk hjulkraft i kurver som funksjon av hjulradius r kan uttrykkes: | |||
<math> | |||
Q_{tillatt}=5,26\cdot r \cdot \left( {\sigma_{brudd}\over v} \right)^2 \cdot 10^{-7} \ \ (kN) | |||
</math> | |||
Den tillatte minste hjulradius som funksjon av hjulkraft eller kvasistatisk hjulkraft kan uttrykkes: | |||
<math> | |||
r_{tillatt}=1,90\cdot Q \cdot \left( {v\over \sigma_{brudd}} \right)^2 \cdot 10^{6} \ \ (mm) | |||
</math> | |||
Her betyr: | |||
υ er en sikkerhetsfaktor; i tilfellet for El 18 kan denne verdien settes lik 1,10. | |||
Vertikalkraften Q er enten statisk kraft på rett linje eller kvasistatisk kraft i kurver; dvs. i kurver må det kvasistatiske tillegget trekkes fra for å fastsette den tillatte hjulkraft. | |||
I utpregede strekningsavsnitt hvor bremsing og traksjon forekommer, blir belastninger på skinnehodet større. Kryp i lengderetningen vil opptre. I tillegg oppstår kryp i tverretningen i kurver med små radier. Aspektene fører til større opptredende hovedspenninger i en dybde av 4 – 6 mm under overflaten av skinnehodet. I dette tilfellet avtar ikke skjærspenningene raskt av. Forholdet fører til høyere slitasje. | |||
I kurver med små radier R < 500 m bør den tillatte akselkraft eller hjulkraft reduseres med ca. 20 % i forhold til den beregnede kraft som framkommer i ovennevnte formler. | |||
=== Belastning iht. Hertz teori === | |||
I Hertz modell blir det antatt en elliptisk kontaktflate; dvs. ikke rektangulært som i den forenklede modell. Den maksimale spenning i middelpunktet i kontaktellipsen uttrykkes ved følgende formel: | |||
<math> | |||
p_0={3\over 2}\cdot {N\over \pi a b} | |||
</math> | |||
N er normalkraften; på rett strekning er det imidlertid tillatt å benytte hjulkraften Q uten at feilberegningen blir for stor da kontaktpunktsvinkelen normalt er liten. | |||
Trykkfordelingen i den elliptiske kontaktflate er vist i figur 11.3. | |||
[[Fil:Figur_11.3.PNG|600px|thumb||center|<caption>Figur 11.3 Flatetrykk i en tredimensjonal metode iht. Hertz</caption>]] | |||
Formelen vil føre til høyere kontaktspenninger enn de som beregnes med den simplifiserte metode. Formelen gir imidlertid et nøyaktigere resultat og er derfor mer relevant. Det er av den grunn nødvendig å etablere et annet regime for vurdering. Dette skjer ved anvendelse av Shakedown diagrammet. | |||
I figur 11.4 er dette diagrammet anskueliggjort: | |||
[[Fil:Figur_11.4.PNG|600px|thumb||center|<caption> Figur 11.4 Shakedown diagrammet </caption>]] | |||
Abscissen i Shakedown diagrammet viser friksjonskoeffisienten μ; dvs. forholdet mellom resulterende tangential krypkraft og normalkraft. For rett strekning kan med tilstrekkelig nøyaktighet vertikalkraften benyttes (i stedet for normalkraften). For tangentialkraften legges til grunn at det handler om ren glidning av hjulet i skinnens lengderetning med en konstant friksjonskoeffisient μ. Lav friksjonskoeffisient indikerer våte eller smurte skinner og høy friksjonskoeffisient beskriver tørre skinner. | |||
Ordinaten indikerer kvotienten flatetrykket p<sub>0</sub> i kontaktflaten i forhold til kapasitet på skjær ke i stålet i skinnehodet. | |||
Flyt under overflaten i skinnehodet (eller i det indre av skinnehodet) vil inntreffe ved vedvarende høye belastninger for µ ≤ 0,30. For tørre skinner (µ > 0,30) opptrer flyt i overflaten av skinnehodet ved gjentatte høye belastninger. | |||
Det skilles mellom punktkontakt og linjekontakt. | |||
I ovennevnte diagram benyttes forholdet mellom p<sub>0</sub> og k<sub>e</sub>. Utelatt i vurderingen så langt er skinnestålets kvalitet og dermed kapasitet for k<sub>e</sub>. Som allerede nevn kan følgende verdier benyttes: | |||
{| class="wikitable" style="text-align:center" width="700px" | |||
|- | |||
|Stålkvalitet p<sub>0</sub> (N/mm<sup>2</sup>)|| 700|| 900|| 1100 | |||
|- | |||
|Skjærkapasitet k<sub>e</sub> (N/mm<sup>2</sup>)|| 205|| 260|| 320 | |||
|} | |||
I et dokument for Rail Safety & Standards Board | |||
“Research Programme | |||
Engineering | |||
Management and understanding of | |||
Rolling contact fatigue | |||
Literature Review” | |||
peker artikkelforfatterne (blant annet professor A. Kapoor fra Newcastle University) på det faktum at på overflaten av skinnehodet, så blir svært ofte belastningen vesentlig høyere enn den nominelle Hertz belastning (ifølge denne teori) og at riss dermed vil oppstå. I samme artikkel blir vist en utgave av Shakedown diagrammet som er gjengitt under. Den heltrukne linjen er Shakedown diagram for normale skinner. Det er synlig at kontaktspenningene vurderes å kunne anta grenseverdier opp mot 1000 N/mm<sup>2</sup> for en friksjonskoeffisient μ på inntil 0,15 for så å avta med høyere koeffisienter (mer tørre skinner). | |||
En skinne i normal kvalitet antas å ha strekkfasthet på 900 N/mm<sup>2</sup>, dvs. kvalitet R 260 Mn. | |||
[[Fil:Figur_07.5.PNG|600px|thumb||center|<caption> Figur 7.5 Shakedown for skinner i vanlig stålkvalitet og for hodeherdede skinner etter A. Kapoor (A. Kapoor er en meget respektert ekspert for aspekter knyttet til kontaktmekanikken hujl/skinne) </caption>]] | |||
For μ = 0,30 blir antatt en grenseverdi for kontaktspenning lik ca. 800 N/mm<sup>2</sup>. Ved anvendelse av samme forholdstall n = 3,76 mellom anbefalt maksimal skjærkapasitet og kontaktspenning avledet av normalkraften, gir dette en skjærkapasitet på ca. 230 N/mm<sup>2</sup>. | |||
=== Ikke elliptiske kontaktflater i hjul/skinne kontaktmekanikken === | |||
Det er dokumentert at det for visse geometrier i hjul/skinne kontaktmekanikken forekommer ikke elliptiske kontaktflater. Aspektet gjelder for eksempel for kombinasjonen av nominelt hjulprofil S1002 og nominelt profil i skinnehode til skinne 60E1 i området for løpeflaten på skinnehodet. | |||
For skinne 60E1 endrer krumningen i profilradiene på skinnehodet seg abrupt på en slik måte at det oppstår ikke elliptiske kontaktflater. Det er utgitt presentasjoner mht. dette teamet, men det vil føre for langt å gå inn på aspektet her. | |||
[[Fil:Figur_11.5.PNG|600px|thumb||center|<caption> Figur 11.5 Ikke elliptisk kontaktflate med fordeling av belastningstrykket) </caption>]] | |||
=== Forutsetninger iht. Hertz teori === | |||
Det skal i det etterfølgende gjøres noen simplifiserte beregninger av kontaktflate mellom hjul og skinne iht. teorier til Hertz. Det antas dermed en elliptisk kontaktflate ved framføring av materiellet på rett linje eller i kurver med store radier. Ellipsens store halvakse er i tverretningen av skinneprofilet og den lille halvakse er i skinnens lengderetning, dvs. i kjøreretningen til materiellet. Videre antas en elliptisk fordeling av kontaktspenningene over den elliptiske flate. | |||
Normalkraften må først beregnes. På rett linje for begge skinner og i innerstreng i sirkelkurver er normalkraften tilnærmet lik den vertikale hjulkraft og kan uttrykkes ved: | |||
<math> | |||
N_i=Q_i \cdot cos \gamma_i\approx Q_i | |||
</math> | |||
Her er γ<sub>i</sub> kontaktpunktsvinkelen | |||
Normalkraften i ytterstreng i kurver er definert i figur 11.6. | |||
[[Fil:Figur_11.6.PNG|600px|thumb||center|<caption> Figur 11.6 Beregning av normalkraft i ytterstreng (v = venstre = y = ytre)</caption>]] | |||
Følgende gjelder for vektorsummen mht. Q<sub>y</sub>: | |||
<math> | |||
Q_y=N_y\cdot cos\gamma_y +(-F_{\eta y})\cdot sin\gamma_y | |||
</math> | |||
Videre gjelder (definisjon av positiv retning for kryp): | |||
<math> | |||
F_{\eta y}=-\mu\cdot N_y | |||
</math> | |||
Dermed blir: | |||
<math> | |||
Q_y=N_y\cos \gamma_y+\mu\cdot N_y\cdot sin\gamma_y | |||
</math> | |||
Med utgangspunkt i kjent vertikalkraft Q<sub>y</sub>, kjent kontaktpunktsvinkel γ<sub>y</sub> og kjent friksjonskoeffisient μ kan normalkraften Ny for ytterstreng i kurver med små radier beregnes. | |||
<math> | |||
N_Y= {Q_Y\over (cos \gamma_y+\mu\cdot sin\gamma_Y)} \ \ (kN) | |||
</math> | |||
Det gjøres oppmerksom på at ovennevnte betraktninger er utført noe forenklet. | |||
Med fastsettelse av normalkraften er grunnlaget lagt for beregning av kontaktarealet og spenningene i kontaktflaten for skinner i kurver; i ovennevnte tilfelle ytterskinner. | |||
I kurver med små radier må kontaktflaten beskrives ved hulkilen til hjulbanen til hjulet og ved kjørekanten til skinnehodet til ytre skinne. Dette forholdet gjør beregningsprosedyrene vesentlig mer omfattende og vil ikke bli gjengitt her. | |||
Etterfølgende betraktninger gjelder i kontaktpunktet hjul – skinne for rett linje og i kurver med store radier under forutsetning av små tøyninger i sporkonstruksjonen og vil bli benyttet i forbindelse med beregninger av kontaktspenninger. | |||
Iht. Hertz teori vil den elastiske deformasjon av stålet til hjul og skinne skape en elliptisk kontaktflate. Dimensjonene på kontaktellipsen bestemmes av normalkraften og forholdet mellom aksene til ellipsen bestemmes av kurvaturen til hjulbaneprofilet og profilet på skinnehodet. | |||
Krumningsradier til skinnehodet i tverretningen og i lengderetningen samt for hjulets hjulbane er retningsgivende. Det vises til figur 11.7. Den elliptiske flate er vist i figur 11.8. | |||
[[Fil:Figur_11.7.PNG|600px|thumb||center|<caption> Figur 11.7 Kurveradier for skinnehodet i langsgående retning r<small>ξR</small> og i tverretningen r<small>ƞR</small> samt til hjulet for hjulradius r<sub>ξ</sub> og krumningen r<sub>ƞ</sub> i hjulbane </caption>]] | |||
<small></small> | |||
[[Fil:Figur_11.8.PNG|600px|thumb||center|<caption> Figur 11.8 Den elliptiske kontaktflate til Hertz med halvaksene a og b </caption>]] | |||
<small></small> | |||
Mht. beregningene må elastisitetsmodulen E og tverrkontraksjonstallet (Poisson’ ratio) for hjul og skinne tas i betraktning. Normalkraften er N og i samsvar med Hertz teori kan ellipsens halvakser a og b beregnes. Dette er vist i det etterfølgende. | |||
<math> | |||
a=m\cdot\sqrt[3]{{3\over 2}\cdot{N\cdot (1-v^2)\over E\cdot(A+B)}} | |||
</math> | |||
<math> | |||
b=n\cdot\sqrt[3]{{3\over 2}\cdot{N\cdot (1-v^2)\over E\cdot(A+B)}} | |||
</math> | |||
Funksjonene A og B er gitt ved: | |||
<math> | |||
A={1\over2}\cdot\left({1\over r_{\eta R}}+{1\over r_\eta}\right) | |||
</math> | |||
r<sub>ηR</sub> er radius til skinnehodet i tverretningen og r<sub>η</sub> er radius til hjulbanen lateralt. | |||
<math> | |||
B={1\over2}\cdot\left({1\over r_{\xi R}}+{1\over r_\xi}\right)\approx {1\over 2r_\xi}\approx {1\over 2r_0} | |||
</math> | |||
Termen r<sub>ξR</sub> er radius til skinnen i lengderetningen og r<sub>ξ</sub> er hjulets radius. | |||
Med tilstrekkelig nøyaktighet kan r<sub>ξR</sub>≈∞ og r<sub>ξ</sub>≈r<sub>0</sub>. | |||
m and n er faktorer som må beregnes med utgangspunkt i funksjonen: | |||
<math> | |||
\Theta = arccos\left({A-B\over A+B}\right) | |||
</math> | |||
Verdiene for m og n er gitt i tabeller som funksjon av Θ (<sup>0</sup>). | |||
Arealet av den elliptiske kontaktflate kan dermed uttrykkes: | |||
<math> | |||
A_e=\pi\cdot a\cdot b | |||
</math> | |||
Kontakttrykket uttrykt ved normalkraften i kontaktflaten er gitt ved følgende ligning: | |||
<math> | |||
\sigma_\zeta(\xi , \eta)={3\over 2}\cdot {N\over A_e}\cdot \sqrt{1-\left({\xi\over a}\right)^2-\left( {\eta\over b}\right)^2} | |||
</math> | |||
Dersom fordelingen av kontakttrykket antas å være ellipsoid, kan det maksimale trykket i origo til den elliptiske kontaktflate beregnes: | |||
<math> | |||
\sigma_{\zeta,max}={3\over 2}\cdot {N\over A_e} | |||
</math> | |||
Følgende relasjoner kan utledes: | |||
a er proporsjonal til N<sup>1/3</sup>. | |||
b er proporsjonal til N<sup>1/3</sup>. | |||
A<sub>e</sub> er proporsjonal til N<sup>2/3</sup>. | |||
σ<sub>ζ,max</sub> er proporsjonal til N<sup>1/3</sup>. | |||
Ovennevnte relasjoner er en meget viktig erkjennelse. Hypotesen innebærer at dersom normalkraften N dobles til 2 N, så øker den maksimale kontaktspenning i origo til ellipseflaten med faktor 2<sup>1/3</sup>≈1,26. Dersom konsekvensene av en økning i aksellasten skal vurderes, må dette faktum tas med i betraktningene. Noen relasjoner som er aktuell for El 18, er gitt i tabell under: | |||
{| class="wikitable" style="text-align:center" width="700px" | |||
|+ Tabell Forhold mellom normalkraft, økning i akselkraft og økning i maksimal spenning i kontaktflaten | |||
|- | |||
!Lokomotiv | |||
!El 17 | |||
!El 18 | |||
!Fiktiv El | |||
|- | |||
|Akselkraft (kN) | |||
|160 | |||
|213 | |||
|320 | |||
|- | |||
|Økning i akselkraft | |||
|1,000 | |||
|1,33 | |||
|2,00 | |||
|- | |||
|Økning i spenning σ<sub>ξ, max</sub> | |||
|1,00 | |||
|1,10 | |||
|1,26 | |||
|} | |||
Det er meget viktig å være klar over at kontaktspenningene vil øke med 10 % ved økning av akselkraft fra 160 kN til 213 kN, dvs. en økning på 33 % i forbindelse med overgang fra El 17 til El 18. | |||
Den elliptiske kontaktflate får en ellipsoide fordeling av trykket. Dette er vist i figur 11.9. | |||
[[Fil:Figur_11.9.PNG|600px|thumb||center|<caption> Figur 11.9 Elliptisk kontaktflate og ellipsoide spenningsfordeling </caption>]] | |||
<small></small> | |||
Ved prosedyrer kan halvaksene beregnes med utgangspunkt i hjulbanens og skinnehodets kurvaturer i tverretning og i lengderetning samt normalkraften og dermed fastsettes belastningsflaten. | |||
Her betyr: | |||
N Normalkraft (som er forskjellig fra hjulkraften Q) | |||
Ae Den elliptiske kontaktflate | |||
a, b Ellipsens halvakser | |||
ξ, η Ellipsens koordinatretninger (i lengderetning og i tverretning av skinneprofilet) | |||
=== Beregning, forenklet metode === | |||
Ved denne metoden beregnes det midlere flatetrykket qmean. Det antas rett linje og kurver med store radier. Det benyttes hjulkraft Q (ikke kvasistatisk hjulkraft). I kurver med små radier blir de opptredende belastninger ca. 1,15 ganger større på grunn av et beskjedent kvasistatisk tillegg. | |||
Det forutsettes en hjulradius lik 550 mm for lokomotivet (traksjonsmateriell). | |||
Det oppstår en tilleggsbelastning på skinnehodet i strekninger med bremsing og traksjon. I tillegg inntreffer tverrkryp i kurver med små radier. Begge aspektene gjelder for Flåmsbana. Imidlertid vil disse parametere ikke føre til større opptredende belastninger i en dybde av 4 – 6 mm under skinnehodet relatert til hovedspenningene. Gjennom opptreden av de langsgående kreftene og tverrkreftene avtar ikke skjærspenningene raskt som er tilfelle ved ren rulling. Kreftene i begge retninger forårsaket ved bremsing og traksjon fører derimot til mer slitasje i berøringspunktet hjul / skinne samt til materialflyt i randsonen til skinnehodet. Forholdet skal imidlertid ikke føre til hurtigere hendelse av materialflyt i skinnehodet (shelling) i en dybde av 4 – 6 mm. | |||
Nedenstående beregninger gjennomføres derfor uten innflytelse av traksjon og bremsing da det er de vertikale spenninger mot skinnehodet som er av interesse. | |||
'''<big>Tilfelle I.2.1 Dimensjonering for aksellast lik 21,3 tonn; hjullast lik 10,65 tonn (hjulkraft lik 106,50 kN) for skinnekvalitet R 200 Mn:</big>''' | |||
<math> | |||
q_{mean}=1374\cdot\sqrt{Q\over r} \ {N\over mm^2} | |||
</math> | |||
<math> | |||
q_{mean}=1374\cdot\sqrt{ 106,50\over 550}=605 \ {N\over mm^2} | |||
</math> | |||
Opptredende maksimal skjærkapasitet basert på q<sub>MEAN</sub> (ikke q<sub>MAX</sub>): | |||
<math> | |||
\tau_{max}=412\cdot\sqrt{Q\over r} \ {N\over mm^2} | |||
</math> | |||
<math> | |||
\tau_{max} =412\cdot\sqrt {106,50\over 550}=180 \ {N\over mm^2} | |||
</math> | |||
Anbefalt maksimal verdi for tillatt skjærkapasitet for skinnestål i kvalitet 700 basert på q<sub>MEAN</sub>: | |||
<math> | |||
\tau_{tillat}\approx 205 \ {N\over mm^2} \ \ > \ \ 180 \ {N\over mm^2} | |||
</math> | |||
Kontroll av tillatt anbefalt maksimal verdi for hjulkraft for skinnestål i kvalitet 900 basert på q<sub>MEAN</sub> med sikkerhetsfaktor υ = 1,10: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
Q_{tillatt}=5,26\cdot r\cdot \left( {\sigma_{brudd}\over \upsilon}\right)^2 \cdot 10^{-7} \ \ (kN) | |||
</math></center> || align="right" | | |||
|} | |||
Kontroll av tillatt anbefalt minste hjulradius for skinnestål i kvalitet 700 basert på q<sub>MEAN</sub> | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
r_{tillatt}= 1,90 \cdot Q \left( {\upsilon \over \sigma_{brudd}} \right)^2 \cdot 10^6 \ \ (mm) | |||
</math></center> || align="right" | | |||
|} | |||
Belastningen på skinnehodet i kontaktflaten blir mindre enn anbefalte verdier. | |||
I kurvene opptrer et kvasistatisk tillegg som er fastsatt til 8,50 kN. Det kvasistatiske tillegget < 10 % av nominell hjulkraft og dermed beskjedent. I tillegg vil kontaktflaten være mer utpreget elliptisk med ellipsoid spenningsfordeling. Spenningen q<sub>max</sub> i middelpunktet av ellipsen vurderes til å være 1,15 · q<sub>MEAN</sub> . Antakelsen betraktes å være konservativ. | |||
Dette gir: | |||
<math> | |||
q_{maks,kurve}=1,15\cdot 605=696 \ {N\over mm^2} | |||
</math> | |||
Fiktiv hjulkraft: | |||
<math> | |||
Q_{FIKTIV}={q^2_{maks \ kurve}\cdot r\over 1374^2}={696^2\cdot 550\over 1374^2}=141,00 \ kN | |||
</math> | |||
Nødvendig hjulradius: | |||
<math> | |||
r_{tillatt}=1,90\cdot 141,00\cdot \left({1,10\over 700}\right)^2 \cdot 10^6=662 \ mm \ \ > \ \ | |||
550 \ mm | |||
</math> | |||
Det kreves dermed en relativt stor hjuldiameter. Spørsmålet er hvorvidt relevant hypotesen er. Dette vil bli belyst senere. | |||
<big> | |||
'''Tilfelle I.2.2 Dimensjonering for aksellast lik 21,3 tonn; hjullast lik 10,65 tonn (hjulkraft lik 106,50 kN) for skinnekvalitet R 260 Mn'''</big> | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
q_{mean}=1374 \cdot \sqrt{Q \over r} \ \ \left({N\over mm^2} \right) | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
q_{mean}=1374 \cdot \sqrt{106,50 \over 550}=605 \ \ \left({N\over mm^2} \right) | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\tau_{max}=412 \cdot \sqrt{Q \over r} \ \ \left({N\over mm^2} \right) | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\tau_{max}=412 \cdot \sqrt{106,50 \over 550}=180 \ \ \left({N\over mm^2} \right) | |||
</math></center> || align="right" | | |||
|} | |||
Anbefalt maksimal verdi for tillatt skjærkapasitet for skinnestål i kvalitet 900 basert på q<sub>MEAN</sub> : | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\tau_{tillatt}\approx 260 \ {N\over mm^2} \ \ > \ \ 180 \ {N\over mm^2} | |||
</math></center> || align="right" | | |||
|} | |||
Kontroll av tillatt anbefalt maksimal verdi for hjulkraft for skinnestål i kvalitet 900 basert på q<sub>MEAN</sub> med sikkerhetsfaktor υ = 1,10: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
Q_{tillatt}=5,26\cdot r\cdot \left( {\sigma_{brudd}\over \upsilon}\right)^2 \cdot 10^{-7} \ \ (kN) | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
Q_{tillatt}=5,26\cdot 550 \cdot \left( {900\over 1,10}\right)^2 \cdot 10^{-7} = 193,60 \ \ (kN) | |||
</math></center> || align="right" | | |||
|} | |||
Kontroll av tillatt anbefalt minste hjulradius for skinnestål i kvalitet 900 basert på q<sub>MEAN</sub> : | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
r_{tillatt}= 1,90 \cdot Q \left( {\upsilon \over \sigma_{brudd}} \right)^2 \cdot 10^6 \ \ (mm) | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
r_{tillatt}= 1,90 \cdot 106,50\cdot \left( {110 \over 900}\right)^2 \cdot 10^6=303 \ \ (mm) | |||
</math></center> || align="right" | | |||
|} | |||
I kurvene opptrer et kvasistatisk tillegg som er fastsatt til 8,50 kN. Det kvasistatiske tillegget < 10 % av nominell hjulkraft og dermed beskjedent. I tillegg vil kontaktflaten være elliptisk med ellipsoid spenningsfordeling. Spenningen q<sub>max</sub> i middelpunktet av ellipsen vurderes til å være 1,15 · q<sub>MEAN</sub>. | |||
Dette gir: | |||
<math> | |||
q_{maks,kurve}=1,15\cdot 605=696 \ {N\over mm^2} | |||
</math> | |||
Fiktiv hjulkraft: | |||
<math> | |||
Q_{FIKTIV}={q^2_{maks \ kurve}\cdot r\over 1374^2}={696^2\cdot 550\over 1374^2}=141,00 \ kN | |||
</math> | |||
Nødvendig hjulradius: | |||
<math> | |||
r_{tillatt}=1,90\cdot 141,00\cdot \left({1,10\over 900}\right)^2 \cdot 10^6=400 \ mm | |||
</math> | |||
Det framgår at skinnekvalitet R 260 Mn (900 N/mm2) er greit. | |||
<big>'''Tilfelle I.2.3 Dimensjonering for aksellast lik 21,3 tonn; hjullast lik 10,65 tonn (hjulkraft lik 106,50 kN) for skinnekvalitet R350 HT'''</big> | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
q_{mean}=1374 \cdot \sqrt{Q \over r} \ \ \left({N\over mm^2} \right) | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
q_{mean}=1374 \cdot \sqrt{106,50 \over 550}=605 \ \ \left({N\over mm^2} \right) | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\tau_{max}=412 \cdot \sqrt{Q \over r} \ \ \left({N\over mm^2} \right) | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\tau_{max}=412 \cdot \sqrt{106,50 \over 550}=180 \ \ \left({N\over mm^2} \right) | |||
</math></center> || align="right" | | |||
|} | |||
Anbefalt maksimal verdi for tillatt skjærkapasitet for skinnestål i kvalitet 900 basert på q<sub>MEAN</sub>: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\tau_{tillatt}\approx 320 \ {N\over mm^2} \ \ > \ \ 180 \ {N\over mm^2} | |||
</math></center> || align="right" | | |||
|} | |||
Kontroll av tillatt anbefalt maksimal verdi for hjulkraft for skinnestål i kvalitet 1100 basert på q<sub>MEAN</sub> med sikkerhetsfaktor υ = 1,10: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
Q_{tillatt}=5,26\cdot r\cdot \left( {\sigma_{brudd}\over \upsilon}\right)^2 \cdot 10^{-7} \ \ (kN) | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
Q_{tillatt}=5,26\cdot 550\cdot \left( {1100\over 1,10}\right)^2 \cdot 10^{-7}=290,00 \ \ (kN) \ \ > \ \ 106,50 \ kN | |||
</math></center> || align="right" | | |||
|} | |||
Kontroll av tillatt anbefalt minste hjulradius for skinnestål i kvalitet 900 basert på q<sub>MEAN</sub>: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
r_{tillatt}= 1,90 \cdot Q \left( {\upsilon \over \sigma_{brudd}} \right)^2 \cdot 10^6 \ \ (mm) | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
r_{tillatt}= 1,90 \cdot 106,50 \left( {1,10 \over 1100 } \right)^2 \cdot 10^6 = 202,40\ \ (mm) | |||
</math></center> || align="right" | | |||
|} | |||
I kurvene opptrer et kvasistatisk tillegg som er fastsatt til 8,50 kN. Det kvasistatiske tillegget < 10 % av nominell hjulkraft og dermed beskjedent. I tillegg vil kontaktflaten være elliptisk med ellipsoid spenningsfordeling. Spenningen q<sub>max</sub> i middelpunktet av ellipsen vurderes til å være 1,15 · q<sub>MEAN</sub>. | |||
Dette gir: | |||
<math> | |||
q_{maks,kurve}=1,15\cdot 605=696 \ {N\over mm^2} | |||
</math> | |||
Fiktiv hjulkraft: | |||
<math> | |||
Q_{FIKTIV}={q^2_{maks \ kurve}\cdot r\over 1374^2}={696^2\cdot 550\over 1374^2}=141,00 \ kN | |||
</math> | |||
Nødvendig hjulradius: | |||
<math> | |||
r_{tillatt}=1,90\cdot 141,00\cdot \left({1,10\over 1100}\right)^2 \cdot 10^6=268 \ mm | |||
</math> | |||
Det framgår at skinnekvalitet R 350 HT er greit. | |||
Sammenstilling av beregningene er gitt i tabell. | |||
{| class="wikitable" style="text-align:center" width="900px" | |||
|+ Tabell Belastning i hjul/skinne kontaktmekanikk for kontaktspenning og skjærspenning for hjulkraft lik 106,50 kN: | |||
|- | |||
! colspan=6| akselkraft: 213 kN; hjulkraft = 106,50 kN; hjulradius = 550 mm; rett linje og store radier beregningene er utført i formler som baserer seg på midlere trykk q<sub>MEAN</sub> | |||
|- | |||
|Stålkvalitet | |||
|(N/mm<sup>2</sup>) | |||
|700 | |||
|900 | |||
|1100 | |||
|Kommentarer | |||
|- | |||
|Tillatt skjærkapasitet | |||
|τ<sub>tillatt</sub> (N/mm<sup>2</sup>) | |||
|205 | |||
|260 | |||
|320 | |||
| | |||
|- | |||
|Beregnet kontaktspenning | |||
|q<sub>MEAN</sub> (N/mm<sup>2</sup>) | |||
|605 | |||
|605 | |||
|605 | |||
| | |||
|- | |||
|Beregnet skjærspenning | |||
|τ<sub>max</sub> (N/mm<sup>2</sup>) | |||
|180 | |||
|180 | |||
|180 | |||
| | |||
|- | |||
|Tillatt største hjulkraft | |||
|Q (kN) | |||
|117,10 | |||
|193,60 | |||
|290,00 | |||
| | |||
|- | |||
|Tillatt minste hjulradius; | |||
rett strekning | |||
|r (mm) | |||
|500 | |||
|303,30 | |||
|202,40 | |||
|Hjulradius for stålkvalitet 900 og 1100 ikke realistisk | |||
|- | |||
|Tillatt minste hjulradius; | |||
små kurver | |||
|r + α · r (mm) | |||
|662 | |||
|400 | |||
|268 | |||
|Hjulradius for stålkvalitet 1100 ikke realistisk | |||
|} | |||
Under hensyntagen til ovennevnte er nominell hjuldiameter r = 1125 mm for belastning på skinner i stålkvalitet R260 Mn med strekkfasthet 900 N/mm2 og i stålkvalitet R350 HT med strekkfasthet 1100 N/mm<sup>2</sup> greit. | |||
For skinner i stålkvalitet R200 behøves ideelt en hjuldiameter på over 660 mm. I det etterfølgende vil aspektet bli belyst og vurdert grundigere. | |||
=== Beregning iht. Hertz teori === | |||
Det gjennomføres beregninger med tverrsnittsprofil for skinnehodet i uslitt tilstand. Da beregningene utføres på rett strekning, anvendes radius i løpebaneområdet for skinneprofilet; dvs. r<sub>ƞ R</sub> = 300 mm = 0,30 m. Profilet er vist i figur 11.10 under. Skinneradius i lengderetningen er ∞. | |||
[[Fil:Figur_11.10.PNG|600px|thumb||center|<caption> Figur 11.10 Det antas kontaktflate i løpebaneområdet til skinnehodet; dvs. r = 300 mm </caption>]] | |||
[[Fil:Figur_11.11.PNG|600px|thumb||center|<caption> Figur 11.11 Hjulprofil P8A, B eller C benyttes trolig på El 18 </caption>]] | |||
<small></small> | |||
Hjulradius antas å være r<sub>ξ</sub> = 0,55 m: dvs. hjuldiameter er 1,10 m. | |||
For profilet til hjulbanen antas 3 forskjellige kurver; r<sub>ƞ</sub> = 0,36 m; r<sub>ƞ</sub> = 0,50 m; r<sub>ƞ</sub> = ∞ m. | |||
Belastningene beregnes for en statisk lasttilstand; N = 106,50. | |||
Det oppstår en tilleggsbelastning på skinnehodet i strekninger med bremsing og traksjon. I tillegg inntreffer tverrkryp i kurver med små radier. Begge aspektene gjelder for Flåmsbana. Imidlertid vil disse parametere ikke føre til større opptredende belastninger i en dybde av 4 – 6 mm under skinnehodet relatert til hovedspenningene. Gjennom opptreden av de langsgående kreftene og tverrkreftene avtar ikke skjærspenningene raskt som er tilfelle ved ren rulling. Kreftene i begge retninger forårsaket ved bremsing og traksjon fører derimot til mer slitasje i berøringspunktet hjul / skinne samt til materialflyt i randsonen til skinnehodet. Forholdet skal imidlertid ikke føre til hurtigere hendelse av materialflyt i skinnehodet (shelling) i en dybde av 4 – 6 mm. | |||
Nedenstående beregninger gjennomføres derfor uten innflytelse av traksjon og bremsing da det er de vertikale spenninger mot skinnehodet som er av interesse. | |||
<big>'''Tilfelle II.2.4 Hertz; tverrprofil i hjulbane r<sub>ƞ</sub> = 0,36 m'''</big> | |||
Normalkraft på skinne for rett strekning: N = 106,50 kN | |||
Tverrkontraksjonstallet (eller Poissons forholdstall): υ = 0,30 | |||
Stålets elastisitetsmodul: E = 2,10 · 10<sup>5</sup> N/mm2 | |||
Kurven til skinne i horisontal retning (tverrprofil): r<sub>ƞ R</sub> = 0,30 m | |||
Kurven til skinnehodet i langsgående retning: r<sub>ξ R</sub> = ∞ | |||
Kurven til hjulbane i hjulet i tverretning: r<sub>ƞ</sub> = 0,36 m | |||
Hjulradius: r<sub>ξ</sub> = 0,55 m | |||
Funksjonene A og B er gitt ved: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
A= {1\over 2}\cdot \left({1\over r_{\eta R}}- {1\over r_\eta}\right) ={1\over 2}\cdot \left({1\over 0,30 }- {1\over 0,36}\right)=0,28 | |||
</math></center> || align="right" | | |||
|} | |||
r<sub>ηR</sub> er radius til skinnehodet i tverretningen og r er radius til hjulbanen tverretning. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
B= {1\over 2}\cdot \left({1\over r_{\xi R}}- {1\over r_\xi}\right) \approx{1\over 2 r_\xi}\approx{1\over 2 r_0}={1\over 2\cdot 0,55}=0,90 | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\Theta = arccos\left({0,28-0,90\over 0,28 + 0,90}\right)=121^0 | |||
</math></center> || align="right" | | |||
|} | |||
m = 0,705 og n = 1,505 | |||
'''N = 106,50 kN''' | |||
Termene a og b beregnes. Dette er vist i det etterfølgende for hjulkraft lik 106,50 kN. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
a=m\cdot \sqrt[3]{{3\over 2}\cdot{N\cdot (1-v^2)\over E\cdot (A+B)}}=0.705\cdot\sqrt[3]{{3\over 2}\cdot{106,50\cdot 10^3 \cdot(1-0,30^2)\over 2,10\cdot 10^{11}\cdot (0,28 +0,90)}}=0,705\cdot 8,37\cdot10^{-3}=5,90 \ mm | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
b=n\cdot \sqrt[3]{{3\over 2}\cdot{N\cdot (1-v^2)\over E\cdot (A+B)}}=1,505 \cdot\sqrt[3]{{3\over 2}\cdot{106,50\cdot 10^3 \cdot(1-0,30^2)\over 2,10\cdot 10^{11}\cdot (0,28 +0,90)}}=1,505\cdot 8,37\cdot10^{-3}=12,60 \ mm | |||
</math></center> || align="right" | | |||
|} | |||
Arealet av den elliptiske kontaktflate blir: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
A_e=\pi\cdot a\cdot b=\pi \cdot 5,90 \cdot 12,60=233 \ mm^2 | |||
</math></center> || align="right" | | |||
|} | |||
Termen a er halvakse i skinnehodets lengderetning og b er halvakse i skinnehodets tverretning. Aspektet betyr at den elliptiske flate er langstrakt i skinnehodets tverretning. | |||
Maksimal trykkspenning i kontaktflaten: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\sigma_{\xi ,maks}={3\over2}\cdot {106,50\cdot 10^3\over 233}=686 \ {N\over mm^2} | |||
</math></center> || align="right" | | |||
|} | |||
For skinne med stålkvalitet 700 N/mm2 er kapasitet på skjær τ<sub>tillatt</sub> = 205 N/mm<sup>2</sup>. | |||
I Shakedown diagrammet dannes forholdet: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
{\sigma_{\xi ,maks}\over \tau_{tillatt}}={686\over 205}=3,34 | |||
</math></center> || align="right" | | |||
|} | |||
For skinne med stålkvalitet 900 N/mm2 er kapasitet på skjær τ<sub>tillatt</sub> = 260 N/mm<sup>2</sup>. | |||
I Shakedown diagrammet dannes forholdet: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
{\sigma_{\xi ,maks}\over \tau_{tillatt}}={686\over 260}=2,63 | |||
</math></center> || align="right" | | |||
|} | |||
For skinne med stålkvalitet 1100 N/mm<sup>2</sup> er kapasitet på skjær τ<sub>tillatt</sub> = 320 N/mm<sup>2</sup>. | |||
I Shakedown diagrammet dannes forholdet: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
{\sigma_{\xi ,maks}\over \tau_{tillatt}}={686\over 320}=2,14 | |||
</math></center> || align="right" | | |||
|} | |||
''' | |||
<big>Tilfelle II.2.5 Hertz; tverrprofil i hjulbane r<sub>ƞ</sub> = 0,50 m</big>''' | |||
Normalkraft på skinne for rett strekning: N = 106,50 kN | |||
Tverrkontraksjonstallet (eller Poissons forholdstall): υ = 0,30 | |||
Stålets elastisitetsmodul: E = 2,15 · 105 N/mm<sup>2</sup> | |||
Kurven til skinne i horisontal retning (tverrprofil): r<sub>ƞ</sub> R = 0,30 m | |||
Kurven til skinnehodet i langsgående retning: r<sub>ξ</sub> R = ∞ | |||
Kurven til hjulbane i hjulet i tverretning: rƞ = 0,50 m | |||
Hjulradius: r<sub>ξ</sub> = 0,55 m | |||
Funksjonene A og B er gitt ved: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
A= {1\over 2}\cdot \left({1\over r_{\eta R}}- {1\over r_\eta}\right) ={1\over 2}\cdot \left({1\over 0,30 }- {1\over 0,50}\right)=0,67 | |||
</math></center> || align="right" | | |||
|} | |||
r<sub>ηR</sub> er radius til skinnehodet i tverretningen og r<sub>η</sub> er radius til hjulbanen lateralt. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
B= {1\over 2}\cdot \left({1\over r_{\xi R}}- {1\over r_\xi}\right)\approx {1\over 2r_\xi}\approx {1\over 2r_0}={1\over 2\sdot 0,55}=0,90 | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\Theta=arccos\left( {0,67-0,90\over0,67+0,90}\right)=98^0 | |||
</math></center> || align="right" | | |||
|} | |||
m = 0,910 og n = 1,100 | |||
'''N = 106,50 kN''' | |||
Termene a og b beregnes. Dette er vist i det etterfølgende for hjulkraft lik 106,50kN. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
a=m\cdot \sqrt[3]{{3\over 2}\cdot{N\cdot (1-v^2)\over E\cdot (A+B)}}=0.910\cdot\sqrt[3]{{3\over 2}\cdot{106,50\cdot 10^3 \cdot(1-0,30^2)\over 2,10\cdot 10^{11}\cdot (0,67 +0,90)}}=0,910\cdot 7,61\cdot 10^{-3}=6,93 \ mm | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
b=n\cdot \sqrt[3]{{3\over 2}\cdot{N\cdot (1-v^2)\over E\cdot (A+B)}}=1,100 \cdot\sqrt[3]{{3\over 2}\cdot{106,50\cdot 10^3 \cdot(1-0,30^2)\over 2,10\cdot 10^{11}\cdot (0,67 +0,90)}}=1,100\cdot 7,61\cdot10^{-3}=8,37 \ mm | |||
</math></center> || align="right" | | |||
|} | |||
Arealet av den elliptiske kontaktflate blir: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
A_e=\pi\cdot a\cdot b=\pi\cdot 6,93\cdot8,37=182 \ mm^2 | |||
</math></center> || align="right" | | |||
|} | |||
Termen a er halvakse i skinnehodets tverrprofil og b er halvakse i skinnehodets lengderetning. Aspektet betyr at den elliptiske kontaktflate er langstrakt i skinnehodets tverretning. | |||
Maksimal trykkspenning i kontaktflaten: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\sigma_{\xi ,maks}={3\over2}\cdot {106,50\cdot 10^3\over 182}=878 \ {N\over mm^2} | |||
</math></center> || align="right" | | |||
|} | |||
For skinne med stålkvalitet 700 N/mm2 er kapasitet på skjær τtillatt = 205 N/mm<sup>2</sup>. | |||
I Shakedown diagrammet dannes forholdet: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
{\sigma_{\xi ,maks}\over \tau_{tillatt}}={878\over 205}=4,28 | |||
</math></center> || align="right" | | |||
|} | |||
For skinne med stålkvalitet 900 N/mm2 er kapasitet på skjær τtillatt = 260 N/mm<sup>2</sup>. | |||
I Shakedown diagrammet dannes forholdet: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
{\sigma_{\xi ,maks}\over \tau_{tillatt}}={878\over 260}=3,38 | |||
</math></center> || align="right" | | |||
|} | |||
For skinne med stålkvalitet 1100 N/mm<sup>2</sup> er kapasitet på skjær τtillatt = 320 N/mm<sup>2</sup>. | |||
I Shakedown diagrammet dannes forholdet: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
{\sigma_{\xi ,maks}\over \tau_{tillatt}}={878\over 320}=2,74 | |||
</math></center> || align="right" | | |||
|} | |||
<big>'''Tilfelle II.2.6 Hertz; tverrprofil i hjulbane r<sub>ƞ</sub> = ∞ m'''</big> | |||
Normalkraft på skinne for rett strekning: N = 106,50 kN | |||
Tverrkontraksjonstallet (eller Poissons forholdstall): υ = 0,30 | |||
Stålets elastisitetsmodul: E = 2,15 · 10<sup>5</sup> N/mm2 | |||
Kurven til skinne i horisontal retning (tverrprofil): r<sub>ƞ R</sub> = 0,30 m | |||
Kurven til skinnehodet i langsgående retning: r<sub>ξ R</sub> = ∞ | |||
Kurven til hjulbane i hjulet i tverretning: r<sub>ƞ</sub> = ∞ | |||
Hjulradius: r<sub>ξ</sub> = 0,55 m | |||
Funksjonene A og B er gitt ved: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
A= {1\over 2}\cdot \left({1\over r_{\eta R}}- {1\over r_\eta}\right) ={1\over 2}\cdot \left({1\over 0,30 }- {1\over \infty}\right)=1,67 | |||
</math></center> || align="right" | | |||
|} | |||
r<sub>ηR</sub> er radius til skinnehodet i tverretningen og r<sub>η</sub> er radius til hjulbanen lateralt. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
B= {1\over 2}\cdot \left({1\over r_{\xi R}}- {1\over r_\xi}\right)\approx {1\over 2r_\xi}\approx {1\over 2r_0}={1\over 2\sdot 0,55}=0,90 | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\Theta=arccos\left( {1,67-0,90\over 1,67+0,90}\right)=60,60^0 | |||
</math></center> || align="right" | | |||
|} | |||
m = 1,450 og n = 0,715 | |||
'''N = 106,50 kN''' | |||
Termene a og b beregnes. Dette er vist i det etterfølgende for hjulkraft lik 103,50 kN. | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
a=m\cdot \sqrt[3]{{3\over 2}\cdot{N\cdot (1-v^2)\over E\cdot (A+B)}}=1,450\cdot\sqrt[3]{{3\over 2}\cdot{106,50\cdot 10^3 \cdot(1-0,30^2)\over 2,10\cdot 10^{11}\cdot (1,67 +0,90)}}=1,450\cdot 7,61\cdot 10^{-3}=11,00 \ mm | |||
</math></center> || align="right" | | |||
|} | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
b=n\cdot \sqrt[3]{{3\over 2}\cdot{N\cdot (1-v^2)\over E\cdot (A+B)}}=0,715 \cdot\sqrt[3]{{3\over 2}\cdot{106,50\cdot 10^3 \cdot(1-0,30^2)\over 2,10\cdot 10^{11}\cdot (1,67 +0,90)}}=0,715 \cdot 7,61\cdot10^{-3}=5,44 \ mm | |||
</math></center> || align="right" | | |||
|} | |||
Arealet av den elliptiske kontaktflate blir: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
A_e=\pi\cdot a\cdot b=\pi\cdot 11,00\cdot5,44=188 \ mm^2 | |||
</math></center> || align="right" | | |||
|} | |||
Termen a er halvakse i skinnehodets tverrprofil og b er halvakse i skinnehodets lengderetning. Aspektet betyr at i dette tilfellet så er den elliptiske kontaktflate langstrakt i skinnehodets lengderetning. | |||
Maksimal trykkspenning i kontaktflaten: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\sigma_{\xi ,maks}={3\over2}\cdot {106,50\cdot 10^3\over 188}=850 \ {N\over mm^2} | |||
</math></center> || align="right" | | |||
|} | |||
For skinne med stålkvalitet 700 N/mm2 er kapasitet på skjær τtillatt = 205 N/mm<sup>2</sup>. | |||
I Shakedown diagrammet dannes forholdet: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
{\sigma_{\xi ,maks}\over \tau_{tillatt}}={850\over 205}=4,15 | |||
</math></center> || align="right" | | |||
|} | |||
For skinne med stålkvalitet 900 N/mm2 er kapasitet på skjær τ<sub>tillatt</sub> = 260 N/mm<sup>2</sup>. | |||
I Shakedown diagrammet dannes forholdet: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
{\sigma_{\xi ,maks}\over \tau_{tillatt}}={850\over 260}=3,27 | |||
</math></center> || align="right" | | |||
|} | |||
For skinne med stålkvalitet 1100 N/mm<sup>2</sup> er kapasitet på skjær τtillatt = 320 N/mm<sup>2</sup>. | |||
I Shakedown diagrammet dannes forholdet: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
{\sigma_{\xi ,maks}\over \tau_{tillatt}}={850\over 320}=2,66 | |||
</math></center> || align="right" | | |||
|} | |||
For tangentbelastningen blir det lagt til grunn ren glidning i skinnens lengderetning og tverretning med en konstant friksjonskoeffisient μ. Abscissen beskriver i denne sammenheng den resulterende friksjonskoeffisient som uttrykkes ved: | |||
{|width="100%" | |||
|- | |||
|<center><math> | |||
\mu=\sqrt{\mu_\xi^2 +\mu_\eta^2} | |||
</math></center> || align="right" | | |||
|} | |||
Beregningen er utført for en kontaktspenning på spor på rett linje. Dermed kan til en viss grad grafene for punktkontakt; dvs. graf C for øvre innspillgrense. Inntil en friksjonskoeffisient μ = 0,30 er kapasiteten for skjærspenningen i orden. For høyere friksjonskoeffisient μ; dvs. tørre skinner vil det bli slitasje i overflaten på skinnehodet. | |||
[[Fil:Figur_11.4.PNG|600px|thumb||center|<caption> Figur Shakedown diagram </caption>]] | |||
<small></small> | |||
Beregningene er sammen fattet i tabell under. | |||
{| class="wikitable" style="text-align:center" width="900px" | |||
|+ Tabell Beregning av kontaktspenninger i hjul/skinne med ulike parametervariasjoner | |||
|- | |||
! | |||
! | |||
!Hjulbane | |||
tverretning | |||
!Hjul | |||
radius | |||
!Skinne | |||
tverretning | |||
!Skinne | |||
lengde | |||
!Kontakt | |||
flate | |||
!Trykk | |||
spenning | |||
!Skjær | |||
kapasit | |||
!Forhold | |||
|- | |||
|Stål | |||
kvalitet | |||
(N/mm<sup>2</sup>) | |||
|Hjul | |||
kraft | |||
(kN) | |||
|r<sub>ƞ</sub> | |||
(m) | |||
|r<sub>ξ</sub> | |||
(m) | |||
|r<sub>ƞ R</sub> | |||
(m) | |||
|r<sub>ξ R</sub> | |||
(m) | |||
|A<sub>e</sub> | |||
(mm2) | |||
|σ<sub>ξ maks | |||
</sub> | |||
(mm<sup>2</sup>) | |||
|τ<sub>tillatt</sub> | |||
(mm<sup>2</sup>) | |||
| | |||
|- | |||
|rowspan=3|700 | |||
|rowspan=3|106 | |||
|0,36 | |||
|rowspan=3|0,55 | |||
|rowspan=3|0,30 | |||
|rowspan=3|∞ | |||
|223 | |||
|716 | |||
|rowspan=3|205 | |||
|3,50 | |||
|- | |||
|0,50 | |||
|182 | |||
|878 | |||
|4,28 | |||
|- | |||
|∞ | |||
|188 | |||
|850 | |||
|4,14 | |||
|- | |||
|rowspan=3|900 | |||
|rowspan=3|106 | |||
|0,36 | |||
|rowspan=3|0,55 | |||
|rowspan=3|0,30 | |||
|rowspan=3|∞ | |||
|223 | |||
|716 | |||
|rowspan=3|260 | |||
|2,76 | |||
|- | |||
|0,50 | |||
|182 | |||
|878 | |||
|3,38 | |||
|- | |||
|∞ | |||
|188 | |||
|850 | |||
|3,27 | |||
|- | |||
|rowspan=3|1100 | |||
|rowspan=3|106 | |||
|0,36 | |||
|rowspan=3|0,55 | |||
|rowspan=3|0,30 | |||
|rowspan=3|∞ | |||
|223 | |||
|716 | |||
|rowspan=3|320 | |||
|2,24 | |||
|- | |||
|0,50 | |||
|182 | |||
|878 | |||
|2,74 | |||
|- | |||
|∞ | |||
|188 | |||
|850 | |||
|2,66 | |||
|} | |||
=== Konklusjoner=== | |||
Det er utført beregninger av belastning på hjul/skinne kontaktflate og på skjær etter anerkjente metoder under antakelse om elliptisk kontaktflate for rett strekning og i kurver med store radier. | |||
Beregningene gjelder ikke for kurver med små radier. Det er imidlertid gjort en antakelse om høyere belastning i skinnehodet i kontaktflaten og på skjær med en faktor lik 1,15. | |||
Det er lagt til grunn en skinne med kurveradius i tverrprofilet på 0,30 m i løpebaneområdet. Videre er det antatt 3 ulike profil i løpebaneområdet for hjulprofilet: | |||
r<sub>ƞ</sub> = 0,36 m; 0,50 m; ∞ m | |||
Det er tatt utgangspunkt i hjuldiameter på 1100 mm; dvs. hjulradius lik 550 mm. Krumningsradius i lengderetningen på skinnene er ∞. | |||
Ikke overraskende oppstår de minste belastningene hvor tverrprofilene for skinnehodet og hjulbane tilpasses hverandre ved at belastningsbåndet blir bredere. Den største belastningen oppstår ved et teoretisk konisk hjulbaneprofil; dvs. for r<sub>ƞ</sub> = ∞ m. | |||
Det er å anta at det dynamiske gangløpet i spordynamikken fungerer best ved et konisk hjulprofil. Det er i denne sammenheng ikke tatt stilling til løpedynamikken. | |||
En sammenstilling for oversikt er gitt i tabell 9.6. Tabellen er vist sammen med Shakedown diagrammet for oversiktens skyld. | |||
Det er vist at et hjulbaneprofil med radius r<sub>ƞ</sub> = 0,36 m gir størst kontaktflate og dermed minst belastning i kontaktforholdet hjul/skinne. | |||
Et hjulbaneprofil med radius r<sub>ƞ</sub> = 0,50 m gir betydelig mindre kontaktflate og dermed betydelig større belastning i kontaktforholdet hjul/skinne enn med radius r<sub>ƞ</sub> = 0,36 m. | |||
Det samme forholdet gjør seg gjeldende for r<sub>ƞ</sub> = ∞. | |||
'''Skinnekvalitet R 200 Mn (strekkfasthet 700 N/mm<sup>2</sup>)''' | |||
På rett strekning og i kurver med store radier for skinnekvalitet R 200 Mn med bruddfasthet 700 N/mm<sup>2</sup> anses Shakedown forholdet lik 3,50 for et hjulbaneprofil med r<sub>ƞ</sub> = 0,36 m å være helt greit for fuktige til halvtørre skinner med friksjonskoeffisient inntil μ = 0,35. For tørrere skinner må forventes materialflyt på skinnehodets overflate. | |||
For hjulbaneprofil med r<sub>ƞ</sub> > 0,36 m blir Shakedown forholdet større. For fuktige skinner med friksjonskoeffisient inntil 0,30 er forholdet ikke kritisk. For høyere friksjonskoeffisient μ, dvs. tørrere skinner kan materialflyt i overflaten av skinnehodet forventes. | |||
I kurver med små radier vil de samme forholdene gjøre seg gjeldende. Shakedown forholdet vil for r<sub>ƞ</sub> anta en verdi opp mot 4,0. Aspektet medfører at for r<sub>ƞ</sub> = 0,36 m bør μ < 0,30 for å hindre materialflyt. Skinnene må dermed være litt fuktige. For hjulbaneprofil med større radier antar kontaktspenningene høye verdier i kurver og det vil uansett være fare for opptreden av materialflyt i overflaten av skinnehodet for tørre skinner og i det indre av skinnehodet for bløtere skinner. | |||
'''Skinnekvalitet R 260 Mn (strekkfasthet 900 N/mm<sup>2</sup>)''' | |||
Iht. resultat av beregningene vist i tabell for rett linje forventes normalt slitasjeforløp mht. hastighet for skinner på rett strekning og i kurver med små radier. Et hjulbaneprofil med r<sub>ƞ</sub> = 0,36 m er allikevel bedre enn hjulbaneprofil med større radier. | |||
'''Skinnekvalitet R 350 HT (strekkfasthet 1100 N/mm<sup>2</sup>)''' | |||
Det gjelder de samme vurderinger som foran. Hastigheten i slitasjeforløpet forventes å være langsommere. | |||
'''Endring i spenningene som funksjon av endring av aksellast''' | |||
Det er vist i det foregående vist endringer av spenning i kontaktpunktet hjul/skinne som følge av endring av aksellast. Det vises til tabell. | |||
{| class="wikitable" style="text-align:center" width="700px" | |||
|+ | |||
|- | |||
!Lokomotiv | |||
!El 17 | |||
!El 18 | |||
!Fiktiv El | |||
|- | |||
|Akselkraft (kN) | |||
|160 | |||
|213 | |||
|320 | |||
|- | |||
|Økning i akselkraft | |||
|1,000 | |||
|1,33 | |||
|2,00 | |||
|- | |||
|Økning i spenning σ<sub>ξ, max</sub> | |||
|1,00 | |||
|1,10 | |||
|1,26 | |||
|} | |||
Ved en økning av akselkraft fra 160 kN for El 17 til en akselkraft på 213 kN for El 18 blir det en økning i spenningene på 10 %. Akselkraftøkningen er på 33 %. | |||
Økningen antas ikke å være dramatisk. | |||
Ifølge BANEDATA INNSYN Overbygning Skinner finnes ca. 10 000 m skinner i kvalitet R 200 Mn (700 N/mm<sup>2</sup>). Oversikten viser at disse er lagt i sporet omkring 1965. Skinnene har dermed hatt en liggetid i sporet på ca. 50 år. Dette må bety at skinnene har klart seg relativt bra. | |||
En økning i spenningene på 10 % på grunn av økning av akselkraften på lokomotivene med henholdsvis 4 og 8 aksler i togstammen vil naturlig nok fremskynde slitasje; men det forventes ingen dramatisk økning i hastigheten. | |||
Det er tatt utgangspunkt i radier for hjulbanene r<sub>ƞ</sub> = 0,36 m, 0,50 m og ∞. Det kan synes å være noe inkonsekvent å anta radiene 0,50 m og ∞ m. Hjulbaneprofilet vil tilpasse seg skinneprofilet og en radius lik 0,36 m vil av naturlige årsaker opptre mest. Det eksisterer derfor et relativt bredt kontaktbånd i kontaktflaten hjul /skinne som bidrar til mindre stressende spenninger. | |||
El 18 har nominell hjuldiameter lik 1125 mm. El 17 har nominell hjuldiameter 1100 mm. Forskjellen er ubetydelig for den økning i lasten som er definert. | |||
== Bremsekrefter == | |||
Det beregnes krefter som oppstår i forbindelse med bremsing av toget på et lasket spor med fall i en gradient lik 55 mm/m. Det vurderes 2 tilfeller: | |||
*Nødvendig bremsekraft for opprettholdelse av konstant hastighet | |||
*Nødvendig bremsekraft for nedbremsing til full stopp | |||
Det vurderes tilstand med hensyn til adhesjonen: | |||
*αB i linje i fall med gradient s (mm/m) | |||
Det betraktes et bremset tog med eventuelle blokkbremser/bremseskiver og med bruk av El brems med oppgitt verdi (150,00 kN). | |||
Flåmsbana er meget kurverik og derfor oppstår gangdynamisk motstand. I tillegg vil også inntreffe luftmotstand. I det etterfølgende vil disse aspektene bli neglisjert. | |||
=== Bremsekraft ved El – brems for konstant hastighet === | |||
Det gjennomføres en beregning for å undersøke om kapasiteten ved El brems er tilstrekkelig. Det legges til grunn at prinsippet gir bremsede moment for hjulakslene som igjen indikerer bremsekrefter mellom hjul og skinner. Aspektet medfører at adhesjonen får betydning. | |||
Det må tas hensyn til trykkraften F<sub>X</sub> mellom traksjonsenheten og vognene. Gradienten vil være s = 55 mm/m. | |||
Retardasjonen r<sub>X</sub> for opprettholdelse av konstant hastighet v når lokomotivet skal bremse alene (som løslok): | |||
<math> | |||
r_X=g\cdot s=9,81\cdot {55 \over 1000}=0,54 {m\over s^2} | |||
</math> | |||
Nødvendig adhesjon αB beregnes (for løslok): | |||
<math> | |||
\alpha_B={r_X\over g}={0,54\over 9,81}=0,055 | |||
</math> | |||
Trykkraft F<sub>X</sub> mellom bremset lokomotiv og vogner beregnes. For et lokomotiv benyttes 3 vogner. Det legges til grunn en masse for hver vogn m<sub>O</sub> = 47.000 kg. | |||
Den ekvivalente masse for vognene beregnes med en dynamisk stivhetsfaktor κ<sub>O</sub> = 1,10. Den ekvivalente masse blir: | |||
<math> | |||
m_{eO}=m_O\cdot(1+k_O)=47000\cdot 1,10=51700 \ kg | |||
</math> | |||
For 3 vogner blir den ekvivalente masse: | |||
<math> | |||
\sum m_{eO}=3\cdot 51700=155100 \ kg | |||
</math> | |||
Trykkraft mellom 3 vogner og bremset lokomotiv hvor kurve- og luftmotstand neglisjeres: | |||
<math> | |||
F_X=(\sum m_{eO})\cdot r_X=155100\cdot 0,54=84,00 \ kN | |||
</math> | |||
Bremset kraft for det bremsede lokomotiv for opprettholdelse av konstant hastighet med 3 vogner ubremset: | |||
<math> | |||
F_{\alpha B}=m_B\cdot r_X+ F_X=21300\cdot 4\cdot 0,54\cdot 10^{-3}+84,00=46,00+84,00=130,00 \ kN | |||
</math> | |||
Kapasitet for El brems er 150 kN. | |||
Adhesjonen for det bremsede lokomotivet blir dermed: | |||
<math> | |||
\alpha_B = {r_X\over g}+{F_X\over m_B\cdot g} | |||
</math> | |||
<math> | |||
\alpha_B = {0,54\over 9,81}+{84,00\over 21300\cdot 4\cdot 9,81}=0,055+0,101=0,155 | |||
</math> | |||
Det er synlig at behovet for adhesjon øker fra 0,055 for lokomotivet alene til 0,155 når all bremsing skal foregå hos lokomotivet. Det er klart at α<sub>B</sub> = 0,155 er absolutt øvre grense for adhesjon på Flåmsbana. På grunn av driftsmessige årsaker med bl. annet fuktige skinner bør αB ha lavere verdi. | |||
Kapasitet for El brems er angitt til 150 kN. Utnyttelse av denne bremsekraften gir: | |||
<math> | |||
r_X={F_{\alpha B}\over m_B+m_{eO}} | |||
</math> | |||
<math> | |||
r_X={150\cdot 10^3\over 21300\cdot 4+155700 }={150\cdot 10^3\over 240900}=0,63 \ {m\over s^2} | |||
</math> | |||
Adhesjonen blir da: | |||
<math> | |||
\alpha_B={0,63\over 9,81}+0,101=0,064+0,101=0,165 | |||
</math> | |||
Denne verdien vil bli benyttet for å vurdere sannsynlighet for skinnevandring i lasket spor. | |||
Det er synlig at ved bremsing ned til full stopp kreves i tillegg mekanisk brems som i dette tilfellet er en pneumatisk brems. | |||
=== Vurdering av skinnevandring ved bremsing for opprettholdelse av konstant hastighet === | |||
Med grunnlag i en El brems på 150 kN og tilhørende nødvendig adhesjonskoeffisient α<sub>B</sub> = 0,165 skal vurderes sannsynlighet for skinnevandring ved framføring i konstant hastighet i lasket spor. | |||
Med α<sub>B</sub> = 0,165 er skinnene halvfuktige/halvtørre. | |||
Langsgående skinnespenninger på grunn av temperaturendringer vurderes ikke da sporet er lasket. | |||
En modell for vurdering er vist i figur 12.1. | |||
[[Fil:Figur_12.1.PNG|600px|thumb||center|<caption> Figur 12.1 Belastning på sporet på grunn av adhesjonskrefter </caption>]] | |||
<small></small> | |||
Det defineres følgende parametere: | |||
Hjulkraft: Q (kN) | |||
Adhesjon ved bremsing: α<sub>B</sub> | |||
Fordeling av hjulkraft over sville: Q<sub>1</sub>; Q<sub>2</sub>; Q<sub>3</sub> )kN) | |||
Friksjonskoeffisient mellom skinne og sville: μ<sub>M</sub> | |||
Friksjonskoeffisient mellom sville og pukk: μ | |||
Vertikalkraft mot pukk: N (kN) | |||
Motstandskraft i pukk mot sville: H (kN); ikke angitt, men inntegnet | |||
Hjulkraft er satt til Q = 115 kN; det er da tatt hensyn til kvasistatisk tillegg og til skjevlast. Adhesjonskoeffisienten er satt til 0,165; dvs. at kapasitet på El brems er utnyttet. | |||
Adhesjonskraft mot topp skinne fra hvert hjul: | |||
<math> | |||
\alpha_B\cdot Q=0,165\cdot 115,00=19,00 \ kN | |||
</math> | |||
Klemkraften i befestigelsen bør ha så høy kapasitet at klemkraften må bidra til at skinnen ikke beveger seg i forhold til svillen. Det blir tatt utgangspunkt i en klemkraft i befestigelsen på 6 kN. Det finnes en del HeyBack befestigelse i sporet. Videre er sporet lasket slik at skinnene vil utvide seg ved oppvarming og trekke seg sammen ved lavere temperaturer. Det opptrer dermed en bevegelse i skinnene inntil gapet mellom 2 skinneender blir lukket ved oppvarming. Skinnene vil trekke seg sammen ved overgang til kaldere temperaturer. Kravet til klemkraft er av den grunn lavere enn ved helsveist spor. Skinnene er allikevel bundet sammen ved laskene med bolter. | |||
På grunn av svilleavstand og normal fordeling av hjulkraften på elastisk spor forutsettes at 3 sviller aktiviseres for å ta opp adhesjonen. Dette gir 6 fjærer med samlet klemkraft: | |||
<math> | |||
2\cdot 3\cdot 6,00=36,00 \ kN \ > \ 19,00 \ kN | |||
</math> | |||
Det må erkjennes at fjærene i befestigelsen i midtre sville får større belastninger enn nabofjærene; men til gjengjeld er vertikalkraften større slik at friksjonskoeffisienten får større betydning. | |||
På grunn av type befestigelse antas ingen friksjon mellom skinne og mellomlegg/sville som kan gi ytterligere bistand mot bevegelse av skinne i forhold til sville. | |||
På grunn av elastisiteten i sporet vil hjulkraften fordele seg over 3 sviller: | |||
<math> | |||
Q_1=Q_3={1\over 4}\cdot 115,00=28,75 \ kN | |||
</math> | |||
<math> | |||
Q_2={1\over 2}\cdot 115,00=57,50 \ kN | |||
</math> | |||
Det benyttes tresviller med vekt på 70 kg. Den vertikale tilleggskraft fra hver sville: | |||
<math> | |||
\Delta Q={1\over 2}\cdot 70\cdot 10\cdot 10^{-3}=0,35 \ kN | |||
</math> | |||
Horisontal motstandskraft i pukken for bevegelse av sville (halv lengde): | |||
<math> | |||
H=2,00 \ kN | |||
</math> | |||
For 3 sviller: | |||
<math> | |||
H=6,00 \ kN | |||
</math> | |||
Samlet vertikalkraft: | |||
<math> | |||
N=115,00+3\cdot 0,35=116,00 \ kN | |||
</math> | |||
Skinnevekten er ikke tatt med. | |||
Den samlede horisontale kraft i lengderetningen fra adhesjonen er: | |||
<math> | |||
\alpha_B\cdot Q=19,00 \ kN | |||
</math> | |||
Nødvendig friksjonskoeffisient mellom 3 sviller og pukklaget i ballastsengen for å hindre svillevandring med skinner: | |||
<math> | |||
\mu={\alpha_B\cdot Q\over N}={19,00-6,00\over 116,00}=0,112 | |||
</math> | |||
Denne friksjonskoeffisienten er meget lav og vil normalt kunne oppfylles. | |||
Det skulle således ikke være fare for skinnevandring i bremset tilstand i et lasket spor. | |||
=== Nødvendig kraft for nedbremsing til full stopp === | |||
Ved nedbremsing til full stopp på linje i fall med gradient s (mm/m) beregnes den samlede retardasjon for et tog hvor adhesjonskoeffisienten utnyttes ved pneumatisk brems: | |||
<math> | |||
r_x= g\cdot(\alpha_B-s)=9,81\cdot\left({0,135-{55\over 1000}}\right)=0,79 \ {m\over s^2} | |||
</math> | |||
Det legges til grunn en adhesjonskoeffisient α<sub>B</sub> = 0,135; dvs. halvfuktige/halvtørre skinner. Nødvendig bremsekraft for 3 vogner mot skinne hvor kurvemotstand neglisjeres, beregnes. | |||
<math> | |||
F_{\alpha B}=\sum_{i=}^{n_{pB}}F_{\alpha Bi}=r_X\cdot (m_{\alpha VOGNER}) | |||
</math> | |||
<math> | |||
F_{\alpha B} =\sum_{i=}^{n_{pB}}F_{\alpha Bi}=0,79 (3\cdot 47000 )=111 \ kN | |||
</math> | |||
Det er til sammen 24 hjul for de 3 vognene. Dette gir en gjennomsnittlig bremsekraft for hvert hjul mot skinner: | |||
<math> | |||
F_{\alpha B} = {111,00\over 24}=4,63 \ kN | |||
</math> | |||
Nødvendig bremsekraft for lokomotivet mot skinne hvor kurvemotstand neglisjeres, beregnes: | |||
<math> | |||
F_{\alpha B}=\sum_{i=}^{n_{pB}}F_{\alpha Bi}=r_X\cdot (m_{\alpha LOKOMOTIV}) | |||
</math> | |||
<math> | |||
F_{\alpha B}=\sum_{i=}^{n_{pB}}F_{\alpha Bi}=0,79\cdot 85200=67,31 \ kN | |||
</math> | |||
Det er til sammen 8 hjul i lokomotivet. Dette gir en gjennomsnittlig bremsekraft for hvert hjul mot skinner: | |||
<math> | |||
F_{\alpha B}=\sum_{i=}^{n_{pB}}F_{\alpha Bi}=0,79 (3\cdot 47000 )=111 \ kN | |||
</math> | |||
Ekvivalent masse eller massetreghetsmoment for alle 3 vogner: | |||
<math> | |||
3\cdot m_{eB,VOGN}=3\cdot m_B\dot(1+\kappa_B)=3\cdot 47000\cdot (1+0,10)=155100 \ kg | |||
</math> | |||
Ekvivalent masse eller massetreghetsmoment for lokomotivet: | |||
<math> | |||
m_{eB,LOKOMOTIV}= m_B\dot(1+\kappa_B)=85200\cdot (1+0,10)=93720 \ kg | |||
</math> | |||
For vognene blir det bremsede moment for et hjulpar: | |||
<math> | |||
M_{B,HJULPAR,VOGN}=3\cdot m_{eB}\cdot r_X\cdot r_B\cdot {1\over 12}=155100\cdot 0,79\cdot {0,84\over 2}\cdot {1\over 12}=4,30 \ kNm | |||
</math> | |||
Tilsvarende for lokomotivet: | |||
<math> | |||
M_{LOKOMOTIV}= m_{eB}\cdot r_X\cdot r_B\cdot {1\over 4}=93720\cdot 0,79\cdot {1,10\over 2}\cdot {1\over 4}=10,20 \ kNm | |||
</math> | |||
Det tas ikke stilling til hvilke type bremser som benyttes; blokkbremser, bremseskiver eller annet. Det legges til grunn blokkbremser i de etterfølgende beregninger. Ved lik bremsing på alle hjulpar blir bremsekraften mellom blokkbrems og hjul for vogner: | |||
<math> | |||
F_{Bi}={3\cdot m_{eB, VOGN}\cdot r_X\over n_{pB}}={155100\cdot 0,79\over 2 \cdot 12}=5,10 \ kN | |||
</math> | |||
For lokomotiv gjelder: | |||
<math> | |||
F_{B \ LOKOMOTIV}={ m_{eB, LOKOMOTIV}\cdot r_X\over n_{pB}}={93720\cdot 0,79\over 2 \cdot 4}=9,25 \ kN | |||
</math> | |||
For en hastighet V<sub>0</sub> = 30 km/h (eller v<sub>0</sub> = 8,33 m/s) beregnes bremsetiden til (r<sub>X</sub> = 0,79 m/s<sup>2</sup>): | |||
<math> | |||
t_B={v_0\over r_X}={8,33\over 0,79}=11s | |||
</math> | |||
Bremselengde beregnes til: | |||
<math> | |||
s_B={v_0^2\over 2\cdot r_X}={8,33^2\over 2\cdot 0,79}=44m | |||
</math> | |||
Det er opplyst at pneumatisk brems og El brems i kombinasjon kan oppnå en retardasjon på opp mot r<sub>X</sub> = 1,84 m/s<sup>2</sup>. Da begge typene er å betrakte som adhesjonsavhengige bremser, må skinnene være relativt tørre eller det kan oppstå glidning inntil grense for glidevern. Det vurderes at det inntreffer bare unntaksvis. | |||
=== Vurdering av skinnevandring ved nedbremsing til full stopp === | |||
På grunn av spredning av bremsekraften på alle hjul forventes ikke skinnevandring eller bare en beskjeden skinnevandring | |||
== Traksjon == | |||
Det skal utføres noen enkle beregninger for traksjonskrefter utøvet av lokomotivet i akselerasjonsfasen og for opprettholdelse av konstant hastighet i stigning. Det blir antatt en akselkraft fra lokomotivet lik 213 kN og en akselkraft fra vogner lik 117,50 kN. Det legges til grunn at et lokomotiv skal trekke 3 vogner. | |||
Flåmsbana har en høy gradient for stigning og er samtidig meget kurverik med små radier (R = 150 m). Dermed utøves det stor motstand for framføring. Sporet har en lasket konstruksjon (ikke helsveist). | |||
De enkelte parametere for motstand er: | |||
*mekanisk gangmotstand D<sub>M</sub> som er størst ved igangsetting (lavere når toget er i bevegelse) | |||
*kurvemotstand D<sub>K</sub> | |||
*luftmotstand D<sub>L</sub> som settes sammen av flere faktorer og er en del av grunnmotstanden | |||
*stigningsmotstand D<sub>S</sub> | |||
=== Mekanisk gangmotstand === | |||
Litteraturen angir formler for beregning av mekanisk gangmotstand. Med en beskjeden masse fra lokomotiv og vogner kombinert med lav hastighet vil denne motstanden være lav. | |||
Samlet masse: | |||
<math> | |||
m_{ LOKOMOTIV+VOGNER}=m_T=85200+3\cdot 47000=226200 \ kg | |||
</math> | |||
Hastigheten er v = 8,33 m/s. | |||
Det utføres ikke beregninger av denne motstanden; den vurderes å være: | |||
<math> | |||
D_M=5,00 \ kN | |||
</math> | |||
=== Kurvemotstand === | |||
Det benyttes en vanlig brukt formel: | |||
<math> | |||
D_K={6,50\over R-60}\cdot 226200=16,40 \ kN | |||
</math> | |||
Det er et spørsmål om ovennevnte formel gjelder for så små kurveradier. I litteraturen legges til grunn en radius R ≥ 300 m. Imidlertid, i mangel av bedre underlag benyttes denne formelen. | |||
=== Luftmotstand som del i grunnmotstanden === | |||
Det benyttes den enkle formel for spesifikk motstand: | |||
<math> | |||
w_0=2,40+{V^2\over 1300}=2,40+{30^2\over 1300}=2,40+0,70=3,10 \ {N\over kN} | |||
</math> | |||
Togets samlede luftmotstand: | |||
<math> | |||
D_L=m_T\cdot g\cdot w_0=226200\cdot 10\cdot 3,10\cdot 10^{-3}=7,00 \ kN | |||
</math> | |||
=== Stigningsmotstand=== | |||
Gradienten på Flåmsbana er 55 mm/m. | |||
Stigningsmotstanden blir: | |||
<math> | |||
D_S=m_T\cdot g\cdot {s\over 1000}=226200\cdot 10\cdot {55\over 1000}=125 \ kN | |||
</math> | |||
=== Samlet motstand: === | |||
Den samlede motstand beregnes: | |||
<math> | |||
D=D_M+D_K+D_L+D_S=5,00+16,40+7,00+125,00=153,40 \ kN | |||
</math> | |||
Det er synlig at stigningsforholdene utgjør en betydelig andel av motstanden. | |||
Følgende ligning kan benyttes for beregning av nødvendig adhesjon: | |||
<math> | |||
\alpha_D={m_D+m_{eO}\over m_{\alpha D}\cdot g}\cdot a_X+{D\over m_{\alpha D}\cdot g} | |||
</math> | |||
I ovennevnte ligning er termen m<sub>e O</sub> vognenes ekvivalente masse: | |||
<math> | |||
m_{e0}=(1+\kappa)m_{VOGNER}=1,10\cdot 3\cdot 47000=155100 \ kg | |||
</math> | |||
Da alle akslene på lokomotivet har traksjon, er m<sub>D</sub> = m<sub>α D</sub>. | |||
Adhesjonskoeffisienten vil ha en verdi i området 0,15 – 0,20 ved normale forhold på skinnehodet (verken helt tørt eller helt fuktig). | |||
Det antas en akselerasjon a<sub>X</sub> = 0,10 m/s<sup>2</sup>. Dette gir adhesjonsverdi for opprettholdelse av konstant hastighet (hastighetsendringen er svært liten så den betraktes som konstant): | |||
<math> | |||
\alpha_D={85200+155100\over 85200\cdot 10}\cdot 0,10+{153,40\cdot 10^3\over 85200\cdot 10}=0,028+0,180=0,21 | |||
</math> | |||
Adhesjonen er temmelig bra utnyttet dersom den er antatt riktig. | |||
Det undersøkes om en høyere akselerasjon er mulig for å nå hastigheten hurtigere. Det kan for eksempel bli tatt utgangspunkt i en aksellerasjonstid på 30 sekunder for å nå hastighet V = 30 km/h eller v = 8,33 m/s. | |||
<math> | |||
a_X={v\over t}={8,33\over 30}=0,28 \ {m\over s^2} | |||
</math> | |||
Adhesjonen blir: | |||
<math> | |||
\alpha_D={85200+155100\over 85200\cdot 10}\cdot 0,28+{153,40\cdot 10^3\over 85200\cdot 10}=0,079+0,180=0,26 | |||
</math> | |||
Det kreves en høyere adhesjonskoeffisient. Skinnene skal i dette tilfellet være tørrere. Det er et spørsmål hvor realistisk dette tilfellet er. | |||
Nødvendig trekkraft fra lokomotivet blir da: | |||
<math> | |||
F_\alpha=\alpha_D\cdot m_{LOKOMOTIV}\cdot g=0,26\cdot85200\cdot 10=221,50 \ kN | |||
</math> | |||
Kraften fordeles på 4 aksler eller 8 hjul. | |||
For hvert hjul utøves en adhesjonskraft mot skinnene: | |||
<math> | |||
{1\over 8}\cdot F_\alpha ={1\over 8}\cdot 221,50=27,70 \ kN | |||
</math> | |||
Det blir tatt utgangspunkt i en klemkraft på 6 kN. Det regnes med at hjulkraften fordeles på 3 sviller. Dette gjelder også den langsgående trekkraft fra lokomotivet. Det blir da til sammen 6 fjærer som gir en samlet klemkraft: | |||
<math> | |||
2\cdot 3\cdot 6,00=36,00 \ kN \ > \ 27,70 \ kN | |||
</math> | |||
På grunn av elastisitet i sporet vil hjulkraften fordele seg over 3 sviller: | |||
<math> | |||
Q_1=Q_3=0,25\cdot 115,00=28,75 \ kN | |||
</math> | |||
<math> | |||
Q_2=0,50\cdot 57,50 \ kN | |||
</math> | |||
Det benyttes tresviller med vekt på 70 kg. Den vertikale tilleggskraft fra hver sville: | |||
<math> | |||
\Delta Q={1\over 2}\cdot 70\cdot 10\cdot 10^{-3}=0,35 \ kN | |||
</math> | |||
Horisontal motstandskraft i pukken for bevegelse av sville (halv lengde): | |||
<math> | |||
H=2,00 \ kN | |||
</math> | |||
For 3 sviller: | |||
<math> | |||
H=6,00 \ kN | |||
</math> | |||
Samlet vertikalkraft: | |||
<math> | |||
N=115,00+3\cdot 0,35=116,00 \ kN | |||
</math> | |||
Skinnevekten er ikke tatt med. | |||
Nødvendig friksjonskoeffisient mellom 3 sviller og pukklaget i ballastsengen for å hindre svillevandring med skinner: | |||
<math> | |||
\mu ={{1\over 8}\cdot F_\alpha -H\over N}={27,70-6,00\over 116,00}=0,19 | |||
</math> | |||
Denne friksjonskoeffisienten er meget lav og vil normalt kunne oppfylles. | |||
Det skulle således normalt ikke være fare for skinnevandring ved utførelse i traksjon for et lasket spor. | |||
== Vurderinger mht. skinnevandring ved nedbremsing og traksjon av materiell i lasket spor ved avvik i nøytraltemperatur == | |||
Skinnene er spenningsfrie på grunn av temperatur ved nøytraltemperatur og det finnes da et gap mellom skinneendene for 2 naboskinner i varmerommet i et lasket spor. Ved svakere klemkraft i befestigelsen kan det komme til bevegelse av skinnene inntil gapet tettes ved temperaturstigning. Tilsvarende vil ved lavere temperaturer gapet bli større. På grunn av disse forholdene innføres store strekk- og trykkrefter i skinnene. Dette aspektet vil da føre til skinnevandring. Arbeidsdiagrammet for skinner i lasket spor ved temperaturendringer er vist i figur 14.1. | |||
Erfaringer som er gjort på Ofotbanen og som også er vist ved målinger i et DAMILL AB målesystem, bekrefter at skinner blir belastet med langsgående krefter i en relativt stor avstand foran lokomotivet ved traksjon i forbindelse med framføring. Sporet betraktes på dette stedet som ubelastet (ikke vertikal belastning fra materiellet). Skinnegangen kan da bli trukket innover og dermed endres nøytraltemperaturen. Sporet på Ofotbanen er helsveist. | |||
Dersom en slik erfaringsoverføring legges til grunn, blir det nødvendig å vurdere | |||
*Krypkrefter ved framføring på belastet skinne på grunn av lokomotivet og langsgående krefter på grunn av temperaturendringer (avvik i nøytraltemperatur) | |||
*Krypkrefter på ubelastet naboskinne (gjennom skjøten) og langsgående krefter på grunn av temperaturendringer (avvik i nøytraltemperatur) | |||
Flåmsbana har lasket sporkonstruksjon og er dermed bundet sammen ved lasker. Laskene med bolter kan overføre en kraft på ca. 100 kN. I samsvar med erfaringene på Ofotbanen kan det ikke utelukkes at den ubelastede naboskinne til belastet skinne fra lokomotivet blir utsatt for langsgående krefter forårsaket av traksjon. Aspektet kan medføre en kraft fra hvert hjul på 27,70 kN (beregnet i kapittel foran). 4 hjul vil gi en samlet kraft på ca. 100 kN for hver skinnestreng, altså den kapasitet som laskeboltene har. | |||
Skinnene har en lengde på 40 m som medfører ca. 60 sviller med befestigelse. Dersom naboskinnen betraktes som ubelastet fra toget og motstand mot forskyvning av sporet er antatt til H = 2 kN (halv svillebredde), så blir samlet motstand mot skinnevandring lik 120 kN > 100 kN. Befestigelsen regnes å ha kapasitet mht. den langsgående kraft forårsaket av lokomotivet. For nøytraltemperatur skulle da skinnevandring på grunn av traksjon normalt ikke forekomme (se foregående kapittel); eller skinnevandringen skulle bli beskjeden. | |||
Dersom temperatur avviker fra nøytraltemperatur, medfører dette aspektet langsgående krefter i skinnene. Utøvelse av traksjon for akselerasjon vil i tillegg føre til langsgående krypkrefter. Samlet kan disse 2 aspektene forårsake skinnevandring og at sporet blir trukket innover. Dette kan inntreffe for ubelastet og belastet skinne fra lokomotivet. Ved overgang fra El 17 til El 18 øker aksellasten med en faktor 1,33. Aspektet vil gi en økning i adhesjonskraften for samme adhesjonskoeffisient. Imidlertid vil den økte aksellasten virke stabiliserende. | |||
Skjøtåpningene må kontrolleres og om nødvendig justeres. Når skjøtåpninger er blitt for store eller for små, skyldes dette i regelen enten skinnevandring eller lasken som kan gi for stor eller for liten friksjon. I slike tilfeller må det foretas skjøtregulering, rensing og smøring av laskekammeret og tilskruing av laskene. Varmeromstabellen må følges. | |||
[[Fil:Figur_14.1.PNG|600px|thumb||center|<caption> Figur 14.1 Arbeidsdiagrammet for skinner i lasket spor ved temperaturendringer</caption>]] | |||
<small></small> | |||
== Termisk belastning == | |||
Det skal gis en vurdering av termisk belastning relatert til lokomotivet for 21,3 tonns aksellast. Linjen har en helning med gradient på 55 mm/m og det utøves derfor både traksjons- og bremsekrefter. | |||
Når et hjul ruller på skinnen, er det ingen forskjell i hastighet i den felles kontaktflaten som eksisterer mellom punkter på hjulet og punkter på skinnen. Derimot når hjulet skal utføre traksjon eller skal bremse, så oppstår det forskjell i hastigheter i kontakten. Aspektet fører til varmeutvikling. Den last som overføres ved aksellast, får betydning. Selv ved relativt små forskjeller i hastighet kan dette gi stor varmeeffekt som igjen kan resultere i forhøyet temperatur særlig i hjulet. Det kommer dermed til en effektutvikling. | |||
Særlig høye temperaturer kommer til syne for traksjonshjul på lokomotiv. | |||
De maksimale temperaturer oppstår naturlig nok i den elliptiske kontaktflate på overflaten. Den høyere temperaturen avtar raskt i dybden i skinnehodet. | |||
En nøyere analyse bekrefter at hjul og skinne blir belastet ulikt ved en betraktning av fordelingen av spenningene som følge av normal- og tangentialkrefter når også temperaturspenningene tas hensyn til. Ved traksjon oppstår normalt en høyere belastning på skinnen. Ved bremsing blir belastningen på hjulet høyere. | |||
Effektutvikling mellom hjul og skinne utledes av formelen: | |||
<math> | |||
P=\left\vert v\cdot F \right\vert | |||
</math> | |||
Her betyr termene v glidningshastighet og F tangentialkraft langs skinnen. | |||
Tangentialkraften F utledes av: | |||
<math> | |||
F=\mu\cdot N | |||
</math> | |||
Termen N er normalkraften: | |||
<math> | |||
N={1\over 2}\cdot m\cdot g={1\over 2}\cdot 21,3\cdot 10^3\cdot 10=106,50 \ kN | |||
</math> | |||
Som maksimalverdi for stigning av temperatur i kontaktflaten mellom hjul og skinne ved rent lengdekryp for rene overflater (for eksempel ikke rue flater på skinnehodet) angir litteraturen følgende forenklede formel ved traksjon fra lokomotiv: | |||
<math> | |||
\Theta_{max}=0,62\cdot \mu\cdot p_0\cdot \left\vert \upsilon_\xi \right\vert \cdot \sqrt{a\cdot v_0\over \lambda \cdot \rho \cdot c} | |||
</math> | |||
De enkelte termer skal forklares: | |||
Friksjonskoeffisient: <math> \mu \ \ (-) </math> | |||
Spenning i middelpunkt i kontaktflate: <math> p_0 \ \ \ \left({N\over mm^2}\right) </math> | |||
Kryp i lengderetning: <math> \left\vert \upsilon_\xi\right\vert \ \ (-) </math> | |||
Halvakse i elliptisk kontaktflate: <math> a \ \ \ (mm)) </math> | |||
Framføringshastighet: <math> v_0 \left({m\over s}\right) </math> | |||
Varmeledningsevne for stål: <math> \lambda \left({W\over K\cdot m}\right) </math> | |||
Tetthet for stål: <math> \rho \left({kg\over m^3}\right) </math> | |||
Spesifikk varmekapasitet: <math> c \left({J\over K\cdot kg}\right) </math> | |||
I ovennevnte termer betyr: | |||
Kelvin grader: K | |||
J er enhet i Joule: <math> \left({kg\cdot m^2\over s^2}=kg\cdot {m\over s^2}\cdot m=Nm\right) </math> | |||
W er enhet i watt: <math> \left({J\over s}={kg\cdot m^2\over s^3} \right) </math> | |||
Det skal utføres en dimensjonsanalyse for formelen for stigning av temperaturen: | |||
<math> | |||
\Theta=(-)\cdot \left( {N\over m^2}\right)\cdot (-)\cdot\sqrt{m\cdot{m\over s}\over {W\over k\cdot m }\cdot {kg\over m^3}\cdot{J\over K\cdot kg }} | |||
</math> | |||
Termen K (Kelvingrader) kan trekkes ut fra rotuttrykket. Innføring for W og J gir: | |||
<math> | |||
\Theta=(-)\cdot \left( {N\over m^2}\right)\cdot (-)\cdot\sqrt{m\cdot{m\over s}\over {{kg\cdot m^2\over s^3}\over m}\cdot {kg\over m^3}\cdot{{kg\cdot m^2\over s^2}\over kg}} | |||
</math> | |||
<math> | |||
\Theta=(-)\cdot \left( {N\over m^2}\right)\cdot (-)\cdot K\cdot \sqrt{m^2\over {{kg\cdot m^2\over s^2}\over m}\cdot {kg\over m^3}\cdot{{kg\cdot m^2\over s^2}\over kg}} | |||
</math> | |||
<math> | |||
\Theta=(-)\cdot \left( {N\over m^2}\right)\cdot (-)\cdot K\cdot {1\over {kg\cdot m^2\over s^2} } \sqrt{m^2\over {m\over m}\cdot {kg\over m^3}\cdot{ m\over kg}} | |||
</math> | |||
<math> | |||
\Theta=(-)\cdot \left( {N\over m^2}\right)\cdot (-)\cdot K\cdot {1\over {kg\cdot m^2\over s^2} } \cdot m^2 | |||
</math> | |||
<math> | |||
\Theta=K\cdot {N\over m^2}\cdot {m^2\over N}=K \ \ \ grader | |||
</math> | |||
Det er dermed vist at formelen gir riktige dimensjoner og at den kan anvendes. Det legges merke til at halvaksen i den elliptiske kontaktflate a må ha dimensjon i (m) og at p<sub>0</sub> har dimensjon i (N/m<sup>2</sup>). | |||
Det gjennomføres et beregningseksempel med formelen for et lokomotiv med traksjon: | |||
<math> | |||
\Theta_{max}=0,62\cdot \mu \cdot p_0\cdot \left\vert \upsilon_\xi \right\vert \cdot \sqrt{a\cdot v_0\over \lambda\cdot \rho\cdot c} \ \ (K) | |||
</math> | |||
Følgende inngangsdata: | |||
Friksjon: μ = 0,30 (-) | |||
Flatetrykk hjul/skinne: p<sub>0</sub> = 686 N/mm<sup>2</sup> = 686 · 106 N/m2 | |||
Krypkoeffisient: v<sub>ξ</sub> = 0,05 (5 %) | |||
Halvakse i ellipse: a = 5,90 mm = 0,0059 m | |||
Hastighet: v<sub>0</sub> = 30 m/s | |||
Parameter λ: λ = 50 W/mK | |||
Parameter ρ: ρ = 7850 kg/m<sup>3</sup> | |||
Parameter c: c = 450 J/kgK | |||
Parameterverdier innsatt i ligning: | |||
<math> | |||
\Theta_{max}=0,62\cdot 0,30 \cdot 686\cdot 10^6 \cdot \left\vert 0,05 \right\vert \cdot \sqrt{0,0059\cdot 30\over 50\cdot 7850\cdot 450}=202^0 \ \ (K) | |||
</math> | |||
Det er særlig hjulbanen som vil få denne temperaturen da hjulet blir utsatt for vedvarende bremsing. | |||
== Vurdering av sidestabilitet ved Prud`Hommes formel == | |||
prEN 14363 definerer grenseverdi for lateral kraft som kan forårsake sideforskyvning av sporet. Denne styringskraften er den laterale resultant av venstre og høyre hjulkraft til en aksel. På grunn av sporkonstruksjonen benyttes en faktor k = 0,85 i Prud`Hommes formel for Flåmsbana: | |||
<math> | |||
\sum Y_{j \ maks}=0,85\cdot \left( 10+{2\over3}\cdot Q_0\right) \ (kN) | |||
</math> | |||
Innsatt i formel for El 18 gir: | |||
<math> | |||
\sum Y_{j \ maks}=0,85\cdot \left( 10+{2\over3}\cdot 106,50\right)=68,85 \ kN | |||
</math> | |||
Den maksimale styringskraft som El 18 kan utøve for å unngå sideforskyvning av sporet ved normale forhold er 68,85 kN. Kraften har en lengde på 2 meter i vinduet og evalueres i et lavpass filter på 20 Hz. | |||
Det skal bli gjort et forsøk på å vurdere hvilken styringskraft som El 18 utøver (pragmatisk betraktning). | |||
Styringskraften beregnes etter følgende formel: | |||
<math> | |||
\sum Y_{j \ maks} =Y_{ytre \ hjul}-Y_{indre \ hjul} | |||
</math> | |||
EN 13103 og EN 1304 betrakter Y<sub>indre</sub> hjul som en friksjonskraft. Normene definerer: | |||
<math> | |||
Y_2 =Y_{indre \ hjul}=0,175\cdot m_1\cdot g=0,175\cdot 21300\cdot 10\cdot 10^{-3}=37 \ kN | |||
</math> | |||
Det er i kapittel foran beregnet en kvasistatisk kraft Y<sub>KV.STAT.</sub> = 74,55 kN iht. ligningssystemet i EN 13103 og EN 13104. Denne kraften skulle tilsvare Y<sub>ytre hjul</sub>. | |||
Dette skulle medføre en styringskraft ∑Y<sub>j maks</sub> = 37,55 kN < 68,85 kN. Selv om El 18 har gode radielle styringsegenskaper, så er resultatet optimistisk. Kraften er trolig større. | |||
Det er 2 usikre faktorer: | |||
Det er lagt til grunn en friksjonskoeffisient på indre skinnestreng lik 0,350 fra et hjul. Aspektet forutsetter relativt tørre skinner. En mindre friksjonskoeffisient ville bidra til høyere ∑Y<sub>j maks</sub>. Dette fordi sentrifugalkraften og kraft fra støtfaktor vil få større innflytelse. | |||
For det andre hersker det usikkerhet i om formelverket i EN 13103 eller 13104 samsvarer med de krefter som blir evaluert i EN 14363 i et lavpassfilter på 20 Hz. | |||
Imidlertid konkluderes det med at kapasiteten til sporet mot sideforskyvning er tilstrekkelig god nok. | |||
== Vurdering av (Y/Q) ved dynamisk belastning == | |||
EN 14363 fastsetter kvotienten for avsporing til å være vurdert i et lavpass filter på 20 Hz: | |||
<math> | |||
\left({Y\over Q}\right)_{j,a,max}=0,80 | |||
</math> | |||
I kapitlet for beregning av dynamiske Q og Y krefter er det benyttet følgende verdier for kreftene: | |||
Q<sub>DYN</sub> = 184,00 kN | |||
Y<sub>DYN</sub> = 96,00 kN | |||
Y<sub>DYN</sub> vurderes å være meget høy. Med de radielle styringsegenskaper som El 18 har, er verdien lavere; selv i kurver med R = 150 m. | |||
Anvendelse av formel gir: | |||
<math> | |||
\left({Y\over Q}\right)_{j,a,max}={96,00\over 184,00}=0,52< 0,80 | |||
</math> | |||
Det må påpekes at det hersker usikkerhet i om formelverket i Zimmermanns metode samsvarer med evalueringsprosessen i EN 14363 (vurdering i lavpass filter på 20 Hz). | |||
Imidlertid er sikkerhet mot avsporing tilstrekkelig god. | |||
== Vurdering av (Y/Q) ved statisk belastning i svært lav hastighet (hjulavlastning) == | |||
Nadals formel gjelder: | |||
<math> | |||
{Y_a\over Q_a}< {tg\gamma_a-\mu\over 1+\mu\cdot tg\gamma_a} | |||
</math> | |||
[[Fil:Figur_18.1.PNG|600px|thumb||center|<caption> Figur 18.1 Anskueliggjøring for beregning av avsporing i Nadals formel</caption>]] | |||
<small></small> | |||
Det legges til grunn at El 18 har et hjulprofil som gir flensvinkel på 68° - 70°. For en friksjonskoeffisient μ = 0,36 blir | |||
<math> | |||
\left({Y\over Q}\right)_{ytre}=1,20 | |||
</math> | |||
En typisk overgangskurve på Flåmsbana har en lengde L = 20 og overhøyde D = 50 mm. Aspektet gir en gradient i overhøyderampen på 1 : 400. Imidlertid ved overgang til en sirkelkurve med R = 150 m bør også overhøyderampen ha slak helning. | |||
Videre har trolig boggiene i El 18 torsjonsegenskaper som gir sikker framføring ved hjulavlastning i overhøyderamper som har større gradienter (gradient 1 : 333 forekommer). | |||
Det konkluderes med at avsporingsfare iht. Nadals formel under normale forhold ikke vil forekomme. | |||
== Delta r kriteriet == | |||
På en bane med kurveradier R = 150 m er det nødvendig at Δ r kriteriet oppfylles i størst mulig grad. | |||
∆r – kriteriet beskriver differanse i radius på hjulbanene til et hjulsett iht. formel: | |||
<math> | |||
\Delta r=2\cdot \gamma\cdot y= {r\cdot s\over R} | |||
</math> | |||
∆r uttrykkes som funksjon av konisitet og horisontal forskyvning i retning mot ytterstreng i sirkelkurven eller som en funksjon av hjulradius r og sporvidde s i sirkelkurve. I ovennevnte ligning er R radius i sirkelkurve regnet fra origo til innerstreng. | |||
Differanse i radius på hjulbanene er nødvendig fordi det er forskjell mellom radius til ytre skinnestreng og indre skinnestreng i en sirkelkurve. Det vises til figur 19.1. | |||
[[Fil:Figur_19.1.PNG|600px|thumb||center|<caption> Figur 19.1 Differanse i rulleradius ved gjennomløp i kurver</caption>]] | |||
<small></small> | |||
I figur 19.2 er vist ∆r som funksjon av hjulradius og kurveradius med konstant sporvidde. | |||
[[Fil:Figur_19.2.PNG|600px|thumb||center|<caption>Figur 19.2 Nødvendig differanse i hjulradius for indre og ytre hjul ved gjennomløp i sirkelkurver</caption>]] | |||
<small> | |||
</small> | |||
Det er av betydning at ∆r – kriteriet overholdes i størst mulig grad for at de krypkrefter som ellers ville oppstå i samspillet hjulsett/spor, skal holdes under kontroll. | |||
Dersom hjulradius er 550 mm, beregnes nødvendig Δr til 5,50 mm for kurveradius R = 150 m. | |||
Det blir bedt om en redegjørelse om i hvilken grad NSB iverksetter tiltak for best mulig overholdelse av kriteriet. | |||
== Radiell styringsindeks == | |||
En annen parameter av betydning er ∆x–kriteriet som i geometrisk henseende er et vilkår for radiell innstilling av hjulsett i kurver. Forholdet kan uttrykkes ved formel: | |||
<math> | |||
\Delta x={a\cdot s\over 4\cdot R} | |||
</math> | |||
Dette er anskueliggjort i figur 20.1. | |||
[[Fil:Figur_20.1.PNG|600px|thumb||center|<caption>Figur 20.1 Definisjon av ∆x-kriteriet</caption>]] | |||
<small></small> | |||
a er avstand mellom hjulsettene i en boggi. | |||
s er avstand mellom hjulene i hjulsettet. | |||
R er kurvens radius. | |||
Parameteren ∆x er vist grafisk i figur 20.2. | |||
∆x uttrykker den avstand som senterlinje for det ytre hjulet i hjulsettet må være foran det indre hjulet sett i forhold til en linje vinkelrett på vognens lengdeakse. Tilsvarende må senterlinjen til det indre hjulet være Δx bak den samme linje. Den totale avstand blir dermed 2Δx. Dette er en betingelse for å oppnå radiell styring av hjulsettet i kurven. | |||
[[Fil:Figur_20.2.PNG|600px|thumb||center|<caption>Figur 20.2 Beregning av Δx</caption>]] | |||
<small></small> | |||
<small></small> | |||
For kurveradius lik 150 m beregnes Δx til 7 mm for en boggi med hjulavstand lik 2,8 m. | |||
Beregningen innebærer at hjulene i ytterstreng må gå 14 mm fra hverandre og hjulene på innerstreng må gå 14 mm til hverandre (nærme seg hverandre). | |||
Det blir bedt om en redegjørelse om i hvilken grad NSB iverksetter tiltak for best mulig overholdelse av kriteriet. | |||
== Opprettholdelse av sporvidde vurdert ut fra kurveradius, skinneslitasje og kontakt av svilleskrue for befestigelsen mot trematerialet til tresviller == | |||
Det er av betydning at sporvidden holdes innenfor de mål som regelverket foreskriver for å unngå avsporing. Aspektet medfører at svilleskruene må ha kontakt med materialet i svillene. Tester kan utføres med et definert dreiemoment som er beskrevet i regelverket for vedlikehold. | |||
Måling med målevogn, dvs. måling i belastet spor vil gi informasjon om opptredende sporvidde og om svilleskruene er i kontakt med trevirke i svillene. | |||
I benyttet spor med små radier med tresviller kan opptredende sporvidde settes sammen av 4 komponenter: | |||
*Nominell sporvidde | |||
*Utvidelse av nominell sporvidde i kurver med små radier gjennom bormønsteret | |||
*Slitte skinnehoder på skinnene (særlig for ytre skinnestreng) | |||
*Slark i skruehullene (som ikke må forekomme) | |||
Et slitasjebilde for ytterstreng og innerstreng er vist på side 21. Slitasjen i tverrprofilet i ytterstreng er betydelig. Skjeggdannelsen på indre streng framkommer tydelig i bilde på samme side. | |||
Nominell sporvidde er 1435 mm. | |||
For kurver med radier R ≥ 300 m benyttes nominell sporvidde lik 1435 mm. For kurver med radier 200 m < R < 300 m utvides sporvidden med 5 mm til 1440 mm. For kurver med radier R ≤ 200 m settes sporvidde til 1445 mm. | |||
I klasse K3 eller lavere foreskriver regelverket et tillatt avvik fra grunnverdien som er 1435 mm, på 15 mm i vedlikeholdsgrense. Tiltaksgrensen er 30 mm og umiddelbar grense er 35 mm. | |||
Sporvidden ved vedlikeholdsgrense blir 1450 mm og ved tiltaksgrense 1465 mm. Større sporvidder må ikke forekomme. | |||
Økning i aksellast fra El 17 til El 18 (opptil 21,3 tonn) medfører større vertikalt trykk mot befestigelsen og en økning i horisontalkraft spesielt i kurver. Skruene i anlegg mot trematerialet må motstå denne økningen slik at avsporing unngås. Retningen til den resulterende kraft fra El 18 vil ikke være mer ugunstig enn retningen fra El 17. | |||
Råte og mekanisk slitasje vil over tid føre til at svilleskruene mister sitt feste i svillene. Dersom skruene på flere sviller etter hverandre mangler feste, vil dette kunne medføre farlig sporutvidelse og velting av skinnen med avsporing som resultat. | |||
Ved bare mekanisk slitasje vil tap av feste foregå meget langsomt og svillen får relativt lang levetid i sporet. | |||
I regelverket for vedlikehold i overbygningen er det referert til metoder for å utbedre manglende feste for svilleskruer. | |||
For vurdering av om svillen er blitt utsatt for råte, kan målediagrammene for sporvidde over flere perioder anvendes. Dersom utvidelsen av sporvidde er blitt betydelig mellom 2 målinger, er dette en indikator på at svillen er blitt utsatt for råteangrep. | |||
I et slikt tilfelle må tester utføres med et definert dreiemoment på svilleskruene som er beskrevet i regelverket for vedlikehold i overbygningen. Samme regelverk beskriver også metode for rehabilitering. | |||
Bidet under (figur 20.1) er et illustrasjonsbilde som ikke er hentet fra Flåmsbana (har ingen ting med Flåmsbana å gjøre). | |||
[[Fil:Figur_21.1.PNG|600px|thumb||center|<caption>Figur 21.1 Illustrasjonsbilde av skadet tresville; bildet har ingen ting med Flåmsbana å gjøre</caption>]] | |||
<small></small> | |||
Målediagrammene fra en måling datert 31.05.2012 for Flåmsbana viser stor variasjon i målt sporvidde i belastet spor (med ROGER 1000). Sporvidden varierer fra ca. 1435 mm til 1465 mm på enkelte steder. Verdier i intervallet 1445 mm – 1455 mm forekommer meget hyppig. | |||
Det er forbundet med usikkerhet å vurdere faren for avsporing ved stor sporvidde som er forårsaket av råte og mekanisk slitasje ved å studere diagrammene bare fra en måling. | |||
Imidlertid er en sporvidde på ca. 1445 – 1450 mm å betrakte som normalt på Flåmsbana. Aspektet har sammenheng med selve bormønsteret i tresvillene og slitasje i skinnehodet i ytterstreng. | |||
For å hindre mulig tendens til avsporing bør målediagrammene de siste periodene gjennomgås for å undersøke om det ved enkelte steder på banestrekningen er en abrupt utvikling i sporvidde. På disse stedene må feste av skruene kontrolleres opp mot dreiemomentet og eventuelt tiltak iverksettes for rehabilitering. | |||
I figur 21.2 er vist et utsnitt av sporvidden over en lengde på ca. 400 m målt med målevogn, dvs. måling i belastet spor. Sporvidden varierer fra nær 1435 mm på rett linje til ca. 1455 mm i sirkel- og overgangskurver. Det finnes en maksimalverdi på 1465 mm registrert i sirkelkurve. | |||
[[Fil:Figur_21.2.PNG|600px|thumb||center|<caption>Figur 20.2 Måling av sporvidde i belastet spor</caption>]] | |||
<small></small> | |||
Iht. teknisk regelverk settes den reelle sporvidde lik 1435 + 10 = 1445 mm. På side 21 er vist et representativt slitasjeprofil for ytterstreng i en kurve. Slitasjeprofilet er registrert ved km 338,950. Slitasjemålet kan settes til ca. 15 mm. Samlet sporvidde skulle dermed bli ca. 1460 mm. | |||
Målediagrammet i figur 21.2 er hentet fra ca. km 340,450 til ca. km 340,850. Bortsett fra ett målepunkt (ca. km 340,450) holder sporvidden seg godt innenfor maksimalgrensene. Diagrammet tyder på at tresvillene er i god stand. Det gjøres oppmerksom på at målingene er utført i belastet tilstand med målevogn ROGER 1000 som har en aksellast på 16 tonn. El 18 er tyngre med aksellast på 21,30 tonn. | |||
Den overveiende konklusjon er at på enkelte steder hvor sporvidden er målt opp til 1465 mm, så bør skruene kontrolleres på dreiemoment iht. bestemmelsene i regelverket og eventuelt at utbedringer gjennomføres. | |||
'''Forholdet R/D/g (sirkelkurve, overhøyde, vindskjevhet i overgangskurve)''' | |||
Iht. løfteskjema er vindskjeheten meget lav; flere steder 1 : 400. Diagrammene fra målevognkjøringen viser vindskjevhet < 10 mm for 2 meters verdier og < 31 mm for 9 meters verdier. | |||
'''Stabilitet''' | |||
På grunn av lav hastighet vil instabilt løp ikke oppstå. | |||
| Linje 3 373: | Linje 9 677: | ||
---------------------- | |||
'''Referanser''' | |||
(1) Evert Andersson; Mats Berg: Järnvägssystem och spårfordon, Stockholm 2001 | |||
(2) Evert Andersson; Mats Berg; Sebastian Stichel: Spårfordons dynamik, Stockholm 2002 | |||
(3) Klaus Knothe; Sebastian Stichel: Schienenfahrzeugdynamik, Springer Verlag, Berlin 2003 | |||
(4) Fritz Fastenrath; VERLAG ERNST & SOHN: Die Eisenbahnschiene, BERLIN, MÜNCHEN, DüSSELDORF | |||
(5) Klaus Knothe; Ernst&Sohn: Gleisdynamik, Berlin 2001 | |||
(6) Coenraad Esveld: Modern Railway Track, Second Edition, Nederland 2001 | |||
(7) Klaus Knothe; ZEV Glasers Annalen: Beanspruchungen von Schienen unter statischen, dynamischen und thermischen Belastungen, april 2003 | |||
(8) prEN 14363:2012: Railway applications – Testing and Simulations for the acceptance of | |||
running characteristics of railway vehicles – Running Behaviour and stationary tests | |||
(9) EN 13103 og EN 13104 | |||
Siste sideversjon per 4. feb. 2025 kl. 08:09
Innledning
El 18 vurderes å bli satt inn i trafikk som trekkmateriell for vogner på Flåmsbana til erstatning for El 17.
Aspektet gir en betydelig økning av aksellasten; fra 16,0 tonn for El 17 til 21,3 tonn for El 18. NGI har utført et prosjekt for å undersøke stabilitet i fyllinger, støttemurer med mer. Det er dokumentert at det ikke er fare for utglidninger. NGI anbefaler allikevel å overvåke steder hvor det kan være mulighet for utglidning under spesielle forhold.
Flåmsbana har en krevende geometri. I langsgående retning er det fall/stigning på 55 mm/m. Det finnes et stort antall av kurver med små radier; R = 200 m med D = 50 mm og R = 150 m med D = 50 mm. Kurveradius ned mot 130 m finnes også.
Med sin kurvatur faller Flåmsbana utenfor rammene i EN 14363. Det kreves dermed særskilte vurderinger.
Flåmsbana er klassifisert i overbygningsklasse b. Iht. teknisk regelverk tillates vogner i persontog å ha en aksellast på 18 tonn ved framføring i 100 km/h. Denne hastigheten er ikke aktuell på Flåmsbana på grunn av kurvaturen. Hastigheten settes til 30 km/h.
I teknisk regelverk i tabell for kombinasjon for tillatt aksellast og hastighet er det definert underpunkter som kommer til anvendelse
- maks aksellast for lokomotiv i persontog er 22,5 tonn
- den totale masse av toget skal ikke overstige maksimal nominell aksellast x antall aksler x 1,02 (lokomotiv i persontog holdes utenfor i denne beregning)
Kulepunktene innebærer at lokomotiv med aksellast inntil 22,50 tonn kan benyttes til framføring av vogner på Flåmsbana. El 18 har en aksellast lik 21,3 tonn.
Det legges til grunn at det ved målevognkjøring i den senere tid er verifisert at Flåmsbana har en sporkvalitet som minst er i samsvar med retningslinjene for tillatte avvik for bestemmende sporkvalitetsparametere gitt for den hastighetsavhengige kvalitetsklasse for sikker framføring av togmateriell. Aspektet innebærer at kvalitetsparameterne ikke overskrider verdier i grense for vedlikehold; eventuelt for tiltak. Det legges også til grunn at komponenter i sporet er i en slik forfatning at El 18 kan framføres. Aspektet har særlig gyldighet for tresviller.
En viktig parameter er den faktiske sporvidde målt i lastet tilstand med målevogn. Sporvidden må bli vurdert i sammenheng med reell sporvidde (nominell + utvidelse på grunn av kurvatur), skinneslitasje og svilleskruens kontakt med trevirke i svillene.
En annen parameter er vindskjevhet i overgangskurve sett i sammenheng med tilhørende sirkelkurve og overhøyde i sirkelkurven.
Parametere for sporkonstruksjonen
På grunn av de små kurveradiene har Flåmsbana lasket spor.
Skinner er 49E1 overveiende i kvalitet R 260 Mn med strekkfastheten min. 880 N/mm2. Skinner av samme profil i kvalitet R 200 Mn finnes også. Min. strekkfasthet for denne skinnekvaliteten er 680 N/mm2. Hodeherdede skinner er også registrert.
Ifølge BANADATA Innsyn Overbygning finnes ca. 10.000 til 11.000 meter skinnestreng i kvalitet R 200 Mn. Disse er lagt i sporet omkring 1965. Skinner i kvalitet R 260 Mn er lagt i sporet på et senere tidspunkt.
Det er undersøkt om skinnene i kvalitet R 200 Mn ligger på steder på strekningen som gir mindre belastning. Til dette formålet er benyttet løfteskjema og BANADATA Innsyn Overbygning. Iht. stikkprøver er det ikke funnet en slik sammenheng.
Tresviller i bøk og furu av relativt nyere dato er lagt i sporet.
Betongsville Bet-NSB-Enhetssville forekommer også.
Sviileavstanden er overveiende 640 mm.
En del av befestigelsen på sporet er av en type Pandrol og beskrives som god. En annen type som benyttes, er Hey-Back. Erfaringer tilsier at Hey-Back befestigelsen har en svakere klemkraft enn Pandrol befestigelsen.
Konklusjoner
Det legges til grunn en overbygningsstandard iht. beskrivelse i BANADATA Innsyn Overbygning og at sporet opprettholdes i en kvalitet som er i samsvar med den kvalitetsklasse som gjelder for Flåmsbana basert på målinger med målevogn.
Videre legges til grunn normale klimatiske forhold. Ved eventuelt ekstremvær som kan virke nedbrytende på overbygningskonstruksjonen, må trafikk med El 18 vurderes.
Det er utført beregninger og/eller vurderinger for følgende aspekter for den laskede sporkonstruksjonen på Flåmsbana:
- Belastning på momentbøyning av skinner på elastisk underlag ved vertikalkrefter (rett strekning)
- Belastning på momentbøyning av skinner i kurver ved vertikal- og horisontalkrefter
- Belastning på befestigelse
- Belastning i skjøter i lasket spor på elastisk underlag
- Belastning ved hjulslag og belastning på lasker i skjøter
- Kontaktmekanikk, belastning på skinnehodet i hjul/skinne i kontaktflate
- Belastning ved bremsing for konstant hastighet og nedbremsing til full stopp
- Belastning ved traksjon for akselerasjon og konstant hastighet
- Vurderinger mht. skinnevandring ved oppbremsing og traksjon av materiell i lasket spor ved nøytraltemperatur
- Vurderinger mht. skinnevandring ved oppbremsing og traksjon av materiell i lasket spor ved avvik i nøytraltemperatur
- Termisk oppvarming (særlig av hjulbane)
- Vurdering av sidestabilitet ved Prud`Hommes formel
- Vurdering av (Y/Q) ved dynamisk belastning
- Vurdering av (Y/Q) ved statisk belastning ved lav hastighet (hjulavlastning)
- Delta r kriteriet
- Vurdering av radiell styringsindeks
- Opprettholdelse av sporvidde vurdert ut fra kurveradius, skinneslitasje og kontakt av svilleskrue for befestigelsen mot trematerialet til tresviller
- Forholdet R/D/g (sirkelkurve, overhøyde, vindskjevhet i overgangskurve)
- Stabilitet
Det er innledningsvis for flere temaer beskrevet en teoretisk orientering som grunnlag for de formler som er anvendt i beregningene.
Belastning på momentbøyning av skinner på rett strekning
På rett strekning og i kurver med store radier oppstår spenninger i dynamisk tilstand i skinnefot i symmetriaksen som er lavere enn tillatt anbefalt spenningskapasitet for skinner i kvalitet R 200 Mn og i kvalitet R 260 Mn. Det skulle derfor ikke være fare for utmatting.
Det påpekes at den kvasistatiske kraft QKV.ST. vurderes i samsvar med tilhørende kvasistatisk kraft i EN 14363 evaluert i et lavpassfilter på 20 Hz. Denne kraften er en 50 % kraft og forekommer derfor svært ofte.
Den dynamiske kraft QDYN vurderes i samsvar med tilhørende dynamisk kraft i EN 14363 evaluert i et lavpassfilter på 20 Hz. Denne kraften er en 99,85 % kraft og forekommer dermed meget sjeldent.
Beregningene er utført med nominelt skinneprofil og dermed nominelt treghetsmoment. Med den slitasje som er registrert og vist i slutten av dette kapittel, så er bæreevnen svakere enn ved nominelt profil. Det forventes imidlertid ikke utmatting i underkant skinnefot i symmetriaksen.
Belastning på momentbøyning av skinner i kurver ved vertikal- og horisontalkrefter
I kurver med små radier opptrer en kombinasjon av eksentrisk virkende vertikale krefter og horisontale krefter på skinnehodet. I en kvasistatisk vurdering er de beregnede spenninger i kant av skinnehode og skinnefot tolererbare og akseptable i skinnekvalitet R 200 Mn og R 260 Mn. De kvasistatiske spenninger er å oppfatte som 50 % verdier i en statistisk vurdering og opptrer dermed ofte. De kvasistatiske spenninger er tolererbare.
Dynamisk betraktning for eksentrisk virkende vertikalkrefter og horisontale krefter gir beregningsmessig meget høye spenninger i kantene på skinnehodet og i skinnefot. De beregnede spenninger overskrider anbefalte grenseverdier; særlig gjelder dette for skinnekvalitet R 200 Mn. Plastiske deformasjoner vil kunne opptre teoretisk. Imidlertid er det nødvendig å være oppmerksom på de beregnede dynamiske spenningene er å oppfatte som 99,85 % verdier i en vurdering i et lavpassfilter på 20 Hz i samsvar med betingelsene i EN 14363 og at de derfor opptrer meget sjeldent og har lokal opptreden. De største beregnede spenningene som opptrer i underkant skinnefot i punkt C (det vises til figur i relevant kapittel), har en størrelse på 344,10 N/mm2; dvs. ca. 50 % av strekkfastheten for skinnestål R 200 Mn.
I tillegg til krefter fra rullende materiell opptrer også belastning forårsaket av kurveradius, egenspenninger og temperaturspenninger. I særlige tilfeller kan da den resulterende spenning bli opp mot 480 N/mm2. Imidlertid er det nødvendig å være oppmerksom på at temperaturspenningene sjeldent opptrer med maksimale verdier. Aspektet vil ha betydning for sannsynlighet for opptreden av plastisk deformasjon i punkt C på skinneprofilet (det vises til figur i gjeldende kapittel).
Det er også å bemerke at skinner i kvalitet R 200 Mn har ligget i sporet siden ca. 1965. Ifølge BANADATA Innsyn finnes ca. 10.000 – 11.000 løpemeter skinner i denne kvaliteten. Øvrige skinner har kvalitet R 260 Mn og er lagt i sporet på et senere tidspunkt.
Beregningene er utført med nominelt skinneprofil og dermed nominelt treghetsmoment. Med den slitasje som er registrert og vist i slutten av dette kapittel, så er bæreevnen svakere enn ved nominelt profil. Det forventes imidlertid ikke plastiske deformasjoner på sensitive steder i profilet.
Belastning på befestigelse
På grunn av kurver med radier R = 150 m opptrer horisontale og vertikale krefter i befestigelsen. Aspektet gir en resulterende kraft rettet mot befestigelsen. Det forventes ikke en økning i helningsvinkelen for virkningslinjen for den resulterende kraft fra det tyngre lokomotivet El 18 sammenlignet med virkningslinjen for de kombinasjonskrefter som oppstår ved framføring av det lettere lokomotivet El 17. Aspektet har sammenheng med de radielle styringsegenskaper til boggiene i El 18. Med El 17 eksisterer betydelig erfaring for virkning på befestigelsen. Imidlertid vil det trolig bli en økning i de horisontale krefter fra El 18 på grunn av større aksellast. Aspektet kan føre til hurtigere opptreden av slitasje i skruehullene på tresvillene på grunn av treets mekaniske egenskaper. Det er derfor nødvendig å føre kontroll med skruene ved for eksempel utøvelse av et definert dreiemoment (som beskrevet i Teknisk Regelverk).
Belastninger fra hjulslag og belastning på skjøter i lasket spor på elastisk underlag og i sporveksler
Det er vurdert 4 aspekter:
- Kraft ved hjulslag på tresviller på elastisk underlag
- Støtkrefter i skinneskjøter i lasket spor
- Belastning i svevende skjøter i lasket spor
- Belastning i sporveksler (krysspiss og braketter)
Kraft ved hjulslag på tresviller på elastisk underlag
Målinger av tester i bl. annet. ORE D 161 viser at ved en aksellast på 22,50 tonn så øker slagkraften med 30 kN/mm for tresviller på elastisk underlag ved framføringshastighet på 30 km/h.
Slagkraften skulle dermed anta en verdi på ca. 45,00 kN. Dette er ikke urovekkende.
Støtkrefter i skinneskjøter i lasket spor
Overgang fra eksisterende lokomotiv El 17 med aksellast 16 tonn til nytt lokomotiv El 18 med aksellast 21,3 tonn gir en økning i støtkreftene P1 og P2 på om lag en faktor lik 1,15 for hastighet V = 30 km/h. Økningen i lasten har en faktor lik 1,33.
Økningen i støtlasten oppfattes ikke å være dramatisk.
Belastning i svevende skjøter i lasket spor
For svevende skjøter opptrer store belastninger i stållaskene vurdert etter en konservativ metode. Det er imidlertid nødvendig å være oppmerksom på at laskene har anlegg mot overkant skinnefot og underkant skinnehode. Stållaskene opptrer dermed ikke som teoretisk virkende fritt bærende bjelker. Store belastninger kan imidlertid føre til utmatting ved skruehullene på grunn av dynamiske belastninger.
Belastning i sporveksler (krysspiss og braketter)
En enkel betraktning viser at støtkraft i krysspiss vil øke med en faktor lik 1,15 ved overgang fra El 17 til El 18. Ved ofte passeringer må det forventes hurtigere nedbrytning av krysspiss.
I områder for ledeskinner kan det forekomme at ledeskinnen blir belastet bare på horisontale krefter da de vertikale kreftene fra hjulbane overføres til hovedskinne. Ledeskinnene er festet til underliggende sville og blir dermed utkraget. Ved stor horisontal belastning kan det derfor inntreffe brudd i brakettfot ved små sporveksler. Det er ikke mulig å konkretisere om dette vil skje; sannsynligheten er meget lav. Men brakettene må overvåkes.
Belastning på skinnehodet
Følgende tabell viser økning i spenning i kontaktflaten som funksjon av økning av aksellasten:
| Lokomotiv | El 17 | El 18 | Fiktiv El |
|---|---|---|---|
| Akselkraft (kN) | 160 | 213 | 320 |
| Økning i akselkraft | 1,000 | 1,33 | 2,00 |
| Økning i spenning σξ, max | 1,00 | 1,10 | 1,26 |
En økning av aksellast fra 16 tonn til 21,3 tonn (økning lik 1,33) gir en økning i kontaktspenningene på 1,10 under forutsetning av samme hjuldiameter.
En økning i spenningene på 10 % på grunn av økning av akselkraften på lokomotivene med henholdsvis 4 og 8 aksler i togstammen vil naturlig fremskynde nedbrytning; men det forventes ingen dramatisk økning i hastigheten for slitasje.
Det er tatt utgangspunkt i radier for hjulbanene til hjulene rƞ = 0,36 m, 0,50 m og ∞ m i beregningene. Det kan synes å være noe inkonsekvent å anta radiene 0,50 m og ∞ m. Hjulbaneprofilet vil tilpasse seg skinneprofilet og en radius lik omtrent 0,36 m vil av naturlige årsaker opptre mest. Det eksisterer derfor et relativt bredt kontaktbånd i kontaktflaten hjul /skinne som bidrar til mindre stressende spenninger.
El 18 har nominell hjuldiameter 1125 mm. El 17 har nominell hjuldiameter 1100 mm. Forskjellen er ubetydelig for den økning i lasten som er definert.
Bremsekrefter
Kapitlet omhandler 2 aspekter:
- Bremsing for opprettholdelse av konstant hastighet og vurdering for skinnevandring
- Nedbremsing til full stopp og vurdering for skinnevandring
Det er tatt hensyn til kriterier for nødvendig adhesjonsforhold.
I beregningene er det lagt til grunn at det benyttes El brems med kraft 150 kN for opprettholdelse av konstant hastighet under hensyntagen til nødvendig adhesjon.
For nedbremsing til full stopp er det i beregningene benyttet en modell med bruk av pneumatisk brems. Det er ikke tatt stilling til hvilke typer pneumatisk brems som brukes (i beregningene legges til grunn blokkbremser; dette behøver ikke å være riktig).
Det er vurdert at skinnevandring trolig ikke vil oppstå ved bremsing for opprettholdelse av konstant hastighet i lasket spor på Flåmsbana.
Det er vurdert at det vil kunne inntreffe en beskjeden skinnevandring ved nedbremsing til full stopp i det laskete spor. Aspektet er imidlertid en funksjon av klemkraften i befestigelsen. Det er rapportert at særlig Pandrol PR 341 A er i god stand og dette skulle dermed medføre høy klemkraft.
Traksjon
Kapitlet omhandler 2 aspekter:
- Traksjon for opprettholdelse av konstant hastighet og vurdering for skinnevandring
- Traksjon for akselerasjon til definert hastighet og vurdering for skinnevandring
I beregningene er lagt til grunn mekanisk gangmotstand, kurvemotstand, luftmotstand og stigningsmotstand.
Det er vurdert at det vil kunne inntreffe en beskjeden skinnevandring ved traksjon i et lasket spor.
Vurderinger mht. skinnevandring ved nedbremsing og traksjon av materiell i lasket spor ved avvik i nøytraltemperatur
Ved nøytraltemperatur i skinnene forventes ingen eller en beskjeden skinnevandring (se foregående kapitler).
Dersom temperatur avviker fra nøytraltemperatur, medfører dette aspektet langsgående krefter i skinnene. Utøvelse av traksjon for akselerasjon vil i tillegg føre til langsgående krypkrefter. Samlet kan disse 2 aspektene forårsake skinnevandring og at sporet blir trukket innover i kurve. Dette kan inntreffe både for ubelastet naboskinne og belastet skinne fra lokomotivet i det laskede sporet. Ved overgang fra El 17 til El 18 øker aksellasten med en faktor 1,33. Aspektet vil gi en økning i adhesjonskraften for samme adhesjonskoeffisient. Imidlertid vil den økte aksellasten virke stabiliserende.
Skjøtåpningene må kontrolleres og om nødvendig justeres. Når skjøtåpninger er blitt for store eller for små, skyldes dette i regelen enten skinnevandring eller lasken som kan gi for stor eller for liten friksjon. I slike tilfeller må det foretas skjøtregulering, rensing og smøring av laskekammeret og tilskruing av laskene. Varmeromstabellen må følges.
Termisk oppvarming (særlig av hjulbane)
Det er beregnet den termiske oppvarming av særlig hjulbane ved vedvarende bremsing.
Vurdering av sidestabilitet ved Prud`Hommes formel
Den maksimale styringskraft som El 18 kan utøve for å unngå sideforskyvning av sporet ved normale forhold er 68,85 kN. Kraften har en lengde på 2 meter i vinduet og evalueres i et lavpass filter på 20 Hz.
I mangel av informasjon benyttes formelverket i EN 13103 og EN 13014 for beregning av styringskraften som kan betraktes som sideforskyvningskraft i Prud’ Hommes formel. Dette skulle medføre = 37,55 kN < 68,85 kN. Selv om El 18 har gode radielle styringsegenskaper, så er resultatet optimistisk. Kraften er trolig større.
Det vurderes imidlertid at kapasitet mot sideforskyvning er tilstrekkelig god nok.
Vurdering av (Y/Q) ved dynamisk belastning
I mangel av informasjon er beregnet (Y/Q)j, a, max i dynamisk tilstand:
De beregnede verdiene for YDYN og QDYN er hentet fra kapitlet for kalkulasjon av disse parametere i forbindelse med beregning av spenninger i skinne når skinnen fungerer som bærebjelke.
Det er ingen fare for avsporing.
Vurdering av (Y/Q) ved statisk belastning ved lav hastighet (hjulavlastning)
Det legges til grunn at El 18 har et hjulprofil som gir flensvinkel på 68° - 70°. For en friksjonskoeffisient μ = 0,36 blir
En typisk overgangskurve på Flåmsbana har en lengde L = 20 m og overhøyde D = 50 mm. Aspektet gir en gradient i overhøyderampen på 1 : 400. Imidlertid ved overgang til en sirkelkurve med R = 150 m bør også overhøyderampen ha slak helning. Diagrammene fra målevognkjøring gir høyere verdier for vindskjevhet i belastet tilstand.
Det eksisterer ingen fare for avsporing i kvasistatisk tilstand under forutsetning av at El 18 har foreskrevne verdier mht. torsjonsegenskaper.
Delta r (∆r)-kriteriet
Dersom hjulradius er 550 mm, beregnes nødvendig Δr til 5,50 mm for kurveradius R = 150 m.
Det blir bedt om en redegjørelse om i hvilken grad NSB iverksetter tiltak for best mulig overholdelse av kriteriet.
Vurdering av radiell styringsindeks
For kurveradius lik 150 m beregnes Δx til 7 mm for en boggi med hjulavstand lik 2,8 m.
Beregningen innebærer at hjulene i ytterstreng må gå 14 mm fra hverandre og hjulene på innerstreng må gå 14 mm til hverandre (nærme seg hverandre).
Det blir bedt om en redegjørelse om i hvilken grad NSB iverksetter tiltak for best mulig overholdelse av kriteriet.
Opprettholdelse av sporvidde vurdert ut fra kurveradius, skinneslitasje og kontakt av svilleskrue for befestigelsen mot trematerialet til tresviller
Det er av betydning at sporvidden holdes innenfor de mål som regelverket foreskriver for å unngå avsporing. Aspektet medfører at svilleskruene må ha kontakt med materialet i svillene. Tester kan utføres med et definert dreiemoment som er beskrevet i regelverket for vedlikehold.
Måling med målevogn over flere perioder, dvs. måling i belastet spor vil gi informasjon om opptredende sporvidde og om svilleskruene er i kontakt med trevirke i svillene. En eventuell abrupt endring fra en periode til neste periode kan tyde på at svillen er blitt utsatt for råte.
Den overveiende konklusjon er at på enkelte steder hvor sporvidden er målt opp til 1465 mm, så bør skruene kontrolleres på dreiemoment iht. bestemmelsene i regelverket og eventuelt at utbedringer gjennomføres.
Forholdet R/D/g (sirkelkurve, overhøyde, vindskjevhet i overgangskurve)
Iht. løfteskjema er vindskjeheten meget lav; flere steder 1 : 400. Diagrammene fra målevognkjøringen viser vindskjevhet < 10 mm for 2 meters verdier og < 31 mm for 9 meters verdier.
Stabilitet
På grunn av lav hastighet vil instabilt løp ikke oppstå.
Tilrådning
Det konkluderes med at El 18 kan benyttes for framføring og trekking av vogner i passasjertrafikk på Flåmsbana. Iht. informasjon fra NSB må det benyttes ett lokomotiv for maksimalt inntil 3 vogner. Dette er også bekreftet i de beregninger som er gjennomført; både med hensyn til skinnegangens adhesjon og kapasitet for øvrig for relevante parametere for sporet. På grunn av gradienten på 55 mm/m er dette også nødvendig.
Ved flere vogner må det benyttes 2 lokomotiv (for inntil 6 vogner). Ett lokomotiv må gå foran og det andre må gå bak i togstammen av vogner slik at traksjons- og bremsekreftene blir spredd. Gjennomførte beregninger med grunnlag i overbygningens armering bekrefter at dette tiltaket er nødvendig.
Beregningene dokumenterer at i alle fall 4 parametere krever oppmerksomhet:
- Det forventes kun en litt hurtigere hastighetsøkning for nedbrytning av sporet og for slitasje på alle komponenter i sporet; i særlig grad gjelder dette skinner.
- Belastning i kontaktflaten i hjul/skinne mekanikken får en økning på 10 % med samme hjuldiameter ved overgang fra El 17 med 16 tonns aksellast til El 18 med 21,3 tonns aksellast. Det forventes et bredt bånd i kontaktflaten slik at denne økningen skulle kunne være tolererbar; også for skinner i kvalitet R 200 Mn. Lastøkningen fra lokomotivet er 33 %.
En togstamme bestående av et lokomotiv av type El 17 og 3 vogner har en samlet vekt:
En togstamme bestående av et lokomotiv av type El 18 og 3 vogner har en samlet vekt:
- Økning i prosent blir 9,7. For vognene er benyttet den ekvivalente masse med en faktor lik 1,10. Under ellers like adhesjonsforhold behøves en tilsvarende økning i bremse- og trekkraft. Økningen oppfattes ikke å være alarmerende.
- Støtkrefter i laskede skjøter og i krysspiss i sporveksel får en forventet økning på 15 % fra El 18 i forhold til El 17. Denne økningen forventes ikke å være dramatisk.
På grunn av overbygningens konstruksjon må det utøves kontroll ved framføring i den forstand at ikke mer traksjons- og bremsekraft enn nødvendig benyttes. Det må utøves streng kontroll med hensyn til sluring og glidning.
Både operatør og infrastruktur må holde banen under oppsikt. Det anbefales at det utarbeides et program for korttidsovervåking og langtidsovervåking av overbygningen i samsvar med de anbefalinger som er gitt fra NGI vedr. støttemurer, fyllinger med mer.
For sporet bør følgende aspekter underlegges spesiell overvåking:
- De laskede skjøtene med åpninger må kontrolleres og om nødvendig justeres
- I svevende skjøter (dersom slike forekommer) kontrolleres laskene på utmatting
- Skruene i skruehullene i tresvillene må kontrolleres på nødvendig dreiemoment iht. regelverket
- Tresvillenes bestandighet kontrolleres; særlig i kurver
- Observasjon av eventuell skinnevandring som kan resultere i et innover trukket spor
- Overvåkning av nøytraltemperatur
- Utvikling av slitasje på skinnehodet i skinnene
- Abrupt endring av sporvidde fra en måling til neste måling i belastet spor med målevogn
NSB blir bedt om en redegjørelse for hvordan det er tenkt i best mulig grad å etterkomme krav til Δ r kriteriet og til radiell styringsindeks.
Belastningsparametere
Kapitlet redegjør i stikkordsform for parametere som må tas hensyn til i en vurdering av belastning på sporet og som bør iakttas i relevante beregningsmodeller. Kapitlet er ment å være allmenngyldig og er ikke spesielt laget for Flåmsbana.
Sporet har til oppgave:
- Fungere som kjørevei; togmateriellet er bundet til sporet
- Fungere som bærebjelke på elastisk underlag (ballast med underbygning)
Hovedfaktorer som belaster sporet
- Trafikk (årlig tonnasje på sporet)
- Aksellast
- Traksjon og bremsing
- Hastighet
Faktorer som må vektlegges i framføring
- Materiellets løpedynamiske egenskaper
- Hjul/ skinne kontakt mekanikk
- Sporets dynamiske virkning
- Dynamisk profil til materiellet
- Linjebelastning
Vurdering av aksellaster; linjelaster
- Aksellast for lokomotiv
- Aksellast for vogner med passasjerer og gods
- Linjelast (geometrisk utforming av lokomotiv og vogn)
Ballastspor
Overbygning
- Tverrsvilleoverbygning
- Ballastskuldre (bredde)
- Formasjonsplan (bredde)
- Høyde av ballast
Komponenter i sporet:
- Skinner
- Sviller
- Befestigelse
- Ballast
- Sporveksler
- Skjøter
Viktige parametere for å ta opp belastningene fra rullende materiell
- Skinner
- ° Vekt (treghetsmoment), stålkvalitet (i kurver)
- ° Statisk og dynamisk belastningsevne
- Sviller
- ° Svilleavstand, statisk og dynamisk belastningsevne
- Befestigelse
- ° Tilstrekkelig klemkraft, nødvendig kvalitet i komponenter
- Ballast
- ° Kvalitet, utseende på steinene (form), riktig fraksjonering, tykkelse av ballast
- Sporveksler
- ° Belastningsevne i alle komponenter; særlig de som blir belastet med støt
- Skjøter
- ° Skjøter
- ° Belastningsevne på støt
Overbygningens elastisitet
- Vurdering av ballastsiffer eller ballaststivhet
- ° Belastningsevne for skinner på momentbøyning
- Variasjon av ballastsiffer eller ballaststivhet som funksjon av årstid (sommer, høst, vinter, vår, endring av temperaturer og variasjon av nedbørsmengder)
Sporgeometri og hastighet
- Minste kurveradius i sporet
- Maksimal vertikal helning av gradient i lengderetning
- Minste kurveradius i sporveksler
- Optimal overhøyde i kurver relatert til balansert hastighet; eventuelt til hastighet i sammenheng med manglende overhøyde eller overskuddshøyde
- Helning i overhøyderampe i overgangskurver
- Minste lengde for trasseringselementer (rett strekning, kurver, overgangskurver)
- Enklest mulig geometri i kombinasjoner
- ° Unngå for eksempel horisontal sirkelkurve og overgangskurve i vertikalradier i lavbrekk og høybrekk
Vognmateriell
- Opphengsystemer (fjærer og dempere)
- Avstand mellom hjulsettene i to eller tre – akslede boggier for lokomotiv og vogner
- Boggiene kjennes ved radiell styringsevne
- Konisitetsbetraktninger (ikke avgjørende for kurverike baner med overveiende små radier)
- Delta r kriteriet i kurver; eventuell radiell styringsindeks
Lokomotiv
- Opphengsystemer (fjærer og dempere)
- Vil være to – akslede boggier
- Boggiene kjennetegnes ved radiell styringsevne
- Utnyttelse av adhesjon
- Sluregrense
- Konisitetsbetraktninger (ikke avgjørende)
- Delta r kriteriet i kurver; eventuelt radiell styringsindeks
Bremsing
- El brems
- Skivebremser
- Blokkbremser
- Bremsing for overholdelse av konstant hastighet
- Bremsing for stopp
Traksjon
- For opprettholdelse av konstant hastighet i stigning
- For akselerasjon for realisering av definert hastighet i stigning
Opptredende belastninger på sporet i definerte tilstander
- Statisk
- Kvasistatisk
- Dynamisk
Belastninger fra rullende materiell
- Vertikale krefter
- Laterale krefter
- Støtkrefter
- Traksjons- og bremsekrefter
- ° Langsgående krefter i sporet; krypkrefter (skinnevandring)
- ° Skjærkrefter på skinnehodet
- ° Varmeutvikling på skinnehodet
- ° Varmeutvikling på hjulbane
Øvrige krefter utøves ved:
- Temperaturvariasjoner
- Værforhold
- Egenkrefter i komponenter (skinner)
Mulig opptreden av uønskede hendelser
- Innover rettet forskyvning av sporet i små kurver
- Brukne deler i komponenter
- Merkbar skinnevandring
- Gliding av mellomleggsplate i sviller (gjelder bare betongsviller)
Modelleringer og beregninger
- Enklere og mer sofistikerte modeller
- ° Statisk modell med koeffisienter for dynamisk tillegg
- ° Modell som beregner dynamisk belastning på grunn av irregulariteter
- ° Simulering
- Vertikallaster i statisk, kvasistatisk og dynamisk tilstand
- ° Momenter og spenninger i skinner
- ° Belastning på befestigelse, sviller, ballast
- Kombinasjon av vertikal- og lateralkrefter i kvasistatisk og dynamisk tilstand
- ° Momenter og spenninger i skinner
- ° Belastning på befestigelse, sviller, ballast
- Ballastsifferet for optimalisering av overbygningens elastisitet
- Belasting på skinnehodet (hjul/skinne kontaktmekanikk)
- ° hjuldiameter
- Støtbelastninger på steder og komponenter hvor slike belastninger oppstår (P1 og P2 krefter)
- Krypkrefter ved traksjon og bremsing
- ° Shakedown diagram
- Skinneslitasje
- Motstand mot skinnevandring
- Motstand mot sideforskyvning av sporet
Slitasje og skader på skinnehodet
- Generell slitasje
- Forskjellige typer av skader på skinnehodet
Nedbrytningsmekanismer
- Tonnasje
- Aksellast
- Hastighet
- Traksjon og bremsing
Vedlikehold (tunge operasjoner) og øvrig vedlikehold
- Sliping av skinnehodet for eliminering av rifler, bølger, head-checks, shelling, squats
- Pakking, justering, stabilisering
- Ballastrensning
- Stedvis eller punktvis reparasjoner
RAMS i sporet knyttet til komponenter
- Pålitelighet (Reliability)
- Tilgjengelighet (Availability)
- Effektivt vedlikehold (Maintainability)
- ° Utforming av komponenter i sporet
- Sikkerhet (Safety)
Underbygning
Bæreevne
- Fyllinger
- Stabilitet
- Frostsikring
- Stikkrenner
- Drenering
- Rassikring
- Bruer
- Konstruksjonsprofil
- Lastmodell for bruer
- Definisjon av linjelast for formasjonsplanet; betydning for stabilitet i fyllinger
Bilder av slitte skinneprofil i indre og ytre skinnestreng målt på Flåmsbana er vist på neste side. Det er betydelig slitasje på side på ytre skinnestreng og skjeggdannelse av skinnehodet på indre skinnestreng. Bildene er registret den 16.10.2009.
Slitasjeprofilene gir reduksjon i treghetsmomentene til skinneprofilene og dermed også til redusert bæreevne for spor lagt på elastisk underlag. Tapet av treghetsmomentet er imidlertid ikke av en slik karakter at det vil oppstå utmatting i underkant skinnefot i symmetriaksen ved belastning av vertikale laster. Spenningene som er beregnet, er til dels betydelig lavere enn maksimale tillatte verdier. Videre er det innbygget sikkerhetsmarginer i beregningsmodellene.
I kurver vurderes det at plastiske deformasjoner i kantene på skinnehodet og skinnefot ved kombinasjonslaster vertikalt og horisontalt i dynamisk tilstand trolig ikke vil forekomme. Det påpekes også i dette tilfelle at beregningsmodellene har innebyggede sikkerhetsmarginer. Dynamiske belastninger som er beregnet, er 99,85 % av maksimale belastninger og som derfor forekommer sjeldent og også har lokal opptreden.
Det legges til grunn at mengde av stålslitasje i skinnehodet med utgangspunkt i slitasjeprofilene iht. regelverket ikke blir overskredet. Jernbaneverket har et betydelig erfaringsgrunnlag vedr. bæreevne for slitte skinneprofil (49 kgs skinner) for aksellaster på inntil 22,50 tonn; også i kurver med små radier. Det er gjort den erfaring at slitte skinneprofil (49 kgs skinner) innenfor tillatte slitasjegrenser slik de defineres i regelverket tåler belastning fra aksler med aksellast lik 22,50 tonn > 21,30 tonn.
Kort beskrivelse av El 18
Figur 6.1 viser et bilde av El 18.
Følgende data er registrert:
Lengde over buffer: 18500 mm
Total hjulstand: 13800 mm
Boggihjulstand: 2800 mm
Drivhjuldiameter: 1125 mm
Tjenestevekt: 85,2 tonn
Aksellast: 21,3 tonn
For sammenligning har El 17 nominell diameter på drivhjulet lik 1100 mm.
Det legges til grunn at vognene med passasjerer har en aksellast lik 11.750 kg.
Kapasitet på bruer og fyllinger
Bæreevne for bruer
Linjelast:
Konsentrert linjelast over boggi:
Konsentrert linjelast over boggiende – buffer:
El 18 tilfredsstiller alle krav til last på bruer.
Stabilitet i fyllinger og skjæringer
NGI har levert en rapport som omhandler stabilitet med tyngre lokomotiver.
Det gis en vurdering av effekt av økt aksellast basert på målte vibrasjoner og forskyvninger for fyllinger og støttemurer.
Konklusjonene er at målingene viser ingen indikasjon på permanent deformasjon etter togpasseringene. Jernbaneverket har imidlertid registrert flere setninger i sporet og deformasjoner i en av murene. Det anbefales derfor at det etableres et program for langtidsovervåking av murene for eventuelle registreringer av deformasjons- og setningsutvikling.
Modell for beregning av bøyemomenter på skinner
Skinner skal fungere som bærebjelke for rullende materiell. Skinner med sviller i en fiktiv langsvilleoverbygning er lagt på en ballastseng med elastiske egenskaper. Av den grunn vil skinner bli belastet på bøyemomenter. I figur 8.1 er vist prinsippet for oppbygging av en konvensjonell tverrsvilleoverbygning. Komponentene er skinner, befestigelse, sviller og pukk.
Grunnleggende parametere
De grunnleggende parametere i beregningsmetodikken beskrives kort:
- Etablering av belastet svilleflate i ballastert spor
- Etablering av statisk fjærstivhet, statisk ballaststivhet og statisk ballastsiffer
- Etablering av elastisk sjikt
- Beregning av dynamisk ballaststivhet
Etablering av belastet svilleflate i ballastert spor
Det legges til grunn kontaktflaten mellom sville og ballastlaget. På grunn av det lave hastighetsnivået er det tilstrekkelig å betrakte skinnen som kontinuerlig opplagret på en fiktiv langsville. I en slik langsville må den fiktive bredde beregnes. Følgende parametere inngår:
Svilleavstand: a (mm)
Ubelastet midtdel av sville: m (mm)
Bredde av sville: b1 (mm)
Svillelengde: l (mm)
Fiktiv bredde av langsville: b (mm)
Med disse parametere beregnes den medvirkende svillebredde b for den fiktive langsvilleoverbygning:
Arealet av belastet flate i underkant sville er:
Figur 8.2 illustrerer aspektet.
Etablering av statisk fjærstivhet (punktstivhet) k, statisk ballaststivhet (linjestivhet) β og statisk ballastsiffer (flatestivhet) C; sammenhenger
Fjærstivheten, ballaststivheten og ballastsifferet er viktige parametere for beregning av belastning på skinner utsatt for momentbøyning. Uavhengig av dimensjoneringsmetode som benyttes, anvendes enten ballaststivheten eller ballastsifferet med utgangspunkt i fjærstivhet.
Det etableres sammenhengene som vist i formel under.
Termen k beskriver en fjærstivhet (N/mm) eller punktstivhet.
Termen β som er ballaststivhet, defineres ved:
Ballaststivheten beskriver dermed en linjefjær i vertikalplanet. Termen a er avstanden mellom svillene. Ballastsifferet defineres:
Ballastsifferet blir en bladfjær. Termen F er belastet flate av sville mot ballastlaget.
Omregning gir:
Ballaststivheten uttrykt ved balastsifferet C:
Figur 8.3 gir et bilde av de ulike begrepene.
I figur 8.3 kan termen k betraktes som punktfjær; summen av alle punktfjærene kan betraktes som linjefjær i vertikalplanet over lengde x; ved anvendelse av bredde bc (fiktiv bredde av langsville) etableres bladfjær som er identisk med ballastsifferet C.
Det legges til grunn at ballastsifferet C registreres som kvotient flatetrykk/nedsenkning av sville under forutsetning av løs forbindelse av sville til ballast; dvs. at svillen til en viss grad betraktes som hengende. Dette kommer til syne i figur 8.4 ved at svillen får en nedsenkning før svillen utøver belastning på ballastunderlaget. Ballastsifferet beskrives dermed ved vinkelkoeffisienten α for den rette linje. Aspektet er en tilnærming.
Etablering av elastiske sjikt
I en overbygningskonstruksjon er det mulig å bygge inn flere elastiske sjikt.
For en overbygning som består av tresviller, vil det i praksis eksistere et elastisk sjikt som er ballasten. I et slikt tilfelle uttrykkes ganske enkelt ballastsifferet, fjærstivheten og ballaststivheten:
C (N/mm3) k (N/mm) β (N/mm2)
I en overbygningskonstruksjon hvor det er betongsviller, finnes det et mellomlegg i gummi mellom skinne og betongsville. Mellomlegget har til oppgave å redusere spissbelastninger fra rullende hjul ved framføring av tog på betongsvillen. I et slikt tilfelle er det 2 elastiske sjikt; gummimellomlegget mellom skinne og sville samt ballastlaget med undergrunn. De resulterende elastiske egenskaper beregnes ved seriekopling av de elastiske sjiktene.
For beregning av det resulterende ballastsifferet blir prosedyren som redegjort for under da de enkelte fjærelementene er konstruert i en seriekobling:
Termen krp er stivheten til gummielementet i mellomlegget. Videre er kb stivheten i ballastlaget med underbygning.
Ballaststivheten β blir tilsvarende:
I en avansert overbygningskonstruksjon kan svillene bli påmontert gummimatter i underkant av sville. Dermed eksisterer et 3. elastisk sjikt som er svillematten. Under forutsetning av at ballastlaget med underbygning beskrives som en ballastblokk med masse og elastisitet, blir formelverket tilsvarende (antakelse om seriekobling av fjærelementene):
Her betyr:
Stivhet til mellomlegget i gummi: krp
Stivhet til svillematte: ksp
Stivhet til ballastlaget mot underbygning: kb
Ved betraktning med ballaststivheten β blir tilsvarende:
En variant beskrives ved anvendelse av ballastmatter som legges i formasjonsplanet. Dersom ballastsjiktet mellom en svillematte og ballastmatte betraktes som en blokk uten elastiske egenskaper, etableres også i dette tilfellet et system med 3 elastiske sjikt. Det nederste elastiske sjiktet består da av ballastmatte og undergrunn med stivhet kf. Formlene blir tilsvarende som over:
Termen βf er stivheten til ballastmattene lagt i formasjonsplanet; dvs. at undergrunnen også har innflytelse. Figur 8.5 gir en oversikt over aspektet.
En siste variant beskrives ved mellomlegg i gummi mellom skinne og sville og ballastmatte lagt i formasjonsplanet; dvs. at elastisk svillematte ikke påføres underside av sville. I stedet påføres et relativt hardt underlag i gummi som tjener til å skåne betong og pukk for spissbelastninger.
Da blir ligningene:
Beregning av dynamisk ballastsiffer eller dynamisk ballaststivhet
Det statiske ballastsifferet C (N/mm3), eventuelt den statiske ballaststivhet β (N/mm2) for overbygningen gjelder bare for et materiell som står stille.
Ved framføring av materiellet i sporet med hastighet endrer sporets karakteristikker seg slik at det må benyttes tilsvarende dynamiske parametere CDYN, eventuelt βDYN. Det er forbundet med omfangsrike algoritmer i en kompleks analyse for å beregne disse parameterne. Aspektet har sammenheng med at også dempingsegenskapene og opptredende frekvenser må bli tatt hensyn til. Imidlertid ved lave hastigheter vil ikke endringene bli så framtredende.
I denne studien vil ved dimensjonering bli benyttet de statiske parametere. Senere vil en beregning for de dynamiske parametere bli fulgt opp.
Interessante frekvensområder i vekselvirking rullende materiell – spor
Det skal diskuteres interessante frekvensområder som oppstår i en vekselvirking av rullende materiell og spor for Malmbanen ved tunge aksellaster. Figur 8.6 illustrerer aspektet.
Det oppstår en mengde ulike frekvenser med forskjellige bølgelengder som påvirker sporet i samtidighet ved framføring av togmateriell. Aspektet fører til dynamiske belastninger på sporkonstruksjonen:
- Tilfelle I: Rifler og bølger på skinnehodet
- Tilfelle II: Svilleavstand (sporet har en annen elastisitet over sville enn mellom svillene)
- Tilfelle III: Bøyelinje ved nedsenkning av skinne under belastning på grunn av elastisitet
- Tilfelle IV: Globale bølgelengder i sporet med vertikale amplituder; disse betraktes i området 3 – 25 m
Parametere som bidrar til nedsenkning av sporet og som forårsaker dynamiske belastninger og i særlig grad til tunge akselerasjonsbevegelser av skinnene under påvirkning fra rullende materiell:
- Tilfelle V: Hengende sviller
Tilfellene er illustrert i figurene 8.7, 8.8, 8.9, 8.10 og 8.11.
Det er synlig at algoritmene blir svært omfattende dersom alle tilfellene skal modelleres for samtidighet i opptreden (som skjer i sann tilstand). Det blir vanligvis søkt etter forenklinger.
I tillegg vurderes støtkrefter på grunn av hjulslag. På elastisk spor medfører støtet en kraftig kortvarig økning av bøyemomentet på skinnen. I et frosset spor blir slaget teoretisk uendelig stort og aspektet kan føre til skinnebrudd.
Ovennevnte aspekter krever omfattende modelleringer for beregning av resulterende beskatningsparametere. Da ulike bøyelinjer med forskjellige lengder opptrer under tilstandene i samtidighet, må ideelt matematiske Fourier rekker anvendes for nøyaktig modellering. Dette gjennomføres ikke i dette beregningsheftet. Det blir derimot søkt etter forenklinger.
Det skisseres 2 modeller for beregning av belastning på komponenter på sporet med grunnlag i bøyemomenter på skinner:
- DAF for dynamisk belastning basert på Zimmermanns metode
- Dynamisk modell som anvender vognens karakteristikker og irregulariteter i sporet
Enkel modell (DAF MODELL basert på Zimmermanns metode)
Det er utviklet en modell for betraktning av en tilleggsfaktor for beregning av dynamisk vertikalkraft med utgangspunkt i den statiske hjulkraft. Den hastighetsavhengige faktor er forskjellig for passasjervogner og godsvogner. Videre influerer vurdering av sporkvaliteten og hastigheten på relevant faktor.
Beregninger kan gjennomføres uten algebracomputersystemer (lommekalkulator er tilstrekkelig).
Følgende ligning blir benyttet:
Termen Q0 er statisk kraft fra hjul. I kurvekjøring benyttes kvasistatisk hjulkraft på grunn av omlagring av kreftene:
DAF er betegnelse for dynamisk innflytelsesfaktor (Dynamic Amplification Factor).
Det beregnes først en hastighetsavhengig faktor:
Dernest vurderes sporets standard:
Produktet av hastighetsavhengig faktor og sporets standard definerer faktor for standardavviket σ.
Alternativt kan faktor for standardavviket beregnes ved kjent vertikalfeil s i sporet:
Endelig defineres multiplikasjonsfaktor for standardavviket:
Dynamisk innflytelsesfaktor DAF:
Den resulterende dynamiske kraft blir dermed:
Formelverk for beregninger av belastning på overbygningens komponenter
I det etterfølgende er vist formelverket i Zimmermanns metode.
Det må først beregnes en grunnverdi L for langsvilleoverbygningen:
Her betyr:
L er grunnverdi for langsvilleoverbygning (mm)
E er elastisitetsmodul for skinnestålet (N/mm2)
IX-X er skinneprofilets treghetsmoment (mm4)
b er medvirkende bredde av fiktiv lengdebjelke (mm)
C er sporets statiske ballastsiffer (N/mm3)
Anvendelse av sporets statiske ballastsiffer gjelder for togmateriell som ikke er i bevegelse. For tog i bevegelse skal det fortrinnsvis benyttes det dynamiske ballastsiffer. Det dynamiske ballastsifferet er høyere enn det statiske fordi sporet stivner litt ved framføring. Normalt antas at CDYN er 10 til 50 % høyere enn CSTAT. I formelverket beskrevet under benyttes en nøytral betegnelse C.
I formelverket under menes med enkeltlast bare denne lasten eller enkeltlast med et kvasistatisk tillegg ved omlagring av vertikalkrefter på ytre og indre skinnestreng på grunn av sentrifugalkraften ved framføring i kurver.
Direkte under enkeltlast beregnes nedsenkning eller deformasjon av skinnen:
Direkte under enkeltlast beregnes bøyemomentet i statisk og dynamisk tilstand ved DAF:
Spenning i underkant skinnefot i statisk og dynamisk tilstand:
Bøyelinjens halve lengde beregnes:
Ved lang bøyelinje vil naboaksel få innflytelse på betraktet sted for dimensjonering (vanligvis direkte under betraktet enkeltlast) og dermed på belastningen på skinne. Dette tas hensyn til ved anvendelse av koeffisienter i tabell som er blitt utledet av influenslinjer.
Det etableres forholdet:
Termen x er avstand fra det betraktede stedet hvor hjullasten virker til et sted med avstand x fra dette stedet; x kan for eksempel beskrive avstanden mellom 2 hjulsett.
For nednøyning av skinne gjelder:
For momentberegning gjelder:
Parameterne ƞ og µ kan avleses i tabeller i handbøker.
Dynamiske parametere:
Formelverk for beregning av trykk i underkant sville og i befestigelsesområdet for sville iht. Zimmermanns metode og dynamisk faktor iht. Eisenmann:
Trykk mot underkant sville under enkeltlast:
Dersom nabolast må betraktes, blir formelen:
Belastning på sville i befestigelsesområdet i statisk og dynamisk tilstand:
Under hensyntagen til nabolast blir formelen:
Algoritmer for relative betraktninger med utgangspunkt i referanseparametere
Det eksisterer matematiske avhengigheter med hensyn til bestemmende parametere i sporet i Zimmermanns metode. Utgangspunktet er gitte kjente referanseparametere.
Referanseparametere er:
- Treghetsmoment til skinneprofil: IREF (mm4)
- Motstandsmoment til skinneprofil: WREF (mm3)
- Resulterende ballastsiffer: CREF (N/mm3)
- Svilleavstand: aREF (mm)
- Svilleflate: FREF (mm2)
Det kan påvises sammenhenger for spenning i underkant i skinnefot; i nedsenkning av skinne og trykk mot ballast fra sville som gitt i tabell 8.1.
| K σ | K y | K p | |
|---|---|---|---|
| I; W |
|
||
| C | |||
| a | |||
| F | |||
Dersom referanseverdiene er kjent, kan verdier for dimensjonerende parametere beregnes.
En modell for betraktning av frekvensrelatert opptreden av vertikalkrefter; endimensjonal modell med en frihetsgrad
En relativ enkel modell for beregning av dynamisk vertikalkraft under hensyntagen til irregulariteter definert ved bølgelengder i sporet for konstant hastighet defineres. For vognen legges det til grunn en endimensjonal modell med en frihetsgrad; dvs. en vogn med kun primæroppheng. Dette er en vanlig konstruksjon for godsvogner; dvs. at vognkasse ligger på boggiramme. Dersom det skulle være et sekundæroppheng, så ville bevegelsene til vognkasse bli så lave at det dynamiske bidraget fra vognkasse kan elimineres. Bare den statiske vekt må medtas.
For vurdering av vognens påvirkning benyttes en fiktiv modell. Framgangsmåten forklares i det etterfølgende:
Her betyr følgende:
QDYN er resulterende vertikalkraft (kN)
Q0 er statisk hjulkraft (kN); eventuelt benyttes den kvasistatiske hjulkraft (kN)
Q0 er statisk hjulkraft (kN)
QdLF er lavfrekvent dynamisk kraft forårsaket av vognkasse og boggiramme (kN)
QdHF er høyfrekvent dynamisk kraft forårsaket av uavfjæret masse til hjulsats (kN)
mc er masse til vognkasse og boggi (kg)
mw er uavfjæret masse til hjulsats (kg)
g er tyngdens akselerasjon (m/s2)
ac er akselerasjonen til vognkasse; eventuelt sammen med boggiramme (m/s2)
v er framføringshastighet til vogn (m/s)
er annen derivert av irregularitet av vertikal sporfeil; dvs. krumning
Brøkuttrykket beskriver belastning på grunn av rifler og bølger i sporet. Det erkjennes bruk av overføringsfunksjoner.
QHENG beskriver belastning på grunn av hengende sviller.
I tillegg kan også kraft fra hjulslag virke.
De enkelte leddene i formelen skal gjennomgås.
Beregning av vognkassens akselerasjon
Det er greit å beregne akselerasjonen ac til vognkassen gjennom egnet formel idet det tas hensyn til vognkassens oppheng i en modell med en frihetsgrad.
Først beregnes opptredende vinkelfrekvens for framføring på grunn av bølgelengden i sporet:
ω er vinkelfrekvens for resonans hvor c er karakteristikk for fjærstivhet og mC er masse av avfjæret vogn:
Forholdet mellom opptredende frekvens og resonansfrekvens er:
Den relative demping D under hensyntagen til demperkarakteristikk d:
Akselerasjonen ac beregnes under forutsetning av neglisjering av opptredende fasevinkler:
Parameter for bevegelse av uavfjæret masse
Parameteren kan også uttrykkes ved
Dermed er det mulig å beregne den dynamiske kraft på skinnegangen når irregulariteten i vertikal retning i sporet ved definert bølgelengde er kjent. Termen L er bølgelengde i sporet.
Modell for beregning av vertikalkraft ved irregulariteter på skinnehodet
Modellen tar hensyn til sammenknytning mellom hjul og skinne over kontaktbetingelsene. Hertzian fjærstivhet i kombinasjon med sporets irregularitet blir benyttet til å definere kontaktkraften.
En resulterende deformasjon blir uttrykt ved differansen i forskyvningen av hjul, skinne og irregulariteten i skinne:
Ligningen formulerer at den resulterende irregularitet kan beregnes ved en forskyvning av skinnen nedover i vertikal retning, ved en bevegelse av hjulsatsen oppover i vertikal retning og ved sammentrykking av kontaktfjæren.
Det er fordelaktig å framskaffe overføringsfunksjonene da bevegelsene uttrykkes i forhold til disse. Variasjonen av kraften Q iht. irregulariteten tas med:
Dermed kan den variable kraft ∆Q beregnes:
∆z er den målte irregularitet, Hr er reseptansen for skinne (m/N), Hw er reseptansen for hjulsatsen (m/N) og kh (kN/mm) er reseptansen for Hertz kontakt.
∆Q representerer variasjonen i det dynamiske krafttillegget med frekvensen
Termen l er lende av bølge på skinnehodet.
Når uttrykket i parentesen er lik 1, får ∆Q sin maksimale verdi.
Det framgår av ovennevnte formel at en kompleks analyse er nødvendig. Med informasjon om verdier på amplitudene, lengde l av riflene og hastigheten kan det dynamiske tillegget beregnes.
Rifler og bølger vil opptre ved framføring med høye aksellaster og det regnes med et dynamisk tillegg på 10 % av aksellasten; dvs. 40 kN:
Verdien er å betrakte som relativt lav; dette skyldes den lave framføringshastigheten på 60 km/h.
Det vises i denne sammenheng til en artikkel i ZEVS Glaser Annalen:
“Stresses in rails due to static, dynamic and thermal loadings”
Artikkelen er på tysk.
Hensyntagen til hengende sviller (vaskesviller)
Effekt av hengende sviller er økt belastning på skinner, sviller og ballast og større krefter i hjul / skinne kontaktflaten relatert til hjul skinne kontaktmekanikken. I IAVSD (International Association of Vehicle Systems Dynamics) i 2009 i Stockholm ble det presentert hva hengende sviller gir i økt belastning. Resultatene er basert på numerisk simulering.
Når det gjelder selve skinnen, kan deformasjonen øke med opp til 60 % (naturlig nok) og økning av belastning i skinnefot kan bli opp til 26 %. Mest ille er imidlertid de store akselerasjonsbevegelsene til skinnene.
Det regnes med et beskjedent tillegg på ca. 10 % av statisk hjulkraft. Det forutsettes at konstruksjonen og byggingen av overbygningen blir utført på en måte som gir nødvendig drenering:
Endelig formel
Den endelige formel for beregning av dynamisk vertikalkraft uttrykkes ved:
Det gjelder:
Dermed blir formelen:
En endimensjonal modell med to frihetsgrader har enda en term. Aspektet gir tilkjenne at det finnes to masser som er avfjæret. Disse er vognkasse og boggiramme. Uavfjæret masse vil være hjulsettet med hjulskivene. Formelen vil da bli:
Illustrasjon av de enkelte termer i formel
Første term er selvforklarende. Termen viser samlet kraft for vognkasse med boggiramme og hjulsats uttrykt ved deres masser og tyngdens akselerasjon.
Figur 8.12 illustrerer term nummer 2 som beskriver det dynamiske tillegget fra vognkasse under hensyntagen til vognkassens vertikale akselerasjon. Bølgelengde med vertikal amplitude i sporet har betydning. Dette vil framgå av formelverket.
Figur 8.13 illustrerer det dynamiske tillegget fra uavfjæret masse (hjulsats) som beveger seg på et spor med vertikal sporfeil (amplitude) over en bølgelengde L (term nummer 3 i formel). Bølgelengder betraktes i området 3 – 25 m.
Term nummer 4 beskriver en høyfrekvent bevegelse på grunn av rifler og bølger i skinnehodet. På grunn av det lave hastighetsnivået vil denne kraften uttrykt i prosent av akselkraft ikke bli alt for stor. Men på grunn av den høye aksellasten får kraften allikevel en størrelse. Figur 8.15 illustrerer situasjonen. Beregninger må gjennomføres i en kompleks analyse og dimensjonerende parametere framstilles som funksjon av hastighetsavhengige frekvenser med lengder på riflene og bølgene.
Term nummer 5 er selvforklarende. Hengende sviller eller vaskesviller betyr at det ikke er fast og kontinuerlig kontakt mellom sville og ballast. Under forutsetning av tilfredsstillende dreneringsforhold og i forbindelse med pakking med etterfølgende stabilisering av sporet forventes sjeldent opptreden av hengende sviller. Det er i beregningene allikevel tatt med et lite bidrag til den dynamiske kraft.
I tillegg kan det forekomme hjulslag på hjulbanen. Hjulslaget vil gi et kortvarig høyt spissmoment på elastisk underlag.
På frosset underlag vil det opptre et uelastisk støt som gir meget høye støtkrefter.
Formelverk for beregning av dimensjonerende parametere
Modellen tar hensyn til belastning på sporets komponenter som funksjon av longitudinelle bølgelengder i sporet ved beskrivelse av et cosinusspor samt rifler og bølger på skinnehodet i tillegg til opptreden av hengende sviller.
Formelverket benytter ballaststivheten β i dimensjon (N/mm2). I Zimmermanns metode inngår tradisjonelt ballastsifferet C i dimensjon (N/mm3). Verdier for denne parameteren i overbygningskonstruksjonen er mer kjent for enn verdiene for ballaststivheten.
I de etterfølgende beregninger vil det bli antatt verdier for C. En omregning til β blir nødvendig. Algoritmene beskrives for å anskueliggjøre sammenhengen.
Det gjentas:
Det defineres:
Faktor utrykkes:
Termen er den inverse verdi av grunnverdi L for langsvilleoverbygningen i Zimmermanns metode:
Bøyelinjens halve lengde beregnes:
Denne formelen sammenlignes med formel i Zimmermanns metode:
Det skal også demonstreres samsvar for nedbøyningsberegning. Utgangspunkt er Zimmermanns formel (på generelt grunnlag):
Relasjonene er dermed bevist.
Det er vist at bøyelinens halve bølgelengde blir beregnet etter samme prosedyre som for Zimmermanns metode.
Dermed etableres forholdet (som for Zimmermann):
Termen L er grunnverdien for en fiktiv langsvilleoverbygning beregnet etter formel i Zimmermanns metode. Det vises til denne metoden.
Faktorene ƞ og µ avleses i tabell.
Direkte under enkeltlast beregnes nedsenking eller deformasjon av skinnen:
Dersom nabolast må betraktes, blir formelen:
Direkte under enkeltlast beregnes bøyemomentet i statisk og dynamisk tilstand:
For beregning av det dynamiske momentet skal strengt tatt den dynamiske ballaststivhet βDYN benyttes. Den dynamiske stivhet er litt forskjellig fra den statiske stivhet da sporet normalt stivner litt når toget framføres. I formel under er imidlertid benyttet den statiske stivhet β. Feilen er ikke særlig stor på grunn av lav hastighet.
Dersom nabolast må betraktes, blir formelen:
Spenning i underkant skinnefot i statisk og dynamisk tilstand:
Dersom nabolast må betraktes, blir formelen:
Den statiske og dynamiske kraft i befestigelsesområdet på sville under enkeltlast uttrykkes ved:
En beregning i dynamisk tilstand krever dimensjonering i en kompleks analyse. En slik analyse medfører omfangsrike algoritmer. Analysen gjennomføres ikke her.
I stedet benyttes den dynamiske kraft QDYN beregnet ifølge den avanserte metode som tar hensyn til bølgelengder i sporet. Det anvendes kvasistatiske stivhetsparametere til sporet. Aspektet medfører en tilnærmelse. Formelen blir under enkeltlast:
Det foretas en dimensjonsanalyse:
Formelen blir mer krevende dersom nabolast må tas med. Imidlertid gjelder uttrykket generelt:
Dermed blir formelen:
Trykket mot svillens underside utledes av RSTATISK og RDYN (tilnærmede formler):
Dersom nabosville tas med, blir uttrykket tilsvarende:
Sammendrag av belastninger på skinne
Samtlige belastningsparametere beskrives.
Skinnen betraktes som en uendelig lang bjelke på elastisk underlag
Figur 8.17 beskriver modellen:
Figur 8.18 gir en beskrivelse av nedsenknings- og momentkurve til skinnen på elastisk underlag.
Spenningsbildet i skinnetverrsnittet ved sentrisk belastning av hjulkraft Q er vist i figur 8.19, romertall I.
Egenspenninger
Det opptrer egenspenninger som oppstår i forbindelse med retteprosessen ved produksjon av skinner. Figur 8.20 viser fordelingen av egenspenningene i tverrsnittet i skinnen. Variasjonen mht. strekkspenninger og trykkspenninger i tverrsnittet er vist.
Temperaturspenninger
Endringer i temperaturen gir opphav til longitudinelle spenninger i tverrsnittet i skinneprofilet. Normalt har skinnen en nøytraltemperatur på 20° - 24 °C. Kraften på Temperaturspenningene beregnes med følgende formel:
Her betyr:
P er longitudinell kraft i skinnen (kN)
αth er utvidelseskoeffisienten i lengderetningen for stål som settes til 1,15 · 10-5 · (1/°C)
∆T er temperaturendring (°C) i forhold til skinnens nøytraltemperatur
A er tverrsnittsarealet (mm2)
Smiths diagram og resulterende spenninger
I figur 8.21 er vist Smiths diagram for vurdering av tillatt spenning i underkant skinnefot i symmetriaksen ved sentrisk vertikal belastning i korrodert tilstand.
Den dynamiske belastning må betraktes sammen med egenspenning i skinnestålet og spenninger på grunn av temperaturvariasjoner. Videre trekkes inn spenning i skinne som opptrer i brukonstruksjoner hvor det ikke er glideskjøter.
Det framkommer følgende ligning:
Her betyr:
zul σd F er tillatt spenning i underkant av skinnefot i symmetriaksen på utmatting forårsaket av den dynamiske vertikale hjulkraft ved framføring av materiellet.
σE er egenspenning i skinnestålet
σT er temperaturspenning
σBT er spenning i skinne som opptrer i brukonstruksjoner hvor glideskjøter ikke er installert
zul σ er tillatt resulterende spenning i skinnen
σDYN FOT er beregnet dynamisk spenning på grunn av kraft fra hjul ved framføring
γ er sikkerhetsfaktor
I Smiths diagram finnes også følgende betegnelser:
σBV er spenning som antas å opptre i skinnen fra bremsing og traksjon fra materiell på bruer
σU er minimumsbelastning ved utmattingstester i benk
σA er maksimalspenning for belastning ved utmattingstester i benk
Den tillatte trafikkspenning inkludert sikkerhetsfaktor for skinne 60E1 i kvalitet 900 er zul σd F = 200 N/mm2.
I beregningene benyttes en sikkerhetsfaktor ϒ = 1,1. Det vil da gjelde for skinnekvalitet R 260 Mn:
For skinnekvalitet R 200 Mn gjelder:
Polygonal Wöhler kurve
Dersom den beregnede eller opptredende spenning er mindre eller lik den tillatte trafikkspenning zul σdF , så kan levetiden for skinnen bli tilnærmet uendelig lang relatert til belastning på momentbøyning. Dette er vist i den polygonale Wöhler kurve:
En lang levetid i sporet forutsetter normalt vedlikehold som regelmessig sliping av skinner, pakking og justering av sporet.
Lasttilfelle I.1: 21,3 tonns aksellast, skinne 49E1, svilleavstand 640 mm, tresviller, vekt 70 kg, svillelengde 2500 mm, bølgelengde 10 m
I.1.1 Zimmermanns metode med dynamisk tilleggsfaktor DAF; Cb = 0,15 N/mm2
Det gjennomføres en beregning med skinne 49E1 og sville med vekt 70 kg og svilleavstand a = 640 mm.
Del 1: Svilleflate
Belastet svilleflate:
Fiktiv medvirkende bredde:
Del 2: Elastisitetsegenskaper i overbygning
Elastisitet i ballastsengen og overbygning (antakelse):
Det er vekselvis Heyback og Pandrol befestigelse på tresviller med tilhørende underlagsplater. Det legges til grunn at mellomleggene ikke bidrar til elastisitet i befestigelsen og i sporet. Den totale elastisitet er derfor lik ballastens elastisitet.
Del 3: Beregning av karakteristisk lengde L ved valg av skinneprofil
Det velges skinne 49E1:
Treghetsmoment: IX – X = 1819 ·104 mm4
IY – Y = 320 · 104 mm4
Motstandsmoment: WX – X = 248 · 103 mm3
WY – Y = 51,2 · 103 mm3
Vekt: G = 49 kg/m
Elastisitetsmodul: E = 2,15 · 105 N/mm2
Beregning av karakteristisk lengde ved anvendelse av statisk ballastsiffer:
Halv bølgelengde:
Det er ingen belastning fra naboaksel for den aksel som betraktes.
Beregning for rett linje og store kurveradier
Del 4: Lastberegning:
Statisk betraktning
Statisk akselkraft:
Statisk hjulkraft:
Det legges på et beskjedent kvasistatisk tillegg:
Kvasistatisk betraktning
Kvasistatisk kraft blir:
Nedbøyning beregnet med statisk ballastsiffer:
Moment:
Spenning i underkant skinnefot, symmetriakse:
Trykk mot underkant sville under enkeltlast:
Belastning på sville i befestigelsen:
Dynamisk betraktning
Dynamisk tilleggsfaktor DAF
Antatt sporstandard:
Statistisk sikkerhet:
Dynamisk tilleggsfaktor:
Dynamisk vertikalkraft:
Dynamisk moment:
Dynamisk spenning i underkant skinnefot i symmetriaksen:
Sikkerhetsfaktor er bestemt til 1,10:
Trykk mot underkant sville under enkeltlast
Belastning på sville i befestigelsen:
Beregningene er sammenfattet i tabell (se under)
| Skinneprofil | 49E1 | 49E1 |
|---|---|---|
| Skinnekvalitet for bøyning (N/mm2) | 700 | 900 |
| Ballastsiffer C (N/mm3) | 0,15 | 0,15 |
| Hastighet (km/h) | 30 | 30 |
| Karakteristisk L (mm) | 720 | 720 |
| (3/4) x Π x L (mm) | 1822 | 1822 |
| Akselkraft (kN) | 213 | 213 |
| Qqst (kN) | 106,50 | 106,50 |
| Nedbøying yKV:ST. fra betraktet hjul for QKV.ST. (mm) | 1,27 | 1,27 |
| Bøyemoment MKV.ST. (kNm) | 19,80 | 19,80 |
| Belastning i skinnefot symmetriakse, σ (N/mm2) | 80,00 | 80,00 |
| Trykk mot underkant sville (N/mm2) | 0,19 | 0,19 |
| Skinnesetekraft (kN) | 37,50 | 37,50 |
| Dynamisk tilleggsfaktor (-) | 1,60 | 1,60 |
| QDYN (kN) | 176,00 | 176,00 |
| Bøyemoment (kNm) | 31,60 | 31,60 |
| Spenning σ dyn (N/mm2) | 128,00 | 128,00 |
| 1,1 x σ dyn (N/mm2) | 141,00 | 141,00 |
| tillatt σ dyn (N/mm2) | 160,00 | 200,00 |
| Egenspenninger (N/mm2) | 80,00 | 80,00 |
| Temperaturspenning | 100,00 | 100,00 |
| Svilletrykk p dyn (N/mm2) | 0,30 | 0,30 |
| Svillesetekraft R dyn (kN) | 60,00 | 60,00 |
På rett strekning og i kurver med store radier oppstår spenninger i dynamisk tilstand i skinnefot i symmetriaksen som er lavere enn tillatt tilrådelig spenningskapasitet for skinner i kvalitet R200Mn og i kvalitet R260Mn. Det skulle derfor ikke være fare for utmatting.
Det påpekes at den kvasistatiske kraft QKV.ST. vurderes i samsvar med tilhørende kvasistatisk kraft i EN 14363 evaluert i et lavpassfilter på 20 Hz. Denne kraften er en 50 % verdi kraft.
Den dynamiske kraft QDYN vurderes i samsvar med tilhørende dynamisk kraft i EN 14363 evaluert i et lavpassfilter på 20 Hz. Denne kraften er en 99,85 % kraft og forekommer dermed meget sjeldent.
Beregning i kurver med små radier; R = 150 m; D = 50 mm; V = 30 km/h
Det blir antatt en framføringshastighet V = 30 km/h tilsvarende v = 8,33 m/s. For en kurve med R = 150 m og D = 50 mm beregnes en liten ukompensert sideakselerasjon og overskuddshøyde:
Med en aksellast mLOK AKSEL = 21300 kg og aq = 0,14 m/s2 blir sentrifugal kraften:
Med tyngdepunktshøyde h = 2,00 m og sporvidde s = 1,50 m blir den kvasistatiske tilleggskraft:
Det regnes med et kvasistatisk tillegg på ΔQ = 8,50 kN > 4,00 kN på grunn av kurvekjøring og beskjeden eksentrisk last på lokomotivet.
Dette gir kvasistatisk kraft:
Vurderinger av spenningstilstand for kombinasjon av vertikale og laterale krefter
For beregning av spenninger i fot av skinne for vertikale krefter benyttes den kvasistatiske og dynamiske tilstand. I Zimmermanns metode beregnes den kvasistatiske vertikale kraft og denne gis et tillegg (DAF = dynamic implification factor) for fastsettelse av den dynamiske vertikale kraft. Metoden er meget enkel og har dermed en del svakheter. Zimmermanns metode gir ingen opplysninger om frekvensrelaterte tilstander.
For en kombinasjon av vertikale og laterale krefter blir aspektet meget omfattende. De vertikale kreftene bestemmes normalt i dynamisk tilstand når disse opptrer alene. For de laterale kreftene er det nødvendig med en vurdering.
Det kan antas 3 innfallsvinkler:
- Grenseverdi for YKV.STAT: bestemt i norm
- Anvendelse av EN 13104 for traksjonsaksler for bestemmelse av Y krefter
- Anvendelse av resultat fra tester El 18
Bestemmelse av dynamisk tilleggsfaktor (DAF) for beregning av YDYN:
- Dimensjonerende YKV.STAT. med tillegg av DAF (dynamic amplification factor)
Grenseverdi for YKV.STAT. bestemt i norm for aksellaster ved forsøk
60 kN er en høy verdi i kvasistatisk tilstand og opptrer trolig for trekkmateriell og ikke for vogner med løpeboggier. Det må legges til at denne verdien sammenlignes med evaluering av målt midlere (50 % verdi) verdi i et lavpassfilter på 20 Hz.
Den kvasistatiske laterale kraft i kombinasjon med den vertikale kraft vil gi store spenninger i dimensjonerende hjørner i skinneprofilet. Plastiske deformasjoner vil kunne forekomme.
Anvendelse av EN 13104 for traksjonsaksler for bestemmelse av Y krefter
Systemskisse for beregning av lateral kraft Y1 er vist i figur I1.
Dersom kraften Y1 er fra førende hjul på førende aksel, angir EN 13104 følgende formel for beregning av denne parameteren for masser i bevegelse (bremsing og traksjon er ikke inkludert):
Det kreves en forklaring på hvordan denne kraften er utledet. Termen Y2 er friksjonskraft mellom hjul og skinne på indre skinnestreng og har en verdi lik:
Denne kraften forutsettes å være i likevekt med føringskraften P på ytre skinnestreng.
Videre legges til grunn en støtfaktor:
Endelig gjennomkjører akselen kurver med en ukompensert sideakselerasjon lik 1,0 m/s2 (i normen):
Dermed blir den ytre laterale kraft Y1
Termen m1 er vognkassens masse med last på en aksel. Dersom denne settes til 21,30 tonn, blir Y kraften:
Det er i ovennevnte beregning lagt til grunn en ukompensert sideakselerasjon aq = 1,00 m/s2. El 18 kjører gjennom kurvene med langsommere hastighet på Flåmsbana. For V = 30 km/h opptrer det en beskjeden ukompensert sideakselerasjon aq = 0,14 m/s2.
Ved en slik forutsetning blir den laterale kraften:
Det er et spørsmål om denne kraften skal vurderes som kvasistatisk eller dynamisk. Normen angir lave verdier for tillatte spenninger som framkommer ved dividering med en sikkerhetsfaktor.
Det bør nevnes at virkning av høy ukompensert sideakselerasjon og dermed høy sentrifugalkraft ifølge utallige målinger ikke fører til tilsvarende høy føringskraft på kanten av skinnehodet sammenlignet med framføring med lav aq. Dette skyldes trolig at friksjonen av føringskraften mot skinnehodet er større ved lav ukompensert sideakselerasjon enn ved høy aq. Dermed utlignes forskjellen mht. føringskraften og tilhørende lateral spenning.
Anvendelse av resultat fra tester for El 18
En tredje innfallsvinkel er å benytte rapporter fra gjennomførte tester. Det vites ikke om slike tester er gjennomført i Norge eller i andre land. Imidlertid har El 18 en boggi med gode radielle styringsegenskaper i kurver.
Grenseverdi for Y KV.STAT. bestemt i norm for høyere aksellaster ved forsøk med tillegg av DAF (dynamic amplification factor)
Dynamisk innflytelsesfaktor DAF:
Den statistiske sikkerhet er t = 3. Hastighetsinnflytelse bestemmes til φ = 1 og sporets standard i lateral retning vurderes til å være ϕ = 0,20.
Dermed blir DAF = 0,60.
Formel for dynamisk lateral kraft er:
Det er nevnt 3 innfallsvinkler for vurdering av den kvasistatiske Y kraft
Kraft i norm: YKV.STAT. = 60,00 kN
Kraft i EN 13104: Y = 56,32 kN
Kraft i test (maks. verdi): mangler opplysninger
Kraften på 60 kN i norm er høy og gjelder i hovedsak for lokomotiv. Vogner med løpeaksler vil gi lavere verdier. I det etterfølgende fastsettes:
Det gjennomføres i det etterfølgende en fullstendig beregning med utgangspunkt i vertikal og lateral kraft i kvasistatisk og dynamisk tilstand.
Samvirke av eksentrisk hjulkraft Q og høy lateral kraft Y kan føre til betydelige spenninger på bøyning i kantene på skinnehode og skinnefot. Dette gjelder punktene A, B, C og D som er vist i figur 8.19. Denne tilstanden oppstår i hovedsak i kurver med små radier i sporet og i sporveksler med små radier ved passering av tunge lokomotiv. Ved tunge aksellaster i godsvogner med enkle boggikonstruksjoner (ikke tilstrekkelig gode radielle styringsegenskaper) vil betydelige spenningsnivåer opptre.
I litteraturen diskuteres om beregninger på utmatting i dynamisk tilstand er nødvendig da antallet av slike situasjoner vanligvis er begrenset og har lokal opptreden i en kurve. Imidlertid på Flåmsbana med et stort antall av kurveradier (ned mot R = 150 m) vil lokale spenningsmaksima opptre og det vil alltid være en mulighet for opptreden av plastisk deformasjon dersom ytelsesgrensen for stålet blir overskredet et tilstrekkelig antall ganger.
Det er hensiktsmessig å foreta en dekomponering av kraftbildet som vist i figur 8.1. Spenningsbildene i tverrsnittet på profilet er vist.
Det opptrer ulike momenter.
Bøyemoment på grunn av vertikalkraft Q i senter skinne på skinnehodet (kvasistatisk og dynamisk):
Torsjonsmoment på grunn av eksentrisk angrepspunkt for vertikalkraft Q og angrepspunkt for lateral kraft Y (kvasistatisk og dynamisk):
Hovedspenningene kan beregnes.
Bøyningsspenning i skinnehode:
Bøyningsspenning i skinnefot:
Delspenning I på grunn av tverrsnittform av skinneprofilet for dynamisk kraft Q:
Delspenning II på grunn av torsjonsmomentet MT:
Delspenning III på grunn av lateral kraft Y:
Den resulterende spenning I hver lokalisering uttrykkes:
Faktorene λ med indekser for skinneprofil 49E1, 54E3 og 60E1 er gitt I litteraturen:
| Skinneprofil | Koeffisienter for beregning av spenninger i skinneprofil ved kombinerte laster Q og Y | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| h (cm) | e (cm) | λOH(cm-3) | λ1H(cm-2) | λ2H (cm-3) | λ3H (cm-2) | λOF (cm-3) | λ2F (cm -3) | λ3F(cm-2)
| |
| 49E1 | 9,90 | 3,35 | 0,0020 | 0,054 | 0,016 | 0,160 | 0,0040 | 0,0152 | 0,2980 |
| 54E3 | 10,20 | 3,35 | 0,0017 | 0,049 | 0,014 | 0,140 | 0,0036 | 0,0131 | 0,2610 |
| 60E1 | 12,90 | 3,60 | 0,0018 | 0,050 | 0,017 | 0,110 | 0,0027 | 0,0126 | 0,2290 |
For skinne i kvalitet R 260 Mn gjelder følgende grenseverdier for anbefalte tillatte spenninger:
I punktene A og B: 325 N/mm2
I punktene C og D: 250 N/mm2
I symmetriakse i fot: 200 N/mm2
For skinne i kvalitet R200Mn vurderes for Flåmsbana følgende grenseverdier for anbefalte
tillatte spenninger:
I punktene A og B: 285 N/mm2
I punktene C og D: 210 N/mm2
I symmetriakse i fot: 160 N/mm2
Spenningene gjelder i dynamisk tilstand ved vedvarende opptreden av belastninger.
Spenninger i skinneprofil ved bøyning på grunn av kurveradius
I kurver med små radier opptrer i tillegg horisontale bøyningsmomenter som må beregnes. Følgende ligninger benyttes:
Termene betyr:
E: elastisitetsmodul for stål (N/mm2)
bHODE: bredde av skinnehode (mm)
bFOT: bredde av skinnefot (mm)
R: kurveradius (mm)
Kvasistatisk vurdering
Iht. foregående beregninger for vertikal last:
Torsjonsmoment MT:
Delspenningene beregnes:
De resulterende spenninger blir:
Dynamisk vurdering
Iht. foregående beregninger for vertikal kraft:
Torsjonsmomentet blir:
Delspenningene beregnes:
De resulterende spenninger blir:
Spenninger i bøyning på grunn av kurveradius
R =150 m
Egenspenninger
Egenspenninger bestemmes:
Temperaturspenninger
Temperaturspenningene kan være trykkspenninger eller strekkspenninger og er konstant over hele tverrsnittet når de opptrer.
Eventuelt:
Kvasistatisk vurdering
Resulterende spenninger blir:
Dynamisk vurdering
Det gjentas følgende vedr. anbefalte tillatte spenninger:
- For skinne i kvalitet R 260 Mn gjelder følgende grenseverdier for anbefalte tillatte spenninger:
I punktene A og B: 325 N/mm2
I punktene C og D: 250 N/mm2
I symmetriakse i fot: 200 N/mm2
- For skinne i kvalitet R200Mn vurderes for Flåmsbana følgende grenseverdier for anbefalte tillatte spenninger:
I punktene A og B: 285 N/mm2
I punktene C og D: 210 N/mm2
I symmetriakse i fot: 160 N/mm2
De anbefalte spenningene gjelder i dynamisk tilstand ved vedvarende opptreden av belastninger.
De beregnede spenningene er å betrakte som 99,85 % verdier og forekommer derfor sjeldent.
Det er dermed ikke overhengende fare for opptreden av plastiske deformasjoner.
Beregningene er sammenfattet i tabeller i det etterfølgende.
Den første tabellen viser de beregnede belastninger i kvasistatisk tilstand.
Den andre tabellen viser de beregnede belastninger i dynamisk tilstand
| Kvasistatisk betraktning | Spor (49E1 og a = 640 mm)
Radius R = 150 m, D = 50 mm, V = 30 km/h I = 22 mm (aq = 0,14 m/s2) Skinnekvalitet R 200 Mn; 700 N/mm2 |
Spor (49E1 og a = 640 mm)
Radius R = 150m, D = 50 med mer V = 30 km/h I = 22 mm (aq = 0,14 m/s2) Skinnekvalitet R 260 Mn; 900 N/mm2
| ||
|---|---|---|---|---|
| Krefter (kN) | Målt | Beregnet | Målt | Beregnet |
| P (kN) | 213,00 | 213,00 | ||
| QSTATIKK (kN) | 106,50 | 106,50 | ||
| ΔQSTATIKK (kN) | 8,50 | 8,50 | ||
| QKV.STATIKK (kN) | 115,00 | 115,00 | ||
| QDYN (kN) | ||||
| YKV.STATIKK (kN) | 60,00 | 60,00 | ||
| YDYN (kN) | ||||
| Y/Q)2m DYN | ||||
| CTOTAL (N/mm3) | 0,15 | 0,15 | ||
| Svilleavstand | 640 mm | 640 mm | ||
| L | 720 mm | 720 mm | ||
| ¾ x Π x L | 1822 mm | 1822 mm | ||
| Beregninger av belastninger på skinneprofil | ||||
| Kvasistatisk bøyemoment | 20,70 kNm | 20,70 kNm | ||
| Hovedspenninger | 41,40 N/mm
82,80 N/mm2 |
1282,80 N/mm2
82,80 N/mm2 | ||
| Torsjonsmoment | 2,09 kNm | 2,09 kNm | ||
| Delspenninger | 62,10 N/mm2
0 |
62,10 N/mm2
0 | ||
| 33,50 N/mm2
31,80 N/mm2 |
33,50 N/mm2
31,80 N/mm2 | |||
| 96,00 N/mm2
179,00 N/mm2 |
96,00 N/mm2
179,00 N/mm2 | |||
| Resulterende
spenninger på bøyepåkjenning |
31,00 N/mm2 | 131,00 N/mm2 | ||
| - 102,00 N/mm2 | - 102,00 N/mm2 | |||
| 215,30 N/mm2 | 215,30 N/mm2 | |||
| -49,70 N/mm2 | -49,70 N/mm2 | |||
| Grenseverdi for spenning | ; | |||
| ; | ||||
| Egenspenninger | I
σRC, D |
-40 N/mm2
-60 N/mm2 |
-40 N/mm2
- 60 N/mm2 | |
| Temperatur | σTEMP | 100 N/mm2 | 100 N/mm2 | |
| Bøyning i kurver | ± 48,00 N/mm2 | ± 48,00 N/mm2 | ||
| ± 90,00 N/mm2 | ± 90,00 N/mm2 | |||
| Dynamisk betraktning | Spor (49E1 og a = 640 mm)
Radius R = 150 m, D = 50 mm, V = 30 km/h I = 22 mm (aq = 0,14 m/s2) Skinnekvalitet R 200 Mn; 700 N/mm2 |
Spor (49E1 og a = 640 mm)
Radius R = 150m, D = 50 med mer V = 30 km/h I = 22 mm (aq = 0,14 m/s2) Skinnekvalitet R 260 Mn; 900 N/mm2
| ||
|---|---|---|---|---|
| Krefter (kN) | Målt | Beregnet | Målt | Beregnet |
| P (kN) | 213,00 | 213,00 | ||
| QSTATIKK (kN) | 106,50 | 106,50 | ||
| ΔQSTATIKK (kN) | 8,50 | 8,50 | ||
| QKV.STATIKK (kN) | 115,00 | 115,00 | ||
| QDYN (kN) | 184,00 | 184,00 | ||
| YKV.STATIKK (kN) | 60,00 | 60,00 | ||
| YDYN (kN) | 96,00 | 96,00 | ||
| Y/Q)2m DYN | ||||
| CTOTAL (N/mm3) | 0,15 | 0,15 | ||
| Svilleavstand | 640 mm | 640 mm | ||
| L | 720 mm | 720 mm | ||
| ¾ x Π x L | 1822 mm | 1822 mm | ||
| Beregninger av belastninger på skinneprofil | ||||
| Dynamisk bøyemoment | 33,10 kNm | 33,10 kNm | ||
| Hovedspenninger | 66,20 N/mm2
132,40 N/mm2 |
66,20 N/mm2
132,40 N/mm2 | ||
| Torsjonsmoment | 3,34 kNm | 3,34 kNm | ||
| Delspenninger | 99,40 N/mm2
0 |
99,40 N/mm2
0 | ||
| 53,40 N/mm2
50,80 N/mm2 |
53,40 N/mm2
50,80 N/mm2 | |||
| 153,60 N/mm2
286,00 N/mm2 |
153,60 N/mm2
286,00 N/mm2 | |||
| Resulterende
spenninger på bøyepåkjenning |
208,70 N/mm2 | 208,70 N/mm2 | ||
| - 163,00 N/mm2 | - 163,00 N/mm2 | |||
| 344,10 N/mm2 | 344,10 N/mm2 | |||
| -80,00 N/mm2 | -80,00 N/mm2 | |||
| Grenseverdi for spenning | ; | ± 285 N/mm2 | ± 325 N/mm2 | |
| ; | ± 210 N/mm2 | ± 250 N/mm2 | ||
| Egenspenninger | σR A, B
σR C, D |
-40 N/mm2
-60 N/mm2 |
-40 N/mm2
- 60 N/mm2 | |
| Temperatur | σTEMP | 100 N/mm2 | 100 N/mm2 | |
| Bøyning i kurver | ± 48,00 N/mm2 | ± 48,00 N/mm2 | ||
| ± 90,00 N/mm2 | ± 90,00 N/mm2 | |||
Det skal formuleres kommentarer til beregningene.
På rett strekning og i kurver med store radier oppstår spenninger i dynamisk tilstand i skinnefot i symmetriaksen som er lavere enn tillatt tilrådelig spenningskapasitet for skinner i kvalitet R 200Mn og i kvalitet R 260Mn. Det skulle derfor ikke være fare for utmatting.
Det påpekes at den kvasistatiske kraft QKV.ST. vurderes i samsvar med tilhørende kvasistatisk kraft i EN 14363 evaluert i et lavpassfilter på 20 Hz. Denne kraften er en 50 % verdi knyttet til belastningen.
Den dynamiske kraft QDYN vurderes i samsvar med tilhørende dynamisk kraft i EN 14363 evaluert i et lavpassfilter på 20 Hz. Denne kraften er en 99,85 % verdi og forekommer dermed meget sjeldent.
I kurver med små radier opptrer en kombinasjon av eksentrisk virkende vertikalkrefter og horisontale krefter. I en kvasistatisk vurdering er de beregnede spenninger i kant av skinnehode og skinnefot tolererbare og akseptable i skinnekvalitet R 200 Mn og R 260 Mn. De kvasistatiske spenninger er å oppfatte som 50 % verdier i en statistisk vurdering og opptrer dermed ofte.
Dynamisk betraktning for eksentrisk virkende vertikalkrefter og horisontale krefter gir beregningsmessig meget høye spenninger i kantene på skinnehode og i skinnefot. De beregnede spenninger overskrider anbefalte grenseverdier; særlig gjelder dette for skinnekvalitet R 200 Mn. Plastiske deformasjoner vil kunne opptre teoretisk. Imidlertid er det nødvendig å være oppmerksom på de beregnede dynamiske spenningene er å oppfatte som 99,85 % verdier i en vurdering i et lavpassfilter på 20 Hz og at de derfor opptrer meget sjeldent og har lokal opptreden. De største spenningene som opptrer i underkant skinnefot i punkt C har en størrelse på 344,10 N/mm2; dvs. ca. 50 % av strekkfastheten for skinnestål R 200 Mn.
I tillegg til belastningen fra rullende materiell opptrer også belastning forårsaket av kurveradius, egenspenninger og temperaturspenninger. I særlige tilfeller kan da resulterende spenning bli opp mot 480 N/mm2. Imidlertid er det da nødvendig å være oppmerksom på at temperaturspenningene sjeldent opptrer med maksimale verdier. Aspektet vil ha betydning for sannsynlighet for opptreden av plastisk deformasjon i punkt C.
Det er også å bemerke at skinner i kvalitet R200 Mn har ligget i sporet siden ca. 1965. Ifølge BANADATA Innsyn finnes ca. 10.000 – 11.000 løpemeter skinner i denne kvaliteten. Øvrige skinner har kvalitet R900 Mn og er lagt i sporet på et senere tidspunkt.
Det blir dermed et spørsmål hvorfor skinnene i R 200 Mn ennå ligger i sporet.
I.1.2 Beregning i henhold til modell med en frihetsgrad
El 18 består av et lokomotiv med avfjæret vognkasse, avfjæret boggiramme og uavfjæret hjulsett.
Det beregnes de dynamiske vertikale krefter med utgangspunkt i nedennevnte formel. Det tas dermed i betrakting den vertikale akselerasjon av lokomotivets vognkasse.
For ikke å gjøre beregningen for omstendelig blir vognen og boggiramme vurdert som en avfjæret masse i samvirke. Med den lave hastighet som eksisterer på Flåmsbana, er dette greit.
EN 14363 setter en grenseverdi for den vertikale akselerasjon til 3 m/s2 for bevegelse av vognkasser i lokomotiv. Denne verdien benyttes i det etterfølgende.
Det gjennomføres en beregning som tar hensyn til vognkassens karakteristiske parametere og irregulariteter i sporet:
Termen kan omskrives:
Det regnes med følgende verdier for parametere:
Masse av vogn og delvis boggi på et hjulsett: mC = 20300 kg
Masse av hjulsett og delvis boggi (uavfjæret masse): mW = 1000 kg
Tyngdens akselerasjon: g = ca. 10 m/s2
Vognkassens vertikale akselerasjon med boggiramme: aC (skal beregnes); (m/s2)
Framføringshastighet: v (m/s)
Vertikal irregularitet i sporet: z (m)
Bølgelengde i sporet (cosinusspor): L (m)
Overføringsfunksjon for rifler og bølger på skinne (se formel)
Statisk hjulkraft av lokomotiv:
Kvasistatisk tillegg:
Kvasistatisk hjulkraft:
Vognkassens dimensjonerende parametere inkludert boggiramme på et hjulsett:
Demperkarakteristikk (antatt): d = 80 kNs/m
Karakteristikk for fjærstivhet: c = 1080 kN/m
Sporkarakteristikker:
Bølgelengde i cosinusspor (belastet spor): L = 10 m
Vertikal irregularitet i skinne: z = 0,05 m
Framføringshastighet: V = 30 km/h (v = 8,3 m/s)
Omløpshastighet:
Vognens egenfrekvens inkludert boggiramme relatert til en aksel (antakelse om lik fordeling):
Dimensjonsløs frekvens for bevegelse:
Dempingsgrad:
Vertikale akselerasjonsbevegelser til vognkasse med boggiramme:
Vertikalbevegelse til vognkasse med boggiramme:
I det etterfølgende settes vognkassens akselerasjon over boggi lik grenseverdi i EN 14363 til aC = 3,00 m/s2 > 2,30 m/s2. Det gjentas at verdiene for demperkarakteristikk og fjærkarakteristikk er antatt.
Dynamisk kraft fra avfjæret vognkasse med boggiramme på grunn av vertikal akselerasjonsbevegelse:
Dynamisk kraft fra hjulsett (uavfjæret masse):
Kraft fra rifler og bølger på skinnehodet:
Overføringsverdi:
Kraft på grunn av hengende sviller:
Resulterende dynamisk kraft på skinne:
Beregning av belastning i henhold til formler i avansert metode
Resulterende statisk ballastsiffer er beregnet til:
Fjærstivhet k er beregnet til:
Ballaststivheten beregnes med svilleavstand a = 640 mm:
Produkt av elastisitetsmoment og treghetsmoment:
Deformasjon av skinne ved statisk last:
Dynamisk moment:
Dynamisk spenning i underkant skinne:
Sikkerhetsfaktor er bestemt til 1,10:
Kraft på sville i befestigelse blir:
Trykk mot underside sville:
Beregningsmetoden gir en dypere analyse av virkningen av de ulike opptredende laster og krefter og dermed en bedre forståelse av hva som skjer i sporet; i dette tilfellet på rett strekning.
På grunn av den lave hastigheten blir beregningsresultatene omtrent de samme som for Zimmermanns metode med dynamisk tillegg.
Det må imidlertid ikke være tvil om hvilken metode som er den beste; det er den avanserte metode.
Belastning i befestigelse
Sporet på Flåmsbana er lagt ut med tresviller. Det finnes overveiende 2 befestigelser:
- Pandrol (trolig PR 341 A)
- Hey – Back (trolig HBFJ49)
Figur 9.1 viser befestigelse av type Hey – Back.
På grunn av kurver med radier R = 150 m opptrer horisontale og vertikale krefter i befestigelsen. Aspektet gir en resulterende kraft rettet mot befestigelsen. Det forventes ikke en økning i helningsvinkelen for virkningslinjen for den resulterende kraft fra det tyngre lokomotivet El 18 sammenlignet med virkningslinjen for de kombinasjonskrefter som oppstår ved framføring av det lettere lokomotivet El 17. Med El 17 eksisterer betydelig erfaring for virkning på befestigelsen.
Imidlertid vil det trolig bli en økning i de horisontale krefter fra El 18 på grunn av større tyngde. Aspektet kan føre til hurtigere opptreden av slitasje i skruehullene på tresvillene på grunn av treets mekaniske egenskaper. Det er derfor nødvendig å føre kontroll med skruene ved for eksempel utøvelse av et dreiemoment (som beskrevet i regelverket).
Belastninger fra hjulslag og belastning på skjøter i lasket spor på elastisk underlag og i sporveksler
Kraft ved hjulslag på tresviller på elastisk underlag
Selve slagenergien ved hjulslag er ikke særlig stor; den er i første rekke avhengig av størrelsen på det flate partiet på hjulet og av vognmassen. Slagkraften kan imidlertid bli meget stor og forårsake et kortvarig opptredende bøyemoment av betydelig størrelse.
Det dynamiske moment er i det foregående beregnet til MDYN = 33,45 kNm. Dette momentet innbefatter også parametere som korte rifler og bølger på skinnehodet samt svevende sviller.
Det blir tatt utgangspunkt i et hjul med radius r = 550 mm (litt benyttet) og en lengde på det flate partiet på 80 mm. Det blir da antatt et tilfelle som er dårligere enn gjeldende verdi i retningslinjene (60 mm).
Beregninger gir:
Pilhøyde i det flate partiet beregnes til:
Målinger av tester i bl. annet. ORE D 161 viser at ved en aksellast på 22,50 tonn så øker slagkraften med 30 kN/mm for tresviller på elastisk underlag ved framføringshastighet på 30 km/h.
Slagkraften skulle dermed anta en verdi på ca. 45,00 kN. Dette er ikke urovekkende.
Støtkrefter i skinneskjøter i lasket spor
På grunn av de små kurveradier på Flåmsbana er det overveiende lasket spor på hele strekningen (det finnes mellomliggende partier med sveiste skjøter).
I skjøtene opptrer støtkrefter P1 og P2.
Ved irregulariteter på skinnehodet og hjulbane vil det ved framføring av materiell oppstå støt- eller slagkrefter. Slike krefter vil særlig oppstå i laskede skjøter, men også i forbindelse med hjulslag og andre defekter på hjulbane, korte bølgelengder på skinnehodet, diskrete irregulariteter samt sveiste skjøter i for eksempel sporveksler og i vilkårlig opptredende ruhet på skinnehodet.
Litteraturen beskriver støtkreftene ved P1 og P2. Eksempler er vist i figurene 10.1 og 10.2.
P1 opptrer umiddelbart på skinnehodet og kan forårsake høye frekvenser og har et mønster som gjør at skinne og hjul beveger seg ut av fase.
Følgende formel er vist:
Her betyr:
P0 er statisk hjulkraft; dvs. identisk med Q0 (kN)
2 α totale vinkel i fordypningen av irregulariteten (rad)
v er hastighet (m/s)
kH er lineariteten i Hertz kontaktstivhet (N/m)
mT1 er effektiv ekvivalent spormasse for beregning av P1 (kg)
mU er uavfjæret masse av hjulsats (kg)
Modell for beregning av slagkrefter og støtkrefter er vist i figur 10.3.
P2 opptrer litt senere i overbygningskonstruksjonen og forårsaker skade og nedbrytning av denne. Følgende formel gjelder:
I tillegg til ovennevnte betegnelser betyr:
mT2 er ekvivalent medsvingende spormasse for beregning av P2 (kg)
kT2 er ekvivalent sporstivhet for beregning av P2 (N/m)
cT er ekvivalent spordemping for beregning av P2 (Ns/m)
Litteraturen beskriver også en enklere formel:
Her betyr:
λ er dimensjonsløs faktor avhengig av sporpakking (≤ 1)
k er sporets stivhet som er beregnet til 37,50 N/m
Slagkreftene eller støtkreftene blir i det vesentligste en funksjon av hjulkrat og hastighet.
I eksisterende situasjon er hjullasten omtrent 10,65 tonn og hastigheten er 30 km/h.
Tabell under gir oversikt over kilder til opphav av P1 og P2 krefter og tiltak som må iverksettes.
| Type av irregularitet | Utøvende kraft | Vedlikeholdstiltak |
|---|---|---|
| Hjulslag og defekter på hjul | P1; P2 | hjuldreining |
| Korte bølgelengder på skinnehodet | P1; P2 | Sliping
(slag- og støtkrefter blir normalt ikke dimensjonerende) |
| Diskrete irregulariteter i sveise-skjøter, laskede skjøter, sporveksler | P1; P2; rullende materiell | Utretting; sliping, pakking |
| Vilkårlig opptredende ruhet på skinnehodet | P1; P2 | Sliping |
| Vilkårlig opptredende feil i ballast | Rullende materiell | Pakking
|
Tabell P1 og P2 krefter og vedlikehold
Det skal gjennomføres en beregning for eksisterende og framtidig situasjon.
Følgende parameterverdier antas for ny situasjon:
Statisk hjulkraft: P0 = 106,50 kN
2 x vinkel for skjøt: 2 α = 20 mrad = 0,02 radianer
Hertzian kontakt fjærstivhet: kH = 1,40 · 109 N/m
Effektiv spormasse: mT1 = 2000 · 0,60 · 0,30 · 1,20 = 432 kg
Uavfjæret masse av et halvt hjulsett: mU = 500 kg
Hastighet er: V = 30 km/h = 8,33 m/s
Kraften beregnes:
Følgende parameterverdier antas for eksisterende lokomotiv El 17:
Statisk hjulkraft: P0 = 80 kN
2 x vinkel for skjøt: 2 α = 20 mrad = 0,02 radianer
Hertzian kontakt fjærstivhet: kH = 1,40 · 109 N/m
Effektiv spormasse: mT1 = 2000 · 0,60 · 0,30 · 1,20 = 432 kg
Uavfjæret masse av et halvt hjulsett: mU = 400 kg
Hastighet er: V = 30 km/h = 8,33 m/s
Overgang fra eksisterende lokomotiv med aksellast lik 16 tonn og hastighet lik 30 km/h til nytt lokomotiv med aksellast lik 21,3 tonn og hastighet lik 30 km/h gir en økning i P1 og P2 på om lag en faktor lik 1,15. Økningen i last har en faktor lik 1,33.
Belastning i svevende skjøter i lasket spor
En skjøt i et lasket spor kan få opplegg på 3 ulike måter. I tilfellet av svevende skjøt oppstår et moment på bøyning mellom svillene. En slik skjøt er vist i figur 10.4.
Av de 3 mulige oppleggsmetodene er det bare tilfelle a) som er kritisk. Aspektet henger sammen med at treghetsmomentet til laskene samlet er mindre enn treghetsmomentet til skinnen. På grunn av konstruksjonen kan alternativt skinnene betraktes som utkraget fra sville til skjøt. Det vil derfor bli en større nedsenkning av skinnen når tog passerer over skjøten.
Spennvidde regnet mellom de ytre boltene er om lag 430 mm. Den reelle lysåpning er ca. 250 mm.
Overgang fra El 17 til El 18 gir en lastøkning på en faktor lik 1,33.
Den dynamiske hjulkraft er QDYN = 176,00 kN (se beregninger foran). Momentet blir:
Formelen er hentet fra Modern Railway Track og termen L er den karakteristiske lengde som er beregnet foran.
Det er foran beregnet et moment på bøyning i dynamisk tilstand for skinner på elastisk underlag lik 31,60 kNm. Dette moment gir en spenning i underkant skinnefot i symmetriaksen σDYN = 141,00 N/mm2. Spenningen i dynamisk tilstand oppfattes som moderat; dette gjelder også for kvalitet R 200 Mn (bruddfasthet lik 680 N/mm2).
Momentet over skjøtåpningen er mindre enn i sporet; 20,40 kNm < 31,60 kNm.
Treghetsmomentet for 2 laskede skjøter er:
Spenningen i laskene blir:
Tilsvarende spenning fra El 17:
Spenningene er beregnet konservativt; dvs. etter en metode som har innebygget mye sikkerhet. De beregnede spenningene representerer de absolutt høyeste verdiene som kan aksepteres; dette gjelder for belastning fra El 18. Stållaskene blir forspente med 4 bolter.
Stållaskene støtter seg på konsollene på skinnefot i overkantkant og på skinnehodet i underkant. Stållaskene behøver dermed ikke å overta belastningen tilsvarende en fritt bærende bjelke. Boltehullene er imidlertid et svakt punkt og dynamiske belastninger kan føre til at utmatting kan inntreffe.
Krefter i sporveksler
Støtkrefter i krysspiss i sporveksel forventes å øke med 15 % ved overgang fra El 17 til El 18. Ved ofte passeringer vil aspektet føre til en noe hurtigere slitasje i krysspissen.
I områder for ledeskinner kan det forekomme at ledeskinnen blir belastet bare på horisontale krefter da de vertikale kreftene fra hjulbane overføres til hovedskinne. Ledeskinnene er festet til underliggende sville og blir dermed utkraget. Ved stor horisontal belastning kan det derfor inntreffe brudd i brakettfot ved små sporveksler. Det er ikke mulig å konkretisere om dette vil skje; sannsynligheten er meget lav. Men brakettene må overvåkes. De nedenstående bilder er hentet fra Ofotbanen og tjener til kunnskapsoverføring.
Belastning på skinnehodet
Kapitlet inneholder beregner av kontaktspenningene relatert til hjul/skinne kontaktmekanikken. Beregningene er utført i henhold til en forenklet metode og til en mer detaljert metode.
For den forenklede metode antas en rektangulær kontaktflate med et gjennomsnittlig flatetrykk.
For den mer detaljerte metode legges til grunn en elliptisk kontaktflate med en ellipsoide trykkfordeling.
Det er kjent at kontaktflaten i mange operative forhold er ikke – elliptisk. Ikke elliptiske kontaktflater oppstår for eksempel for skinne 60E1 i kombinasjon med hjul S1002 for nominelle tverrprofil. Ikke elliptiske kontaktmodeller krever anvendelse av sofistiske beregningsmetoder iht. Kalkers teorier som ikke blir vurdert her.
Forenklet studie
Denne metoden tar utgangspunkt i et jevnt fordelt trykk i kontaktflaten mellom hjul og skinne. Litteraturen bekrefter at for hjul med diameter mellom 600 mm og 1200 mm kan en simplifisert todimensjonal metode anvendes for beregninger av spenninger i skinnehodet. Alle radier som inngår i beregningene, blir antatt å være uendelige. Unntaket er radius til hjulet som må benyttes. Kontaktarealet blir dermed rektangulært og kontaktbelastningene har form som en semi elliptisk sylinder. Det vises til figur 11.1.
I denne forenklede metode benyttes det midlere trykket qmean i kontaktflaten. Det er foreslått følgende formel:
Her betyr:
Q er statisk eller kvasistatisk hjulkraft (kN)
r er hjulradius (mm)
2 b er lengde av kontaktflate mellom hjul og skinne (mm)
E er stålets elastisitetsmodul (N/mm2)
v er Poissons ratio eller tverrkontraksjonen for stålet
For E = 2,15 · 105 N/mm2, v = 0,3 og b = 6 mm (2 b = 12 mm) oppnås en praktisk formel:
Den maksimale skjærspenning opptrer på tvers av skinnehodet. I lengderetningen vil skjærspenningen avta litt på grunn av belastning fra bøyemomenter.
Uttrykt ved qmean beregnes skjærspenning:
For en skinne med stålkvalitet 900 N/mm2 er den anbefalte maksimale skjærspenning ved gjentatt belastning:
Dvs. at skjærkapasiteten kan utrykkes ved den klassisk kjente tilnærming
Forholdet mellom flytespenning og tillatt skjærspenning blir dermed:
Dersom dette forholdstallet overføres for andre stålkvaliteter, kan tilsvarende anbefalte maksimale skjærspenninger for slike stålkvaliteter angis. For hodeherdede skinner i kvalitet 1100 N/mm2 kan den tillatte anbefalte maksimale skjærspenning settes høyere:
For bløtere skinner i kvalitet 700 N/mm2 kan den tillatte anbefalte maksimale skjærspenning vurderes til:
Med ovenfor angitte formler kan den nødvendige hjulradius beregnes for å unngå for store kontaktspenninger og skjærspenninger i skinnehodet. Spørsmålet er hvilken hjulradius som skal legges til grunn; et helt nytt hjul levert fra leverandør eller et hjul som er halvt eller delvis utnyttet, dvs. midlere eller delvis utnyttet hjuldiameter før hjulet må skrotes.
Den største tillatte hjulkraft eller kvasistatisk hjulkraft i kurver som funksjon av hjulradius r kan uttrykkes:
Den tillatte minste hjulradius som funksjon av hjulkraft eller kvasistatisk hjulkraft kan uttrykkes:
Her betyr:
υ er en sikkerhetsfaktor; i tilfellet for El 18 kan denne verdien settes lik 1,10.
Vertikalkraften Q er enten statisk kraft på rett linje eller kvasistatisk kraft i kurver; dvs. i kurver må det kvasistatiske tillegget trekkes fra for å fastsette den tillatte hjulkraft.
I utpregede strekningsavsnitt hvor bremsing og traksjon forekommer, blir belastninger på skinnehodet større. Kryp i lengderetningen vil opptre. I tillegg oppstår kryp i tverretningen i kurver med små radier. Aspektene fører til større opptredende hovedspenninger i en dybde av 4 – 6 mm under overflaten av skinnehodet. I dette tilfellet avtar ikke skjærspenningene raskt av. Forholdet fører til høyere slitasje.
I kurver med små radier R < 500 m bør den tillatte akselkraft eller hjulkraft reduseres med ca. 20 % i forhold til den beregnede kraft som framkommer i ovennevnte formler.
Belastning iht. Hertz teori
I Hertz modell blir det antatt en elliptisk kontaktflate; dvs. ikke rektangulært som i den forenklede modell. Den maksimale spenning i middelpunktet i kontaktellipsen uttrykkes ved følgende formel:
N er normalkraften; på rett strekning er det imidlertid tillatt å benytte hjulkraften Q uten at feilberegningen blir for stor da kontaktpunktsvinkelen normalt er liten.
Trykkfordelingen i den elliptiske kontaktflate er vist i figur 11.3.
Formelen vil føre til høyere kontaktspenninger enn de som beregnes med den simplifiserte metode. Formelen gir imidlertid et nøyaktigere resultat og er derfor mer relevant. Det er av den grunn nødvendig å etablere et annet regime for vurdering. Dette skjer ved anvendelse av Shakedown diagrammet.
I figur 11.4 er dette diagrammet anskueliggjort:
Abscissen i Shakedown diagrammet viser friksjonskoeffisienten μ; dvs. forholdet mellom resulterende tangential krypkraft og normalkraft. For rett strekning kan med tilstrekkelig nøyaktighet vertikalkraften benyttes (i stedet for normalkraften). For tangentialkraften legges til grunn at det handler om ren glidning av hjulet i skinnens lengderetning med en konstant friksjonskoeffisient μ. Lav friksjonskoeffisient indikerer våte eller smurte skinner og høy friksjonskoeffisient beskriver tørre skinner.
Ordinaten indikerer kvotienten flatetrykket p0 i kontaktflaten i forhold til kapasitet på skjær ke i stålet i skinnehodet.
Flyt under overflaten i skinnehodet (eller i det indre av skinnehodet) vil inntreffe ved vedvarende høye belastninger for µ ≤ 0,30. For tørre skinner (µ > 0,30) opptrer flyt i overflaten av skinnehodet ved gjentatte høye belastninger.
Det skilles mellom punktkontakt og linjekontakt.
I ovennevnte diagram benyttes forholdet mellom p0 og ke. Utelatt i vurderingen så langt er skinnestålets kvalitet og dermed kapasitet for ke. Som allerede nevn kan følgende verdier benyttes:
| Stålkvalitet p0 (N/mm2) | 700 | 900 | 1100 |
| Skjærkapasitet ke (N/mm2) | 205 | 260 | 320 |
I et dokument for Rail Safety & Standards Board
“Research Programme
Engineering
Management and understanding of
Rolling contact fatigue
Literature Review”
peker artikkelforfatterne (blant annet professor A. Kapoor fra Newcastle University) på det faktum at på overflaten av skinnehodet, så blir svært ofte belastningen vesentlig høyere enn den nominelle Hertz belastning (ifølge denne teori) og at riss dermed vil oppstå. I samme artikkel blir vist en utgave av Shakedown diagrammet som er gjengitt under. Den heltrukne linjen er Shakedown diagram for normale skinner. Det er synlig at kontaktspenningene vurderes å kunne anta grenseverdier opp mot 1000 N/mm2 for en friksjonskoeffisient μ på inntil 0,15 for så å avta med høyere koeffisienter (mer tørre skinner).
En skinne i normal kvalitet antas å ha strekkfasthet på 900 N/mm2, dvs. kvalitet R 260 Mn.
For μ = 0,30 blir antatt en grenseverdi for kontaktspenning lik ca. 800 N/mm2. Ved anvendelse av samme forholdstall n = 3,76 mellom anbefalt maksimal skjærkapasitet og kontaktspenning avledet av normalkraften, gir dette en skjærkapasitet på ca. 230 N/mm2.
Ikke elliptiske kontaktflater i hjul/skinne kontaktmekanikken
Det er dokumentert at det for visse geometrier i hjul/skinne kontaktmekanikken forekommer ikke elliptiske kontaktflater. Aspektet gjelder for eksempel for kombinasjonen av nominelt hjulprofil S1002 og nominelt profil i skinnehode til skinne 60E1 i området for løpeflaten på skinnehodet.
For skinne 60E1 endrer krumningen i profilradiene på skinnehodet seg abrupt på en slik måte at det oppstår ikke elliptiske kontaktflater. Det er utgitt presentasjoner mht. dette teamet, men det vil føre for langt å gå inn på aspektet her.
Forutsetninger iht. Hertz teori
Det skal i det etterfølgende gjøres noen simplifiserte beregninger av kontaktflate mellom hjul og skinne iht. teorier til Hertz. Det antas dermed en elliptisk kontaktflate ved framføring av materiellet på rett linje eller i kurver med store radier. Ellipsens store halvakse er i tverretningen av skinneprofilet og den lille halvakse er i skinnens lengderetning, dvs. i kjøreretningen til materiellet. Videre antas en elliptisk fordeling av kontaktspenningene over den elliptiske flate.
Normalkraften må først beregnes. På rett linje for begge skinner og i innerstreng i sirkelkurver er normalkraften tilnærmet lik den vertikale hjulkraft og kan uttrykkes ved:
Her er γi kontaktpunktsvinkelen
Normalkraften i ytterstreng i kurver er definert i figur 11.6.
Følgende gjelder for vektorsummen mht. Qy:
Videre gjelder (definisjon av positiv retning for kryp):
Dermed blir:
Med utgangspunkt i kjent vertikalkraft Qy, kjent kontaktpunktsvinkel γy og kjent friksjonskoeffisient μ kan normalkraften Ny for ytterstreng i kurver med små radier beregnes.
Det gjøres oppmerksom på at ovennevnte betraktninger er utført noe forenklet.
Med fastsettelse av normalkraften er grunnlaget lagt for beregning av kontaktarealet og spenningene i kontaktflaten for skinner i kurver; i ovennevnte tilfelle ytterskinner.
I kurver med små radier må kontaktflaten beskrives ved hulkilen til hjulbanen til hjulet og ved kjørekanten til skinnehodet til ytre skinne. Dette forholdet gjør beregningsprosedyrene vesentlig mer omfattende og vil ikke bli gjengitt her.
Etterfølgende betraktninger gjelder i kontaktpunktet hjul – skinne for rett linje og i kurver med store radier under forutsetning av små tøyninger i sporkonstruksjonen og vil bli benyttet i forbindelse med beregninger av kontaktspenninger.
Iht. Hertz teori vil den elastiske deformasjon av stålet til hjul og skinne skape en elliptisk kontaktflate. Dimensjonene på kontaktellipsen bestemmes av normalkraften og forholdet mellom aksene til ellipsen bestemmes av kurvaturen til hjulbaneprofilet og profilet på skinnehodet.
Krumningsradier til skinnehodet i tverretningen og i lengderetningen samt for hjulets hjulbane er retningsgivende. Det vises til figur 11.7. Den elliptiske flate er vist i figur 11.8.
Mht. beregningene må elastisitetsmodulen E og tverrkontraksjonstallet (Poisson’ ratio) for hjul og skinne tas i betraktning. Normalkraften er N og i samsvar med Hertz teori kan ellipsens halvakser a og b beregnes. Dette er vist i det etterfølgende.
Funksjonene A og B er gitt ved:
rηR er radius til skinnehodet i tverretningen og rη er radius til hjulbanen lateralt.
Termen rξR er radius til skinnen i lengderetningen og rξ er hjulets radius.
Med tilstrekkelig nøyaktighet kan rξR≈∞ og rξ≈r0.
m and n er faktorer som må beregnes med utgangspunkt i funksjonen:
Verdiene for m og n er gitt i tabeller som funksjon av Θ (0).
Arealet av den elliptiske kontaktflate kan dermed uttrykkes:
Kontakttrykket uttrykt ved normalkraften i kontaktflaten er gitt ved følgende ligning:
Dersom fordelingen av kontakttrykket antas å være ellipsoid, kan det maksimale trykket i origo til den elliptiske kontaktflate beregnes:
Følgende relasjoner kan utledes:
a er proporsjonal til N1/3.
b er proporsjonal til N1/3.
Ae er proporsjonal til N2/3.
σζ,max er proporsjonal til N1/3.
Ovennevnte relasjoner er en meget viktig erkjennelse. Hypotesen innebærer at dersom normalkraften N dobles til 2 N, så øker den maksimale kontaktspenning i origo til ellipseflaten med faktor 21/3≈1,26. Dersom konsekvensene av en økning i aksellasten skal vurderes, må dette faktum tas med i betraktningene. Noen relasjoner som er aktuell for El 18, er gitt i tabell under:
| Lokomotiv | El 17 | El 18 | Fiktiv El |
|---|---|---|---|
| Akselkraft (kN) | 160 | 213 | 320 |
| Økning i akselkraft | 1,000 | 1,33 | 2,00 |
| Økning i spenning σξ, max | 1,00 | 1,10 | 1,26
|
Det er meget viktig å være klar over at kontaktspenningene vil øke med 10 % ved økning av akselkraft fra 160 kN til 213 kN, dvs. en økning på 33 % i forbindelse med overgang fra El 17 til El 18.
Den elliptiske kontaktflate får en ellipsoide fordeling av trykket. Dette er vist i figur 11.9.
Ved prosedyrer kan halvaksene beregnes med utgangspunkt i hjulbanens og skinnehodets kurvaturer i tverretning og i lengderetning samt normalkraften og dermed fastsettes belastningsflaten.
Her betyr:
N Normalkraft (som er forskjellig fra hjulkraften Q)
Ae Den elliptiske kontaktflate
a, b Ellipsens halvakser
ξ, η Ellipsens koordinatretninger (i lengderetning og i tverretning av skinneprofilet)
Beregning, forenklet metode
Ved denne metoden beregnes det midlere flatetrykket qmean. Det antas rett linje og kurver med store radier. Det benyttes hjulkraft Q (ikke kvasistatisk hjulkraft). I kurver med små radier blir de opptredende belastninger ca. 1,15 ganger større på grunn av et beskjedent kvasistatisk tillegg.
Det forutsettes en hjulradius lik 550 mm for lokomotivet (traksjonsmateriell).
Det oppstår en tilleggsbelastning på skinnehodet i strekninger med bremsing og traksjon. I tillegg inntreffer tverrkryp i kurver med små radier. Begge aspektene gjelder for Flåmsbana. Imidlertid vil disse parametere ikke føre til større opptredende belastninger i en dybde av 4 – 6 mm under skinnehodet relatert til hovedspenningene. Gjennom opptreden av de langsgående kreftene og tverrkreftene avtar ikke skjærspenningene raskt som er tilfelle ved ren rulling. Kreftene i begge retninger forårsaket ved bremsing og traksjon fører derimot til mer slitasje i berøringspunktet hjul / skinne samt til materialflyt i randsonen til skinnehodet. Forholdet skal imidlertid ikke føre til hurtigere hendelse av materialflyt i skinnehodet (shelling) i en dybde av 4 – 6 mm.
Nedenstående beregninger gjennomføres derfor uten innflytelse av traksjon og bremsing da det er de vertikale spenninger mot skinnehodet som er av interesse.
Tilfelle I.2.1 Dimensjonering for aksellast lik 21,3 tonn; hjullast lik 10,65 tonn (hjulkraft lik 106,50 kN) for skinnekvalitet R 200 Mn:
Opptredende maksimal skjærkapasitet basert på qMEAN (ikke qMAX):
Anbefalt maksimal verdi for tillatt skjærkapasitet for skinnestål i kvalitet 700 basert på qMEAN:
Kontroll av tillatt anbefalt maksimal verdi for hjulkraft for skinnestål i kvalitet 900 basert på qMEAN med sikkerhetsfaktor υ = 1,10:
Kontroll av tillatt anbefalt minste hjulradius for skinnestål i kvalitet 700 basert på qMEAN
Belastningen på skinnehodet i kontaktflaten blir mindre enn anbefalte verdier.
I kurvene opptrer et kvasistatisk tillegg som er fastsatt til 8,50 kN. Det kvasistatiske tillegget < 10 % av nominell hjulkraft og dermed beskjedent. I tillegg vil kontaktflaten være mer utpreget elliptisk med ellipsoid spenningsfordeling. Spenningen qmax i middelpunktet av ellipsen vurderes til å være 1,15 · qMEAN . Antakelsen betraktes å være konservativ.
Dette gir:
Fiktiv hjulkraft:
Nødvendig hjulradius:
Det kreves dermed en relativt stor hjuldiameter. Spørsmålet er hvorvidt relevant hypotesen er. Dette vil bli belyst senere.
Tilfelle I.2.2 Dimensjonering for aksellast lik 21,3 tonn; hjullast lik 10,65 tonn (hjulkraft lik 106,50 kN) for skinnekvalitet R 260 Mn
Anbefalt maksimal verdi for tillatt skjærkapasitet for skinnestål i kvalitet 900 basert på qMEAN :
Kontroll av tillatt anbefalt maksimal verdi for hjulkraft for skinnestål i kvalitet 900 basert på qMEAN med sikkerhetsfaktor υ = 1,10:
Kontroll av tillatt anbefalt minste hjulradius for skinnestål i kvalitet 900 basert på qMEAN :
I kurvene opptrer et kvasistatisk tillegg som er fastsatt til 8,50 kN. Det kvasistatiske tillegget < 10 % av nominell hjulkraft og dermed beskjedent. I tillegg vil kontaktflaten være elliptisk med ellipsoid spenningsfordeling. Spenningen qmax i middelpunktet av ellipsen vurderes til å være 1,15 · qMEAN.
Dette gir:
Fiktiv hjulkraft:
Nødvendig hjulradius:
Det framgår at skinnekvalitet R 260 Mn (900 N/mm2) er greit.
Tilfelle I.2.3 Dimensjonering for aksellast lik 21,3 tonn; hjullast lik 10,65 tonn (hjulkraft lik 106,50 kN) for skinnekvalitet R350 HT
Anbefalt maksimal verdi for tillatt skjærkapasitet for skinnestål i kvalitet 900 basert på qMEAN:
Kontroll av tillatt anbefalt maksimal verdi for hjulkraft for skinnestål i kvalitet 1100 basert på qMEAN med sikkerhetsfaktor υ = 1,10:
Kontroll av tillatt anbefalt minste hjulradius for skinnestål i kvalitet 900 basert på qMEAN:
I kurvene opptrer et kvasistatisk tillegg som er fastsatt til 8,50 kN. Det kvasistatiske tillegget < 10 % av nominell hjulkraft og dermed beskjedent. I tillegg vil kontaktflaten være elliptisk med ellipsoid spenningsfordeling. Spenningen qmax i middelpunktet av ellipsen vurderes til å være 1,15 · qMEAN.
Dette gir:
Fiktiv hjulkraft:
Nødvendig hjulradius:
Det framgår at skinnekvalitet R 350 HT er greit.
Sammenstilling av beregningene er gitt i tabell.
| akselkraft: 213 kN; hjulkraft = 106,50 kN; hjulradius = 550 mm; rett linje og store radier beregningene er utført i formler som baserer seg på midlere trykk qMEAN | |||||
|---|---|---|---|---|---|
| Stålkvalitet
|
(N/mm2)
|
700 | 900 | 1100 | Kommentarer |
| Tillatt skjærkapasitet | τtillatt (N/mm2) | 205 | 260 | 320 | |
| Beregnet kontaktspenning | qMEAN (N/mm2) | 605 | 605 | 605 | |
| Beregnet skjærspenning | τmax (N/mm2) | 180 | 180 | 180 | |
| Tillatt største hjulkraft | Q (kN) | 117,10 | 193,60 | 290,00 | |
| Tillatt minste hjulradius;
rett strekning |
r (mm) | 500 | 303,30 | 202,40 | Hjulradius for stålkvalitet 900 og 1100 ikke realistisk |
| Tillatt minste hjulradius;
små kurver |
r + α · r (mm) | 662 | 400 | 268 | Hjulradius for stålkvalitet 1100 ikke realistisk |
Under hensyntagen til ovennevnte er nominell hjuldiameter r = 1125 mm for belastning på skinner i stålkvalitet R260 Mn med strekkfasthet 900 N/mm2 og i stålkvalitet R350 HT med strekkfasthet 1100 N/mm2 greit.
For skinner i stålkvalitet R200 behøves ideelt en hjuldiameter på over 660 mm. I det etterfølgende vil aspektet bli belyst og vurdert grundigere.
Beregning iht. Hertz teori
Det gjennomføres beregninger med tverrsnittsprofil for skinnehodet i uslitt tilstand. Da beregningene utføres på rett strekning, anvendes radius i løpebaneområdet for skinneprofilet; dvs. rƞ R = 300 mm = 0,30 m. Profilet er vist i figur 11.10 under. Skinneradius i lengderetningen er ∞.
Hjulradius antas å være rξ = 0,55 m: dvs. hjuldiameter er 1,10 m.
For profilet til hjulbanen antas 3 forskjellige kurver; rƞ = 0,36 m; rƞ = 0,50 m; rƞ = ∞ m.
Belastningene beregnes for en statisk lasttilstand; N = 106,50.
Det oppstår en tilleggsbelastning på skinnehodet i strekninger med bremsing og traksjon. I tillegg inntreffer tverrkryp i kurver med små radier. Begge aspektene gjelder for Flåmsbana. Imidlertid vil disse parametere ikke føre til større opptredende belastninger i en dybde av 4 – 6 mm under skinnehodet relatert til hovedspenningene. Gjennom opptreden av de langsgående kreftene og tverrkreftene avtar ikke skjærspenningene raskt som er tilfelle ved ren rulling. Kreftene i begge retninger forårsaket ved bremsing og traksjon fører derimot til mer slitasje i berøringspunktet hjul / skinne samt til materialflyt i randsonen til skinnehodet. Forholdet skal imidlertid ikke føre til hurtigere hendelse av materialflyt i skinnehodet (shelling) i en dybde av 4 – 6 mm.
Nedenstående beregninger gjennomføres derfor uten innflytelse av traksjon og bremsing da det er de vertikale spenninger mot skinnehodet som er av interesse.
Tilfelle II.2.4 Hertz; tverrprofil i hjulbane rƞ = 0,36 m
Normalkraft på skinne for rett strekning: N = 106,50 kN
Tverrkontraksjonstallet (eller Poissons forholdstall): υ = 0,30
Stålets elastisitetsmodul: E = 2,10 · 105 N/mm2
Kurven til skinne i horisontal retning (tverrprofil): rƞ R = 0,30 m
Kurven til skinnehodet i langsgående retning: rξ R = ∞
Kurven til hjulbane i hjulet i tverretning: rƞ = 0,36 m
Hjulradius: rξ = 0,55 m
Funksjonene A og B er gitt ved:
rηR er radius til skinnehodet i tverretningen og r er radius til hjulbanen tverretning.
m = 0,705 og n = 1,505
N = 106,50 kN
Termene a og b beregnes. Dette er vist i det etterfølgende for hjulkraft lik 106,50 kN.
Arealet av den elliptiske kontaktflate blir:
Termen a er halvakse i skinnehodets lengderetning og b er halvakse i skinnehodets tverretning. Aspektet betyr at den elliptiske flate er langstrakt i skinnehodets tverretning.
Maksimal trykkspenning i kontaktflaten:
For skinne med stålkvalitet 700 N/mm2 er kapasitet på skjær τtillatt = 205 N/mm2.
I Shakedown diagrammet dannes forholdet:
For skinne med stålkvalitet 900 N/mm2 er kapasitet på skjær τtillatt = 260 N/mm2.
I Shakedown diagrammet dannes forholdet:
For skinne med stålkvalitet 1100 N/mm2 er kapasitet på skjær τtillatt = 320 N/mm2.
I Shakedown diagrammet dannes forholdet:
Tilfelle II.2.5 Hertz; tverrprofil i hjulbane rƞ = 0,50 m
Normalkraft på skinne for rett strekning: N = 106,50 kN
Tverrkontraksjonstallet (eller Poissons forholdstall): υ = 0,30
Stålets elastisitetsmodul: E = 2,15 · 105 N/mm2
Kurven til skinne i horisontal retning (tverrprofil): rƞ R = 0,30 m
Kurven til skinnehodet i langsgående retning: rξ R = ∞
Kurven til hjulbane i hjulet i tverretning: rƞ = 0,50 m
Hjulradius: rξ = 0,55 m
Funksjonene A og B er gitt ved:
rηR er radius til skinnehodet i tverretningen og rη er radius til hjulbanen lateralt.
m = 0,910 og n = 1,100
N = 106,50 kN
Termene a og b beregnes. Dette er vist i det etterfølgende for hjulkraft lik 106,50kN.
Arealet av den elliptiske kontaktflate blir:
Termen a er halvakse i skinnehodets tverrprofil og b er halvakse i skinnehodets lengderetning. Aspektet betyr at den elliptiske kontaktflate er langstrakt i skinnehodets tverretning.
Maksimal trykkspenning i kontaktflaten:
For skinne med stålkvalitet 700 N/mm2 er kapasitet på skjær τtillatt = 205 N/mm2.
I Shakedown diagrammet dannes forholdet:
For skinne med stålkvalitet 900 N/mm2 er kapasitet på skjær τtillatt = 260 N/mm2.
I Shakedown diagrammet dannes forholdet:
For skinne med stålkvalitet 1100 N/mm2 er kapasitet på skjær τtillatt = 320 N/mm2.
I Shakedown diagrammet dannes forholdet:
Tilfelle II.2.6 Hertz; tverrprofil i hjulbane rƞ = ∞ m
Normalkraft på skinne for rett strekning: N = 106,50 kN
Tverrkontraksjonstallet (eller Poissons forholdstall): υ = 0,30
Stålets elastisitetsmodul: E = 2,15 · 105 N/mm2
Kurven til skinne i horisontal retning (tverrprofil): rƞ R = 0,30 m
Kurven til skinnehodet i langsgående retning: rξ R = ∞
Kurven til hjulbane i hjulet i tverretning: rƞ = ∞
Hjulradius: rξ = 0,55 m
Funksjonene A og B er gitt ved:
rηR er radius til skinnehodet i tverretningen og rη er radius til hjulbanen lateralt.
m = 1,450 og n = 0,715
N = 106,50 kN
Termene a og b beregnes. Dette er vist i det etterfølgende for hjulkraft lik 103,50 kN.
Arealet av den elliptiske kontaktflate blir:
Termen a er halvakse i skinnehodets tverrprofil og b er halvakse i skinnehodets lengderetning. Aspektet betyr at i dette tilfellet så er den elliptiske kontaktflate langstrakt i skinnehodets lengderetning.
Maksimal trykkspenning i kontaktflaten:
For skinne med stålkvalitet 700 N/mm2 er kapasitet på skjær τtillatt = 205 N/mm2.
I Shakedown diagrammet dannes forholdet:
For skinne med stålkvalitet 900 N/mm2 er kapasitet på skjær τtillatt = 260 N/mm2.
I Shakedown diagrammet dannes forholdet:
For skinne med stålkvalitet 1100 N/mm2 er kapasitet på skjær τtillatt = 320 N/mm2.
I Shakedown diagrammet dannes forholdet:
For tangentbelastningen blir det lagt til grunn ren glidning i skinnens lengderetning og tverretning med en konstant friksjonskoeffisient μ. Abscissen beskriver i denne sammenheng den resulterende friksjonskoeffisient som uttrykkes ved:
Beregningen er utført for en kontaktspenning på spor på rett linje. Dermed kan til en viss grad grafene for punktkontakt; dvs. graf C for øvre innspillgrense. Inntil en friksjonskoeffisient μ = 0,30 er kapasiteten for skjærspenningen i orden. For høyere friksjonskoeffisient μ; dvs. tørre skinner vil det bli slitasje i overflaten på skinnehodet.
Beregningene er sammen fattet i tabell under.
| Hjulbane
tverretning |
Hjul
radius |
Skinne
tverretning |
Skinne
lengde |
Kontakt
flate |
Trykk
spenning |
Skjær
kapasit |
Forhold | ||
|---|---|---|---|---|---|---|---|---|---|
| Stål
kvalitet (N/mm2) |
Hjul
kraft (kN) |
rƞ
(m) |
rξ
(m) |
rƞ R
(m) |
rξ R
(m) |
Ae
(mm2) |
σξ maks
(mm2) |
τtillatt
(mm2) |
|
| 700 | 106 | 0,36 | 0,55 | 0,30 | ∞ | 223 | 716 | 205 | 3,50 |
| 0,50
|
182 | 878 | 4,28 | ||||||
| ∞
|
188 | 850 | 4,14 | ||||||
| 900 | 106 | 0,36 | 0,55 | 0,30 | ∞ | 223 | 716 | 260 | 2,76 |
| 0,50
|
182 | 878 | 3,38 | ||||||
| ∞
|
188 | 850 | 3,27 | ||||||
| 1100 | 106 | 0,36 | 0,55 | 0,30 | ∞ | 223 | 716 | 320 | 2,24 |
| 0,50
|
182 | 878 | 2,74 | ||||||
| ∞
|
188 | 850 | 2,66 |
Konklusjoner
Det er utført beregninger av belastning på hjul/skinne kontaktflate og på skjær etter anerkjente metoder under antakelse om elliptisk kontaktflate for rett strekning og i kurver med store radier.
Beregningene gjelder ikke for kurver med små radier. Det er imidlertid gjort en antakelse om høyere belastning i skinnehodet i kontaktflaten og på skjær med en faktor lik 1,15.
Det er lagt til grunn en skinne med kurveradius i tverrprofilet på 0,30 m i løpebaneområdet. Videre er det antatt 3 ulike profil i løpebaneområdet for hjulprofilet:
rƞ = 0,36 m; 0,50 m; ∞ m
Det er tatt utgangspunkt i hjuldiameter på 1100 mm; dvs. hjulradius lik 550 mm. Krumningsradius i lengderetningen på skinnene er ∞.
Ikke overraskende oppstår de minste belastningene hvor tverrprofilene for skinnehodet og hjulbane tilpasses hverandre ved at belastningsbåndet blir bredere. Den største belastningen oppstår ved et teoretisk konisk hjulbaneprofil; dvs. for rƞ = ∞ m.
Det er å anta at det dynamiske gangløpet i spordynamikken fungerer best ved et konisk hjulprofil. Det er i denne sammenheng ikke tatt stilling til løpedynamikken.
En sammenstilling for oversikt er gitt i tabell 9.6. Tabellen er vist sammen med Shakedown diagrammet for oversiktens skyld.
Det er vist at et hjulbaneprofil med radius rƞ = 0,36 m gir størst kontaktflate og dermed minst belastning i kontaktforholdet hjul/skinne.
Et hjulbaneprofil med radius rƞ = 0,50 m gir betydelig mindre kontaktflate og dermed betydelig større belastning i kontaktforholdet hjul/skinne enn med radius rƞ = 0,36 m.
Det samme forholdet gjør seg gjeldende for rƞ = ∞.
Skinnekvalitet R 200 Mn (strekkfasthet 700 N/mm2)
På rett strekning og i kurver med store radier for skinnekvalitet R 200 Mn med bruddfasthet 700 N/mm2 anses Shakedown forholdet lik 3,50 for et hjulbaneprofil med rƞ = 0,36 m å være helt greit for fuktige til halvtørre skinner med friksjonskoeffisient inntil μ = 0,35. For tørrere skinner må forventes materialflyt på skinnehodets overflate.
For hjulbaneprofil med rƞ > 0,36 m blir Shakedown forholdet større. For fuktige skinner med friksjonskoeffisient inntil 0,30 er forholdet ikke kritisk. For høyere friksjonskoeffisient μ, dvs. tørrere skinner kan materialflyt i overflaten av skinnehodet forventes.
I kurver med små radier vil de samme forholdene gjøre seg gjeldende. Shakedown forholdet vil for rƞ anta en verdi opp mot 4,0. Aspektet medfører at for rƞ = 0,36 m bør μ < 0,30 for å hindre materialflyt. Skinnene må dermed være litt fuktige. For hjulbaneprofil med større radier antar kontaktspenningene høye verdier i kurver og det vil uansett være fare for opptreden av materialflyt i overflaten av skinnehodet for tørre skinner og i det indre av skinnehodet for bløtere skinner.
Skinnekvalitet R 260 Mn (strekkfasthet 900 N/mm2)
Iht. resultat av beregningene vist i tabell for rett linje forventes normalt slitasjeforløp mht. hastighet for skinner på rett strekning og i kurver med små radier. Et hjulbaneprofil med rƞ = 0,36 m er allikevel bedre enn hjulbaneprofil med større radier.
Skinnekvalitet R 350 HT (strekkfasthet 1100 N/mm2)
Det gjelder de samme vurderinger som foran. Hastigheten i slitasjeforløpet forventes å være langsommere.
Endring i spenningene som funksjon av endring av aksellast
Det er vist i det foregående vist endringer av spenning i kontaktpunktet hjul/skinne som følge av endring av aksellast. Det vises til tabell.
| Lokomotiv | El 17 | El 18 | Fiktiv El |
|---|---|---|---|
| Akselkraft (kN) | 160 | 213 | 320 |
| Økning i akselkraft | 1,000 | 1,33 | 2,00 |
| Økning i spenning σξ, max | 1,00 | 1,10 | 1,26
|
Ved en økning av akselkraft fra 160 kN for El 17 til en akselkraft på 213 kN for El 18 blir det en økning i spenningene på 10 %. Akselkraftøkningen er på 33 %.
Økningen antas ikke å være dramatisk.
Ifølge BANEDATA INNSYN Overbygning Skinner finnes ca. 10 000 m skinner i kvalitet R 200 Mn (700 N/mm2). Oversikten viser at disse er lagt i sporet omkring 1965. Skinnene har dermed hatt en liggetid i sporet på ca. 50 år. Dette må bety at skinnene har klart seg relativt bra.
En økning i spenningene på 10 % på grunn av økning av akselkraften på lokomotivene med henholdsvis 4 og 8 aksler i togstammen vil naturlig nok fremskynde slitasje; men det forventes ingen dramatisk økning i hastigheten.
Det er tatt utgangspunkt i radier for hjulbanene rƞ = 0,36 m, 0,50 m og ∞. Det kan synes å være noe inkonsekvent å anta radiene 0,50 m og ∞ m. Hjulbaneprofilet vil tilpasse seg skinneprofilet og en radius lik 0,36 m vil av naturlige årsaker opptre mest. Det eksisterer derfor et relativt bredt kontaktbånd i kontaktflaten hjul /skinne som bidrar til mindre stressende spenninger.
El 18 har nominell hjuldiameter lik 1125 mm. El 17 har nominell hjuldiameter 1100 mm. Forskjellen er ubetydelig for den økning i lasten som er definert.
Bremsekrefter
Det beregnes krefter som oppstår i forbindelse med bremsing av toget på et lasket spor med fall i en gradient lik 55 mm/m. Det vurderes 2 tilfeller:
- Nødvendig bremsekraft for opprettholdelse av konstant hastighet
- Nødvendig bremsekraft for nedbremsing til full stopp
Det vurderes tilstand med hensyn til adhesjonen:
- αB i linje i fall med gradient s (mm/m)
Det betraktes et bremset tog med eventuelle blokkbremser/bremseskiver og med bruk av El brems med oppgitt verdi (150,00 kN).
Flåmsbana er meget kurverik og derfor oppstår gangdynamisk motstand. I tillegg vil også inntreffe luftmotstand. I det etterfølgende vil disse aspektene bli neglisjert.
Bremsekraft ved El – brems for konstant hastighet
Det gjennomføres en beregning for å undersøke om kapasiteten ved El brems er tilstrekkelig. Det legges til grunn at prinsippet gir bremsede moment for hjulakslene som igjen indikerer bremsekrefter mellom hjul og skinner. Aspektet medfører at adhesjonen får betydning.
Det må tas hensyn til trykkraften FX mellom traksjonsenheten og vognene. Gradienten vil være s = 55 mm/m.
Retardasjonen rX for opprettholdelse av konstant hastighet v når lokomotivet skal bremse alene (som løslok):
Nødvendig adhesjon αB beregnes (for løslok):
Trykkraft FX mellom bremset lokomotiv og vogner beregnes. For et lokomotiv benyttes 3 vogner. Det legges til grunn en masse for hver vogn mO = 47.000 kg.
Den ekvivalente masse for vognene beregnes med en dynamisk stivhetsfaktor κO = 1,10. Den ekvivalente masse blir:
For 3 vogner blir den ekvivalente masse:
Trykkraft mellom 3 vogner og bremset lokomotiv hvor kurve- og luftmotstand neglisjeres:
Bremset kraft for det bremsede lokomotiv for opprettholdelse av konstant hastighet med 3 vogner ubremset:
Kapasitet for El brems er 150 kN.
Adhesjonen for det bremsede lokomotivet blir dermed:
Det er synlig at behovet for adhesjon øker fra 0,055 for lokomotivet alene til 0,155 når all bremsing skal foregå hos lokomotivet. Det er klart at αB = 0,155 er absolutt øvre grense for adhesjon på Flåmsbana. På grunn av driftsmessige årsaker med bl. annet fuktige skinner bør αB ha lavere verdi.
Kapasitet for El brems er angitt til 150 kN. Utnyttelse av denne bremsekraften gir:
Adhesjonen blir da:
Denne verdien vil bli benyttet for å vurdere sannsynlighet for skinnevandring i lasket spor. Det er synlig at ved bremsing ned til full stopp kreves i tillegg mekanisk brems som i dette tilfellet er en pneumatisk brems.
Vurdering av skinnevandring ved bremsing for opprettholdelse av konstant hastighet
Med grunnlag i en El brems på 150 kN og tilhørende nødvendig adhesjonskoeffisient αB = 0,165 skal vurderes sannsynlighet for skinnevandring ved framføring i konstant hastighet i lasket spor.
Med αB = 0,165 er skinnene halvfuktige/halvtørre.
Langsgående skinnespenninger på grunn av temperaturendringer vurderes ikke da sporet er lasket.
En modell for vurdering er vist i figur 12.1.
Det defineres følgende parametere:
Hjulkraft: Q (kN)
Adhesjon ved bremsing: αB
Fordeling av hjulkraft over sville: Q1; Q2; Q3 )kN)
Friksjonskoeffisient mellom skinne og sville: μM
Friksjonskoeffisient mellom sville og pukk: μ
Vertikalkraft mot pukk: N (kN)
Motstandskraft i pukk mot sville: H (kN); ikke angitt, men inntegnet
Hjulkraft er satt til Q = 115 kN; det er da tatt hensyn til kvasistatisk tillegg og til skjevlast. Adhesjonskoeffisienten er satt til 0,165; dvs. at kapasitet på El brems er utnyttet.
Adhesjonskraft mot topp skinne fra hvert hjul:
Klemkraften i befestigelsen bør ha så høy kapasitet at klemkraften må bidra til at skinnen ikke beveger seg i forhold til svillen. Det blir tatt utgangspunkt i en klemkraft i befestigelsen på 6 kN. Det finnes en del HeyBack befestigelse i sporet. Videre er sporet lasket slik at skinnene vil utvide seg ved oppvarming og trekke seg sammen ved lavere temperaturer. Det opptrer dermed en bevegelse i skinnene inntil gapet mellom 2 skinneender blir lukket ved oppvarming. Skinnene vil trekke seg sammen ved overgang til kaldere temperaturer. Kravet til klemkraft er av den grunn lavere enn ved helsveist spor. Skinnene er allikevel bundet sammen ved laskene med bolter.
På grunn av svilleavstand og normal fordeling av hjulkraften på elastisk spor forutsettes at 3 sviller aktiviseres for å ta opp adhesjonen. Dette gir 6 fjærer med samlet klemkraft:
Det må erkjennes at fjærene i befestigelsen i midtre sville får større belastninger enn nabofjærene; men til gjengjeld er vertikalkraften større slik at friksjonskoeffisienten får større betydning.
På grunn av type befestigelse antas ingen friksjon mellom skinne og mellomlegg/sville som kan gi ytterligere bistand mot bevegelse av skinne i forhold til sville.
På grunn av elastisiteten i sporet vil hjulkraften fordele seg over 3 sviller:
Det benyttes tresviller med vekt på 70 kg. Den vertikale tilleggskraft fra hver sville:
Horisontal motstandskraft i pukken for bevegelse av sville (halv lengde):
For 3 sviller:
Samlet vertikalkraft:
Skinnevekten er ikke tatt med.
Den samlede horisontale kraft i lengderetningen fra adhesjonen er:
Nødvendig friksjonskoeffisient mellom 3 sviller og pukklaget i ballastsengen for å hindre svillevandring med skinner:
Denne friksjonskoeffisienten er meget lav og vil normalt kunne oppfylles.
Det skulle således ikke være fare for skinnevandring i bremset tilstand i et lasket spor.
Nødvendig kraft for nedbremsing til full stopp
Ved nedbremsing til full stopp på linje i fall med gradient s (mm/m) beregnes den samlede retardasjon for et tog hvor adhesjonskoeffisienten utnyttes ved pneumatisk brems:
Det legges til grunn en adhesjonskoeffisient αB = 0,135; dvs. halvfuktige/halvtørre skinner. Nødvendig bremsekraft for 3 vogner mot skinne hvor kurvemotstand neglisjeres, beregnes.
Det er til sammen 24 hjul for de 3 vognene. Dette gir en gjennomsnittlig bremsekraft for hvert hjul mot skinner:
Nødvendig bremsekraft for lokomotivet mot skinne hvor kurvemotstand neglisjeres, beregnes:
Det er til sammen 8 hjul i lokomotivet. Dette gir en gjennomsnittlig bremsekraft for hvert hjul mot skinner:
Ekvivalent masse eller massetreghetsmoment for alle 3 vogner:
Ekvivalent masse eller massetreghetsmoment for lokomotivet:
For vognene blir det bremsede moment for et hjulpar:
Tilsvarende for lokomotivet:
Det tas ikke stilling til hvilke type bremser som benyttes; blokkbremser, bremseskiver eller annet. Det legges til grunn blokkbremser i de etterfølgende beregninger. Ved lik bremsing på alle hjulpar blir bremsekraften mellom blokkbrems og hjul for vogner:
For lokomotiv gjelder:
For en hastighet V0 = 30 km/h (eller v0 = 8,33 m/s) beregnes bremsetiden til (rX = 0,79 m/s2):
Bremselengde beregnes til:
Det er opplyst at pneumatisk brems og El brems i kombinasjon kan oppnå en retardasjon på opp mot rX = 1,84 m/s2. Da begge typene er å betrakte som adhesjonsavhengige bremser, må skinnene være relativt tørre eller det kan oppstå glidning inntil grense for glidevern. Det vurderes at det inntreffer bare unntaksvis.
Vurdering av skinnevandring ved nedbremsing til full stopp
På grunn av spredning av bremsekraften på alle hjul forventes ikke skinnevandring eller bare en beskjeden skinnevandring
Traksjon
Det skal utføres noen enkle beregninger for traksjonskrefter utøvet av lokomotivet i akselerasjonsfasen og for opprettholdelse av konstant hastighet i stigning. Det blir antatt en akselkraft fra lokomotivet lik 213 kN og en akselkraft fra vogner lik 117,50 kN. Det legges til grunn at et lokomotiv skal trekke 3 vogner.
Flåmsbana har en høy gradient for stigning og er samtidig meget kurverik med små radier (R = 150 m). Dermed utøves det stor motstand for framføring. Sporet har en lasket konstruksjon (ikke helsveist).
De enkelte parametere for motstand er:
- mekanisk gangmotstand DM som er størst ved igangsetting (lavere når toget er i bevegelse)
- kurvemotstand DK
- luftmotstand DL som settes sammen av flere faktorer og er en del av grunnmotstanden
- stigningsmotstand DS
Mekanisk gangmotstand
Litteraturen angir formler for beregning av mekanisk gangmotstand. Med en beskjeden masse fra lokomotiv og vogner kombinert med lav hastighet vil denne motstanden være lav.
Samlet masse:
Hastigheten er v = 8,33 m/s.
Det utføres ikke beregninger av denne motstanden; den vurderes å være:
Kurvemotstand
Det benyttes en vanlig brukt formel:
Det er et spørsmål om ovennevnte formel gjelder for så små kurveradier. I litteraturen legges til grunn en radius R ≥ 300 m. Imidlertid, i mangel av bedre underlag benyttes denne formelen.
Luftmotstand som del i grunnmotstanden
Det benyttes den enkle formel for spesifikk motstand:
Togets samlede luftmotstand:
Stigningsmotstand
Gradienten på Flåmsbana er 55 mm/m. Stigningsmotstanden blir:
Samlet motstand:
Den samlede motstand beregnes:
Det er synlig at stigningsforholdene utgjør en betydelig andel av motstanden. Følgende ligning kan benyttes for beregning av nødvendig adhesjon:
I ovennevnte ligning er termen me O vognenes ekvivalente masse:
Da alle akslene på lokomotivet har traksjon, er mD = mα D.
Adhesjonskoeffisienten vil ha en verdi i området 0,15 – 0,20 ved normale forhold på skinnehodet (verken helt tørt eller helt fuktig).
Det antas en akselerasjon aX = 0,10 m/s2. Dette gir adhesjonsverdi for opprettholdelse av konstant hastighet (hastighetsendringen er svært liten så den betraktes som konstant):
Adhesjonen er temmelig bra utnyttet dersom den er antatt riktig.
Det undersøkes om en høyere akselerasjon er mulig for å nå hastigheten hurtigere. Det kan for eksempel bli tatt utgangspunkt i en aksellerasjonstid på 30 sekunder for å nå hastighet V = 30 km/h eller v = 8,33 m/s.
Adhesjonen blir:
Det kreves en høyere adhesjonskoeffisient. Skinnene skal i dette tilfellet være tørrere. Det er et spørsmål hvor realistisk dette tilfellet er.
Nødvendig trekkraft fra lokomotivet blir da:
Kraften fordeles på 4 aksler eller 8 hjul.
For hvert hjul utøves en adhesjonskraft mot skinnene:
Det blir tatt utgangspunkt i en klemkraft på 6 kN. Det regnes med at hjulkraften fordeles på 3 sviller. Dette gjelder også den langsgående trekkraft fra lokomotivet. Det blir da til sammen 6 fjærer som gir en samlet klemkraft:
På grunn av elastisitet i sporet vil hjulkraften fordele seg over 3 sviller:
Det benyttes tresviller med vekt på 70 kg. Den vertikale tilleggskraft fra hver sville:
Horisontal motstandskraft i pukken for bevegelse av sville (halv lengde):
For 3 sviller:
Samlet vertikalkraft:
Skinnevekten er ikke tatt med. Nødvendig friksjonskoeffisient mellom 3 sviller og pukklaget i ballastsengen for å hindre svillevandring med skinner:
Denne friksjonskoeffisienten er meget lav og vil normalt kunne oppfylles.
Det skulle således normalt ikke være fare for skinnevandring ved utførelse i traksjon for et lasket spor.
Vurderinger mht. skinnevandring ved nedbremsing og traksjon av materiell i lasket spor ved avvik i nøytraltemperatur
Skinnene er spenningsfrie på grunn av temperatur ved nøytraltemperatur og det finnes da et gap mellom skinneendene for 2 naboskinner i varmerommet i et lasket spor. Ved svakere klemkraft i befestigelsen kan det komme til bevegelse av skinnene inntil gapet tettes ved temperaturstigning. Tilsvarende vil ved lavere temperaturer gapet bli større. På grunn av disse forholdene innføres store strekk- og trykkrefter i skinnene. Dette aspektet vil da føre til skinnevandring. Arbeidsdiagrammet for skinner i lasket spor ved temperaturendringer er vist i figur 14.1.
Erfaringer som er gjort på Ofotbanen og som også er vist ved målinger i et DAMILL AB målesystem, bekrefter at skinner blir belastet med langsgående krefter i en relativt stor avstand foran lokomotivet ved traksjon i forbindelse med framføring. Sporet betraktes på dette stedet som ubelastet (ikke vertikal belastning fra materiellet). Skinnegangen kan da bli trukket innover og dermed endres nøytraltemperaturen. Sporet på Ofotbanen er helsveist.
Dersom en slik erfaringsoverføring legges til grunn, blir det nødvendig å vurdere
- Krypkrefter ved framføring på belastet skinne på grunn av lokomotivet og langsgående krefter på grunn av temperaturendringer (avvik i nøytraltemperatur)
- Krypkrefter på ubelastet naboskinne (gjennom skjøten) og langsgående krefter på grunn av temperaturendringer (avvik i nøytraltemperatur)
Flåmsbana har lasket sporkonstruksjon og er dermed bundet sammen ved lasker. Laskene med bolter kan overføre en kraft på ca. 100 kN. I samsvar med erfaringene på Ofotbanen kan det ikke utelukkes at den ubelastede naboskinne til belastet skinne fra lokomotivet blir utsatt for langsgående krefter forårsaket av traksjon. Aspektet kan medføre en kraft fra hvert hjul på 27,70 kN (beregnet i kapittel foran). 4 hjul vil gi en samlet kraft på ca. 100 kN for hver skinnestreng, altså den kapasitet som laskeboltene har.
Skinnene har en lengde på 40 m som medfører ca. 60 sviller med befestigelse. Dersom naboskinnen betraktes som ubelastet fra toget og motstand mot forskyvning av sporet er antatt til H = 2 kN (halv svillebredde), så blir samlet motstand mot skinnevandring lik 120 kN > 100 kN. Befestigelsen regnes å ha kapasitet mht. den langsgående kraft forårsaket av lokomotivet. For nøytraltemperatur skulle da skinnevandring på grunn av traksjon normalt ikke forekomme (se foregående kapittel); eller skinnevandringen skulle bli beskjeden.
Dersom temperatur avviker fra nøytraltemperatur, medfører dette aspektet langsgående krefter i skinnene. Utøvelse av traksjon for akselerasjon vil i tillegg føre til langsgående krypkrefter. Samlet kan disse 2 aspektene forårsake skinnevandring og at sporet blir trukket innover. Dette kan inntreffe for ubelastet og belastet skinne fra lokomotivet. Ved overgang fra El 17 til El 18 øker aksellasten med en faktor 1,33. Aspektet vil gi en økning i adhesjonskraften for samme adhesjonskoeffisient. Imidlertid vil den økte aksellasten virke stabiliserende.
Skjøtåpningene må kontrolleres og om nødvendig justeres. Når skjøtåpninger er blitt for store eller for små, skyldes dette i regelen enten skinnevandring eller lasken som kan gi for stor eller for liten friksjon. I slike tilfeller må det foretas skjøtregulering, rensing og smøring av laskekammeret og tilskruing av laskene. Varmeromstabellen må følges.
Termisk belastning
Det skal gis en vurdering av termisk belastning relatert til lokomotivet for 21,3 tonns aksellast. Linjen har en helning med gradient på 55 mm/m og det utøves derfor både traksjons- og bremsekrefter.
Når et hjul ruller på skinnen, er det ingen forskjell i hastighet i den felles kontaktflaten som eksisterer mellom punkter på hjulet og punkter på skinnen. Derimot når hjulet skal utføre traksjon eller skal bremse, så oppstår det forskjell i hastigheter i kontakten. Aspektet fører til varmeutvikling. Den last som overføres ved aksellast, får betydning. Selv ved relativt små forskjeller i hastighet kan dette gi stor varmeeffekt som igjen kan resultere i forhøyet temperatur særlig i hjulet. Det kommer dermed til en effektutvikling.
Særlig høye temperaturer kommer til syne for traksjonshjul på lokomotiv.
De maksimale temperaturer oppstår naturlig nok i den elliptiske kontaktflate på overflaten. Den høyere temperaturen avtar raskt i dybden i skinnehodet.
En nøyere analyse bekrefter at hjul og skinne blir belastet ulikt ved en betraktning av fordelingen av spenningene som følge av normal- og tangentialkrefter når også temperaturspenningene tas hensyn til. Ved traksjon oppstår normalt en høyere belastning på skinnen. Ved bremsing blir belastningen på hjulet høyere.
Effektutvikling mellom hjul og skinne utledes av formelen:
Her betyr termene v glidningshastighet og F tangentialkraft langs skinnen.
Tangentialkraften F utledes av:
Termen N er normalkraften:
Som maksimalverdi for stigning av temperatur i kontaktflaten mellom hjul og skinne ved rent lengdekryp for rene overflater (for eksempel ikke rue flater på skinnehodet) angir litteraturen følgende forenklede formel ved traksjon fra lokomotiv:
De enkelte termer skal forklares:
Friksjonskoeffisient:
Spenning i middelpunkt i kontaktflate:
Kryp i lengderetning:
Halvakse i elliptisk kontaktflate:
Framføringshastighet:
Varmeledningsevne for stål:
Tetthet for stål:
Spesifikk varmekapasitet:
I ovennevnte termer betyr:
Kelvin grader: K
J er enhet i Joule:
W er enhet i watt:
Det skal utføres en dimensjonsanalyse for formelen for stigning av temperaturen:
Termen K (Kelvingrader) kan trekkes ut fra rotuttrykket. Innføring for W og J gir:
Det er dermed vist at formelen gir riktige dimensjoner og at den kan anvendes. Det legges merke til at halvaksen i den elliptiske kontaktflate a må ha dimensjon i (m) og at p0 har dimensjon i (N/m2).
Det gjennomføres et beregningseksempel med formelen for et lokomotiv med traksjon:
Følgende inngangsdata:
Friksjon: μ = 0,30 (-)
Flatetrykk hjul/skinne: p0 = 686 N/mm2 = 686 · 106 N/m2
Krypkoeffisient: vξ = 0,05 (5 %)
Halvakse i ellipse: a = 5,90 mm = 0,0059 m
Hastighet: v0 = 30 m/s
Parameter λ: λ = 50 W/mK
Parameter ρ: ρ = 7850 kg/m3
Parameter c: c = 450 J/kgK
Parameterverdier innsatt i ligning:
Det er særlig hjulbanen som vil få denne temperaturen da hjulet blir utsatt for vedvarende bremsing.
Vurdering av sidestabilitet ved Prud`Hommes formel
prEN 14363 definerer grenseverdi for lateral kraft som kan forårsake sideforskyvning av sporet. Denne styringskraften er den laterale resultant av venstre og høyre hjulkraft til en aksel. På grunn av sporkonstruksjonen benyttes en faktor k = 0,85 i Prud`Hommes formel for Flåmsbana:
Innsatt i formel for El 18 gir:
Den maksimale styringskraft som El 18 kan utøve for å unngå sideforskyvning av sporet ved normale forhold er 68,85 kN. Kraften har en lengde på 2 meter i vinduet og evalueres i et lavpass filter på 20 Hz.
Det skal bli gjort et forsøk på å vurdere hvilken styringskraft som El 18 utøver (pragmatisk betraktning).
Styringskraften beregnes etter følgende formel:
EN 13103 og EN 1304 betrakter Yindre hjul som en friksjonskraft. Normene definerer:
Det er i kapittel foran beregnet en kvasistatisk kraft YKV.STAT. = 74,55 kN iht. ligningssystemet i EN 13103 og EN 13104. Denne kraften skulle tilsvare Yytre hjul.
Dette skulle medføre en styringskraft ∑Yj maks = 37,55 kN < 68,85 kN. Selv om El 18 har gode radielle styringsegenskaper, så er resultatet optimistisk. Kraften er trolig større.
Det er 2 usikre faktorer:
Det er lagt til grunn en friksjonskoeffisient på indre skinnestreng lik 0,350 fra et hjul. Aspektet forutsetter relativt tørre skinner. En mindre friksjonskoeffisient ville bidra til høyere ∑Yj maks. Dette fordi sentrifugalkraften og kraft fra støtfaktor vil få større innflytelse.
For det andre hersker det usikkerhet i om formelverket i EN 13103 eller 13104 samsvarer med de krefter som blir evaluert i EN 14363 i et lavpassfilter på 20 Hz.
Imidlertid konkluderes det med at kapasiteten til sporet mot sideforskyvning er tilstrekkelig god nok.
Vurdering av (Y/Q) ved dynamisk belastning
EN 14363 fastsetter kvotienten for avsporing til å være vurdert i et lavpass filter på 20 Hz:
I kapitlet for beregning av dynamiske Q og Y krefter er det benyttet følgende verdier for kreftene:
QDYN = 184,00 kN
YDYN = 96,00 kN
YDYN vurderes å være meget høy. Med de radielle styringsegenskaper som El 18 har, er verdien lavere; selv i kurver med R = 150 m.
Anvendelse av formel gir:
Det må påpekes at det hersker usikkerhet i om formelverket i Zimmermanns metode samsvarer med evalueringsprosessen i EN 14363 (vurdering i lavpass filter på 20 Hz).
Imidlertid er sikkerhet mot avsporing tilstrekkelig god.
Vurdering av (Y/Q) ved statisk belastning i svært lav hastighet (hjulavlastning)
Nadals formel gjelder:
Det legges til grunn at El 18 har et hjulprofil som gir flensvinkel på 68° - 70°. For en friksjonskoeffisient μ = 0,36 blir
En typisk overgangskurve på Flåmsbana har en lengde L = 20 og overhøyde D = 50 mm. Aspektet gir en gradient i overhøyderampen på 1 : 400. Imidlertid ved overgang til en sirkelkurve med R = 150 m bør også overhøyderampen ha slak helning.
Videre har trolig boggiene i El 18 torsjonsegenskaper som gir sikker framføring ved hjulavlastning i overhøyderamper som har større gradienter (gradient 1 : 333 forekommer).
Det konkluderes med at avsporingsfare iht. Nadals formel under normale forhold ikke vil forekomme.
Delta r kriteriet
På en bane med kurveradier R = 150 m er det nødvendig at Δ r kriteriet oppfylles i størst mulig grad.
∆r – kriteriet beskriver differanse i radius på hjulbanene til et hjulsett iht. formel:
∆r uttrykkes som funksjon av konisitet og horisontal forskyvning i retning mot ytterstreng i sirkelkurven eller som en funksjon av hjulradius r og sporvidde s i sirkelkurve. I ovennevnte ligning er R radius i sirkelkurve regnet fra origo til innerstreng.
Differanse i radius på hjulbanene er nødvendig fordi det er forskjell mellom radius til ytre skinnestreng og indre skinnestreng i en sirkelkurve. Det vises til figur 19.1.
I figur 19.2 er vist ∆r som funksjon av hjulradius og kurveradius med konstant sporvidde.
Det er av betydning at ∆r – kriteriet overholdes i størst mulig grad for at de krypkrefter som ellers ville oppstå i samspillet hjulsett/spor, skal holdes under kontroll.
Dersom hjulradius er 550 mm, beregnes nødvendig Δr til 5,50 mm for kurveradius R = 150 m.
Det blir bedt om en redegjørelse om i hvilken grad NSB iverksetter tiltak for best mulig overholdelse av kriteriet.
Radiell styringsindeks
En annen parameter av betydning er ∆x–kriteriet som i geometrisk henseende er et vilkår for radiell innstilling av hjulsett i kurver. Forholdet kan uttrykkes ved formel:
Dette er anskueliggjort i figur 20.1.
a er avstand mellom hjulsettene i en boggi.
s er avstand mellom hjulene i hjulsettet.
R er kurvens radius.
Parameteren ∆x er vist grafisk i figur 20.2.
∆x uttrykker den avstand som senterlinje for det ytre hjulet i hjulsettet må være foran det indre hjulet sett i forhold til en linje vinkelrett på vognens lengdeakse. Tilsvarende må senterlinjen til det indre hjulet være Δx bak den samme linje. Den totale avstand blir dermed 2Δx. Dette er en betingelse for å oppnå radiell styring av hjulsettet i kurven.
For kurveradius lik 150 m beregnes Δx til 7 mm for en boggi med hjulavstand lik 2,8 m.
Beregningen innebærer at hjulene i ytterstreng må gå 14 mm fra hverandre og hjulene på innerstreng må gå 14 mm til hverandre (nærme seg hverandre).
Det blir bedt om en redegjørelse om i hvilken grad NSB iverksetter tiltak for best mulig overholdelse av kriteriet.
Opprettholdelse av sporvidde vurdert ut fra kurveradius, skinneslitasje og kontakt av svilleskrue for befestigelsen mot trematerialet til tresviller
Det er av betydning at sporvidden holdes innenfor de mål som regelverket foreskriver for å unngå avsporing. Aspektet medfører at svilleskruene må ha kontakt med materialet i svillene. Tester kan utføres med et definert dreiemoment som er beskrevet i regelverket for vedlikehold.
Måling med målevogn, dvs. måling i belastet spor vil gi informasjon om opptredende sporvidde og om svilleskruene er i kontakt med trevirke i svillene.
I benyttet spor med små radier med tresviller kan opptredende sporvidde settes sammen av 4 komponenter:
- Nominell sporvidde
- Utvidelse av nominell sporvidde i kurver med små radier gjennom bormønsteret
- Slitte skinnehoder på skinnene (særlig for ytre skinnestreng)
- Slark i skruehullene (som ikke må forekomme)
Et slitasjebilde for ytterstreng og innerstreng er vist på side 21. Slitasjen i tverrprofilet i ytterstreng er betydelig. Skjeggdannelsen på indre streng framkommer tydelig i bilde på samme side.
Nominell sporvidde er 1435 mm.
For kurver med radier R ≥ 300 m benyttes nominell sporvidde lik 1435 mm. For kurver med radier 200 m < R < 300 m utvides sporvidden med 5 mm til 1440 mm. For kurver med radier R ≤ 200 m settes sporvidde til 1445 mm.
I klasse K3 eller lavere foreskriver regelverket et tillatt avvik fra grunnverdien som er 1435 mm, på 15 mm i vedlikeholdsgrense. Tiltaksgrensen er 30 mm og umiddelbar grense er 35 mm.
Sporvidden ved vedlikeholdsgrense blir 1450 mm og ved tiltaksgrense 1465 mm. Større sporvidder må ikke forekomme.
Økning i aksellast fra El 17 til El 18 (opptil 21,3 tonn) medfører større vertikalt trykk mot befestigelsen og en økning i horisontalkraft spesielt i kurver. Skruene i anlegg mot trematerialet må motstå denne økningen slik at avsporing unngås. Retningen til den resulterende kraft fra El 18 vil ikke være mer ugunstig enn retningen fra El 17.
Råte og mekanisk slitasje vil over tid føre til at svilleskruene mister sitt feste i svillene. Dersom skruene på flere sviller etter hverandre mangler feste, vil dette kunne medføre farlig sporutvidelse og velting av skinnen med avsporing som resultat.
Ved bare mekanisk slitasje vil tap av feste foregå meget langsomt og svillen får relativt lang levetid i sporet.
I regelverket for vedlikehold i overbygningen er det referert til metoder for å utbedre manglende feste for svilleskruer.
For vurdering av om svillen er blitt utsatt for råte, kan målediagrammene for sporvidde over flere perioder anvendes. Dersom utvidelsen av sporvidde er blitt betydelig mellom 2 målinger, er dette en indikator på at svillen er blitt utsatt for råteangrep.
I et slikt tilfelle må tester utføres med et definert dreiemoment på svilleskruene som er beskrevet i regelverket for vedlikehold i overbygningen. Samme regelverk beskriver også metode for rehabilitering.
Bidet under (figur 20.1) er et illustrasjonsbilde som ikke er hentet fra Flåmsbana (har ingen ting med Flåmsbana å gjøre).
Målediagrammene fra en måling datert 31.05.2012 for Flåmsbana viser stor variasjon i målt sporvidde i belastet spor (med ROGER 1000). Sporvidden varierer fra ca. 1435 mm til 1465 mm på enkelte steder. Verdier i intervallet 1445 mm – 1455 mm forekommer meget hyppig. Det er forbundet med usikkerhet å vurdere faren for avsporing ved stor sporvidde som er forårsaket av råte og mekanisk slitasje ved å studere diagrammene bare fra en måling.
Imidlertid er en sporvidde på ca. 1445 – 1450 mm å betrakte som normalt på Flåmsbana. Aspektet har sammenheng med selve bormønsteret i tresvillene og slitasje i skinnehodet i ytterstreng.
For å hindre mulig tendens til avsporing bør målediagrammene de siste periodene gjennomgås for å undersøke om det ved enkelte steder på banestrekningen er en abrupt utvikling i sporvidde. På disse stedene må feste av skruene kontrolleres opp mot dreiemomentet og eventuelt tiltak iverksettes for rehabilitering.
I figur 21.2 er vist et utsnitt av sporvidden over en lengde på ca. 400 m målt med målevogn, dvs. måling i belastet spor. Sporvidden varierer fra nær 1435 mm på rett linje til ca. 1455 mm i sirkel- og overgangskurver. Det finnes en maksimalverdi på 1465 mm registrert i sirkelkurve.
Iht. teknisk regelverk settes den reelle sporvidde lik 1435 + 10 = 1445 mm. På side 21 er vist et representativt slitasjeprofil for ytterstreng i en kurve. Slitasjeprofilet er registrert ved km 338,950. Slitasjemålet kan settes til ca. 15 mm. Samlet sporvidde skulle dermed bli ca. 1460 mm.
Målediagrammet i figur 21.2 er hentet fra ca. km 340,450 til ca. km 340,850. Bortsett fra ett målepunkt (ca. km 340,450) holder sporvidden seg godt innenfor maksimalgrensene. Diagrammet tyder på at tresvillene er i god stand. Det gjøres oppmerksom på at målingene er utført i belastet tilstand med målevogn ROGER 1000 som har en aksellast på 16 tonn. El 18 er tyngre med aksellast på 21,30 tonn.
Den overveiende konklusjon er at på enkelte steder hvor sporvidden er målt opp til 1465 mm, så bør skruene kontrolleres på dreiemoment iht. bestemmelsene i regelverket og eventuelt at utbedringer gjennomføres.
Forholdet R/D/g (sirkelkurve, overhøyde, vindskjevhet i overgangskurve)
Iht. løfteskjema er vindskjeheten meget lav; flere steder 1 : 400. Diagrammene fra målevognkjøringen viser vindskjevhet < 10 mm for 2 meters verdier og < 31 mm for 9 meters verdier.
Stabilitet
På grunn av lav hastighet vil instabilt løp ikke oppstå.
Referanser
(1) Evert Andersson; Mats Berg: Järnvägssystem och spårfordon, Stockholm 2001
(2) Evert Andersson; Mats Berg; Sebastian Stichel: Spårfordons dynamik, Stockholm 2002
(3) Klaus Knothe; Sebastian Stichel: Schienenfahrzeugdynamik, Springer Verlag, Berlin 2003
(4) Fritz Fastenrath; VERLAG ERNST & SOHN: Die Eisenbahnschiene, BERLIN, MÜNCHEN, DüSSELDORF
(5) Klaus Knothe; Ernst&Sohn: Gleisdynamik, Berlin 2001
(6) Coenraad Esveld: Modern Railway Track, Second Edition, Nederland 2001
(7) Klaus Knothe; ZEV Glasers Annalen: Beanspruchungen von Schienen unter statischen, dynamischen und thermischen Belastungen, april 2003
(8) prEN 14363:2012: Railway applications – Testing and Simulations for the acceptance of running characteristics of railway vehicles – Running Behaviour and stationary tests
(9) EN 13103 og EN 13104