Aksialkrefter i helsveist spor: Forskjell mellom sideversjoner
(slettet linjeskift) |
|||
| (46 mellomliggende versjoner av 2 brukere er ikke vist) | |||
| Linje 2: | Linje 2: | ||
==Innledning== | ==Innledning== | ||
Den første jernbane som ble åpnet i England i 1826 hadde skinnelengder | Den første jernbane som ble åpnet i England i 1826 hadde skinnelengder | ||
mindre enn 5 m. Produksjonstekniske fremskritt har siden gjort det mulig åfremstille stadig lengre skinnelengder. I 1945 var skinnelengdene økt til 20 m | mindre enn 5 m. Produksjonstekniske fremskritt har siden gjort det mulig åfremstille stadig lengre skinnelengder. I 1945 var skinnelengdene økt til 20 m og rundt 1960 til 40 m. I dag fremstilles det helvalsede skinner på 120 m. Tidlig på 1900-tallet ble det utviklet metoder for å sveise sammen skinner slik at skinner kunne skjøtes uten bruk av lasker. Til tross for dette våget man ikke å sveise sammen lengre skinnelengder enn 30-40 m. Helt frem til midten av vårt århundre var det vanlig å skjøte skinnene sammen med lasker. En lasket skjøt forårsaker store slagpåkjenninger som bryter ned både sporkomponenter og rullende materiell. | ||
og rundt 1960 til 40 m. I dag fremstilles det helvalsede skinner på 120 m. | |||
Tidlig på 1900-tallet ble det utviklet metoder for å sveise sammen skinner slik | Rundt 1950 (1960 i Norge) ble det satt i gang med å sveise skinner sammen til kontinuerlige strenger, dvs. helsveiste skinner. Dette var mulig pga. bedre ballast, sviller, og fremfor alt bedre befestigelse som holdt skinnene bedre fast, og gjorde sporet stivere sideveis. | ||
at skinner kunne skjøtes uten bruk av lasker. Til tross for dette våget man | |||
ikke å sveise sammen lengre skinnelengder enn 30-40 m. Helt frem til | I dag er over 95 % av Jernbaneverkets hovedspor helsveist spor. Innføring av helsveiste skinner er kanskje det viktigste sportekniske fremskritt i dette århundret. Det helsveiste sporet har medført en dramatisk reduksjon i slitasje på både sporet og det rullende materiell. Men det helsveiste sporet har introdusert nye problemstillinger som kan føre til alvorlig sikkerhetsrisiko dersom de ikke behandles på riktig måte. Problemene knytter seg til de store aksialkreftene som blir låst inne i skinnene. Disse kreftene medfører økt fare for skinnebrudd om vinteren og solslyng i sommerhalvåret. | ||
midten av vårt århundre var det vanlig å skjøte skinnene sammen med lasker. | |||
En lasket skjøt forårsaker store slagpåkjenninger som bryter ned både | |||
Aksialkrefter i helsveiste skinner spor kan forårsakes av følgende faktorer: | Aksialkrefter i helsveiste skinner spor kan forårsakes av følgende faktorer: | ||
*temperaturendringer i skinnene | *temperaturendringer i skinnene | ||
| Linje 29: | Linje 13: | ||
*forflytning av sporet i horisontalplanet | *forflytning av sporet i horisontalplanet | ||
*utvalsing (plastisk deformasjon) i skinnehodet | *utvalsing (plastisk deformasjon) i skinnehodet | ||
De store trykkreftene som oppstår i et helsveist spor ved høye | |||
skinnetemperaturer stiller store krav til sporets komponenter. Sporet må ha | De store trykkreftene som oppstår i et helsveist spor ved høye skinnetemperaturer stiller store krav til sporets komponenter. Sporet må ha tilstrekkelig motstand mot sideveis utknekking for å unngå solslyng. Dette blir behandlet i kapittel 7, “Sporets sidemotstand”. | ||
tilstrekkelig motstand mot sideveis utknekking for å unngå solslyng. Dette blir | |||
behandlet i kapittel 7, “Sporets sidemotstand”. | |||
==Aksialkrefter pga. temperaturendringer== | ==Aksialkrefter pga. temperaturendringer== | ||
'''Lengdeforandring ved temperaturendring''' | '''Lengdeforandring ved temperaturendring''' | ||
[[Fil:Lengdeforandring ved temperaturendring.PNG|thumb|300px|Figur 5.1: Lengdeforandring ved temperaturendring]] | |||
[[Fil:Lengdeforandring ved kraftpåvirkning.PNG|thumb|300px|Figur 5.2:Lengdeforandring ved kraftpåvirkning]] | |||
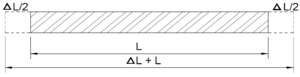
En skinne som ligger fritt opplagret vil forandre lengde når temperaturen i skinnen forandrer seg (figur 5.1). Skinnen vil utvide seg når temperaturen øker og krympe når temperaturen synker. Lengdeendring avhengig av | En skinne som ligger fritt opplagret vil forandre lengde når temperaturen i skinnen forandrer seg (figur 5.1). Skinnen vil utvide seg når temperaturen øker og krympe når temperaturen synker. Lengdeendring avhengig av | ||
| Linje 50: | Linje 34: | ||
{|width="45%" | {|width="45%" | ||
|- | |- | ||
| | |L = opprinnelig lengde [m] | ||
|- | |- | ||
| | |ΔL = lengdeendring [m] | ||
|- | |- | ||
| | |α = lengdeutvidelseskoeffisient = 1,15*10<sup>-5</sup> [m/°C*m] | ||
|- | |- | ||
| | |Δt = temperaturendring [°C]. | ||
|} | |} | ||
| Linje 66: | Linje 50: | ||
vi forandre skinnens lengde (figur 5.2). Lengdeendringen er avhengig av | vi forandre skinnens lengde (figur 5.2). Lengdeendringen er avhengig av | ||
aksialspenningen i skinnen og kan uttrykkes ved hjelp av formel 5.2. | aksialspenningen i skinnen og kan uttrykkes ved hjelp av formel 5.2. | ||
{|width="45%" | {|width="45%" | ||
| Linje 79: | Linje 60: | ||
hvor: | hvor: | ||
{|width="45%" | {|width="45%" | ||
| | |L = opprinnelig lengde [mm] | ||
|- | |- | ||
| | | ΔL = lengdeendring [mm] | ||
|- | |- | ||
| | | σ= aksialspenning=P/A [N/mm<sup>2</sup>] | ||
|- | |- | ||
| | | E = elastisitetsmodul=2,07*10<sup>5</sup>[N/mm<sup>2</sup>] | ||
|- | |- | ||
| | |P = aksialkraft [N] | ||
|- | |- | ||
| | | A = skinnens tverrsnittsareal [mm<sup>2</sup>]. | ||
|} | |} | ||
| Linje 106: | Linje 87: | ||
|<math> \alpha \cdot t \cdot L= {\sigma \cdot L \over E}</math> | |<math> \alpha \cdot t \cdot L= {\sigma \cdot L \over E}</math> | ||
|- | |- | ||
| | |||
|<math> \Updownarrow</math> | |<math> \Updownarrow</math> | ||
| | |||
|(5.3) | |(5.3) | ||
|- | |- | ||
| Linje 119: | Linje 102: | ||
{| | {| | ||
|<math> \sigma =2,4 \Delta t [N/mm^2]</math> | |<math> \sigma =2,4 \Delta t [N/mm^2]</math> | ||
| | |||
| | |||
| | |||
| | |||
| | |||
| | |||
| | |||
|(5.4) | |(5.4) | ||
|- | |- | ||
|} | |} | ||
For hver grad temperaturendring i en helsveist skinne vil aksialspenningen | For hver grad temperaturendring i en helsveist skinne vil aksialspenningen | ||
altså endres med 2,4 N/mm | altså endres med 2,4 N/mm<sup>2. | ||
'''Aksialkrefter''' | '''Aksialkrefter''' | ||
Aksialkreftene som oppstår finner vi ved å multiplisere med skinnens | Aksialkreftene som oppstår finner vi ved å multiplisere med skinnens | ||
tverrsnittsareal. S54 og UIC60 skinner har tverrsnittsareal på hhv. 6950 | tverrsnittsareal. S54 og UIC60 skinner har tverrsnittsareal på hhv. 6950 mm<sup>2</sup> | ||
og 7686 | og 7686 mm<sup>2</sup>. 1 grads temperaturøkning medfører dermed en kraftøkning på | ||
16680 N (1,6 tonn) for S54-skinne og 18446 N (1,8 tonn) for UIC60 - skinne. | 16680 N (1,6 tonn) for S54-skinne og 18446 N (1,8 tonn) for UIC60 - skinne. | ||
Et tyngre skinneprofil medfører m.a.o. større aksialkrefter i et helsveist spor. | Et tyngre skinneprofil medfører m.a.o. større aksialkrefter i et helsveist spor. | ||
| Linje 140: | Linje 131: | ||
fører til mindre trykkrefter i skinnene ved høye temperaturer om sommeren, | fører til mindre trykkrefter i skinnene ved høye temperaturer om sommeren, | ||
mens strekkreftene blir desto større ved kulde om vinteren. Ved JBV er | mens strekkreftene blir desto større ved kulde om vinteren. Ved JBV er | ||
nøytraltemperaturen satt til + | nøytraltemperaturen satt til + 21˚C . | ||
'''Middeltemperaturen''' | '''Middeltemperaturen''' | ||
| Linje 147: | Linje 138: | ||
middeltemperaturen, dvs. den skinnetemperaturen som ligger midt i mellom | middeltemperaturen, dvs. den skinnetemperaturen som ligger midt i mellom | ||
høyeste og laveste påregnelige skinnetemperatur. For de fleste steder i | høyeste og laveste påregnelige skinnetemperatur. For de fleste steder i | ||
Norge regner vi med at skinnetemperaturen kan nå opp til + | Norge regner vi med at skinnetemperaturen kan nå opp til + 55˚C og ned til | ||
-30 | -30 ˚C. Dette gir en middeltemperatur på + 15˚C. Når nøytraltemperaturen er | ||
satt | satt 6˚C høyere skyldes dette at vi ønsker en større sikkerhet mot solslyng. | ||
Dette fordi solslyng anses som en større avsporingsrisiko enn skinnebrudd. | Dette fordi solslyng anses som en større avsporingsrisiko enn skinnebrudd. | ||
| Linje 159: | Linje 150: | ||
arbeidsoperasjonen kalles nøytralisering og blir behandlet i L534 - | arbeidsoperasjonen kalles nøytralisering og blir behandlet i L534 - | ||
”Produksjonsteknikk”. Under nøytralisering ved JBV kan nøytraltemperaturen | ”Produksjonsteknikk”. Under nøytralisering ved JBV kan nøytraltemperaturen | ||
tilordnes innenfor en toleranse på ± | tilordnes innenfor en toleranse på ± 3˚C, dvs. innenfor temperaturområdet + | ||
18 - | 18 - 24˚C. Dette kalles nøytraltemperaturområdet. | ||
===Maksimale trykk og strekkrefter=== | ===Maksimale trykk og strekkrefter=== | ||
| Linje 175: | Linje 166: | ||
|- | |- | ||
|S49 | |S49 | ||
|6350 mm | |6350 mm<sup>2 | ||
|777 kN | |777 kN | ||
|518 kN | |518 kN | ||
|- | |- | ||
|S54 | |S54 | ||
|6950 mm | |6950 mm<sup>2 | ||
|850 kN | |850 kN | ||
|567 kN | |567 kN | ||
|- | |- | ||
|UIC60 | |UIC60 | ||
|7686 | |7686 mm<sup>2 | ||
|941 kN | |941 kN | ||
|627 kN | |627 kN | ||
| Linje 195: | Linje 186: | ||
===Pusteparti=== | ===Pusteparti=== | ||
[[Fil:Pusteparti.PNG|thumb|300px|Figur 5.3: Pusteparti]] | |||
Hittil har vi bare sett på hva som skjer inne i et helsveist spor hvor | Hittil har vi bare sett på hva som skjer inne i et helsveist spor hvor | ||
motstanden mot langsgående bevegelse av skinnene er så stor at skinnene | motstanden mot langsgående bevegelse av skinnene er så stor at skinnene | ||
| Linje 204: | Linje 196: | ||
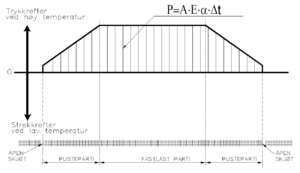
er fullstendig hindret fra å bevege seg. Dette partiet kalles pustepartiet (figur | er fullstendig hindret fra å bevege seg. Dette partiet kalles pustepartiet (figur | ||
5.3). | 5.3). | ||
I pustepartiet vil spenningene i skinnene gradvis bygges opp i pustepartiet | I pustepartiet vil spenningene i skinnene gradvis bygges opp i pustepartiet | ||
inntil full bevegelseshindring inntreffer. | inntil full bevegelseshindring inntreffer. | ||
| Linje 212: | Linje 204: | ||
====Ballastmotstand==== | ====Ballastmotstand==== | ||
[[Fil:Ballastmotstand.PNG|thumb|300px|Figur 5.4: Ballastmotstand]] | |||
Ballastmotstand er definert som den motstand skinnen møter når den | Ballastmotstand er definert som den motstand skinnen møter når den | ||
beveger seg eller prøver å bevege seg i sporets lengderetning. Bevegelse i | beveger seg eller prøver å bevege seg i sporets lengderetning. Bevegelse i | ||
| Linje 227: | Linje 220: | ||
ved å dividere med svilleavstanden. Det er vanlig å regne ballastmotstanden | ved å dividere med svilleavstanden. Det er vanlig å regne ballastmotstanden | ||
pr. skinnestreng, dvs. pr. halve sville | pr. skinnestreng, dvs. pr. halve sville | ||
{| | {| | ||
|<math> Ballastmotstand={motstand pr. halve sville \over svilleavstand} [N/m] </math> | |<math> Ballastmotstand={motstand pr. halve sville \over svilleavstand} [N/m] </math> | ||
| | |||
| | |||
| | |||
| | |||
| | |||
| | |||
|(5.5) | |(5.5) | ||
|} | |} | ||
| Linje 238: | Linje 240: | ||
konstant verdi på ca. 9 kN etter 4 - 6 mm bevegelse. Med svilleavstand på | konstant verdi på ca. 9 kN etter 4 - 6 mm bevegelse. Med svilleavstand på | ||
0,6 m gir dette en ballastmotstand på 7,5 kN/m (pr. skinnestreng). | 0,6 m gir dette en ballastmotstand på 7,5 kN/m (pr. skinnestreng). | ||
Det er vanlig å regne ballastmotstanden i et normalt konsolidert spor med | Det er vanlig å regne ballastmotstanden i et normalt konsolidert spor med | ||
| Linje 254: | Linje 254: | ||
====Lengde av pusteparti==== | ====Lengde av pusteparti==== | ||
[[Fil:Lengde av pusteparti i spor med S54 skinner.PNG|thumb|300px|Figur 5.5 Lengde av pusteparti i spor med S54 skinner]] | |||
Lengden av et pusteparti er avhengig av ballastmotstanden og hvor stor | Lengden av et pusteparti er avhengig av ballastmotstanden og hvor stor | ||
aksialkraft vi har i det fastlåste partiet. Dersom vi antar en konstant | aksialkraft vi har i det fastlåste partiet. Dersom vi antar en konstant | ||
| Linje 260: | Linje 261: | ||
{| | {| | ||
|<math> a={P-R \over r} [N/m] </math> | |<math> a={P-R \over r} [N/m] </math> | ||
| | |||
| | |||
| | |||
| | |||
| | |||
| | |||
|(5.6) | |(5.6) | ||
|} | |} | ||
| Linje 284: | Linje 291: | ||
aksialkraft vi har i det fastlåste partiet. Dersom vi antar en konstant | aksialkraft vi har i det fastlåste partiet. Dersom vi antar en konstant | ||
ballastmotstand kan vi beregne lengden av pustepartiet etter formel 5.6. | ballastmotstand kan vi beregne lengden av pustepartiet etter formel 5.6. | ||
a P R | |||
r | <math> a={P-R \over r} </math> (5.6) | ||
Motstanden i evt. lask kan settes til ca. 100 kN. Figur 5.5 viser hvor lange | Motstanden i evt. lask kan settes til ca. 100 kN. Figur 5.5 viser hvor lange | ||
pustepartiene blir i et S54-spor avhengig av ballastmotstanden og | pustepartiene blir i et S54-spor avhengig av ballastmotstanden og | ||
| Linje 292: | Linje 299: | ||
representerer en ballastmotstand [kN/m]. Det er i diagrammet sett bort fra | representerer en ballastmotstand [kN/m]. Det er i diagrammet sett bort fra | ||
motstand i evt. lask. | motstand i evt. lask. | ||
For et normalt godt konsolidert spor kan vi få pustepartier på opptil 80 -100 | For et normalt godt konsolidert spor kan vi få pustepartier på opptil 80 -100 | ||
| Linje 304: | Linje 310: | ||
====Bruddåpning ved skinnebrudd==== | ====Bruddåpning ved skinnebrudd==== | ||
[[Fil:Kraftlikevekt i et skinneelement.PNG|thumb|300px|Figur 5.6: Kraftlikevekt i et skinneelement]] | |||
Når det oppstår skinnebrudd ved lav temperatur vil det oppstå en | Når det oppstår skinnebrudd ved lav temperatur vil det oppstå en | ||
bruddåpning som resultat av at bruddet utløser pustepartier hvor skinnene | bruddåpning som resultat av at bruddet utløser pustepartier hvor skinnene | ||
| Linje 312: | Linje 319: | ||
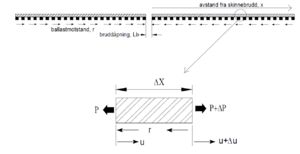
avstand x fra bruddstedet. Dersom r er ballastmotstanden, x er avstand fra | avstand x fra bruddstedet. Dersom r er ballastmotstanden, x er avstand fra | ||
bruddstedet og P er aksialkraften i skinnen har vi at: | bruddstedet og P er aksialkraften i skinnen har vi at: | ||
{| | |||
|<math>\Delta P = r \cdot \Delta x</math> | |||
|- | |||
|<math>\Updownarrow</math> | |||
|(5.7) | |||
|- | |||
|<math>{\operatorname{d} \!P \over \operatorname{d} \!x} = r</math> | |||
|} | |||
Dersom Δu er lengdeendring i skinneelementet vil Δu/Δx representere den | Dersom Δu er lengdeendring i skinneelementet vil Δu/Δx representere den | ||
| Linje 322: | Linje 335: | ||
må vi trekke fra den termiske andelen. Dermed kan vi finne aksialkraften P: | må vi trekke fra den termiske andelen. Dermed kan vi finne aksialkraften P: | ||
{| | |||
|<math> P = A \cdot E \cdot[{\operatorname{d}\!u\over\operatorname{d}\!x}- \alpha \cdot \Delta t]</math> | |||
| | |||
| | |||
| | |||
| | |||
|(5.8) | |||
|} | |||
Ved å sette inn formel 5.8 i formel 5.7 får vi følgende differensialligning: | Ved å sette inn formel 5.8 i formel 5.7 får vi følgende differensialligning: | ||
{| | |||
|<math> A \cdot E \cdot {d^2 u \over dx^2}=r</math> | |||
| | |||
| | |||
| | |||
| | |||
|(5.9) | |||
|} | |||
Løsningen av 5.9 kan uttrykkes som: | Løsningen av 5.9 kan uttrykkes som: | ||
{| | |||
|<math> u={f \over 2 \cdot A \cdot E}\cdot x^2+c_1\cdot x+c_2</math> | |||
| | |||
| | |||
| | |||
| | |||
|(5.10) | |||
|} | |||
Skinnebruddet utløser bevegelse i skinnene i hele pustepartiets lengde a. | Skinnebruddet utløser bevegelse i skinnene i hele pustepartiets lengde a. | ||
Dette gir oss følgende grensebetingelser: | Dette gir oss følgende grensebetingelser: | ||
{| | |||
|ved x=0 | |||
| | |||
| | |||
| | |||
| | |||
|<math> P = 0 \Leftrightarrow {\operatorname{d}\!u\over\operatorname{d}\!x}= \alpha \cdot \Delta t</math> | |||
|} | |||
{| | |||
|ved x=a | |||
| | |||
| | |||
| | |||
| | |||
|<math> u=0 </math> og <math>{\operatorname{d}\!u\over\operatorname{d}\!x}=0 </math> | |||
|} | |||
De 3 grensebetingelsene bestemmer a, c1 og c2. Det endelige uttrykket for u | De 3 grensebetingelsene bestemmer a, c1 og c2. Det endelige uttrykket for u | ||
og a blir dermed: | og a blir dermed: | ||
{| | |||
|<math> u={r \over 2 \cdot A \cdot E}\cdot (x-a)^2</math> | |||
| | |||
| | |||
| | |||
| | |||
|<math>0<x<a</math> | |||
| | |||
| | |||
| | |||
| | |||
|(5.11) | |||
|} | |||
{| | |||
|<math> a={A \cdot E \cdot \alpha \cdot \Delta t \over r}</math> | |||
| | |||
| | |||
| | |||
| | |||
| | |||
| | |||
|(5.12) | |||
|} | |||
Bruddåpning ved skinnebrudd vil være 2 ganger skinnens bevegelse ved | Bruddåpning ved skinnebrudd vil være 2 ganger skinnens bevegelse ved | ||
bruddstedet, dvs: | bruddstedet, dvs: | ||
{| | |||
|<math> L_B=2 \cdot u_{x=0}={r \cdot a^2 \over A \cdot E}</math> | |||
| | |||
| | |||
| | |||
| | |||
| | |||
| | |||
|(5.13) | |||
|} | |||
Ved å sette 5.12 inn i 5.13 får vi følgende uttrykk for bruddåpningens | Ved å sette 5.12 inn i 5.13 får vi følgende uttrykk for bruddåpningens | ||
størrelse: | størrelse: | ||
{| | |||
|<math> L_B={A \cdot E \cdot \alpha^2 \cdot {\Delta t}^2 \over r}</math> | |||
| | |||
| | |||
| | |||
| | |||
| | |||
| | |||
|(5.14) | |||
|} | |||
{| | |||
|L<sub>B</sub>= bruddåpning [mm] | |||
|- | |||
| A=skinnens tverrsnittsareal [mm<sup>2</sup>] | |||
|- | |||
|E=elastisitetesmodul [2,07*10<sup>5</sup> N/mm<sup>2</sup>] | |||
|- | |||
|a=utvidelseskoeffisient [1,15*10<sup>-5</sup> m/°C*m] | |||
|- | |||
|Δt = temp.forskjell nøytraltemperatur-skinnetemperatur ved brudd [°C] | |||
|- | |||
|r=ballastmotstand [N/mm] | |||
|} | |||
Vi ser at bruddåpningen er omvendt proporsjonal med ballastmotstanden og | Vi ser at bruddåpningen er omvendt proporsjonal med ballastmotstanden og | ||
| Linje 358: | Linje 464: | ||
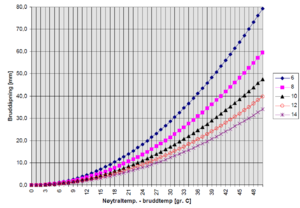
Figur 5.7 viser bruddåpning ved skinnebrudd i et spor med S54-skinner. De | Figur 5.7 viser bruddåpning ved skinnebrudd i et spor med S54-skinner. De | ||
forskjellige linjene i diagrammet representerer ballastmotstanden [kN/m]. | forskjellige linjene i diagrammet representerer ballastmotstanden [kN/m]. | ||
[[Fil:Bruddåpning ved skinnebrudd i spor med S54-skinner.PNG|thumb|center|300px|Figur 5.7: Bruddåpning ved skinnebrudd i spor med S54-skinner]] | |||
Figur 5.7 Bruddåpning ved skinnebrudd i spor med S54-skinner | |||
==Aksialkrefter pga. skinnevandring== | ==Aksialkrefter pga. skinnevandring== | ||
| Linje 383: | Linje 488: | ||
'''Beregningsmodell''' | '''Beregningsmodell''' | ||
[[Fil:Beregning av krefter ved skinnevandring.PNG|thumb|300px|Figur 5.8: Beregning av krefter ved skinnevandring]] | |||
Ved Krakow tekniske universitet i Polen er det utarbeidet en modell for | Ved Krakow tekniske universitet i Polen er det utarbeidet en modell for | ||
beregning av restkrefter som oppstår i skinnene ved oppbremsing, “CREEP”. | beregning av restkrefter som oppstår i skinnene ved oppbremsing, “CREEP”. | ||
| Linje 389: | Linje 494: | ||
oppbremsing i spor med hhv. 15, 10, og 5 ‰ fall. I dette eksemplet er det | oppbremsing i spor med hhv. 15, 10, og 5 ‰ fall. I dette eksemplet er det | ||
valgt en vertikal last på 86,25 kN/m i en lengde på 640 m. | valgt en vertikal last på 86,25 kN/m i en lengde på 640 m. | ||
Figuren viser kraftøkninger opp til 180 kN ved oppbremsing i spor med 15 ‰ | Figuren viser kraftøkninger opp til 180 kN ved oppbremsing i spor med 15 ‰ | ||
fall. Dersom sporet har UIC60 skinner, tilsvarer dette en reduksjon av | fall. Dersom sporet har UIC60 skinner, tilsvarer dette en reduksjon av | ||
nøytraltemperaturen på | nøytraltemperaturen på 10˚C. | ||
'''Skinnevandring i dobbeltspor''' | '''Skinnevandring i dobbeltspor''' | ||
| Linje 420: | Linje 523: | ||
==Aksialkrefter pga. sideforflytning== | ==Aksialkrefter pga. sideforflytning== | ||
[[Fil:Sideforflytning av sporet.PNG|thumb|300px|Figur 5.9: Sideforflytning av sporet]] | |||
[[Fil:Figur5.10.PNG|thumb|150px|Figur 5.10]] | |||
[[Fil:Endring av nøytraltemperatur.PNG|thumb|300px|Figur 5.11: Endring av nøytraltemperatur ved sideforflytning]] | |||
Ved sideforflytning av sporet i kurver endrer vi lengden av skinnene i det | Ved sideforflytning av sporet i kurver endrer vi lengden av skinnene i det | ||
partiet som blir flyttet, dvs. at skinnene blir strukket, eller trykket sammen. | partiet som blir flyttet, dvs. at skinnene blir strukket, eller trykket sammen. | ||
| Linje 426: | Linje 532: | ||
vil det medføre en økning i nøytraltemperaturen. | vil det medføre en økning i nøytraltemperaturen. | ||
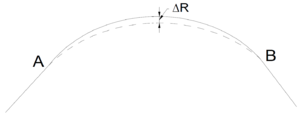
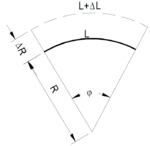
Figur 5.10 viser en sirkelsektor med vinkel ﬩,radius R og en skinnelengde | |||
Figur 5.10 viser en sirkelsektor med vinkel | |||
(buelengde) L. Dersom vi sideforflytter sporet med DR endres skinnelengden | (buelengde) L. Dersom vi sideforflytter sporet med DR endres skinnelengden | ||
DL. Formel 5.15 og formel 5.16 viser sammenhengen mellom radius og | DL. Formel 5.15 og formel 5.16 viser sammenhengen mellom radius og | ||
skinnelengde. | skinnelengde. | ||
{| | |||
|<math> L={R \cdot \pi \cdot \phi \over 180} </math> | |||
| | |||
| | |||
| | |||
|(5.15) | |||
|} | |||
{| | |||
|<math> \Delta L= {\Delta R \cdot \pi \cdot \phi \over 180} </math> | |||
| | |||
| | |||
| | |||
|(5.16) | |||
|} | |||
Lengdeendringen ΔL som finner sted påvirker nøytraltemperaturen i | Lengdeendringen ΔL som finner sted påvirker nøytraltemperaturen i | ||
skinnene. Sammenhengen mellom lengdeendring og temperaturendring i | skinnene. Sammenhengen mellom lengdeendring og temperaturendring i | ||
skinnene finner vi i formel 5.1. Vi kan da sette opp følgende ligning: | skinnene finner vi i formel 5.1. Vi kan da sette opp følgende ligning: | ||
{| | |||
|<math> L \cdot \alpha \cdot \Delta t={\Delta R \cdot \pi \cdot \phi \over 180} </math> | |||
|- | |||
| | |||
|<math>\Updownarrow </math> | |||
| | |||
|- | |||
|<math>\Delta t ={\Delta R \cdot \pi \cdot \phi \over 180 \cdot L \cdot \alpha}</math> | |||
|} | |||
Ved å sette inn formel 5.15 for skinnelengden L får vi videre: | Ved å sette inn formel 5.15 for skinnelengden L får vi videre: | ||
{| | |||
|<math> \Delta t={\Delta R \cdot \pi \cdot \phi \over 180 \cdot({ R \cdot \pi \cdot \phi \over 180}) \cdot \alpha} </math> | |||
|- | |||
| | |||
|<math>\Updownarrow </math> | |||
| | |||
|- | |||
|<math>\Delta t ={\Delta R \over R \cdot \alpha}</math> | |||
| | |||
| | |||
| | |||
|(5.17) | |||
|} | |||
{| | |||
|Δt = endring i nøytraltemperatur [°C] | |||
|- | |||
|R = kurveradius [m] | |||
|- | |||
|ΔR = sideforflyttning [m] | |||
|- | |||
|α= lengdeutvidelseskoeffisient [1,15*10<sup>-5</sup>m/m*°C ] | |||
|} | |||
Figur 5.11 viser sammenhengen mellom sideforflytning og endring av | Figur 5.11 viser sammenhengen mellom sideforflytning og endring av | ||
| Linje 515: | Linje 661: | ||
==Aksialkrefter i sporveksler== | ==Aksialkrefter i sporveksler== | ||
[[Fil:Aksialkrefter.PNG|thumb|300px|Figur 5.12: Aksialkrefter i 1:12 sporveksel målt i Tyskland]] | |||
I helsveiste sporveksler får vi tilleggskrefter som følge av at to spor går over i | I helsveiste sporveksler får vi tilleggskrefter som følge av at to spor går over i | ||
et spor. Tungene utgjør frie ender i sporvekselen slik at aksialkraften ved | et spor. Tungene utgjør frie ender i sporvekselen slik at aksialkraften ved | ||
| Linje 522: | Linje 669: | ||
Målinger gjort i Tyskland viser at aksialkreftene i sporveksler øker med opptil | Målinger gjort i Tyskland viser at aksialkreftene i sporveksler øker med opptil | ||
40% ved stokkskinneskjøt (figur 5.12). | 40% ved stokkskinneskjøt (figur 5.12). | ||
Selve sporvekselen er som regel meget stiv i horisontalplanet slik at det er | Selve sporvekselen er som regel meget stiv i horisontalplanet slik at det er | ||
| Linje 541: | Linje 686: | ||
===Bruer uten glideskjøt=== | ===Bruer uten glideskjøt=== | ||
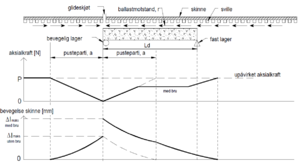
[[Fil:Aksialkraft og bevegelse.PNG|thumb|300px|Figur 5.13: aksialkraft og bevegelse i skinner på bru uten glideskjøt]] | |||
Når en bru uten glideskjøt beveger seg overføres krefter gjennom ballast og | Når en bru uten glideskjøt beveger seg overføres krefter gjennom ballast og | ||
sviller til skinnene. Kraften som overføres påvirker aksialkraften til skinnene. | sviller til skinnene. Kraften som overføres påvirker aksialkraften til skinnene. | ||
| Linje 552: | Linje 698: | ||
symmetriakse, der avstanden til sporet utenfor brua som “holder” igjen er | symmetriakse, der avstanden til sporet utenfor brua som “holder” igjen er | ||
størst. | størst. | ||
'''Maksimal tilleggskraft''' | '''Maksimal tilleggskraft''' | ||
| Linje 562: | Linje 706: | ||
evt. relativ bevegelse mellom ballast og brukar. | evt. relativ bevegelse mellom ballast og brukar. | ||
{| | |||
|<math> \Delta P = {Ld \cdot r \over 2} </math> | |||
| | |||
| | |||
| | |||
|(5.18) | |||
|} | |||
{| | |||
|ΔP= tileggskraft pga bruas bevegelse [N] | |||
|- | |||
|Ld=bruas dilatasjonslengde [m] | |||
|- | |||
|r=ballastmotstand [N/m] | |||
|} | |||
Vi ser at tilleggskraften øker proporsjonalt med dilatasjonslengden og | Vi ser at tilleggskraften øker proporsjonalt med dilatasjonslengden og | ||
| Linje 570: | Linje 728: | ||
skinner på brua vil dette tilsvare en økning på 37 % av maksimal strekkraft | skinner på brua vil dette tilsvare en økning på 37 % av maksimal strekkraft | ||
om vinteren, og en økning på 55 % av maksimal trykkraft om sommeren | om vinteren, og en økning på 55 % av maksimal trykkraft om sommeren | ||
(forutsatt nøytraltemperatur = + | (forutsatt nøytraltemperatur = +21˚C). | ||
Den store økningen i trykkrefter vi kan få fører til økt fare for solslyng. På | Den store økningen i trykkrefter vi kan få fører til økt fare for solslyng. På | ||
| Linje 592: | Linje 750: | ||
===Bruer med glideskjøt=== | ===Bruer med glideskjøt=== | ||
[[Fil:Aksialkraft og lengdebevegelse.PNG|thumb|300px|Figur 5.14: Aksialkraft og lengdebevegelse i skinner på bru med glideskjøt]] | |||
For å unngå for store tillegg i skinnenes aksialkraft må det installeres | For å unngå for store tillegg i skinnenes aksialkraft må det installeres | ||
glideskjøt når bruas dilatasjonslengde blir stor. Ved JBV er kravet at det skal | glideskjøt når bruas dilatasjonslengde blir stor. Ved JBV er kravet at det skal | ||
| Linje 597: | Linje 756: | ||
gjennomgående ballast, og over 100 m for bruer uten ballast. Glideskjøter | gjennomgående ballast, og over 100 m for bruer uten ballast. Glideskjøter | ||
monteres alltid ved bruas bevegelige lager der bruas lengdeendring er størst. | monteres alltid ved bruas bevegelige lager der bruas lengdeendring er størst. | ||
'''Pustepartier''' | '''Pustepartier''' | ||
| Linje 612: | Linje 769: | ||
glideskjøten på en betongbru med dilatasjonslengde på 400 m. | glideskjøten på en betongbru med dilatasjonslengde på 400 m. | ||
'''Eksempel | '''Eksempel''' | ||
{| | |||
|Dilatasjonslengde Ld = 400 m | |||
|- | |||
|Skinneprofil: UIC60, A= 7686 mm<sup>2</sup> | |||
|- | |||
|Ballastmotstand: 7 kN/m = 7 N/mm | |||
|- | |||
|Utvidelseskoeffisient skinne, a<sub>s</sub> = 1,15*10<sup>-5</sup> | |||
|- | |||
|Utvidelseskoeffisient bru, a<sub>b</sub> = 1,0*10<sup>-5</sup> | |||
|- | |||
|Maks temperaturvariasjon skinne, Δt<sub>s</sub> = ± 45˚C | |||
|- | |||
|Maks temperaturvariasjon bru, Δt<sub>b</sub> = ± 20˚C | |||
|} | |||
Maksimallengden av pustepartiene som glideskjøten utløser kan beregnes | Maksimallengden av pustepartiene som glideskjøten utløser kan beregnes | ||
ved hjelp av formel 5.6: | ved hjelp av formel 5.6: | ||
{| | |||
|<math> a ={P \over r}={A \cdot E \cdot \alpha_{s} \cdot \Delta t_{s} \over r}</math> | |||
|} | |||
{| | |||
|<math> ={7686 mm^{2} \cdot 2,07 \cdot 10^5 N/mm^2 \cdot 1,15 \cdot 10^{-5} \cdot 45 \over 7 N/mm}= 117621 mm = 118 m</math> | |||
|} | |||
Maksimal lengdeendring av begge skinnestrenger pga. “pusting” ved | Maksimal lengdeendring av begge skinnestrenger pga. “pusting” ved | ||
| Linje 623: | Linje 804: | ||
skinnebrudd) ved hjelp av formel 5.14: | skinnebrudd) ved hjelp av formel 5.14: | ||
{| | |||
|<math> 2 \cdot \Delta l_{maks}={A \cdot E \cdot \alpha_{s}^2 \cdot \Delta t_{s}^2 \over r}</math> | |||
|} | |||
{| | |||
|<math> ={7686 mm^{2} \cdot 2,07 \cdot 10^5 N/mm^2 (\cdot 1,15 \cdot 10^{-5})^2 \cdot 45^2 \over 7 N/mm}= 61 mm</math> | |||
|} | |||
Vi antar at skinnene følger brukonstruksjonens bevegelse i pustepartiets | Vi antar at skinnene følger brukonstruksjonens bevegelse i pustepartiets | ||
lengde. Det maksimale lengdeendringsbidraget fra bruas bevegelse blir da: | lengde. Det maksimale lengdeendringsbidraget fra bruas bevegelse blir da: | ||
{| | |||
|<math> \Delta l_{bru}=(Ld-a) \cdot \alpha_{b} \cdot \Delta t_{b}</math> | |||
|} | |||
{| | |||
|<math> =(400m-118m) \cdot 10^{-5} \cdot 20 =0,0564 m= 56 mm</math> | |||
|} | |||
Total bevegelse i glideskjøten blir da: 2*(61 mm+56 mm)=234 mm | |||
I eksemplet over er det ikke tatt hensyn til den bevegelsesmotstand brua | I eksemplet over er det ikke tatt hensyn til den bevegelsesmotstand brua | ||
møter i brulagrene og evt. kryp i betongen. | møter i brulagrene og evt. kryp i betongen. | ||
==Litteraturhenvisninger== | ==Litteraturhenvisninger== | ||
*1. Krefter i helsveist spor | *1. Sørlie,Per Hermann. ''Krefter i helsveist spor'',1992 | ||
*2. Overbygning - regler for bygging Jernbaneverkets regelverk JD 531 - 1998 | *2. Jernbaneverket. ''Overbygning - regler for bygging'', Jernbaneverkets regelverk JD 531 - 1998 | ||
*3. Overbygning - regler for vedlikehold Jernbaneverkets regelverk JD 532 - 1998 | *3. Jernbaneverket. ''Overbygning - regler for vedlikehold'', Jernbaneverkets regelverk JD 532 - 1998 | ||
*4. Improved knowledge of forces in CWR Track ERRI D202 Report 3, 1995 | *4. ''Improved knowledge of forces in CWR Track ERRI D202 Report 3'', 1995 | ||
*5. Modern Railway Track | *5. Esveld, Coenraad. ''Modern Railway Track'', 1989 | ||
*6. Die Eisenbahnschiene | *6. Fastenrath, Fritz. ''Die Eisenbahnschiene'', 1977 | ||
*7. Auswirkungen einer nicht gleichmässigen Schienentemperatur auf das gleis | *7. Eisenmann, Josef & Leykauf, Günther. ''Auswirkungen einer nicht gleichmässigen Schienentemperatur auf das gleis'', Eisenbahningeneur 40 (1989) | ||
*8. Brücken als Störstellen für das gleis | *8. Eisenmann, Josef & Leykauf, Günther. ''Brücken als Störstellen für das gleis'', Eisenbahningeneur 38 (1987) | ||
*9. Longitudinal rail forces: The effect of braking and Acceleration | *9. Zarembski, Allan. ''Longitudinal rail forces: The effect of braking and Acceleration'', Railway Track&Structures desember 1994 | ||
*10.A better understanding of continuos welded rail track | *10. Esveld, Coenraad. ''A better understanding of continuos welded rail track'', Rail Engineering International Edition nr. 4 1996 | ||
Siste sideversjon per 23. okt. 2024 kl. 08:13
__NUMBEREDHEADINGS__
Innledning
Den første jernbane som ble åpnet i England i 1826 hadde skinnelengder mindre enn 5 m. Produksjonstekniske fremskritt har siden gjort det mulig åfremstille stadig lengre skinnelengder. I 1945 var skinnelengdene økt til 20 m og rundt 1960 til 40 m. I dag fremstilles det helvalsede skinner på 120 m. Tidlig på 1900-tallet ble det utviklet metoder for å sveise sammen skinner slik at skinner kunne skjøtes uten bruk av lasker. Til tross for dette våget man ikke å sveise sammen lengre skinnelengder enn 30-40 m. Helt frem til midten av vårt århundre var det vanlig å skjøte skinnene sammen med lasker. En lasket skjøt forårsaker store slagpåkjenninger som bryter ned både sporkomponenter og rullende materiell.
Rundt 1950 (1960 i Norge) ble det satt i gang med å sveise skinner sammen til kontinuerlige strenger, dvs. helsveiste skinner. Dette var mulig pga. bedre ballast, sviller, og fremfor alt bedre befestigelse som holdt skinnene bedre fast, og gjorde sporet stivere sideveis.
I dag er over 95 % av Jernbaneverkets hovedspor helsveist spor. Innføring av helsveiste skinner er kanskje det viktigste sportekniske fremskritt i dette århundret. Det helsveiste sporet har medført en dramatisk reduksjon i slitasje på både sporet og det rullende materiell. Men det helsveiste sporet har introdusert nye problemstillinger som kan føre til alvorlig sikkerhetsrisiko dersom de ikke behandles på riktig måte. Problemene knytter seg til de store aksialkreftene som blir låst inne i skinnene. Disse kreftene medfører økt fare for skinnebrudd om vinteren og solslyng i sommerhalvåret.
Aksialkrefter i helsveiste skinner spor kan forårsakes av følgende faktorer:
- temperaturendringer i skinnene
- skinnevandring
- forflytning av sporet i horisontalplanet
- utvalsing (plastisk deformasjon) i skinnehodet
De store trykkreftene som oppstår i et helsveist spor ved høye skinnetemperaturer stiller store krav til sporets komponenter. Sporet må ha tilstrekkelig motstand mot sideveis utknekking for å unngå solslyng. Dette blir behandlet i kapittel 7, “Sporets sidemotstand”.
Aksialkrefter pga. temperaturendringer
Lengdeforandring ved temperaturendring
En skinne som ligger fritt opplagret vil forandre lengde når temperaturen i skinnen forandrer seg (figur 5.1). Skinnen vil utvide seg når temperaturen øker og krympe når temperaturen synker. Lengdeendring avhengig av temperaturendring kan uttrykkes ved hjelp av formel 5.1.
| (5.1) |
der:
| L = opprinnelig lengde [m] |
| ΔL = lengdeendring [m] |
| α = lengdeutvidelseskoeffisient = 1,15*10-5 [m/°C*m] |
| Δt = temperaturendring [°C]. |
Lengdeforandring ved kraftpåvirkning
Dersom vi påfører en ytre kraft i skinnens lengderetning, trykk eller strekk, vil vi forandre skinnens lengde (figur 5.2). Lengdeendringen er avhengig av aksialspenningen i skinnen og kan uttrykkes ved hjelp av formel 5.2.
| (5.2) |
hvor:
| L = opprinnelig lengde [mm] |
| ΔL = lengdeendring [mm] |
| σ= aksialspenning=P/A [N/mm2] |
| E = elastisitetsmodul=2,07*105[N/mm2] |
| P = aksialkraft [N] |
| A = skinnens tverrsnittsareal [mm2]. |
Aksialspenninger
Inne i et helsveist sporavsnitt blir skinnene helt hindret fra å bevege seg pga. friksjonskrefter mellom skinne og sviller og mellom sville og ballast. Ved temperaturendringer vil det derfor opptre aksialspenninger i skinnene i stedet for en lengdeforandring. Vi kan finne et uttrykk for aksialspenningene som opptrer ved å kombinere formel 5.1 og formel 5.2, dvs. forlengelse pga. temperaturendring = forlengelse pga. påført ytre kraft = 0
| (5.3) | |||
Vi ser at aksialspenningene bare er avhengige av temperaturvariasjonen. Skinnelengden er uten betydning. Utvidelseskoeffisienten a og elastisitetsmodulen E kan vi regne som konstante innenfor det temperaturområdet som er aktuelt. Ved å sette inn verdiene for disse faktorene får vi følgende enkle uttrykk:
| (5.4) |
For hver grad temperaturendring i en helsveist skinne vil aksialspenningen altså endres med 2,4 N/mm2.
Aksialkrefter
Aksialkreftene som oppstår finner vi ved å multiplisere med skinnens tverrsnittsareal. S54 og UIC60 skinner har tverrsnittsareal på hhv. 6950 mm2 og 7686 mm2. 1 grads temperaturøkning medfører dermed en kraftøkning på 16680 N (1,6 tonn) for S54-skinne og 18446 N (1,8 tonn) for UIC60 - skinne. Et tyngre skinneprofil medfører m.a.o. større aksialkrefter i et helsveist spor.
Nøytraltemperatur
For å oppnå tilstrekkelig kontroll med kreftene som oppstår i et helsveist spor. er det fastlagt en skinnetemperatur hvor aksialspenningene skal være lik null. Denne temperaturen kalles nøytraltemperaturen. Ved fastsettelse av nøytraltemperaturen må man balansere behovet for sikkerhet mot solslyng opp mot behovet for sikkerhet mot skinnebrudd. En høy nøytraltemperatur fører til mindre trykkrefter i skinnene ved høye temperaturer om sommeren, mens strekkreftene blir desto større ved kulde om vinteren. Ved JBV er nøytraltemperaturen satt til + 21˚C .
Middeltemperaturen
Ved fastsetting av nøytraltemperaturen er det tatt utgangspunkt i middeltemperaturen, dvs. den skinnetemperaturen som ligger midt i mellom høyeste og laveste påregnelige skinnetemperatur. For de fleste steder i Norge regner vi med at skinnetemperaturen kan nå opp til + 55˚C og ned til -30 ˚C. Dette gir en middeltemperatur på + 15˚C. Når nøytraltemperaturen er satt 6˚C høyere skyldes dette at vi ønsker en større sikkerhet mot solslyng. Dette fordi solslyng anses som en større avsporingsrisiko enn skinnebrudd.
Nøytralisering og nøytraltemperaturområdet
Riktig nøytraltemperatur i skinnene tilordnes ved å feste og sveise skinnene sammen ved nøytraltemperatur, eller etter kunstig forlenging av skinnene til en lengde som medfører spenningsfri tilstand ved nøytraltemperatur. Denne arbeidsoperasjonen kalles nøytralisering og blir behandlet i L534 - ”Produksjonsteknikk”. Under nøytralisering ved JBV kan nøytraltemperaturen tilordnes innenfor en toleranse på ± 3˚C, dvs. innenfor temperaturområdet + 18 - 24˚C. Dette kalles nøytraltemperaturområdet.
Maksimale trykk og strekkrefter
Tabell 5.1 viser de maksimale trykk- og strekkrefter vi kan forvente dersom vi forutsetter en nøytraltemperatur på + 21˚C, laveste skinnetemperatur -30˚C og høyeste skinnetemperatur +55˚C.
| Skinneprofil | Tverrsnittsareal | Strekkraft (Δt= 51˚C) | Trykkraft (Δt = 34˚C) |
|---|---|---|---|
| S49 | 6350 mm2 | 777 kN | 518 kN |
| S54 | 6950 mm2 | 850 kN | 567 kN |
| UIC60 | 7686 mm2 | 941 kN | 627 kN |
Maksimalkreftene i tabell 5.1 gjelder for en skinnestreng. De langsgående kreftene for hele sporet blir altså dobbelt så store. Merk også at vi kan få større maksimalkrefter dersom nøytraltemperaturen ikke er som forutsatt.
Pusteparti
Hittil har vi bare sett på hva som skjer inne i et helsveist spor hvor motstanden mot langsgående bevegelse av skinnene er så stor at skinnene er helt fastlåst. Ved hver ende av et helsveist spor, dvs. ved åpne skjøter, vil det ikke være noe som hindrer en bevegelse av skinnen i lengderetningen (bortsett fra evt. motstand i lask). Når vi beveger oss bort fra den åpne skjøten vil det gradvis bygges opp motstand mot bevegelse inntil motstanden er så stor at skinnene er fullstendig hindret fra å bevege seg. Dette partiet kalles pustepartiet (figur 5.3).
I pustepartiet vil spenningene i skinnene gradvis bygges opp i pustepartiet inntil full bevegelseshindring inntreffer. Motstanden mot lengdeforskyvning utgjøres av friksjonen mellom sville og ballast eller mellom skinne og sville. Denne motstanden betegnes som ballastmotstand.
Ballastmotstand
Ballastmotstand er definert som den motstand skinnen møter når den beveger seg eller prøver å bevege seg i sporets lengderetning. Bevegelse i lengderetningen kan foregå på to måter:
1. skinnene “sklir” gjennom befestigelsen mens svillene står i ro
2. skinnene beveger seg sammen med svillene relativt til ballasten
Ved moderne befestigelse er som regel friksjonen mellom skinne og sville betydelig større enn mellom sville og ballast. Bevegelse i pustepartiet vil da skje ved at svillene beveger seg i forhold til ballasten. Ballastmotstanden uttrykkes gjerne ved motstand pr. lengdeenhet. Dersom vi kjenner motstanden som hver enkelt sville yter, finner vi ballastmotstanden ved å dividere med svilleavstanden. Det er vanlig å regne ballastmotstanden pr. skinnestreng, dvs. pr. halve sville
| (5.5) |
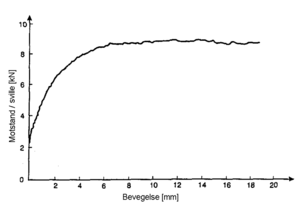
Figur 5.4 viser ballastmotstanden målt av British Rail på et betongsvillespor
med Pandrol befestigelse. Vi ser at motstanden ved små forskyvninger er
avhengig av hvor stor bevegelse som finner sted, mens motstanden når en
konstant verdi på ca. 9 kN etter 4 - 6 mm bevegelse. Med svilleavstand på
0,6 m gir dette en ballastmotstand på 7,5 kN/m (pr. skinnestreng).
Det er vanlig å regne ballastmotstanden i et normalt konsolidert spor med god befestigelse til 7-10 kN/m pr. skinnestreng. Ballastmotstanden kan imidlertid variere sterkt. Nyjustert spor kan ha langt lavere ballastmotstand mens spor med frosset ballast kan ha ballastmotstand opp til 15 - 20 kN/m pr. skinnestreng. Moderne befestigelsessystemer har en typisk forskyvningsmotstand på 10 - 15 kN pr. befestigelsespunkt, noe som gir en motstand på 17 - 25 kN/m ved 60 cm svilleavstand. For spor med dårlig befestigelse som yter dårlig lengdeforskyvningsmotstand kan imidlertid motstand mellom sville og skinne bli bestemmende ballastmotstand ved at skinnene beveger seg relativt til svillene.
Lengde av pusteparti
Lengden av et pusteparti er avhengig av ballastmotstanden og hvor stor aksialkraft vi har i det fastlåste partiet. Dersom vi antar en konstant ballastmotstand kan vi beregne lengden av pustepartiet etter formel 5.6.
| (5.6) |
hvor:
| a = pustepartiets lengde [m] |
| P = kraft i fastlåst parti av helsveist spor [N] |
| R = motstand i evt. lask [N] |
| r = ballastmotstand [N/m]. |
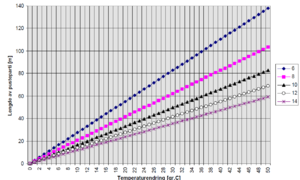
Motstanden i evt. lask kan settes til ca. 100 kN. Figur 5.5 viser hvor lange pustepartiene blir i et S54-spor avhengig av ballastmotstanden og temperaturendring i forhold til nøytraltemperaturen. Hver linje i diagrammet representerer en ballastmotstand [kN/m]. Det er i diagrammet sett bort fra motstand i evt. lask.
Lengde av pusteparti
Lengden av et pusteparti er avhengig av ballastmotstanden og hvor stor aksialkraft vi har i det fastlåste partiet. Dersom vi antar en konstant ballastmotstand kan vi beregne lengden av pustepartiet etter formel 5.6.
(5.6)
Motstanden i evt. lask kan settes til ca. 100 kN. Figur 5.5 viser hvor lange pustepartiene blir i et S54-spor avhengig av ballastmotstanden og temperaturendring i forhold til nøytraltemperaturen. Hver linje i diagrammet representerer en ballastmotstand [kN/m]. Det er i diagrammet sett bort fra motstand i evt. lask.
For et normalt godt konsolidert spor kan vi få pustepartier på opptil 80 -100 m, mens vi for et spor med dårlig ballastmotstand gjerne kan få pustepartier på opp til 130-140 m ved ekstremt lave skinnetemperaturer. Det er viktig å være klar over at vi utløser pustepartier med tilhørende bevegelse av skinnene hver gang vi bryter skinnestrengen som f.eks. ved skinnebrudd eller når vi kapper skinnene for å legge inn et skinnekapp. Dersom vi ikke tar hensyn til dette når vi sveiser skinnene sammen igjen vil vi ikke oppnå riktig nøytraltemperatur i området hvor det har vært langsgående bevegelse av skinnene.
Bruddåpning ved skinnebrudd
Når det oppstår skinnebrudd ved lav temperatur vil det oppstå en bruddåpning som resultat av at bruddet utløser pustepartier hvor skinnene beveger seg fra hverandre. Størrelsen av bruddåpningen vil være en funksjon av ballastmotstanden og hvor stor aksialkraften var i skinnen når bruddet oppsto. Figur 5.6 viser kraftlikevekt i et skinneelement, u som befinner seg i en avstand x fra bruddstedet. Dersom r er ballastmotstanden, x er avstand fra bruddstedet og P er aksialkraften i skinnen har vi at:
| (5.7) | |
Dersom Δu er lengdeendring i skinneelementet vil Δu/Δx representere den totale aksialspenning i elementet. Den termiske andel av aksialspenningen er aΔt hvor a er utvidelseskoeffisienten og Δt er temperaturendring i forhold til nøytraltemperaturen. For å finne den mekaniske andel av aksialspenningen må vi trekke fra den termiske andelen. Dermed kan vi finne aksialkraften P:
| (5.8) |
Ved å sette inn formel 5.8 i formel 5.7 får vi følgende differensialligning:
| (5.9) |
Løsningen av 5.9 kan uttrykkes som:
| (5.10) |
Skinnebruddet utløser bevegelse i skinnene i hele pustepartiets lengde a. Dette gir oss følgende grensebetingelser:
| ved x=0 |
| ved x=a | og |
De 3 grensebetingelsene bestemmer a, c1 og c2. Det endelige uttrykket for u og a blir dermed:
| (5.11) |
| (5.12) |
Bruddåpning ved skinnebrudd vil være 2 ganger skinnens bevegelse ved bruddstedet, dvs:
| (5.13) |
Ved å sette 5.12 inn i 5.13 får vi følgende uttrykk for bruddåpningens størrelse:
| (5.14) |
| LB= bruddåpning [mm] |
| A=skinnens tverrsnittsareal [mm2] |
| E=elastisitetesmodul [2,07*105 N/mm2] |
| a=utvidelseskoeffisient [1,15*10-5 m/°C*m] |
| Δt = temp.forskjell nøytraltemperatur-skinnetemperatur ved brudd [°C] |
| r=ballastmotstand [N/mm] |
Vi ser at bruddåpningen er omvendt proporsjonal med ballastmotstanden og øker med kvadratet av temperaturforskjellen mellom nøytraltemperatur og bruddtemperatur. Figur 5.7 viser bruddåpning ved skinnebrudd i et spor med S54-skinner. De forskjellige linjene i diagrammet representerer ballastmotstanden [kN/m].
Aksialkrefter pga. skinnevandring
Når tog akselererer eller bremser ned blir det ledet langsgående krefter fra toget til skinnene. Forsøk gjort i USA viser at aksialkrefter opp til 260 kN blir overført til skinnene ved oppbremsing og akselerasjon av tunge godstog. Skinnevandring er en gradvis lengdeforskyvning av skinnene som resulterer i endring av nøytraltemperaturen. Problemet er størst på steder hvor det vanligvis oppstår kraftig oppbremsing eller akselerasjon (foran signaler, sterk stigning/fall mm.).
Tilleggskrefter og restkrefter
Krefter som overføres ved bremsing og akselerasjon kan ikke alene utløse solslyng eller skinnebrudd, men ved et fra før av høyt spenningsnivå i skinnene kan disse tilleggskreftene bidra i negativ retning. Tester (også fra USA) viser at akselerasjon/bremsing ikke bare overfører krefter i det toget passerer, men at restkrefter på opp til 45 kN blir “igjen” i skinnene etter at toget har passert. Dette beror på at det har funnet sted en langsgående bevegelse i skinnene (Resultatene fra tester utført i USA med tunge godstog kan selvfølgelig ikke overføres direkte til europeiske forhold med langt lavere aksellaster og togvekter).
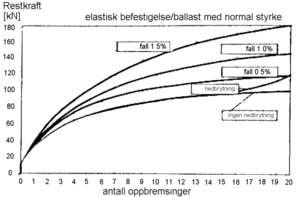
Beregningsmodell
Ved Krakow tekniske universitet i Polen er det utarbeidet en modell for beregning av restkrefter som oppstår i skinnene ved oppbremsing, “CREEP”. Figur 5.8 viser et eksempel av beregninger etter denne modellen ved oppbremsing i spor med hhv. 15, 10, og 5 ‰ fall. I dette eksemplet er det valgt en vertikal last på 86,25 kN/m i en lengde på 640 m.
Figuren viser kraftøkninger opp til 180 kN ved oppbremsing i spor med 15 ‰ fall. Dersom sporet har UIC60 skinner, tilsvarer dette en reduksjon av nøytraltemperaturen på 10˚C.
Skinnevandring i dobbeltspor
Også i spor uten stigning og oppbremsing/akselerasjon kan vi ha skinnevandring. Skinnene vandrer i kjøreretningen og forekommer følgelig hovedsaklig på dobbeltsporstrekninger. Årsaken til denne bevegelsen synes å være sporets bølgebevegelse i vertikalplanet ved togpassering. Løftebølgen foran hjulet forårsaker en tøyning av skinnefoten. Tøyningen resulterer i en liten bevegelse forover av skinnen fordi forskyvningsmotstanden er mindre her enn under den belastede delen av sporet. Når hjulet har passert, vil skinnen bak hjulet igjen bevege seg noe forover pga. at skinnefoten trekker seg sammen igjen.
Dynamisk forskyvningsmotstand
Skinnevandring motvirkes først og fremst gjennom å anvende befestigelse og ballast med god lengdeforskyvningsmotstand. I avsnitt 2.3.1 så vi på den statiske forskyvningsmotstanden til ballast og befestigelse, dvs. motstand mot langsgående bevegelse uten vertikale laster. Skinnevandring er imidlertid avhengig av den dynamiske forskyvningsmotstanden, dvs. motstand ved togpassering. Den dynamiske forskyvningsmotstanden i befestigelsen ligger normalt langt lavere enn den statiske. Befestigelsens forskjellige egenskaper blir behandlet i L533 “Sporets komponenter”, kap. 4.
Aksialkrefter pga. sideforflytning
Ved sideforflytning av sporet i kurver endrer vi lengden av skinnene i det partiet som blir flyttet, dvs. at skinnene blir strukket, eller trykket sammen. Dersom vi flytter sporet innover i kurven som vist på figur 5.9, vil dette medføre en reduksjon i nøytraltemperaturen. Dersom vi flytter kurven utover, vil det medføre en økning i nøytraltemperaturen.
Figur 5.10 viser en sirkelsektor med vinkel ﬩,radius R og en skinnelengde (buelengde) L. Dersom vi sideforflytter sporet med DR endres skinnelengden DL. Formel 5.15 og formel 5.16 viser sammenhengen mellom radius og skinnelengde.
| (5.15) |
| (5.16) |
Lengdeendringen ΔL som finner sted påvirker nøytraltemperaturen i skinnene. Sammenhengen mellom lengdeendring og temperaturendring i skinnene finner vi i formel 5.1. Vi kan da sette opp følgende ligning:
Ved å sette inn formel 5.15 for skinnelengden L får vi videre:
| (5.17) |
| Δt = endring i nøytraltemperatur [°C] |
| R = kurveradius [m] |
| ΔR = sideforflyttning [m] |
| α= lengdeutvidelseskoeffisient [1,15*10-5m/m*°C ] |
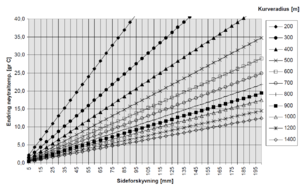
Figur 5.11 viser sammenhengen mellom sideforflytning og endring av nøytraltemperaturen ved forskjellige kurveradier.
Eks: En sideforflytning på 10 cm i en kurve med radius = 300 m vil medføre en endring av nøytraltemperaturen på 28˚C.
Sporjustering i kaldt vær
Vi ser at nøytraltemperaturen blir mest påvirket ved sideforflytning i kurver med små radier. Problemer med at sporet flytter seg i kurver er utbredt i Norge. Dette skyldes i hovedsak sporjustering i kaldt vær hvor strekkreftene i skinnene er så store at sporjusteringsmaskinen ikke klarer å legge sporet tilbake der det skal være, men trekker sporet innover i kurven. Men også manglende ballastskulder kan føre til at sporet flytter seg innover i streng kulde.
Det er derfor viktig at temperaturgrensene for sporjustering overholdes [JD 532, kap 10]. Justering av sporet skal bare utføres innenfor temperaturområder som angitt i tabell 5.2.
| Kurveradius | Toleranse |
|---|---|
| R < 350 m | 15 mm |
| 351 m < R < 500 m | 20 mm |
| 501 m < R < 750 m | 30 mm |
| R > 750 m | 40 mm |
| Kurveradius | Temperaturintervall |
|---|---|
| ≥800 m | 0 - +35˚C |
| 400 - 800 m | +5 - +30˚C |
| ≤ 400 m | +10 - +30˚C |
VUL/GVUL
For å holde kontroll med aksialkreftene i skinnene er det helt nødvendig å vite hvor sporet ligger i forhold til posisjonen sporet hadde ved nøytralisering. Det er derfor nødvendig med et kontrollsystem hvor man kan måle inn sporets posisjon i forhold til referansepunkter i terrenget (VUL/GVUL). Hvordan disse systemene er bygd opp beskrives i L531 “Sporets trase”, kap.7. JD 532 setter grenser for hvor stort avvik sporets sidebeliggenhet kan ha (tabell 5.3). Derom disse grensene overskrides, må sporet bakses på plass, eller evt. må sporet nøytraliseres på nytt.
Aksialkrefter i sporveksler
I helsveiste sporveksler får vi tilleggskrefter som følge av at to spor går over i et spor. Tungene utgjør frie ender i sporvekselen slik at aksialkraften ved tungespiss vil være lik 0. Aksialkreftene i tungestrengen overføres i stedet gjennom svillene til skinnene som går kontinuerlig gjennom sporvekselen. Hvor store krefter som overføres er avhengig av hvor stive svillene er. Målinger gjort i Tyskland viser at aksialkreftene i sporveksler øker med opptil 40% ved stokkskinneskjøt (figur 5.12).
Selve sporvekselen er som regel meget stiv i horisontalplanet slik at det er liten fare for utknekking her. Derimot er sporet foran stokkskinneskjøt spesielt utsatt for solslyng ettersom kraftøkningen også påvirker sporet utenfor sporvekselen.
Aksialkrefter i skinner på bruer
I likhet med skinnene er også bruer utsatt for temperaturendringer. De fleste bruer er utstyrt med et eller flere bevegelige lagre slik at lengdebevegelse av brua tillates ved temperaturendring. Selv om det er forholdsvis små forskjeller i utvidelseskoeffisient for bru og skinne, vil den store forskjellen i oppvarmings- og avkjølingshastighet føre til relativ bevegelse mellom bru og skinne. Dessuten har vi forskjellige ekstremtemperaturer for bru og skinne. Relativ bevegelse mellom bru og skinne fører til en overlagring av aksialkrefter i skinnene.
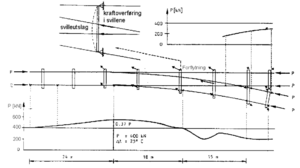
Bruer uten glideskjøt
Når en bru uten glideskjøt beveger seg overføres krefter gjennom ballast og sviller til skinnene. Kraften som overføres påvirker aksialkraften til skinnene. Figur 5.13 viser et forenklet bilde av aksialkraft og lengdebevegelse i en bru med et spenn. Vi ser at bevegelse av brua fører til en økning av aksialkraft ved bruas bevegelige lager, mens vi får en kraftreduksjon ved det faste lageret. Bevegelse av brua påvirker ikke bare kraftbildet i skinnene inne på brua, men også sporet utenfor blir påvirket. Brubevegelsens påvirkning av skinnenes aksialkraft er forbundet med en lengdebevegelse av skinnene. Den største bevegelsen finner sted ved bruas symmetriakse, der avstanden til sporet utenfor brua som “holder” igjen er størst.
Maksimal tilleggskraft
Hvor store krefter som kan overføres er avhengig av bruas dilatasjonslengde og ballastmotstanden. Formel 5.18 gir maksimal tilleggskraft ved det bevegelige lageret. Vi forutsetter her konstant ballastmotstand og ser bort fra evt. relativ bevegelse mellom ballast og brukar.
| (5.18) |
| ΔP= tileggskraft pga bruas bevegelse [N] |
| Ld=bruas dilatasjonslengde [m] |
| r=ballastmotstand [N/m] |
Vi ser at tilleggskraften øker proporsjonalt med dilatasjonslengden og
ballastmotstanden. For bruer med gjennomgående ballast kan vi regne med
en ballastmotstand på 7 kN/m. For en bru med dilatasjonslengde på 100 m
gir dette en maksimal kraftoverføring på 350 kN. Dersom vi har UIC60-
skinner på brua vil dette tilsvare en økning på 37 % av maksimal strekkraft
om vinteren, og en økning på 55 % av maksimal trykkraft om sommeren
(forutsatt nøytraltemperatur = +21˚C).
Den store økningen i trykkrefter vi kan få fører til økt fare for solslyng. På brua har som regel sporet god sideforskyvningsmotstand. Det er spesielt sporet på land ved det bevegelige lageret som er utsatt.
Om vinteren kan frosset ballast føre til høyere ballastmotstand. Dermed øker kraftoverføringen og vi kan få svært høye strekkspenninger i skinnene i ugunstige tilfeller, noe som øker faren for skinnebrudd.
På mange stålbruer er brusvillene festet direkte til brua. Det er da lengdeforskyvningsmotstanden i befestigelsen som avgjør hvor store krefter brua kan overføre til skinnene. Ved “vanlig” type befestigelse får vi uakseptable store tilleggskrefter. Skinner på stålbruer uten ballast og uten glideskjøt er derfor som regel festet med en spesiell type befestigelse som tillater skinnene å bevege seg relativt fritt i forhold til svillene. Dvs. at ballastmotstanden, og dermed kraftoverføringen blir svært liten. Ulempen med denne type befestigelse er at vi kan få store bruddåpninger ved evt. skinnebrudd. Det er derfor begrensninger i hvor lange lengder man kan ha denne type befestigelse. Ved JBV tillates maks. 100 m.
Bruer med glideskjøt
For å unngå for store tillegg i skinnenes aksialkraft må det installeres glideskjøt når bruas dilatasjonslengde blir stor. Ved JBV er kravet at det skal være glideskjøt dersom dilatasjonslengden er over 120 m for bruer med gjennomgående ballast, og over 100 m for bruer uten ballast. Glideskjøter monteres alltid ved bruas bevegelige lager der bruas lengdeendring er størst.
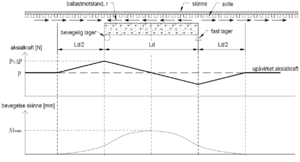
Pustepartier
Figur 5.14 viser aksialkraft og bevegelse i skinner på en bru med 1 spenn og glideskjøt. Ved glideskjøten kan skinnene bevege seg helt fritt i lengderetningen, noe som fører til at aksialkraften faller til 0. De frie endene som glideskjøten representerer medfører pustepartier med lengdebevegelse av skinnene.
Ulempen med glideskjøter er at vi får store bevegelser av sviller og skinner ved skjøten. Etterfølgende eksempel viser hvor store bevegelser vi får ved glideskjøten på en betongbru med dilatasjonslengde på 400 m.
Eksempel
| Dilatasjonslengde Ld = 400 m |
| Skinneprofil: UIC60, A= 7686 mm2 |
| Ballastmotstand: 7 kN/m = 7 N/mm |
| Utvidelseskoeffisient skinne, as = 1,15*10-5 |
| Utvidelseskoeffisient bru, ab = 1,0*10-5 |
| Maks temperaturvariasjon skinne, Δts = ± 45˚C |
| Maks temperaturvariasjon bru, Δtb = ± 20˚C |
Maksimallengden av pustepartiene som glideskjøten utløser kan beregnes
ved hjelp av formel 5.6:
Maksimal lengdeendring av begge skinnestrenger pga. “pusting” ved
glideskjøten finner vi (på samme måte som vi fant bruddåpning ved
skinnebrudd) ved hjelp av formel 5.14:
Vi antar at skinnene følger brukonstruksjonens bevegelse i pustepartiets lengde. Det maksimale lengdeendringsbidraget fra bruas bevegelse blir da:
Total bevegelse i glideskjøten blir da: 2*(61 mm+56 mm)=234 mm
I eksemplet over er det ikke tatt hensyn til den bevegelsesmotstand brua møter i brulagrene og evt. kryp i betongen.
Litteraturhenvisninger
- 1. Sørlie,Per Hermann. Krefter i helsveist spor,1992
- 2. Jernbaneverket. Overbygning - regler for bygging, Jernbaneverkets regelverk JD 531 - 1998
- 3. Jernbaneverket. Overbygning - regler for vedlikehold, Jernbaneverkets regelverk JD 532 - 1998
- 4. Improved knowledge of forces in CWR Track ERRI D202 Report 3, 1995
- 5. Esveld, Coenraad. Modern Railway Track, 1989
- 6. Fastenrath, Fritz. Die Eisenbahnschiene, 1977
- 7. Eisenmann, Josef & Leykauf, Günther. Auswirkungen einer nicht gleichmässigen Schienentemperatur auf das gleis, Eisenbahningeneur 40 (1989)
- 8. Eisenmann, Josef & Leykauf, Günther. Brücken als Störstellen für das gleis, Eisenbahningeneur 38 (1987)
- 9. Zarembski, Allan. Longitudinal rail forces: The effect of braking and Acceleration, Railway Track&Structures desember 1994
- 10. Esveld, Coenraad. A better understanding of continuos welded rail track, Rail Engineering International Edition nr. 4 1996