Underbygning/Frost: Forskjell mellom sideversjoner
(Ny side: == Innledning == Telehiv med tilhørende hastighetsnedsettelser og forsinkelser i togtrafikken er et velkjent problem. Jernbanen har slitt med dette gjennom alle år, og vesentlige tiltak ...) |
(rettet referanse) |
||
| (21 mellomliggende versjoner av 3 brukere er ikke vist) | |||
| Linje 1: | Linje 1: | ||
__NUMBEREDHEADINGS__ | |||
== Innledning == | == Innledning == | ||
| Linje 34: | Linje 35: | ||
I dette avsnittet beskrives de fysiske mekanismene som fører til telehiv og telefarlige jordarter beskrives. I tillegg deles jordartene inn i telefarlighetsklasser. | I dette avsnittet beskrives de fysiske mekanismene som fører til telehiv og telefarlige jordarter beskrives. I tillegg deles jordartene inn i telefarlighetsklasser. | ||
| Linje 41: | Linje 40: | ||
Tre faktorer er nødvendige for at telehiv skal kunne oppstå: | Tre faktorer er nødvendige for at telehiv skal kunne oppstå: | ||
Tilgang på vann | *Tilgang på vann | ||
Temperatur i jordarten under frysepunktet for vann | *Temperatur i jordarten under frysepunktet for vann | ||
Telefarlig jordart | *Telefarlig jordart | ||
Dersom èn av disse faktorene ikke er tilstede vil telehiv ikke kunne opptre. | Dersom èn av disse faktorene ikke er tilstede vil telehiv ikke kunne opptre. | ||
| Linje 49: | Linje 48: | ||
Det er to faktorer som bidrar til størrelsen på telehiv: | Det er to faktorer som bidrar til størrelsen på telehiv: | ||
≈ 9% utvidelse av porevann under frysing | *≈ 9% utvidelse av porevann under frysing | ||
dannelse av islinser ved frysefronten | *dannelse av islinser ved frysefronten | ||
Det at porevannet i jordartene utvider seg med 9% når det fryser ble lenge sett på som årsaken til telehiv. Hovedårsaken til telehiv er imidlertid at ekstra vann suges opp til frysefronten og fryser ut som rene lag av is (islinser). Dannelsen av islinser kan gi en ekspansjon som langt overstiger volumøkingen av porevannet. | Det at porevannet i jordartene utvider seg med 9% når det fryser ble lenge sett på som årsaken til telehiv. Hovedårsaken til telehiv er imidlertid at ekstra vann suges opp til frysefronten og fryser ut som rene lag av is (islinser). Dannelsen av islinser kan gi en ekspansjon som langt overstiger volumøkingen av porevannet. | ||
| Linje 60: | Linje 59: | ||
En jordart regnes som telefarlig hvis den har evne til å trekke opp vann kapilært og skille det ut som islinser ved frysfronten. Telefarlighet av jordartene er knyttet opp til porestørrelsen. | En jordart regnes som telefarlig hvis den har evne til å trekke opp vann kapilært og skille det ut som islinser ved frysfronten. Telefarlighet av jordartene er knyttet opp til porestørrelsen. | ||
I finkornige og finstoffholdige jordarter (silt, leire og morene) er porene så små at isen møter hindring mot å trenge ned i poresystemet. Overflatespenningen mellom is og vann og små poreradier fører til at frysepunktet for vann synker under | I finkornige og finstoffholdige jordarter (silt, leire og morene) er porene så små at isen møter hindring mot å trenge ned i poresystemet. Overflatespenningen mellom is og vann og små poreradier fører til at frysepunktet for vann synker under 0<sup>o</sup>C. Da oppstår et undertrykk (sug) i porene under isfronten. Undertrykket bidrar til at det trekkes opp vann til frysefronten fra underliggende jordlag eller fra grunnvannet. Telemekanismen i finkornige jordarter er en meget komplisert prosess. Det praktiske resultatet er imidlertid at vanninnholdet øker og at det dannes mer eller mindre rene islag i jorda. | ||
I silt kan det under ugunstige betingelser utvikles betydelige islinser, enten jevnt fordelt i mange tynne skikt eller konsentrert i flere centimeter tykke islag. I leire vil den lave permeabiliteten begrense vanntransporten. I feite leirer oppstår det også en krymping av leirmaterialet mellom islinsene på grunn av at vann suges ut og konsentreres i islinsene. Det kan derfor bli relativt liten telehiving i homogen leire. Men i leire som er sprukket eller lagdelt kan det tilføres rikelig med vann til å utvikle store islinser. | I silt kan det under ugunstige betingelser utvikles betydelige islinser, enten jevnt fordelt i mange tynne skikt eller konsentrert i flere centimeter tykke islag. I leire vil den lave permeabiliteten begrense vanntransporten. I feite leirer oppstår det også en krymping av leirmaterialet mellom islinsene på grunn av at vann suges ut og konsentreres i islinsene. Det kan derfor bli relativt liten telehiving i homogen leire. Men i leire som er sprukket eller lagdelt kan det tilføres rikelig med vann til å utvikle store islinser. | ||
| Linje 73: | Linje 72: | ||
I Norge er det vanlig å dele jordartene inn i 4 klasser etter bæreevneegenskapene i teleløsningsperioden: | I Norge er det vanlig å dele jordartene inn i 4 klasser etter bæreevneegenskapene i teleløsningsperioden: | ||
T1 | T1 = Ikke telefarlig | ||
T2 | |||
T3 | T2 = Litt telefarlig | ||
T4 | |||
T3 = Middels telefarlig | |||
T4 = Meget telefarlig | |||
Når en jordart betegnes som ikke telefarlig, betyr det at en underbygning som består av denne jordarten under normale forhold ikke vil utsettes for heving og synking når jorden fryser og tiner. | Når en jordart betegnes som ikke telefarlig, betyr det at en underbygning som består av denne jordarten under normale forhold ikke vil utsettes for heving og synking når jorden fryser og tiner. | ||
| Linje 82: | Linje 84: | ||
Når frosten trenger ned i en telefarlig jordart, oppstår islinser som følge av kapillær vannoppsuging fra underliggende lag. Dette medfører at formasjonsplanet (FP) løftes under nedfrysningen, og synker i tineperioden. Dette kalles for telehiv. Telehivet blir trolig størst jo tidligere på vinteren frosten trenger ned i telefarlig grunn. Dette fordi telehivdannelsen tar tid, da vann hele tiden må transporteres til frysefronten for å øke telehivet. | Når frosten trenger ned i en telefarlig jordart, oppstår islinser som følge av kapillær vannoppsuging fra underliggende lag. Dette medfører at formasjonsplanet (FP) løftes under nedfrysningen, og synker i tineperioden. Dette kalles for telehiv. Telehivet blir trolig størst jo tidligere på vinteren frosten trenger ned i telefarlig grunn. Dette fordi telehivdannelsen tar tid, da vann hele tiden må transporteres til frysefronten for å øke telehivet. | ||
Jordmaterialer som anvendes i frostsonen, skal være av typen "Ikke telefarlig". Telefarlighet bedømmes ut fra den korngradering materialet har, se tabell .1. | Jordmaterialer som anvendes i frostsonen, skal være av typen "Ikke telefarlig". Telefarlighet bedømmes ut fra den korngradering materialet har, se tabell 6.1. | ||
Tabell 6.1 Norsk telefarlighetsklassifisering | Tabell 6.1 Norsk telefarlighetsklassifisering | ||
{| class="wikitable" width="45%" | |||
|- | |||
! rowspan="2" |Benevnelse !! rowspan="2" | Telekasse !! colspan="2" | Masseprosent (av materiale < 19,0 mm) !! rowspan="2" |Eksempel på jordarter | |||
|- | |||
! < 0,02 mm || < 0,2 mm | |||
|- | |||
| Ikke telefarlig || align="center" | T1 ||align="center" | <math>\le 3 \%</math> || || Sand | |||
Grus | |||
Torv | |||
Myrjord | |||
|- | |||
| Litt telefarlig || align="center" | T2 || align="center" | <math> > 3 - 12 \le \%</math> || || Sand | |||
< | |||
Sand | |||
Grus | Grus | ||
Morene (sandig, grusig) | Morene (sandig, grusig) | ||
Middels telefarlig | |- | ||
T3 | | Middels telefarlig || align="center" | T3 || align="center" | <math> > 12 \%</math> || align="center" | <math> > 50 \%</math> || Sand | ||
> 12 % | |||
< 50 % | |||
Sand | |||
Morene (leirig) | Morene (leirig) | ||
Leire med mer enn 40 % < 0,002 mm | Leire med mer enn 40 % < 0,002 mm | ||
Meget | |- | ||
T4 | | Meget telefarlig || align="center" | T4 || align="center" |<math> > 12 \%</math> || align="center" |<math>> 50 \%</math> || Leire med mindre enn 40 % < 0,002 | ||
> 12 % | |||
> 50 % | |||
Leire med mindre enn 40 % < 0, | |||
Silt | Silt | ||
Morene (siltig) | Morene (siltig) | ||
|} | |||
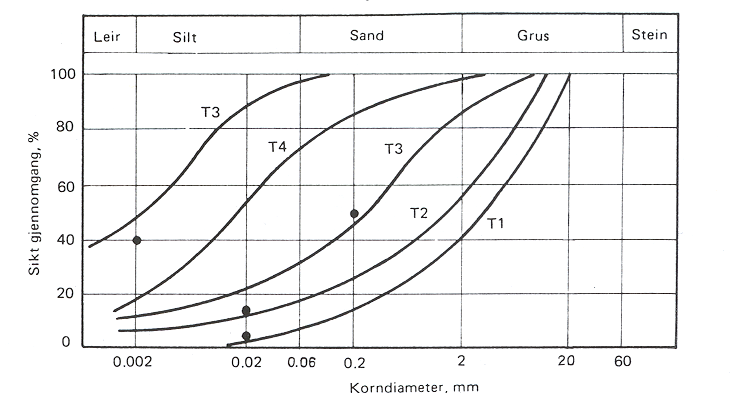
Telefarlighetskriteriet kan uttrykkes slik: "For at et materiale ikke skal være telefarlig, må masseprosenten av materialet < 0,02 mm ikke være større enn 3% beregnet av materiale som passerer 19 mm sikt". I figur 6.1 vises eksempler på korngraderingskurver for materialer innen de forskjellige telefarlighetsgruppene. | |||
[[Fil:Fig521-601.png|800px]] | |||
Figur 6.1 Eksempler på kornfordelingskurver for jordmaterialer innen de enkelte telefarlighetsgrupper | Figur 6.1 Eksempler på kornfordelingskurver for jordmaterialer innen de enkelte telefarlighetsgrupper | ||
| Linje 140: | Linje 133: | ||
Følgende formel gir tilnærmet kapillær stigehøyde for jordarter: | Følgende formel gir tilnærmet kapillær stigehøyde for jordarter: | ||
{| width="300px" align="center" | |||
|- | |||
| h<sub>c</sub> = <math>\frac {0,3} {e \cdot d_10}</math> || (6.1) | |||
|} | |||
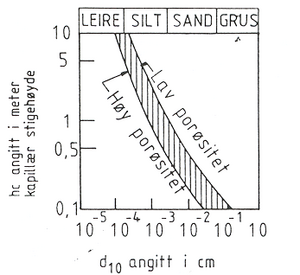
hvor e er materialets poretall gitt ved e = <math>\frac {V_p} {V} (\%)</math> og er et uttrykk for andelen ”hulrom” mellom kornene i jordarten. d10 angir kornstørrelsen for et materiale ved 10 % gjennomgang på et kvadratsikt, dvs. d<sub>10</sub> betyr at 10% av materialet har mindre korndiameter enn d<sub>10</sub> | |||
I figur 6.2 er det samme forholdet vist utregnet for varierende materialer. | |||
[[Fil:Fig521-602.png|300px]] | |||
Figur 6.2 Kapillær stigehøyde i jord | Figur 6.2 Kapillær stigehøyde i jord | ||
== Frostdimensjonering == | == Frostdimensjonering == | ||
=== Grunnlag for termisk dimensjonering === | === Grunnlag for termisk dimensjonering === | ||
==== Varmestrøm gjennom vegg ==== | ==== Varmestrøm gjennom vegg ==== | ||
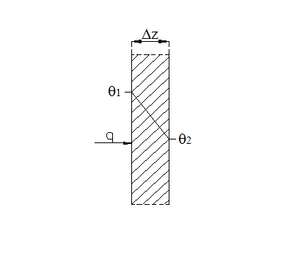
Frostdimensjonering tar utgangspunkt i vanlige betraktninger av varmestrøm gjennom en vegg, jf. figur .3. Ved en gitt temperaturgradient, dvs. ved en konstant temperaturforskjell mellom de to sidene av veggen, vil varmestrømmen gjennom veggen være konstant, og kan uttrykkes slik: | Frostdimensjonering tar utgangspunkt i vanlige betraktninger av varmestrøm gjennom en vegg, jf. figur 6.3. Ved en gitt temperaturgradient, dvs. ved en konstant temperaturforskjell mellom de to sidene av veggen, vil varmestrømmen gjennom veggen være konstant, og kan uttrykkes slik: | ||
{| width="300px" align="center" | |||
|- | |||
| q = <math>\frac {\lambda (\theta_2 - \theta_1)} {\Delta Z}</math> || (6.2) | |||
|} | |||
der: | |||
*<math>\lambda </math>er veggens varmeledningsevne, | |||
*<math>(\theta_2 - \theta_1)</math> er temperaturforskjell mellom de to sidene av veggen, og | |||
*<math>\Delta Z</math> er veggens tykkelse. | |||
[[Fil:Fig521-603.png|300px]] | |||
Figur 6.3 Varmestrøm gjennom en vegg | Figur 6.3 Varmestrøm gjennom en vegg | ||
==== Varmelagring ==== | ==== Varmelagring ==== | ||
Varmelagring i et legeme ved tilførsel av en varmemengde | Varmelagring i et legeme ved tilførsel av en varmemengde Q er gitt ved følgende sammenheng: | ||
{| width="300px" align="center" | |||
|- | |||
| <math>(\theta_2 - \theta_1) \cdot C \cdot V = Q</math> || (6.3) | |||
|} | |||
der: | der: | ||
*<math>(\theta_2 - \theta_1)</math> er temperaturforskjell i legemet før og etter varmetilføringen, | |||
*C er legemets volumetriske varmekapasitet, | |||
*V er legemets volum | |||
En tilført varmemengde gir altså en temperaturøkning i legemet avhengig av den volumetriske varmekapasitet. | En tilført varmemengde gir altså en temperaturøkning i legemet avhengig av den volumetriske varmekapasitet. | ||
| Linje 176: | Linje 189: | ||
Frysing eller tining av et materiale som inneholder vann frigjør eller binder en varmemengde proporsjonal med materialets frysevarme: | Frysing eller tining av et materiale som inneholder vann frigjør eller binder en varmemengde proporsjonal med materialets frysevarme: | ||
{| width="300px" align="center" | |||
|- | |||
| <math>Q = L \cdot V</math> || (6.4) | |||
|} | |||
L | der: | ||
*Q er frigjort varme, | |||
*L er volumetrisk frysevarme, og | |||
*V er volum som tiner eller fryser. | |||
=== Grunnlag for frostdimensjonering | L kan skrives som <math>W \cdot \rho_d \cdot l</math>, | ||
hvor: | |||
*w er vektandel vann, | |||
*<math>\rho_d</math> er tørr romvekt for materialet, og | |||
*l er vannets frysevarme (= 4,2 MJ/m<sup>3</sup>). | |||
=== Grunnlag for frostdimensjonering === | |||
==== Frostmengde og ”hundreårsfrosten” ==== | ==== Frostmengde og ”hundreårsfrosten” ==== | ||
Frostmengder beregnes med enheten | Frostmengder beregnes med enheten h<sup>o</sup>C eller ”frosttimegrader”, som er et uttrykk for summen av produktet av døgnmiddeltemperaturen og antall timer i frostperioden. Eksempel: Hvis det i et døgn er gjennomsnittlig 10 minusgrader, blir døgnets frostmengde 24 h x 10 = 240 frosttimegrader. | ||
Hundreårsfrosten, | Hundreårsfrosten, F<sub>100</sub>, er for mange et velkjent begrep. Vi avgrenser oss her til å definere begrepet slik det defineres i Bane NORs tekniske regelverk. F<sub>100</sub> er den frostmengde som «antas å bli overskredet én gang i løpet av en periode på 100 år». Vi kan for ordens skyld føye til «én - og akkurat én». | ||
Dette er en teoretisk definisjon av hundreårsfrosten. Ved å akseptere hundreårsfrosten som dimensjoneringskriterium, aksepterer vi samtidig at gjennomfrysing av underbygningen kan forekomme én gang hvert hundreår i snitt. | Dette er en teoretisk definisjon av hundreårsfrosten. Ved å akseptere hundreårsfrosten som dimensjoneringskriterium, aksepterer vi samtidig at gjennomfrysing av underbygningen kan forekomme én gang hvert hundreår i snitt. | ||
| Linje 199: | Linje 220: | ||
Selv om definisjonen av hundreårsfrosten er enkel og eksakt, kan det diskuteres hvilken tallmessig størrelse «hundreårsfrosten» egentlig har. Det finnes bare pålitelig statistisk materiale for en begrenset periode for denne type meteorologiske registreringer. Det finnes også bare et begrenset antall målestasjoner, og ikke alltid der jernbanen går, eller planlegges bygget. Det benyttes også flere forskjellige statistiske metoder som ikke alltid gir samme svar osv. Endelig kan det hende at klimaet generelt endrer seg fortere enn at det går an å snakke med presisjon om noe som skal inntreffe én gang hvert hundreår i gjennomsnitt. | Selv om definisjonen av hundreårsfrosten er enkel og eksakt, kan det diskuteres hvilken tallmessig størrelse «hundreårsfrosten» egentlig har. Det finnes bare pålitelig statistisk materiale for en begrenset periode for denne type meteorologiske registreringer. Det finnes også bare et begrenset antall målestasjoner, og ikke alltid der jernbanen går, eller planlegges bygget. Det benyttes også flere forskjellige statistiske metoder som ikke alltid gir samme svar osv. Endelig kan det hende at klimaet generelt endrer seg fortere enn at det går an å snakke med presisjon om noe som skal inntreffe én gang hvert hundreår i gjennomsnitt. | ||
I | I Bane NORs tekniske regelverk er det også bestemmelse om at en skal benytte F<sub>100</sub> som utgangspunkt for beregning av F<sub>20</sub> og F<sub>10</sub>, med følgende sammenhenger: | ||
F<sub>20</sub> = 0.85 x F<sub>100</sub> (”tyveårsfrosten”) | |||
F<sub>10</sub> = 0.75 x F<sub>100</sub> (”tiårsfrosten”) | |||
Dette utgjør nok en viss forenkling i forhold til reelle klimatiske forhold. | Dette utgjør nok en viss forenkling i forhold til reelle klimatiske forhold. F<sub>20</sub> ligger noen steder noe nærmere F<sub>100</sub>, mens andre steder er det motsatte tilfelle. | ||
==== Faktorer som påvirker frostnedtrengning ==== | ==== Faktorer som påvirker frostnedtrengning ==== | ||
Mange faktorer påvirker frostnedtrengning i en jernbanekonstruksjon. En oversikt over de viktigste faktorene er vist i tabell .2 | Mange faktorer påvirker frostnedtrengning i en jernbanekonstruksjon. En oversikt over de viktigste faktorene er vist i tabell 6.2 | ||
Tabell 6.2 Faktorer som påvirker frostnedtrengning i en jernbanekonstruksjon | Tabell 6.2 Faktorer som påvirker frostnedtrengning i en jernbanekonstruksjon | ||
Klimatiske forhold | |||
Banekonstruksjon | {| class="wikitable" width="45%" | ||
Materiale i over- og underbygning | |- | ||
Klimasone | ! Klimatiske forhold !! Banekonstruksjon !! Materiale i over- og underbygning | ||
Frostmengde i luft | |- | ||
Årsmiddeltemperatur | | | ||
Temperatur i grunnen | *Klimasone | ||
Forholdet mellom frostmengde i luft og på fyllingens overflate | **Frostmengde i luft | ||
Temperatur forutgående sommer | **Årsmiddeltemperatur | ||
Nedbør forutgående høst | *Temperatur i grunnen | ||
Snø og vindforhold | *Forholdet mellom frostmengde i luft og på fyllingens overflate | ||
Lokale klimavariasjoner | *Temperatur forutgående sommer | ||
Skydekke eller klar himmel | *Nedbør forutgående høst | ||
Drenering | *Snø og vindforhold | ||
Tverrprofil utforming | *Lokale klimavariasjoner | ||
Lagtykkelse | *Skydekke eller klar himmel | ||
Tetting av grøfteskråning | | | ||
Skjæringsdybde | *Drenering | ||
Undergrunn | *Tverrprofil utforming | ||
Stikkrenner | *Lagtykkelse | ||
Underganger | *Tetting av grøfteskråning | ||
Kulverter | *Skjæringsdybde | ||
Tørr romvekt og porøsitet avh. av: | *Undergrunn | ||
gradering: | *Stikkrenner | ||
dmaks | *Underganger | ||
finstoffinnhold | *Kulverter | ||
åpen/tett struktur | | | ||
kompakteringsgrad: | *Tørr romvekt og porøsitet avh. av: | ||
kompakteringsarbeid | **gradering: | ||
tykkelse ved utlegging | ***dmaks | ||
Vanninnhold | ***finstoffinnhold | ||
Bergart | ***åpen/tett struktur | ||
**kompakteringsgrad: | |||
***kompakteringsarbeid | |||
***tykkelse ved utlegging | |||
*Vanninnhold | |||
*Bergart | |||
|} | |||
Noen av faktorene kan måles og tallfestes, slik som årsmiddeltemperatur og frostmengde, selv om også disse faktorene kan variere betydelig over en gitt jernbanestrekning. Andre faktorer vil være avhengige av utførelse og kontroll, slik som tørr romvekt og maksimal kornstørrelse, dmaks. Noen faktorer har store årlige variasjoner. | Noen av faktorene kan måles og tallfestes, slik som årsmiddeltemperatur og frostmengde, selv om også disse faktorene kan variere betydelig over en gitt jernbanestrekning. Andre faktorer vil være avhengige av utførelse og kontroll, slik som tørr romvekt og maksimal kornstørrelse, dmaks. Noen faktorer har store årlige variasjoner. | ||
| Linje 249: | Linje 277: | ||
Det teoretiske grunnlaget for frostdimensjonering av konstruksjoner i grunnen er omfattende, og er til dels også bygget på empiri hva angår jordvarme og meteorologiske forutsetninger. Her medtas en forenklet oppsummering av teorien for frostsikring som bakgrunn for å forstå frostproblematikken generelt, basert på metode beskrevet i ”Frost i jord” (1976). | Det teoretiske grunnlaget for frostdimensjonering av konstruksjoner i grunnen er omfattende, og er til dels også bygget på empiri hva angår jordvarme og meteorologiske forutsetninger. Her medtas en forenklet oppsummering av teorien for frostsikring som bakgrunn for å forstå frostproblematikken generelt, basert på metode beskrevet i ”Frost i jord” (1976). | ||
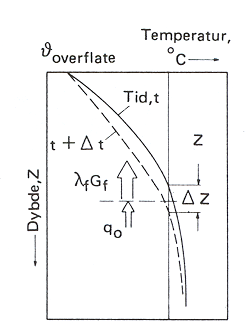
En varmestrømsbetraktning av en liten økning i frostdybde sier at varmestrømmen består av to bidrag, se også figur .4: | En varmestrømsbetraktning av en liten økning i frostdybde sier at varmestrømmen består av to bidrag, se også figur 6.4: | ||
Frysevarme (L•Δz) som frigjøres ved faseovergangen når vannet i underbygningsmassene fryser til is. | Frysevarme (L•Δz) som frigjøres ved faseovergangen når vannet i underbygningsmassene fryser til is. | ||
Jordvarme ( | Jordvarme (q<sub>0</sub>•Δt) som strømmer opp fra undergrunnen i det tilhørende aktuelle tidsrommet. | ||
[[Fil:Fig521-604.png|300px]] | |||
Figur 6.4 Varmebalanse ved frysefronten over et lite tidsrom Δt | Figur 6.4 Varmebalanse ved frysefronten over et lite tidsrom Δt | ||
Betraktet over hele frostperioden utgjør frysevarmen jordlagets frysemotstand. Tilsvarende kalles bidraget fra utstrømmende jordvarme jordvarmens frostmotstand. | Betraktet over hele frostperioden utgjør frysevarmen jordlagets frysemotstand. Tilsvarende kalles bidraget fra utstrømmende jordvarme jordvarmens frostmotstand. | ||
| Linje 260: | Linje 291: | ||
Til sammen utgjør jordlagets frysemotstand ned til frysefronten og jordvarmens frostmotstand den frostmengden som jernbanen utsettes for på overflaten. | Til sammen utgjør jordlagets frysemotstand ned til frysefronten og jordvarmens frostmotstand den frostmengden som jernbanen utsettes for på overflaten. | ||
Likning .5 uttrykker sammenhengen ble vist i figur .4. | Likning 6.5 uttrykker sammenhengen ble vist i figur 6.4. | ||
{| width="350px" align="center" | |||
|- | |||
| <math>L \cdot \Delta Z + q_0 \cdot \Delta t = \lambda_f \cdot G_f \cdot \Delta t</math> || (6.5) | |||
|} | |||
der: L er volumetrisk frysevarme (= | der: | ||
*L er volumetrisk frysevarme (<math>= W \cdot \rho_d \cdot l</math>) [Wh/m<sup>3</sup>] | |||
*w er vektandel vann | |||
*<math>\rho_d</math> er tørr romvekt | |||
*l er frysevarme av vann | |||
*q<sub>0</sub> er varmestrøm fra ufrosne jordlag | |||
*<math>\lambda_f</math> er varmeledningsevne av frosset jord | |||
*G<sub>f</sub> er temperaturgradient over frysefronten, og | |||
*t er tid. | |||
Med ord betyr dette: | Med ord betyr dette: | ||
| Linje 277: | Linje 314: | ||
Frysevarme + jordvarme = varme som ledes bort fra frysefronten. | Frysevarme + jordvarme = varme som ledes bort fra frysefronten. | ||
Formel .5 kan omregnes, bl.a. ved en integrering over frostperioden samt ved å neglisjere varmelagring i frosne jordlag, slik at en har følgende: | Formel 6.5 kan omregnes, bl.a. ved en integrering over frostperioden samt ved å neglisjere varmelagring i frosne jordlag, slik at en har følgende: | ||
Jordlagets frysemotstand + jordvarmens frostmotstand = frostmengden på overflaten. | Jordlagets frysemotstand + jordvarmens frostmotstand = frostmengden på overflaten. | ||
| Linje 283: | Linje 320: | ||
Dimensjonering av en lagdelt jernbanekonstruksjon vil derfor si å finne nødvendig tykkelse av lagene for at telefronten ikke skal gå gjennom disse, og ned i underliggende telefarlige masser. | Dimensjonering av en lagdelt jernbanekonstruksjon vil derfor si å finne nødvendig tykkelse av lagene for at telefronten ikke skal gå gjennom disse, og ned i underliggende telefarlige masser. | ||
Nødvendige parametre som vi selv må velge for dimensjoneringen, er varmeledningsevnen til materialene ( | Nødvendige parametre som vi selv må velge for dimensjoneringen, er varmeledningsevnen til materialene (<math>\lambda</math>),vanninnhold (w) og tetthet av materialene (<math>\rho_d</math>). I tillegg er det nødvendig med empirisk verdi for varmestrøm (Watzingers tall W<sub>t</sub>) og jordvarmemengde (Q<sub>0</sub>), og som finnes i diagrammer i figur 6.6 (fra ”Frost i jord nr. 17, 1976”). | ||
==== Manuell beregningsmetode etter ”Frost i jord” ==== | ==== Manuell beregningsmetode etter ”Frost i jord” ==== | ||
| Linje 290: | Linje 327: | ||
Total frysemotstand F er gitt ved: | Total frysemotstand F er gitt ved: | ||
{| width="300px" align="center" | |||
|- | |||
| <math>F =\sum \Omega_i + E</math> || (6.6) | |||
|} | |||
der: F er total frysemotstand, | der: | ||
*F er total frysemotstand, | |||
*<math>\sum \Omega_i</math>i er summen av frysemotstand i ulike lag, og | |||
*E er jordvarmens frostmotstand. | |||
Jordvarmens frysemotstand E er gitt ved: | Jordvarmens frysemotstand E er gitt ved: | ||
{| width="300px" align="center" | |||
|- | |||
| <math>E =W_t \cdot R_{max} \cdot Q_0 + E</math> || (6.7) | |||
|} | |||
der: | |||
*Wt er Watzingers tall (empirisk, se figur 6.6), | |||
*R<sub>max</sub> er varmestrømmotstand ved største tillatte frostdybde, og | |||
*Q<sub>0</sub> er jordvarmemengde, | |||
og hvor varmestrømmotstanden R<sub>max</sub> er gitt ved: | |||
{| width="350px" align="center" | |||
|- | |||
| <math>R_{max} =\sum_{i=1}^n \frac {\Delta Z} {\lambda_i}=\frac {\Delta_1} {\lambda_1} + \cdots + \frac {\Delta Z_n} {\lambda_n}</math> || (6.8) | |||
|} | |||
der: | |||
*R<sub>max</sub> er varmestrømmotstand ved største frostdybde, | |||
*<math>\Delta Z_n</math> er lagtykkelse i lag nr. i, og | |||
*<math>\lambda_i</math> er varmeledningsevne i lag nr. i. | |||
Frysemotstanden <math>\Omega_n</math> i lag nr. n er gitt ved: | |||
{| width="350px" align="center" | |||
|- | |||
| <math>\Omega_n =L_n \cdot \Delta Z_n (\sum_{i=1}^{n-} \frac {\Delta_i} {\lambda_i} + \frac {\Delta Z_n} {2 \lambda_n})</math> || (6.9) | |||
|} | |||
der: | der: | ||
*<math>\Delta Z_i</math> er lagtykkelse i lag nr. i, | |||
*<math>\lambda_i</math> er varmeledningsevne i lag nr. i, og | |||
*L<sub>n</sub> er frysevarme i lag n, | |||
og hvor frysevarmen | og hvor frysevarmen L<sub>n</sub> i det enkelte lag er gitt ved: | ||
{| width="350px" align="center" | |||
|- | |||
| <math>L_n = \frac {W_n} {100} \cdot \rho_{dn} \cdot l</math> || (6.10) | |||
|} | |||
der: | der: | ||
*W<sub>n</sub> er vanninnhold i lag nr. n (vektprosent), | |||
*l er frysevarme i vann (=93 Wh/kg), og | |||
*<math>\rho_{dn}</math> er densitet av lag nr. n. | |||
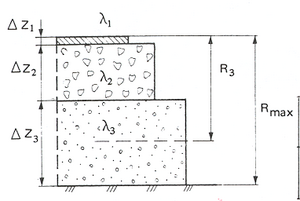
Beregning av varmestrømmotstand i en lagvis oppbygget konstruksjon som vist i figur .5 er vist nedenfor. | Beregning av varmestrømmotstand i en lagvis oppbygget konstruksjon som vist i figur 6.5 er vist nedenfor. | ||
[[Fil:Fig521-605.png|300px]] | |||
Figur 6.5 Varmestrømmotstand i lagene 1 - 3. | Figur 6.5 Varmestrømmotstand i lagene 1 - 3. | ||
| Linje 338: | Linje 400: | ||
For lag nr. 1 er frysemotstanden gitt ved: | For lag nr. 1 er frysemotstanden gitt ved: | ||
{| width="350px" align="center" | |||
|- | |||
| <math>\Omega_1 = L_1 \frac {\Delta Z_{1x} \Delta Z_1} {2\lambda_1}</math> || (6.11) | |||
|} | |||
For lag nr. 2 er frysemotstanden gitt ved: | For lag nr. 2 er frysemotstanden gitt ved: | ||
{| width="350px" align="center" | |||
|- | |||
| <math>\Omega_2 = L_2 \cdot \Delta Z_2 (\frac {\Delta Z_1} {\lambda_1} + \frac {\Delta Z_1} {2\lambda_2})</math> || (6.12) | |||
|} | |||
For lag nr. 3 er frysemotstanden gitt ved: | For lag nr. 3 er frysemotstanden gitt ved: | ||
{| width="350px" align="center" | |||
|- | |||
| <math>\Omega_3 = L_3 \cdot \Delta Z_3 (\frac {\Delta Z_1} {\lambda_1} + \frac {\Delta Z_1} {\lambda_2} + \frac {\Delta Z_3} {2\lambda_3})</math> || (6.13) | |||
|} | |||
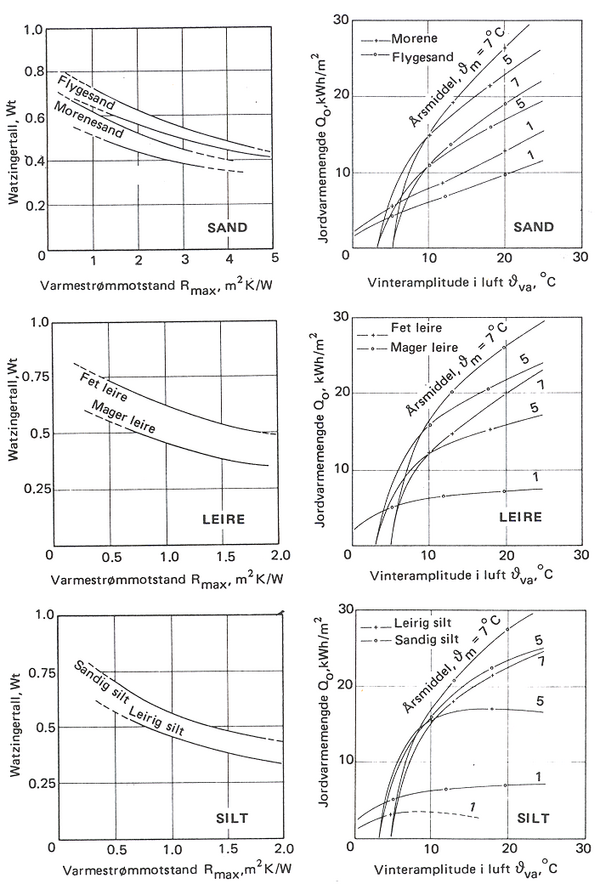
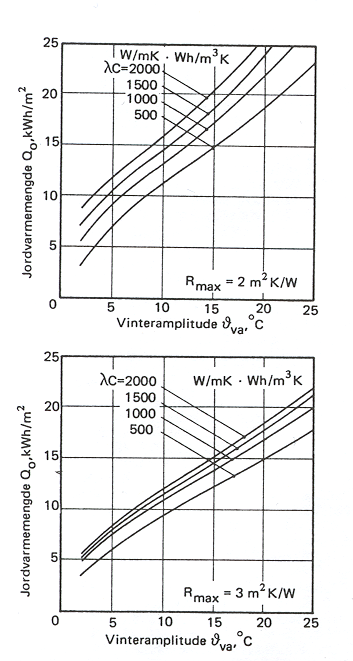
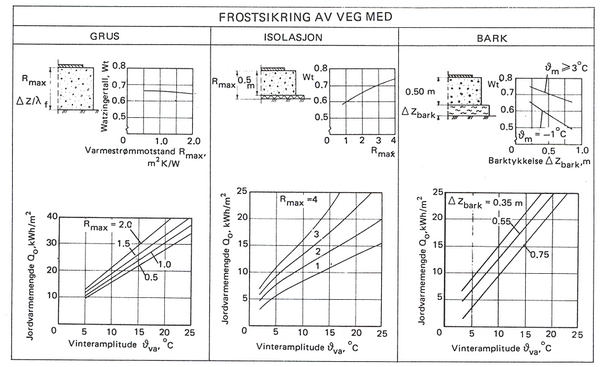
Med dette formelapparatet og ved hjelp av diagrammene nedenfor for bl.a. det empiriske Watzingers tall, kan frysemotstanden F finnes. Dette forutsetter at egnede parametre for materialer og klima (frostmengde osv.) er kjent. | Med dette formelapparatet og ved hjelp av diagrammene nedenfor for bl.a. det empiriske Watzingers tall, kan frysemotstanden F finnes. Dette forutsetter at egnede parametre for materialer og klima (frostmengde osv.) er kjent. | ||
| Linje 353: | Linje 427: | ||
[[Fil:Fig521-606-1.png|600px]] | |||
[[Fil:Fig521-606-2.png|400px]] | |||
[[Fil:Fig521-606-3.png|600px]] | |||
Figur 6.6 Diagrammer for Watzingers tall W<sub>t</sub> og varmestrømmotstand R<sub>max</sub> | |||
Før regneeksempler skal vi bl.a. se litt på vurdering av parametrene varmeledningsevne og vanninnhold. | Før regneeksempler skal vi bl.a. se litt på vurdering av parametrene varmeledningsevne og vanninnhold. | ||
=== Materialparametre === | === Materialparametre === | ||
De viktige parametrene for frostdimensjonering er varmeledningsevne | De viktige parametrene for frostdimensjonering er varmeledningsevne <math>\lambda</math> og vanninnhold. Disse parametrene er i stor grad bestemt av den type materialer vi bygger med, men i noen grad også av dreneringsløsning. Når det gjelder valg av densitet for de forskjellige materialer, vises til erfaringsverdier for komprimerte masser. | ||
==== Varmeledningsevne ==== | ==== Varmeledningsevne ==== | ||
| Linje 376: | Linje 448: | ||
I tillegg vil stor kornstørrelse (steinstørrelse) kunne spille negativt inn, fordi steinmaterialet i seg selv har høy varmeledningsevne. Hvis hele lagtykkelsen i underbygningen besto av en enkelt stein, ville varmeledningsevnen to-/tredobles i forhold til i steinmasser hvor lagtykkelsen er 2-3 ganger så stor som maksimal steinstørrelse. | I tillegg vil stor kornstørrelse (steinstørrelse) kunne spille negativt inn, fordi steinmaterialet i seg selv har høy varmeledningsevne. Hvis hele lagtykkelsen i underbygningen besto av en enkelt stein, ville varmeledningsevnen to-/tredobles i forhold til i steinmasser hvor lagtykkelsen er 2-3 ganger så stor som maksimal steinstørrelse. | ||
Forøvrig spiller også fordeling av mineraltyper i steinmaterialene inn. Kvarts har høy varmeledningsevne ( | Forøvrig spiller også fordeling av mineraltyper i steinmaterialene inn. Kvarts har høy varmeledningsevne (<math>\lambda \approx</math>10 W/m<sup>2</sup>K), og kvartsinnhold i steinmaterialene kan gi stort utslag på varmeledningsevnen. Feltspat har derimot liten varmeledningsevne (<math>\lambda \approx</math>2 W/m<sup>2</sup>K). | ||
==== Vanninnhold ==== | ==== Vanninnhold ==== | ||
| Linje 395: | Linje 467: | ||
For isolasjonsmaterialer som XPS er det kun varmeledningsevnen som har betydning, i det vanninnholdet mhp. frysemotstand er neglisjerbart (gjelder moderne plater av XPS med lukkede porer; tidligere har vannopptak i diverse platetyper som styrofoam vært betydelig). Derimot må vanninnholdet vurderes hvis lettklinker benyttes som frostsikring. | For isolasjonsmaterialer som XPS er det kun varmeledningsevnen som har betydning, i det vanninnholdet mhp. frysemotstand er neglisjerbart (gjelder moderne plater av XPS med lukkede porer; tidligere har vannopptak i diverse platetyper som styrofoam vært betydelig). Derimot må vanninnholdet vurderes hvis lettklinker benyttes som frostsikring. | ||
Orienterende verdier for noen massetyper (over GV) er vist i tabell .3. Som man vil se, er variasjonene store, og mye innsats må derfor gjøres nettopp i parametervalget. | Orienterende verdier for noen massetyper (over GV) er vist i tabell 6.3. Som man vil se, er variasjonene store, og mye innsats må derfor gjøres nettopp i parametervalget. | ||
Tabell 6.3 Orienterende verdier for vanninnhold og varmeledningsevne for noen vanlige materialer i jernbanen | Tabell 6.3 Orienterende verdier for vanninnhold og varmeledningsevne for noen vanlige materialer i jernbanen | ||
0 | {| class="wikitable" width="45%" | ||
|- | |||
! Materiale !! Vanninnhold | |||
[%] | |||
! Varmeledningsevne <math>\lambda</math> | |||
[J/m<sup>2</sup>K] | |||
|- | |||
| Ballastpukk || align="center" |2 - 4 || align="center" |0,8 - 1,1 | |||
|- | |||
| Sand || align="center" |4 - 12 || align="center" |0,8 - 2,2 | |||
|- | |||
| Grus / sandig grus || align="center" |2 - 8 || align="center" |0,7 - 2,0 | |||
|- | |||
| rowspan="2" | Stein || align="center" |0,5 - 2 | |||
(ensgradert) | |||
| rowspan="2" align="center" |0,6 - 2,0 | |||
|- | |||
| align="center" |1 - 4 | |||
(velgradert | |||
|- | |||
| Lettklinker || align="center" |1 - 3 || align="center" |~ 0.15 | |||
(«tørr») | |||
|- | |||
| XPS-plater || align="center" |~ 0 || align="center" |0.037 | |||
(dimensjonerende) | |||
|} | |||
=== Grunnundersøkelser === | === Grunnundersøkelser === | ||
| Linje 441: | Linje 515: | ||
Som vist innledningsvis, er korngraderingen avgjørende for telefarligheten. Det betyr at undersøkelse av materialets korngradering er vesentlig for å bestemme telefarlighet av materialet. Det benyttes forskjellige typer undersøkelser for å klassifisere materialet ut fra korngradering: | Som vist innledningsvis, er korngraderingen avgjørende for telefarligheten. Det betyr at undersøkelse av materialets korngradering er vesentlig for å bestemme telefarlighet av materialet. Det benyttes forskjellige typer undersøkelser for å klassifisere materialet ut fra korngradering: | ||
Tørrsikting: Velegnet for sand / grus | *Tørrsikting: Velegnet for sand / grus | ||
Våtsikting: Benyttes for å få skilt ut finere materiale fra grovere, men gir ikke fordeling innen de forskjellige fraksjoner av finere materiale < 0,074mm. | *Våtsikting: Benyttes for å få skilt ut finere materiale fra grovere, men gir ikke fordeling innen de forskjellige fraksjoner av finere materiale < 0,074mm. | ||
Slemmeanalyse/hydrometeranalyse (evt. ”falling drop”-metoden): Benyttes for å finne korngraderingskurve for materialer med innhold av silt og leire. | *Slemmeanalyse/hydrometeranalyse (evt. ”falling drop”-metoden): Benyttes for å finne korngraderingskurve for materialer med innhold av silt og leire. | ||
For å kartlegge telefarlighet i masser med noe finstoffinnhold (for eksempel finsand med noe siltinnhold), vil det ofte være behov for å utføre nettopp sistnevnte analyse. | For å kartlegge telefarlighet i masser med noe finstoffinnhold (for eksempel finsand med noe siltinnhold), vil det ofte være behov for å utføre nettopp sistnevnte analyse. | ||
=== Undersøkelse av varmeledningsevne === | === Undersøkelse av varmeledningsevne === | ||
Normalt vil det ikke være mulig å undersøke varmeledning av naturlige materialer til bruk i jernbanens underbygning i hvert enkelt tilfelle/prosjekt. Imidlertid er det mulig å gjøre dette i laboratorium, og NGI | Normalt vil det ikke være mulig å undersøke varmeledning av naturlige materialer til bruk i jernbanens underbygning i hvert enkelt tilfelle/prosjekt. Imidlertid er det mulig å gjøre dette i laboratorium, og NGI utførte på oppdrag fra Jernbaneverket flere forsøk i plateapparat (såkalte ”kasseforsøk”) på slutten av 1990-tallet for å undersøke egenskapene til bl.a. sprengstein. | ||
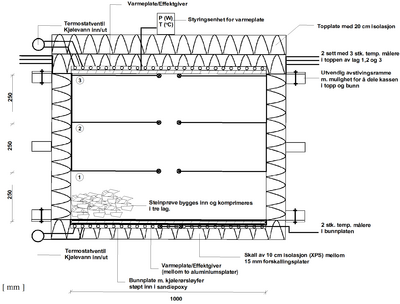
Målingene er utført i en instrumentert og godt isolert forsøkskasse med mål 100 | Målingene er utført i en instrumentert og godt isolert forsøkskasse med mål 100<math>\cdot</math>100<math>\cdot</math>75 cm<sup>3</sup>, vist på figur 6.7. Steinmaterialene som ønskes testet bygges lagvis inn i kassen og komprimeres. Steinprøvene som ble testet er sprengstein av ulike fraksjoner, ballastpukk og maskinkult. | ||
[[Fil:Fig521-607.png|400px]] | |||
Figur 6.7 Plateapparat for måling av varmeledningsevne i steinfylling | Figur 6.7 Plateapparat for måling av varmeledningsevne i steinfylling | ||
Forsøkskassen er utstyrt med en varmeplate i toppen og en bunnplate med kjølerør. Selve forsøket består deretter av avlesninger av temperatur og effektforbruk fram mot stasjonær varmestrøm gjennom prøven. Når tykkelsen av prøven er kjent kan materialets varmeledningsevne beregnes. I denne sammenheng vil det ikke gås nærmere inn på forsøksprosedyren. Resultatene fra forsøkene er innarbeidet i erfaringsverdiene gitt i avsnitt 4.3.3, tabell .3. | Forsøkskassen er utstyrt med en varmeplate i toppen og en bunnplate med kjølerør. Selve forsøket består deretter av avlesninger av temperatur og effektforbruk fram mot stasjonær varmestrøm gjennom prøven. Når tykkelsen av prøven er kjent kan materialets varmeledningsevne beregnes. I denne sammenheng vil det ikke gås nærmere inn på forsøksprosedyren. Resultatene fra forsøkene er innarbeidet i erfaringsverdiene gitt i avsnitt 4.3.3, tabell 6.3. | ||
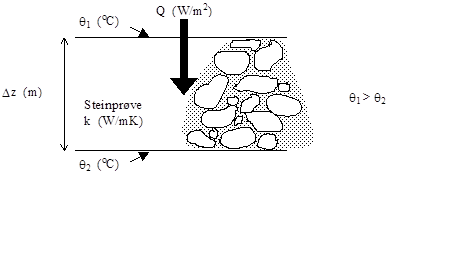
De første forsøkene ble utført for kun å bestemme steinmaterialenes varmeledningsevne. Prinsippet for måling av varmeledningsevne er vist i figur .8, der varm side er plassert på toppen, jf. beskrivelsen ovenfor. | De første forsøkene ble utført for kun å bestemme steinmaterialenes varmeledningsevne. Prinsippet for måling av varmeledningsevne er vist i figur 6.8, der varm side er plassert på toppen, jf. beskrivelsen ovenfor. | ||
[[Fil:Fig521-608.png|500px]] | |||
Figur 6.8 Prinsipp for måling av varmeledningsevne ved stasjonær varmestrøm i plateapparat (dvs. måling av varmeledning uten konveksjon) | Figur 6.8 Prinsipp for måling av varmeledningsevne ved stasjonær varmestrøm i plateapparat (dvs. måling av varmeledning uten konveksjon) | ||
| Linje 465: | Linje 542: | ||
For en steinfylling in-situ vil det imidlertid også være andre effekter som har stor betydning for fyllingens frostisolerende evne. De viktigste andre effekter er: | For en steinfylling in-situ vil det imidlertid også være andre effekter som har stor betydning for fyllingens frostisolerende evne. De viktigste andre effekter er: | ||
Indre konveksjon | *Indre konveksjon | ||
Utstråling til atmosfæren | *Utstråling til atmosfæren | ||
Kald luft som blåser inn i fyllingen | *Kald luft som blåser inn i fyllingen | ||
Steinfyllingens varmekapasitet | *Steinfyllingens varmekapasitet | ||
Latent varme | *Latent varme | ||
Generelt vil det for drenerte steinfyllinger være finstoffinnhold, kvartsinnhold, vanninnhold og porøsitet/total romvekt som bestemmer varmeledningsevnen. | Generelt vil det for drenerte steinfyllinger være finstoffinnhold, kvartsinnhold, vanninnhold og porøsitet/total romvekt som bestemmer varmeledningsevnen. | ||
| Linje 475: | Linje 552: | ||
Med bakgrunn i telehiv på nybygde banestrekninger i løpet av 1990-tallet var det en viss sammenheng mellom steder hvor telehivene oppsto og hvilke massetyper som var lagt ut i forsterknings- og frostsikringslaget. Tendensen var slik at de vesentligste telehivene ble registrert på strekninger med grove ensgraderte steinmasser, og mistanken om at konveksjon spilte en vesentlig rolle ble ytterligere forsterket. Med dette som bakgrunn ble det gjennomført nye forsøk i NGIs forsøkskasse. | Med bakgrunn i telehiv på nybygde banestrekninger i løpet av 1990-tallet var det en viss sammenheng mellom steder hvor telehivene oppsto og hvilke massetyper som var lagt ut i forsterknings- og frostsikringslaget. Tendensen var slik at de vesentligste telehivene ble registrert på strekninger med grove ensgraderte steinmasser, og mistanken om at konveksjon spilte en vesentlig rolle ble ytterligere forsterket. Med dette som bakgrunn ble det gjennomført nye forsøk i NGIs forsøkskasse. | ||
Forsøkskassen ble da ombygd slik det også kunne foretas målinger med den varme siden på bunnen av kassen (det er for øvrig denne ombygde kassen som er vist på figur .7). | Forsøkskassen ble da ombygd slik det også kunne foretas målinger med den varme siden på bunnen av kassen (det er for øvrig denne ombygde kassen som er vist på figur 6.7). | ||
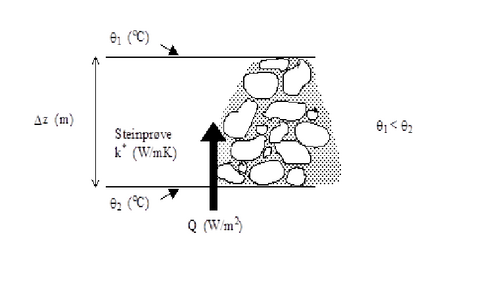
Dersom bunnen av prøvematerialet har høyere temperatur enn toppen av prøven, vil konvektiv varmeoppgang oppstå som følge av tetthetsforskjellen mellom varm (lett) luft og kald (tyngre) luft. Når en kjent stasjonær varmestrøm passerer da gjennom prøven, og det er mulig å måle temperaturforskjellen mellom topp og bunn. Varmetap med både varmeledning og bidrag fra naturlig tetthetsdrevet konveksjon kan da måles. Dette prinsippet er vist i figur .9. | Dersom bunnen av prøvematerialet har høyere temperatur enn toppen av prøven, vil konvektiv varmeoppgang oppstå som følge av tetthetsforskjellen mellom varm (lett) luft og kald (tyngre) luft. Når en kjent stasjonær varmestrøm passerer da gjennom prøven, og det er mulig å måle temperaturforskjellen mellom topp og bunn. Varmetap med både varmeledning og bidrag fra naturlig tetthetsdrevet konveksjon kan da måles. Dette prinsippet er vist i figur 6.9. | ||
[[Fil:Fig521-609.png|500px]] | |||
Figur 6.9 Prinsipp for måling av varmetap med både varmeledning og bidrag fra tetthetsdrevet konveksjon i plateapparat | Figur 6.9 Prinsipp for måling av varmetap med både varmeledning og bidrag fra tetthetsdrevet konveksjon i plateapparat | ||
Det er gjennomført slike forsøk på ballastpukk (25 – 63 mm), ensgradert maskinkult (20 – 120 mm) og velgradert sprengstein (0 – 250mm). Resultatene fra disse målingene uten bidrag fra konveksjon, er vist i tabell .4. Resultater fra målinger, jf. prinsipp i figur .9, med konveksjonens bidrag er vist i tabell .5. | Det er gjennomført slike forsøk på ballastpukk (25 – 63 mm), ensgradert maskinkult (20 – 120 mm) og velgradert sprengstein (0 – 250mm). Resultatene fra disse målingene uten bidrag fra konveksjon, er vist i tabell 6.4. Resultater fra målinger, jf. prinsipp i figur 6.9, med konveksjonens bidrag er vist i tabell 6.5. | ||
Tabell 6.4 Resultater fra utførte forsøk uten naturlig konveksjon (dvs. kun varmeledningsevne) | Tabell 6.4 Resultater fra utførte forsøk uten naturlig konveksjon (dvs. kun varmeledningsevne) | ||
Fraksjon | {| class="wikitable" width="45%" style="text-align: center;" | ||
|- | |||
Total romvekt | | Fraksjon | ||
(mm) | |||
Porøsitet | | Kvartsinnhold | ||
(%) | |||
| Total romvekt | |||
( | (kN/m<sup>3</sup>) | ||
(%) | | h<sub>tot</sub>/d<sub>maks</sub> | ||
( | | Porøsitet | ||
(%) | |||
| Vanninhold | |||
(%) | |||
| Varmeledn.tall | |||
(W/mK) | |||
|- | |||
| 25 - 63 || 23,2 || 16,5 || 11,9 || 38 || ~0 || 0,79 - 0,83 | |||
|- | |||
| 20 - 120 || 21,4 || 17,4 || 6,3 || 34 || ~0 || 0,82 - 0,91 | |||
|- | |||
| 0 - 250 || || 22,5 || 3 || 18 || 3,2 || 1,6 | |||
|} | |||
Tabell 6.5 Resultater fra utførte forsøk der naturlig konveksjon kan oppstå | Tabell 6.5 Resultater fra utførte forsøk der naturlig konveksjon kan oppstå | ||
Fraksjon | {| class="wikitable" width="45%" style="text-align: center;" | ||
|- | |||
| Fraksjon | |||
(mm) | |||
| <math>\Delta T</math> | |||
(<sup>0</sup>C) | |||
| T<sub>middel</sub> | |||
( | (<sup>0</sup>C) | ||
( | | R<sub>a</sub> | ||
( | (-) | ||
| Nu<sup>teoretisk</sup> | |||
(-) | |||
| k<sup>*</sup> | |||
(W/mK) | |||
| Nu<sup>forsøk</sup> | |||
(-) | (-) | ||
|- | |||
| 25 - 63 || 13,2 | |||
21,0 | |||
23,0 | |||
20 | | 20,8 | ||
35 | 27,0 | ||
1 | |||
0 | 30,0 | ||
1 | | 35,5 | ||
54,0 | |||
58,6 | |||
| 1,0 | |||
1,2 | |||
1,3 | |||
| 0,83 | |||
1,20 | |||
1,35 | |||
| 1,04 | |||
1,50 | |||
1 | |||
1 | |||
1 | |||
1,69 | |||
|- | |||
| 20 - 120 || 14,0 | |||
1 | 22,5 | ||
1 | | 21,0 | ||
1 | 24,8 | ||
| 32,7 | |||
51,8 | |||
21 | | 1,0 | ||
1,0 | |||
1 | | 1,82 | ||
0 | 1,82 | ||
1 | | 1,13 | ||
1,13 | |||
|- | |||
| 0 - 250 ||18,0 | |||
23,5 | |||
| 21,0 | |||
23,5 | |||
| 6,5 | |||
8,4 | |||
| 1,0 | |||
1,0 | |||
| 1,82 | |||
1,82 | |||
| 1,13 | |||
1,13 | |||
|} | |||
Ra eller Rayleightallet er et forholdstall mellom oppdriftskrefter og viskøse krefter. k* er en parameter beregnet med formelverk som for varmeledning men benyttet for situasjonen der konveksjon kan oppstå. Nu eller Nusselt tallet er et mål på hvor mye den totale varmetransporten øker pga. naturlig konveksjon sammenlignet med ren varmeledning. | Ra eller Rayleightallet er et forholdstall mellom oppdriftskrefter og viskøse krefter. k* er en parameter beregnet med formelverk som for varmeledning men benyttet for situasjonen der konveksjon kan oppstå. Nu eller Nusselt tallet er et mål på hvor mye den totale varmetransporten øker pga. naturlig konveksjon sammenlignet med ren varmeledning. | ||
Fra ovennevnte forsøk ser vi at ved temperaturgradienter på 20 | Fra ovennevnte forsøk ser vi at ved temperaturgradienter på 20<sup>0</sup>C eller mer, vil effekten fra konveksjonen spille en vesentlig rolle for de ensgradert massene av ballastpukk og maskinkult. Resultatene tilsvarer at materialene får ca. 50 – 70% høyere varmeledingsevne ved de nevnte temperaturgradienter enn ved forsøkene uten naturlig konveksjon. | ||
For velgradert sprengstein måles det kun mindre forskjeller. Forsøket viser betydningen av å velge velgraderte masser til bruk i frostfundamentet når det i dimensjoneringen forutsettes at varmeledning er den dominerende årsaken til frostnedtrengning. | For velgradert sprengstein måles det kun mindre forskjeller. Forsøket viser betydningen av å velge velgraderte masser til bruk i frostfundamentet når det i dimensjoneringen forutsettes at varmeledning er den dominerende årsaken til frostnedtrengning. | ||
| Linje 601: | Linje 677: | ||
Følgende eksempler gjennomregnes: | Følgende eksempler gjennomregnes: | ||
Først ser vi på effekten av å benytte grus (eksempel A) hhv. sprengstein (eksempel B) i underbygningen. | *Først ser vi på effekten av å benytte grus (eksempel A) hhv. sprengstein (eksempel B) i underbygningen. | ||
Deretter ser vi på effekt av å isolere sporet med XPS-plater | *Deretter ser vi på effekt av å isolere sporet med XPS-plater | ||
Først legges XPS-platen over et gruslag (eksempel C). | **Først legges XPS-platen over et gruslag (eksempel C). | ||
Deretter legger vi isolasjonsplaten på traubunn (eksempel D), og ser om «faktorenes orden» er likegyldig. | **Deretter legger vi isolasjonsplaten på traubunn (eksempel D), og ser om «faktorenes orden» er likegyldig. | ||
Helt til slutt tar vi utgangspunkt i eksempel B, men legger inn et beskjedent sandlag nederst i konstruksjonen som filterlag (eks. E). | *Helt til slutt tar vi utgangspunkt i eksempel B, men legger inn et beskjedent sandlag nederst i konstruksjonen som filterlag (eks. E). | ||
Pukklaget på 0.5 m er konstant med de samme parametre i alle eksemplene. I tillegg er antatt vinteramplitude på 15 | Pukklaget på 0.5 m er konstant med de samme parametre i alle eksemplene. I tillegg er antatt vinteramplitude på 15<sup>0</sup>C i alle eksemplene. | ||
| Linje 614: | Linje 690: | ||
I det første regneeksemplet ser vi på en enkel, klassisk jernbanekonstruksjon med grus som frostsikringslag. | I det første regneeksemplet ser vi på en enkel, klassisk jernbanekonstruksjon med grus som frostsikringslag. | ||
Lag | {| class="wikitable" width="35%" | ||
Materiale | |- | ||
| Lag || Materiale || <math>\Delta Z</math> || <math>\lambda_f</math> || W || <math>\rho_d</math> | |||
|- | |||
W | | [nr] || || [m] || [W/mK] ||[%] || [kg/m<sup>3</sup>] | ||
|- | |||
[nr] | | 1 || Ballastpukk || 0,5 || 0,9 || 1,5 || 1500 | ||
|- | |||
| 2 || Grus || 1,2 || 1,6 || 5 ||1800 | |||
|} | |||
Det er antatt et Watzingers tall | Det er antatt et Watzingers tall W<sub>t</sub> på 0.65, og en jordvarmemengde Q<sub>0</sub> på 25.000. | ||
Innsetting i formelapparatet over gir følgende: | Innsetting i formelapparatet over gir følgende: | ||
Frysemotstand: | *Frysemotstand: <math>\sum \Omega</math> = 10.393 h<sup>0</sup>C | ||
Jordvarmens frostmotstand: | *Jordvarmens frostmotstand: E = 18.958 h<sup>0</sup>C | ||
Konstruksjonen motstår en frostmengde på: | *Konstruksjonen motstår en frostmengde på: <math>\sum \Omega</math> + E = 29.351 h<sup>0</sup>C | ||
Frostdimensjonering tar utgangspunkt i frostmengde i luft. På grunn av lavere overflatetemperatur må fratrekkes ca. 5000 | Frostdimensjonering tar utgangspunkt i frostmengde i luft. På grunn av lavere overflatetemperatur må fratrekkes ca. 5000 h<sup>0</sup>C fra resultatet ovenfor, slik at konstruksjonen kan tåle en dimensjonerende frostmengde på F = 25.000 h<sup>0</sup>C. Dette må kontrolleres mot kurvene i regelverket. | ||
Eksempel B | Eksempel B | ||
Vi bytter nå ut grus med sprengstein med langt lavere vanninnhold. Samtidig antar vi da at varmeledningsevnen er litt lavere enn for grus, men antatt store steiner gjør at varmeledningsevnen fortsatt antas å ha en høy verdi. | Vi bytter nå ut grus med sprengstein med langt lavere vanninnhold. Samtidig antar vi da at varmeledningsevnen er litt lavere enn for grus, men antatt store steiner gjør at varmeledningsevnen fortsatt antas å ha en høy verdi. | ||
Lag | {| class="wikitable" width="35%" | ||
Materiale | |- | ||
| Lag || Materiale || <math>\Delta Z</math> || <math>\lambda_f</math> || W || <math>\rho_d</math> | |||
|- | |||
W | | [nr] || || [m] || [W/mK] ||[%] || [kg/m<sup>3</sup>] | ||
|- | |||
[nr] | | 1 || Ballastpukk || 0,5 || 1,0 || 2,0 || 1500 | ||
|- | |||
| 2 || sprengstein || 1,2 || 1,5 || 0,5 ||1900 | |||
|} | |||
Ved innsetting i formelapparatet får vi: | Ved innsetting i formelapparatet får vi: | ||
Frysemotstand: | *Frysemotstand: <math>\sum \Omega</math> = 1.303 h<sup>0</sup>C | ||
Jordvarmens frostmotstand: E = 21.125 | *Jordvarmens frostmotstand: E = 21.125 h<sup>0</sup>C | ||
Konstruksjonen motstå en frostmengde på: | *Konstruksjonen motstå en frostmengde på: <math>\sum \Omega</math> + E = 22.428 h<sup>0</sup>C | ||
Altså betydelig dårligere frostisolasjon enn for grustilfellet. Forskjellen ligger i dette beregningstilfellet hovedsakelig i at vi har antatt et svært lavt vanninnhold i sprengsteinslaget, og vi mister derved et vesentlig frysevarmebidrag. | Altså betydelig dårligere frostisolasjon enn for grustilfellet. Forskjellen ligger i dette beregningstilfellet hovedsakelig i at vi har antatt et svært lavt vanninnhold i sprengsteinslaget, og vi mister derved et vesentlig frysevarmebidrag. | ||
Reduksjon for lavere overflatetemperatur tilsier at konstruksjonen er tilstrekkelig for en dimensjonerende frostmengde i luft på ca. 17.000 | Reduksjon for lavere overflatetemperatur tilsier at konstruksjonen er tilstrekkelig for en dimensjonerende frostmengde i luft på ca. 17.000 h<sup>0</sup>C. | ||
Eksempel C | Eksempel C | ||
I dette eksemplet er det tenkt innlagt isolasjonsplate av XPS over et gruslag. Vi antar at platen ikke opptar vann. XPS-platen er egentlig 60 mm tykk, men må reduseres til 50 mm ved beregning, pga. antatt inntrykking av stein i platen og sammenpressing. | I dette eksemplet er det tenkt innlagt isolasjonsplate av XPS over et gruslag. Vi antar at platen ikke opptar vann. XPS-platen er egentlig 60 mm tykk, men må reduseres til 50 mm ved beregning, pga. antatt inntrykking av stein i platen og sammenpressing. | ||
Lag | {| class="wikitable" width="35%" | ||
|- | |||
| Lag || Materiale || <math>\Delta Z</math> || <math>\lambda_f</math> || W || <math>\rho_d</math> | |||
|- | |||
| [nr] || || [m] || [W/mK] ||[%] || [kg/m<sup>3</sup>] | |||
|- | |||
| 1 || Ballastpukk || 0,5 || 1,0 || 2,0 || 1500 | |||
|- | |||
| 2 || XPS || 0,05 || 0,037 || 0 ||40 | |||
|- | |||
| 3 || Grus || 0,80 || 1,6 || 5 ||1800 | |||
|} | |||
Innsetting i formelapparatet gir: | Innsetting i formelapparatet gir: | ||
Frysemotstand: | *Frysemotstand: <math>\sum \Omega</math> = 17.010 h<sup>0</sup>C | ||
Jordvarmens frostmotstand: E = 23.073 | *Jordvarmens frostmotstand: E = 23.073 h<sup>0</sup>C | ||
Konstruksjonen kan motstå en frostmengde på: | *Konstruksjonen kan motstå en frostmengde på: <math>\sum \Omega</math> + E = 40.083 h<sup>0</sup>C | ||
Reduksjon for lutftemperatur gjøres som tidligere, slik at konstruksjonen med de gitte forutsetninger kan tåle dimensjonerende frostmengde i luft på ca. 35.000 | |||
Reduksjon for lutftemperatur gjøres som tidligere, slik at konstruksjonen med de gitte forutsetninger kan tåle dimensjonerende frostmengde i luft på ca. 35.000 h<sup>0</sup>C. | |||
| Linje 735: | Linje 771: | ||
Her skal vi sjekke om det har noen betydning hvor de ulike lagene plasseres i frostfundamentet. Vi antar en oppbygging av konstruksjon med lag som i eksempel C, men vi bytter om rekkefølgen, og legger isolasjonsplaten helt nede på traubunn. Forøvrig er alle parametre like. | Her skal vi sjekke om det har noen betydning hvor de ulike lagene plasseres i frostfundamentet. Vi antar en oppbygging av konstruksjon med lag som i eksempel C, men vi bytter om rekkefølgen, og legger isolasjonsplaten helt nede på traubunn. Forøvrig er alle parametre like. | ||
{| class="wikitable" width="35%" | |||
|- | |||
| Lag || Materiale || <math>\Delta Z</math> || <math>\lambda_f</math> || W || <math>\rho_d</math> | |||
|- | |||
| [nr] || || [m] || [W/mK] ||[%] || [kg/m<sup>3</sup>] | |||
|- | |||
| 1 || Ballastpukk || 0,5 || 1,0 || 2,0 || 1500 | |||
|- | |||
| 2 || Grus || 0,80 || 1,8 || 6 ||1800 | |||
|- | |||
| 3 || XPS || 0,05 || 0,037 || 0 ||40 | |||
|} | |||
Innsetting i formelapparatet gir: | |||
*Frysemotstand: <math>\sum \Omega</math> = 355 h<sup>0</sup>C | |||
*Jordvarmens frostmotstand: E = 23.073 h<sup>0</sup>C | |||
*Konstruksjonen kan motstå en frostmengde på: <math>\sum \Omega</math> + E = 23.428 h<sup>0</sup>C | |||
Et svært interessant – og tankevekkende - resultat! Bare ved å bytte om rekkefølgen på lagene mistet vi hele 16.500 | Et svært interessant – og tankevekkende - resultat! Bare ved å bytte om rekkefølgen på lagene mistet vi hele 16.500 h<sup>0</sup>C i frostmotstand i forhold til forrige eksempel! Vi får her ikke utnyttet det høye vanninnholdet i gruslaget effektivt, fordi den frigjorte varmen ikke lenger blir holdt tilbake av isolasjonsplatene, slik som i eksempelet foran. | ||
Eksempel E | Eksempel E | ||
Til slutt erstatter vi 15 cm sprengstein i eksempel B med et sandlag på 15 cm. Sandlaget legges nederst i trauet, som et filterlag. Sand holder på mye vann, og vi antar samtidig en relativt høy varmeledningsevne. | Til slutt erstatter vi 15 cm sprengstein i eksempel B med et sandlag på 15 cm. Sandlaget legges nederst i trauet, som et filterlag. Sand holder på mye vann, og vi antar samtidig en relativt høy varmeledningsevne. | ||
Lag | {| class="wikitable" width="35%" | ||
|- | |||
| Lag || Materiale || <math>\Delta Z</math> || <math>\lambda_f</math> || W || <math>\rho_d</math> | |||
|- | |||
| [nr] || || [m] || [W/mK] ||[%] || [kg/m<sup>3</sup>] | |||
|- | |||
| 1 || Ballastpukk || 0,5 || 1,0 || 2,0 || 1500 | |||
|- | |||
| 2 || Sprengstein|| 1,05 || 1,5 || 0,5 || 1800 | |||
|- | |||
| 3 || Sand || 0,15 || 2,0 || 10 ||1600 | |||
|} | |||
Frysemotstand: | *Frysemotstand: <math>\sum \Omega</math> = 3.455 h<sup>0</sup>C | ||
Jordvarmens frostmotstand: E = 20.719 | *Jordvarmens frostmotstand: E = 20.719 h<sup>0</sup>C | ||
Konstruksjonen kan motstå en frostmengde på: | *Konstruksjonen kan motstå en frostmengde på: <math>\sum \Omega</math> + E = 24.175 h<sup>0</sup>C | ||
Dette er ca. 2.000 | Dette er ca. 2.000 h<sup>0</sup>C mer enn i eksempel B, hvor det ble brukt bare sprengstein. Lar vi sandlaget være 30 cm tykt, vinner vi ytterligere ca. 2.000 h<sup>0</sup>C, og bedringen i frostmotstand begynner nå virkelig å monne. Virkelig høy gevinst får vi når vi legger inn et fuktig lag som torv, sviller, bark e.l. Denne teknikken utnyttes ikke på nye jernbaner i dag, men er i bruk innen vegbygging. | ||
=== Oppsummering av beregningseksemplene === | === Oppsummering av beregningseksemplene === | ||
De enkle eksemplene kan føre oss frem til en slags oppsummering av de vesentligste punkter ved dimensjoneringsmetodikken: | De enkle eksemplene kan føre oss frem til en slags oppsummering av de vesentligste punkter ved dimensjoneringsmetodikken: | ||
Det er ikke tilfeldig hvilken lagrekkefølge som benyttes ved oppbygging av banelegemet. Regelen er enkel: Våte lag nederst, tørre og isolerende lag øverst. (En løsning som er nøye utregnet etter dette prinsippet kan miste mye av sin effekt hvis noen i anleggsperioden plutselig finner ut at det er mer praktisk å f.eks. legge isolasjonsplater på traubunn.) | *Det er ikke tilfeldig hvilken lagrekkefølge som benyttes ved oppbygging av banelegemet. Regelen er enkel: Våte lag nederst, tørre og isolerende lag øverst. (En løsning som er nøye utregnet etter dette prinsippet kan miste mye av sin effekt hvis noen i anleggsperioden plutselig finner ut at det er mer praktisk å f.eks. legge isolasjonsplater på traubunn.) | ||
Lavt vanninnhold gir generelt dårlig frostsikring. Vi har ikke her regnet på eksempler helt uten vanninnhold, men ved store frostmengder vil lagtykkelsene etterhvert bli så store at det ikke kan være fornuftig å benytte bare konvensjonelle masser. En må da ty til isolasjonsløsninger eller materialer med høyt vanninnhold. | *Lavt vanninnhold gir generelt dårlig frostsikring. Vi har ikke her regnet på eksempler helt uten vanninnhold, men ved store frostmengder vil lagtykkelsene etterhvert bli så store at det ikke kan være fornuftig å benytte bare konvensjonelle masser. En må da ty til isolasjonsløsninger eller materialer med høyt vanninnhold. | ||
Parametre som benyttes i regnemodellene må velges med omhu da de har stor betydning for resultatet. Man kan ved beregninger vise at telesikringen er tilstrekkelig i nesten ethvert tverrsnitt ved valg av passende eller upassende parametre. Derfor er det på valg av parametre innsatsen bør legges. Regnemodeller og beregnings-programmer finnes det flere av, men forutsetningen for et godt resultat er omtanke ved vurdering av varmeledning og vanninnhold, samt ved vurdering av den reelle frostpåkjenning på stedet. Samtidig gjør beregningsprogrammer det mulig å utføre følsmohetsstudier, hvilket er sterkt å anbefale i flere tilfeller. | *Parametre som benyttes i regnemodellene må velges med omhu da de har stor betydning for resultatet. Man kan ved beregninger vise at telesikringen er tilstrekkelig i nesten ethvert tverrsnitt ved valg av passende eller upassende parametre. Derfor er det på valg av parametre innsatsen bør legges. Regnemodeller og beregnings-programmer finnes det flere av, men forutsetningen for et godt resultat er omtanke ved vurdering av varmeledning og vanninnhold, samt ved vurdering av den reelle frostpåkjenning på stedet. Samtidig gjør beregningsprogrammer det mulig å utføre følsmohetsstudier, hvilket er sterkt å anbefale i flere tilfeller. | ||
== Frostsikring av nye baneanlegg == | == Frostsikring av nye baneanlegg == | ||
| Linje 829: | Linje 832: | ||
Vi må fastlegge følgende før vi kan gjennomføre dimensjonering: | Vi må fastlegge følgende før vi kan gjennomføre dimensjonering: | ||
Hvilken frostmengde skal vi frostsikre sporet mot? Det vil for jernbane si at vi også må vite hva slags standard vi bygger for, og selvsagt geografisk lokalisering. | *Hvilken frostmengde skal vi frostsikre sporet mot? Det vil for jernbane si at vi også må vite hva slags standard vi bygger for, og selvsagt geografisk lokalisering. | ||
Hvilke materialer skal vi bygge med, og hvilke frosttekniske parametre skal vi benytte for de materialene som velges? | *Hvilke materialer skal vi bygge med, og hvilke frosttekniske parametre skal vi benytte for de materialene som velges? | ||
=== Dimensjonerende frostmengde === | === Dimensjonerende frostmengde === | ||
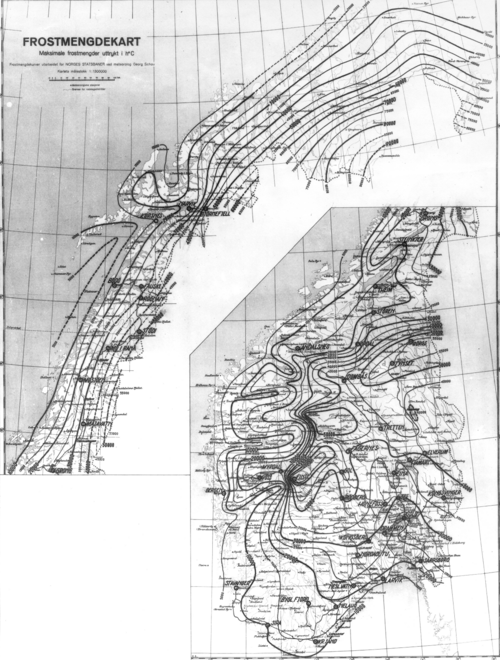
Bane NOR hadde tidligere i sitt regelverk tatt med et frostmengdekart over hvilke frostmengder det skal dimensjoneres for ut fra hvor i landet jernbanestrekningen skal bygges. Dette kartet ble laget for NSB på 1960-tallet, og er ikke endret vesentlig siden. Kartet er utarbeidet av Meteorologisk institutt. Skal man prosjektere en jernbanestrekning, kan en altså finne den aktuelle hundreårsfrost på kartet. Evt. reduksjon av frostmengde utføres hvis dimensjonerende hastighet er lav, jf. avsnitt 4.2.1. Frostmengdekartet er vist på figur 6.10. | |||
[[Fil:Fig521-610.png|500px]] | |||
Figur 6.10 Maksimale frostmengder i Norge | |||
Overflatetemperaturen på jernbanesporet kan være 2-3 | Overflatetemperaturen på jernbanesporet kan være 2-3<sup>0</sup>C lavere enn lufttemperaturen om vinteren, hvilket man derfor må korrigere for ved beregninger. Ved beregning av dimensjonerende frostmengde justeres frostmengden for lavere overflatetemperatur avhengig av varighet av frostperioden. En justering på 5-6000 h<sup>0</sup>C er ofte noenlunde riktig på Østlandet. For å få en verdi for dette, kan vi ta utgangspunkt i frostperiodens varighet, og multiplisere antall timer med differansen i luft- og overflatetemperatur. Ved utarbeidelse av dimensjoneringskurver for nye baneanlegg, jf. avsnitt 5, er det tatt hensyn til dette forholdet. | ||
Frostmengdekartet | Frostmengdekartet egner seg dårlig til detaljert planlegging. Det er derfor behov for å benytte andre kilder, for eksempel Vegvesenets håndbok 018, for å finne detaljert informasjon om F<sub>100</sub> for den enkelte kommune. | ||
=== Frostsikring og banetype === | === Frostsikring og banetype === | ||
Den frostmengde et jernbanespor frostsikres for avhenger av hvilken hastighetsavhengige kvalitetsklasse sporet skal ha. Dette skyldes at en evt. telekul får større konsekvenser med økende hastighet. | Den frostmengde et jernbanespor frostsikres for avhenger av hvilken hastighetsavhengige kvalitetsklasse sporet skal ha. Dette skyldes at en evt. telekul får større konsekvenser med økende hastighet. | ||
Tabell .6 viser prinsipper for frostdimensjonering av hovedspor. Hvilken frostmengde sporet må dimensjoneres etter, variererer med dimensjonerende toghastighet. | Tabell 6.6 viser prinsipper for frostdimensjonering av hovedspor. Hvilken frostmengde sporet må dimensjoneres etter, variererer med dimensjonerende toghastighet. | ||
Tabell 6.6 Dimensjonerende frostmengde og sporets kvalitetsklasse | Tabell 6.6 Dimensjonerende frostmengde og sporets kvalitetsklasse | ||
Kvalitetsklasse | {| class="wikitable" width="45%" | ||
Dimensjonerende hastighet, | |- | ||
Dimensjonerende frostmengde, | | Kvalitetsklasse || Dimensjonerende hastighet, V<sub>dim</sub> || Dimensjonerende frostmengde, F<sub>d</sub> | ||
K0 - K1 | |- | ||
| K0 - K1 || <math>V_{dim} \ge 125 km/h</math> || F<sub>100</sub> | |||
|- | |||
K2 - K4 | | K2 - K4 || <math>45 km/h \le V_{dim} \ge 125 km/h</math> || F<sub>20</sub> | ||
45 km/h | |- | ||
| K5-baner || <math>V_{dim} \le 40 km/h</math> || F<sub>10</sub> | |||
K5-baner | |} | ||
Kvalitetsklassene K0-K5 er baner med forskjellig standard, og hvor krav til frostsikring følgelig varierer. | Kvalitetsklassene K0-K5 er baner med forskjellig standard, og hvor krav til frostsikring følgelig varierer. | ||
Vi ser at det alltid benyttes | Vi ser at det alltid benyttes F<sub>100</sub> for frostsikring av baner hvor dimensjonerende hastighet er større enn 120 km/h. Alle nye viktige banestrekninger, som Østfold- og Vestfoldbanen, er K0-baner. | ||
Maksimal hastighet for en banestrekning er som regel fastsatt lenge før det er aktuelt å utføre frostdimensjonering. Med andre ord vil det være gitt i det enkelte prosjekt hvorvidt en kan redusere kravet i forhold til hundreårsfrosten | Maksimal hastighet for en banestrekning er som regel fastsatt lenge før det er aktuelt å utføre frostdimensjonering. Med andre ord vil det være gitt i det enkelte prosjekt hvorvidt en kan redusere kravet i forhold til hundreårsfrosten | ||
=== Prinsipp for frostisolering ved jernbanen === | === Prinsipp for frostisolering ved jernbanen === | ||
Hovedprinsippet for frostisolering av jernbane har vært å plassere et fuktig lag av frostsikre masser langt nede i konstruksjonen, som dekkes med et tørt isolerende lag. F.eks. vil et fyllingsprofil bygget opp av grus med ballastpukk øverst følge dette prinsippet. Grusen inneholder relativt mye vann, og kan avgi mye frysevarme når frosten trenger ned. Ballastpukken er tørr, og isolerer godt. | Hovedprinsippet for frostisolering av jernbane har vært å plassere et fuktig lag av frostsikre masser langt nede i konstruksjonen, som dekkes med et tørt isolerende lag. F.eks. vil et fyllingsprofil bygget opp av grus med ballastpukk øverst følge dette prinsippet. Grusen inneholder relativt mye vann, og kan avgi mye frysevarme når frosten trenger ned. Ballastpukken er tørr, og isolerer godt. | ||
| Linje 883: | Linje 885: | ||
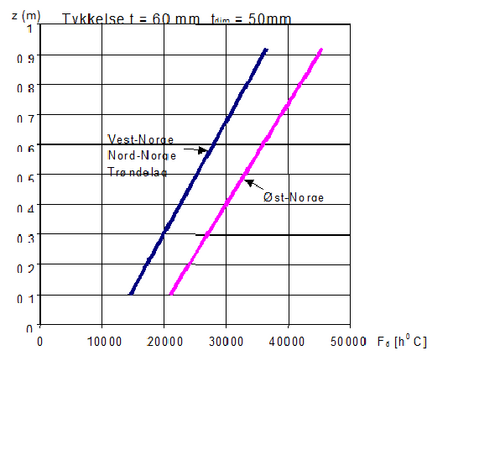
Jernbanens regelverk har i flere tiår hatt kurver for dimensjonering av frostfundament ut fra dimensjonerende frostmengde. Utgangspunktet er at det benyttes grus under 0.5 m ballast. Det er gjengitt to forskjellige dimensjoneringskurver, én for Øst-Norge og én for resten av landet. Forskjellen ligger i at magasinert sommervarme er større i Østlandsområdet enn ellers i landet når vinteren setter inn. | Jernbanens regelverk har i flere tiår hatt kurver for dimensjonering av frostfundament ut fra dimensjonerende frostmengde. Utgangspunktet er at det benyttes grus under 0.5 m ballast. Det er gjengitt to forskjellige dimensjoneringskurver, én for Øst-Norge og én for resten av landet. Forskjellen ligger i at magasinert sommervarme er større i Østlandsområdet enn ellers i landet når vinteren setter inn. | ||
Dimensjoneringskurver i gjeldende regelverk er vist i figur .11 og .12. Figur .11 viser kurve for grus uten isolasjonsplater (dvs. masseskifting i eksisterende spor eller bygging av nye spor), mens .12 viser kurver for etterisolering av eksisterende bane. Det er én kurve for 5 cm isolasjon, og én for 9 cm (effektiv tykkelse av platen redusert for 1 cm sammenpressing og pukkinntrengning). Virkelig platetykkelse skal være hhv. 6 cm og 10 cm. | Dimensjoneringskurver i gjeldende regelverk er vist i figur 6.11 og 6.12. Figur 6.11 viser kurve for grus uten isolasjonsplater (dvs. masseskifting i eksisterende spor eller bygging av nye spor), mens 6.12 viser kurver for etterisolering av eksisterende bane. Det er én kurve for 5 cm isolasjon, og én for 9 cm (effektiv tykkelse av platen redusert for 1 cm sammenpressing og pukkinntrengning). Virkelig platetykkelse skal være hhv. 6 cm og 10 cm. | ||
Ved bruk av sprengstein som frostsikring har regelen vært at en skal multiplisere nødvendig lagtykkelse for grus med 1.3 (både frostsikringslag og forsterkningslag regnes inn i lagtykkelsen). Kurven for sprengstein er senere revidert, og faktoren for tykkelse av sprengsteinslag i forhold til grus er øket til 1.6, på bakgrunn av nye kunnskaper og erfaringer ved bruk av sprengstein i underbygningen. Det åpnes likevel for å gjøre beregninger uavhengig av kurven, og derved for optimalisering av løsninger / materialvalg mv. | Ved bruk av sprengstein som frostsikring har regelen vært at en skal multiplisere nødvendig lagtykkelse for grus med 1.3 (både frostsikringslag og forsterkningslag regnes inn i lagtykkelsen). Kurven for sprengstein er senere revidert, og faktoren for tykkelse av sprengsteinslag i forhold til grus er øket til 1.6, på bakgrunn av nye kunnskaper og erfaringer ved bruk av sprengstein i underbygningen. Det åpnes likevel for å gjøre beregninger uavhengig av kurven, og derved for optimalisering av løsninger / materialvalg mv. | ||
=== Dimensjonering av frostsikringslag av grus === | === Dimensjonering av frostsikringslag av grus === | ||
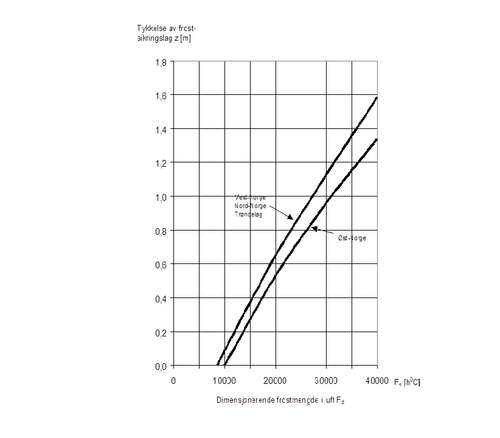
Total tykkelse av forsterkningslag og frostsikringslag av sand eller grus under ballast dimensjoneres etter figur .11. Dimensjoneringskurvene er utarbeidet for norske forhold etter UIC-blad nr. 719. Forholdene er gunstigere i Øst-Norge enn i resten av landet pga. større magasinert sommervarme i Øst-Norge. Sand i filterlaget betraktes frostteknisk som grus. | Total tykkelse av forsterkningslag og frostsikringslag av sand eller grus under ballast dimensjoneres etter figur 6.11. Dimensjoneringskurvene er utarbeidet for norske forhold etter UIC-blad nr. 719. Forholdene er gunstigere i Øst-Norge enn i resten av landet pga. større magasinert sommervarme i Øst-Norge. Sand i filterlaget betraktes frostteknisk som grus. | ||
[[Fil:Fig521-611.png|500px]] | |||
Figur 6.11 Dimensjoneringskurver for total tykkelse, z, av forsterknings- og frostsikringslag av grus | Figur 6.11 Dimensjoneringskurver for total tykkelse, z, av forsterknings- og frostsikringslag av grus | ||
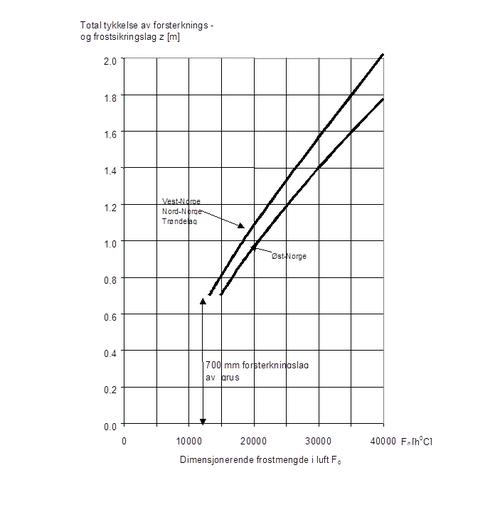
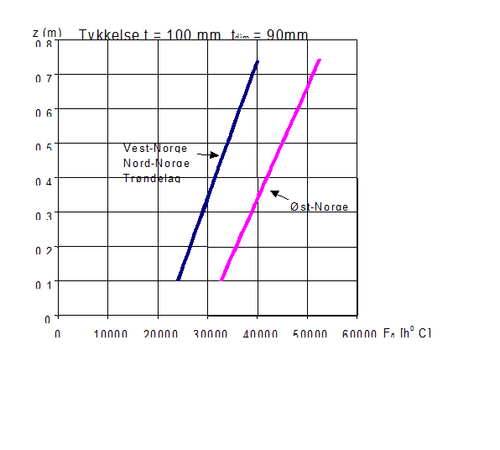
Figur .12 viser dimensjoneringskurver for frostsikringslag av grus, under forutsetning av at det i tillegg benyttes 700 mm forsterkningslag av sprengstein. | Figur 6.12 viser dimensjoneringskurver for frostsikringslag av grus, under forutsetning av at det i tillegg benyttes 700 mm forsterkningslag av sprengstein. | ||
[[Fil:Fig521-612.png|500px]] | |||
Figur 6.12 Dimensjoneringskurver for frostsikringslag av grus, i tillegg til 700 mm forsterkningslag med sprengstein | Figur 6.12 Dimensjoneringskurver for frostsikringslag av grus, i tillegg til 700 mm forsterkningslag med sprengstein | ||
=== Dimensjonering av frostsikringslag av sprengstein === | === Dimensjonering av frostsikringslag av sprengstein === | ||
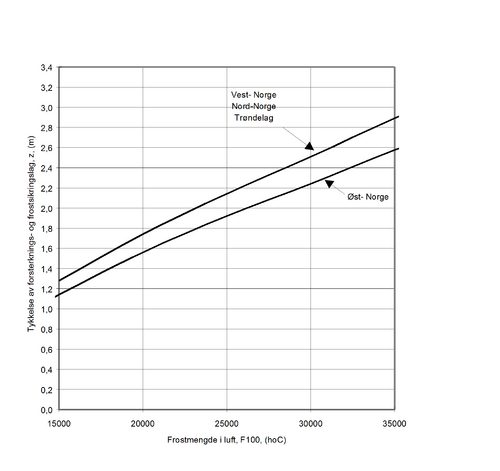
Ved dimensjonering av frostsikringslag av sprengstein er det avgjørende å ta tilstrekkelig hensyn til at de termiske egenskapene generelt er usikre og at det kan opptre betydelig variasjon i egenskapene både lokalt og fra anlegg til anlegg. Ved å sikre seg mot ekstremt ugunstige egenskaper kan kurven som svarer til 1,6 x | Ved dimensjonering av frostsikringslag av sprengstein er det avgjørende å ta tilstrekkelig hensyn til at de termiske egenskapene generelt er usikre og at det kan opptre betydelig variasjon i egenskapene både lokalt og fra anlegg til anlegg. Ved å sikre seg mot ekstremt ugunstige egenskaper kan kurven som svarer til 1,6 x Z<sub>grus</sub> gitt i figur 6.13 benyttes. Kurven gjelder for dimensjonering av tykkelse av frostsikrings- og forsterkningslag med sprengstein, under forutsetning av at følgende er tilfredsstilt: | ||
steinmassene er velgraderte, slik at bl.a. indre konveksjon forhindres | *steinmassene er velgraderte, slik at bl.a. indre konveksjon forhindres | ||
overflate og grøfteskråninger av banelegemet tettes, slik at varmetap ved konveksjon og frostinntrengning fra siden minimaliseres. | *overflate og grøfteskråninger av banelegemet tettes, slik at varmetap ved konveksjon og frostinntrengning fra siden minimaliseres. | ||
Dimensjoneringskurven gjelder for det aktuelle konseptet med 700 mm forsterkningslag av stein | Dimensjoneringskurven gjelder for det aktuelle konseptet med 700 mm forsterkningslag av stein 0 - 300 mm og frostsikringslag av stein med maksimal steinstørrelse 500 mm eller inntil 2/3 av lagtykkelsen. | ||
Inngangsdata for dimensjoneringskurven er 100 års frostmengde i luft. Effekten av temperaturforskjell mellom luft og overflate er inkludert i kurven gitt i figur .13. | Inngangsdata for dimensjoneringskurven er 100 års frostmengde i luft. Effekten av temperaturforskjell mellom luft og overflate er inkludert i kurven gitt i figur 6.13. | ||
Det er likevel helt klart at bruk av sprengstein i frostsikring er forbundet med større usikkerhet enn alternative løsninger med bruk av grus, isolasjonsprodukter eller varmeakkumulerende bunnlag. Bl.a. er følgende faktorer ikke inkludert i dimensjoneringskurven: | Det er likevel helt klart at bruk av sprengstein i frostsikring er forbundet med større usikkerhet enn alternative løsninger med bruk av grus, isolasjonsprodukter eller varmeakkumulerende bunnlag. Bl.a. er følgende faktorer ikke inkludert i dimensjoneringskurven: | ||
"steinreir" som følge av separasjon ved uheldig utlegging eller ensgraderte masser | *"steinreir" som følge av separasjon ved uheldig utlegging eller ensgraderte masser | ||
store steiner (kan gi kuldebroer gjennom fyllingen) | *store steiner (kan gi kuldebroer gjennom fyllingen) | ||
indre konveksjon som følge av åpen struktur i sprengsteinsmassene (i | *indre konveksjon som følge av åpen struktur i sprengsteinsmassene (i Bane NORs tekniske regelverk kreves det imidlertid bruk av velgraderte masser som vil ta høyde for denne effekten) | ||
Ved bruk av spesielt gunstige masser, kan lagtykkelsen beregnes spesielt. Ved bruk av spesielt ugunstige masser, skal lagtykkelsen beregnes spesielt. | Ved bruk av spesielt gunstige masser, kan lagtykkelsen beregnes spesielt. Ved bruk av spesielt ugunstige masser, skal lagtykkelsen beregnes spesielt. | ||
| Linje 917: | Linje 925: | ||
Å sikre et høyt fuktighetsnivå i bunnen av frostfundamentet av sprengstein vil bedre frostmotstanden. Dette kan f.eks. oppnås ved innlegging av gruspute eller filterlag av sand. | Å sikre et høyt fuktighetsnivå i bunnen av frostfundamentet av sprengstein vil bedre frostmotstanden. Dette kan f.eks. oppnås ved innlegging av gruspute eller filterlag av sand. | ||
[[Fil:Fig521-613.png|500px]] | |||
Figur 6.13 Dimensjoneringskurve for total tykkelse av forsterknings- og frostsikringslag av sprengstein | Figur 6.13 Dimensjoneringskurve for total tykkelse av forsterknings- og frostsikringslag av sprengstein | ||
== | == Tiltak mot telehiv på eksisterende baner == | ||
Dette avsnittet omhandler frostsikring av eksisterende baner. Dette innbefatter planlegging av etterisolering når telehiv har oppstått, samt beskrivelse av forebyggende tiltak. | Dette avsnittet omhandler frostsikring av eksisterende baner. Dette innbefatter planlegging av etterisolering når telehiv har oppstått, samt beskrivelse av forebyggende tiltak. | ||
| Linje 927: | Linje 938: | ||
Som grunnlag for å planlegge frostsikring er det viktig å skaffe seg opplysninger om størrelsen og utstrekningen av telehivet, grunnforholdene og oppbygging av underbygningen på stedet. Regelverket for underbygning beskriver derfor at telenivellement og grunnundersøkelser skal utføres som forundersøkelse for planlegging av frostsikring. Opptegningen av observasjonene er standardisert, og skal utføres som et lengdeprofil med angivelse av linjens kilometrering (pælenr.). Følgende data presenteres: | Som grunnlag for å planlegge frostsikring er det viktig å skaffe seg opplysninger om størrelsen og utstrekningen av telehivet, grunnforholdene og oppbygging av underbygningen på stedet. Regelverket for underbygning beskriver derfor at telenivellement og grunnundersøkelser skal utføres som forundersøkelse for planlegging av frostsikring. Opptegningen av observasjonene er standardisert, og skal utføres som et lengdeprofil med angivelse av linjens kilometrering (pælenr.). Følgende data presenteres: | ||
telehiv opptegnes i målestokk 1:5 for en eller flere vintre registrert ved nivellement | *telehiv opptegnes i målestokk 1:5 for en eller flere vintre registrert ved nivellement | ||
eventuell skoring angis i mm som høyeste skore innenfor hvert skoringsfelt | *eventuell skoring angis i mm som høyeste skore innenfor hvert skoringsfelt | ||
undersøkelse av ballast og undergrunn. Resultatet opptegnes i høydemålestokk 1:20 | *undersøkelse av ballast og undergrunn. Resultatet opptegnes i høydemålestokk 1:20 | ||
angivelse av skjæring eller fylling | *angivelse av skjæring eller fylling | ||
karakteristiske tverrprofiler i målestokk 1:200 | *karakteristiske tverrprofiler i målestokk 1:200 | ||
Valg av utførelsesmåte for frostsikring fastlegges av en geoteknisk sakkyndig, sammen med vedlikeholdsansvarlig for banen. | Valg av utførelsesmåte for frostsikring fastlegges av en geoteknisk sakkyndig, sammen med vedlikeholdsansvarlig for banen. | ||
| Linje 944: | Linje 955: | ||
Brukte impregnerte sviller har i nedgravd tilstand lang levetid i sporet. Trykkfastheten og deformasjonsegenskapene er tilfredsstillende hos tresvillene. Svillene skal legges på tvers under midtre del av sporet. På sidene skal det legges langsgående sviller. For å unngå oppressing av finmateriale mellom svillene, skal det legges fiberduk under svillelaget. | Brukte impregnerte sviller har i nedgravd tilstand lang levetid i sporet. Trykkfastheten og deformasjonsegenskapene er tilfredsstillende hos tresvillene. Svillene skal legges på tvers under midtre del av sporet. På sidene skal det legges langsgående sviller. For å unngå oppressing av finmateriale mellom svillene, skal det legges fiberduk under svillelaget. | ||
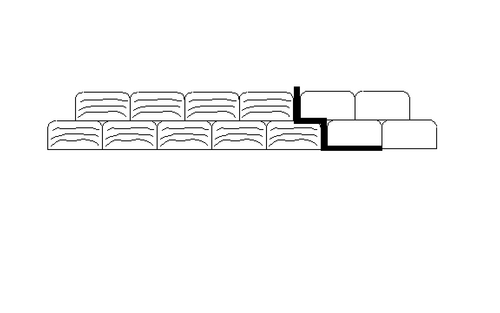
Svilletrauet kan virke som drensgrøft, og det kan oppstå grunnbrudd. Grunnbruddet oppstår p.g.a. vanntrykket på trauveggene ved overgang fra skjæring til fylling. For å unngå dette, skal det legges inn tverrgående sperresjikt av 0,15 mm plastfolie for hver 10 m hvor banen ligger i større stigning enn 10 ‰, se figur .14. | Svilletrauet kan virke som drensgrøft, og det kan oppstå grunnbrudd. Grunnbruddet oppstår p.g.a. vanntrykket på trauveggene ved overgang fra skjæring til fylling. For å unngå dette, skal det legges inn tverrgående sperresjikt av 0,15 mm plastfolie for hver 10 m hvor banen ligger i større stigning enn 10 ‰, se figur 6.14. | ||
[[Fil:Fig521-614.png|500px]] | |||
Figur 6.14 Sperresjikt av plastfolie | Figur 6.14 Sperresjikt av plastfolie | ||
Frostsikringens bredde skal ved bruk av sviller være minimum 4 m. Tykkelsen på frostsikringslaget dimensjoneres etter tabell .7. | Frostsikringens bredde skal ved bruk av sviller være minimum 4 m. Tykkelsen på frostsikringslaget dimensjoneres etter tabell 6.7. | ||
Tabell 6.7 Antall lag sviller | Tabell 6.7 Antall lag sviller | ||
{| class="wikitable" width="45%" style="text-align: center;" | |||
|- | |||
| Dimensjonerende frostmengde (h<sup>0</sup>C) || Antall lag sviller | |||
|- | |||
| 5000 – 15000 | |||
15000 – 25000 | |||
25000 – 40000 | |||
| 1 | |||
25000 – 40000 | |||
1 | |||
2 | 2 | ||
3 | 3 | ||
|} | |||
=== Frostsikring med isolasjonsmaterialer === | === Frostsikring med isolasjonsmaterialer === | ||
De første kunstige isolasjonsmaterialene var plater av ekspandert polystyren. I de senere årene er det ekstrudert polystyren som er mest brukt. Plater som benyttes skal være KFK- frie plater av ekstrudert polystyren. | De første kunstige isolasjonsmaterialene var plater av ekspandert polystyren. I de senere årene er det ekstrudert polystyren som er mest brukt. Plater som benyttes skal være KFK- frie plater av ekstrudert polystyren. | ||
Kvalitetskrav knyttet til trykkstyrke og densitet er gitt i tabell .8 | Kvalitetskrav knyttet til trykkstyrke og densitet er gitt i tabell 6.8 | ||
Tabell 6.8 Krav knyttet til trykkstyrke og densitet av isolasjonsplater | Tabell 6.8 Krav knyttet til trykkstyrke og densitet av isolasjonsplater | ||
Kvalitetskrav | {| class="wikitable" width="45%" | ||
Min. tykkelse (mm) | |- | ||
Trykkstyrke (kN/ | | Kvalitetskrav || Min. tykkelse (mm) || Trykkstyrke (kN/m<sup>2</sup>) || Densitet (kg/m<sup>3</sup>) | ||
Densitet (kg/ | |- | ||
Plater av ekstrudert polystyren | | Plater av ekstrudert | ||
60 | polystyren | ||
min. 400 ved 5 % deformasjon* | | 60 || min. 400 ved 5 % deformasjon* || min. 38 | ||
min. 38 | |} | ||
* Trykkstyrken måles på 50 mm prøveterninger | * Trykkstyrken måles på 50 mm prøveterninger | ||
| Linje 988: | Linje 1 001: | ||
Anvendelse av polystyrenplater til frostisolasjon, er i alminnelighet mest aktuelt i forbindelse med ballastrensing og bruk av ballastrenseverk. Under platene skal det ligge igjen pukk, grus eller sand i minst 0,1 m tykkelse. I motsatt fall skal det velges en arbeidsmetode som tillater grusfilter eller fiberduk innlagt under platene. På sprengsteinsfyllinger er det normalt filterlag på traubunn. Kravet om 0,1 m tykkelse pukk, grus eller sand faller da bort. | Anvendelse av polystyrenplater til frostisolasjon, er i alminnelighet mest aktuelt i forbindelse med ballastrensing og bruk av ballastrenseverk. Under platene skal det ligge igjen pukk, grus eller sand i minst 0,1 m tykkelse. I motsatt fall skal det velges en arbeidsmetode som tillater grusfilter eller fiberduk innlagt under platene. På sprengsteinsfyllinger er det normalt filterlag på traubunn. Kravet om 0,1 m tykkelse pukk, grus eller sand faller da bort. | ||
Platene må minimum være 60 mm tykke. Dimensjonerende tykkelse regnes 10 mm mindre enn platetykkelsen p.g.a. pukknedtrengning og sammentrykking. Figur .15 og .16 viser dimensjoneringskurver for kombinasjonen isolasjon og grus. Diagrammene angir tykkelsen på nødvendig gruslag under 60 mm og 100 mm skumplate. Det er forutsatt at varmeledningstallet for isolasjonsplatene er 0,037 W/mK. For isolasjonsmaterialer av ekstrudert polystyren, tilsvarer dette et fuktopptak på 5 - 10 volumprosent. | Platene må minimum være 60 mm tykke. Dimensjonerende tykkelse regnes 10 mm mindre enn platetykkelsen p.g.a. pukknedtrengning og sammentrykking. Figur 6.15 og 6.16 viser dimensjoneringskurver for kombinasjonen isolasjon og grus. Diagrammene angir tykkelsen på nødvendig gruslag under 60 mm og 100 mm skumplate. Det er forutsatt at varmeledningstallet for isolasjonsplatene er 0,037 W/mK. For isolasjonsmaterialer av ekstrudert polystyren, tilsvarer dette et fuktopptak på 5 - 10 volumprosent. | ||
Frostdybden avhenger av akkumulert sommervarme. Det er derfor forskjellige dimensjoneringskurver for Øst-Norge og resten av landet. | Frostdybden avhenger av akkumulert sommervarme. Det er derfor forskjellige dimensjoneringskurver for Øst-Norge og resten av landet. | ||
| Linje 995: | Linje 1 008: | ||
[[Fil:Fig521-615.png|500px]] | |||
Figur 6.15 Tykkelse av gruslag under 60 mm isolasjonsplater | Figur 6.15 Tykkelse av gruslag under 60 mm isolasjonsplater | ||
[[Fil:Fig521-616.png|500px]] | |||
Figur 6.16 Tykkelse av gruslag under 100 mm isolasjonsplater | Figur 6.16 Tykkelse av gruslag under 100 mm isolasjonsplater | ||
| Linje 1 004: | Linje 1 022: | ||
=== Utførelse av frostsikring med isolasjonsplater === | === Utførelse av frostsikring med isolasjonsplater === | ||
Ved leggingen må det være minimum 0,3 m avstand mellom underkant sville og overkant plate. Platene legges uten sprekker. Avvik fra dette kan være aktuelt på spesielle utkilingspartier (overganger). Figur .17 viser prinsippet for etterisolering med XPS-plater. Nødvendig omfang av isoleringen vurderes i hvert enkelt tilfelle. Tetting av sideskråninger utføres | Ved leggingen må det være minimum 0,3 m avstand mellom underkant sville og overkant plate. Platene legges uten sprekker. Avvik fra dette kan være aktuelt på spesielle utkilingspartier (overganger). Figur 6.17 viser prinsippet for etterisolering med XPS-plater. Nødvendig omfang av isoleringen vurderes i hvert enkelt tilfelle. Tetting av sideskråninger utføres iht. Bane NORs tekniske regelverk JD 520, kap. 6 Banelegeme. | ||
[[Fil:Fig521-617.png|800px]] | |||
Figur 6.17 Etterisolering med XPS-plater. Prinsippskisse | Figur 6.17 Etterisolering med XPS-plater. Prinsippskisse | ||
| Linje 1 016: | Linje 1 036: | ||
Telehivet blir redusert p.g.a. | Telehivet blir redusert p.g.a. | ||
frostfundamentets tykkelse øker slik at det kreves større frostmengde for gjennomfrysing | *frostfundamentets tykkelse øker slik at det kreves større frostmengde for gjennomfrysing | ||
ballastlaget får bedre drenering, blir tørrere og får dermed bedre isolasjonsevne | *ballastlaget får bedre drenering, blir tørrere og får dermed bedre isolasjonsevne | ||
økt avstand til grunnvannsspeilet. | *økt avstand til grunnvannsspeilet. | ||
NB: Smale fyllinger på eldre baner er en vesentlig årsak til solslyng. Sporløfting må derfor ikke foretas, uten samtidig utvidelse av fyllingsprofilet jf. | NB: Smale fyllinger på eldre baner er en vesentlig årsak til solslyng. Sporløfting må derfor ikke foretas, uten samtidig utvidelse av fyllingsprofilet jf. Bane NORs tekniske regelverk JD520, kap 6 Banelegeme og JD 530, kap. 10 Ballast. | ||
=== Ballastrensing === | === Ballastrensing === | ||
Ballastrensing er i mange tilfeller en effektiv og tilstrekkelig forebygging mot telehiving. Dette er tilfelle der hvor telehivingen vesentlig skyldes forurenset ballast. Karakteristisk ved dette er oppumping av finmateriale rundt svillene (vaskesviller). Dette kan ofte være tilfelle ved lite elastisk underbygning, som fjellskjæringer og bruer med betongtrau. | Ballastrensing er i mange tilfeller en effektiv og tilstrekkelig forebygging mot telehiving. Dette er tilfelle der hvor telehivingen vesentlig skyldes forurenset ballast. Karakteristisk ved dette er oppumping av finmateriale rundt svillene (vaskesviller). Dette kan ofte være tilfelle ved lite elastisk underbygning, som fjellskjæringer og bruer med betongtrau. | ||
== Bygging av nytt spor inntil eksisterende spor == | == Bygging av nytt spor inntil eksisterende spor == | ||
| Linje 1 053: | Linje 1 070: | ||
Hvis formasjonsplanet bli tettet med finstoff i anleggsperioden, bør det foretas harving eller avskraping av formasjonsplanet, slik at det ikke oppstår fare for telehiv i dette laget, og for å sikre de drenerende egenskapene i underbygningen. | Hvis formasjonsplanet bli tettet med finstoff i anleggsperioden, bør det foretas harving eller avskraping av formasjonsplanet, slik at det ikke oppstår fare for telehiv i dette laget, og for å sikre de drenerende egenskapene i underbygningen. | ||
== Litteraturhenvisninger == | |||
1. NIF-kurs 1997 – Frost i jord – sikring mot teleskader, NGF/NBF/NIF (1997) | 1. NIF-kurs 1997 – Frost i jord – sikring mot teleskader, NGF/NBF/NIF (1997) | ||
| Linje 1 062: | Linje 1 079: | ||
3. NGI rapport nr. 960054-1. Måling av varmeledningsevne i sprengstein, august 1996 | 3. NGI rapport nr. 960054-1. Måling av varmeledningsevne i sprengstein, august 1996 | ||
4. NGI rapport nr. 982519-1. Måling av varmetap i ballastpukk, maskinkult og sprengstein, september 1999 | 4. [[Medium:Måling av varmetap i ulike steinfyllingsfraksjoner NGI 1999.pdf|NGI rapport nr. 982519-1. Måling av varmetap i ballastpukk, maskinkult og sprengstein, september 1999]] | ||
5. [[Medium:Telehiv Vinteren 1995-96 Rapport.pdf|Telehiv vinteren 1995/96 - nye regler for frostfundament, NSB Bane Hovedkontoret Teknisk kontor 1.7.1996, rapport og vedleggsrapport]] | |||
6. [[Medium:Telehiv 1996-97 Rapport.pdf|Telehiv 1996/97, Jernbaneverket Direktoratet, Teknisk myndighet 8.4.1997]] | |||
Siste sideversjon per 21. aug. 2024 kl. 08:38
__NUMBEREDHEADINGS__
Innledning
Telehiv med tilhørende hastighetsnedsettelser og forsinkelser i togtrafikken er et velkjent problem. Jernbanen har slitt med dette gjennom alle år, og vesentlige tiltak er også utført for å redusere eller eliminere problemene. Likevel har det på 1990-tallet vært store problemer med frost og telehiv på helt nye baneanlegg.
Videre er det også tilbakevendende problemer med telehiv på våre eldre jernbanestrekninger, selv om mye er gjort for å hindre dette. Vanlige løsninger benyttet for utbedring av frostproblemer ved eksisterende baner blir også drøftet i kapitlet.
Jernbanens problem med tele i grunnen
Nedenfor beskrives de hovedproblemstillinger vedrørende frost som er typiske for jernbaner i Norge.
Problemer på grunn av telehiv
En sammenlikning mellom teleproblematikken for vei og jernbane kan være naturlig innledningsvis. Telehiv er velkjent for de fleste bilister på norske veier. Dette påvirker imidlertid biltrafikken minimalt (så lenge fjærene fungerer), mens derimot redusert bæreevne under teleløsning om våren kan gjøre veien uframkommelig (reduserte aksellaster osv.). Jernbanetrafikken påvirkes derimot kraftig selv ved mindre telehiv, noe som de reisende selv kan registrere. Følgen blir nedsatt hastighet, dårlig komfort og forsinkelselser, samt kostbart vedlikehold for jernbanen. Teleløsningsproblematikk er derimot ikke noe vesentlig problem for jernbanen.
Et moment som gjør telehiv på jernbane ekstra problematisk, er at det normalt er vanskelig å komme til for å få gjort nødvendige utbedringsarbeider i sporet, dvs. etterisolasjon, masseutskifting eller annet. Selv for vanlig vedlikehold som bytting av sviller og skinner, pukksupplering mv. er det som regel kamp mot klokken for å få utført arbeider mellom togavgangene. Omkjøringsalternativer finnes sjelden på jernbanen, og derved er det ekstra viktig å unngå at det oppstår telehiv på sporet i første omgang.
Historisk tilbakeblikk
Både banenes underbygning og overbygning har gjennomgått store forandringer gjennom jernbanens historie, dvs. fra 1850-tallet her til lands. Tidligere var det ikke uvanlig at ballasten ble lagt ut rett på underliggende grunn, med mindre denne var meget bløt, og derfor måtte skiftes ut. Dermed kunne en oppleve at det lå telefarlige masser høyt opp i banelegemet, faktisk helt oppunder ballasten. Dette er selvsagt uaktuelt for nye baner. Tykkelsen på underbygningen av f.eks. steinmasser under ballastlaget er som regel minst én meter, som oftest mer.
Dreneringsløsningen er også endret kraftig, i det en tidligere ofte baserte seg på et udrenert trau. I skjæringer har uttrauingen i naturlig grunn også endret seg vesentlig. Tidligere ble trauet gravd ut i en begrenset bredde (gjerne 4 m) og dybde under sporet. I dag graves trauet normalt ut samtidig som skjæringen for øvrig (traubredde > 10 m), og det legges som regel lukket drenering på nivå under traubunn uansett.
Etterhvert med økende krav til toghastigheter ble problemene med telehiv også tydeligere. Ved større hastigheter gjør de fysiske lover at en ujevnhet i skinnegangen merkes stadig sterkere.
Overgangen til betongsviller og helsveiset spor har gjort at det er blitt vanskelig å justere sporet om vinteren ved skoring (innlegging av plater mellom sville og skinne for mindre høydejustering av sporet). Dessuten har ballastpukken, så tørr den enn kan se ut når den ligger i sporet, den uvane å fryse sammen om vinteren. Det gjør det vanskelig å justere sporet under normale vinterforhold.
For å hindre telehiv på eksisterende spor er det gjennom tidene forsøkt mange forskjellige utbedringsløsninger, såkalt teleforebygging. En mye brukt metode er innlegging av torvbunter i sporet. Andre kjente metoder er innlegging av lokomotivslagg, innlegging av brukte sviller, masseskifting med grus, og med tiden kom også bruken av isolerende plater av kunstige materialer som XPS o.l. I mindre grad er det også benyttet bark og kutterflis til isolasjonsformål.
All den tid det i flere tiår ikke ble bygget nye baner her i landet, sier det seg selv at det i stor grad var de eksisterende baner som ble utbedret ved hjelp av ovennevnte tiltak. Metodene, og da særlig ilegging av torvballer, er likevel benyttet også på nybygde spor. F.eks. ble det ved utvidelse av sporet mellom Skøyen og Asker til dobbeltspor lagt ned betydelige mengder torv, og tilsvarende ved bygging av Nordlandsbanen. Frem til midten av 1970-tallet var over 600 km jernbanespor frostsikret her i landet med de nevnte metoder.
Forskningsaktiviteten på feltet frost var svært intens i NSB på 1950- og 60-tallet, og både forskjellige materialer og utførelsesmetoder ble studert i utstrakt grad ved Geoteknisk kontor. Metodene man valgte for utbedring av isolasjonen viste seg effektive, og problemene med telehiv ble i stor grad løst.
Noe telehivproblemer om vinteren har det nok likevel vært ved jernbanen hele tiden, men det var først på midten av 1990-tallet at en plutselig fikk fornyet fokus på dette feltet. Som tidligere nevnt var årsaken de meget omfattende, og fra massemedia velkjente, telehivproblemene på de nye banestrekningene på Østfold- og Vestfoldbanen. Hovedårsaken til dette var at andre byggematerialer ble tatt i bruk i banenes frostfundament (hovedsakelig sprengstein) og alle frosttekniske egenskaper var ikke godt nok dokumentert. Dette satte på nytt fokus på frostforskningen i siste halvdel av 1990-tallet, se også avsnitt 4.5.
Mekanismer for frysing og teledannelse i jord
I dette avsnittet beskrives de fysiske mekanismene som fører til telehiv og telefarlige jordarter beskrives. I tillegg deles jordartene inn i telefarlighetsklasser.
Teledannelse i jordmaterialer
Tre faktorer er nødvendige for at telehiv skal kunne oppstå:
- Tilgang på vann
- Temperatur i jordarten under frysepunktet for vann
- Telefarlig jordart
Dersom èn av disse faktorene ikke er tilstede vil telehiv ikke kunne opptre.
Det er to faktorer som bidrar til størrelsen på telehiv:
- ≈ 9% utvidelse av porevann under frysing
- dannelse av islinser ved frysefronten
Det at porevannet i jordartene utvider seg med 9% når det fryser ble lenge sett på som årsaken til telehiv. Hovedårsaken til telehiv er imidlertid at ekstra vann suges opp til frysefronten og fryser ut som rene lag av is (islinser). Dannelsen av islinser kan gi en ekspansjon som langt overstiger volumøkingen av porevannet.
Når islinsene smelter om våren, oppstår et vannoverskudd i jorda. Dette gir nedsatt styrke og mindre motstand mot deformasjon ved belastning. Nedsatt bæreevne grunnet oppbløting i teleløsningsperioden er en av de viktigste skadeårsakene på norske veger. For jernbaneanlegg er det som tidligere nevnt telehiv som er klart mest kritisk.
Telefarlig jord
En jordart regnes som telefarlig hvis den har evne til å trekke opp vann kapilært og skille det ut som islinser ved frysfronten. Telefarlighet av jordartene er knyttet opp til porestørrelsen.
I finkornige og finstoffholdige jordarter (silt, leire og morene) er porene så små at isen møter hindring mot å trenge ned i poresystemet. Overflatespenningen mellom is og vann og små poreradier fører til at frysepunktet for vann synker under 0oC. Da oppstår et undertrykk (sug) i porene under isfronten. Undertrykket bidrar til at det trekkes opp vann til frysefronten fra underliggende jordlag eller fra grunnvannet. Telemekanismen i finkornige jordarter er en meget komplisert prosess. Det praktiske resultatet er imidlertid at vanninnholdet øker og at det dannes mer eller mindre rene islag i jorda.
I silt kan det under ugunstige betingelser utvikles betydelige islinser, enten jevnt fordelt i mange tynne skikt eller konsentrert i flere centimeter tykke islag. I leire vil den lave permeabiliteten begrense vanntransporten. I feite leirer oppstår det også en krymping av leirmaterialet mellom islinsene på grunn av at vann suges ut og konsentreres i islinsene. Det kan derfor bli relativt liten telehiving i homogen leire. Men i leire som er sprukket eller lagdelt kan det tilføres rikelig med vann til å utvikle store islinser.
I grovkornige jordarter, slik som sand og grus, er det så store sammenhengende åpninger i poresystemet at volumutvidelsen ved utfrysing av porevannet vanligvis blir tatt opp ved fortrengning av porevann inn i den ufrosne delen av jorda. I slike materialer oppstår det derfor vanligvis ikke telehiving. I litt mer finkornige jordarter (fin sand, grov silt) kan det skje en innfrysing av vannet i porene. I så fall oppstår en telehiving som svarer til 9% av porevolumet hvis metningsgraden er høy. Med metningsgrad menes hvor stor del av de disponible porene i jordarten som er fylt med vann.
I masser med stor tilgang på vann kan det oppstå stort telehiv også i finstoff-fattige materialer som normal ikke regnes som telefarlig. Problemet er vanligvis forbundet med grunnvann som strømmer opp mot frysefronten i skjæringer eller naturlige forsenkninger i terrenget.
På overflaten kan grunnvann som trenger fram i dagen bygge opp betydelige ismasser om vinteren (iskjøving). Slike ismasser kan gi store belastninger der de kommer i kontakt med konstruksjoner.
Telefarlighetsklassifisering
I Norge er det vanlig å dele jordartene inn i 4 klasser etter bæreevneegenskapene i teleløsningsperioden:
T1 = Ikke telefarlig
T2 = Litt telefarlig
T3 = Middels telefarlig
T4 = Meget telefarlig
Når en jordart betegnes som ikke telefarlig, betyr det at en underbygning som består av denne jordarten under normale forhold ikke vil utsettes for heving og synking når jorden fryser og tiner.
Når frosten trenger ned i en telefarlig jordart, oppstår islinser som følge av kapillær vannoppsuging fra underliggende lag. Dette medfører at formasjonsplanet (FP) løftes under nedfrysningen, og synker i tineperioden. Dette kalles for telehiv. Telehivet blir trolig størst jo tidligere på vinteren frosten trenger ned i telefarlig grunn. Dette fordi telehivdannelsen tar tid, da vann hele tiden må transporteres til frysefronten for å øke telehivet.
Jordmaterialer som anvendes i frostsonen, skal være av typen "Ikke telefarlig". Telefarlighet bedømmes ut fra den korngradering materialet har, se tabell 6.1.
Tabell 6.1 Norsk telefarlighetsklassifisering
| Benevnelse | Telekasse | Masseprosent (av materiale < 19,0 mm) | Eksempel på jordarter | |
|---|---|---|---|---|
| < 0,02 mm | < 0,2 mm | |||
| Ikke telefarlig | T1 | Sand
Grus Torv Myrjord | ||
| Litt telefarlig | T2 | Sand
Grus Morene (sandig, grusig) | ||
| Middels telefarlig | T3 | Sand
Morene (leirig) Leire med mer enn 40 % < 0,002 mm | ||
| Meget telefarlig | T4 | Leire med mindre enn 40 % < 0,002
Silt Morene (siltig) | ||
Telefarlighetskriteriet kan uttrykkes slik: "For at et materiale ikke skal være telefarlig, må masseprosenten av materialet < 0,02 mm ikke være større enn 3% beregnet av materiale som passerer 19 mm sikt". I figur 6.1 vises eksempler på korngraderingskurver for materialer innen de forskjellige telefarlighetsgruppene.
Figur 6.1 Eksempler på kornfordelingskurver for jordmaterialer innen de enkelte telefarlighetsgrupper
Som nevnt i avsnitt 3.2 har altså grovkornige masser som sand og grus har liten kapillær sugeevne, og derfor liten evne til å suge opp vann fra et dyptliggende grunnvannsspeil. Finkornige jordarter som silt og leire har stor kapillær sugeevne, og kan suge vann opp fra et grunnvannsspeil som kan ligge flere titalls meter under terreng.
Det er interessant å merke seg at siltinnholdet kan sies å ha størst betydning for telefarligheten, selv om leire, som har de minste kapillarrørene, har større kapillær sugeevne. Årsaken er at leire, samtidig som materialet kan løfte vann flere titalls meter, er så tett at tilført vannmengde til frysefronten, og derved mulighet for islinseproduksjon, er liten. Silt har fortsatt høy sugeevne, samtidig som materialets permeabilitet er høy. Siltmasser tilfører derfor raskt nytt vann til frysefronten når det dannes islinser i frysesonen.
Følgende formel gir tilnærmet kapillær stigehøyde for jordarter:
| hc = | (6.1) |
hvor e er materialets poretall gitt ved e = og er et uttrykk for andelen ”hulrom” mellom kornene i jordarten. d10 angir kornstørrelsen for et materiale ved 10 % gjennomgang på et kvadratsikt, dvs. d10 betyr at 10% av materialet har mindre korndiameter enn d10
I figur 6.2 er det samme forholdet vist utregnet for varierende materialer.
Figur 6.2 Kapillær stigehøyde i jord
Frostdimensjonering
Grunnlag for termisk dimensjonering
Varmestrøm gjennom vegg
Frostdimensjonering tar utgangspunkt i vanlige betraktninger av varmestrøm gjennom en vegg, jf. figur 6.3. Ved en gitt temperaturgradient, dvs. ved en konstant temperaturforskjell mellom de to sidene av veggen, vil varmestrømmen gjennom veggen være konstant, og kan uttrykkes slik:
| q = | (6.2) |
der:
- er veggens varmeledningsevne,
- er temperaturforskjell mellom de to sidene av veggen, og
- er veggens tykkelse.
Figur 6.3 Varmestrøm gjennom en vegg
Varmelagring
Varmelagring i et legeme ved tilførsel av en varmemengde Q er gitt ved følgende sammenheng:
| (6.3) |
der:
- er temperaturforskjell i legemet før og etter varmetilføringen,
- C er legemets volumetriske varmekapasitet,
- V er legemets volum
En tilført varmemengde gir altså en temperaturøkning i legemet avhengig av den volumetriske varmekapasitet.
Frysevarme
Frysing eller tining av et materiale som inneholder vann frigjør eller binder en varmemengde proporsjonal med materialets frysevarme:
| (6.4) |
der:
- Q er frigjort varme,
- L er volumetrisk frysevarme, og
- V er volum som tiner eller fryser.
L kan skrives som ,
hvor:
- w er vektandel vann,
- er tørr romvekt for materialet, og
- l er vannets frysevarme (= 4,2 MJ/m3).
Grunnlag for frostdimensjonering
Frostmengde og ”hundreårsfrosten”
Frostmengder beregnes med enheten hoC eller ”frosttimegrader”, som er et uttrykk for summen av produktet av døgnmiddeltemperaturen og antall timer i frostperioden. Eksempel: Hvis det i et døgn er gjennomsnittlig 10 minusgrader, blir døgnets frostmengde 24 h x 10 = 240 frosttimegrader.
Hundreårsfrosten, F100, er for mange et velkjent begrep. Vi avgrenser oss her til å definere begrepet slik det defineres i Bane NORs tekniske regelverk. F100 er den frostmengde som «antas å bli overskredet én gang i løpet av en periode på 100 år». Vi kan for ordens skyld føye til «én - og akkurat én».
Dette er en teoretisk definisjon av hundreårsfrosten. Ved å akseptere hundreårsfrosten som dimensjoneringskriterium, aksepterer vi samtidig at gjennomfrysing av underbygningen kan forekomme én gang hvert hundreår i snitt.
Selv om definisjonen av hundreårsfrosten er enkel og eksakt, kan det diskuteres hvilken tallmessig størrelse «hundreårsfrosten» egentlig har. Det finnes bare pålitelig statistisk materiale for en begrenset periode for denne type meteorologiske registreringer. Det finnes også bare et begrenset antall målestasjoner, og ikke alltid der jernbanen går, eller planlegges bygget. Det benyttes også flere forskjellige statistiske metoder som ikke alltid gir samme svar osv. Endelig kan det hende at klimaet generelt endrer seg fortere enn at det går an å snakke med presisjon om noe som skal inntreffe én gang hvert hundreår i gjennomsnitt.
I Bane NORs tekniske regelverk er det også bestemmelse om at en skal benytte F100 som utgangspunkt for beregning av F20 og F10, med følgende sammenhenger:
F20 = 0.85 x F100 (”tyveårsfrosten”)
F10 = 0.75 x F100 (”tiårsfrosten”)
Dette utgjør nok en viss forenkling i forhold til reelle klimatiske forhold. F20 ligger noen steder noe nærmere F100, mens andre steder er det motsatte tilfelle.
Faktorer som påvirker frostnedtrengning
Mange faktorer påvirker frostnedtrengning i en jernbanekonstruksjon. En oversikt over de viktigste faktorene er vist i tabell 6.2
Tabell 6.2 Faktorer som påvirker frostnedtrengning i en jernbanekonstruksjon
| Klimatiske forhold | Banekonstruksjon | Materiale i over- og underbygning |
|---|---|---|
|
|
|
Noen av faktorene kan måles og tallfestes, slik som årsmiddeltemperatur og frostmengde, selv om også disse faktorene kan variere betydelig over en gitt jernbanestrekning. Andre faktorer vil være avhengige av utførelse og kontroll, slik som tørr romvekt og maksimal kornstørrelse, dmaks. Noen faktorer har store årlige variasjoner.
Jordvarme og frysevarme
Det teoretiske grunnlaget for frostdimensjonering av konstruksjoner i grunnen er omfattende, og er til dels også bygget på empiri hva angår jordvarme og meteorologiske forutsetninger. Her medtas en forenklet oppsummering av teorien for frostsikring som bakgrunn for å forstå frostproblematikken generelt, basert på metode beskrevet i ”Frost i jord” (1976).
En varmestrømsbetraktning av en liten økning i frostdybde sier at varmestrømmen består av to bidrag, se også figur 6.4:
Frysevarme (L•Δz) som frigjøres ved faseovergangen når vannet i underbygningsmassene fryser til is. Jordvarme (q0•Δt) som strømmer opp fra undergrunnen i det tilhørende aktuelle tidsrommet.
Figur 6.4 Varmebalanse ved frysefronten over et lite tidsrom Δt
Betraktet over hele frostperioden utgjør frysevarmen jordlagets frysemotstand. Tilsvarende kalles bidraget fra utstrømmende jordvarme jordvarmens frostmotstand.
Til sammen utgjør jordlagets frysemotstand ned til frysefronten og jordvarmens frostmotstand den frostmengden som jernbanen utsettes for på overflaten.
Likning 6.5 uttrykker sammenhengen ble vist i figur 6.4.
| (6.5) |
der:
- L er volumetrisk frysevarme () [Wh/m3]
- w er vektandel vann
- er tørr romvekt
- l er frysevarme av vann
- q0 er varmestrøm fra ufrosne jordlag
- er varmeledningsevne av frosset jord
- Gf er temperaturgradient over frysefronten, og
- t er tid.
Med ord betyr dette:
Frysevarme + jordvarme = varme som ledes bort fra frysefronten.
Formel 6.5 kan omregnes, bl.a. ved en integrering over frostperioden samt ved å neglisjere varmelagring i frosne jordlag, slik at en har følgende:
Jordlagets frysemotstand + jordvarmens frostmotstand = frostmengden på overflaten.
Dimensjonering av en lagdelt jernbanekonstruksjon vil derfor si å finne nødvendig tykkelse av lagene for at telefronten ikke skal gå gjennom disse, og ned i underliggende telefarlige masser.
Nødvendige parametre som vi selv må velge for dimensjoneringen, er varmeledningsevnen til materialene (),vanninnhold (w) og tetthet av materialene (). I tillegg er det nødvendig med empirisk verdi for varmestrøm (Watzingers tall Wt) og jordvarmemengde (Q0), og som finnes i diagrammer i figur 6.6 (fra ”Frost i jord nr. 17, 1976”).
Manuell beregningsmetode etter ”Frost i jord”
Nedenfor gis en beregningsmetode og formler for dimensjonering etter ”Frost i jord”.
Total frysemotstand F er gitt ved:
| (6.6) |
der:
- F er total frysemotstand,
- i er summen av frysemotstand i ulike lag, og
- E er jordvarmens frostmotstand.
Jordvarmens frysemotstand E er gitt ved:
| (6.7) |
der:
- Wt er Watzingers tall (empirisk, se figur 6.6),
- Rmax er varmestrømmotstand ved største tillatte frostdybde, og
- Q0 er jordvarmemengde,
og hvor varmestrømmotstanden Rmax er gitt ved:
| (6.8) |
der:
- Rmax er varmestrømmotstand ved største frostdybde,
- er lagtykkelse i lag nr. i, og
- er varmeledningsevne i lag nr. i.
Frysemotstanden i lag nr. n er gitt ved:
| (6.9) |
der:
- er lagtykkelse i lag nr. i,
- er varmeledningsevne i lag nr. i, og
- Ln er frysevarme i lag n,
og hvor frysevarmen Ln i det enkelte lag er gitt ved:
| (6.10) |
der:
- Wn er vanninnhold i lag nr. n (vektprosent),
- l er frysevarme i vann (=93 Wh/kg), og
- er densitet av lag nr. n.
Beregning av varmestrømmotstand i en lagvis oppbygget konstruksjon som vist i figur 6.5 er vist nedenfor.
Figur 6.5 Varmestrømmotstand i lagene 1 - 3.
For lag nr. 1 er frysemotstanden gitt ved:
| (6.11) |
For lag nr. 2 er frysemotstanden gitt ved:
| (6.12) |
For lag nr. 3 er frysemotstanden gitt ved:
| (6.13) |
Med dette formelapparatet og ved hjelp av diagrammene nedenfor for bl.a. det empiriske Watzingers tall, kan frysemotstanden F finnes. Dette forutsetter at egnede parametre for materialer og klima (frostmengde osv.) er kjent.
Figur 6.6 Diagrammer for Watzingers tall Wt og varmestrømmotstand Rmax
Før regneeksempler skal vi bl.a. se litt på vurdering av parametrene varmeledningsevne og vanninnhold.
Materialparametre
De viktige parametrene for frostdimensjonering er varmeledningsevne og vanninnhold. Disse parametrene er i stor grad bestemt av den type materialer vi bygger med, men i noen grad også av dreneringsløsning. Når det gjelder valg av densitet for de forskjellige materialer, vises til erfaringsverdier for komprimerte masser.
Varmeledningsevne
For en bestemt gradering av et materiale er vanninnholdet den faktor som i sterkest grad styrer varmeledningsevnen. Økende vanninnhold gir som nevnt økende varmeledningsevne.
Økende komprimering øker også varmeledningsevnen.
I tillegg vil stor kornstørrelse (steinstørrelse) kunne spille negativt inn, fordi steinmaterialet i seg selv har høy varmeledningsevne. Hvis hele lagtykkelsen i underbygningen besto av en enkelt stein, ville varmeledningsevnen to-/tredobles i forhold til i steinmasser hvor lagtykkelsen er 2-3 ganger så stor som maksimal steinstørrelse.
Forøvrig spiller også fordeling av mineraltyper i steinmaterialene inn. Kvarts har høy varmeledningsevne (10 W/m2K), og kvartsinnhold i steinmaterialene kan gi stort utslag på varmeledningsevnen. Feltspat har derimot liten varmeledningsevne (2 W/m2K).
Vanninnhold
Det er svært avgjørende å anta et fornuftig vanninnhold i massene. Både frysevarme og varmeledning påvirkes av dette, og gale vurderinger her kan gjøre resten av dimensjoneringen svært usikker.
Økt vanninnhold fører til økt varmeledningsevne, og derved i første omgang til redusert frostsikring. Imidlertid foregriper vi regneeksemplene som følger med å slå fast at vanninnholdets betydning for frostsikringen vanskelig kan overvurderes, fordi det under fryseprosessen av vann utvikles frysevarme. Totalt sett betyr derfor høyere vanninnhold i konvensjonelle masser normalt forbedret frostsikring. Vanninnholdet styres av flere faktorer, hvorav korngradering helt klart er vesentlig. Høyt finstoffinnhold vil øke materialets evne til å holde på vann. Valgt dreneringsløsning spiller også inn. Lukket drenering under traubunn vil redusere vanninnholdet i frostsikringslaget. Man kan i tillegg forvente at masser nærmest overflaten (lengst fra grunnvannsspeilet) er tørrere enn masser lenger ned mot traubunn.
Vanninnholdet i grusmasser er forholdsvismessig høyt, og generelt er ikke f.eks. 5-7 % vann (regnet i vekt av tørr masse) i et sandig grusmateriale uvanlig høyt. Økende avstand til grunnvannsspeilet reduserer vanninnholdet.
I ballastpukk, som med tiden stadig har fått grovere gradering, er vanninnholdet på dagens sortering neppe særlig over 2%. Grovere gradering på ballastpukken enn tidligere gir antatt noe lavere vanninnhold.
For grove sprengsteinsmasser har vi lite erfaringstall fra jernbane vedrørende vanninnhold. Det har selvsagt også med praktiske problemer å gjøre: Når steinstørrelsen er f.eks. 0.5 m er det praktisk vanskelig å ta representative prøver, og å måle vanninnholdet. Noe erfaring har en imidlertid fra mindre prøver av materiale i fraksjon 32-120 mm, som er gravd opp fra sporet på Skogerparsellen / Vestfoldbanen. Her var vanninnholdet så vidt over 1%. Antagelser om vanninnhold fra 0.5% til 1.5 % for svært ensgradert masse, og noe høyere for velgraderte steinmasser med en del finstoff, kan være en pekepinn.
Oppsummering om parametervalg
Vi ser at valg av parametre vil ha stor betydning for resultatet. Skal vi regne riktig, bør vi ikke både forutsette lav varmeledningsevne, og samtidig utnytte frysevarmen fra et høyt vanninnhold.
For isolasjonsmaterialer som XPS er det kun varmeledningsevnen som har betydning, i det vanninnholdet mhp. frysemotstand er neglisjerbart (gjelder moderne plater av XPS med lukkede porer; tidligere har vannopptak i diverse platetyper som styrofoam vært betydelig). Derimot må vanninnholdet vurderes hvis lettklinker benyttes som frostsikring.
Orienterende verdier for noen massetyper (over GV) er vist i tabell 6.3. Som man vil se, er variasjonene store, og mye innsats må derfor gjøres nettopp i parametervalget.
Tabell 6.3 Orienterende verdier for vanninnhold og varmeledningsevne for noen vanlige materialer i jernbanen
| Materiale | Vanninnhold
[%] |
Varmeledningsevne
[J/m2K] |
|---|---|---|
| Ballastpukk | 2 - 4 | 0,8 - 1,1 |
| Sand | 4 - 12 | 0,8 - 2,2 |
| Grus / sandig grus | 2 - 8 | 0,7 - 2,0 |
| Stein | 0,5 - 2
(ensgradert) |
0,6 - 2,0 |
| 1 - 4
(velgradert | ||
| Lettklinker | 1 - 3 | ~ 0.15
(«tørr») |
| XPS-plater | ~ 0 | 0.037
(dimensjonerende) |
Grunnundersøkelser
For å kunne vurdere og beregne behov for frostisolasjon må grunnforholdene være undersøkt. Under forutsetning av at massene i banefundamentet er forskriftsmessige, dvs. ikke telefarlige, er det jordarten i naturlig grunn, samt tilgangen på vann, som er avgjørende for om det skal kunne foregå telehiv.
Med andre ord er det behov for å kjenne til type jordarter og beliggenhet av grunnvannsspeilet.
Prøvetaking
Prøvetaking kan gjøres med sylinderprøvetaker (uforstyrrede prøver), men ofte vil det også være aktuelt med skovlprøvetaking (forstyrrede prøver). Prøver bør tas minimum til dybde hvor det ikke lenger vil være frost i jorden etter at det aktuelle anlegg er bygget (eks: hensyn til frostnedtrengning under planlagt kulvert).
Laboratorieundersøkelser
Som vist innledningsvis, er korngraderingen avgjørende for telefarligheten. Det betyr at undersøkelse av materialets korngradering er vesentlig for å bestemme telefarlighet av materialet. Det benyttes forskjellige typer undersøkelser for å klassifisere materialet ut fra korngradering:
- Tørrsikting: Velegnet for sand / grus
- Våtsikting: Benyttes for å få skilt ut finere materiale fra grovere, men gir ikke fordeling innen de forskjellige fraksjoner av finere materiale < 0,074mm.
- Slemmeanalyse/hydrometeranalyse (evt. ”falling drop”-metoden): Benyttes for å finne korngraderingskurve for materialer med innhold av silt og leire.
For å kartlegge telefarlighet i masser med noe finstoffinnhold (for eksempel finsand med noe siltinnhold), vil det ofte være behov for å utføre nettopp sistnevnte analyse.
Undersøkelse av varmeledningsevne
Normalt vil det ikke være mulig å undersøke varmeledning av naturlige materialer til bruk i jernbanens underbygning i hvert enkelt tilfelle/prosjekt. Imidlertid er det mulig å gjøre dette i laboratorium, og NGI utførte på oppdrag fra Jernbaneverket flere forsøk i plateapparat (såkalte ”kasseforsøk”) på slutten av 1990-tallet for å undersøke egenskapene til bl.a. sprengstein.
Målingene er utført i en instrumentert og godt isolert forsøkskasse med mål 10010075 cm3, vist på figur 6.7. Steinmaterialene som ønskes testet bygges lagvis inn i kassen og komprimeres. Steinprøvene som ble testet er sprengstein av ulike fraksjoner, ballastpukk og maskinkult.
Figur 6.7 Plateapparat for måling av varmeledningsevne i steinfylling
Forsøkskassen er utstyrt med en varmeplate i toppen og en bunnplate med kjølerør. Selve forsøket består deretter av avlesninger av temperatur og effektforbruk fram mot stasjonær varmestrøm gjennom prøven. Når tykkelsen av prøven er kjent kan materialets varmeledningsevne beregnes. I denne sammenheng vil det ikke gås nærmere inn på forsøksprosedyren. Resultatene fra forsøkene er innarbeidet i erfaringsverdiene gitt i avsnitt 4.3.3, tabell 6.3.
De første forsøkene ble utført for kun å bestemme steinmaterialenes varmeledningsevne. Prinsippet for måling av varmeledningsevne er vist i figur 6.8, der varm side er plassert på toppen, jf. beskrivelsen ovenfor.
Figur 6.8 Prinsipp for måling av varmeledningsevne ved stasjonær varmestrøm i plateapparat (dvs. måling av varmeledning uten konveksjon)
For en steinfylling in-situ vil det imidlertid også være andre effekter som har stor betydning for fyllingens frostisolerende evne. De viktigste andre effekter er:
- Indre konveksjon
- Utstråling til atmosfæren
- Kald luft som blåser inn i fyllingen
- Steinfyllingens varmekapasitet
- Latent varme
Generelt vil det for drenerte steinfyllinger være finstoffinnhold, kvartsinnhold, vanninnhold og porøsitet/total romvekt som bestemmer varmeledningsevnen.
Med bakgrunn i telehiv på nybygde banestrekninger i løpet av 1990-tallet var det en viss sammenheng mellom steder hvor telehivene oppsto og hvilke massetyper som var lagt ut i forsterknings- og frostsikringslaget. Tendensen var slik at de vesentligste telehivene ble registrert på strekninger med grove ensgraderte steinmasser, og mistanken om at konveksjon spilte en vesentlig rolle ble ytterligere forsterket. Med dette som bakgrunn ble det gjennomført nye forsøk i NGIs forsøkskasse.
Forsøkskassen ble da ombygd slik det også kunne foretas målinger med den varme siden på bunnen av kassen (det er for øvrig denne ombygde kassen som er vist på figur 6.7).
Dersom bunnen av prøvematerialet har høyere temperatur enn toppen av prøven, vil konvektiv varmeoppgang oppstå som følge av tetthetsforskjellen mellom varm (lett) luft og kald (tyngre) luft. Når en kjent stasjonær varmestrøm passerer da gjennom prøven, og det er mulig å måle temperaturforskjellen mellom topp og bunn. Varmetap med både varmeledning og bidrag fra naturlig tetthetsdrevet konveksjon kan da måles. Dette prinsippet er vist i figur 6.9.
Figur 6.9 Prinsipp for måling av varmetap med både varmeledning og bidrag fra tetthetsdrevet konveksjon i plateapparat
Det er gjennomført slike forsøk på ballastpukk (25 – 63 mm), ensgradert maskinkult (20 – 120 mm) og velgradert sprengstein (0 – 250mm). Resultatene fra disse målingene uten bidrag fra konveksjon, er vist i tabell 6.4. Resultater fra målinger, jf. prinsipp i figur 6.9, med konveksjonens bidrag er vist i tabell 6.5.
Tabell 6.4 Resultater fra utførte forsøk uten naturlig konveksjon (dvs. kun varmeledningsevne)
| Fraksjon
(mm) |
Kvartsinnhold
(%) |
Total romvekt
(kN/m3) |
htot/dmaks | Porøsitet
(%) |
Vanninhold
(%) |
Varmeledn.tall
(W/mK) |
| 25 - 63 | 23,2 | 16,5 | 11,9 | 38 | ~0 | 0,79 - 0,83 |
| 20 - 120 | 21,4 | 17,4 | 6,3 | 34 | ~0 | 0,82 - 0,91 |
| 0 - 250 | 22,5 | 3 | 18 | 3,2 | 1,6 |
Tabell 6.5 Resultater fra utførte forsøk der naturlig konveksjon kan oppstå
| Fraksjon
(mm) |
(0C) |
Tmiddel
(0C) |
Ra
(-) |
Nuteoretisk
(-) |
k*
(W/mK) |
Nuforsøk
(-) |
| 25 - 63 | 13,2
21,0 23,0 |
20,8
27,0 30,0 |
35,5
54,0 58,6 |
1,0
1,2 1,3 |
0,83
1,20 1,35 |
1,04
1,50 1,69 |
| 20 - 120 | 14,0
22,5 |
21,0
24,8 |
32,7
51,8 |
1,0
1,0 |
1,82
1,82 |
1,13
1,13 |
| 0 - 250 | 18,0
23,5 |
21,0
23,5 |
6,5
8,4 |
1,0
1,0 |
1,82
1,82 |
1,13
1,13 |
Ra eller Rayleightallet er et forholdstall mellom oppdriftskrefter og viskøse krefter. k* er en parameter beregnet med formelverk som for varmeledning men benyttet for situasjonen der konveksjon kan oppstå. Nu eller Nusselt tallet er et mål på hvor mye den totale varmetransporten øker pga. naturlig konveksjon sammenlignet med ren varmeledning.
Fra ovennevnte forsøk ser vi at ved temperaturgradienter på 200C eller mer, vil effekten fra konveksjonen spille en vesentlig rolle for de ensgradert massene av ballastpukk og maskinkult. Resultatene tilsvarer at materialene får ca. 50 – 70% høyere varmeledingsevne ved de nevnte temperaturgradienter enn ved forsøkene uten naturlig konveksjon.
For velgradert sprengstein måles det kun mindre forskjeller. Forsøket viser betydningen av å velge velgraderte masser til bruk i frostfundamentet når det i dimensjoneringen forutsettes at varmeledning er den dominerende årsaken til frostnedtrengning.
Regneeksempler
Vi skal nå se på noen regneeksempler. Formelgrunnlag som er benyttet er det samme som vist i avsnitt 4.2. Metoden som er benyttet er bare én av flere mulige regnemetoder, men tar hensyn til både jordvarmebidrag og frysevarme.
I handelen finnes også beregningsprogrammer, hvor sporets geometri kan modelleres todimensjonalt.
Det dimensjoneres ikke her for noen spesiell frostmengde. Vi ser heller på effekten av forskjellige oppbygninger, med varierende materialer i underbygningen. Hvis vi skal dimensjonere for en spesiell frostmengde, kan samme metodikk benyttes, men vi må gjenta beregningen med varierende lagtykkelser til vi er fornøyd. For konstruksjoner som består av bare ett lag er det mulig å dimensjonere direkte ved hjelp av formelapparatet ut fra gitt dimensjonerende frostmengde.
Følgende eksempler gjennomregnes:
- Først ser vi på effekten av å benytte grus (eksempel A) hhv. sprengstein (eksempel B) i underbygningen.
- Deretter ser vi på effekt av å isolere sporet med XPS-plater
- Først legges XPS-platen over et gruslag (eksempel C).
- Deretter legger vi isolasjonsplaten på traubunn (eksempel D), og ser om «faktorenes orden» er likegyldig.
- Helt til slutt tar vi utgangspunkt i eksempel B, men legger inn et beskjedent sandlag nederst i konstruksjonen som filterlag (eks. E).
Pukklaget på 0.5 m er konstant med de samme parametre i alle eksemplene. I tillegg er antatt vinteramplitude på 150C i alle eksemplene.
Eksempel A
I det første regneeksemplet ser vi på en enkel, klassisk jernbanekonstruksjon med grus som frostsikringslag.
| Lag | Materiale | W | |||
| [nr] | [m] | [W/mK] | [%] | [kg/m3] | |
| 1 | Ballastpukk | 0,5 | 0,9 | 1,5 | 1500 |
| 2 | Grus | 1,2 | 1,6 | 5 | 1800 |
Det er antatt et Watzingers tall Wt på 0.65, og en jordvarmemengde Q0 på 25.000.
Innsetting i formelapparatet over gir følgende:
- Frysemotstand: = 10.393 h0C
- Jordvarmens frostmotstand: E = 18.958 h0C
- Konstruksjonen motstår en frostmengde på: + E = 29.351 h0C
Frostdimensjonering tar utgangspunkt i frostmengde i luft. På grunn av lavere overflatetemperatur må fratrekkes ca. 5000 h0C fra resultatet ovenfor, slik at konstruksjonen kan tåle en dimensjonerende frostmengde på F = 25.000 h0C. Dette må kontrolleres mot kurvene i regelverket.
Eksempel B Vi bytter nå ut grus med sprengstein med langt lavere vanninnhold. Samtidig antar vi da at varmeledningsevnen er litt lavere enn for grus, men antatt store steiner gjør at varmeledningsevnen fortsatt antas å ha en høy verdi.
| Lag | Materiale | W | |||
| [nr] | [m] | [W/mK] | [%] | [kg/m3] | |
| 1 | Ballastpukk | 0,5 | 1,0 | 2,0 | 1500 |
| 2 | sprengstein | 1,2 | 1,5 | 0,5 | 1900 |
Ved innsetting i formelapparatet får vi:
- Frysemotstand: = 1.303 h0C
- Jordvarmens frostmotstand: E = 21.125 h0C
- Konstruksjonen motstå en frostmengde på: + E = 22.428 h0C
Altså betydelig dårligere frostisolasjon enn for grustilfellet. Forskjellen ligger i dette beregningstilfellet hovedsakelig i at vi har antatt et svært lavt vanninnhold i sprengsteinslaget, og vi mister derved et vesentlig frysevarmebidrag.
Reduksjon for lavere overflatetemperatur tilsier at konstruksjonen er tilstrekkelig for en dimensjonerende frostmengde i luft på ca. 17.000 h0C.
Eksempel C I dette eksemplet er det tenkt innlagt isolasjonsplate av XPS over et gruslag. Vi antar at platen ikke opptar vann. XPS-platen er egentlig 60 mm tykk, men må reduseres til 50 mm ved beregning, pga. antatt inntrykking av stein i platen og sammenpressing.
| Lag | Materiale | W | |||
| [nr] | [m] | [W/mK] | [%] | [kg/m3] | |
| 1 | Ballastpukk | 0,5 | 1,0 | 2,0 | 1500 |
| 2 | XPS | 0,05 | 0,037 | 0 | 40 |
| 3 | Grus | 0,80 | 1,6 | 5 | 1800 |
Innsetting i formelapparatet gir:
- Frysemotstand: = 17.010 h0C
- Jordvarmens frostmotstand: E = 23.073 h0C
- Konstruksjonen kan motstå en frostmengde på: + E = 40.083 h0C
Reduksjon for lutftemperatur gjøres som tidligere, slik at konstruksjonen med de gitte forutsetninger kan tåle dimensjonerende frostmengde i luft på ca. 35.000 h0C.
Eksempel D
Her skal vi sjekke om det har noen betydning hvor de ulike lagene plasseres i frostfundamentet. Vi antar en oppbygging av konstruksjon med lag som i eksempel C, men vi bytter om rekkefølgen, og legger isolasjonsplaten helt nede på traubunn. Forøvrig er alle parametre like.
| Lag | Materiale | W | |||
| [nr] | [m] | [W/mK] | [%] | [kg/m3] | |
| 1 | Ballastpukk | 0,5 | 1,0 | 2,0 | 1500 |
| 2 | Grus | 0,80 | 1,8 | 6 | 1800 |
| 3 | XPS | 0,05 | 0,037 | 0 | 40 |
Innsetting i formelapparatet gir:
- Frysemotstand: = 355 h0C
- Jordvarmens frostmotstand: E = 23.073 h0C
- Konstruksjonen kan motstå en frostmengde på: + E = 23.428 h0C
Et svært interessant – og tankevekkende - resultat! Bare ved å bytte om rekkefølgen på lagene mistet vi hele 16.500 h0C i frostmotstand i forhold til forrige eksempel! Vi får her ikke utnyttet det høye vanninnholdet i gruslaget effektivt, fordi den frigjorte varmen ikke lenger blir holdt tilbake av isolasjonsplatene, slik som i eksempelet foran.
Eksempel E Til slutt erstatter vi 15 cm sprengstein i eksempel B med et sandlag på 15 cm. Sandlaget legges nederst i trauet, som et filterlag. Sand holder på mye vann, og vi antar samtidig en relativt høy varmeledningsevne.
| Lag | Materiale | W | |||
| [nr] | [m] | [W/mK] | [%] | [kg/m3] | |
| 1 | Ballastpukk | 0,5 | 1,0 | 2,0 | 1500 |
| 2 | Sprengstein | 1,05 | 1,5 | 0,5 | 1800 |
| 3 | Sand | 0,15 | 2,0 | 10 | 1600 |
- Frysemotstand: = 3.455 h0C
- Jordvarmens frostmotstand: E = 20.719 h0C
- Konstruksjonen kan motstå en frostmengde på: + E = 24.175 h0C
Dette er ca. 2.000 h0C mer enn i eksempel B, hvor det ble brukt bare sprengstein. Lar vi sandlaget være 30 cm tykt, vinner vi ytterligere ca. 2.000 h0C, og bedringen i frostmotstand begynner nå virkelig å monne. Virkelig høy gevinst får vi når vi legger inn et fuktig lag som torv, sviller, bark e.l. Denne teknikken utnyttes ikke på nye jernbaner i dag, men er i bruk innen vegbygging.
Oppsummering av beregningseksemplene
De enkle eksemplene kan føre oss frem til en slags oppsummering av de vesentligste punkter ved dimensjoneringsmetodikken:
- Det er ikke tilfeldig hvilken lagrekkefølge som benyttes ved oppbygging av banelegemet. Regelen er enkel: Våte lag nederst, tørre og isolerende lag øverst. (En løsning som er nøye utregnet etter dette prinsippet kan miste mye av sin effekt hvis noen i anleggsperioden plutselig finner ut at det er mer praktisk å f.eks. legge isolasjonsplater på traubunn.)
- Lavt vanninnhold gir generelt dårlig frostsikring. Vi har ikke her regnet på eksempler helt uten vanninnhold, men ved store frostmengder vil lagtykkelsene etterhvert bli så store at det ikke kan være fornuftig å benytte bare konvensjonelle masser. En må da ty til isolasjonsløsninger eller materialer med høyt vanninnhold.
- Parametre som benyttes i regnemodellene må velges med omhu da de har stor betydning for resultatet. Man kan ved beregninger vise at telesikringen er tilstrekkelig i nesten ethvert tverrsnitt ved valg av passende eller upassende parametre. Derfor er det på valg av parametre innsatsen bør legges. Regnemodeller og beregnings-programmer finnes det flere av, men forutsetningen for et godt resultat er omtanke ved vurdering av varmeledning og vanninnhold, samt ved vurdering av den reelle frostpåkjenning på stedet. Samtidig gjør beregningsprogrammer det mulig å utføre følsmohetsstudier, hvilket er sterkt å anbefale i flere tilfeller.
Frostsikring av nye baneanlegg
I dette avsnittet gjennomgås kort hvilke forutsetninger og bestemmelser som gjelder for frostsikring av jernbanespor.
Vi må fastlegge følgende før vi kan gjennomføre dimensjonering:
- Hvilken frostmengde skal vi frostsikre sporet mot? Det vil for jernbane si at vi også må vite hva slags standard vi bygger for, og selvsagt geografisk lokalisering.
- Hvilke materialer skal vi bygge med, og hvilke frosttekniske parametre skal vi benytte for de materialene som velges?
Dimensjonerende frostmengde
Bane NOR hadde tidligere i sitt regelverk tatt med et frostmengdekart over hvilke frostmengder det skal dimensjoneres for ut fra hvor i landet jernbanestrekningen skal bygges. Dette kartet ble laget for NSB på 1960-tallet, og er ikke endret vesentlig siden. Kartet er utarbeidet av Meteorologisk institutt. Skal man prosjektere en jernbanestrekning, kan en altså finne den aktuelle hundreårsfrost på kartet. Evt. reduksjon av frostmengde utføres hvis dimensjonerende hastighet er lav, jf. avsnitt 4.2.1. Frostmengdekartet er vist på figur 6.10.
Figur 6.10 Maksimale frostmengder i Norge
Overflatetemperaturen på jernbanesporet kan være 2-30C lavere enn lufttemperaturen om vinteren, hvilket man derfor må korrigere for ved beregninger. Ved beregning av dimensjonerende frostmengde justeres frostmengden for lavere overflatetemperatur avhengig av varighet av frostperioden. En justering på 5-6000 h0C er ofte noenlunde riktig på Østlandet. For å få en verdi for dette, kan vi ta utgangspunkt i frostperiodens varighet, og multiplisere antall timer med differansen i luft- og overflatetemperatur. Ved utarbeidelse av dimensjoneringskurver for nye baneanlegg, jf. avsnitt 5, er det tatt hensyn til dette forholdet.
Frostmengdekartet egner seg dårlig til detaljert planlegging. Det er derfor behov for å benytte andre kilder, for eksempel Vegvesenets håndbok 018, for å finne detaljert informasjon om F100 for den enkelte kommune.
Frostsikring og banetype
Den frostmengde et jernbanespor frostsikres for avhenger av hvilken hastighetsavhengige kvalitetsklasse sporet skal ha. Dette skyldes at en evt. telekul får større konsekvenser med økende hastighet.
Tabell 6.6 viser prinsipper for frostdimensjonering av hovedspor. Hvilken frostmengde sporet må dimensjoneres etter, variererer med dimensjonerende toghastighet.
Tabell 6.6 Dimensjonerende frostmengde og sporets kvalitetsklasse
| Kvalitetsklasse | Dimensjonerende hastighet, Vdim | Dimensjonerende frostmengde, Fd |
| K0 - K1 | F100 | |
| K2 - K4 | F20 | |
| K5-baner | F10 |
Kvalitetsklassene K0-K5 er baner med forskjellig standard, og hvor krav til frostsikring følgelig varierer.
Vi ser at det alltid benyttes F100 for frostsikring av baner hvor dimensjonerende hastighet er større enn 120 km/h. Alle nye viktige banestrekninger, som Østfold- og Vestfoldbanen, er K0-baner.
Maksimal hastighet for en banestrekning er som regel fastsatt lenge før det er aktuelt å utføre frostdimensjonering. Med andre ord vil det være gitt i det enkelte prosjekt hvorvidt en kan redusere kravet i forhold til hundreårsfrosten
Prinsipp for frostisolering ved jernbanen
Hovedprinsippet for frostisolering av jernbane har vært å plassere et fuktig lag av frostsikre masser langt nede i konstruksjonen, som dekkes med et tørt isolerende lag. F.eks. vil et fyllingsprofil bygget opp av grus med ballastpukk øverst følge dette prinsippet. Grusen inneholder relativt mye vann, og kan avgi mye frysevarme når frosten trenger ned. Ballastpukken er tørr, og isolerer godt.
Det samme prinsippet har ligget til grunn når NSB gjennom flere tiår har lagt torv i sporet i frostsikringsøyemed. Torv har ekstremt høyt vanninnhold, og gir følgelig meget høy frysemotstand. Nedlegging av isolasjonsplater umiddelbart under ballastpukken på strekninger med grus følger samme prinsipp. Da er det imidlertid isolasjonsevnen over det vannholdige laget som forbedres.
Det må på denne bakgrunn kunne sies at den økte bruken av sprengstein har medført løsninger som fra et frostteknisk synspunkt ikke er optimale.
Frostsikring etter dimensjoneringskurver
Jernbanens regelverk har i flere tiår hatt kurver for dimensjonering av frostfundament ut fra dimensjonerende frostmengde. Utgangspunktet er at det benyttes grus under 0.5 m ballast. Det er gjengitt to forskjellige dimensjoneringskurver, én for Øst-Norge og én for resten av landet. Forskjellen ligger i at magasinert sommervarme er større i Østlandsområdet enn ellers i landet når vinteren setter inn.
Dimensjoneringskurver i gjeldende regelverk er vist i figur 6.11 og 6.12. Figur 6.11 viser kurve for grus uten isolasjonsplater (dvs. masseskifting i eksisterende spor eller bygging av nye spor), mens 6.12 viser kurver for etterisolering av eksisterende bane. Det er én kurve for 5 cm isolasjon, og én for 9 cm (effektiv tykkelse av platen redusert for 1 cm sammenpressing og pukkinntrengning). Virkelig platetykkelse skal være hhv. 6 cm og 10 cm.
Ved bruk av sprengstein som frostsikring har regelen vært at en skal multiplisere nødvendig lagtykkelse for grus med 1.3 (både frostsikringslag og forsterkningslag regnes inn i lagtykkelsen). Kurven for sprengstein er senere revidert, og faktoren for tykkelse av sprengsteinslag i forhold til grus er øket til 1.6, på bakgrunn av nye kunnskaper og erfaringer ved bruk av sprengstein i underbygningen. Det åpnes likevel for å gjøre beregninger uavhengig av kurven, og derved for optimalisering av løsninger / materialvalg mv.
Dimensjonering av frostsikringslag av grus
Total tykkelse av forsterkningslag og frostsikringslag av sand eller grus under ballast dimensjoneres etter figur 6.11. Dimensjoneringskurvene er utarbeidet for norske forhold etter UIC-blad nr. 719. Forholdene er gunstigere i Øst-Norge enn i resten av landet pga. større magasinert sommervarme i Øst-Norge. Sand i filterlaget betraktes frostteknisk som grus.
Figur 6.11 Dimensjoneringskurver for total tykkelse, z, av forsterknings- og frostsikringslag av grus
Figur 6.12 viser dimensjoneringskurver for frostsikringslag av grus, under forutsetning av at det i tillegg benyttes 700 mm forsterkningslag av sprengstein.
Figur 6.12 Dimensjoneringskurver for frostsikringslag av grus, i tillegg til 700 mm forsterkningslag med sprengstein
Dimensjonering av frostsikringslag av sprengstein
Ved dimensjonering av frostsikringslag av sprengstein er det avgjørende å ta tilstrekkelig hensyn til at de termiske egenskapene generelt er usikre og at det kan opptre betydelig variasjon i egenskapene både lokalt og fra anlegg til anlegg. Ved å sikre seg mot ekstremt ugunstige egenskaper kan kurven som svarer til 1,6 x Zgrus gitt i figur 6.13 benyttes. Kurven gjelder for dimensjonering av tykkelse av frostsikrings- og forsterkningslag med sprengstein, under forutsetning av at følgende er tilfredsstilt:
- steinmassene er velgraderte, slik at bl.a. indre konveksjon forhindres
- overflate og grøfteskråninger av banelegemet tettes, slik at varmetap ved konveksjon og frostinntrengning fra siden minimaliseres.
Dimensjoneringskurven gjelder for det aktuelle konseptet med 700 mm forsterkningslag av stein 0 - 300 mm og frostsikringslag av stein med maksimal steinstørrelse 500 mm eller inntil 2/3 av lagtykkelsen.
Inngangsdata for dimensjoneringskurven er 100 års frostmengde i luft. Effekten av temperaturforskjell mellom luft og overflate er inkludert i kurven gitt i figur 6.13.
Det er likevel helt klart at bruk av sprengstein i frostsikring er forbundet med større usikkerhet enn alternative løsninger med bruk av grus, isolasjonsprodukter eller varmeakkumulerende bunnlag. Bl.a. er følgende faktorer ikke inkludert i dimensjoneringskurven:
- "steinreir" som følge av separasjon ved uheldig utlegging eller ensgraderte masser
- store steiner (kan gi kuldebroer gjennom fyllingen)
- indre konveksjon som følge av åpen struktur i sprengsteinsmassene (i Bane NORs tekniske regelverk kreves det imidlertid bruk av velgraderte masser som vil ta høyde for denne effekten)
Ved bruk av spesielt gunstige masser, kan lagtykkelsen beregnes spesielt. Ved bruk av spesielt ugunstige masser, skal lagtykkelsen beregnes spesielt.
Å sikre et høyt fuktighetsnivå i bunnen av frostfundamentet av sprengstein vil bedre frostmotstanden. Dette kan f.eks. oppnås ved innlegging av gruspute eller filterlag av sand.
Figur 6.13 Dimensjoneringskurve for total tykkelse av forsterknings- og frostsikringslag av sprengstein
Tiltak mot telehiv på eksisterende baner
Dette avsnittet omhandler frostsikring av eksisterende baner. Dette innbefatter planlegging av etterisolering når telehiv har oppstått, samt beskrivelse av forebyggende tiltak.
Planlegging av frostsikring
Som grunnlag for å planlegge frostsikring er det viktig å skaffe seg opplysninger om størrelsen og utstrekningen av telehivet, grunnforholdene og oppbygging av underbygningen på stedet. Regelverket for underbygning beskriver derfor at telenivellement og grunnundersøkelser skal utføres som forundersøkelse for planlegging av frostsikring. Opptegningen av observasjonene er standardisert, og skal utføres som et lengdeprofil med angivelse av linjens kilometrering (pælenr.). Følgende data presenteres:
- telehiv opptegnes i målestokk 1:5 for en eller flere vintre registrert ved nivellement
- eventuell skoring angis i mm som høyeste skore innenfor hvert skoringsfelt
- undersøkelse av ballast og undergrunn. Resultatet opptegnes i høydemålestokk 1:20
- angivelse av skjæring eller fylling
- karakteristiske tverrprofiler i målestokk 1:200
Valg av utførelsesmåte for frostsikring fastlegges av en geoteknisk sakkyndig, sammen med vedlikeholdsansvarlig for banen.
De gamle jernbanene er bygd med grusballast. Ved senere overgang til pukk, er vanligvis linjen løftet slik at det ligger et filterlag av grus under pukken. Innlegging av grus er som regel uaktuelt for frostsikringsformål p.g.a. store masseutskiftninger og driftsforstyrrelser.
Tresviller
Brukte impregnerte sviller har i nedgravd tilstand lang levetid i sporet. Trykkfastheten og deformasjonsegenskapene er tilfredsstillende hos tresvillene. Svillene skal legges på tvers under midtre del av sporet. På sidene skal det legges langsgående sviller. For å unngå oppressing av finmateriale mellom svillene, skal det legges fiberduk under svillelaget.
Svilletrauet kan virke som drensgrøft, og det kan oppstå grunnbrudd. Grunnbruddet oppstår p.g.a. vanntrykket på trauveggene ved overgang fra skjæring til fylling. For å unngå dette, skal det legges inn tverrgående sperresjikt av 0,15 mm plastfolie for hver 10 m hvor banen ligger i større stigning enn 10 ‰, se figur 6.14.
Figur 6.14 Sperresjikt av plastfolie
Frostsikringens bredde skal ved bruk av sviller være minimum 4 m. Tykkelsen på frostsikringslaget dimensjoneres etter tabell 6.7.
Tabell 6.7 Antall lag sviller
| Dimensjonerende frostmengde (h0C) | Antall lag sviller |
| 5000 – 15000
15000 – 25000 25000 – 40000 |
1
2 3 |
Frostsikring med isolasjonsmaterialer
De første kunstige isolasjonsmaterialene var plater av ekspandert polystyren. I de senere årene er det ekstrudert polystyren som er mest brukt. Plater som benyttes skal være KFK- frie plater av ekstrudert polystyren.
Kvalitetskrav knyttet til trykkstyrke og densitet er gitt i tabell 6.8
Tabell 6.8 Krav knyttet til trykkstyrke og densitet av isolasjonsplater
| Kvalitetskrav | Min. tykkelse (mm) | Trykkstyrke (kN/m2) | Densitet (kg/m3) |
| Plater av ekstrudert
polystyren |
60 | min. 400 ved 5 % deformasjon* | min. 38 |
- Trykkstyrken måles på 50 mm prøveterninger
Anvendelse av polystyrenplater til frostisolasjon, er i alminnelighet mest aktuelt i forbindelse med ballastrensing og bruk av ballastrenseverk. Under platene skal det ligge igjen pukk, grus eller sand i minst 0,1 m tykkelse. I motsatt fall skal det velges en arbeidsmetode som tillater grusfilter eller fiberduk innlagt under platene. På sprengsteinsfyllinger er det normalt filterlag på traubunn. Kravet om 0,1 m tykkelse pukk, grus eller sand faller da bort.
Platene må minimum være 60 mm tykke. Dimensjonerende tykkelse regnes 10 mm mindre enn platetykkelsen p.g.a. pukknedtrengning og sammentrykking. Figur 6.15 og 6.16 viser dimensjoneringskurver for kombinasjonen isolasjon og grus. Diagrammene angir tykkelsen på nødvendig gruslag under 60 mm og 100 mm skumplate. Det er forutsatt at varmeledningstallet for isolasjonsplatene er 0,037 W/mK. For isolasjonsmaterialer av ekstrudert polystyren, tilsvarer dette et fuktopptak på 5 - 10 volumprosent.
Frostdybden avhenger av akkumulert sommervarme. Det er derfor forskjellige dimensjoneringskurver for Øst-Norge og resten av landet.
For ekstremt kalde strøk kan det være nødvendig med spesiell dimensjonering.
Figur 6.15 Tykkelse av gruslag under 60 mm isolasjonsplater
Figur 6.16 Tykkelse av gruslag under 100 mm isolasjonsplater
Utførelse av frostsikring med isolasjonsplater
Ved leggingen må det være minimum 0,3 m avstand mellom underkant sville og overkant plate. Platene legges uten sprekker. Avvik fra dette kan være aktuelt på spesielle utkilingspartier (overganger). Figur 6.17 viser prinsippet for etterisolering med XPS-plater. Nødvendig omfang av isoleringen vurderes i hvert enkelt tilfelle. Tetting av sideskråninger utføres iht. Bane NORs tekniske regelverk JD 520, kap. 6 Banelegeme.
Figur 6.17 Etterisolering med XPS-plater. Prinsippskisse
Løfting av sporet
Sporløfting er et effektivt og velprøvd middel mot telehiv. Gjennom 1950 og -60-tallet ble dette virkemidlet benyttet på lange strekninger langs våre jernbaner, og med dette ble også telehivproblemene vesentlig redusert.
Telehivet blir redusert p.g.a.
- frostfundamentets tykkelse øker slik at det kreves større frostmengde for gjennomfrysing
- ballastlaget får bedre drenering, blir tørrere og får dermed bedre isolasjonsevne
- økt avstand til grunnvannsspeilet.
NB: Smale fyllinger på eldre baner er en vesentlig årsak til solslyng. Sporløfting må derfor ikke foretas, uten samtidig utvidelse av fyllingsprofilet jf. Bane NORs tekniske regelverk JD520, kap 6 Banelegeme og JD 530, kap. 10 Ballast.
Ballastrensing
Ballastrensing er i mange tilfeller en effektiv og tilstrekkelig forebygging mot telehiving. Dette er tilfelle der hvor telehivingen vesentlig skyldes forurenset ballast. Karakteristisk ved dette er oppumping av finmateriale rundt svillene (vaskesviller). Dette kan ofte være tilfelle ved lite elastisk underbygning, som fjellskjæringer og bruer med betongtrau.
Bygging av nytt spor inntil eksisterende spor
Basert på erfaringer som er gjort ved større jernbaneprosjekter pekes til slutt på noen spesielle problemstillinger hva angår frostsikring relatert til bygging av nytt spor inntil eksisterende spor.
Koblingspunkter mv
Spesielt ved koblingspunkter kan det oppstå problemer med telehiv på grunn av at det finnes telefarlige masser i tidligere spor som av anleggsmessige og driftsmessige årsaker ikke fjernes. Typisk er at det ligger en kile av slike masser igjen mellom sporene på et nytt dobbeltspor, og at en derfor får teleproblemer.
Det må derfor legges vesentlig vekt på at arbeider med masseskifting planlegges og utføres slik at telefarlige masser fjernes i nødvendig utstrekning.
Hvis problemet er å få gravet dypt nok i nærheten av trafikkert spor, kan alternativet være en isolasjonsløsning i mindre dybde.
Alternativt kan også seksjonsvis utgraving benyttes, evt. også i kombinasjon med jordarmeringsløsninger som gjør det mulig å masseskifte helt inntil tilbakefylte masser.
Masseutskifting av eksisterende spor
Noen ganger er situasjonen den motsatte i forhold til problemstillingen over, og man bør helst la eksisterende spor ligge i ro.
Dette kan f.eks. være når underbygningen for eksisterende spor består av sandige grusmasser. Å utføre masseutskifting med sprengstein når nyanlegget kommer vil i slike tilfeller, som en vil forstå av eksemplene foran, føre til langt dårligere frostsikring og derved telehivsproblemer, fordi innskiftede sprengsteingsmasser har minimalt vanninnhold.
Et annet problem er når nytt spor bygges ved siden av eksisterende, og dette er frostsikret med torv. Det eksisterende sporet ligger da udrenert. Det er da viktig å passe på at nybyggingen ikke medfører utdrenering av torven (f.eks. pga. dypdrenering). Resultatet vil i tilfelle bli urolig spor med setninger etter hvert som torven råtner opp, men også teleproblemer fordi vanninnholdet synker.
Formasjonsplan
Ved bygging av jernbane vil ofte formasjonsplanet bli benyttet som anleggsvei. Dette vil i mange situasjoner føre til forurensning av formasjonsplanet med finstoff. Generelt bør derfor bruk av formasjonsplanet som anleggsveg unngås, og hvis mulig, bør anleggsvegen bygges ved siden av selve traséen.
Hvis formasjonsplanet bli tettet med finstoff i anleggsperioden, bør det foretas harving eller avskraping av formasjonsplanet, slik at det ikke oppstår fare for telehiv i dette laget, og for å sikre de drenerende egenskapene i underbygningen.
Litteraturhenvisninger
1. NIF-kurs 1997 – Frost i jord – sikring mot teleskader, NGF/NBF/NIF (1997)
2. Frost i jord nr. 17, Vegdirektoratet/NTNF (1976)
3. NGI rapport nr. 960054-1. Måling av varmeledningsevne i sprengstein, august 1996
6. Telehiv 1996/97, Jernbaneverket Direktoratet, Teknisk myndighet 8.4.1997