Kortslutningsstrømmer: Forskjell mellom sideversjoner
(Rettet opp syntaksfeil. Litt generell redigering.) |
|||
| (4 mellomliggende revisjoner av samme bruker vises ikke) | |||
| Linje 38: | Linje 38: | ||
{|width="45%" | {|width="45%" | ||
|- | |- | ||
| <math>jX_d^'=\frac {U_0}{I_k^'}</math> || align=right | 2 | | <math>jX_d^{'}=\frac {U_0}{I_k^{'}}</math> || align=right | 2 | ||
|} | |} | ||
| Linje 74: | Linje 74: | ||
{|width="45%" | {|width="45%" | ||
|- | |- | ||
| <math>E^'=U+jI_G\cdot X_d^'</math> || align=right | 5 | | <math>E^{'}=U+jI_G\cdot X_d^{'}</math> || align=right | 5 | ||
|} | |} | ||
| Linje 84: | Linje 84: | ||
{|width="45%" | {|width="45%" | ||
|- | |- | ||
| <math>I^'=\frac {E^'}{jX_d^'}</math> || align=right | 6 | | <math>I^{'}=\frac {E^{'}}{jX_d^{'}}</math> || align=right | 6 | ||
|} | |} | ||
| Linje 181: | Linje 181: | ||
=== Beregninger av transient kortslutningsstrøm=== | === Beregninger av transient kortslutningsstrøm=== | ||
Den totale transiente kortslutningstrømmen i feilstedet når flere omformere er i drift i omformerstasjonen og det tas hensyn til bidrag fra de nærmeste matestasjonene blir: | Den totale transiente kortslutningstrømmen i feilstedet når flere omformere er i drift i omformerstasjonen og det tas hensyn til bidrag fra de nærmeste matestasjonene blir: | ||
{|width="45%" | {|width="45%" | ||
|- | |- | ||
| <math>I_{k, total}=\sum_{omf.i drift} I_k + \sum_{ | | <math>I_{k, total}=\sum_{omf.i drift} I_k + \sum_{naerl. omf.} I_{k, KL}</math> || align=right | 9 | ||
|} | |} | ||
hvor | hvor første ledd representerer det totale transiente bidrag fra omformerstasjonen rett ved kortslutningen. Andre ledd representerer det totale bidrag fra nærliggende omformerstasjoner | ||
Andre ledd representerer det totale bidrag fra nærliggende omformerstasjoner | |||
==== Beregning av kortslutningsstrøm fra generatorer==== | ==== Beregning av kortslutningsstrøm fra generatorer==== | ||
| Linje 201: | Linje 194: | ||
1. Først beregnes maksimal laststrøm for generator, som er gitt av den maksimale ytelsen til generatoren (6-min. verdi): | 1. Først beregnes maksimal laststrøm for generator, som er gitt av den maksimale ytelsen til generatoren (6-min. verdi): | ||
{|width="45%" | {|width="45%" | ||
| Linje 207: | Linje 199: | ||
| <math>I_G=\frac {S_{max}}{U_G}</math> || align=right | 10 | | <math>I_G=\frac {S_{max}}{U_G}</math> || align=right | 10 | ||
|} | |} | ||
2. Deretter beregnes spenningen bak den transiente reaktansen med likning .5. Her antas laststrømmens effektfaktor cos<math>\varphi</math> lik generatorens merkeverdi. | 2. Deretter beregnes spenningen bak den transiente reaktansen med likning .5. Her antas laststrømmens effektfaktor cos<math>\varphi</math> lik generatorens merkeverdi. | ||
3. Beregner transient kortslutningsstrøm ut fra transformator gitt av | 3. Beregner transient kortslutningsstrøm ut fra transformator gitt av | ||
{|width="45%" | {|width="45%" | ||
|- | |- | ||
| <math> | | <math>I_{kg+tr}^{'}=\frac {E^{'}}{x_d^{'}+x_t}\cdot \frac {U_{ref}}{U_{kl}}</math> || align=right | 11 | ||
|} | |} | ||
Strømmen er referert til 15 kV siden av transformatoren. | Strømmen er referert til 15 kV siden av transformatoren. | ||
| Linje 228: | Linje 217: | ||
|- | |- | ||
| U<sub>kl</sub>: || spenningen på kontaktledningssiden av transformatoren, vanlig å benytte 16 kV | | U<sub>kl</sub>: || spenningen på kontaktledningssiden av transformatoren, vanlig å benytte 16 kV | ||
|} | |} | ||
===== Regneeksempel transient kortslutningsstrøm===== | ===== Regneeksempel transient kortslutningsstrøm===== | ||
Her følger utregninger for 5,8 MVA-generator | |||
Her følger utregninger for 5,8 MVA generator | |||
1. | 1. | ||
{|width="45%" | {|width="45%" | ||
|- | |- | ||
| <math>I_G=\frac {8,0 MVA}{4,0 kV}=2,0 kA</math> || align=right | 12 | | <math>I_G=\frac {8,0 MVA}{4,0 kV}=2,0 kA</math> || align=right | 12 | ||
|} | |} | ||
2. For å beregne E’ må først Zref finnes for generatoren. Denne finnes ved | 2. For å beregne E’ må først Zref finnes for generatoren. Denne finnes ved | ||
{|width="45%" | {|width="45%" | ||
| Linje 254: | Linje 235: | ||
| <math>Z_{ref}=\frac {U_N^2}{S_N}=\frac {(4,0\cdot 10^3)^2}{4,0\cdot 10^6}=4,0 \Omega</math> || align=right | 13 | | <math>Z_{ref}=\frac {U_N^2}{S_N}=\frac {(4,0\cdot 10^3)^2}{4,0\cdot 10^6}=4,0 \Omega</math> || align=right | 13 | ||
|} | |} | ||
Deretter beregnes | Deretter beregnes | ||
| Linje 263: | Linje 243: | ||
Setter inn i likning 5 og får | Setter inn i likning 5 og får | ||
{|width="75%" | {|width="75%" | ||
|- | |- | ||
| <math>E^'=U+jX_d^'\cdot I_G=4,0+j0,5\cdot 2,0e^{-36,87}=(4,6+j0,80)kV</math> || align=right | 14 | | <math>E^{'}=U+jX_d^{'}\cdot I_G=4,0+j0,5\cdot 2,0e^{-36,87}=(4,6+j0,80)kV</math> || align=right | 14 | ||
|} | |} | ||
3. Beregner deretter den transiente kortslutningsstrømmen, Ik’, ved å sette inn i likning 11. | 3. Beregner deretter den transiente kortslutningsstrømmen, Ik’, ved å sette inn i likning 11. | ||
| Linje 276: | Linje 254: | ||
<math>X_t=e_t\cdot Z_{ref}=0,0335 \cdot 4=0,134</math> | <math>X_t=e_t\cdot Z_{ref}=0,0335 \cdot 4=0,134</math> | ||
{|width="75%" | {|width="75%" | ||
|- | |- | ||
| <math>I_{kg+tr}^'=\frac {E^'}{x_d^'+x_t}\cdot \frac {U_{ref}}{U_{kl}}=\frac {(4,60+j0,80)\cdot 10^3}{j(0,5+0,134)}\cdot \frac {4,0\cdot 10^3}{16 \cdot 10^3}=1841,11e^{-j80,1} A</math> || align=right | 15 | | <math>I_{kg+tr}^{'}=\frac {E^{'}}{x_d^{'}+x_t}\cdot \frac {U_{ref}}{U_{kl}}=\frac {(4,60+j0,80)\cdot 10^3}{j(0,5+0,134)}\cdot \frac {4,0\cdot 10^3}{16 \cdot 10^3}=1841,11e^{-j80,1} A</math> || align=right | 15 | ||
|} | |} | ||
På samme måte som over regnes den subtransiente kortslutningsstrømmen ut ved å bruke likningene for det subtransiente systemet, likning 3 og 4. I likning 11 erstattes x<sub>d</sub>’ med x<sub>d</sub>’’. For transformatoren benyttes samme reaktans ved transient analyse som ved subtransient analyse. | På samme måte som over regnes den subtransiente kortslutningsstrømmen ut ved å bruke likningene for det subtransiente systemet, likning 3 og 4. I likning 11 erstattes x<sub>d</sub>’ med x<sub>d</sub>’’. For transformatoren benyttes samme reaktans ved transient analyse som ved subtransient analyse. | ||
Resultater for hver enkelt omformertype er regnet ut i ref.[1]. | Resultater for hver enkelt omformertype er regnet ut i ref.[1]. | ||
==== Bidrag fra nærliggende omformere==== | ==== Bidrag fra nærliggende omformere==== | ||
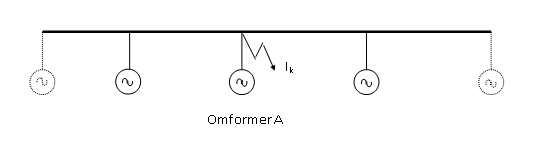
Når det oppstår en kortslutning ved en omformerstasjon vil normalt den største andelen av feilstrømmen komme fra denne omformerstasjonen. Jernbaneverkets kontaktledningsanlegg er i normaldrift samkjørt til enhver tid. Av den grunn vil feilstrømmen også få bidrag fra de nærmeste omformerstasjonene. Størrelsen på dette bidraget til den totale feilstrømmen minker med avstand til de nærmeste omformerstasjonene. De fleste av Jernbaneverkets omformerstasjoner ligger langs banestrekninger uten stjernepunkt, som angitt i figur 6. | Når det oppstår en kortslutning ved en omformerstasjon vil normalt den største andelen av feilstrømmen komme fra denne omformerstasjonen. Jernbaneverkets kontaktledningsanlegg er i normaldrift samkjørt til enhver tid. Av den grunn vil feilstrømmen også få bidrag fra de nærmeste omformerstasjonene. Størrelsen på dette bidraget til den totale feilstrømmen minker med avstand til de nærmeste omformerstasjonene. De fleste av Jernbaneverkets omformerstasjoner ligger langs banestrekninger uten stjernepunkt, som angitt i figur 6. | ||
[[Fil:Fig542-406.png|600px]] | [[Fil:Fig542-406.png|600px]] | ||
Figur 6 Omformerstasjoner langs Jernbaneverkets kontaktledningsanlegg | Figur 6 Omformerstasjoner langs Jernbaneverkets kontaktledningsanlegg | ||
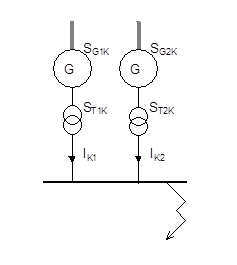
Ved beregning av den totale feilstrømmen, I<sub>k</sub>, ved feilstedet, må det lages modeller av systemet. Omformerstasjonen, A, nærmest feilstedet, figur .6, kan modelleres med den transiente spenningen E’ bak den transiente reaktansen, x<sub>d'</sub>. Når avstanden til de to nærmeste omformerstasjonene er over 60 km, kan disse modelleres som stive spenningskilder på 16,2 kV, da det er så stor demping i kontaktledningsanlegget at resultatet vil ha god nok nøyaktighet. Ved kortere avstander bør de nærmeste omformerstasjonene bli modellert som omformer A. | Ved beregning av den totale feilstrømmen, I<sub>k</sub>, ved feilstedet, må det lages modeller av systemet. Omformerstasjonen, A, nærmest feilstedet, figur .6, kan modelleres med den transiente spenningen E’ bak den transiente reaktansen, x<sub>d'</sub>. Når avstanden til de to nærmeste omformerstasjonene er over 60 km, kan disse modelleres som stive spenningskilder på 16,2 kV, da det er så stor demping i kontaktledningsanlegget at resultatet vil ha god nok nøyaktighet. Ved kortere avstander bør de nærmeste omformerstasjonene bli modellert som omformer A. | ||
| Linje 314: | Linje 282: | ||
Dersom en kortslutning ikke oppstår rett utenfor en omformerstasjon, må impedansen i kontaktledningsanlegget, Z<sub>kl</sub>, tas med for utregning av kortslutningsstrømmen i likning 11. Det er da viktig å huske at impedansene for generator og transformator er referert generatorsiden av transformatoren. For å regne om Z<sub>kl</sub> til denne siden av transformatoren benyttes likningen under: | Dersom en kortslutning ikke oppstår rett utenfor en omformerstasjon, må impedansen i kontaktledningsanlegget, Z<sub>kl</sub>, tas med for utregning av kortslutningsstrømmen i likning 11. Det er da viktig å huske at impedansene for generator og transformator er referert generatorsiden av transformatoren. For å regne om Z<sub>kl</sub> til denne siden av transformatoren benyttes likningen under: | ||
{|width="45%" | {|width="45%" | ||
| Linje 320: | Linje 287: | ||
| <math>Z_{kl,gen}=Z_{kl}\cdot \frac {U_{ref}}{U_{kl}}</math> || align=right | 16 | | <math>Z_{kl,gen}=Z_{kl}\cdot \frac {U_{ref}}{U_{kl}}</math> || align=right | 16 | ||
|} | |} | ||
hvor: | hvor: | ||
| Linje 329: | Linje 295: | ||
Dette gir følgene formel for kortslutningsstrømmen: | Dette gir følgene formel for kortslutningsstrømmen: | ||
{|width="45%" | {|width="45%" | ||
|- | |- | ||
| <math>I_{kg+tr}^'=\frac {E^'}{X_d^'+X_{tr}+Z_{kl,gen}}\cdot \frac {U_{ref}}{U_{kl}}</math> || align=right | 17 | | <math>I_{kg+tr}^{'}=\frac {E^{'}}{X_d^{'}+X_{tr}+Z_{kl,gen}}\cdot \frac {U_{ref}}{U_{kl}}</math> || align=right | 17 | ||
|} | |} | ||
Betraktningen over om avstand fra omformeren gjelder også ved denne kortslutningsberegningen. Er avstanden fra omformeren til feilstedet over 60 km, benyttes en stiv spenningskilde som modell for omformeren istedenfor likningen over. | Betraktningen over om avstand fra omformeren gjelder også ved denne kortslutningsberegningen. Er avstanden fra omformeren til feilstedet over 60 km, benyttes en stiv spenningskilde som modell for omformeren istedenfor likningen over. | ||
| Linje 341: | Linje 305: | ||
===== Regneeksempel total transient kortslutningsstrøm===== | ===== Regneeksempel total transient kortslutningsstrøm===== | ||
Ved å ta utgangspunkt i figur 6 skal den totale transiente kortslutningsstrømmen beregnes ved en kortslutning rett utenfor omformerstasjon A. For å forenkle beregningene består denne omformerstasjonen av to 5,8 MVA aggregat. De to nabo-omformerstasjonene ligger 60 km fra omformerstasjon A. Disse kan derfor modelleres som to stive spenningskilder. Som impedans i kontaktledningsanlegget benyttes Z=0,21+j0,21 <math>\Omega</math>/km. | Ved å ta utgangspunkt i figur 6 skal den totale transiente kortslutningsstrømmen beregnes ved en kortslutning rett utenfor omformerstasjon A. For å forenkle beregningene består denne omformerstasjonen av to 5,8 MVA aggregat. De to nabo-omformerstasjonene ligger 60 km fra omformerstasjon A. Disse kan derfor modelleres som to stive spenningskilder. Som impedans i kontaktledningsanlegget benyttes Z=0,21+j0,21 <math>\Omega</math>/km. | ||
For å finne den totale transiente kortslutningsstrømmen benyttes likning 9. | For å finne den totale transiente kortslutningsstrømmen benyttes likning 9. | ||
<math>I_{k, total}=\sum_{omf.i drift} I_k + \sum_{naerl. omf.} I_{k, KL}</math> | |||
<math>I_{k, total}=\sum_{omf.i drift} I_k + \sum_{ | |||
Den transiente kortslutningsstrømmen for 5,8 MVA aggregatet er beregnet i avsnitt 3.2.1.1, I<sub>k</sub>’=1841,1 A med vinkel –80,1<sup>o</sup>. Begge aggregatene vil gi samme bidrag. | Den transiente kortslutningsstrømmen for 5,8 MVA aggregatet er beregnet i avsnitt 3.2.1.1, I<sub>k</sub>’=1841,1 A med vinkel –80,1<sup>o</sup>. Begge aggregatene vil gi samme bidrag. | ||
Strømmen fra de to omformerstasjonene som gir bidrag, finnes ved hjelp av: | Strømmen fra de to omformerstasjonene som gir bidrag, finnes ved hjelp av: | ||
{|width="75%" | {|width="75%" | ||
| Linje 362: | Linje 322: | ||
Begge omformerstasjonene gir like store bidrag. Dette gir total transient kortslutningsstrøm: | Begge omformerstasjonene gir like store bidrag. Dette gir total transient kortslutningsstrøm: | ||
{|width="75%" | {|width="75%" | ||
|- | |- | ||
| <math>I_{k,total}=\sum_{omf.i drift} I_k + \sum_{ | | <math>I_{k,total}=\sum_{omf.i drift} I_k + \sum_{naerl. omf.} I_{k, KL}=2\cdot 1841,1e^{-j80,1}+2\cdot909,14e^{-j45}=5274,48e^{-68,67}A</math> || align=right | 19 | ||
|} | |} | ||
Siste sideversjon per 24. mai 2024 kl. 08:10
__NUMBEREDHEADINGS__
INNLEDNING
Dette kapittelet inneholder beregningsmetode for bestemmelse av kortslutningsstrøm på 15 kV siden i en roterende omformerstasjon. Beregning av kortslutningsstrømmer fra statiske omformerstasjoner er også behandlet.
Mye av teorien er hentet fra kompendium i Elektriske kraftsystemer, NTH [3] og Lundbergs lærebok i elektroteknikk [6].
Dette kapittelet er en bearbeiding av ”Kortslutningsdata 1-fase i det norske jernbanenettet”, [1].
Bakgrunnen for å beregne kortslutningsytelsene i nettet er for å kunne dimensjonere vern og jordingsanlegg godt nok. Ved disse dimensjoneringene er det viktig å kjenne både maksimal og minimal kortslutningsstrøm.
Den totale transiente kortslutningsstrømmen i feilstedet, vil være den maksimale kortslutningsstrømmen. Ved utregning av den minimale kortslutningsstrømmen, ser man på kortslutningsstrømmen ut fra den omformerstasjonen hvor vernet er plassert, og man tar hensyn til at alle aggregater nødvendig vis ikke er innkoblet på tidspunktet hvor feilen inntreffer.
Forutsetninger for beregninger på Jernbaneverkets omformeraggregater
For å kunne beregne den maksimale kortslutningsstrøm som kan forekomme på Jernbaneverkets kontaktledningsanlegg, er det nødvendig å finne den maksimale kortslutningsstrøm ut fra de enkelte omformerstasjonene. De aller fleste omformerstasjonene består av flere omformeraggregater, dette gjør at den totale kortslutningsytelsen ut fra en omformerstasjon består av summen av ytelsen fra hvert enkelt aggregat.
For å finne maksimal kortslutningsytelse ut fra et roterende omformeraggregat benyttes samme teori som for generatorer i vannkraftverk. Dette betyr at det kan ses på generatorsiden av omformeren alene, uten innvirkning fra det matende 3-fase nett. Den mekaniske koblingen (akslingen) mellom motor og generator er så treg at den ikke vil rekke å overføre energi av betydelig størrelse fra 3-fase nettet.
For de statiske omformeraggregatene er det andre parametre som virker inn på kortslutningsstrømmen.
TEORI
Kortslutningsforløp for roterende frekvensomformere
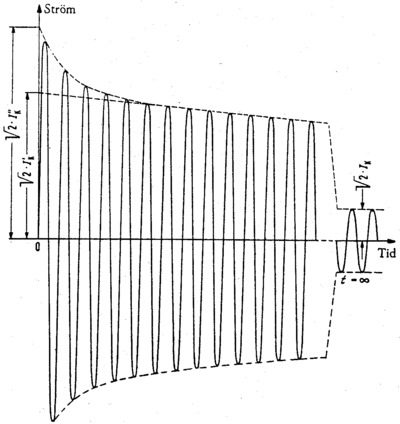
Et kortslutningsforløp deles opp i en subtransient, transient og stasjonær del, se figur 1.
Den subtransiente kortslutningsstrømmen, Ik’’ , er definert som effektivverdien av kortslutningsstrømmens vekselstrømsledd i første øyeblikk etter kortslutningen. Den subtransiente perioden strekker seg kun over noen millisekunder. Synkronmaskinens subtransiente reaktans xd’’ er definert som forholdet mellom klemmespenningen før kortslutning og strømmen ved kortslutning fra tomgang.
| 1 |
Den transiente kortslutningsstrøm, Ik’, er den effektivverdi vekselstrømsleddet ville hatt rett etter kortslutningen hvis den transiente periode hadde startet ved t=0. Synkronmaskinens transiente reaktans, xd’, er definert som forholdet mellom klemmespenningen før kortslutning og den transiente kortslutningsstrømmen ved kortslutning fra tomgang.
| 2 |
På samme måte er synkronmaskinens synkronreaktans, xd , definert som forholdet mellom klemmespenning før kortslutning og den stasjonære kortslutningsstrømmen ved kortslutning fra tomgang. Stasjonær kortslutningsstrøm starter når den transiente kortslutningsstrømmen har dødd ut, anslagsvis rundt 1 sekund etter kortslutning.
Subtransient kortslutningsstrøm
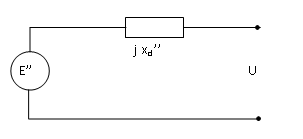
Hvis man skal beregne subtransient kortslutningsstrøm i en generator, kan generatoren ekvivaleres med Thevenin-ekvivalenten, hvor den subtransiente reaktansen, xd’’, er ekvivalentens seriereaktans. Spenningen bak denne reaktansen, E’’ , er en fiktiv spenning i synkronmaskinen som er like stor før og etter feilen. Figur 2 viser Thevenin-ekvivalenten for synkrongenerator for den subtransiente periode:
Utfra dette kan denne spenningen beregnes ved stasjonær drift før feilen oppstår, etter likning 3:
| 3 |
hvor
IG er den strømmen generatoren er belastet med.
I følge Thevenins teorem er E’’ en konstant. Ved feil kan strømmen da beregnes i første øyeblikk fra likningen 3. Feilbetingelsen gir U som funksjon av I. Ved kortslutning er U=0. Dette gir:
| 4 |
Ik’’ er her begynnelsesverdien for den subtransiente strømmen. Ekvivalenten og likningene ovenfor er gyldige bare i de første millisekunder etter at feilen inntreffer.
Transient kortslutningsstrøm
Skal strømmer og spenninger beregnes i den transiente perioden, må det brukes en annen Thevenin-ekvivalent . I den perioden er det en spenning E’ bak den transiente reaktansen, xd’, som er konstant fra situasjonen før feilen inntraff. E’ er tilsvarende E’’ en fiktiv spenning som man tenker seg i synkronmaskinen til enhver tid. Den kan beregnes ut fra de stasjonære forhold før feilen inntraff:
| 5 |
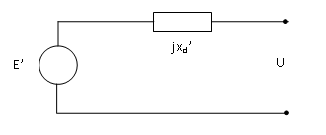
Thevenin-ekvivalenten for transient periode er vist i figur 3.
Når det skal ses på den transiente perioden ser man bort fra den subtransiente perioden og forutsetter E’ konstant fra situasjonen før kortslutningen og frem til den transiente perioden inntreffer. Ved en feil kan en da beregne kortslutningsstrømmen ved å bruke likningen 5 og sette U = 0:
| 6 |
Ik’ er startverdien for feilstrømmen i den transiente periode.
Stasjonær kortslutningsstrøm
Den stasjonære kortslutningsstrømmen beregnes på tilsvarende måte som subtransient og transient feilstrøm. I stasjonær tilstand ekvivaleres synkrongeneratoren med spenningen Ef bak den synkrone reaktansen, xd,. Ef er tilsvarende E’ og E’’ en fiktiv spenning som man tenker seg i synkronmaskinen til enhver tid. Den kan beregnes ut fra de stasjonære forholdene før feilen inntraff.
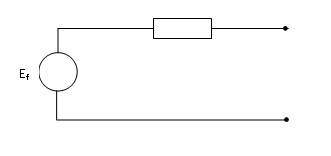
Den stasjonære periode kan forenkles til Thevenin-ekvivalent vist i figur 4:
På likningsform blir dette:
| 7 |
og ved kortslutning finnes den stasjonære kortslutningsstrømmen ved å sette U = 0:
| 8 |
Kortslutningsstrømmer fra statiske frekvensomformere
Kortslutningsstrømmen fra de statiske omformerne blir påvirket av strømgrensen i omformerne. Når strømmens toppverdi kommer til strømgrensen blir strømmen klippet og det oppstår en trapesformet strøm. Denne strømmen får en effektivverdi rundt 30 % høyere enn om strømmen hadde vært sinusformet med samme toppverdi. Faktoren på 30 % kommer fra målinger ved Kjelland omformerstasjon.
Klippingen av strømmen starter ved første svitsjing etter kortslutningen, og svitsjefrekvensen i de statiske omformerne er rundt 12-1500 Hz. Dette gir en rask begrensing av strømmens maksimalverdi. Ved kortslutning vil spenningen på omformerens utgang være avhengig av impedansen fra feilstedet til omformeren. Dog vil spenningsregulatoren sørge for at spenningen ikke blir over innstilt verdi, ca. 16,2 kV.
Etter at klippingen av strømmen har startet når strømmen når strømgrensen vil regulatorene i omformeren styre ned spenningen i omformeren til strømmen igjen har blitt sinusformet med toppverdi under strømgrensen. Denne reguleringen tar tid, og kortslutningsvernene skal ha løst ut før omformeren er kommet i denne nye stasjonære driftsformen.
Ved beregninger med kortslutningsstrøm fra statiske omformerstasjoner anbefales det derfor å modellere omformeren med en strømkilde med strømstyrke lik strømgrensen + 30 % når feilstedet er nær den statiske omformeren. Dersom avstanden til feilstedet er slik at dette gir en spenning utenfor omformeren høyere enn 16,2 kV, modelleres den statiske omformeren som en stiv spenningskilde med spenning lik 16,2 kV. Dette blir den samme modellen som for roterende omformerstasjoner langt fra feilstedet.
KORTSLUTNING PÅ GENERATORSIDEN - 15 kV
| Aggregat-type
[MVA] |
SN(original)
[MVA] |
S6 min (overlast)
[MVA] |
cos | UN
[kV] |
Xd
[%] |
Xd’
[%] |
Xd’’
[%] |
ek
[%] |
|---|---|---|---|---|---|---|---|---|
| 3,1 | 2,4 | 4,8 | 0,8 | 3,0 | 97 | 13,5 | 10,9 | 4,72 |
| 5,8 | 4,0 | 8,0 | 0,8 | 4,0 | 93 | 12,5 | 10,9 | 3,35 |
| 7 | 7,0 | 11,0 | 0,85 | 4,5 | 129 | 25,9 | 23,7 | 3,43 |
| 10 ASEA | 10,0 | 14,0 | 0,7 | 5,2 | 139 | 20,7 | 19,0 | 3,3 |
| 10 NEBB | 10,0 | 14,0 | 0,7 | 5,2 | 128 | 30,4 | 25,9 | 3,3 |
På 15 kV siden er kortslutningsytelsen gitt av antall generatorer i drift i omformerstasjonen og impedansen til feilstedet. De nærmeste omformestasjonene gir også bidrag inn mot feilstedet. Dette bidraget minker med økende avstand mellom feilstedet og de nærliggende omformerstasjonene.
På generatorsiden i omformerstasjonene er det vanlig å angi kortslutningsytelsen i nettet i kortslutningsstrøm, og ikke i kortslutningseffekt. Dette er bare en definisjonssak, og de samme regler for beregning gjelder uansett.
Nødvendige data.
For generatorer: SgN, UN , cos , xd, xd’, xd’’
For transformator: StN , ek , Up , Us
Her er
- SgN generatorens merkeeffekt
- UN generatorens merkespenning
- xd generatorens stasjonære kortslutningsreaktans
- xd’ generatorens transiente kortslutningsreaktans
- xd’’ generatorens subtransiente kortslutningsreaktans
- StN transformatorens merkeytelse
- ek 1-fase transformatorens kortslutningsimpedans
- Up Spenningen på primærsiden av transformatoren
- Us Spenningen på sekundærsiden av transformatoren
Ytelser, spenninger og cos er gitt direkte i prøveprotokollene og som påstemplede merkeverdier. Subtransient og transient reaktans er for de fleste omformertypene beregnet fra prøveprotokollene (typeprøve) til omformerne ref.[2]. For enkelte aggregattyper mangler det prøveprotokoller, og der er det brukt data som Adtranz har benyttet i sine simuleringer for Gardermobanen ref.[5], eller data fra en eldre oversikt over de svenske omformerne, sannsynligvis laget av Banverket [4].
Kortslutningsimpedans for transformatorer (ek), er et beregnet gjennomsnitt av flere transformatorer av samme type, data er hentet fra prøveprotokollene. En oversikt som viser de forskjellige omformertyper med merkedata for generatorsiden er vist i tabellform i tabell 1.
Beregninger av transient kortslutningsstrøm
Den totale transiente kortslutningstrømmen i feilstedet når flere omformere er i drift i omformerstasjonen og det tas hensyn til bidrag fra de nærmeste matestasjonene blir:
| 9 |
hvor første ledd representerer det totale transiente bidrag fra omformerstasjonen rett ved kortslutningen. Andre ledd representerer det totale bidrag fra nærliggende omformerstasjoner
Beregning av kortslutningsstrøm fra generatorer
Metode for beregning av transient kortslutningsstrøm i en generator er forklart nedenfor. Skal man beregne den subtransiente eller stasjonære kortslutningsstrømmen, benyttes samme metode, men med generatorreaktanser for den perioden som skal beregnes.
1. Først beregnes maksimal laststrøm for generator, som er gitt av den maksimale ytelsen til generatoren (6-min. verdi):
| 10 |
2. Deretter beregnes spenningen bak den transiente reaktansen med likning .5. Her antas laststrømmens effektfaktor cos lik generatorens merkeverdi.
3. Beregner transient kortslutningsstrøm ut fra transformator gitt av
| 11 |
Strømmen er referert til 15 kV siden av transformatoren.
| Uref: | generatorspenning |
| xt: | transformatorens kortslutningsimpedans, brukes både i stasjonær, transient og subtransient periode |
| Ukl: | spenningen på kontaktledningssiden av transformatoren, vanlig å benytte 16 kV |
Regneeksempel transient kortslutningsstrøm
Her følger utregninger for 5,8 MVA-generator
1.
| 12 |
2. For å beregne E’ må først Zref finnes for generatoren. Denne finnes ved
| 13 |
Deretter beregnes
Xd’=xd’ . Zref=0,125 . 4,0=0,5
Finner vinkelen på bakgrunn av cos, = -36,87o.
Setter inn i likning 5 og får
| 14 |
3. Beregner deretter den transiente kortslutningsstrømmen, Ik’, ved å sette inn i likning 11.
Før det kan settes inn i likningen må xt beregnes,
| 15 |
På samme måte som over regnes den subtransiente kortslutningsstrømmen ut ved å bruke likningene for det subtransiente systemet, likning 3 og 4. I likning 11 erstattes xd’ med xd’’. For transformatoren benyttes samme reaktans ved transient analyse som ved subtransient analyse.
Resultater for hver enkelt omformertype er regnet ut i ref.[1].
Bidrag fra nærliggende omformere
Når det oppstår en kortslutning ved en omformerstasjon vil normalt den største andelen av feilstrømmen komme fra denne omformerstasjonen. Jernbaneverkets kontaktledningsanlegg er i normaldrift samkjørt til enhver tid. Av den grunn vil feilstrømmen også få bidrag fra de nærmeste omformerstasjonene. Størrelsen på dette bidraget til den totale feilstrømmen minker med avstand til de nærmeste omformerstasjonene. De fleste av Jernbaneverkets omformerstasjoner ligger langs banestrekninger uten stjernepunkt, som angitt i figur 6.
Figur 6 Omformerstasjoner langs Jernbaneverkets kontaktledningsanlegg
Ved beregning av den totale feilstrømmen, Ik, ved feilstedet, må det lages modeller av systemet. Omformerstasjonen, A, nærmest feilstedet, figur .6, kan modelleres med den transiente spenningen E’ bak den transiente reaktansen, xd'. Når avstanden til de to nærmeste omformerstasjonene er over 60 km, kan disse modelleres som stive spenningskilder på 16,2 kV, da det er så stor demping i kontaktledningsanlegget at resultatet vil ha god nok nøyaktighet. Ved kortere avstander bør de nærmeste omformerstasjonene bli modellert som omformer A.
Kontaktledningsanlegget modelleres som serieimpedanser med de verdier som er registrert i gamle målinger. Der det mangler dokumentasjon på kontaktledningsanleggets impedanser, benyttes en impedans på Z=0,21 + j0,21 /km, eldre anlegg.
Det er gjort beregninger hvor også de to neste omformerstasjonene (vist stiplet i figur .6) er tatt med i en kortslutningsberegning, men dette ga mikroskopiske utslag på den totale feilstrømmen. Det eneste som skjedde var at man fikk en annen lastdeling i systemet. De “nye” omformerstasjonene lastet av stasjonene mellom seg og feilstedet, mens den totale feilstrømmen ble som før. Ved beregning av minimal kortslutningsstrøm må det tas hensyn til denne lastdelingen.
På enkelte banestrekninger er det i dag installert seriekondensatorbatterier for kompensering av det induktive spenningsfallet i kontaktledningsanlegget. Disse batteriene vil på enkelte steder øke kortslutningsstrømmen når de er innkoblet, mens de andre steder faktisk vil redusere den totale feilstrømmen. Årsaken til at man får slike forhold er at bidraget av feilstrøm fra en naboomformer via et kompensert nett ligger sterkt faseforskjøvet i forhold til bidraget fra den nærmeste omformeren hvis den ikke er kompensert. Når man summerer flere strømmer som er faseforskjøvet i forhold til hverandre, må man summere vektorielt, og da blir summen lavere enn hvis strømmene hadde vært i fase.
For å finne den maksimale kortslutningsstrømmen, bør det gjøres beregninger både med og uten seriekondensatorbatterier for å komme frem til den største feilstrømmen.
Dersom en kortslutning ikke oppstår rett utenfor en omformerstasjon, må impedansen i kontaktledningsanlegget, Zkl, tas med for utregning av kortslutningsstrømmen i likning 11. Det er da viktig å huske at impedansene for generator og transformator er referert generatorsiden av transformatoren. For å regne om Zkl til denne siden av transformatoren benyttes likningen under:
| 16 |
hvor:
Uref: generatorspenningen
Ukl: spenningen på kontaktledningssiden av transformatoren.
Dette gir følgene formel for kortslutningsstrømmen:
| 17 |
Betraktningen over om avstand fra omformeren gjelder også ved denne kortslutningsberegningen. Er avstanden fra omformeren til feilstedet over 60 km, benyttes en stiv spenningskilde som modell for omformeren istedenfor likningen over.
Regneeksempel total transient kortslutningsstrøm
Ved å ta utgangspunkt i figur 6 skal den totale transiente kortslutningsstrømmen beregnes ved en kortslutning rett utenfor omformerstasjon A. For å forenkle beregningene består denne omformerstasjonen av to 5,8 MVA aggregat. De to nabo-omformerstasjonene ligger 60 km fra omformerstasjon A. Disse kan derfor modelleres som to stive spenningskilder. Som impedans i kontaktledningsanlegget benyttes Z=0,21+j0,21 /km.
For å finne den totale transiente kortslutningsstrømmen benyttes likning 9.
Den transiente kortslutningsstrømmen for 5,8 MVA aggregatet er beregnet i avsnitt 3.2.1.1, Ik’=1841,1 A med vinkel –80,1o. Begge aggregatene vil gi samme bidrag.
Strømmen fra de to omformerstasjonene som gir bidrag, finnes ved hjelp av:
| 18 |
Begge omformerstasjonene gir like store bidrag. Dette gir total transient kortslutningsstrøm:
| 19 |
Litteraturhenvisninger
1. Jernbaneverket Bane Energi. Kortslutningsdata 1-fase i det norske jernbanenettet, Bane Energi (1998)
2. ASEA. Prøveprotokoller for ASEA 5.8 (4.0), NEBB 7.0 og NEBB 10.0
3. Faanes, Arnesen, Klevjer. Kompendium Elektriske kraftsystemer, NTH (1987)
4. Siemens. Datablad for omformere Q24/Q25, Q38/Q39, Q48/Q49
5. Adtranz. Systemstudie Oslo-området, prosjekt for Gardermobanen, Adtranz (1997)
6. R. Lundberg. Lærebok i elektroteknikk, del 4 - omformerstasjoner, Svenska Tryckeriaktiebolaget, Stockholm (1959)