Sporjustering: Forskjell mellom sideversjoner
(rettet feil da l var skrevet som ettall 1) |
|||
| (47 mellomliggende revisjoner av samme bruker vises ikke) | |||
| Linje 9: | Linje 9: | ||
[[Fil:L53404-1.png|600px]] | [[Fil:L53404-1.png|center|600px]] | ||
''Figur 1: Banemester Schives apparat for retting av skinnegangen'' | ''Figur 1: Banemester Schives apparat for retting av skinnegangen'' | ||
| Linje 20: | Linje 20: | ||
[[Fil:L53404-2.png|600px]] | [[Fil:L53404-2.png|center|600px]] | ||
''Figur 2: Justeringsarbeid på Dovrebanen i 1920-årene'' | ''Figur 2: Justeringsarbeid på Dovrebanen i 1920-årene'' | ||
Selve metoden går ut på at en kurve kan beskrives vha. såkalt krumningsprofil (XZ-planet) og vinkelprofil (XY-planet), der vinkelprofilet er integrallinjen av krumningsprofilet. Hvis vi deler opp linjen i små nok linjestykker | Selve metoden går ut på at en kurve kan beskrives vha. såkalt krumningsprofil (XZ-planet) og vinkelprofil (XY-planet), der vinkelprofilet er integrallinjen av krumningsprofilet. Hvis vi deler opp linjen i små nok linjestykker ΔL, kan hvert linjestykke på en ujevn strekning tilnærmes med en perfekt sirkelkurve, dvs. med konstant krumning. Målinger av det eksisterende sporet sammenlignes med beregninger på utstukket/teoretisk kurve, og justeringsverdier dannes punkt for punkt. | ||
Målingene av sporet ville typisk bestå av kjeding og avmerking, der kjedelengden var | Målingene av sporet ville typisk bestå av kjeding og avmerking, der kjedelengden var ΔL. Deretter ble pilhøyder målt med manuelt instrument i hvert avmerkede punkt med et egnet måleapparat, som f.eks. vist i figur 3. Samtidig med utstikking ble også gjerne tvangspunkter og karakteristiske trasépunkter målt inn når disse la betingelser for justeringen. | ||
[[Fil:L53404-3.png|600px]] | [[Fil:L53404-3.png|center|600px]] | ||
''Figur 3: Måling av pilhøyder med Höfers apparat'' | ''Figur 3: Måling av pilhøyder med Höfers apparat'' | ||
| Linje 77: | Linje 77: | ||
Størstedelen av dette avsnittet dreier seg om sporjustering som baserer seg på målinger av såkalte pilhøyder. Vi skal se på de prinsipper som ble lagt til grunn ved århundreskiftet og som fortsatt danner basis for de kompliserte beregningene som foretas av dagens høyteknologiske justeringsverktøy. | Størstedelen av dette avsnittet dreier seg om sporjustering som baserer seg på målinger av såkalte pilhøyder. Vi skal se på de prinsipper som ble lagt til grunn ved århundreskiftet og som fortsatt danner basis for de kompliserte beregningene som foretas av dagens høyteknologiske justeringsverktøy. | ||
Detaljer rundt selve målingen av pilhøydene vil ikke bli videre gjennomgått, men det vises til | Detaljer rundt selve målingen av pilhøydene vil ikke bli videre gjennomgått, men det vises til [[Tilstandskontroll]]. | ||
== Nalenz/Höfer/Schramm metode == | == Nalenz/Höfer/Schramm metode == | ||
| Linje 83: | Linje 83: | ||
=== Grunnlag for metoden === | === Grunnlag for metoden === | ||
[[Fil:L53404-4.png|600px]] | [[Fil:L53404-4.png|center|600px]] | ||
''Figur 4: Eksisterende og ønsket kurve - avstand og vinkeldifferanse'' | ''Figur 4: Eksisterende og ønsket kurve - avstand og vinkeldifferanse'' | ||
Figuren viser to kurver med samme hovedtangent, dvs. en utgangsretning hvor de to kurvene sammenfaller. I et vilkårlig punkt (P<sub>1</sub>) på den eksisterende kurven trekker vi dennes normal ned på den ønskede kurven, som gir oss et krysningspunkt (P<sub>2</sub>). Tangentene i disse punktene danner en vinkel vi kaller vinkeldifferansen | Figuren viser to kurver med samme hovedtangent, dvs. en utgangsretning hvor de to kurvene sammenfaller. I et vilkårlig punkt (P<sub>1</sub>) på den eksisterende kurven trekker vi dennes normal ned på den ønskede kurven, som gir oss et krysningspunkt (P<sub>2</sub>). Tangentene i disse punktene danner en vinkel vi kaller vinkeldifferansen Δφ, og vi definerer avstanden mellom punktene til å være kurveavstanden a i punktet P<sub>1</sub>. | ||
Uendelig små buelengder dl langs kurven kan betraktes som rettlinjer og vi kan skrive: | Uendelig små buelengder dl langs kurven kan betraktes som rettlinjer og vi kan skrive: | ||
<math>\text{da}=\text{dl}\cdot \text{tan}{\Delta \phi }</math>''(1)'' | <math>\text{da}=\text{dl}\cdot \text{tan}{\Delta \phi }</math> ''(1)'' | ||
For små vinkler kan vi også tilnærme uttrykket med | For små vinkler kan vi også tilnærme uttrykket med | ||
<math>\text{da}=\text{dl}\cdot \mathit{\Delta \phi }</math>''(2)'' | <math>\text{da}=\text{dl}\cdot \mathit{\Delta \phi }</math> ''(2)'' | ||
Med ønske om å løse ut nettopp avstanden mellom eksisterende og ønsket kurve, kan vi integrere | Med ønske om å løse ut nettopp avstanden mellom eksisterende og ønsket kurve, kan vi integrere | ||
<math>a=\int \mathit{\Delta \phi }\text{dl}</math>''(3)'' | <math>a=\int \mathit{\Delta \phi }\text{dl}</math> ''(3)'' | ||
Ligningen 3 kan benyttes i enhver situasjon der krumningsforholdene er gitt, dvs. hvor | Ligningen 3 kan benyttes i enhver situasjon der krumningsforholdene er gitt, dvs. hvor Δφ kan uttrykkes som en bestemt funksjon. Men dette forholdet er sjelden oppfylt. Vi utfører justering nettopp som følge av ujevne krumningsforhold i sporet. Med disse forutsetningene deler vi opp kurven i ''endelige'', små buelengder Δl og ''summerer'' vinkeldifferansene i et stort nok antall punkter for å finne avstanden mellom kurvene: | ||
<math>a=\mathit{\Delta l}\cdot \sum \mathit{\Delta \phi }</math>''(4)'' | <math>a=\mathit{\Delta l}\cdot \sum \mathit{\Delta \phi }</math> ''(4)'' | ||
Dette er det alminnelige utgangspunktet for å beregne avstanden mellom faktisk og ønsket kurveforløp. For å beregne denne i praksis skal vi i det følgende beregne problemstillingen grafisk. Konklusjonene vil bli gitt i avsnitt 2.1.5. | Dette er det alminnelige utgangspunktet for å beregne avstanden mellom faktisk og ønsket kurveforløp. For å beregne denne i praksis skal vi i det følgende beregne problemstillingen grafisk. Konklusjonene vil bli gitt i avsnitt 2.1.5. | ||
=== Krumnings- og vinkelprofil === | === Krumnings- og vinkelprofil === | ||
Vi skal gå tilbake til situasjonen hvor vi benytter differensialer i stedet for endelige størrelser. Vinkeldifferensialet | Vi skal gå tilbake til situasjonen hvor vi benytter differensialer i stedet for endelige størrelser. Vinkeldifferensialet dφ (ikke det samme som Δφ i 2.1.1) fremkommer av lengdedifferensialet dl og krumningsradien ρ i et punkt: | ||
<math>\mathit{d\phi }=\frac{\text{dl}}{\rho }</math>''(5)'' | <math>\mathit{d\phi }=\frac{\text{dl}}{\rho }</math> ''(5)'' | ||
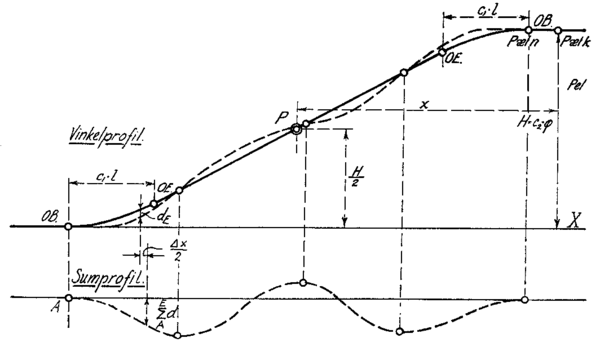
Ved å avsette krumningen (eller pilhøyden) som ordinater (Z) langs lengdeaksen (X) fremkommer ''krumningsprofilet ''(pilhøydediagram), som vist i figur | Ved å avsette krumningen (eller pilhøyden) som ordinater (Z) langs lengdeaksen (X) fremkommer ''krumningsprofilet ''(pilhøydediagram), som vist i figur 5. I tillegg avsettes vinkelen som dannes med utgangspunktet (hovedtangent) langs linjen som ordinater (Y) langs samme lengdeakse. Dette betegnes ''vinkelprofilet''. | ||
[[Fil:L53404-5.png|600px]] | [[Fil:L53404-5.png|center|600px]] | ||
''Figur 5: Krumnings- og vinkelprofil'' | ''Figur 5: Krumnings- og vinkelprofil'' | ||
| Linje 120: | Linje 120: | ||
Ved noen enkle differensialbetraktninger dx og dy for hhv. lengder og vinkler, kan vi vise at: | Ved noen enkle differensialbetraktninger dx og dy for hhv. lengder og vinkler, kan vi vise at: | ||
<math>\frac{\text{dy}}{\text{dx}}=\frac{{c}_{2}}{{c}_{1}}\cdot \frac{1}{\rho }={c}_{3}\cdot \frac{1}{\rho }=z</math>''(6)'' | <math>\frac{\text{dy}}{\text{dx}}=\frac{{c}_{2}}{{c}_{1}}\cdot \frac{1}{\rho }={c}_{3}\cdot \frac{1}{\rho }=z</math> ''(6)'' | ||
(c<sub>1</sub> – c<sub>4</sub> i det følgende er kun målestokksfaktorer, jf. figur | (c<sub>1</sub> – c<sub>4</sub> i det følgende er kun målestokksfaktorer, jf. figur 5 - 6) | ||
Vinkelprofilet, som vi har valgt å benevne y, kan dermed skrives som | Vinkelprofilet, som vi har valgt å benevne y, kan dermed skrives som | ||
<math>y=\int z\text{dx}=\int {c}_{3}\frac{1}{\rho }\text{dx}</math>''(7)'' | <math>y=\int z\text{dx}=\int {c}_{3}\frac{1}{\rho }\text{dx}</math> ''(7)'' | ||
Vinkelprofilet er altså integrallinjen av krumningsprofilet. Dette innebærer at dersom krumningsprofilet kan uttrykkes som funksjon av lengde, så kan vinkelprofilet finnes analytisk ved integrasjon. Neste avsnitt gir eksempler på dette for ulike traséelementer. | Vinkelprofilet er altså integrallinjen av krumningsprofilet. Dette innebærer at dersom krumningsprofilet kan uttrykkes som funksjon av lengde, så kan vinkelprofilet finnes analytisk ved integrasjon. Neste avsnitt gir eksempler på dette for ulike traséelementer. | ||
=== Krumnings- og vinkelprofil for ulike traséelementer === | === Krumnings- og vinkelprofil for ulike traséelementer === | ||
En sirkelkurve har konstant krumning 1/R for konstant radius R. Vi kan da sette, jf. forrige avsnitt, at <math>z={c}_{3}\cdot \frac{1}{R}</math>. | En sirkelkurve har konstant krumning 1/R for konstant radius R. Vi kan da sette, jf. forrige avsnitt, at <math>z={c}_{3}\cdot \frac{1}{R}</math>. | ||
<math>y=\int \frac{{c}_{3}}{R}\text{dx}=\frac{{c}_{3}}{R}\cdot x</math>''(8)'' | For vinkelprofilet får vi da: | ||
<math>y=\int \frac{{c}_{3}}{R}\text{dx}=\frac{{c}_{3}}{R}\cdot x</math> ''(8)'' | |||
Dette er ikke noe annet enn en ''rettlinje'' med en bestemt helning. Det kan vises at venstrekurver vil ha positiv helning, mens høyrekurver vil ha negativ helning i lengderetningen. | Dette er ikke noe annet enn en ''rettlinje'' med en bestemt helning. Det kan vises at venstrekurver vil ha positiv helning, mens høyrekurver vil ha negativ helning i lengderetningen. | ||
Som vi vet er krumningsprofilet til overgangskurver stigende eller synkende rettlinjer, <math>z={c}_{3}\cdot \frac{x}{R\cdot l}</math>. | Som vi vet er krumningsprofilet til overgangskurver stigende eller synkende rettlinjer, <math>z={c}_{3}\cdot \frac{x}{R\cdot l}</math>. | ||
<math>y=\int {c}_{3}\cdot \frac{x}{R\cdot l}\text{dx}={c}_{3}\cdot \frac{{x}^{2}}{2\cdot R\cdot l}</math>''(9)'' | For vinkelprofilet får vi: | ||
<math>y=\int {c}_{3}\cdot \frac{x}{R\cdot l}\text{dx}={c}_{3}\cdot \frac{{x}^{2}}{2\cdot R\cdot l}</math>'' (9)'' | |||
Vinkelprofilet er altså en vanlig (kvadratisk) ''parabel''. | Vinkelprofilet er altså en vanlig (kvadratisk) ''parabel''. | ||
| Linje 145: | Linje 149: | ||
Integreres uttrykkene for vinkelprofilene til hhv. sirkelkurver og overgangkurver, ser vi at integrallinjene til vinkelprofilet er de virkelige kurvene langs hovedtangenten: | Integreres uttrykkene for vinkelprofilene til hhv. sirkelkurver og overgangkurver, ser vi at integrallinjene til vinkelprofilet er de virkelige kurvene langs hovedtangenten: | ||
<math>y={c}_{3}\cdot \frac{{x}^{2}}{2\cdot R}\text{og}y={c}_{3}\cdot \frac{{x}^{3}}{6\cdot R\cdot l}</math>''(10)'' | <math>y={c}_{3}\cdot \frac{{x}^{2}}{2\cdot R}\text{ og }y={c}_{3}\cdot \frac{{x}^{3}}{6\cdot R\cdot l}</math> ''(10)'' | ||
=== Ujevne kurver – kurver som skal justeres === | === Ujevne kurver – kurver som skal justeres === | ||
Etter å ha definert begrepene krumnings- og vinkelprofil i avsnittene 2.1.2 og 2.1.3, skal vi nå returnere til noe av situasjonen beskrevet i 2.1.1, der vi ikke kjenner kurvaturen, men har en geometri som av ulike årsaker har kommet ut av opprinnelig form. Da må den tidligere integrasjonen erstattes av summering, og vi får: | Etter å ha definert begrepene krumnings- og vinkelprofil i avsnittene 2.1.2 og 2.1.3, skal vi nå returnere til noe av situasjonen beskrevet i 2.1.1, der vi ikke kjenner kurvaturen, men har en geometri som av ulike årsaker har kommet ut av opprinnelig form. Da må den tidligere integrasjonen erstattes av summering, og vi får: | ||
<math>y=\sum z\cdot \mathit{\Delta x}=\sum \frac{{c}_{3}}{\rho }\cdot \mathit{\Delta x}=\sum \frac{1}{\rho }\cdot \frac{{c}_{2}}{{c}_{1}}\cdot {c}_{1}\cdot \mathit{\Delta l}={c}_{2}\cdot \mathit{\Delta l}\cdot \sum \frac{1}{\rho }</math>''(11)'' | <math>y=\sum z\cdot \mathit{\Delta x}=\sum \frac{{c}_{3}}{\rho }\cdot \mathit{\Delta x}=\sum \frac{1}{\rho }\cdot \frac{{c}_{2}}{{c}_{1}}\cdot {c}_{1}\cdot \mathit{\Delta l}={c}_{2}\cdot \mathit{\Delta l}\cdot \sum \frac{1}{\rho }</math> ''(11)'' | ||
Krumningen 1/ | Krumningen 1/ρ bestemmes ved pilhøydemåling på bestemte kordelengder. | ||
Vi foretar ingen utledning her, men vinkeprofilets ligning kan pga. forholdet mellom krumning og pilhøyden h skrives som | Vi foretar ingen utledning her, men vinkeprofilets ligning kan pga. forholdet mellom krumning og pilhøyden h skrives som | ||
<math>y={c}_{4}\cdot \sum h</math>''(12)'' | <math>y={c}_{4}\cdot \sum h</math> ''(12)'' | ||
=== Beregning av sumprofil === | === Beregning av sumprofil === | ||
Vi skal nå ta for oss hvordan vi benytter de til nå gjennomgåtte begrepene for å bestemme avstandene mellom eksisterende og ønsket kurve. I figur .6 er vist vinkelprofilet til en eksisterende kurvekombinasjon bestående av rettlinjer i endene, en venstrekrum sirkelkurve og mellomliggende overgangskurver (stiplet kurve). Ønsket/rettet kurve er vist med heltrukken kurve. Sistnevntes vinkelprofil kaller vi balanseprofilet. | Vi skal nå ta for oss hvordan vi benytter de til nå gjennomgåtte begrepene for å bestemme avstandene mellom eksisterende og ønsket kurve. I figur .6 er vist vinkelprofilet til en eksisterende kurvekombinasjon bestående av rettlinjer i endene, en venstrekrum sirkelkurve og mellomliggende overgangskurver (stiplet kurve). Ønsket/rettet kurve er vist med heltrukken kurve. Sistnevntes vinkelprofil kaller vi balanseprofilet. | ||
[[Fil:L53404-6.png|600px]] | [[Fil:L53404-6.png|center|600px]] | ||
| Linje 170: | Linje 174: | ||
For den eksisterende (urettede) kurven har vi | For den eksisterende (urettede) kurven har vi | ||
<math>{F}_{1}=\mathit{\Delta x}\cdot \sum _{1}^{k}y=\mathit{\Delta x}\cdot \sum _{1}^{k}\sum _{1}^{n}z=\mathit{\Delta x}\cdot {c}_{4}\sum _{1}^{k}\sum _{1}^{n}h</math>''(13)'' | <math>{F}_{1}=\mathit{\Delta x}\cdot \sum _{1}^{k}y=\mathit{\Delta x}\cdot \sum _{1}^{k}\sum _{1}^{n}z=\mathit{\Delta x}\cdot {c}_{4}\sum _{1}^{k}\sum _{1}^{n}h</math> ''(13)'' | ||
For balanseprofilet har vi | For balanseprofilet har vi | ||
<math>{F}_{2}=x\cdot H=x\cdot {c}_{4}\sum _{1}^{n}h</math>''(14)'' | <math>{F}_{2}=x\cdot H=x\cdot {c}_{4}\sum _{1}^{n}h</math> ''(14)'' | ||
Kravet om like flater under vinkelprofilene gir: | Kravet om like flater under vinkelprofilene gir: | ||
<math>x=\mathit{\Delta x}\cdot \frac{{c}_{4}\sum _{1}^{k}\sum _{1}^{n}h}{\sum _{1}^{n}h}</math>''(15)'' | <math>x=\mathit{\Delta x}\cdot \frac{{c}_{4}\sum _{1}^{k}\sum _{1}^{n}h}{\sum _{1}^{n}h}</math> ''(15)'' | ||
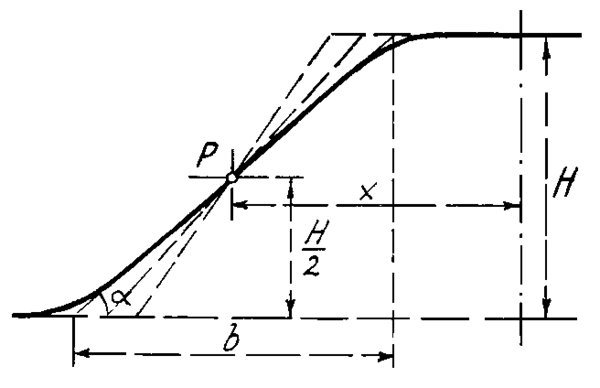
Dette gir punktet P, illustrert i figur 7: | Dette gir punktet P, illustrert i figur 7: | ||
[[Fil:L53404-7.png|600px]] | [[Fil:L53404-7.png|center|600px]] | ||
''Figur 7 Fellespunkt P for alle balanseprofil'' | ''Figur 7 Fellespunkt P for alle balanseprofil'' | ||
| Linje 192: | Linje 196: | ||
Sumprofilets ordinater d gir verdier for å finne den reelle avstanden mellom opprinnelig og rettet kurve: | Sumprofilets ordinater d gir verdier for å finne den reelle avstanden mellom opprinnelig og rettet kurve: | ||
<math>d={c}_{2}\cdot \mathit{\Delta \phi }</math>''(16)'' | <math>d={c}_{2}\cdot \mathit{\Delta \phi }</math> ''(16)'' | ||
Settes dette inn i ligning 4, får vi følgende uttrykk for avstanden mellom kurvene, eller bakseverdier: | Settes dette inn i ligning 4, får vi følgende uttrykk for avstanden mellom kurvene, eller bakseverdier: | ||
<math>a=\mathit{\Delta l}\cdot \sum \mathit{\Delta \phi }=\mathit{\Delta l}\cdot \sum \frac{d}{{c}_{2}}=\frac{\mathit{\Delta l}}{{c}_{2}}\cdot \sum d</math>''(17)'' | <math>a=\mathit{\Delta l}\cdot \sum \mathit{\Delta \phi }=\mathit{\Delta l}\cdot \sum \frac{d}{{c}_{2}}=\frac{\mathit{\Delta l}}{{c}_{2}}\cdot \sum d</math> ''(17)'' | ||
Siden <math>\mathit{\Delta x}={c}_{1}\cdot \mathit{\Delta l}</math>, får vi | Siden <math>\mathit{\Delta x}={c}_{1}\cdot \mathit{\Delta l}</math>, får vi | ||
<math>a=\frac{\mathit{\Delta x}}{{c}_{1}\cdot {c}_{2}}\cdot \sum d</math>''(18)'' | <math>a=\frac{\mathit{\Delta x}}{{c}_{1}\cdot {c}_{2}}\cdot \sum d</math> ''(18)'' | ||
Som vi ser av utledningene over, kan justeringsberegningen også foretas helt analytisk ved å føre opp alle summer fortløpende i en egnet tabell, jf. Rabstad-metoden. Som vi skjønner er arbeidet svært tidkrevende dersom ikke elektronisk regnekraft benyttes. | Som vi ser av utledningene over, kan justeringsberegningen også foretas helt analytisk ved å føre opp alle summer fortløpende i en egnet tabell, jf. Rabstad-metoden. Som vi skjønner er arbeidet svært tidkrevende dersom ikke elektronisk regnekraft benyttes. | ||
| Linje 219: | Linje 223: | ||
Metoden ble regnet som en nokså primitiv måte å beregne sporjustering på. Ved all justering gikk en på akkord med ny pilhøyde. Som ved nyere justeringsalgoritmer (jf. avsnitt 2.3) ble ikke eksakt den kurvaturen man ønsket seg oppnådd. Man måtte derfor akseptere en ”beste” løsning mht. baks kontra ønsket pilhøyde. | Metoden ble regnet som en nokså primitiv måte å beregne sporjustering på. Ved all justering gikk en på akkord med ny pilhøyde. Som ved nyere justeringsalgoritmer (jf. avsnitt 2.3) ble ikke eksakt den kurvaturen man ønsket seg oppnådd. Man måtte derfor akseptere en ”beste” løsning mht. baks kontra ønsket pilhøyde. | ||
[[Fil:L53404-8.jpg|600px]] | [[Fil:L53404-8.jpg|center|600px]] | ||
''Figur 4.8: Matisakalkulatoren (to sammenmonterte) med initiell konfigurasjon'' | ''Figur 4.8: Matisakalkulatoren (to sammenmonterte) med initiell konfigurasjon'' | ||
[[Fil:L53404-9.jpg|600px]] | [[Fil:L53404-9.jpg|center|600px]] | ||
''Figur 4.9: Matisakalkulatoren etter endt "justering"'' | ''Figur 4.9: Matisakalkulatoren etter endt "justering"'' | ||
| Linje 239: | Linje 243: | ||
Når det gjelder størrelsen på beregnet baks, er denne ikke bare avhengig av plasseringen av OB’er og OE’er. Anvendelsen av spline-funksjoner byr på muligheten for å velge en utjevningsgrad for bakseberegningen. Siden spline-funksjoner består av subintervaller av en gitt strekning, vil de variere mye med hvor mange intervaller, eller punkter vi velger at den skal dekke. For bakseberegningens del betyr dette at jo høyere utjevningsgrad vi velger i programmet, dvs. hvor mange intervaller spline-funksjonen skal inneholde, desto bedre tilpasning mellom ønsket og ny pilhøyde får vi. Men dette resulterer også i større bakseverdier. Det kan i tillegg gis en baksekorridor for den aktuelle strekningen, men bakseverdier som tangerer baksekorridoren fører normalt til en dårligere tilpasning mellom ønsket og ny pilhøyde. | Når det gjelder størrelsen på beregnet baks, er denne ikke bare avhengig av plasseringen av OB’er og OE’er. Anvendelsen av spline-funksjoner byr på muligheten for å velge en utjevningsgrad for bakseberegningen. Siden spline-funksjoner består av subintervaller av en gitt strekning, vil de variere mye med hvor mange intervaller, eller punkter vi velger at den skal dekke. For bakseberegningens del betyr dette at jo høyere utjevningsgrad vi velger i programmet, dvs. hvor mange intervaller spline-funksjonen skal inneholde, desto bedre tilpasning mellom ønsket og ny pilhøyde får vi. Men dette resulterer også i større bakseverdier. Det kan i tillegg gis en baksekorridor for den aktuelle strekningen, men bakseverdier som tangerer baksekorridoren fører normalt til en dårligere tilpasning mellom ønsket og ny pilhøyde. | ||
Å variere utjevningsgraden på bakseberegningen er ikke tilrådelig før man har fått låst fast | Å variere utjevningsgraden på bakseberegningen er ikke tilrådelig før man har fått låst fast OB-er og OE-er med en tilfredsstillende løsning. Inntil dette er gjort, anvendes normalt en utjevningsgrad lik 0, dvs. en spline som går gjennom 9 målepunkter. | ||
=== Praktisk eksempel: Baksber benyttet over 1 km spor === | === Praktisk eksempel: Baksber benyttet over 1 km spor === | ||
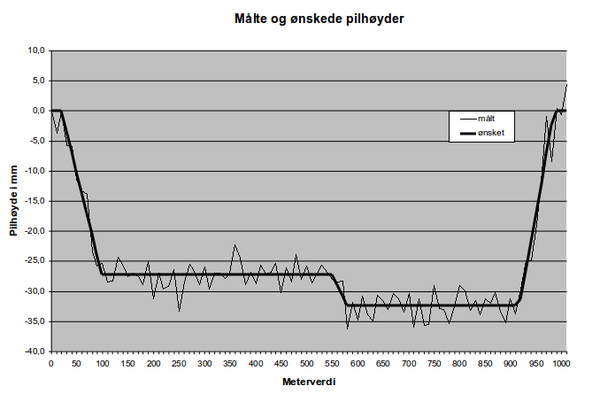
Figur 10 viser utgangssituasjonen for bakseberegning av en 1 km lang sporstrekning: | Figur 10 viser utgangssituasjonen for bakseberegning av en 1 km lang sporstrekning: | ||
[[Fil:L53404-10.png|600px]] | [[Fil:L53404-10.png|center|600px]] | ||
''Figur 4.10: Målte og ønskede pilhøyder'' | ''Figur 4.10: Målte og ønskede pilhøyder'' | ||
| Linje 252: | Linje 256: | ||
''Tabell 1 Tallresultater fra tre ulike bakseberegninger'' | ''Tabell 1 Tallresultater fra tre ulike bakseberegninger'' | ||
{| | {| class="wikitable" style="text-align: center" | ||
|- | |||
| | ! Utjevningsgrad !! Antall spline- målepunkter !! <nowiki>Summe baks [mm]</nowiki> !! <nowiki>Standardavvik [mm]</nowiki> | ||
|- | |||
| -2 || 7 || 352 || 0.61 | |||
|- | |- | ||
| | | 0 || 9 || 700 || 0.50 | ||
| | |||
| | |||
|- | |- | ||
| | | 10 || 19 || 2234 || 0.30 | ||
| | |} | ||
| | |||
| | |||
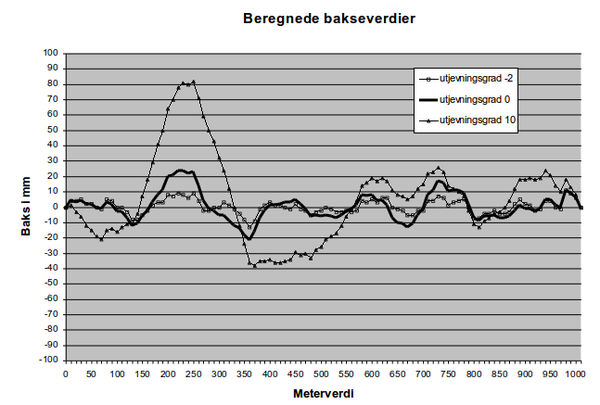
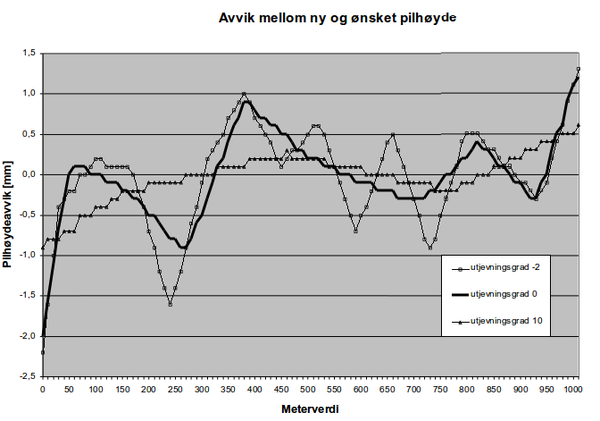
Vi ser tydelig at utjevningsgrad 10 gir meget store bakseverdier utfra figuren, og summe baks blir av en helt annen størrelsesorden enn for de to andre utjevningsgradene. Denne kan derfor utelukkes som endelig beregning for sporjustering. (Bakseverdiene er imidlertid ikke så store at de tangerer baksekorridoren, slik at det resulterer i dårlig overensstemmelse mellom ny og ønsket pilhøyde, jf. fig. 12.) Utjevningsgradene –2 og 0 gir tilsynelatende ingen store forskjeller i baks, med unntak av summe baksen som faktisk står i forholdet 1:2. | |||
Vi ser tydelig at utjevningsgrad 10 gir meget store bakseverdier utfra figuren, og summe baks blir av en helt annen størrelsesorden enn for de to andre utjevningsgradene. Denne kan derfor utelukkes som endelig beregning for sporjustering. (Bakseverdiene er imidlertid ikke så store at de tangerer baksekorridoren, slik at det resulterer i dårlig overensstemmelse mellom ny og ønsket pilhøyde, jf. fig | |||
[[Fil:L53404-11.png|600px]] | [[Fil:L53404-11.png|center|600px]] | ||
''Figur 11: Bakseverdier fra tre bakseberegninger (utj.grad –2,0 og 10)'' | ''Figur 11: Bakseverdier fra tre bakseberegninger (utj.grad –2,0 og 10)'' | ||
| Linje 285: | Linje 276: | ||
I figur 12 ser vi derimot hvor god tilpasning vi ville fått med utjevningsgrad 10 til ønsket pilhøyde. Videre avsløres effekten av forskjellen i standardavvik mellom utjevningsgradene –2 og 0, der –2 gir en langt mindre optimal ny pilhøyde. Valget av beregning som bør benyttes faller derfor på utjevningsgrad 0 i denne enkle betraktningen. | I figur 12 ser vi derimot hvor god tilpasning vi ville fått med utjevningsgrad 10 til ønsket pilhøyde. Videre avsløres effekten av forskjellen i standardavvik mellom utjevningsgradene –2 og 0, der –2 gir en langt mindre optimal ny pilhøyde. Valget av beregning som bør benyttes faller derfor på utjevningsgrad 0 i denne enkle betraktningen. | ||
[[Fil:L53404-12.png|600px]] | [[Fil:L53404-12.png|center|600px]] | ||
''Figur 12: Avvik fra ønsket pilhøyde for tre bakseberegninger | ''Figur 12: Avvik fra ønsket pilhøyde for tre bakseberegninger (utj.grad -2,0 og 10)'' | ||
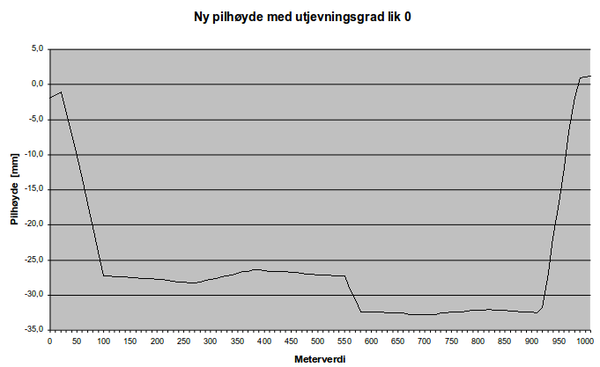
Figur 13 viser den nye pilhøyden etter bakseberegning med utjevningsgrad 0. | Figur 13 viser den nye pilhøyden etter bakseberegning med utjevningsgrad 0. | ||
[[Fil:L53404-13.png|600px]] | [[Fil:L53404-13.png|center|600px]] | ||
''Figur 13: Eksempel på ny pilhøyde (optimalt resultat med utj.grad 0)'' | ''Figur 13: Eksempel på ny pilhøyde (optimalt resultat med utj.grad 0)'' | ||
| Linje 417: | Linje 406: | ||
* Pakking - etterfylling og komprimering av ballast under svillene | * Pakking - etterfylling og komprimering av ballast under svillene | ||
[[Fil:L53404-15.jpg|600px]] | [[Fil:L53404-15.jpg|center|600px]] | ||
''Figur 15: Eksempel på pakkmaskin: Plasser 09-32 CSM'' | ''Figur 15: Eksempel på pakkmaskin: Plasser 09-32 CSM'' | ||
== Måling under justering == | == Måling under justering == | ||
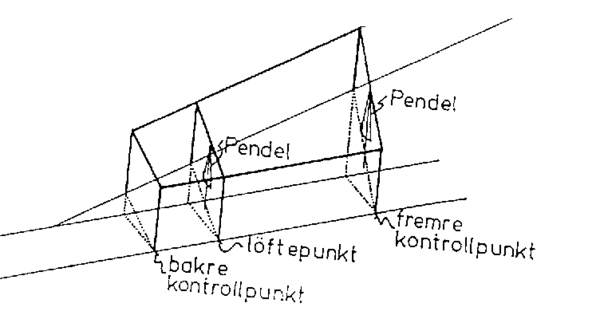
I alminnelighet finnes et separat måle- og løftesystem for hver av skinnestrengene, mens innlegging av overhøyde og overhøyderamper gjøres vha. en elektronisk pendel/inklinometer, jf. figur | I alminnelighet finnes et separat måle- og løftesystem for hver av skinnestrengene, mens innlegging av overhøyde og overhøyderamper gjøres vha. en elektronisk pendel/inklinometer, jf. figur 16. | ||
[[Fil:L53404-16.png|600px]] | [[Fil:L53404-16.png|center|600px]] | ||
''Figur 16: Prinsipp for justering av overhøyde/ innlegging av overhøyderampe'' | ''Figur 16: Prinsipp for justering av overhøyde/ innlegging av overhøyderampe'' | ||
| Linje 431: | Linje 420: | ||
For høydejustering benyttes alltid den såkalte 3-punkts kordemetoden. Måleprinsippet er det samme som ved pilhøydemålinger med målevogn: | For høydejustering benyttes alltid den såkalte 3-punkts kordemetoden. Måleprinsippet er det samme som ved pilhøydemålinger med målevogn: | ||
En målereferanse dannes av en korde mellom to sensorer mot sporet. Disse kan være mekaniske eller optiske. En tredje sensor måler pilhøyden i forhold til korden, jf. figur | En målereferanse dannes av en korde mellom to sensorer mot sporet. Disse kan være mekaniske eller optiske. En tredje sensor måler pilhøyden i forhold til korden, jf. figur 17. Avvik mellom teoretisk og målt verdi for pilhøyden indikerer avvik fra korrekt traséelement og danner grunnlag for korreksjonsverdien ved justeringen. | ||
[[Fil:L53404-17.png|600px]] | [[Fil:L53404-17.png|center|600px]] | ||
''Figur 17: Prinsippskisse av asymmetrisk pilhøydemåling'' | ''Figur 17: Prinsippskisse av asymmetrisk pilhøydemåling'' | ||
| Linje 443: | Linje 432: | ||
For sirkelkurver avhenger den pilhøyden som skal angis for sammenligning med den målte kun av to faktorer: kurveradius og den enkelte pakkmaskinen. Uten å foreta selve utledningen her, kan det vises gjennom utvikling av Taylor-rekker at pilhøyden er gitt ved: | For sirkelkurver avhenger den pilhøyden som skal angis for sammenligning med den målte kun av to faktorer: kurveradius og den enkelte pakkmaskinen. Uten å foreta selve utledningen her, kan det vises gjennom utvikling av Taylor-rekker at pilhøyden er gitt ved: | ||
<center><math>p=\frac{(\frac{ | <center><math>p=\frac{(\frac{l}{2}{)}^{2}}{\mathrm{2R}}-\frac{{b}^{2}}{\mathrm{2R}}=k\frac{l}{R}</math> ''(19)''</center> | ||
Pilhøyden er altså lik en maskinspesifikk konstant k mutliplisert med krumningen. Dermed er det nok for operatøren å mate kurveradien inn i systemet på et eller annet tidspunkt før justering. Alle andre størrelser er kjent. | Pilhøyden er altså lik en maskinspesifikk konstant k mutliplisert med krumningen. Dermed er det nok for operatøren å mate kurveradien inn i systemet på et eller annet tidspunkt før justering. Alle andre størrelser er kjent. | ||
| Linje 450: | Linje 439: | ||
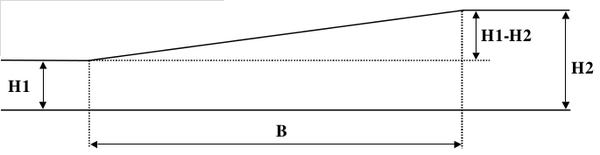
I stedet for 3 punkter og én målebasis benyttes her 4 punkter og to målebasiser. Dermed kan vi måle to forskjellige pilhøyder h og H på to forskjellige steder med en fast, målesystemavhengig avstand. Pilhøydene har altså forskjellig lengde på kordene. Når systemet er inne i ett enkelt traséelement skal forholdet mellom de to pilhøydene være konstant. Hvis ikke tyder det på at kurven ikke er skikkelig justert, og sporet må bakses til forholdet mellom pilhøydene stemmer overens med verdiene gitt i målesystemet. | I stedet for 3 punkter og én målebasis benyttes her 4 punkter og to målebasiser. Dermed kan vi måle to forskjellige pilhøyder h og H på to forskjellige steder med en fast, målesystemavhengig avstand. Pilhøydene har altså forskjellig lengde på kordene. Når systemet er inne i ett enkelt traséelement skal forholdet mellom de to pilhøydene være konstant. Hvis ikke tyder det på at kurven ikke er skikkelig justert, og sporet må bakses til forholdet mellom pilhøydene stemmer overens med verdiene gitt i målesystemet. | ||
<math>H=K\cdot h</math>'' | <math>H=K\cdot h</math> ''(20)'' | ||
der | der | ||
<math>K=\frac{\left(b-a\right)b}{\left(b-a+b\right)\left(b-a+c\right)}</math>''(21)'' | <math>K=\frac{\left(b-a\right)b}{\left(b-a+b\right)\left(b-a+c\right)}</math> ''(21)'' | ||
[[Fil:L53404-18.png|600px]] | [[Fil:L53404-18.png|center|600px]] | ||
''Figur 18: Prinsipp for sidejustering etter 4-punkts kordemetoden'' | ''Figur 18: Prinsipp for sidejustering etter 4-punkts kordemetoden'' | ||
| Linje 467: | Linje 456: | ||
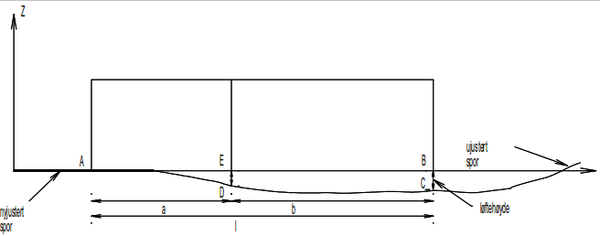
Fig. 19 viser skjematisk hvordan en løfteoperasjon arter seg. Punkt A befinner seg på allerede justert spor. Sporet skal gis et gjennomgående løft lik høyden BC. Sporet ved måle- og arbeidspunktet D løftes, og svillen pakkes slik at punktet ender på rettlinjen AB i punktet E. Matematisk kan dette uttrykkes som: | Fig. 19 viser skjematisk hvordan en løfteoperasjon arter seg. Punkt A befinner seg på allerede justert spor. Sporet skal gis et gjennomgående løft lik høyden BC. Sporet ved måle- og arbeidspunktet D løftes, og svillen pakkes slik at punktet ender på rettlinjen AB i punktet E. Matematisk kan dette uttrykkes som: | ||
<math>{Z}_{n}\left(x)=\frac{b}{l}{Z}_{n}\right(x-a)+\frac{a}{l}{Z}_{0}\left(x+b\right)</math>''(22)'' | <math>{Z}_{n}\left(x)=\frac{b}{l}{Z}_{n}\right(x-a)+\frac{a}{l}{Z}_{0}\left(x+b\right)</math> ''(22)'' | ||
Her skal Z<sub>n</sub> bety den nye høyden etter løftet, mens Z<sub>0</sub> er den opprinnelige høyden. Faktoren a/l er reduksjonsfaktoren som alle feil blir redusert med. | Her skal Z<sub>n</sub> bety den nye høyden etter løftet, mens Z<sub>0</sub> er den opprinnelige høyden. Faktoren a/l er reduksjonsfaktoren som alle feil blir redusert med. | ||
[[Fil:L53404-19.png|600px]] | [[Fil:L53404-19.png|center|600px]] | ||
''Figur 4.19: Prinsippet for justering i høyde etter 3-punktsmetoden'' | ''Figur 4.19: Prinsippet for justering i høyde etter 3-punktsmetoden'' | ||
| Linje 480: | Linje 469: | ||
Som for måling med målevogner, er det vanlig å benytte Fourier-transformasjon for å beskrive sammenhengen i frekvens-/bølgelengdedomenet: | Som for måling med målevogner, er det vanlig å benytte Fourier-transformasjon for å beskrive sammenhengen i frekvens-/bølgelengdedomenet: | ||
<math>\text{FT}\left\lbrace {Z}_{n}\right\rbrace =H\left(\lambda \right)\text{FT}\left\lbrace {Z}_{0}\right\rbrace </math>'' (23)'' | <math>\text{FT}\left\lbrace {Z}_{n}\right\rbrace =H\left(\lambda \right)\text{FT}\left\lbrace {Z}_{0}\right\rbrace </math> '' (23)'' | ||
Overføringsfunksjonen H angir forholdet mellom amplituden til løftet etter og før justeringen som funksjon av bølgelengde. Denne er gitt ved: | Overføringsfunksjonen H angir forholdet mellom amplituden til løftet etter og før justeringen som funksjon av bølgelengde. Denne er gitt ved: | ||
<math>H(\lambda )=\frac{{\mathit{ax}}^{b}}{l-{\mathit{bx}}^{-a}},\text{der}x={e}^{\frac{\mathit{i2p}}{\lambda }}</math>''(24)'' | <math>H(\lambda )=\frac{{\mathit{ax}}^{b}}{l-{\mathit{bx}}^{-a}},\text{der}x={e}^{\frac{\mathit{i2p}}{\lambda }}</math> ''(24)'' | ||
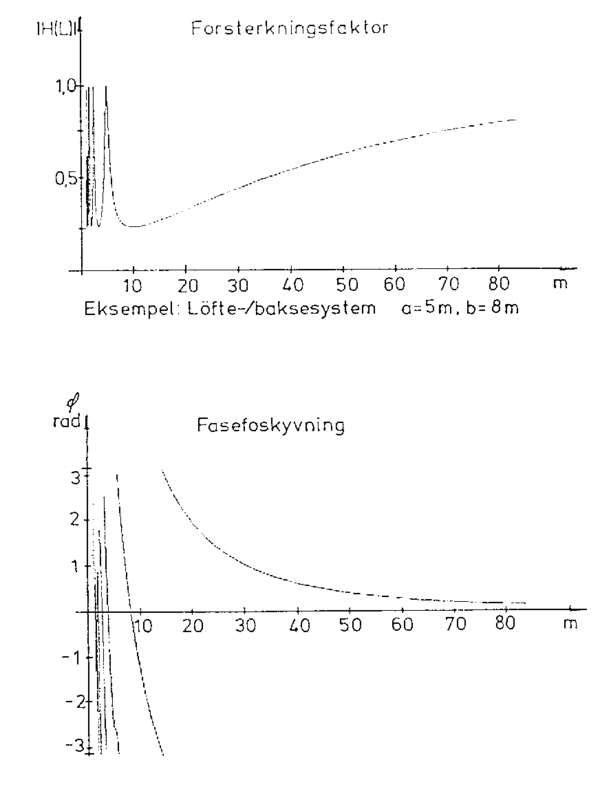
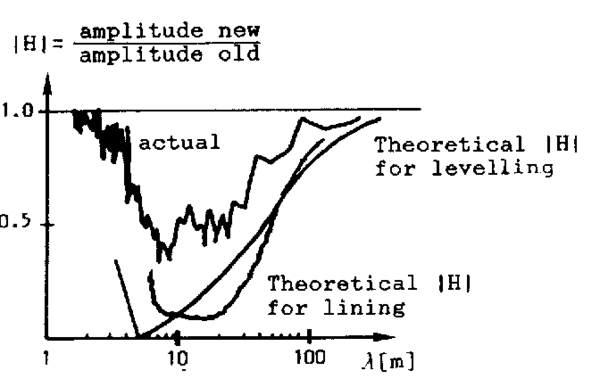
Figur 20 viser et eksempel på en overføringsfunksjon for løft og baks, der også faseforskyvningen for de ulike bølgelengdene er angitt. | Figur 20 viser et eksempel på en overføringsfunksjon for løft og baks, der også faseforskyvningen for de ulike bølgelengdene er angitt. | ||
[[Fil:L53404-20.png|600px]] | [[Fil:L53404-20.png|center|600px]] | ||
''Figur 4.20: Eksempel på overføringsfunksjon for løft/baks'' | ''Figur 4.20: Eksempel på overføringsfunksjon for løft/baks'' | ||
| Linje 507: | Linje 496: | ||
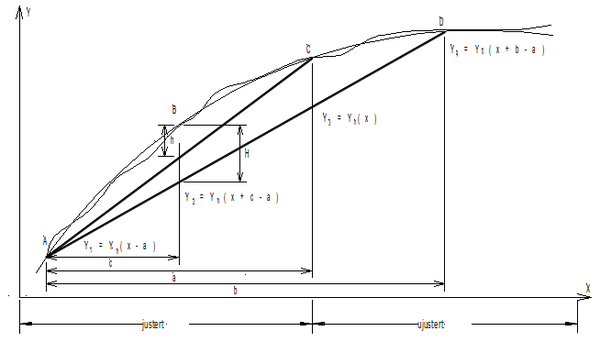
Ved automatbaks følger altså den fremste sensoren, i punkt D, det ujusterte sporet, mens punktene A og B går på nyjustert spor. Dette er indikert i figuren med hhv. ordinatene Y<sub>o</sub> og Y<sub>n</sub> (opprinnelig og ny). Lengdene a, b og c er kjente, så posisjonen til C kan uttrykkes ved posisjonene til A, B og D. På en tilsvarende måte som for 3-punktsmetoden kan vi uttrykke den nye beliggenheten som en funksjon av den gamle: | Ved automatbaks følger altså den fremste sensoren, i punkt D, det ujusterte sporet, mens punktene A og B går på nyjustert spor. Dette er indikert i figuren med hhv. ordinatene Y<sub>o</sub> og Y<sub>n</sub> (opprinnelig og ny). Lengdene a, b og c er kjente, så posisjonen til C kan uttrykkes ved posisjonene til A, B og D. På en tilsvarende måte som for 3-punktsmetoden kan vi uttrykke den nye beliggenheten som en funksjon av den gamle: | ||
<math>\begin{array}{c}{Y}_{n}\left(x)={\text{KY}}_{n}\right(x-a+c)+\left(\frac{b-a-K\left(b-c\right)}{b}\right){Y}_{n}\left(x-a\right) | <math>\begin{array}{c}{Y}_{n}\left(x)={\text{KY}}_{n}\right(x-a+c)+\left(\frac{b-a-K\left(b-c\right)}{b}\right){Y}_{n}\left(x-a\right)+\frac{a-\text{Kc}}{b}{Y}_{o}\left(x+b-a\right)\end{array}</math> ''(25)'' | ||
+\frac{a-\text{Kc}}{b}{Y}_{o}\left(x+b-a\right)\end{array}</math>''(25)'' | |||
Selv om maskinen klarer seg uten innlesing av kurveradius inne i sirkelkurver, må derimot den fremste sensoren (D) påføres en korreksjonsverdi for å oppnå riktig resultat ved overgang fra rettlinje til sirkelkurve, eller omvendt. Noe av det samme gjelder når maskinen passerer en overgangskurve. Pilhøydene endres kontinuerlig fra fremre målepunkt går inn i overgangskurven til bakereste målepunkt forlater overgangskurven. Når alle målepunktene er inne i overgangskurven er ''endringshastigheten'' til pilhøydene konstant. Vi må altså kjenne kurvaturen ved justering også når vi anvender 4-punktsmetoden. Samtidig med korreksjonene er det viktig å merke start- og sluttpunkt for de enkelte traseringselementene på sporet. | Selv om maskinen klarer seg uten innlesing av kurveradius inne i sirkelkurver, må derimot den fremste sensoren (D) påføres en korreksjonsverdi for å oppnå riktig resultat ved overgang fra rettlinje til sirkelkurve, eller omvendt. Noe av det samme gjelder når maskinen passerer en overgangskurve. Pilhøydene endres kontinuerlig fra fremre målepunkt går inn i overgangskurven til bakereste målepunkt forlater overgangskurven. Når alle målepunktene er inne i overgangskurven er ''endringshastigheten'' til pilhøydene konstant. Vi må altså kjenne kurvaturen ved justering også når vi anvender 4-punktsmetoden. Samtidig med korreksjonene er det viktig å merke start- og sluttpunkt for de enkelte traseringselementene på sporet. | ||
| Linje 515: | Linje 503: | ||
Overføringsfunksjonen mellom gammel og ny geometri som kan utledes ved Fourier-transformasjon blir følgende: | Overføringsfunksjonen mellom gammel og ny geometri som kan utledes ved Fourier-transformasjon blir følgende: | ||
<math>H(\lambda )=\frac{\frac{a-\text{Kc}}{b}{x}^{b-a}}{1-{\mathit{Kx}}^{-a+c}-\left(\frac{b-a-K\left(b-c\right)}{b}\right){x}^{-a}}</math>''(26)'' | <math>H(\lambda )=\frac{\frac{a-\text{Kc}}{b}{x}^{b-a}}{1-{\mathit{Kx}}^{-a+c}-\left(\frac{b-a-K\left(b-c\right)}{b}\right){x}^{-a}}</math> ''(26)'' | ||
Fig. 21 viser både teoretisk og virkelig overføringsfunksjon for både løft ved 3-punkts- og baks ved 4-punktsmetoden for pakkmaskinen Plasser & Theurer 07-32. | Fig. 21 viser både teoretisk og virkelig overføringsfunksjon for både løft ved 3-punkts- og baks ved 4-punktsmetoden for pakkmaskinen Plasser & Theurer 07-32. | ||
| Linje 526: | Linje 514: | ||
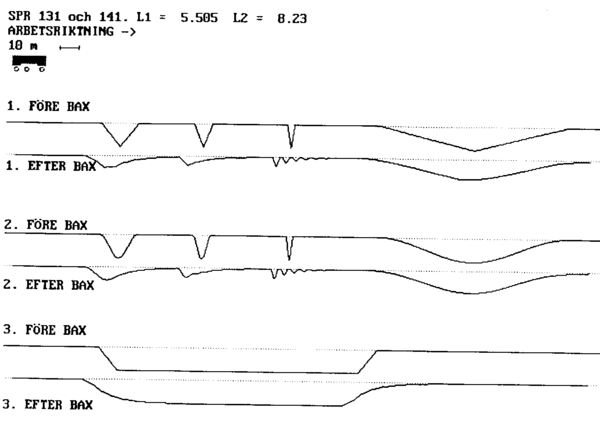
Under er vist et par praktiske eksempler på baks med ulike pakkmaskiner. Både 3-punkts og 4-punktsbaks er benyttet, og første eksempel kan derfor i stor grad sidestilles med løft etter samme metode. | Under er vist et par praktiske eksempler på baks med ulike pakkmaskiner. Både 3-punkts og 4-punktsbaks er benyttet, og første eksempel kan derfor i stor grad sidestilles med løft etter samme metode. | ||
[[Fil:L53404-22.png|600px]] | [[Fil:L53404-22.png|center|600px]] | ||
''Figur 22: Praktisk eksempel: Baks etter 3-punktsmetoden'' | ''Figur 22: Praktisk eksempel: Baks etter 3-punktsmetoden'' | ||
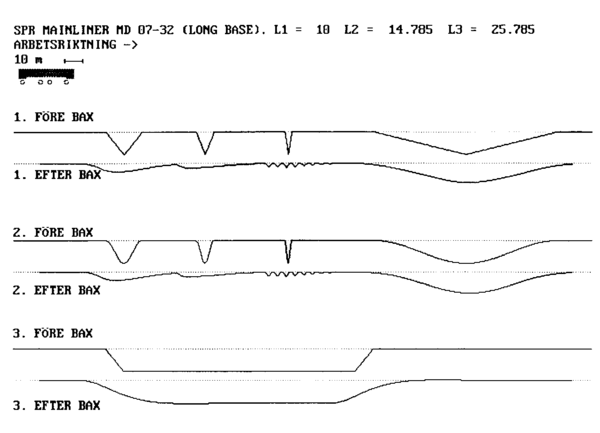
[[Fil:L53404-23.png|600px]] | [[Fil:L53404-23.png|center|600px]] | ||
''Figur 23: Praktisk eksempel: Baks med 4-punktsmetoden'' | ''Figur 23: Praktisk eksempel: Baks med 4-punktsmetoden'' | ||
| Linje 539: | Linje 527: | ||
Bakseaggregatet er som regel sammenbygget med løfteanordningen og består av ruller med dobbelte flenser. Vha. hydrauliske sylindre forskyves skinnegangen sidevegs i ønsket retning. | Bakseaggregatet er som regel sammenbygget med løfteanordningen og består av ruller med dobbelte flenser. Vha. hydrauliske sylindre forskyves skinnegangen sidevegs i ønsket retning. | ||
[[Fil:L53404-24.jpg|600px]] | [[Fil:L53404-24.jpg|center|600px]] | ||
''Figur 24 Løfte- og baksemekanisme'' | ''Figur 24 Løfte- og baksemekanisme'' | ||
| Linje 545: | Linje 533: | ||
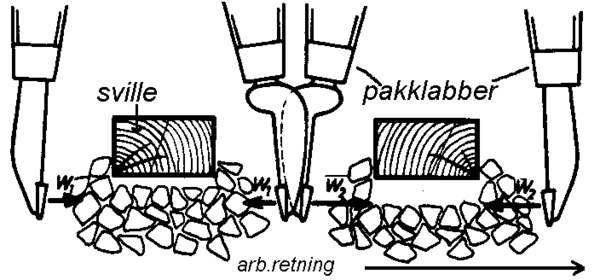
Selve pakkingen skal sørge for å gjenopprette noe av den stabiliteten vi må gi avkall på under justeringen. Prinsippet er illustrert i figur 25. Dog kan ikke sporet lenger regnes som stabilt etter større justeringer. Bestemmelser i forbindelse med stabilitet blir omtalt nærmere i avsnitt 6. | Selve pakkingen skal sørge for å gjenopprette noe av den stabiliteten vi må gi avkall på under justeringen. Prinsippet er illustrert i figur 25. Dog kan ikke sporet lenger regnes som stabilt etter større justeringer. Bestemmelser i forbindelse med stabilitet blir omtalt nærmere i avsnitt 6. | ||
[[Fil:L53404-25.png|600px]] | [[Fil:L53404-25.png|center|600px]] | ||
''Figur 25: Prinsipp for pakking: klemkraft og vibrasjon'' | ''Figur 25: Prinsipp for pakking: klemkraft og vibrasjon'' | ||
| Linje 557: | Linje 545: | ||
Ved maskinell justering er det viktig å påpeke at maskinen, og således målesystemet, ferdes på et spor allerede beheftet med sporgeometriske feil. Fig. 26 illustrerer hva dette kan medføre på rettspor. | Ved maskinell justering er det viktig å påpeke at maskinen, og således målesystemet, ferdes på et spor allerede beheftet med sporgeometriske feil. Fig. 26 illustrerer hva dette kan medføre på rettspor. | ||
[[Fil:L53404-26.png|600px]] | [[Fil:L53404-26.png|center|600px]] | ||
''Figur 26 Målepunkter ved 3- punktsmetoden - feilkilder'' | ''Figur 26 Målepunkter ved 3- punktsmetoden - feilkilder'' | ||
| Linje 563: | Linje 551: | ||
I figuren blir feilen i B justert riktig til B’, men vi ser at når målepunktet A kommer til punktet S, vil målebasisen stå skjevt i forhold til rettlinjen. Hvis ikke maskinen er programmert på forhånd eller benytter ytre referanser utenfor vogna, men styres etter automatbaks, vil maskinen lage en feil i justeringspunktet B (når A har forflyttet seg til S). På tilsvarende måte vil automatbaks etter 4-punktsmetoden heller aldri justere sporet til å bli helt feilfritt. | I figuren blir feilen i B justert riktig til B’, men vi ser at når målepunktet A kommer til punktet S, vil målebasisen stå skjevt i forhold til rettlinjen. Hvis ikke maskinen er programmert på forhånd eller benytter ytre referanser utenfor vogna, men styres etter automatbaks, vil maskinen lage en feil i justeringspunktet B (når A har forflyttet seg til S). På tilsvarende måte vil automatbaks etter 4-punktsmetoden heller aldri justere sporet til å bli helt feilfritt. | ||
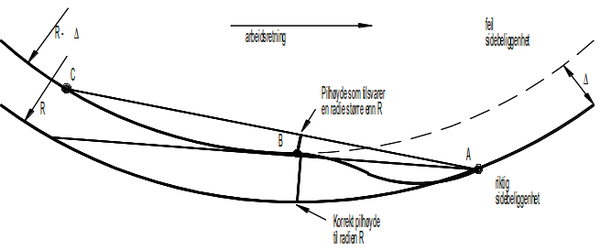
Hvis en feilaktig radius leses inn i systemet i en kurve, får vi en baksefeil. Denne feilen vil asymptotisk nærme seg verdien | Hvis en feilaktig radius leses inn i systemet i en kurve, får vi en baksefeil. Denne feilen vil asymptotisk nærme seg verdien Δ, jf. fig. 27. Som figuren viser, blir baksefeilen i tillegg langt større enn pilhøydefeilen som er innlest. | ||
[[Fil:L53404-27.png|600px]] | [[Fil:L53404-27.png|center|600px]] | ||
''Figur 27: Baksefeil ved innlesing av feil radius - 3-punktsmetoden'' | ''Figur 27: Baksefeil ved innlesing av feil radius - 3-punktsmetoden'' | ||
| Linje 571: | Linje 559: | ||
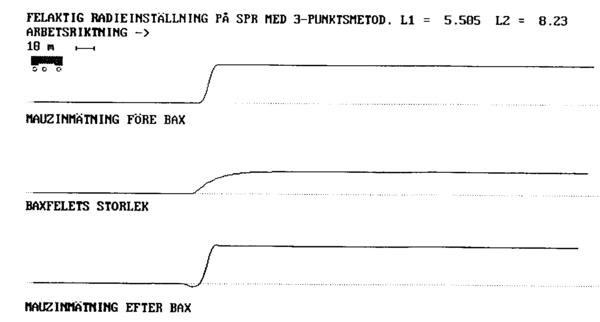
Figur 28 viser et praktisk eksempel på effekten av baksefeil: | Figur 28 viser et praktisk eksempel på effekten av baksefeil: | ||
[[Fil:L53404-28.png|600px]] | [[Fil:L53404-28.png|center|600px]] | ||
''Figur 28: Eksempel på baksefeil ved feil radius - SPR 131'' | ''Figur 28: Eksempel på baksefeil ved feil radius - SPR 131'' | ||
| Linje 580: | Linje 568: | ||
=== Overføringsfunksjonene === | === Overføringsfunksjonene === | ||
En rekke målinger har blitt utført for ulike pakkmaskiner for å kartlegge den såkalte virkelige overføringsfunksjonen. På grunnlag av målinger i sporet ''like etter'' justering/pakking, har funksjoner som den vist i fig | En rekke målinger har blitt utført for ulike pakkmaskiner for å kartlegge den såkalte virkelige overføringsfunksjonen. På grunnlag av målinger i sporet ''like etter'' justering/pakking, har funksjoner som den vist i fig. 21 fremkommet. Fra denne kan man raskt konkludere med at forbedringene etter justering bare er rundt halvparten av det teorien skulle tilsi. I tillegg må det også nevnes at et helt nyjustert spors beliggenhet endres signifikant i den nærmeste tiden etter justering. | ||
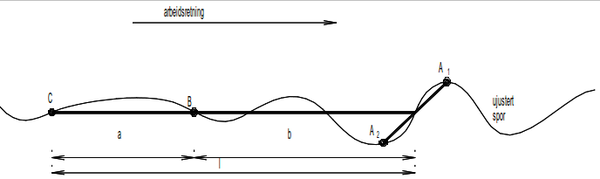
Men vi kan til en viss grad kompensere for overføringsfunksjonenes mangel på fortreffelighet. Ved å dele opp fremre målepunkt A i to målepunkter A<sub>1</sub> og A<sub>2</sub>, kan vi interpolere fram en verdi på A fra disse, som vist i figur | Men vi kan til en viss grad kompensere for overføringsfunksjonenes mangel på fortreffelighet. Ved å dele opp fremre målepunkt A i to målepunkter A<sub>1</sub> og A<sub>2</sub>, kan vi interpolere fram en verdi på A fra disse, som vist i figur 29. Selv om vi i dette benytter totalt 4 målepunkt i praksis, er det fortsatt 3-punktsmetoden maskinen arbeider etter. Som figuren illustrerer, vil periodiske feil med bølgelengde lik 2 ganger avstanden mellom de nye målepunktene reduseres helt. | ||
[[Fil:L53404-29.png|600px]] | [[Fil:L53404-29.png|center|600px]] | ||
''Figur 29: Todeling av fremre målepunkt for forbedret overføringsfunksjon'' | ''Figur 29: Todeling av fremre målepunkt for forbedret overføringsfunksjon'' | ||
| Linje 593: | Linje 581: | ||
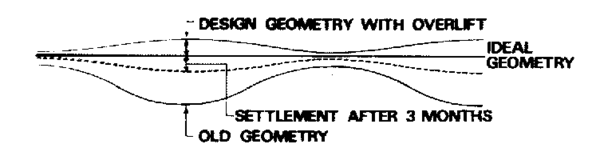
Etter en stund med slike deformasjoner fra nyjustert spor, stabiliserer beliggenheten seg. Men denne prosessen kan pr. definisjon aldri opprettholde eksempelvis en ideell rettlinje i vertikalplanet. For at dette skal bli mulig, må beregningen baseres på et overløft der det er kalkulert med de ovennevnte setningene. | Etter en stund med slike deformasjoner fra nyjustert spor, stabiliserer beliggenheten seg. Men denne prosessen kan pr. definisjon aldri opprettholde eksempelvis en ideell rettlinje i vertikalplanet. For at dette skal bli mulig, må beregningen baseres på et overløft der det er kalkulert med de ovennevnte setningene. | ||
[[Fil:L53404-30.png|600px]] | [[Fil:L53404-30.png|center|600px]] | ||
''Figur 30 Prinsipp for overløft som kompenserer for forutsette setninger'' | ''Figur 30 Prinsipp for overløft som kompenserer for forutsette setninger'' | ||
| Linje 604: | Linje 592: | ||
''Tabell 2: Ulike prinsipper for justering til absolutt beliggenhet for noen forvaltninger i Europa.'' | ''Tabell 2: Ulike prinsipper for justering til absolutt beliggenhet for noen forvaltninger i Europa.'' | ||
{| class="wikitable" testyle="text-align: center | |||
{| | |- | ||
! Justerings-/måleprinsipp !! Forvaltning !! System | |||
|- | |- | ||
| | | '''Utfesting for justering –''' | ||
'''Geodetisk innmåling av spor''' | |||
| | || JBV | ||
DB (Tyskland) | DB (Tyskland) | ||
| Linje 620: | Linje 605: | ||
BV (Sverige) | BV (Sverige) | ||
SNCF (Frankrike) | SNCF (Frankrike) | ||
| | || VUL/GVUL | ||
SurVer - ZVS/GPS | SurVer - ZVS/GPS | ||
|- | |- | ||
| | | '''“Langsehne”''' || DB (Tyskland) | ||
| | |||
NS (Holland) | NS (Holland) | ||
| Linje 635: | Linje 618: | ||
SBB (Sveits) | SBB (Sveits) | ||
ÖBB (Østerrike) | ÖBB (Østerrike) | ||
| | || Driver | ||
Båglaser | Båglaser | ||
|- | |- | ||
| | | '''Integrert måling og justering''' || SBB (Sveits) || Palas | ||
| | |} | ||
| | |||
== Ulike metoder for absolutt justering == | == Ulike metoder for absolutt justering == | ||
=== Utfesting/geodetisk innmåling === | === Utfesting/geodetisk innmåling === | ||
Som måleprinsippet uttrykker, er dette en metode der den aktuelle strekningens faktiske beliggenhet koordinatbestemmes geodetisk, i praksis ved bruk av teodolitt/totalstasjon eller GPS-utstyr. Den teoretiske beliggenheten er koordinatbestemt fra før, og avvikene mellom de to danner grunnlag for løfte-/bakseverdier. Videre kan disse verdiene enten listes, for senere å lese inn manuelt, eller lagres på et dataformat som kan leses av et dataprogram ombord i pakkmaskinen. | Som måleprinsippet uttrykker, er dette en metode der den aktuelle strekningens faktiske beliggenhet koordinatbestemmes geodetisk, i praksis ved bruk av teodolitt/totalstasjon eller GPS-utstyr. Den teoretiske beliggenheten er koordinatbestemt fra før, og avvikene mellom de to danner grunnlag for løfte-/bakseverdier. Videre kan disse verdiene enten listes, for senere å lese inn manuelt, eller lagres på et dataformat som kan leses av et dataprogram ombord i pakkmaskinen. | ||
Ved JBV har vi to metoder for varig utfesting av linjen: VUL og GVUL, som er nærmere beskrevet i | Ved JBV har vi to metoder for varig utfesting av linjen: VUL og GVUL, som er nærmere beskrevet i [[Utfesting av linjen]]. Begge metoder benyttes til å kartlegge sporets absolutte beliggenhet i et ytre referansesystem og kan dermed også benyttes til å regne ut justeringsverdier. | ||
På høyhastighetsbaner (K0) er sporet utfestet med GVUL og dermed koordinatbestemt gjennom en teknisk linjeberegning. Fremgangsmåten der det er utfestet med GVUL blir i første omgang å måle inn sporet fra et geodetisk fastmerkenett. Sporet er teknisk linjeberegnet for sporets ''senterlinje'', og denne må følgelig også måles inn før justering. Til dette kan det benyttes en tralle som kan skyves langs sporet. På tralla er montert et en prismestav hvis fot har beliggenheten spormidt, i grunnriss. Alternativt måles begge skinnestrenger og senterlinjen beregnes i etterkant. Sporets høyde er definert til å være høyden til laveste skinnestreng. Ved bruk av tralla må også instrument for måling av overhøyden benyttes. De samlede måledata gir deretter grunnlaget for justering. | På høyhastighetsbaner (K0) er sporet utfestet med GVUL og dermed koordinatbestemt gjennom en teknisk linjeberegning. Fremgangsmåten der det er utfestet med GVUL blir i første omgang å måle inn sporet fra et geodetisk fastmerkenett. Sporet er teknisk linjeberegnet for sporets ''senterlinje'', og denne må følgelig også måles inn før justering. Til dette kan det benyttes en tralle som kan skyves langs sporet. På tralla er montert et en prismestav hvis fot har beliggenheten spormidt, i grunnriss. Alternativt måles begge skinnestrenger og senterlinjen beregnes i etterkant. Sporets høyde er definert til å være høyden til laveste skinnestreng. Ved bruk av tralla må også instrument for måling av overhøyden benyttes. De samlede måledata gir deretter grunnlaget for justering. | ||
| Linje 678: | Linje 658: | ||
Ved de franske høyhastighetsbanene, SNCF’s TGV, er det utviklet et system som ligner vår egen utfestingsmetode VUL, men det franske systemet holder en langt høyere nøyaktighet pga. de høye hastighetene (300 km/h+). | Ved de franske høyhastighetsbanene, SNCF’s TGV, er det utviklet et system som ligner vår egen utfestingsmetode VUL, men det franske systemet holder en langt høyere nøyaktighet pga. de høye hastighetene (300 km/h+). | ||
[[Fil:L53404-31.jpg|400px]] | [[Fil:L53404-31.jpg|center|400px]] | ||
''Figur 31: Franske TGV med fastmerker mellom sporene'' | ''Figur 31: Franske TGV med fastmerker mellom sporene'' | ||
| Linje 699: | Linje 679: | ||
Som vi ser er dette en on-line prosedyre der justeringen skjer i umiddelbar ettertid av måling. Et problem er dermed at vi ikke har noen kontroll med referansepunktenes kvalitet, f.eks. med hensyn til setninger i mastene de er montert på. I og med at justering foregår fra punkt til punkt, vil evt. feil i referansepunktene, eller feil innstilling av lasersenderens posisjon, kunne medføre langbølgede feil i sporet som vil forplante seg bortover. Lasermålesystemet har heller ingen korreksjoner innlagt for effekter som refraksjon og jordkrumming. | Som vi ser er dette en on-line prosedyre der justeringen skjer i umiddelbar ettertid av måling. Et problem er dermed at vi ikke har noen kontroll med referansepunktenes kvalitet, f.eks. med hensyn til setninger i mastene de er montert på. I og med at justering foregår fra punkt til punkt, vil evt. feil i referansepunktene, eller feil innstilling av lasersenderens posisjon, kunne medføre langbølgede feil i sporet som vil forplante seg bortover. Lasermålesystemet har heller ingen korreksjoner innlagt for effekter som refraksjon og jordkrumming. | ||
[[Fil:L53404-32.png|600px]] | [[Fil:L53404-32.png|center|600px]] | ||
| Linje 706: | Linje 686: | ||
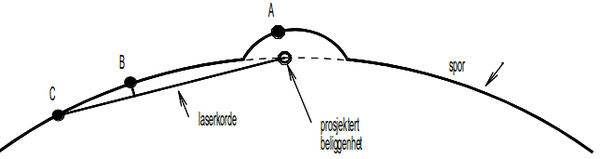
Ved JBV har også laser blitt anvendt ved justering, men da kun for korrigering av rettlinjer. Figur .33 illustrerer prinsippet. I dette tilfellet forholder vi oss ikke til et koordinatbestemt spor, slik at bakseverdier beregnes utfra en laserkorde, men setter opp senderen i enden av en rettlinje. Videre må pakkmaskinen ha korrekt sidebeliggenhet, slik at rettlinjen som oppnås sammenfaller med teoretisk beliggenhet. | Ved JBV har også laser blitt anvendt ved justering, men da kun for korrigering av rettlinjer. Figur .33 illustrerer prinsippet. I dette tilfellet forholder vi oss ikke til et koordinatbestemt spor, slik at bakseverdier beregnes utfra en laserkorde, men setter opp senderen i enden av en rettlinje. Videre må pakkmaskinen ha korrekt sidebeliggenhet, slik at rettlinjen som oppnås sammenfaller med teoretisk beliggenhet. | ||
[[Fil:L53404-33.png|600px]] | [[Fil:L53404-33.png|center|600px]] | ||
''Figur 33: Justering med laser på rettlinje'' | ''Figur 33: Justering med laser på rettlinje'' | ||
| Linje 732: | Linje 712: | ||
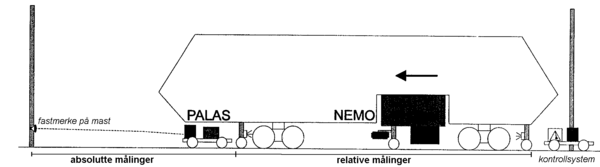
Til slutt samordnes det koordinatbaserte måle- og justeringssystemet (Palas) med et pilhøydebasert system for glatting (NEMO) for å styre løft og baks. I praksis rettes fremste sensor i NEMO inn etter Palas’ beregningsresultater. | Til slutt samordnes det koordinatbaserte måle- og justeringssystemet (Palas) med et pilhøydebasert system for glatting (NEMO) for å styre løft og baks. I praksis rettes fremste sensor i NEMO inn etter Palas’ beregningsresultater. | ||
[[Fil:L53404-34.png|600px]] | [[Fil:L53404-34.png|center|600px]] | ||
''Figur 34: Prinsippskisse for integrert måle- og justeringsmaskin ved SBB'' | ''Figur 34: Prinsippskisse for integrert måle- og justeringsmaskin ved SBB'' | ||
| Linje 768: | Linje 748: | ||
Ovennevnte hastighetsreduksjoner er ikke nødvendig ved bruk av dynamisk sporstabilisator etter arbeidene. | Ovennevnte hastighetsreduksjoner er ikke nødvendig ved bruk av dynamisk sporstabilisator etter arbeidene. | ||
[[Fil: | [[Fil:Sporstabilistaor.jpg|center|400px]] | ||
''Figur 35: Dynamisk sporstabilisator'' | ''Figur 35: Dynamisk sporstabilisator'' | ||
| Linje 786: | Linje 766: | ||
== Sikring mot solslyng == | == Sikring mot solslyng == | ||
For pakking/baksing av helsveist spor gjelder temperaturbegrensninger som er fastsatt i | For pakking/baksing av helsveist spor gjelder temperaturbegrensninger som er fastsatt i [https://trv.jbv.no/wiki/Overbygning/Vedlikehold/Sporjustering_og_stabilisering#Krav_til_sporarbeider Teknisk regelverk - Krav til sporarbeider]. | ||
Ved grove sporfeil der akuttgrensene for vindskjevhet eller sidefeil er overskredet, begrenses justeringen til vedkommende steder og hastighetsreduksjoner gjennomføres i hht. nedenstående punkter. | Ved grove sporfeil der akuttgrensene for vindskjevhet eller sidefeil er overskredet, begrenses justeringen til vedkommende steder og hastighetsreduksjoner gjennomføres i hht. nedenstående punkter. | ||
Dersom ballastprofilet tilfredsstiller betingelsene som er angitt i | Dersom ballastprofilet tilfredsstiller betingelsene som er angitt i [https://trv.jbv.no/wiki/Overbygning/Prosjektering/Ballast Teknisk regelverk - Ballast], skal det etter pakking/baksing i helsveist spor med kurveradier mindre enn 400 m gjennomføres hastighetsreduksjon til 40 km/h eller mindre på alle dager når skinnetemperaturen er over 30<sup>0</sup>C eller kan ventes å bli større enn 30<sup>0</sup>C. Dette gjelder inntil det har passert en samlet trafikkmengde på 50000 bruttotonn siden pakking/baksing ble foretatt. | ||
Hastighetsnedsettelsene er ikke nødvendig ved bruk av dynamisk sporstabilisator. | Hastighetsnedsettelsene er ikke nødvendig ved bruk av dynamisk sporstabilisator. | ||
Dersom ballastprofilet har mindre dimensjoner enn angitt i | Dersom ballastprofilet har mindre dimensjoner enn angitt i [https://trv.jbv.no/wiki/Overbygning/Prosjektering/Ballast Teknisk regelverk - Ballast], skal det etter pakking/baksing i helsveist spor med kurveradier mindre enn 400 m gjennomføres hastighetsnedsettelse til 40 km/h eller mindre inntil det har passert en samlet trafikkmengde på 50000 bruttotonn. Dette gjelder uansett skinnetemperatur. | ||
Ovenstående regler gjelder også for lasket spor med skinnelengder over 30m. | Ovenstående regler gjelder også for lasket spor med skinnelengder over 30m. | ||
| Linje 803: | Linje 783: | ||
== Bakseberegning med BAKSBER == | == Bakseberegning med BAKSBER == | ||
Beregnet dato: 28 - 9 1999 | Beregnet dato: 28 - 9 1999 | ||
UTJEVNINGSGRAD = 0 | |||
UTJEVNINGSGRAD = 0 | FILNAVN = lill1401.bax | ||
KILO- MÅLT ØNSKET NY BAKSVERDIER BAKSEKORRIDOR | |||
FILNAVN = lill1401.bax | METER PILH PILH PILH VENSTRE HØYRE VENSTRE HØYRE | ||
---------------------------------------------------------------- | |||
KILO- MÅLT ØNSKET NY BAKSVERDIER BAKSEKORRIDOR | 24780 -.2 .0 -2.0 0. 100 100 | ||
24790 -3.7 .0 -1.6 4. 100 100 | |||
METER PILH PILH PILH VENSTRE HØYRE VENSTRE HØYRE | 24800 -.2 .0 -1.1 3. 100 100 | ||
24810 -5.7 -3.4 -4.1 4. 100 100 | |||
24820 -5.9 -6.8 -7.1 2. 100 100 | |||
24830 -11.4 -10.2 -10.2 2. 100 100 | |||
24840 -13.2 -13.6 -13.5 0. 100 100 | |||
24850 -13.8 -17.1 -17.0 1. 100 100 | |||
24860 -23.4 -20.5 -20.4 3. 100 100 | |||
24870 -25.7 -23.9 -23.9 2. 100 100 | |||
24880 -25.3 -27.3 -27.3 3. 100 100 | |||
24890 -28.5 -27.3 -27.3 3. 100 100 | |||
24900 -28.3 -27.3 -27.4 7. 100 100 | |||
24910 -24.3 -27.3 -27.4 12. 100 100 | |||
24920 -25.7 -27.3 -27.4 11. 100 100 | |||
24930 -27.6 -27.3 -27.5 6. 100 100 | |||
24940 -27.0 -27.3 -27.5 2. 100 100 | |||
24950 -27.5 -27.3 -27.6 3. 100 100 | |||
24960 -28.8 -27.3 -27.6 8. 100 100 | |||
24970 -25.1 -27.3 -27.7 11. 100 100 | |||
24980 -31.1 -27.3 -27.8 20. 100 100 | |||
24990 -26.9 -27.3 -27.8 21. 100 100 | |||
25000 -29.6 -27.3 -27.9 24. 100 100 | |||
25010 -29.2 -27.3 -28.0 24. 100 100 | |||
25020 -26.4 -27.3 -28.1 22. 100 100 | |||
25030 -33.2 -27.3 -28.1 23. 100 100 | |||
25040 -28.5 -27.3 -28.2 14. 100 100 | |||
25050 -25.5 -27.3 -28.2 4. 100 100 | |||
25060 -26.6 -27.3 -28.1 1. 100 100 | |||
24800 -.2 .0 -1.1 3. 100 100 | 25070 -28.9 -27.3 -27.9 2. 100 100 | ||
25080 -25.9 -27.3 -27.8 5. 100 100 | |||
24810 -5.7 -3.4 -4.1 4. 100 100 | 25090 -29.6 -27.3 -27.6 5. 100 100 | ||
25100 -27.0 -27.3 -27.4 9. 100 100 | |||
24820 -5.9 -6.8 -7.1 2. 100 100 | 25110 -27.0 -27.3 -27.2 12. 100 100 | ||
25120 -27.8 -27.3 -27.1 14. 100 100 | |||
24830 -11.4 -10.2 -10.2 2. 100 100 | 25130 -26.9 -27.3 -26.9 18. 100 100 | ||
25140 -22.2 -27.3 -26.7 22. 100 100 | |||
24840 -13.2 -13.6 -13.5 0. 100 100 | 25150 -24.4 -27.3 -26.6 16. 100 100 | ||
25160 -28.9 -27.3 -26.4 7. 100 100 | |||
24850 -13.8 -17.1 -17.0 1. 100 100 | 25170 -26.8 -27.3 -26.4 2. 100 100 | ||
25180 -28.7 -27.3 -26.5 1. 100 100 | |||
24860 -23.4 -20.5 -20.4 3. 100 100 | 25190 -25.6 -27.3 -26.6 1. 100 100 | ||
25200 -27.1 -27.3 -26.6 2. 100 100 | |||
24870 -25.7 -23.9 -23.9 2. 100 100 | 25210 -26.8 -27.3 -26.7 3. 100 100 | ||
25220 -25.4 -27.3 -26.7 3. 100 100 | |||
24880 -25.3 -27.3 -27.3 3. 100 100 | 25230 -30.1 -27.3 -26.8 5. 100 100 | ||
25240 -26.1 -27.3 -26.8 2. 100 100 | |||
24890 -28.5 -27.3 -27.3 3. 100 100 | 25250 -28.4 -27.3 -26.9 1. 100 100 | ||
25260 -23.8 -27.3 -27.0 6. 100 100 | |||
24900 -28.3 -27.3 -27.4 7. 100 100 | 25270 -28.1 -27.3 -27.0 5. 100 100 | ||
25280 -25.7 -27.3 -27.1 6. 100 100 | |||
24910 -24.3 -27.3 -27.4 12. 100 100 | 25290 -28.6 -27.3 -27.1 5. 100 100 | ||
25300 -27.0 -27.3 -27.1 6. 100 100 | |||
24920 -25.7 -27.3 -27.4 11. 100 100 | 25310 -25.6 -27.3 -27.2 7. 100 100 | ||
25320 -26.8 -27.3 -27.2 5. 100 100 | |||
24930 -27.6 -27.3 -27.5 6. 100 100 | 25330 -28.0 -27.3 -27.2 3. 100 100 | ||
25340 -28.5 -29.0 -29.0 1. 100 100 | |||
24940 -27.0 -27.3 -27.5 2. 100 100 | 25350 -28.3 -30.7 -30.7 1. 100 100 | ||
25360 -36.2 -32.4 -32.4 8. 100 100 | |||
24950 -27.5 -27.3 -27.6 3. 100 100 | 25370 -31.8 -32.4 -32.5 7. 100 100 | ||
25380 -34.7 -32.4 -32.5 8. 100 100 | |||
24960 -28.8 -27.3 -27.6 8. 100 100 | 25390 -30.8 -32.4 -32.5 4. 100 100 | ||
25400 -33.8 -32.4 -32.5 4. 100 100 | |||
24970 -25.1 -27.3 -27.7 11. 100 100 | 25410 -34.9 -32.4 -32.6 1. 100 100 | ||
25420 -30.6 -32.4 -32.6 7. 100 100 | |||
24980 -31.1 -27.3 -27.8 20. 100 100 | 25430 -31.5 -32.4 -32.6 10. 100 100 | ||
25440 -33.0 -32.4 -32.6 11. 100 100 | |||
24990 -26.9 -27.3 -27.8 21. 100 100 | 25450 -30.4 -32.4 -32.7 13. 100 100 | ||
25460 -31.1 -32.4 -32.7 11. 100 100 | |||
25000 -29.6 -27.3 -27.9 24. 100 100 | 25470 -33.4 -32.4 -32.7 5. 100 100 | ||
25480 -30.4 -32.4 -32.7 1. 100 100 | |||
25010 -29.2 -27.3 -28.0 24. 100 100 | 25490 -35.9 -32.4 -32.7 8. 100 100 | ||
25500 -31.1 -32.4 -32.7 11. 100 100 | |||
25020 -26.4 -27.3 -28.1 22. 100 100 | 25510 -35.7 -32.4 -32.6 17. 100 100 | ||
25520 -35.5 -32.4 -32.6 16. 100 100 | |||
25030 -33.2 -27.3 -28.1 23. 100 100 | 25530 -29.1 -32.4 -32.5 10. 100 100 | ||
25540 -32.8 -32.4 -32.4 11. 100 100 | |||
25040 -28.5 -27.3 -28.2 14. 100 100 | 25550 -33.0 -32.4 -32.4 11. 100 100 | ||
25560 -35.3 -32.4 -32.3 9. 100 100 | |||
25050 -25.5 -27.3 -28.2 4. 100 100 | 25570 -32.6 -32.4 -32.2 2. 100 100 | ||
25580 -29.1 -32.4 -32.2 7. 100 100 | |||
25060 -26.6 -27.3 -28.1 1. 100 100 | 25590 -29.9 -32.4 -32.1 9. 100 100 | ||
25600 -33.1 -32.4 -32.0 6. 100 100 | |||
25070 -28.9 -27.3 -27.9 2. 100 100 | 25610 -31.5 -32.4 -32.1 6. 100 100 | ||
25620 -33.9 -32.4 -32.1 5. 100 100 | |||
25080 -25.9 -27.3 -27.8 5. 100 100 | 25630 -31.1 -32.4 -32.2 7. 100 100 | ||
25640 -31.9 -32.4 -32.3 7. 100 100 | |||
25090 -29.6 -27.3 -27.6 5. 100 100 | 25650 -30.3 -32.4 -32.3 6. 100 100 | ||
25660 -33.3 -32.4 -32.4 2. 100 100 | |||
25100 -27.0 -27.3 -27.4 9. 100 100 | 25670 -35.2 -32.4 -32.5 1. 100 100 | ||
25680 -31.3 -32.4 -32.5 1. 100 100 | |||
25110 -27.0 -27.3 -27.2 12. 100 100 | 25690 -33.7 -32.4 -32.6 1. 100 100 | ||
25700 -29.6 -31.4 -31.7 3. 100 100 | |||
25120 -27.8 -27.3 -27.1 14. 100 100 | 25710 -24.9 -26.6 -26.9 1. 100 100 | ||
25720 -24.8 -21.8 -21.9 5. 100 100 | |||
25130 -26.9 -27.3 -26.9 18. 100 100 | 25730 -18.9 -16.9 -16.9 5. 100 100 | ||
25740 -10.1 -12.1 -11.8 1. 100 100 | |||
25140 -22.2 -27.3 -26.7 22. 100 100 | 25750 -.9 -7.3 -6.8 0. 100 100 | ||
25760 -8.4 -2.4 -1.8 11. 100 100 | |||
25150 -24.4 -27.3 -26.6 16. 100 100 | 25770 .4 .0 .9 9. 100 100 | ||
25780 -.6 .0 1.1 6. 100 100 | |||
25160 -28.9 -27.3 -26.4 7. 100 100 | 25790 4.4 .0 1.2 0. 100 100 | ||
---------------------------------------------------------------- | |||
25170 -26.8 -27.3 -26.4 2. 100 100 | SUMME BAKS = 700 STANDARDAVVIK = .50 | ||
25180 -28.7 -27.3 -26.5 1. 100 100 | |||
25190 -25.6 -27.3 -26.6 1. 100 100 | |||
25200 -27.1 -27.3 -26.6 2. 100 100 | |||
25210 -26.8 -27.3 -26.7 3. 100 100 | |||
25220 -25.4 -27.3 -26.7 3. 100 100 | |||
25230 -30.1 -27.3 -26.8 5. 100 100 | |||
25240 -26.1 -27.3 -26.8 2. 100 100 | |||
25250 -28.4 -27.3 -26.9 1. 100 100 | |||
25260 -23.8 -27.3 -27.0 6. 100 100 | |||
25270 -28.1 -27.3 -27.0 5. 100 100 | |||
25280 -25.7 -27.3 -27.1 6. 100 100 | |||
25290 -28.6 -27.3 -27.1 5. 100 100 | |||
25300 -27.0 -27.3 -27.1 6. 100 100 | |||
25310 -25.6 -27.3 -27.2 7. 100 100 | |||
25320 -26.8 -27.3 -27.2 5. 100 100 | |||
25330 -28.0 -27.3 -27.2 3. 100 100 | |||
25340 -28.5 -29.0 -29.0 1. 100 100 | |||
25350 -28.3 -30.7 -30.7 1. 100 100 | |||
25360 -36.2 -32.4 -32.4 8. 100 100 | |||
25370 -31.8 -32.4 -32.5 7. 100 100 | |||
25380 -34.7 -32.4 -32.5 8. 100 100 | |||
25390 -30.8 -32.4 -32.5 4. 100 100 | |||
25400 -33.8 -32.4 -32.5 4. 100 100 | |||
25410 -34.9 -32.4 -32.6 1. 100 100 | |||
25420 -30.6 -32.4 -32.6 7. 100 100 | |||
25430 -31.5 -32.4 -32.6 10. 100 100 | |||
25440 -33.0 -32.4 -32.6 11. 100 100 | |||
25450 -30.4 -32.4 -32.7 13. 100 100 | |||
25460 -31.1 -32.4 -32.7 11. 100 100 | |||
25470 -33.4 -32.4 -32.7 5. 100 100 | |||
25480 -30.4 -32.4 -32.7 1. 100 100 | |||
25490 -35.9 -32.4 -32.7 8. 100 100 | |||
25500 -31.1 -32.4 -32.7 11. 100 100 | |||
25510 -35.7 -32.4 -32.6 17. 100 100 | |||
25520 -35.5 -32.4 -32.6 16. 100 100 | |||
25530 -29.1 -32.4 -32.5 10. 100 100 | |||
25540 -32.8 -32.4 -32.4 11. 100 100 | |||
25550 -33.0 -32.4 -32.4 11. 100 100 | |||
25560 -35.3 -32.4 -32.3 9. 100 100 | |||
25570 -32.6 -32.4 -32.2 2. 100 100 | |||
25580 -29.1 -32.4 -32.2 7. 100 100 | |||
25590 -29.9 -32.4 -32.1 9. 100 100 | |||
25600 -33.1 -32.4 -32.0 6. 100 100 | |||
25610 -31.5 -32.4 -32.1 6. 100 100 | |||
25620 -33.9 -32.4 -32.1 5. 100 100 | |||
25630 -31.1 -32.4 -32.2 7. 100 100 | |||
25640 -31.9 -32.4 -32.3 7. 100 100 | |||
25650 -30.3 -32.4 -32.3 6. 100 100 | |||
25660 -33.3 -32.4 -32.4 2. 100 100 | |||
25670 -35.2 -32.4 -32.5 1. 100 100 | |||
25680 -31.3 -32.4 -32.5 1. 100 100 | |||
25690 -33.7 -32.4 -32.6 1. 100 100 | |||
25700 -29.6 -31.4 -31.7 3. 100 100 | |||
25710 -24.9 -26.6 -26.9 1. 100 100 | |||
25720 -24.8 -21.8 -21.9 5. 100 100 | |||
25730 -18.9 -16.9 -16.9 5. 100 100 | |||
25740 -10.1 -12.1 -11.8 1. 100 100 | |||
25750 -.9 -7.3 -6.8 0. 100 100 | |||
25760 -8.4 -2.4 -1.8 11. 100 100 | |||
25770 .4 .0 .9 9. 100 100 | |||
25780 -.6 .0 1.1 6. 100 100 | |||
25790 4.4 .0 1.2 0. 100 100 | |||
SUMME BAKS = 700 STANDARDAVVIK = .50 | |||
25790 .0 | Nye OB/OE-punkter og radier | ||
Km R | |||
---------------- | |||
24780 .0 | |||
24800 .0 | |||
24880 1831.5 | |||
25330 1831.5 | |||
25360 1543.2 | |||
25698 1543.2 | |||
25765 .0 | |||
25790 .0 | |||
Siste sideversjon per 28. okt. 2021 kl. 08:30
__NUMBEREDHEADINGS__
Innledning
Historikk
Manuell sporjustering
Før sporjusteringsmaskinenes tid var ofte sporjustering et svært krevende arbeid der mye personell var påkrevd. I tillegg til diverse måle- og utfestingsinnretninger måtte det nokså mange personer til for å flytte sporet vha. spett og pakke ballasten med spade og rive.
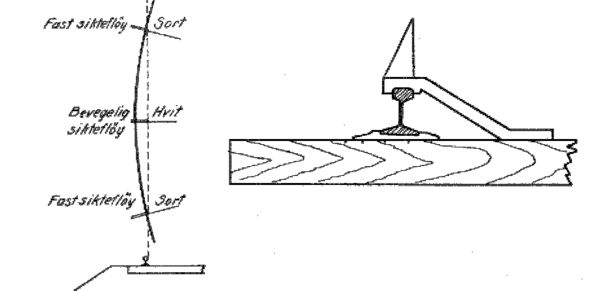
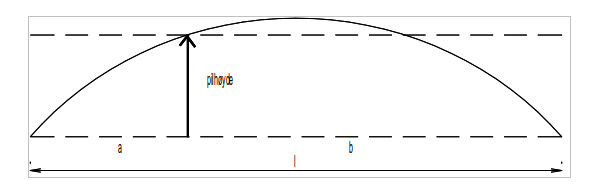
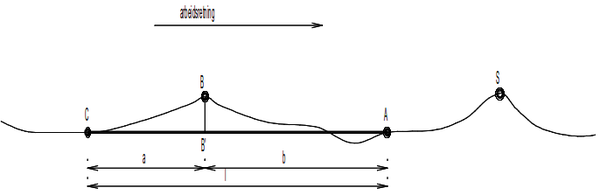
En enkel måte å korrigere skinnegangen på var å anvende et apparat som eksempelvis banemester Schives: Tre sikteskiver, hvorav den midterste kunne beveges et kordeavsett som svarte til kordelengden og den aktuelle radien, ble rettet inn så de tre siktene lå på linje. En slik operasjon krevde imidlertid “en særlig øvet justerformann, som har et godt og skarpt øye”. Deretter ble justeringen foretatt og ballastprofilet tilpasset med spade og jernrive. Til hjelp for sistnevnte arbeid ble også en såkalt skrive, alternativt et stikkmål, dratt etter linjen, som skapte en ripe eller stikkmerker i ballasten som anga profilets bredde.
Figur 1: Banemester Schives apparat for retting av skinnegangen
For større justeringsarbeider og omlegginger lå også et nokså komplisert beregningsarbeid til grunn. Vi skal foreta en prinsipiell utledning litt senere, men noen navn og begreper er verdt å sette i et historisk perspektiv:
Først i 1898, over hundre år etter den kommersielle jernbanenes tilblivelse, innførte jernbane-landmåleren Nalenz metoden med pilhøydemåling og såkalt evolventberegning for kurveretting. Metoden fikk imidlertid svært liten utbredelse i begynnelsen, trolig fordi den var vanskelig for de fleste å forstå. 10 år senere begynte overlandmåler Max Höfer å bearbeide metoden, noe som i 1927 resulterte i en bok. Flere andre anvendte og bearbeidet metoden i tiden som fulgte, også innenfor NSB (Rabstad), men i 1931 fant Dr. ing. Gerhard Schramm frem til en forenkling som bl.a. utelot de kompliserte evolventene. Det er denne metoden som ble gjeldende for ettertidenes kurveretting og som vil beskrives nærmere i avsnitt 2.
Figur 2: Justeringsarbeid på Dovrebanen i 1920-årene
Selve metoden går ut på at en kurve kan beskrives vha. såkalt krumningsprofil (XZ-planet) og vinkelprofil (XY-planet), der vinkelprofilet er integrallinjen av krumningsprofilet. Hvis vi deler opp linjen i små nok linjestykker ΔL, kan hvert linjestykke på en ujevn strekning tilnærmes med en perfekt sirkelkurve, dvs. med konstant krumning. Målinger av det eksisterende sporet sammenlignes med beregninger på utstukket/teoretisk kurve, og justeringsverdier dannes punkt for punkt.
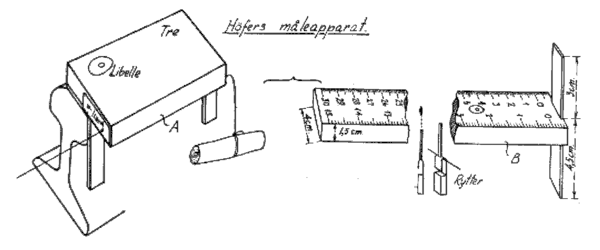
Målingene av sporet ville typisk bestå av kjeding og avmerking, der kjedelengden var ΔL. Deretter ble pilhøyder målt med manuelt instrument i hvert avmerkede punkt med et egnet måleapparat, som f.eks. vist i figur 3. Samtidig med utstikking ble også gjerne tvangspunkter og karakteristiske trasépunkter målt inn når disse la betingelser for justeringen.
Figur 3: Måling av pilhøyder med Höfers apparat
Maskinell justering
Innføringen av maskiner i sporjusteringsarbeidet begynte på slutten av 50-tallet, og dette medførte samtidig et behov for nøyaktig å kunne måle sporets form og tilstand. Til dette ble målevognen Mauzin anskaffet i 1958, som dannet basis for arbeidsprogram for justeringsarbeidene.
Den tekniske utviklingen ble radikal de neste 20 årene og bemanningsbehovet tilsvarende mindre. I det følgende er de såkalte pakkmaskinene delt inn i tre generasjoner.
Den første sporjusteringsmaskinen kom i 1956 og kunne bare underpakke en og en sville av gangen. Selve løftingen måtte utføres manuelt med skrudonkrafter, mens løftehøydene ble fastlagt etter kikkertsikte. Arbeidene krevde hele 18 mann ved siden av maskinen, og pakkekapasiteten var på rundt 300 sviller/ 200 m spor pr. time.
Neste generasjon kom i 1961 og hadde løfteaggregater i tillegg. Løftehøyden ble beregnet med 2 vaiere over skinnene, utspent mellom maskinen og en forvogn ca. 60 m foran i sporet. En måleramme foran på maskinen fulgte med sporet opp ved løfting, og når kontaktblikket festet øverst på denne målerammen berørte de utspente vaierne og fikk elkontakt, ble løftet stoppet. Senere ble vaierne skiftet ut med infrarøde lysstråler. Arbeidslaget for denne maskinen bestod kun av 2 operatører i maskinen og en til høydeinnstilling av forvognen, og kapasiteten var på rundt 450 sviller/300 m spor pr. time.
En stor nyvinning ble utviklet i 1967, da pakkmaskinen også kunne håndtere baksing av sporet vha. innebygde aggregater. Sidevegs retting av sporet var tidligere en svært arbeidskrevende prosess utover å løfte og pakke sporet, ikke minst fordi den økende vekten av komponentene i overbygningen krevde større og større bemanning for å utføre baksing, gjerne 12-14 mann med spett. Kapasiteten økte også betraktelig til hele 700 sviller/450 m spor pr. time.
I senere tid har tilsvarende maskiner blitt utstyrt med kantvibratorer for vibrering av ballastskulderen, laserstrålemottaker for retting av sporet og måleutstyr for både sporets tilstand (pilhøyder, høydefeil og vindskjevheter) og kvaliteten av utført arbeid.
Generelt
Den maskinelle finjusteringen av sporet foretas i dag helautomatisk eller interaktivt med bakgrunn i sporets teoretiske beliggenhet og beregnede justeringsdata. På høyhastighetsbaner (K0) er det et absolutt krav at arbeidsmaskiner med laser, optisk nivellement/løft eller tilsvarende utstyr benyttes, foruten utfesting med GVUL.
Justeringens overordnede formål er å opprettholde en gitt beliggenhet og tilstand for sporet ved å utbedre feil i høyde- og sideretning (løft/baks), samt å stabilisere sporet (pakking). Avhengig av arbeidenes omfang skiller vi mellom:
- Gjennomgående justering: Justering over lengre strekningsavsnitt.
- Stedvis justering: Justering over kortere strekningsavsnitt der sportilstanden er blitt så dårlig at en justering ikke kan vente til neste gjennomgående justering.
De ulike justeringene vil typisk være gitt av alvorlighetsgraden til de sporgeometriske feilene som avdekkes ved målevognskjøring.
Før en maskinell sporjustering kan gjennomføres, må en del sportekniske arbeider være utført i forkant:
- Ballasten må være fordelt og evt. supplert
- Skjøter må utbedres
- Hindringer må fjernes, som skinnekontakter, smøreapparater o.l.
- Alle elektriske sportilkoplinger må være kontrollert
En siste og viktig forberedelse er korreksjon av sporvidden. I avsnitt 3 skal vi derfor gjennomgå justering av sporvidden og manuelle metoder for utbedring av andre sporgeometriske feil, før vi går inn på detaljene for den maskinelle justeringen i avsnitt 4.
Andre tiltak i sporet
I tillegg til sporjustering med forberedende arbeider, jf. beskrivelsen i forrige avsnitt, finnes også en del andre tiltak som er med på å opprettholde en sikker, pålitelig og kostnadseffektiv togfremføring:
- Sliping og høvling av skinner for å beholde et optimalt skinneprofil
- Rensing av ballast
- Vedlikehold av dreneringen langs sporet
- Utskifting av sporets komponenter
Justering utfra pilhøydemålinger
Størstedelen av dette avsnittet dreier seg om sporjustering som baserer seg på målinger av såkalte pilhøyder. Vi skal se på de prinsipper som ble lagt til grunn ved århundreskiftet og som fortsatt danner basis for de kompliserte beregningene som foretas av dagens høyteknologiske justeringsverktøy.
Detaljer rundt selve målingen av pilhøydene vil ikke bli videre gjennomgått, men det vises til Tilstandskontroll.
Nalenz/Höfer/Schramm metode
Som nevnt innledningsvis blir metoden med kurveretting, eller sporjustering, utfra målte pilhøyder kalt ulike navn; Nalenz- eller vinkelbildemetoden, grafisk metode, Nalenz/Höfers metode, Rabstadmetoden. Grunnprinsippet er det samme for alle, men de involverte personene har gjerne videreutviklet metoden som engang ble innført av landmåleren Nalenz. Som beskrevet i 1.1.1 forenklet Dr. ing. Gerhard Schramm metoden i 1931, og denne metoden ble lenge stående for senere anvendelser. I det følgende vil derfor denne varianten av metoden bli nærmere beskrevet. Formlene som inngår er ikke ment som noe beregningsgrunnlag, men som en matematisk beskrivelse av prinsippene for metoden.
Grunnlag for metoden
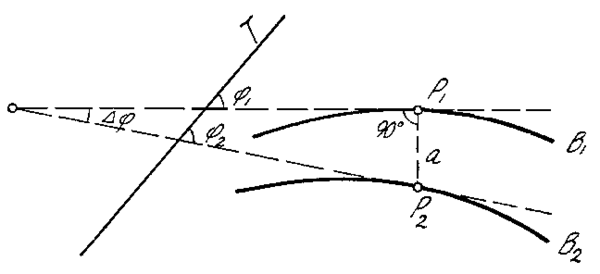
Figur 4: Eksisterende og ønsket kurve - avstand og vinkeldifferanse
Figuren viser to kurver med samme hovedtangent, dvs. en utgangsretning hvor de to kurvene sammenfaller. I et vilkårlig punkt (P1) på den eksisterende kurven trekker vi dennes normal ned på den ønskede kurven, som gir oss et krysningspunkt (P2). Tangentene i disse punktene danner en vinkel vi kaller vinkeldifferansen Δφ, og vi definerer avstanden mellom punktene til å være kurveavstanden a i punktet P1.
Uendelig små buelengder dl langs kurven kan betraktes som rettlinjer og vi kan skrive:
(1)
For små vinkler kan vi også tilnærme uttrykket med
(2)
Med ønske om å løse ut nettopp avstanden mellom eksisterende og ønsket kurve, kan vi integrere
(3)
Ligningen 3 kan benyttes i enhver situasjon der krumningsforholdene er gitt, dvs. hvor Δφ kan uttrykkes som en bestemt funksjon. Men dette forholdet er sjelden oppfylt. Vi utfører justering nettopp som følge av ujevne krumningsforhold i sporet. Med disse forutsetningene deler vi opp kurven i endelige, små buelengder Δl og summerer vinkeldifferansene i et stort nok antall punkter for å finne avstanden mellom kurvene:
(4)
Dette er det alminnelige utgangspunktet for å beregne avstanden mellom faktisk og ønsket kurveforløp. For å beregne denne i praksis skal vi i det følgende beregne problemstillingen grafisk. Konklusjonene vil bli gitt i avsnitt 2.1.5.
Krumnings- og vinkelprofil
Vi skal gå tilbake til situasjonen hvor vi benytter differensialer i stedet for endelige størrelser. Vinkeldifferensialet dφ (ikke det samme som Δφ i 2.1.1) fremkommer av lengdedifferensialet dl og krumningsradien ρ i et punkt:
(5)
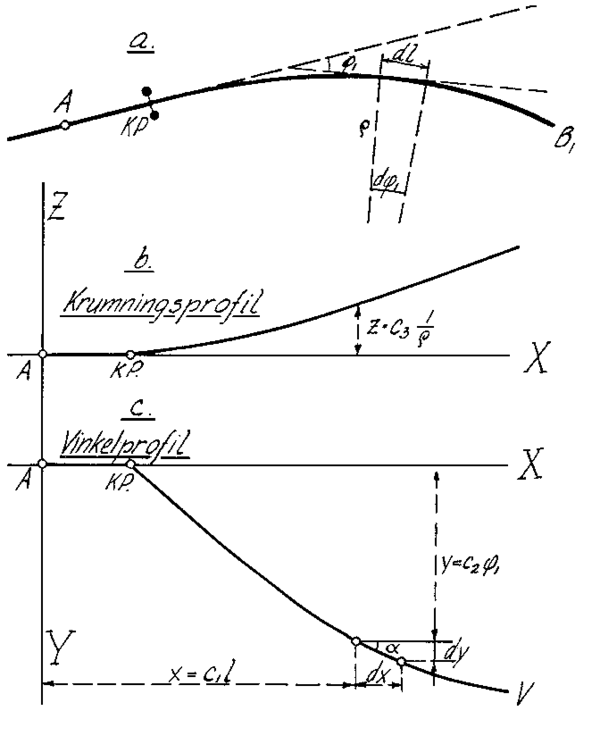
Ved å avsette krumningen (eller pilhøyden) som ordinater (Z) langs lengdeaksen (X) fremkommer krumningsprofilet (pilhøydediagram), som vist i figur 5. I tillegg avsettes vinkelen som dannes med utgangspunktet (hovedtangent) langs linjen som ordinater (Y) langs samme lengdeakse. Dette betegnes vinkelprofilet.
Figur 5: Krumnings- og vinkelprofil
Ved noen enkle differensialbetraktninger dx og dy for hhv. lengder og vinkler, kan vi vise at:
(6)
(c1 – c4 i det følgende er kun målestokksfaktorer, jf. figur 5 - 6)
Vinkelprofilet, som vi har valgt å benevne y, kan dermed skrives som
(7)
Vinkelprofilet er altså integrallinjen av krumningsprofilet. Dette innebærer at dersom krumningsprofilet kan uttrykkes som funksjon av lengde, så kan vinkelprofilet finnes analytisk ved integrasjon. Neste avsnitt gir eksempler på dette for ulike traséelementer.
Krumnings- og vinkelprofil for ulike traséelementer
En sirkelkurve har konstant krumning 1/R for konstant radius R. Vi kan da sette, jf. forrige avsnitt, at .
For vinkelprofilet får vi da:
(8)
Dette er ikke noe annet enn en rettlinje med en bestemt helning. Det kan vises at venstrekurver vil ha positiv helning, mens høyrekurver vil ha negativ helning i lengderetningen.
Som vi vet er krumningsprofilet til overgangskurver stigende eller synkende rettlinjer, .
For vinkelprofilet får vi:
(9)
Vinkelprofilet er altså en vanlig (kvadratisk) parabel.
Integreres uttrykkene for vinkelprofilene til hhv. sirkelkurver og overgangkurver, ser vi at integrallinjene til vinkelprofilet er de virkelige kurvene langs hovedtangenten:
(10)
Ujevne kurver – kurver som skal justeres
Etter å ha definert begrepene krumnings- og vinkelprofil i avsnittene 2.1.2 og 2.1.3, skal vi nå returnere til noe av situasjonen beskrevet i 2.1.1, der vi ikke kjenner kurvaturen, men har en geometri som av ulike årsaker har kommet ut av opprinnelig form. Da må den tidligere integrasjonen erstattes av summering, og vi får:
(11)
Krumningen 1/ρ bestemmes ved pilhøydemåling på bestemte kordelengder.
Vi foretar ingen utledning her, men vinkeprofilets ligning kan pga. forholdet mellom krumning og pilhøyden h skrives som
(12)
Beregning av sumprofil
Vi skal nå ta for oss hvordan vi benytter de til nå gjennomgåtte begrepene for å bestemme avstandene mellom eksisterende og ønsket kurve. I figur .6 er vist vinkelprofilet til en eksisterende kurvekombinasjon bestående av rettlinjer i endene, en venstrekrum sirkelkurve og mellomliggende overgangskurver (stiplet kurve). Ønsket/rettet kurve er vist med heltrukken kurve. Sistnevntes vinkelprofil kaller vi balanseprofilet.
Figur 6: Vinkel- , balanse- og sumprofil for en enkel kurvekombinasjon
Vi tar utgangspunkt i at OB-ene er fastlåst, dvs. at rettlinjene blir liggende. Derav følger det at de to profilene har ordinatdifferanser som opphever hverandre – de balanserer. Grafisk betyr dette at balanseprofilet må utformes slik at det skjærer av like store flater på begge sider av profilet til den eksisterende kurven. Dette vil igjen si at flatene under de to profilene for en bestemt lengde må være like:
For den eksisterende (urettede) kurven har vi
(13)
For balanseprofilet har vi
(14)
Kravet om like flater under vinkelprofilene gir:
(15)
Dette gir punktet P, illustrert i figur 7:
Figur 7 Fellespunkt P for alle balanseprofil
Alle rette linjer gjennom P representerer en bestemt kurveradius, varierende med hvilken vinkel linja har. Med denne grafiske betraktningen er det lett å bestemme visuelt hvilket balanseprofil, og dermed kurveradius, som gir minst mulig flytting av skinnegangen.
Dermed er vi tilbake til problemstillingen som ble omtalt i avsnitt 2.1.1. I et vilkårlig punkt kan vinkeldifferansene leses av vinkelprofilet, og disse kan deretter summeres fortløpende. På denne måten fremkommer sumprofilet, jf. figur 6.
Sumprofilets ordinater d gir verdier for å finne den reelle avstanden mellom opprinnelig og rettet kurve:
(16)
Settes dette inn i ligning 4, får vi følgende uttrykk for avstanden mellom kurvene, eller bakseverdier:
(17)
Siden , får vi
(18)
Som vi ser av utledningene over, kan justeringsberegningen også foretas helt analytisk ved å føre opp alle summer fortløpende i en egnet tabell, jf. Rabstad-metoden. Som vi skjønner er arbeidet svært tidkrevende dersom ikke elektronisk regnekraft benyttes.
Det skal også nevnes at en del problemstillinger ved bruk av metoden ikke er tatt opp her. Blant annet finnes et opphav til unøyaktighet i de tilfeller der to måle-/justeringspunkter ligger på hver sin side av et traseringspunkt. I likhet med sporjusteringsmaskiner krever dette særbehandling gjennom korreksjoner til den alminnelige utregningen beskrevet til nå. Videre vil ikke alltid den analytiske metoden gi ønsket resultat på første forsøk. Da må det legges inn små korreksjoner i ovennevnte tabell for å komme nærmere ønsket pilhøyde for den aktuelle kurven.
Matisakalkulatoren
Før elektronisk regnekraft ble vanlig, fantes andre løsninger som gjorde beregningsarbeidet langt enklere. En av disse var Matisakalkulatoren – en mekanisk innretning som kort fortalt gikk ut på å sette opp målte pilhøyder som skyvependler i en ramme og deretter justere disse til en ”kurvatur” som ga et riktig inntrykk rent visuelt.
Til forskjell fra den matematisk mer omfattende metoden i forrige avsnitt ble kun krumningsprofilet betraktet: Apparatet har 30 par av anvisere som illustrerer pilhøyden på sporet for hver 10. meter. I praksis kunne altså opptil 300 m spor beregnes justert av gangen. Hvert anviserpar består av to plastmarkører som angir pilhøyde, og initielt ble disse satt til hhv. målt pilhøyde og på en linje i flukt med rettlinjer i utkanten av det aktuelle området for justering, jf, figur 8.
Justeringsberegningene bestod i å skru på et bevegelig hjul som kunne variere pilhøydene (dvs. anviserparene), hvorpå den ene av plastmarkørene indikerte den nye pilhøyden, mens den andre anga baksen. For å jevne ut kurvaturen virket apparatet slik at de to nabopilhøydene til den justerte fikk halve utslaget m/ motsatt fortegn. Ved oppnådd resultat ble baksen lest av som forskjellen fra utgangsposisjonen for den ene av markørene i hvert anviserpar, jf. figur 9.
Ved justering måtte man dermed tenke bakover : Man bakset i aktuelt punkt med tanke på det forrige punktets siste pilhøydeverdi. Her er det imidlertid viktig å merke seg at man ikke kom ikke i null ved å gå i én retning – man måtte låse noen endepunkter, i likhet med vinkelbildemetoden.
Bruken av Matisakalkulatoren var en treningssak, i det metoden var fullstendig visuell. Ønsket pilhøyde måtte angis på en slik måte at arealet mellom målt/ønsket pilhøyde ble utjevnet, særlig i overgangskurvene. Dette ble gjort ved å plassere OB/OE-ene til en fastlåst posisjon.
Metoden ble regnet som en nokså primitiv måte å beregne sporjustering på. Ved all justering gikk en på akkord med ny pilhøyde. Som ved nyere justeringsalgoritmer (jf. avsnitt 2.3) ble ikke eksakt den kurvaturen man ønsket seg oppnådd. Man måtte derfor akseptere en ”beste” løsning mht. baks kontra ønsket pilhøyde.
Figur 4.8: Matisakalkulatoren (to sammenmonterte) med initiell konfigurasjon
Figur 4.9: Matisakalkulatoren etter endt "justering"
Vår tids justeringsberegninger
Elektroniske beregningsprogrammer har vært brukt i Norge siden begynnelsen av 1980-tallet da det engelske Hallade-programmet ble kjøpt inn. I 1987 ble programmet Baksber utviklet i NSB. Dette programmet baserer seg på samme sumprofilbetraktning som beskrevet i avsnitt 2.1.5. Imidlertid blir balansepunktet ikke beregnet, men det velges OB/OE-er ved iterativ beregning av baks og resulterende pilhøyde, i interaktiv dialog med brukeren av programmet. Endelig resultat velges når krav til baks og resulterende pilhøyde er tilfredsstillende. Programmet kan håndtere strekninger på inntil 2500 m med 20 meters korder for pilhøydeverdiene.
Bakseverdiene fremkommer ved å først beregne sumprofilet ved fortløpende integrering av differansen mellom målt og ønsket pilhøyde. Dette gir et profil som kun er låst i startpunktet. Deretter integreres dette sumprofilet. Dette gir bakseverdier som ikke kan benyttes da endepunktet på beregningen ikke er låst. Derfor beregnes en ny grunnlinje (erstatter X-akse i figur 6). Denne grunnlinjen beregnes ved å la en kubisk spline-funksjon gå gjennom et gjennomsnitt av et valgt antall punkter fra det integrerte sumprofilet og som sammenfaller med det integrerte sumprofilet i dettes to siste punkter (retningskontroll).
En spline-funksjon g(x) angir kontinuerlige delfunksjoner (i bestemte subintervaller) på polynomform som til sammen tilnærmer en større kontinuerlig funksjon f(x). Per definisjon er alle g(x) flere ganger deriverbare i endepunktene. En kubisk spline-funksjon har kontinuerlige 1.- og 2.deriverte for hele f og kan i alle subintervaller beskrives som et polynom av grad ikke høyere enn tre.
Baksen blir dermed forskjellen mellom spline-funksjonen og det integrerte sumprofilet. Den (annen)deriverte til spline-funksjonen står i tillegg i forhold til forskjellen mellom ny og ønsket pilhøyde.
Når det gjelder størrelsen på beregnet baks, er denne ikke bare avhengig av plasseringen av OB’er og OE’er. Anvendelsen av spline-funksjoner byr på muligheten for å velge en utjevningsgrad for bakseberegningen. Siden spline-funksjoner består av subintervaller av en gitt strekning, vil de variere mye med hvor mange intervaller, eller punkter vi velger at den skal dekke. For bakseberegningens del betyr dette at jo høyere utjevningsgrad vi velger i programmet, dvs. hvor mange intervaller spline-funksjonen skal inneholde, desto bedre tilpasning mellom ønsket og ny pilhøyde får vi. Men dette resulterer også i større bakseverdier. Det kan i tillegg gis en baksekorridor for den aktuelle strekningen, men bakseverdier som tangerer baksekorridoren fører normalt til en dårligere tilpasning mellom ønsket og ny pilhøyde.
Å variere utjevningsgraden på bakseberegningen er ikke tilrådelig før man har fått låst fast OB-er og OE-er med en tilfredsstillende løsning. Inntil dette er gjort, anvendes normalt en utjevningsgrad lik 0, dvs. en spline som går gjennom 9 målepunkter.
Praktisk eksempel: Baksber benyttet over 1 km spor
Figur 10 viser utgangssituasjonen for bakseberegning av en 1 km lang sporstrekning:
Figur 4.10: Målte og ønskede pilhøyder
Figurene 11 og 12 viser hhv. beregnet baks og avvik fra ønsket sporbeliggenhet for tre ulike utjevningsgrader. Som vi var inne på i avsnitt 2.3 regulerer valg av utjevningsgrad størrelsen på den totale baksen, noe som samtidig påvirker overensstemmelsen mellom ny og ønsket pilhøyde. Sistnevnte kan uttrykkes som standardavvik for hele beregningen, og tabell 1 angir tallmessig kompromisset mellom baks og sluttresultat.
Tabell 1 Tallresultater fra tre ulike bakseberegninger
| Utjevningsgrad | Antall spline- målepunkter | Summe baks [mm] | Standardavvik [mm] |
|---|---|---|---|
| -2 | 7 | 352 | 0.61 |
| 0 | 9 | 700 | 0.50 |
| 10 | 19 | 2234 | 0.30 |
Vi ser tydelig at utjevningsgrad 10 gir meget store bakseverdier utfra figuren, og summe baks blir av en helt annen størrelsesorden enn for de to andre utjevningsgradene. Denne kan derfor utelukkes som endelig beregning for sporjustering. (Bakseverdiene er imidlertid ikke så store at de tangerer baksekorridoren, slik at det resulterer i dårlig overensstemmelse mellom ny og ønsket pilhøyde, jf. fig. 12.) Utjevningsgradene –2 og 0 gir tilsynelatende ingen store forskjeller i baks, med unntak av summe baksen som faktisk står i forholdet 1:2.
Figur 11: Bakseverdier fra tre bakseberegninger (utj.grad –2,0 og 10)
I figur 12 ser vi derimot hvor god tilpasning vi ville fått med utjevningsgrad 10 til ønsket pilhøyde. Videre avsløres effekten av forskjellen i standardavvik mellom utjevningsgradene –2 og 0, der –2 gir en langt mindre optimal ny pilhøyde. Valget av beregning som bør benyttes faller derfor på utjevningsgrad 0 i denne enkle betraktningen.
Figur 12: Avvik fra ønsket pilhøyde for tre bakseberegninger (utj.grad -2,0 og 10)
Figur 13 viser den nye pilhøyden etter bakseberegning med utjevningsgrad 0.
Figur 13: Eksempel på ny pilhøyde (optimalt resultat med utj.grad 0)
Det er ikke sikkert at denne sporbeliggenheten ville være god nok i et gitt tilfelle, dvs. om sporkvaliteten er høy nok etter justering, og løsningen ville dermed vært å velge en høyere utjevningsgrad enn 0.
I avsnitt 7.1 er vist utskriften fra beregningen i BAKSBER med utjevningsgraden 0.
Manuell utbedring av sporviddefeil/andre geometrifeil
I dette avsnittet skal vi i hovedsak gå nærmere inn på den manuelle utbedringen av de alminnelige sporgeometriske feil vi finner langs linjen. Hvordan disse feilene måles og gir grunnlag for kvalitetsundersøkelser blir ikke gjennomgått. Det vises til L535 Kap. 4 – Tilstandskontroll.
Sporviddefeil
Årsaker til avvik
Pga. trafikkbelastning vil det ofte forekomme avvik fra den ideelle sporvidden lik 1435 mm. I de fleste tilfeller er problemet sporutvidelser som forekommer som følge av:
- at befestigelsen gir etter på tresviller
- slitasje av isolatorer på betongsviller
- skinneslitasje
- slitasje på mellomlegg / nedgraving i sville
Reduksjoner i sporvidden derimot forårsakes av:
- utvalsing av skinnehodet
- forandring av svillens beliggenhet (skjeve sviller)
Konsekvenser
En del av målet med sporjustering er å gjøre sporet stabilt, og hvis det forekommer store variasjoner i sporvidde vil dette påvirke sidestabiliteten i sporet.
I kontrakurver er de alminnelige kravene til sporutvidelser skjerpet, i og med at for store sporvidder kan føre til ombufring, særlig ved skyving av store togstammer.
Utbedring av for stor sporvidde
Når underlagsplatene har gravd seg ned i tresviller og skapt en sporutvidelse, kan dette rettes opp ved å legge inn såkalte skoringsplater. En midlertidig utbedring er å skru inn strekkbolter, men disse tillates i sporet maksimalt ett år. Hvis utvidelsene er vedvarende og omfattende er svillebytte eneste løsning.
Vedlikeholdet for betongsviller er imidlertid ikke like omfattende. Sporutvidelser som følge av slitte isolatorer utbedres ved å skifte ut isolatorene.
Utbedring av for liten sporvidde
For liten sporvidde som skyldes utvalsing av skinnehodet, kan utbedres ved høvling og/eller skinnesliping, evt. ved svilleregulering.
Vindskjevheter
Et spor er vindskjevt når overhøyden varierer fra punkt til punkt i sporet som vist på figur 14.
Vindskjevheten = (H2-H1)/B i ‰ eller mm/m, der H1 og H2 er overhøyder, B er målebasis.
Figur 14: Definisjon av vindskjevhet
Årsaker og konsekvenser
Vindskjevhet kan skyldes feil i skinnenes høydebeliggenhet eller være tilsiktet i forbindelse med overhøyderamper. Vindskjevhet som feil er som regel langt større enn den tilsiktede (rampestigning) og kan oppstå i spor med telefarlige masser, ustabiliserte spor og etter eller under gravearbeider.
Når en vogn går inn i en overgangskurve og opp en overhøyderampe, vil det fremre, ytterste hjulet påvirkes av en økt kraft, mens det bakre, ytre hjulet vil avlastes. På samme måte får vi motsatt situasjon idet vogna går ut av sirkekurven og ned en overhøyderampe - det fremre, ytre hjulet avlastes. Når denne avlastningen blir stor nok, får vi en avsporing. Avsporingsfaren er dertil også størst i ramper med avtagende overhøyde.
Utbedring av vindskjevheter
For å unngå avsporinger som følge av for stor vindskjevhet, skal sporet være pakket omhyggelig. I de tilfellene justeringsarbeider må utføres umiddelbart, vil det som regel være mest aktuelt å gjøre justeringen manuelt, uten skinnegående justeringsmaskiner. Metodene for slike utbedringsarbeider er:
- justering med håndpakkeutstyr
- skoring vha. gummiplater eller treskorer
- nedgraving av forhøying som forårsaker vindskjevheten
Nedgraving er en mulighet som bare kan utføres ved manuell justering. Ved maskinell justering vil de omkringliggende områdene måtte løftes i stedet til feilen blir fjernet, og dette kan raskt bli langt mer omfattende.
Høyde- og overhøydefeil
Høydefeil blir målt separat for hver av skinnestrengene og betyr kort og godt avvik fra ideell høydebeliggenhet i vertikalkurvaturen. Overhøydefeil er ujevnheter i overhøyden, altså mindre, varierende avvik fra den ideelle overhøyden over en gitt lengde. I mange tilfeller henger disse feilene nøye sammen med de feilene som også avdekkes som vindskjevheter.
Årsaker og konsekvenser
Feil i høydebeliggenheten kan gå begge veger, enten gjennom setninger pga. at underbygningen ikke er tilstrekkelig stabil, eller som forhøyninger pga. telehiv eller annet. Feil oppstår også gjerne som resultat av grov/unøyaktig justering.
Overhøydefeil har ofte en tendens til å vokse. Hvis den tilsiktede overhøyden i en kurve ikke er oppnådd ved en justering, vil belastning av sporet lett kunne påføre kurven ytterligere avvik fra ideell overhøyde.
Dersom følgen av dårlig justering er for stor overhøyde, får vi et større overhøydeoverskudd E enn vi har regnet med for godstogene. Følgelig kan disse forskyve sporet så hardt innover i kurven at det ødelegger sporet. I motsatt fall blir manglende overhøyde I så stor for det raskeste materiellet at vi kan få en avsporing. Brå feil i overhøyden kan også gi feil i sidebeliggenhet (baks).
Utbedring
Høydejusteringen skal utjevne sporets variasjoner i høyderetningen med hensyn til den enkelte skinnes variasjoner i høyderetningen og skinnenes innbyrdes høydenivå. Det skal alltid foretas sidejustering samtidig med høydejustering.
I kurver som gjennomkjøres med liten hastighet, blir sikkerheten mot avsporing bedre når overhøyden reduseres mest mulig eller sløyfes.
Når det i forbindelse med arbeidets utførelse ikke er nødvendig at kurvens ytre streng straks løftes, bør overhøyden være minst 20 mm lavere enn den tilsiktede overhøyde. Den største overhøyde skal da ikke overskride 150‑20 = 130 mm. Det gjenstående løft foretas i forbindelse med finjusteringen.
Når sporet løftes eller senkes, må det ved enden av arbeidsstedet lages en midlertidig stigningsrampe som skal oppfylle følgende krav:
- Stigningen i forhold til opprinnelig trasé (s) skal ikke være større enn 5 ‰.
- Rampen avsluttes i begge ender med vertikalkurver med radier (RV) på minst 1500 m.
- Mellom endene av disse vertikalkurver skal det være en avstand på minst 2,5 m.
For detaljer rundt manuell høydejustering for øvrig vises det til utbedring av vindskjevheter, avsnitt 3.2.2.
Sidefeil
Sidefeil, eller baksefeil, blir som høydefeil målt separat for hver av skinnestrengene (ved pilhøydemålinger) og angir avvik fra ideell beliggenhet i horisontalplanet.
Årsaker og konsekvenser
Brå variasjoner i overhøyden kan medføre sidefeil. Hvis sporet blir forsøkt justert ved svært lave temperaturer, blir sjelden resultatet helt tilfredsstillende, og nye sidefeil skapes.
Hvis utfestingsmetoder benyttes ved maskinell justering, og inngangsdata, sentrering e.l. er beheftet med feil, kan langbølgede sidefeil oppstå.
En dårlig sidegeometri medfører en ubehagelig og slingrende kjøring, som igjen fører til ujevn skinneslitasje og kraftige påkjenninger for befestigelsen. Feil i sidegeometrien kan også utløse solslyng. Når sidefeil blir tilstrekkelig store, oppstår som regel også en sporutvidelse samme sted.
Sidejusteringen skal sikre sporets nødvendige stabilitet og hovedform. Høydejustering skal alltid utføres samtidig med sidejustering.
Utbedring
Sidejusteringen i grovjustert spor kontrolleres i første omgang på øyemål. På steder hvor det forekommer synlige ujevnheter, måles pilhøyden i midten av en 10 m lang snor, både på stedet hvor ujevnheten er iakttatt, og på begge sider av dette stedet i avstander av 5 m. Forskjellene mellom de målte pilhøyder skal ikke være større enn 25 mm.
I sirkelkurver og overgangskurver måles pilhøydene på sporets ytre skinnestreng.
Sideveis sikring av sporet ved avstempling kan tillates når det avstemples mot svilleendene, ikke direkte mot skinnene.
Maskinell sporjustering
Vi var såvidt innom de ulike arbeidene en såkalt pakkmaskin utfører i avsn. 1.1 og skal nå se nærmere på de enkelte justeringene som utføres og de ulike prinsippene som ligger til grunn.
En sporjusteringsmaskin består som regel av 4 forskjellige delsystemer:
- Et målesystem som registrerer feil i sporgeometrien, dvs. avvik fra teoretiske traseringselementer for begge skinnestrenger, både i horisontal- og vertikalplanet. Systemet kan sammenlignes med det som finnes på en målevogn for sporgeometri.
- Et løfte- og baksesystem som fysisk korrigerer feilen ved å løfte eller sideforskyve sporet til en riktigere beliggenhet. Dette systemet er nøye koblet sammen med målesystemet, slik at baks/løft avsluttes når feilene er eliminert.
- Et pakkagregat som bidrar til å stabilisere sporet i korrekt stilling ved å tilføre ballasten energi slik at hulrommene som dannes rundt svillene når sporet løftes eller bakses fylles med omkringliggende ballast.
- En kantvibrator som sørger for kompaktering av ballasten utenfor svilleendene. Dette bidrar til økt sidestabilitet i sporet.
Delt inn noe annerledes, kan vi si at en sporjusteringsmaskin utfører 4 arbeidsoppgaver:
- Måling - målte pilhøyder sammenlignes med teoretiske verdier
- Løft/høydejustering - høydejustering av sporet
- Baks - sidejustering av sporet
- Pakking - etterfylling og komprimering av ballast under svillene
Figur 15: Eksempel på pakkmaskin: Plasser 09-32 CSM
Måling under justering
I alminnelighet finnes et separat måle- og løftesystem for hver av skinnestrengene, mens innlegging av overhøyde og overhøyderamper gjøres vha. en elektronisk pendel/inklinometer, jf. figur 16.
Figur 16: Prinsipp for justering av overhøyde/ innlegging av overhøyderampe
Justerings-/måleprinsipp for løft: 3-punkts kordemetoden
For høydejustering benyttes alltid den såkalte 3-punkts kordemetoden. Måleprinsippet er det samme som ved pilhøydemålinger med målevogn:
En målereferanse dannes av en korde mellom to sensorer mot sporet. Disse kan være mekaniske eller optiske. En tredje sensor måler pilhøyden i forhold til korden, jf. figur 17. Avvik mellom teoretisk og målt verdi for pilhøyden indikerer avvik fra korrekt traséelement og danner grunnlag for korreksjonsverdien ved justeringen.
Figur 17: Prinsippskisse av asymmetrisk pilhøydemåling
I målevognssammenheng benyttes ofte betegnelsen pilhøyde bare når det er snakk om feil i sideretningen, men det er nøyaktig det samme prinsippet som ligger til grunn for å avdekke og justere feil i høyde.
På rettlinje er justeringsprinsippet enkelt. Det midtre målepunktet løftes til det ligger på rettlinjen mellom første og tredje målepunkt. Pilhøydemålingen er altså lik null på korrekt spor.
For sirkelkurver avhenger den pilhøyden som skal angis for sammenligning med den målte kun av to faktorer: kurveradius og den enkelte pakkmaskinen. Uten å foreta selve utledningen her, kan det vises gjennom utvikling av Taylor-rekker at pilhøyden er gitt ved:
Pilhøyden er altså lik en maskinspesifikk konstant k mutliplisert med krumningen. Dermed er det nok for operatøren å mate kurveradien inn i systemet på et eller annet tidspunkt før justering. Alle andre størrelser er kjent.
Justerings-/måleprinsipp for baks: 4-punkts kordemetoden
I stedet for 3 punkter og én målebasis benyttes her 4 punkter og to målebasiser. Dermed kan vi måle to forskjellige pilhøyder h og H på to forskjellige steder med en fast, målesystemavhengig avstand. Pilhøydene har altså forskjellig lengde på kordene. Når systemet er inne i ett enkelt traséelement skal forholdet mellom de to pilhøydene være konstant. Hvis ikke tyder det på at kurven ikke er skikkelig justert, og sporet må bakses til forholdet mellom pilhøydene stemmer overens med verdiene gitt i målesystemet.
(20)
der
(21)
Figur 18: Prinsipp for sidejustering etter 4-punkts kordemetoden
Løft/høydejustering
Rent mekanisk virker det elektronisk styrte løftesystemet vha. hydrauliske sylindere og rulletenger som løfter sporet inntil målt pilhøydefeil er eliminert og grunnløftet gjennomført.
Grunnløftet har sin praktiske årsak i følgende: Ved måling av høydebeliggenheten, vil det teoretisk være behov både å løfte og senke sporet. Men siden kun det første er mulig, må et grunnløft innføres, stort nok til å romme alle justeringer. Et grunnløft er gjerne i størrelsesorden 10-20 cm.
Fig. 19 viser skjematisk hvordan en løfteoperasjon arter seg. Punkt A befinner seg på allerede justert spor. Sporet skal gis et gjennomgående løft lik høyden BC. Sporet ved måle- og arbeidspunktet D løftes, og svillen pakkes slik at punktet ender på rettlinjen AB i punktet E. Matematisk kan dette uttrykkes som:
(22)
Her skal Zn bety den nye høyden etter løftet, mens Z0 er den opprinnelige høyden. Faktoren a/l er reduksjonsfaktoren som alle feil blir redusert med.
Figur 4.19: Prinsippet for justering i høyde etter 3-punktsmetoden
Ved overgang fra rettlinje til sirkelkurve, eller motsatt, er det nødvendig å korrigere målesystemet for å oppnå riktig sporgeometri. En kontinuerlig endring skal påbegynnes når fremre målepunkt når trasépunktet (SE/KP) og avsluttes når bakre målepunkt passerer samme punkt.
Overføringsfunksjon
Som for måling med målevogner, er det vanlig å benytte Fourier-transformasjon for å beskrive sammenhengen i frekvens-/bølgelengdedomenet:
(23)
Overføringsfunksjonen H angir forholdet mellom amplituden til løftet etter og før justeringen som funksjon av bølgelengde. Denne er gitt ved:
(24)
Figur 20 viser et eksempel på en overføringsfunksjon for løft og baks, der også faseforskyvningen for de ulike bølgelengdene er angitt.
Figur 4.20: Eksempel på overføringsfunksjon for løft/baks
Overføringsfunksjonen H pendler mellom en minimumsverdi på 0 - 0.25 og 1. H vil variere utfra den enkelte maskins geometri og sporgeometrifeilenes bølgelengde i sporet, men når bølgelengden øker mot uendelig, vil alltid H gå mot 1.
Hvilken effekt har så overføringsfunksjonen i praksis? H gjenspeiler hvor stor del av feilen som fortsatt gjenstår etter justering. En H = 0.7 gir f.eks. en feilreduksjon på 30%. Ved en ny justering av den samme feilen, rettes ytterligere 21% (0.3·0.7) av den opprinnelige feilen, mens det fortsatt gjenstår 49% (0.7·0.7). Følgelig kan ikke sporjustering der alle elementer i systemet finnes ombord i pakkmaskinen benyttes til fullt ut å eliminere alle sporgeometriske feil. Til dette trengs faste punkter i et ytre referansesystem, noe som blir diskutert i avsnitt 5.
Baks/sidejustering
På helt analogt vis som for løft, fungerer noen ganger baksing også ved at sideforskyvningen avbrytes når differensen mellom målt og teoretisk pilhøyde er eliminert ved trepunktsmåling. For dette justeringsprinsippet vises det til teorien i avsnitt 4.1.1. I det følgende skal vi derimot fokusere videre på 4-punkts-metoden, som oftere er anvendt ved baks.
En annen måte å definere prinsippet fra 4.1.2 på, er å betrakte de 4 målepunktene. Maskinen måler ordinatene Y1, Y2 og Y4, som til sammen definerer en 2.gradskurve. Sporet bakses til best mulig å falle sammen med denne kurven. I praksis betyr det at sporet bakses i punktet C til å ligge på kurven definert av A, B og D, jf. fig. 18.
På rettlinjer blir altså ikke sporet bakset til linjen ABD i punkt C, men fremdeles til sirkelen ABD. Dette innebærer at dersom det er feil i sporet, vil disse avrundes/glattes på en mindre streng måte en ved 3-punktsmetoden. Er derimot maskinen på en perfekt rettlinje med alle 4 målepunkter, er også pilhøydene h og H lik null og maskinen vil ikke foreta noen justering (annet en til en sirkel med radius lik uendelig, som er en rettlinje).
I motsetning til 3-punktsmetoden, trenger ikke kurveradien å være kjent når maskinen befinner seg fullstendig innenfor en sirkelkurve. Den bakser sporet til kurven bestemt av målepunktene A, C og D.
Ved automatbaks følger altså den fremste sensoren, i punkt D, det ujusterte sporet, mens punktene A og B går på nyjustert spor. Dette er indikert i figuren med hhv. ordinatene Yo og Yn (opprinnelig og ny). Lengdene a, b og c er kjente, så posisjonen til C kan uttrykkes ved posisjonene til A, B og D. På en tilsvarende måte som for 3-punktsmetoden kan vi uttrykke den nye beliggenheten som en funksjon av den gamle:
(25)
Selv om maskinen klarer seg uten innlesing av kurveradius inne i sirkelkurver, må derimot den fremste sensoren (D) påføres en korreksjonsverdi for å oppnå riktig resultat ved overgang fra rettlinje til sirkelkurve, eller omvendt. Noe av det samme gjelder når maskinen passerer en overgangskurve. Pilhøydene endres kontinuerlig fra fremre målepunkt går inn i overgangskurven til bakereste målepunkt forlater overgangskurven. Når alle målepunktene er inne i overgangskurven er endringshastigheten til pilhøydene konstant. Vi må altså kjenne kurvaturen ved justering også når vi anvender 4-punktsmetoden. Samtidig med korreksjonene er det viktig å merke start- og sluttpunkt for de enkelte traseringselementene på sporet.
Overføringsfunksjon
Overføringsfunksjonen mellom gammel og ny geometri som kan utledes ved Fourier-transformasjon blir følgende:
(26)
Fig. 21 viser både teoretisk og virkelig overføringsfunksjon for både løft ved 3-punkts- og baks ved 4-punktsmetoden for pakkmaskinen Plasser & Theurer 07-32.
Figur 21: Eksempel på overføringsfunksjon for 3- og 4-punktsmetoden
Eksempler på effekten av maskinell justering
Under er vist et par praktiske eksempler på baks med ulike pakkmaskiner. Både 3-punkts og 4-punktsbaks er benyttet, og første eksempel kan derfor i stor grad sidestilles med løft etter samme metode.
Figur 22: Praktisk eksempel: Baks etter 3-punktsmetoden
Figur 23: Praktisk eksempel: Baks med 4-punktsmetoden
Pakking
Løftingen vi nå har gjennomgått foretas i praksis ved at hver av skinnestrengene uavhengig løftes vha. såkalte hydrauliske løftetallerkener, jf. figur 24. Disse griper under skinnehodet og løfter skinnestrengen til høyden er tilpasset målesystemet.
Bakseaggregatet er som regel sammenbygget med løfteanordningen og består av ruller med dobbelte flenser. Vha. hydrauliske sylindre forskyves skinnegangen sidevegs i ønsket retning.
Figur 24 Løfte- og baksemekanisme
Selve pakkingen skal sørge for å gjenopprette noe av den stabiliteten vi må gi avkall på under justeringen. Prinsippet er illustrert i figur 25. Dog kan ikke sporet lenger regnes som stabilt etter større justeringer. Bestemmelser i forbindelse med stabilitet blir omtalt nærmere i avsnitt 6.
Figur 25: Prinsipp for pakking: klemkraft og vibrasjon
Når skinnen(e) er kommet i riktig posisjon, klemmes ballasten under svillene sammen med såkalte pakklabber. Disse pakker både på innsiden og på utsiden av hver av skinnestrengene. Et pakkaggregat, som betjener én skinnestreng, har gjerne 8 pakklabber fordelt på begge sider av skinnen. Noen maskiner er utstyrt med spesialaggregater for å pakke sporveksler, men disse kan også benyttes på vanlig spor.
I tillegg komprimeres ballasten ytterligere ved at såkalte kantvibratorer komprimerer ballastskuldrene under pakking.
Kvalitet og fallgruver ved justering
Arbeidsmetodikk
Ved maskinell justering er det viktig å påpeke at maskinen, og således målesystemet, ferdes på et spor allerede beheftet med sporgeometriske feil. Fig. 26 illustrerer hva dette kan medføre på rettspor.
Figur 26 Målepunkter ved 3- punktsmetoden - feilkilder
I figuren blir feilen i B justert riktig til B’, men vi ser at når målepunktet A kommer til punktet S, vil målebasisen stå skjevt i forhold til rettlinjen. Hvis ikke maskinen er programmert på forhånd eller benytter ytre referanser utenfor vogna, men styres etter automatbaks, vil maskinen lage en feil i justeringspunktet B (når A har forflyttet seg til S). På tilsvarende måte vil automatbaks etter 4-punktsmetoden heller aldri justere sporet til å bli helt feilfritt.
Hvis en feilaktig radius leses inn i systemet i en kurve, får vi en baksefeil. Denne feilen vil asymptotisk nærme seg verdien Δ, jf. fig. 27. Som figuren viser, blir baksefeilen i tillegg langt større enn pilhøydefeilen som er innlest.
Figur 27: Baksefeil ved innlesing av feil radius - 3-punktsmetoden
Figur 28 viser et praktisk eksempel på effekten av baksefeil:
Figur 28: Eksempel på baksefeil ved feil radius - SPR 131
I avsnittene om de to justeringsprinsippene, var vi inne på hvordan selve målesystemet må påføres korreksjoner når vi beveger oss fra et traséelement til et annet. Dette kan synes nokså enkelt i teorien, men i praksis kan det vise seg vanskelig å mate systemet manuelt med varierende pilhøyder, selv om overgangskurvene har konstant endring av kurvaturen og de nominelle radiene er kjent til enhver tid.
En annen problemstilling der praksis avviker fra teorien, er når løft skal anvendes, etter 3-punktsmetoden, for å generere overhøyderamper. Siden endringen av overhøyde pr. definisjon er lineær, vil lengdeprofilet i teorien kun bestå av rettlinjer. Men dette er ikke mulig i praksis: Sporet vil avrundes i hver ende av overhøyderampen, som om den øyeblikkelige overgangen mellom to traséelementer var en sporgeometrisk feil.
Overføringsfunksjonene
En rekke målinger har blitt utført for ulike pakkmaskiner for å kartlegge den såkalte virkelige overføringsfunksjonen. På grunnlag av målinger i sporet like etter justering/pakking, har funksjoner som den vist i fig. 21 fremkommet. Fra denne kan man raskt konkludere med at forbedringene etter justering bare er rundt halvparten av det teorien skulle tilsi. I tillegg må det også nevnes at et helt nyjustert spors beliggenhet endres signifikant i den nærmeste tiden etter justering.
Men vi kan til en viss grad kompensere for overføringsfunksjonenes mangel på fortreffelighet. Ved å dele opp fremre målepunkt A i to målepunkter A1 og A2, kan vi interpolere fram en verdi på A fra disse, som vist i figur 29. Selv om vi i dette benytter totalt 4 målepunkt i praksis, er det fortsatt 3-punktsmetoden maskinen arbeider etter. Som figuren illustrerer, vil periodiske feil med bølgelengde lik 2 ganger avstanden mellom de nye målepunktene reduseres helt.
Figur 29: Todeling av fremre målepunkt for forbedret overføringsfunksjon
Sporjustering utfra et fast, ytre referansesystem
I det foregående har vi sett hvordan ulike prinsipper, med referansesystem ombord, benyttes til å foreta maskinell justering, samt gjennomgått hvilken kvalitet slike justeringer kan ha. Oppsummert kan vi si at dette er fremgangsmåter som representerer en best mulig glatting av sporet. Men som tidligere nevnt, vil et nyjustert spor raskt komme ut av denne tilstanden idet ethvert tog som passerer den justerte strekningen vil forsøke å presse sporet tilbake til beliggenheten før justeringen.
Etter en stund med slike deformasjoner fra nyjustert spor, stabiliserer beliggenheten seg. Men denne prosessen kan pr. definisjon aldri opprettholde eksempelvis en ideell rettlinje i vertikalplanet. For at dette skal bli mulig, må beregningen baseres på et overløft der det er kalkulert med de ovennevnte setningene.
Figur 30 Prinsipp for overløft som kompenserer for forutsette setninger
En enkel løsning på problemet kunne være å legge en viss andel av avstanden mellom faktisk og teoretisk geometri til løftehøyden. Men en slik prosess krever at den faktiske sporgeometrien er kjent.
Oversikt over noen systemer i Europa
I det følgende skal vi konsentrere oss om metoder for maskinell justering som baserer seg på at et spor er koordinatbestemt i et ytre referansesystem. Slike system vil som regel innebære en signifikant forbedring av justeringskvaliteten, men vi vil se at flere av disse systemene også har sine ulemper mhp. bl.a. ressursbruk. Tabell 2 inneholder noen eksempler på systemer som benyttes i Europa i dag.
Tabell 2: Ulike prinsipper for justering til absolutt beliggenhet for noen forvaltninger i Europa.
| Justerings-/måleprinsipp | Forvaltning | System |
|---|---|---|
| Utfesting for justering –
Geodetisk innmåling av spor |
JBV
DB (Tyskland) BV (Sverige) SNCF (Frankrike) |
VUL/GVUL
SurVer - ZVS/GPS |
| “Langsehne” | DB (Tyskland)
NS (Holland) VR (Finland) SBB (Sveits) ÖBB (Østerrike) |
Driver
Båglaser |
| Integrert måling og justering | SBB (Sveits) | Palas |
Ulike metoder for absolutt justering
Utfesting/geodetisk innmåling
Som måleprinsippet uttrykker, er dette en metode der den aktuelle strekningens faktiske beliggenhet koordinatbestemmes geodetisk, i praksis ved bruk av teodolitt/totalstasjon eller GPS-utstyr. Den teoretiske beliggenheten er koordinatbestemt fra før, og avvikene mellom de to danner grunnlag for løfte-/bakseverdier. Videre kan disse verdiene enten listes, for senere å lese inn manuelt, eller lagres på et dataformat som kan leses av et dataprogram ombord i pakkmaskinen.
Ved JBV har vi to metoder for varig utfesting av linjen: VUL og GVUL, som er nærmere beskrevet i Utfesting av linjen. Begge metoder benyttes til å kartlegge sporets absolutte beliggenhet i et ytre referansesystem og kan dermed også benyttes til å regne ut justeringsverdier.
På høyhastighetsbaner (K0) er sporet utfestet med GVUL og dermed koordinatbestemt gjennom en teknisk linjeberegning. Fremgangsmåten der det er utfestet med GVUL blir i første omgang å måle inn sporet fra et geodetisk fastmerkenett. Sporet er teknisk linjeberegnet for sporets senterlinje, og denne må følgelig også måles inn før justering. Til dette kan det benyttes en tralle som kan skyves langs sporet. På tralla er montert et en prismestav hvis fot har beliggenheten spormidt, i grunnriss. Alternativt måles begge skinnestrenger og senterlinjen beregnes i etterkant. Sporets høyde er definert til å være høyden til laveste skinnestreng. Ved bruk av tralla må også instrument for måling av overhøyden benyttes. De samlede måledata gir deretter grunnlaget for justering.
Selve linjeberegningen foregår vha. programmet SPOROP, et program utviklet i samarbeid med Jernbaneverket hvor innmålte sporkoordinater kobles opp mot dimensjonerende trasékrav for en mest mulig gunstig trasé. En ny linjeberegning vil som regel beregnes utfra ønsket om minst mulig justering kombinert med høyest mulig hastighet. De nye koordinatene settes til slutt ut i terrenget, som regel omregnet til en bakse-/løfteberegning som kan benyttes av en pakkmaskin.
For VUL-strekninger måles horisontale og vertikale avstander fra VUL-merker langs linjen til nærmeste skinne med en såkalt VUL-stav. VUL-merkene, som finnes i fjell, på KL-master og på egne fundament, måles i tillegg inn fra det geodetiske fastmerkenettet for å få en fullgod kobling mellom spor og et ytre referansesystem.
Felles for begge metoder er at de målte data legges inn i tilpasset programvare som beregner justeringsverdier utfra nominelle geometriparametre, optimal linjeføring og krav om ikke altfor store justeringsverdier.
De beregnede justeringsdata leses så inn for å korrigere pakkmaskinens målesystem.
Ved DB i Tyskland finnes et system kalt SurVer. Dette er en manuelt drevet måletralle som effektiviserer målearbeidet. Montert på tralla finnes i første omgang et spesialprisme (RPU) som har styre- og kommunikasjonsutrusting for å kommunisere med en totalstasjon. Her anvendes en såkalt robotstasjon, som vha. servomotorer innretter seg automatisk mot prismet, og denne kan med fordel plasseres som en frioppstilling dersom det finnes tilstrekkelig med fastmerker i nærheten. Dermed kan også fastmerkenettets kvalitet kontrolleres under måling/beregning. I tillegg er prismeenheten koblet mot en PC som har lagret både koordinater på omkringliggende, faste referansepunkt og data for sporgeometrien. Foruten koordinatbestemt posisjon har tralla også utrusting for å måle sporvidde og overhøyde.
Fremgangsmåten er som følger:
- Tralla stoppes og prismet loddes
- RPU (prismet) rettes mot robotstasjonen og måling utføres automatisk
- Måledata overføres til PC og jevnføres med sporvidde og overhøyde
- En koordinatberegning utføres på stedet slik at avvik mellom prosjektert og faktisk beliggenhet påvises direkte
- Data lagres/listes og forestående justering merkes gjerne på skinnene
I nyere tid har også prisme-/totalstasjonsutrustningen på SurVer blitt skiftet ut med kinematisk GPS, både som etterprossesseringsløsning og sanntidsløsning, sistnevnte med krav om radioforbindelse. Dette forenkler kravet til faste referansepunkt betraktelig, men forlanger naturligvis at det finnes god dekning for slik måling på hele den aktuelle strekningen.
De ovenstående metoder har til felles at sporet forhåndsinnmåles før en evt. justering. Vi skjønner umiddelbart at dette er en ressurskrevende fremgangsmåte, og eksempelvis vil det med Surver ZVS ta i underkant av 3 timer å måle inn 1 km spor. En av fordelene er imidlertid at feil i referansepunktene og/eller målingene kan avdekkes innen justering skal utføres.
Ved de franske høyhastighetsbanene, SNCF’s TGV, er det utviklet et system som ligner vår egen utfestingsmetode VUL, men det franske systemet holder en langt høyere nøyaktighet pga. de høye hastighetene (300 km/h+).
Figur 31: Franske TGV med fastmerker mellom sporene
Som vi ser i figur 31, ligger fastmerkene som sorte søyler mellom sporene med svært kort innbyrdes avstand. Ved prosjektering/nybygg settes merkene opp hver 10. meter i kurver (hver 40. meter på rettlinje), for vedlikehold hver 20. meter (eller hver 100.) Ved endring av geometrien settes nye søyler ned, i motsetning til ved VUL, der ny beliggenhet, eller VUL-data, beregnes for samme merke.
For justering beregnes bakse- og løfteverdier etter utjevning av pilhøyder, men intervallene mellom verdiene varierer med kvalitetskravet til den aktuelle linjen.
Langsehne
“Langsehne”, som betyr lang linje, er en metode som ble utviklet i systemet Driver (Holland) og senere i Båglaser (Finland). Systemene baserer seg på faste referansepunkt fra hver 60. - 70. meter (kurver) til hver 150. - 300. meter (rettlinjer), montert på KL-mastene langs linjen. Den lange linja/korden dannes ved at en separat tralle med laserutrustning rulles fram til neste referansepunkt, mens pakkmaskinen står ved det forrige.
Fremgangsmåten er som følger:
- Lasersenderen på tralla justeres inn til prosjektert beliggenhet (etter vinkelrett måling med målebånd til referansepunktet) og rettes mot lasermottakeren på pakkmaskinen
- Laseren registrerer forflytningen i side/høyde fra sville til sville ettersom maskinen går frem (evt. bare måling i første omgang)
- Det korrigeres for krumning i sporet, og deretter styrer laseren hvor mye det skal justeres utfra den teoretiske beliggenheten i forhold til korden
- Når maskinen når igjen tralla, flyttes tralla til neste referansepunkt
Som vi ser er dette en on-line prosedyre der justeringen skjer i umiddelbar ettertid av måling. Et problem er dermed at vi ikke har noen kontroll med referansepunktenes kvalitet, f.eks. med hensyn til setninger i mastene de er montert på. I og med at justering foregår fra punkt til punkt, vil evt. feil i referansepunktene, eller feil innstilling av lasersenderens posisjon, kunne medføre langbølgede feil i sporet som vil forplante seg bortover. Lasermålesystemet har heller ingen korreksjoner innlagt for effekter som refraksjon og jordkrumming.
Figur 32: Prinsipp for Langsehne: justering med laserkorde
Ved JBV har også laser blitt anvendt ved justering, men da kun for korrigering av rettlinjer. Figur .33 illustrerer prinsippet. I dette tilfellet forholder vi oss ikke til et koordinatbestemt spor, slik at bakseverdier beregnes utfra en laserkorde, men setter opp senderen i enden av en rettlinje. Videre må pakkmaskinen ha korrekt sidebeliggenhet, slik at rettlinjen som oppnås sammenfaller med teoretisk beliggenhet.
Figur 33: Justering med laser på rettlinje
Foruten strenge krav til maskinens posisjon og innstillingen av instrumentet, finnes en fallgruve med sistnevnte metode. I enkelte tilfeller finnes korte kurver med svært store radier (>20000 m). Disse kurvene er så slake at overgangskurver og overhøyde er utelatt, samtidig med at målte pilhøyder blir praktisk talt lik null. Å justere disse kurvene som om de var rettlinjer vil raskt skape en stor baksefeil.
Integrert måling og justering
I forrige avsnitt så vi på et justeringssystem som effektiviserte samspillet mellom måling og justering mht. tidsforbruk. Men fortsatt ble noe av målingen utført uavhengig av maskinen (avstanden referansepunkt – sender på måletralle).
Ved SBB i Sveits benyttes imidlertid et integrert system som både måler og justerer i én kontinuerlig operasjon. Systemet kalles Palas og består av følgende:
- måletralle, montert på pakkmaskinen
- laserutrustning for vinkelmåling – RALF
- system for treghetsposisjonering - DRU
- (PC’er)
Kort fortalt oppnår maskinen en absolutt beliggenhet med målesystemet om bord gjennom å måle til fastmerker langs linjen med en innbyrdes avstand på maksimalt 60 m. På samme måte som for Langsehne-prinsippet finnes fortsatt en usikkerhet i at referansesystemet ikke kontrolleres samtidig med at de anvendes, så det må ha god kvalitet og tetthet.
Laserutrustningen om bord (RALF) måler som nevnt vinkler til de ulike fastmerkene langs linjen, og dette utføres helautomatisk ved at laseren søker opp og finner prismer montert på merkene, som monteres og demonteres av en operatør. I og med at metoden forutsetter koordinatbestemt spor, vil sporet til enhver tid ha en kjent, teoretisk retning i forhold til fastmerkene. Avviket mellom målte og teoretiske vinkler vil dermed danne grunnlag for beregning av løfte-/bakseverdier. Målesystemet må også ha kjent posisjon i lengderetningen, og denne oppnås ved vinkelrett avstandsmåling til hvert referansepunkt. Samtidig måles det kontinuerlig mellom punktene med målehjul, i og med at det kan være vanskelig å ha nok referansepunkter i de krappeste kurvene.
Vinkelmålingene trenger imidlertid en referanse utover sporplanet. Når vinkler måles i to dimensjoner, vil disse naturlig nok dreie med sporets beliggenhet og de feil som finnes. Derfor er det nødvendig å relatere målingene til det absolutte horisontal-/og vertikalplanet. Til dette benyttes treghetssystemet ombord (DRU), som gjennom måling av tyngdeakselerasjon finner den treaksede dreiningen til måleutstyret. Systemet støttes i tillegg av en målt GPS-posisjon (lengde, bredde og høyde) for å kunne angi jordakselerasjonen på stedet.
RALF og DRUs mellomliggende posisjon er eksakt kalibrert, og delsystemene er montert på samme plate.
Til slutt samordnes det koordinatbaserte måle- og justeringssystemet (Palas) med et pilhøydebasert system for glatting (NEMO) for å styre løft og baks. I praksis rettes fremste sensor i NEMO inn etter Palas’ beregningsresultater.
Figur 34: Prinsippskisse for integrert måle- og justeringsmaskin ved SBB
Prinsippet med Palas har mange fortrinn sammenlignet med de andre systemene gjennomgått i de øvrige avsnittene. Det integrerte måle- og justeringssystemet opererer kontinuerlig, har få feilkilder og forutsetter liten innsats fra linjepersonell. Den eneste store ulempen er kravet til referansesystem. Det forutsettes fastmerker med innbyrdes avstand mindre enn 60 m, noe som er langt tettere enn for eksempel med Jernbaneverkets normale krav til fastmerkenett. Men ved utvidelse av GPS-systemet om bord, slik at en eksakt posisjon for spormidt kan oppnås, vil behovet for store deler av referansesystemet falle bort.
Sporjustering og stabilitet
Sporets stabilitet er sporets evne til å motstå forskyvninger i side og høyderetning.
Stabilitet generelt
Årsaker til nedsatt stabilitet
Sporets stabilitet kan være nedsatt på grunn av forskjellige mangler i sporets over- og underbygning som f. eks:
- dårlig drenering
- ballastforurensing
- manglende ballastmengde
- manglende formasjonsbredde
- dårlig underbygning
- feil nøytraltemperatur
- sideforskyvning av sporet
Konsekvens av justering
Under justeringsarbeidet løsnes pakkingen av ballasten rundt svillenes ende og sideflater. Dette medfører en reduksjon i sporets stabilitet. Sporet oppnår sin maksimale stabilitet en tid etter justering av sporet er foretatt ved hjelp av trafikkbelastningen eller ved bruk av dynamisk sporstabilisator. Dette gjelder imidlertid ikke på steder med dårlig underbygning, og steder der det har vært store feil i høyde og sidebeliggenhet.
Togpassering over grovjusterte, ikke stabiliserte sporavsnitt
En del arbeider kan i stor grad kan redusere sporets sidemotstand og justeringsstandarden, for eksempel:
- svillefornyelse
- større løft eller senking av sporet
- ballastfornyelse og ballastrensing
- teleforebyggende arbeider og andre gravearbeider under sporet
I disse sporavsnitt nedsettes kjørehastigheten til 40 km/h eller mindre. Togpassering kan for øvrig bare tillates når minstekravene i avsnitt 3.3.2 og 3.4.2 er oppfylt.
Ovennevnte hastighetsreduksjoner er ikke nødvendig ved bruk av dynamisk sporstabilisator etter arbeidene.
Figur 35: Dynamisk sporstabilisator
En dynamisk sporstabilisator gjør ballasten kompakt via skinnene ved at sporet trykkes vertikalt nedover med et akseltrykk på eksempelvis rundt 240 kN, med ulike frekvenser. Maskinen benyttes umiddelbart etter at det er justert med skinnegående pakkmaskin, i og med at denne (ved større justeringsarbeider) opphever rundt 50% av sporets stabilitet. Stabilisatoren kan gjenvinne rundt halvparten av dette tapet igjen dersom sporets tilstand og ballastprofilet holder en god nok kvalitet. For enkelte maskiner tilsvarer bruk av stabilisator en samlet trafikkmengde på 70000 bruttotonn. Som det fremgår av avsnitt 6.3, innebærer dette at saktekjøringer etter justering ikke blir nødvendig.
Før togpassering skal det likevel kontrolleres at kravene det er henvist til over, oppfylles. Bruk av sporstabilisator fritar kun for hastighetsnedsettelse. Før arbeidsstedet forlates, skal det dessuten foretas kontroll etter første togpassering. Når arbeidet blir innstilt i ett eller flere døgn, skal det foretas en kontroll minst én gang pr. døgn. Dette gjelder inntil sporet er pakket med skinnegående justeringsmaskin.
Bestemmelser for større justeringsarbeider
Ved planlegging og under utførelse av arbeidene skal det tas hensyn til følgende:
- Partier hvor ballasten helt eller delvis må fjernes, skal ikke avsluttes ved en laskeskjøt eller mot veidekket i en planovergang. Mellom enden av slike partier og nærmeste laskeskjøt eller nærmeste kant av et veidekke skal det gjenstå en avstand på minst 4 m.
- I en avstand av 4 m fra landkaret for en bru som ikke har gjennomgående ballast, tillates ballasten fjernet helt eller delvis, men bare i den tiden som trengs for gjennomføring av arbeidene. Dvs. ballasten fjernes senest mulig og ballastprofilet settes i stand før arbeidsstedet forlates.
- Når det kan ventes skinnetemperaturer over 300C, skal ballasten ikke fjernes i en avstand av 15 m fra brukaret til en bru uten gjennomgående ballast eller fra veidekket i en planovergang.
- Når sporet skal bakses eller løftes, og når overhøyden skal endres, skal det tas hensyn til minste tverrsnitt og kontaktledningsanlegget.
- Kabler langs sporet må vises spesiell oppmerksomhet slik at ikke driftsforstyrrelser oppstår.
Sikring mot solslyng
For pakking/baksing av helsveist spor gjelder temperaturbegrensninger som er fastsatt i Teknisk regelverk - Krav til sporarbeider.
Ved grove sporfeil der akuttgrensene for vindskjevhet eller sidefeil er overskredet, begrenses justeringen til vedkommende steder og hastighetsreduksjoner gjennomføres i hht. nedenstående punkter.
Dersom ballastprofilet tilfredsstiller betingelsene som er angitt i Teknisk regelverk - Ballast, skal det etter pakking/baksing i helsveist spor med kurveradier mindre enn 400 m gjennomføres hastighetsreduksjon til 40 km/h eller mindre på alle dager når skinnetemperaturen er over 300C eller kan ventes å bli større enn 300C. Dette gjelder inntil det har passert en samlet trafikkmengde på 50000 bruttotonn siden pakking/baksing ble foretatt.
Hastighetsnedsettelsene er ikke nødvendig ved bruk av dynamisk sporstabilisator.
Dersom ballastprofilet har mindre dimensjoner enn angitt i Teknisk regelverk - Ballast, skal det etter pakking/baksing i helsveist spor med kurveradier mindre enn 400 m gjennomføres hastighetsnedsettelse til 40 km/h eller mindre inntil det har passert en samlet trafikkmengde på 50000 bruttotonn. Dette gjelder uansett skinnetemperatur.
Ovenstående regler gjelder også for lasket spor med skinnelengder over 30m.
Hastighetsreduksjonene skal gjennomføres over hele avsnittet hvor arbeidene har foregått samt 50 m til begge sider.
Vedlegg
Bakseberegning med BAKSBER
Beregnet dato: 28 - 9 1999
UTJEVNINGSGRAD = 0 FILNAVN = lill1401.bax KILO- MÅLT ØNSKET NY BAKSVERDIER BAKSEKORRIDOR METER PILH PILH PILH VENSTRE HØYRE VENSTRE HØYRE ---------------------------------------------------------------- 24780 -.2 .0 -2.0 0. 100 100 24790 -3.7 .0 -1.6 4. 100 100 24800 -.2 .0 -1.1 3. 100 100 24810 -5.7 -3.4 -4.1 4. 100 100 24820 -5.9 -6.8 -7.1 2. 100 100 24830 -11.4 -10.2 -10.2 2. 100 100 24840 -13.2 -13.6 -13.5 0. 100 100 24850 -13.8 -17.1 -17.0 1. 100 100 24860 -23.4 -20.5 -20.4 3. 100 100 24870 -25.7 -23.9 -23.9 2. 100 100 24880 -25.3 -27.3 -27.3 3. 100 100 24890 -28.5 -27.3 -27.3 3. 100 100 24900 -28.3 -27.3 -27.4 7. 100 100 24910 -24.3 -27.3 -27.4 12. 100 100 24920 -25.7 -27.3 -27.4 11. 100 100 24930 -27.6 -27.3 -27.5 6. 100 100 24940 -27.0 -27.3 -27.5 2. 100 100 24950 -27.5 -27.3 -27.6 3. 100 100 24960 -28.8 -27.3 -27.6 8. 100 100 24970 -25.1 -27.3 -27.7 11. 100 100 24980 -31.1 -27.3 -27.8 20. 100 100 24990 -26.9 -27.3 -27.8 21. 100 100 25000 -29.6 -27.3 -27.9 24. 100 100 25010 -29.2 -27.3 -28.0 24. 100 100 25020 -26.4 -27.3 -28.1 22. 100 100 25030 -33.2 -27.3 -28.1 23. 100 100 25040 -28.5 -27.3 -28.2 14. 100 100 25050 -25.5 -27.3 -28.2 4. 100 100 25060 -26.6 -27.3 -28.1 1. 100 100 25070 -28.9 -27.3 -27.9 2. 100 100 25080 -25.9 -27.3 -27.8 5. 100 100 25090 -29.6 -27.3 -27.6 5. 100 100 25100 -27.0 -27.3 -27.4 9. 100 100 25110 -27.0 -27.3 -27.2 12. 100 100 25120 -27.8 -27.3 -27.1 14. 100 100 25130 -26.9 -27.3 -26.9 18. 100 100 25140 -22.2 -27.3 -26.7 22. 100 100 25150 -24.4 -27.3 -26.6 16. 100 100 25160 -28.9 -27.3 -26.4 7. 100 100 25170 -26.8 -27.3 -26.4 2. 100 100 25180 -28.7 -27.3 -26.5 1. 100 100 25190 -25.6 -27.3 -26.6 1. 100 100 25200 -27.1 -27.3 -26.6 2. 100 100 25210 -26.8 -27.3 -26.7 3. 100 100 25220 -25.4 -27.3 -26.7 3. 100 100 25230 -30.1 -27.3 -26.8 5. 100 100 25240 -26.1 -27.3 -26.8 2. 100 100 25250 -28.4 -27.3 -26.9 1. 100 100 25260 -23.8 -27.3 -27.0 6. 100 100 25270 -28.1 -27.3 -27.0 5. 100 100 25280 -25.7 -27.3 -27.1 6. 100 100 25290 -28.6 -27.3 -27.1 5. 100 100 25300 -27.0 -27.3 -27.1 6. 100 100 25310 -25.6 -27.3 -27.2 7. 100 100 25320 -26.8 -27.3 -27.2 5. 100 100 25330 -28.0 -27.3 -27.2 3. 100 100 25340 -28.5 -29.0 -29.0 1. 100 100 25350 -28.3 -30.7 -30.7 1. 100 100 25360 -36.2 -32.4 -32.4 8. 100 100 25370 -31.8 -32.4 -32.5 7. 100 100 25380 -34.7 -32.4 -32.5 8. 100 100 25390 -30.8 -32.4 -32.5 4. 100 100 25400 -33.8 -32.4 -32.5 4. 100 100 25410 -34.9 -32.4 -32.6 1. 100 100 25420 -30.6 -32.4 -32.6 7. 100 100 25430 -31.5 -32.4 -32.6 10. 100 100 25440 -33.0 -32.4 -32.6 11. 100 100 25450 -30.4 -32.4 -32.7 13. 100 100 25460 -31.1 -32.4 -32.7 11. 100 100 25470 -33.4 -32.4 -32.7 5. 100 100 25480 -30.4 -32.4 -32.7 1. 100 100 25490 -35.9 -32.4 -32.7 8. 100 100 25500 -31.1 -32.4 -32.7 11. 100 100 25510 -35.7 -32.4 -32.6 17. 100 100 25520 -35.5 -32.4 -32.6 16. 100 100 25530 -29.1 -32.4 -32.5 10. 100 100 25540 -32.8 -32.4 -32.4 11. 100 100 25550 -33.0 -32.4 -32.4 11. 100 100 25560 -35.3 -32.4 -32.3 9. 100 100 25570 -32.6 -32.4 -32.2 2. 100 100 25580 -29.1 -32.4 -32.2 7. 100 100 25590 -29.9 -32.4 -32.1 9. 100 100 25600 -33.1 -32.4 -32.0 6. 100 100 25610 -31.5 -32.4 -32.1 6. 100 100 25620 -33.9 -32.4 -32.1 5. 100 100 25630 -31.1 -32.4 -32.2 7. 100 100 25640 -31.9 -32.4 -32.3 7. 100 100 25650 -30.3 -32.4 -32.3 6. 100 100 25660 -33.3 -32.4 -32.4 2. 100 100 25670 -35.2 -32.4 -32.5 1. 100 100 25680 -31.3 -32.4 -32.5 1. 100 100 25690 -33.7 -32.4 -32.6 1. 100 100 25700 -29.6 -31.4 -31.7 3. 100 100 25710 -24.9 -26.6 -26.9 1. 100 100 25720 -24.8 -21.8 -21.9 5. 100 100 25730 -18.9 -16.9 -16.9 5. 100 100 25740 -10.1 -12.1 -11.8 1. 100 100 25750 -.9 -7.3 -6.8 0. 100 100 25760 -8.4 -2.4 -1.8 11. 100 100 25770 .4 .0 .9 9. 100 100 25780 -.6 .0 1.1 6. 100 100 25790 4.4 .0 1.2 0. 100 100 ---------------------------------------------------------------- SUMME BAKS = 700 STANDARDAVVIK = .50
Nye OB/OE-punkter og radier Km R ---------------- 24780 .0 24800 .0 24880 1831.5 25330 1831.5 25360 1543.2 25698 1543.2 25765 .0 25790 .0
LITTERATURHENVISNINGER
- Enoksen, Løhren og Våge - Sporjustering, Fag 30345 Jernbaneteknikk VK, NTNU Notat nr. 1038 (1997)
- Esveld, Coenraad, Dr. - Modern Railway Track, 446s. (1989)
- Evenmo, Ole - Mekanisering av linjevedlikeholdet, NSB-Teknikk nr. 1 1978
- Gulliksrud, Erik - Sporgeometrijustering, EEU-kurs Jernbaneteknikk, NTH (1992)
- Heje, Kolbjørn - Vei og jernbanebygging, Håndbok for undervisning og praksis, H. Aschehoug & CO, 837s. (1941)
- Jernbaneverket - Overbygning-Vedlikehold, Teknisk regelverk JD 532 (01.01.99)
- Kreyszig, Erwin – Advanced Engineering Mathematics, 4th edition, Ohio State University (1979)
- Kufver, Björn - Baxning med 3-punkts respektive 4-punktsmetod, VTI Notat J 04 (1990)
- Lundén, Sten & Södergren, Björn - Styrning av spårriktare från fast referenssystem, Banverket TB-rapport 96-1 (25.01.96)
- Marriott, D.C. - Improving the performance of track lining and levelling machines, Paper 11031, Proceedings of the Institution of Civil Engineers - Transport (aug. 1996)
- Matisa – Multi-kalkulator für Kurvenkorrekturen, Gebrauchsanweisung
- Schive, Christopher – NSB; Brukerbeskrivelse for programmet BAKSBER, versjon 4.0 (okt. ’88)