Utledning kurveveksler: Forskjell mellom sideversjoner
| Linje 132: | Linje 132: | ||
<div style="width: 100px; margin: 0 auto;"> | <div style="width: 100px; margin: 0 auto;"> | ||
<math> | <math> | ||
R = \frac{2r_0\cdot tan(\alpha/2)}{\alpha\cdot(\frac{r_0}{r} | R = \frac{2r_0\cdot tan(\alpha/2)}{\alpha\cdot(\frac{r_0}{r}\pm1)} | ||
</math> | </math> | ||
</div> | </div> | ||
| Linje 139: | Linje 139: | ||
<div style="width: 100px; margin: 0 auto;"> | <div style="width: 100px; margin: 0 auto;"> | ||
<math> | <math> | ||
r = \frac{r_0}{ | r = \frac{r_0}{1\mp\frac{2r_0\cdot tan(\alpha/2)}{R\alpha}} | ||
</math> | </math> | ||
</div> | </div> | ||
for henholdsvis innoverbøyd | for henholdsvis utoverbøyd og innoverbøyd veksel.</br> | ||
<math>\mp</math> | |||
Sideversjonen fra 19. apr. 2021 kl. 10:51
Utledning, formel for radier, kurveveksel
Her følger utledning av formler for radius i kurveveksler, gitt at dene ene av de to radiene er kjent. Formelgrunnlaget baserer seg på at stigningen i vekslene holdes konstant når den enkle vekselen bøyes.
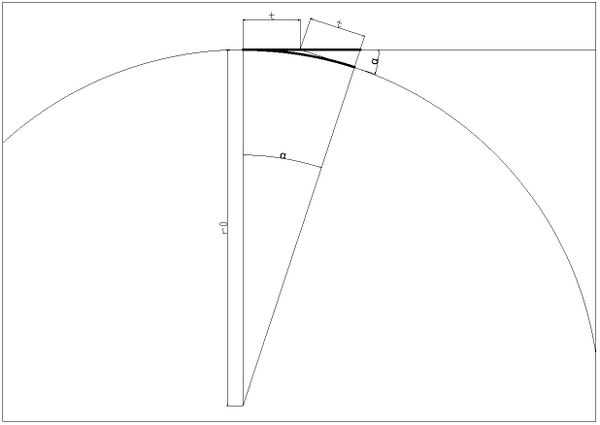
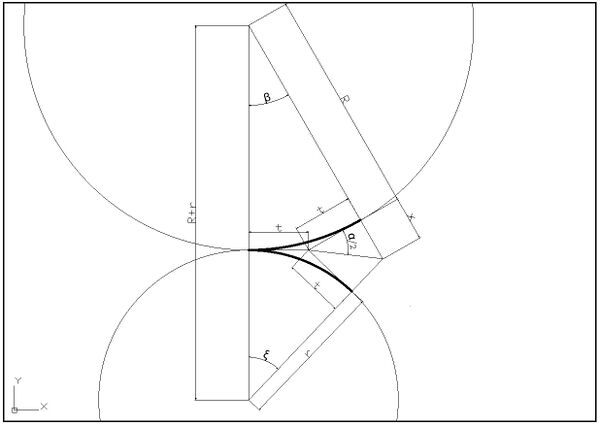
I figuren under vises geometri for en enkel sporveksel med lang kurve og en utoverbøyd kurveveksel.
Siden vinkelen er liten, antas t å være tilnærmet lik både før og etter bøying av den enkle vekselen. Ved å benytte cosinussetningen:
oppnås følgende sammenheng mellom radier og vinkel, :
Videre bearbeiding av denne ligningen gir:
Ved å benytte den trigonometriske identiteten:
gir dette videre:
Fra geometrien i den enkle vekselen, kan vi nå innføre:
Merk at dette er en tilnærming som kun er gyldig når stigningen i vekselen kan ses på som liten.
Ved å også benytte at
får vi
og til slutt
Denne ligningen kan også løses for r, og uttrykket blir da
Alternativ løsning
En mer nøyaktig sammenheng mellom R og r kan oppnås ved å benytte følgende sammenhenger:
og enten
for utoverbøyd veksel, eller
for innoverbøyd veksel.
Dette gir
for henholdsvis utoverbøyd og innoverbøyd veksel.
Dersom det løses for r, blir resulterende ligning
for henholdsvis utoverbøyd og innoverbøyd veksel.