Underbygning/Setninger

__NUMBEREDHEADINGS__

Setninger som problem for jernbaneanlegg

Hvorfor oppstår setninger

Ved bygging på bløt grunn vil det oppstå setninger som følge av økte belastninger. Setninger i bløt grunn utvikles over lang tid og varierer i størrelse med grunnforhold og belastninger. Setninger kan også oppstå på grunn av grunnvannssenkning.

Skadelige setninger for baneanlegg

Setninger i grunnen kan innebære betydelige problemer ved utbygging av jernbaneanlegg på bløt grunn. Moderne jernbaneanlegg beregnet for høye kjørehastigheter har stiv linjeføring og har høye krav til justeringsstandarden for sporet.

For baneanlegg er det differensialsetninger som er kritisk. Brå overganger i grunnforhold kan gi store setningsforskjeller både på tvers og langs av sporet og mellom sporet og mastefundamenter. Høydefeil og vindskjevhet vil kunne oppstå. Dette vil gi økt behov for overvåking og justering av sporet, og kan gjøre det vanskelig med rasjonell drift av baneanlegget. På områder med bløt grunn kan det være både nødvendig og lønnsomt å ta i bruk setningsreduserende fundamenteringsmetoder.

Hvordan løse setningsproblemene

Ved planlegging av nye jernbaneanlegg på bløt grunn er det nødvendig å utarbeide prognoser for framtidige setninger. Med tanke på å sikre ønsket kvalitet av det ferdige baneanlegget er det ideelt sett behov for å besvare disse problemstillingene:

• forventet tidsutvikling av differansesetninger på langs og på tvers av sporet
• forventet utvikling av setningsforskjeller mellom mastefundamentene og sporet

Det er meget vanskelig å gi sikre prognoser for differansesetninger. I praktisk geoteknisk prosjektering blir først og fremst karakteristiske setninger analysert. For jernbaneanlegg vil det innebære analyse av setningenes tidsforløp i karakteristiske tverrprofiler langs planlagt trasé. Slike beregninger gir imidler­tid også et visst grunnlag for å bedømme hvordan eventuelle differanse­setninger i lengderetningen ut­vikler seg med tiden. Nøyaktigheten i en slik bedømmelse vil imidlertid avhenge sterkt både av hvor omfattende grunnundersøkelser som gjøres, og hvilke setningsanalyser som blir utført.

Teorigrunnlag og beregningsmodeller

Hovedprinsipper for setningsberegninger

Mange faktorer påvirker setnings­prosessen, og lasthistorien som jorden utsettes for i byggeperioden kan være kompleks. Det skilles mellom tre prinsipielt forskjellige setnings­bidrag:

• Initialsetninger er de setningene som kommer momentant ved pålasting. I praksis er det vanlig å inkludere alle setninger i løpet av byggeperioden i initialsetningene. For å kunne beregne initialsetninger må man kjenne jordens stivhet.

• Primærsetninger er de setningene som kommer i perioden fra pålasting er utført, til poreovertrykket som tilleggslasten gir, er borte. I praksis er det vanlig å sette starttidspunktet for primærsetningene ved byggeperiodens slutt. For beregning av primærsetninger og tidsforløpet av dem benyttes følgende parametre:
  • konsolideringskoeffisient, Cv
  • prekonsolideringstrykk, pc'
  • initielle effektivspenninger, σz0'
  • kompresjonsmodul, M

Parametrene finnes fra ødometerforsøk på materiale fra prøvetaking (se avsnitt 3.1).

• Sekundærsetninger er tidsavhengige setninger under konstante effektivspen­ninger. Prosessen som gir sekundærsetninger kalles kryp. Normalt ser man bort fra kryp ved setningsberegninger.

I tillegg kommer setninger på grunn av syklisk belastning. Grunnen under et jernbanespor vil bli utsatt for vekslende last. Tunge lokomotiv og godsvogner kan gi kortvarige tilleggsbelastninger. Effekten av disse belastninger er ikke vurdert her.

Spenninger og spenningsendringer i jord

Generelt

Jordas tre faser (fast stoff, vann og luft) vil alle påvirkes av en belastning utenfra. Kornskjelettet vil presses sammen og vannet i porene vil, for tette jordarter, yte stor motstand mot kompresjon. Et økt poretrykk vil oppstå. Dersom det er luft tilstede i porene vil dette virke som en myk fjær og dempe tilveksten av poretrykk. Hvordan jorden som helhet reagerer på belastningen er derfor avhengig av:

• fasesammensetningen (porøsitet, poremetningsgrad)
• kornfordeling (velgradert, ensgradert, korn- og porestørrelse)
• tiden som er løpt etter at årsaken til spenningsendringen oppstod

Begrepene drenert og udrenert henspeiler på i hvilken grad disse faktorer tillater vannet i jorden å unnslippe ved strømning gjennom porene.

Et materiale som oppfører seg drenert vil tillate porevannet å slippe fram slik at poretrykket i materialet forblir det samme både før og etter belastning. En spenningsendring på grunn av ytre belastning vil dermed være en endring i effektivspenning. Normalt vil materialer i fraksjonene grov silt, finsand og grovere oppføre seg drenert.

Et materiale som oppfører seg udrenert vil hindre porevannet i å strømme i porene slik at en endring i poretrykk oppstår like etter belastning. Denne endringen kan i størrelse være maksimalt lik lastendringen, oftest noe mindre. Endringen i spenning på grunn av en belastning blir derfor delvis poretrykks- og effektivspenningsendring. Normalt vil leire og silt oppføre seg udrenert. I slike materialer vil det kreves betydelig tid for at tilveksten i poretrykk skal dreneres bort slik at initiell poretrykkstilstand igjen oppstår.

Effektivspenningsprinsippet

Ved belastning av vannmettet jord, vil det oppstå økte trykk- og skjærspenninger i korn­skjelettet og trykk­øking i porevannet. Den del av de totale spenningene som bæres av korn­skjelet­tet kalles effektiv­spenning, σ'. Vanntrykket kalles poretrykk, u. Effektivspenningene kan ikke måles direkte, men beregnes fra målt eller beregnet totalspenning og poretrykk.

Effektivspen­ningsprin­sippet kan formuleres:

σ' = σ – u

(3.1)

σ'	= effektivspenning
σ	= totalspenninger
u	= poretrykk

Konsolidering

Leire og silt vil som regel oppføre seg udrenert. I slike materialer vil det kreves betydelig tid for at tilveksten i poretrykk skal dreneres bort slik at initiell poretrykkstilstand igjen oppstår. Prosessen som foregår kalles konsolidering og tiden som går med for at poreovertrykket, Δu, skal forsvinne kalles primær konsolideringstid, tp, og kan for leirer være svært lang (opptil flere 10‑år). I takt med at porevannet langsomt presses ut vil effektivspenningene øke og kornskjelettet presses sammen. Setningene i slike masser vil derfor komme gradvis over lang tid.

Parametre for å beregne setninger kan finnes ved hjelp av laboratorieforsøk, se kapittel 3.1.

Viktige begreper i konsolideringsteorien er:

Primær konsolideringstid:	tp = tiden det tar før poreovertrykket skapt av lastpåføringen er borte
Tidsfaktoren, dimensjonsløs tid:	T = t . Cv /H2
Konsolideringskoeffisient:	Cv = material­parameter som bestemmer primærsetningens tidsforløp
Drensvei:	H = drensvei for porevannet
Tid:	t = medgått tid etter spenningsøkning

Sammenhengen mellom drensvei og konsolideringstid er gitt ved formelen tp = TH2/Cv. Tynne sjikt med drenerende masser (sand/grus) kan ha stor innvirkning på konsolideringstiden. Dersom drensveien blir halvert, blir konsolideringstiden bare ¼ i forhold til hva den ville vært med ”full” drensvei.

Prekonsolideringstrykket, pc', er et mål på hvor store effektivspen­ninger det tidligere har vært i jorden. Hvis en leire er prekonsolidert vil den deformere seg mindre ved tilleggs­belast­ning enn en leire som ikke er prekonsolidert. Prekonsolidering kan for eksempel skyldes vekten av is eller fra overliggende masser som senere er erodert bort eller av at grunnvannsspeilet har steget.

Leirer der in situ vertikal effektivspenning er tilnærmet lik prekonsolideringstrykket kalles normal­konsolidert leire (NC-leire). NC-leirer har ofte et "prekonsolideringstrykk" på opp til 1.3 ganger in situ effektivspenning. Dette skyldes ikke reell forbelastning av leiren, men sammentrykking på grunn av egenvekt i løpet av flere tusen år.

Overkonsoliderte leirer (OC-leirer) har lavere in situ vertikal effektivspenning enn prekonsolideringstrykket.

Spenningsmodul

Jordas stivhet beskrives ved modul eller motstand. Modulen bestemmes fra ødometerforsøk. Spenningsmodulen for primærsetning kan uttrykkes ved:

Feil i matematikken (Konverteringsfeil. Tjeneren («cli») rapporterte: «SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "σ" found.in 1:22»): {\displaystyle M = dσ'/ dεp }

(3.2)

Spenningsmodulen, M, kan formuleres ens for alle jordarter:

$M=m\sigma _{a}\ ({\frac {\sigma ^{'}}{\sigma _{a}}})^{1-a}$

(3.3)

m	= modultall som gir informasjon om modulens stør­relse (økning i modul med effektiv­spenningsøkning)
a	= attraksjon, en spenningseksponent som sier hvordan modulen varierer med effektivspen­ning
σ'	= effektivspenning
σa	= referansetrykk, 1 atmosfære, 100 kPa

Modultallet, m, og spenningseksponenten, a, kan bestemmes ved å sette verdiene fra to punkt på modul-effektivspennings-kurven inn i den generelle ligningen.

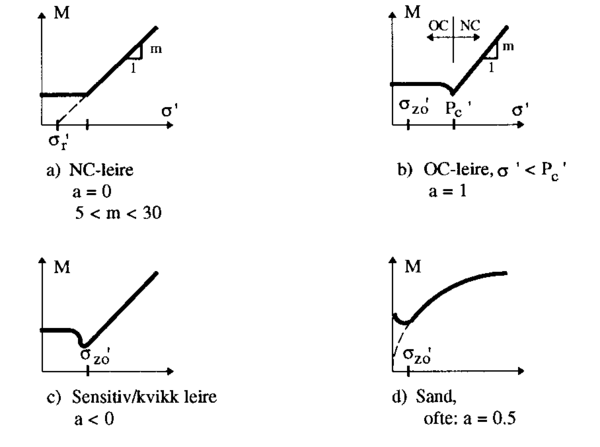
Modul som funksjon av effektivspenning, for forskjellige materialer, er skissert i figur .1.

Figur 3.1 Modul, M, som funksjon av effektivspenning for forskjellige jordarter, prinsipp-skisse.

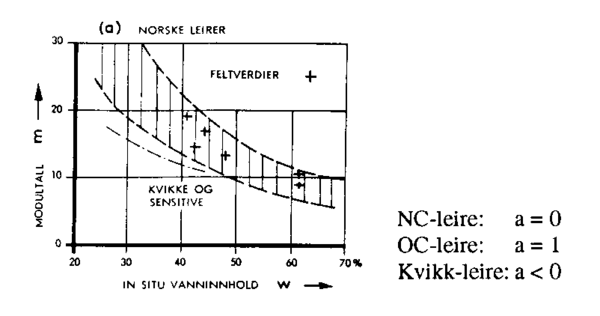
Figur .2 viser erfaringsverdier for norske leirer når det gjelder sammenhengen mellom modultall og vanninnhold.

Figur 3.2 Modultall m, og spenningseksponent a, for norsk leire

Beregningsformler

Primærtøyningen i dybde z er:

$\epsilon _{p}={\frac {\Delta \sigma ^{'}}{M}}$

(OC-leire)

(3.4)

$\epsilon _{p}={\frac {1}{m}}ln({\frac {\sigma ^{'}}{\sigma _{0}^{'}}})$

(NC-leire)

(3.5)

m	modultall
M	spenningsmodul
σ'	effektivspenning
$\sigma _{0}^{'}$	initiell effektivspenning

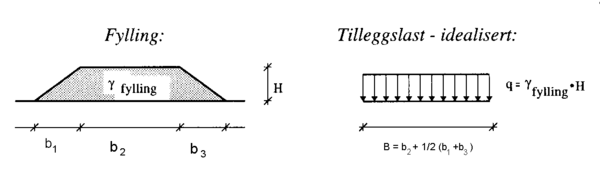
En jernbanefylling kan forenklet betraktes som en stripelast. Stripelasten, q, som jernbanefyllingen påfører grunnen, kan beregnes som vist i figur .3. Stripelasten er en funksjon av fyllingens høyde, H, bredde, B, og egen­vekten av fyllmassene, γfylling.

Figur 3.3 Beregning av stripelast pga. fylling

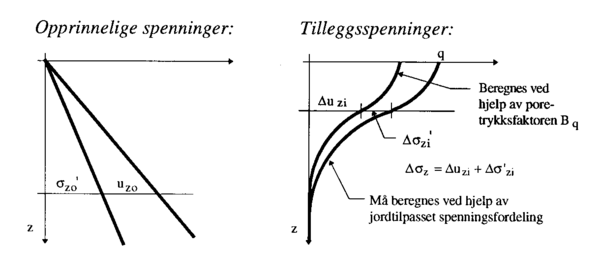
Som grunnlag for setningsberegninger må spenningsfordelingen under fyllingen og poretrykksan­delen av den totale spenningsendringen beregnes. Stripelasten, q, på grunnen, gir en vertikal tilleggsspenning, Δσz, som avtar med dybden under fyllingen. I på­lastings­øyeblikket blir noe av tilleg­gsspen­nin­gen tatt opp av kornskjelettet i form av effektivspen­ningsøkning, Δσzi', resten som pore­trykks­økning, Δuzi. Tilleggsspenningen i en gitt dybde er avhengig av jordart, lastbredde og lastintensitet.

Figur 3.4 Spenningsendringer under stripelast – problemstilling

Størrelsen av de tids­avhengige setningene er avhengig av hvor stor den vertikale effektivspennings­økningen, Δσz', er i forhold til den opprinnelige effektivspenningen, σZ0', og hvor lang tid som går. Setnings­has­tigheten avtar med tiden etter som kornskjelettet blir tettere pakket og hvert leirkorn får en mer stabil posisjon.

Tilleggsspenning som funksjon av dybde Under en stripelast oppstår spenningsspredning. Det vil si at med økende dybde, blir spenningen for­delt over større område enn selve kontaktarealet under fyllingen.

Bløt leire er et plastisk materiale og er dermed "dødt", sammen­lignet med et elastisk. Å bruke elastisk spen­n­ingsfor­deling vil gi for store tilleggsspenninger, særlig dypt under fyllingen, og dermed for store beregnede setninger. I det følgende er det tatt utgangspunkt i jordtilpasset spen­ningsfordeling.

Tilleggsspenninger under fylling på dyp leire Det er i Norge vanlig å benytte Janbus jordtilpassede spenningsfordeling, se figur .5.

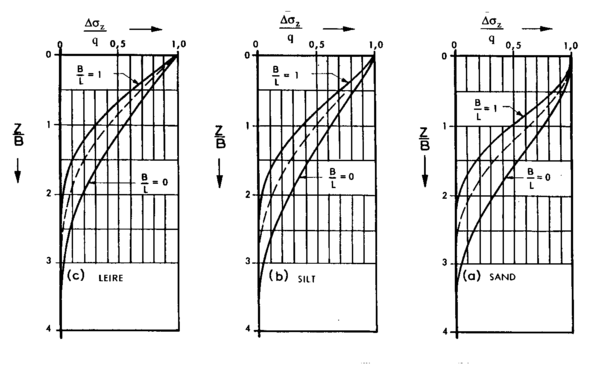
Figur 3.5 Spenningsfordeling for overflatebelastning, tilpasset jordarten sine egenskaper. B = fundamentbredde, L = fundamentlengde, Δz = tilleggsspenning på dybde z, q = stripelast på grunnen Diagrammet benyttes til å beregne tilleggsspenning som funksjon av dybde for forskjellig bredde/ lengde forhold for fyllingen, og for forskjellige materialtyper. For en stripelast gjelder kurven for B/L = 0. Dia­grammet viser at en stripelast gir tilleggsspenninger ned til en dybde tilsvarende ca 3 ganger bredden av stripelasten.

Hvis leirelaget har mindre mektighet enn halve fyllingsbredden kan det regnes med konstant tilleggsspenning med dybden.

Spenningsfordeling i lagdelt jord

Det finnes ikke en enkel, allmenngyldig metode for å beregne spenningsfordeling i lagdelt jord. I praksis benyttes spenningsfordeling for homogen jord - med noen tilpasninger.

I lagdelt grunn er det hovedsakelig de bløte jordartene som gir størst bidrag til setningene over tid. Sandlag i bløt leire øker setningshastigheten vesentlig ved å gi kortere drensvei for overskuddspore­vann, dvs dissipering av poreover­trykk. For å utføre brukbare setningsberegninger er det derfor nødvendig å kjenne lag­grens­er og ha best mulig kunn­skap om tilleggsspenningene i de bløte lagene.

Endring i effektiv vertikalspenning, Δσ'z, i grunnen under en fylling, og resulterende tøyninger i et jordelement på dyp z, er illustrert i figur .6.

Figur 3.6 Endring i effektiv vertikalspenning, z', i grunnen, - og resulterende tøyninger i et jordelement på dyp z

Driving av tunneler kan føre til at vannets veier gjennom grunnen endres, med grunnvannssenkning som følge. Likeså kan utgraving av byggegroper og vei/jernbanetrau føre til permanent grunnvannssenkning. Det er viktig å være obs på dette og installere poretrykksmålinger for å eventuelt kunne igangsette injisering av vann for opprettholdelse av poretrykket. Grunnvannssenkning fører til økning i effektivspenninger som igjen fører til setninger. Se for øvrig regneeksempel side 16.

Setningsberegninger i praksis

Bestemmelse av jordparametre

En setningsanalyse for jernbanekonstruksjon på bløt grunn krever kunnskap om:

beliggenhet og mektighet av jordlag; særlig bløte lag og drenerende lag karakteristisk lagdeling i tverrprofiler setningsparametre

Lagdeling og mektighet av jordlag bestemmes ved tradisjonelle grunnundersøkelser som sonderinger, vingeboring og prøvetaking. Jordas setningsparametre (M, m, Cv og pc’) bestemmes i laboratoriet ved ødometerforsøk. Ødometeret gir en endimensjonal deformasjonstilstand som riktignok er en forenkling av virkeligheten, men samtidig godt tilpasset de vanligste beregningsmodeller for setninger.

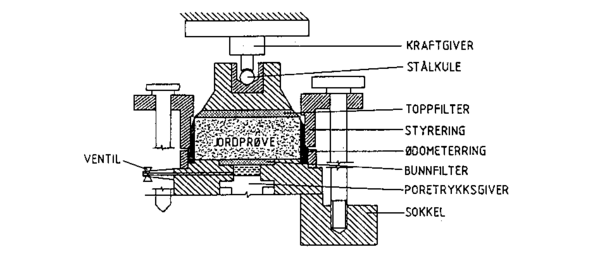
Figur 3.7 Prinsippskisse av ødometercelle

Det benyttes jordprøve fra prøvetaking med 54 mm sylinder. Jordprøven skjæres inn i en ødometerring av stål med diameter 50,5 mm og høyde 20 mm. Ringen hindrer sideutvidelse av prøven. Figur .7 viser prinsippskisse av en ødometercelle.

Prøvestykkene til ødometerforsøkene tas blant de prøvene som er minst forstyrret og slik at en får bestemt setningsegenskapene for alle setningsgivende lag.

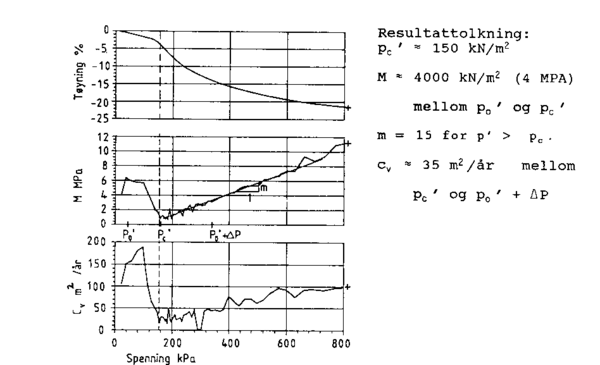
Ødometerforsøk kan utføres med trinnvis eller kontinuerlig belastning. Hver metode har både fordeler og ulemper, og ved tolkning av data er det viktig å vite hvilken metode som er benyttet. Vanligvis registreres spenning, tid og deformasjon, men poretrykk og lateral spenning kan også måles. Resultater fra ødometerforsøk, med tolkning av parametre, er vist i figur .8.

Figur 3.8 Resultater fra ødometerforsøk, med tolkning.

Praktisk beregningsgang

Dersom vi vet hvilke spenninger som er i jorda, hvilke dimensjoner jordlagene har og hvilken stivhet jorda har, kan vi beregne hvordan tøyningen nedover i jorda blir, og derav beregne setningene på overflaten. Beregningene følger følgende prosedyre:

Tabell 3.1 Beregning av setninger

1. Bestemme dybdeprofil for vertikale effektivspenninger,σz0', før bygging. (σZ0' avhenger av grunn­vannsnivå og egenvekt, γ, for jorden).	${\sigma _{z0}}^{'}$
2. Bestemme dybdeprofil for vertikalt effektivspenningstillegg, Δσz', ved endt konsolidering.	Δσ' = Δσ (Etter lang tid : Δu -> 0)
3. Skaffe til veie parametre for jordas motstand mot deformasjon. (Parametrene er avhengig av jordart, spenningsnivå og fyllingens brukstid ut over primær konsolideringstid.)	d σ' = M . dε
4. Beregne tøyning i jordelement i forskjellige dybder i grunnen.	$\epsilon =\int \limits _{\sigma _{0}^{'}}^{\sigma _{0}^{'}+\Delta \sigma ^{'}}{\frac {d\sigma ^{'}}{M}}$
5. Beregne setning­en ved å integrere tøynin­gene over lastens influensdybde.	$\delta =\int \limits _{0}^{H}\epsilon \cdot dz$

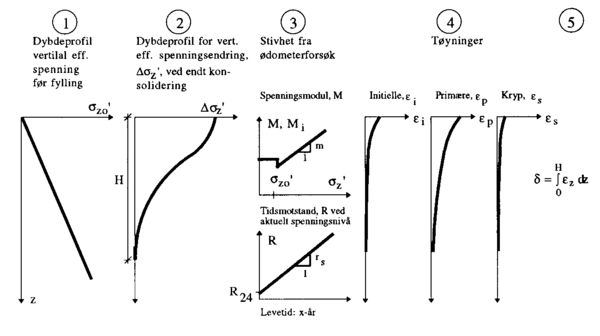
Figur .9 gir en grafisk framstilling av punktene 1-5.

Figur 3.9 Arbeidsgang ved beregning av setninger. Setningene tilsvarer arealet under tøyningskurvene.

Beregningseksempler

Eksempel: Fylling med begrenset utstrekning (f.eks. jernbanefylling)

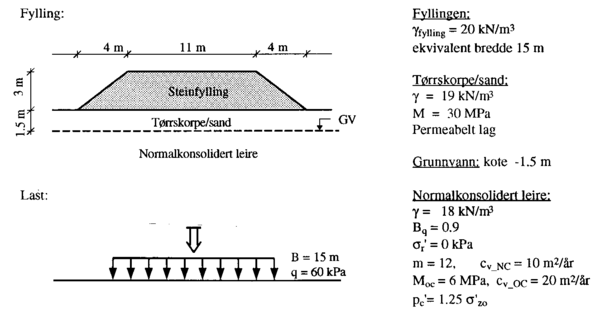
Det er bygget en 3 m høy jernbanefylling for to spor. Grunnen består av 1.5 m med blanding av sand/tørrskorpe over normalkonsolidert leire, se figur .10. Leirdybden er antatt å være større enn influensdybden for stripe­lasten. Leiren har pc' = 1.25 σ’zo. Tørrskorpe/sandlaget er antatt å være så vanngjennomtrengelig at det ikke sinker kon­soliderings­prosessen i den underliggende leiren. Vann fra den normalkon­soliderte leiren dreneres mot underkanten av tørrskorpelaget. Byg­geperioden for fyllingen er antatt å være så kort at vi regner med momentan lastpåføring.

Figur 3.10 Fylling og ekvivalent stripelast

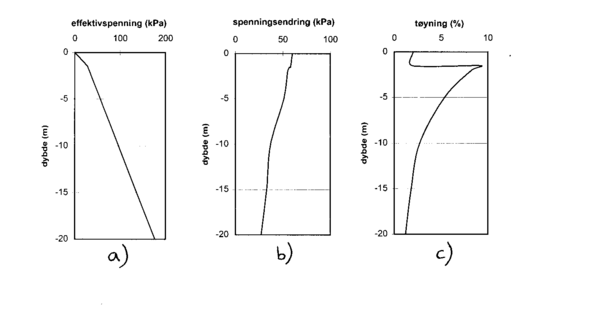
1. Vertikal effektivspenning før fylling, σZ0' er vist i figur .11a. Beregninger:

Feil i matematikken (Konverteringsfeil. Tjeneren («cli») rapporterte: «SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "ø" found.in 1:43»): {\displaystyle {\sigma_{z0}}^'=\mbox{z}_{tørrskorpe/sandlag} \cdot \gamma_{tørrskorpe/sandlag} + (z - z_{tørrskorpe/sandlag}) \cdot \gamma_{NC-leire}^'}

= 1,5·19 + (z – 1,5)·8 = 28,5 kPa + (z – 1,5m)·8kN/m3

2. Vertikal tilleggsspenning, ΔσZ, etter fylling som funksjon av dybde er vist i figur .11b. Det er tatt utgangspunkt i jordart-tilpasset spenningsfordeling i leire (fig. .5). For­holdet mellom bredde og lengde, B/L = 0, fordi jernbanefyllingen har lang utstrekning i forhold til bredde. Beregninger av vertikal tilleggsspenning er vist i tabell 3.2.

     q = zfylling. γfylling = 3. 20 = 60 kPa

3. Parametre for jordas motstand mot deformasjon er gitt i oppgaven.

4. Når vertikal tilleggsspenning er beregnet kan effektivspenning etter pålasting av fylling beregnes, og dermed kan også tøyningen beregnes. Tøyning beregnes etter følgende formler:

$\epsilon ={\frac {\Delta \sigma ^{'}}{M}}$

(for tørrskorpelaget)

(3.6)

$\epsilon ={\frac {1}{m}}\cdot ln({\frac {\sigma ^{'}}{\sigma _{0}^{'}}})$

(for NC-leire)

(3.7)

Tabell 3.2 Beregning av spenninger og tøyninger

z	${\sigma _{z0}}^{'}$	z/B	Δσz/q (avlest fra fig. .5 diagr. c)	Δσz (kPa)	σz’ = σz0’+ Δσz	tøyning %
0	0	0	1,0	60	60	2
1,5	28,5	0,1	0,96	58	86,5	1,93
2	32,5	0,13	0,92	55	87,5	8,25
5	56,5	0,33	0,85	51	107,5	5,36
10	96,5	0,67	0,62	37	133,5	2,7
15	136,5	1	0,55	33	169,5	1,80
20	176,5	1,33	0,45	27	203,5	1,19

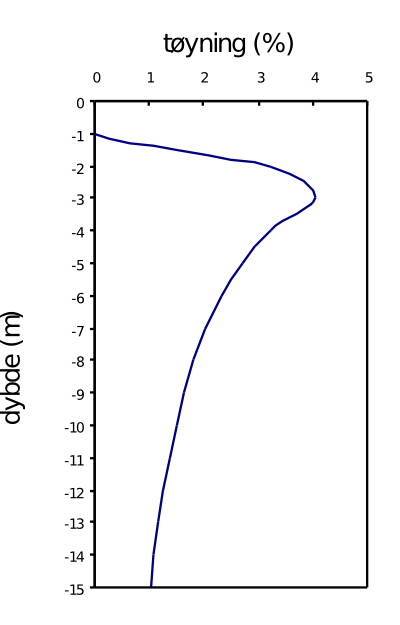
Figur 3.11 Effektivspenning før pålasting, effektivspenningsendring og tøyning-dybde-diagram.

5. Setningene beregnes som arealet under tøyning-dybde-diagrammet.

     Beregnet setning er 65 cm. 

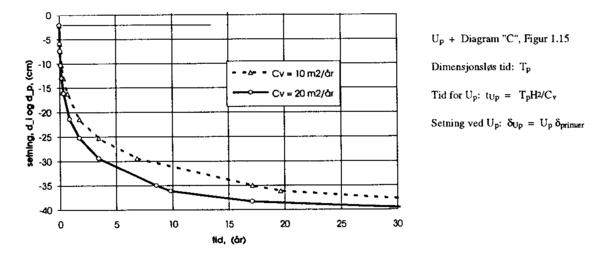
Setningenes tidsforløp Konsolideringskoeffisienten bestemmer hastigheten på konsolideringen. Den aktuelle leiren har Cv =10 m2/år i normalkonsolidert område og Cv =20 m2/år i overkonsolideringsområde. Det er ingen enkel måte å beregne hva som er "gjennomsnittlig" Cv for de aktuelle spenningsintervallene. Primær­setningen er derfor beregnet for de to ytterverdiene av Cv. Utvikling av primærsetning som funksjon av tid er vist i figur .12. Figuren viser at setningshastigheten er størst i starten og avtar etter hvert.

Figur 3.12 Primærsetning som funksjon av tid, for Cv = 10 og 20 m2/år.

Eksempel: Setninger pga. grunnvannssenkning

Grunnforhold: Den øverste meteren består av tørrskorpeleire med  = 18 kN/m3. Fra kote –1 er det NC-leire med 14 meters mektighet over fjell,  = 18 kN/m3, m = 15. Opprinnelig stod grunnvannet til kote ‑1, men pga. utgraving av byggegrop i naboterrenget sank det til kote ‑3.

Tabell .3 viser beregning av tøyninger. Figur .13 viser et tøyning-dybde-diagram som er benyttet til å beregne setningene.

Beregningene er gjort som følger:

Før GV-senkning:	$\sigma _{0}^{'}={\mbox{z}}\cdot \gamma ^{'}={\mbox{z}}\cdot 8$
	$\mu _{0}=(z-1)\cdot 10$
	$\sigma _{0}={\sigma _{0}}^{'}+\mu _{0}$
Etter GV-senkning:	$\mu _{0}=(z-3)\cdot 10$
	${\sigma _{0}}^{'}=\sigma _{0}-\mu _{0}$

Tøyningene er beregnet etter formel .6 og .7. Resultatene er vist i tabell .3.

Tabell 3.3 Beregning av tøyninger pga. grunnvannssenkning.

z	Før			Etter		tøyning
	${\sigma _{0}}^{'}$	$\mu _{0}$	$\sigma _{0}$	U	$\sigma ^{'}=\sigma _{0}-\mu$
0	0	0	0	0	0	0
1	8	0	8	0	8	0
2	16	10	26	0	26	3,24
3	24	20	44	0	44	4,04
4	32	30	62	10	52	3,24
5	40	40	80	20	60	2,70
6	48	50	98	30	68	2,32
7	56	60	116	40	76	2,04
8	64	70	134	50	84	1,81
9	72	80	152	60	92	1,63
10	80	90	170	70	100	1,49
11	88	100	188	80	108	1,37
12	96	110	206	90	116	1,26
13	104	120	224	100	124	1,17
14	112	130	242	110	132	1,10
15	120	140	260	120	140	1,03

Tøyning som funksjon av dybde er framstilt i figur .13. Setninger som følge av grunnvannssenkning er lik arealet under tøyning-dybde-kurven.

Beregnet setning = 27 cm

Figur 3.13 Tøyning-dybde-diagram til beregning av setninger

Tiltak for å redusere setningsproblemer

Behov for setningsreduserende tiltak

Ujevne setninger som oppstår etter at et nytt baneanlegg tas bruk vil forringe banens geometriske standard. Ujevne setninger vil både øke behovet for sporjustering og gi høydefeil i kontaktledningsanlegget. På partier utsatt for ujevne setninger kan det være behov for setningsreduserende tiltak i byggefasen for å hindre uakseptabelt store driftsproblemer.

Behovet for setningsreduserende tiltak må fastlegges med grunnlag i setningsberegninger på prosjekteringsstadiet. For å vurdere setningene i driftsfasen må forventet tidsutvikling av setningene beregnes. Hovedfokus må legges på setninger som er mest skadelige for baneanlegg (se avsnitt 1.2). Da det er ujevne setninger på langs og på tvers av banen som gir sporfeil, vil følgende fyllingspartier på bløt grunn være mest utsatt:

partier med varierende grunnforhold (spesielt overganger mot fast grunn) fyllingsavslutninger inn mot faste konstruksjoner (bruer, kulverter) korte fyllingspartier partier med varierende fyllingshøyde partier med tidligere oppfylling (f.eks. ved breddeutvidelse av eksisterende fylling)

Rent teknisk vil det ofte være mulig å bygge jernbaneanlegg med minimale setninger i driftsfasen. På bløt grunn vil dette kreve omfattende bruk av setningsreduserende tiltak og dermed betydelig økte byggekostnader. Omfanget av tiltak må derfor besluttes ut fra to motstridende hensyn:

Ønske om et mest mulig vedlikeholdsfritt baneanlegg. Ønske om lavest mulige byggekostnader.

For å sikre akseptable byggekostnader og vedlikeholdskostnader for nye baneanlegg på bløt grunn har Jernbaneverket innført setningskrav til bruk ved prosjektering (se avsnitt 5.1). Hensikten er å gi en akseptabel kvalitet av nye banestrekninger på setningsgivende grunn og samtidig unngå unødig store byggekostnader på slike strekninger.

Det samlede behovet for setningsreduserende tiltak på en gitt banestrekning avhenger av en rekke faktorer, særlig:

andel av strekningen som ligger på fylling fyllingshøydene kompressibiliteten av undergrunnen variasjoner i grunnforholdene

Det er normalt størst behov for tiltak for å redusere differansesetninger i banens lengderetning. Sporfeil som skyldes skjevsetninger i tverrprofilet (vindskjevhet og ujevnhet i overhøyden) er imidlertid farligere hvis de først oppstår. Partier med fare for skjevsetning må derfor også undersøkes nøye.

Tiltak for primært å redusere totalsetningene

Tiltakene som er presentert nedenfor har som primær funksjon å redusere anleggets totale setninger. Følgende tiltak er beskrevet:

masseutskifting lette fyllmasser kalksementpæler pæler

Masseutskifting

Masseutskifting kan brukes for å erstatte setningsgivende og lite bæredyktige topplag med stabile masser. Masseutskifting kan utføres ved graving (og eventuell sprengning) og gjenfylling, og ved fortrengning av erstatnings-massene, enten kontinuerlig foran fyllingstippen eller ved nedsprengning av fylling til fast grunn.

Masseutskifting vil være mest aktuelt tiltak på spesielle partier, for eksempel ved:

Ekstremt bløte topplag (torv og organisk leire). Liten, men variabel mektighet av bløte jordlag over fast grunn. I overganger mellom fast og bløt grunn og mellom fylling og skjæring.

Metoden er ikke aktuell dersom leiravsetningen har tykk tørrskorpe. Masseutskifting kan føre til ukontrollerte glidninger og setninger eller hevninger av nærliggende terreng. Faren for at nærliggende eiendom kan ta skade må vurderes i hvert enkelt tilfelle.

Lette fyllmasser

For å redusere tilleggsbelastningene på setningsgivende grunn kan det benyttes lette masser i fyllinga. Aktuelle lette massetyper er:

granulat av ekspandert leire (LECA lettklinker) blokker av ekspandert polystyren (EPS)

Begge disse massetypene har lenge vært brukt i norske vegfyllinger. LECA lettklinker har også vært brukt i jernbanefyllinger. Karakteristiske data for de to materialtypene er vist i tabell .4.

Tabell 3.4 Karakteristiske data for lette fyllmasser

	EPS	Lettklinker
Kvalitet	Trykkstyrke 200 kN/m2 Standard kvalitet (brennbar) og selvslukkende kvalitet (SE)	Gradering 0 – 32 mm
Tørr densitet (fra fabrikk)	30 kg/m3	400 kg/m3
Levering	I blokker à 1.5 – 2.5 m3	Som bulklast
Utleggingsmetode	Manuelt	Med dozer eller med blåseaggregat
Anbefalt romvekt (i setningsanalyser)	1 kN/m3	6 kN/m3 (drenert fylling) 8 kN/m3 (under grunnvann)

Bruksområder for materialene:

Reduksjon av last på undergrunn, både på ny og eventuelt gammel setningsskadet veg/jernbane. Reduksjon av jordtrykk på støttemurer og landkar. Utjevning av differensialsetninger ved overgang til konstruksjoner hvor man ikke vil få setninger. Kompensert fundamentering (dvs. ingen tilleggsbelastning på grunnen) Plassbesparende tiltak.

Det ytterste blokklaget, eventuelt hele fyllingen, skal bestå av brannhemmende (selvslukkende) materiale. (I praksis vil det ofte være praktisk å benytte samme type materiale i hele fyllingen).

Det må kontrolleres at sikkerhet mot oppdrift er tilstrekkelig. EPS-blokkene skal i sin helhet ligge drenert og over høyeste flomvannstand. I skrånende terreng må det legges tilstrekkelig drensledninger for å unngå oppbygging av horisontaltrykk mot EPS-fyllingen.

Kalksementpæler

Kalksementpæler brukes til å forbedre bæreevne og stabilitet av bløt og sensitiv leire til dybder inntil 15-25 meter. Kalk og sement reagerer kjemisk med leira og danner et jordmateriale med større skjærstyrke og stivhet enn den opprinnelige jorden. ”Pælene” settes av en beltegående rigg med borutstyr. Riggen er utstyrt med blandeverktøy, en roterende visp som bores ned til ønsket dybde for underkant pæl før innblandingen av kalk/sement starter. Kalken/sementen blåses ut i jorden gjennom en dyse ved hjelp av trykkluft samtidig som vispen roterer og trekkes opp. Jorden får på denne måten søyler av fastere masse der kalk/sement er blandet inn.

Det finnes mange eksempler på gode erfaringer ved bruk av kalksementpæler som setningsreduserende tiltak. Som stabilitetsbedrende tiltak i skråninger er det blandede erfaringer, se for øvrig kapittel 4 ”stabilitet”.

Følgende er viktig å være klar over ved bruk av metoden:

Kalksementpæler ikke er pæler i ordets egentlige betydning, men søyler av forbedret jord i forhold til omkringliggende masse. Pælene er inhomogene og det kan bare regnes at de tar aksiallast. Det kan ikke forutsettes at pælene tar strekk- og bøyepåkjenning uten at de settes sammen i blokker eller skiver som til sammen har stor skjærkapasitet. Kalk/sement blåses ut ved hjelp av trykkluft. På den måten oppstår poreovertrykk i leira. Ved setting av ks-pæler i skråninger kan dette være problematisk, da skråningen kan bli utstabil pga. det økte poretrykket. Det er viktig å følge opp med poretrykksmålere og stoppe arbeidet dersom det er fare for at skråningen skal rase ut. Ks-pæler i skråninger kan bli en dyr løsning dersom riggen til stadighet stanses pga høyt poretrykk. Hvor godt de kjemiske reaksjonene foregår er avhengig av grunnforholdene og innblandingen. Grunnforhold som kan ha innvirkning på pælenes styrke er - humus - leirinnhold - vanninnhold Leiras sensitivitet har stor betydning for hvor godt innblandingen foregår. Jo mer sensitiv, dess bedre innblanding. Grunnen må ha stor nok bæreevne til at borrigger kan ta seg fram. Før det velges en løsning med bruk av kalksementpæler må en forsikre seg om at det er nok tid til å utføre de nødvendige laboratorieanalysene og at det er tid nok i byggeprosessen til at pælene får herde til ønsket styrke før pålasting. Dimensjonerende styrke som finnes i laboratoriet kan ikke direkte benyttes i beregninger. Ved forsøk i laboratorie oppnås full innblanding, noe som absolutt ikke er tilfelle i felt. Det anbefales derfor at dimensjonerende skjærfasthet ikke settes større enn 100 kPa.

Pæler

I likhet med kalkpæler er også andre pæletyper aktuelle for å føre lastene fra fyllinga ned til større dybde og mindre setningsgivende lag. Aktuelle pæletyper i kombinasjon med fyllinger er nedrammede pæler av betong eller tre. I bløt og sensitiv leire kan nedrammede pæler være en uakseptabel løsning på grunn av poretrykksoppbygging og omrøring under pælerammingen. Nedrammede pæler er vanligvis et dyrere tiltak enn bruk av kalkpæler eller lette fyllmasser.

Tiltak for primært å øke andelen av setninger i byggetida

Tiltakene som er beskrevet i dette avsnittet har som primær funksjon å påskynde setningene, slik at de største setningene kommer i byggeperioden og ikke på ferdig anlegg.

Forbelastning

Forbelastningseffekt kan oppnås ved:

å legge ut fyllmassene tidligere enn vanlig å bygge opp fyllinga med midlertidig overhøyde

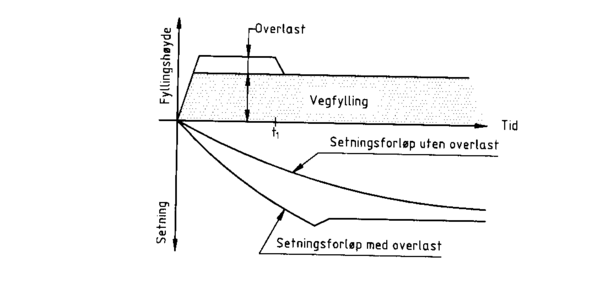
Forbelastningseffekten kan uttrykkes gjennom økt setningsandel i byggetida eller ved økt jordstivhet og reduserte setninger i driftsfasen. En midlertidig overlast er mest effektivt, men fylling med over­høyde vil ofte være vanskelig å utføre på bløt leire uten kombinasjon med stabiliserende tiltak som masseutskifting eller utlegging av motfyllinger. Forbelastning har også vært kombinert med vertikale dren for å redusere tidsperioden og for å sikre stabiliteten.

Forbelastning er vanligvis en rimelig byggemetode. Kostnadene vil være avhengig av hvor langt fyllmassene må transporteres. Har man tid til rådighet, kan massene ofte brukes et annet sted på anlegget når forbelastningen fjernes. For å få best mulig effekt av metoden er det viktig at den blir vurdert tidlig i planfasen (detaljplan), slik at det kan innpasses i driftsopplegget for anlegget.

Figur 3.14 Ideelt setningsforløp for fylling med forbelastning

Vertikale dren

Setninger i lite permeable jordarter, som normalkonsolidert leire og leirig silt, kan påskyndes ved nedsetting av vertikale dren. Dreneringen foregår hovedsakelig gjennom drenene som dimensjoneres slik at det meste av setningene finner sted før overbygningen legges ut. Vertikale dren bør kombineres med forbelastning.

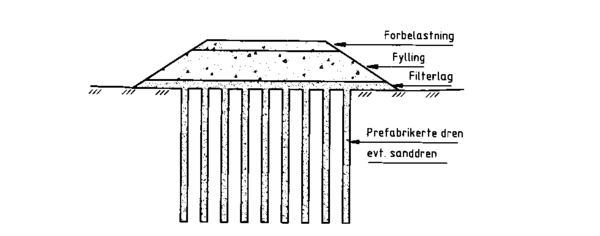
Opprinnelig bestod vertikale dren av sandpæler. I dag benyttes for det meste prefabrikkerte dren på grunn av enklere installering, fleksibilitet og lavere kostnad. Figur .15 viser en prinsipptegning for benyttelsen av vertikale dren under en vegfylling/jernbanefylling.

Figur 3.15 Dypdrenering med vertikale dren)

Vertikale dren er mest effektive i kohesjonsjordarter som i hovedsak er homogene og med konsolideringskoeffisient, Cv < 5 m2/år. Leire med spesielt lavtkrypmotstandstall (rs) egner seg mindre godt for vertikaldrenering. Det samme gjelder grunn med vannførende lag. Dersom vertikaldrenene punkterer et vannførende lag kan setningene bli mye større enn dersom ingen spesielle tiltak hadde blitt utført.

Virkning av stabiliserende tiltak på setninger

I partier med bløt grunn vil man ofte også ha dårlig stabilitet. Tiltak for forbedring av stabiliteten vil kunne deles i to typer tiltak (se kap 4 ”Stabilitet”):

Styrkeforbedring av jorden eller etablering av bærende konstruksjoner. Reduksjon av skjærspenningen i jorden.

Styrkeforbedring av jorden innebærer som regel at også jordas deformasjonsegenskaper blir bedret. Slike stabiliserende tiltak kan derfor ha god effekt for å begrense setninger. Reduksjon av skjærspenningen i jorden ved bruk av lette masser vil også ha positiv effekt med tanke på setninger. Brukes derimot motfylling for å bedre stabiliteten kan dette føre til økte setninger. Planlegging av stabilitet og setninger bør derfor ses i sammenheng.

Typisk effekt og kostnad for aktuelle tiltak

Generelt

Setningsreduserende tiltak kan virke på tre måter:

redusere tilleggsbelastningen (på setningsgivende lag) øke jordstivheten framskynde setningsutviklingen

De to førstnevnte virkemåtene gir reduserte totalsetninger, mens sistnevnte virkemåte øker andelen av setningene i byggetida (og dermed redusert setningsutvikling i driftsfasen).

En oversikt over primære og sekundære virkemåter for mest aktuelle tiltak er vist i tabell .5. Enkelte av tiltakene omtalt i avsnitt 4.2 og 4.3 har flere virkemåter.

Tabell 3.5 Virkemåter for setningsreduserende tiltak

Tiltak/ metode	Virkemåter
	reduserte tilleggsspenninger	økt jordstivhet	raskere setningsutvikling
Masseutskifting		1
Lette fyllmasser	1
Kalksementpæler		1	2
Friksjonspæler	1
Forbelastning		2	1
Vertikale dren			1

1: primær virkemåte 2: sekundær virkemåte

I mange tilfeller kan det være aktuelt å kombinere flere metoder for å oppnå en ønsket setningsreduksjon. For eksempel vil masseutskifting med lette fyllmasser muliggjøre helt eller delvis kompensert fundamentering med små eller ingen tilleggslaster. En annen aktuell kombinasjon er vertikale dren og forbelastning.

Typiske enhetskostnader for noen av tiltakene er vist i tabell .6. Totalkostnadene for tiltakene avhenger selvsagt sterkt av omfanget. I tabell .6 er det gitt eksempler på lm-kostnader for aktuelle tiltak for en 5 meter høy jernbanefylling (dobbeltspor).

Totalkostnadene øker stekt med økende fyllingshøyde. Dette har flere årsaker:

arealet som må forsterkes eller avlastes øker pga. økende fyllingsutslag det skal mer omfattende tiltak til for å oppnå samme setningsreduksjon behovet for setningsreduksjon øker

Kostnadene for å jevne ut brå overganger i grunnforholdene øker eksponensielt med fyllingshøyden. Under høye fyllinger med stort behov for setningsreduksjon, kan det bli meget store tilleggskostnader.

Et eksempel som belyser dette godt er tiltakene som ble utført under de ca 10 meter høye tilløpsfyllingene inn mot den nye Trøgstad bru på Hovedbanen (enkeltspor). Ved byggingen (1996) ble det her benyttet setningsreduserende tiltak for i alt ca 8 mill. kroner. Setningsmålinger tyder på at omfanget av tiltakene burde vært enda større. Liggetiden for fyllingene før banen ble tatt i bruk var imidlertid svært kort i dette tilfellet.

Det skal likevel være ekstremt bløt grunn før det er økonomisk lønnsomt å forlenge ei luftig jernbanebru i stedet for å foreta nødvendige grunnforsterkningstiltak slik at høye tilløpsfyllinger kan bygges.

Tabell 3.6 Typiske enhetspriser for setningsreduserende tiltak (1999‑priser) samt kostnadseksempler for en 5 meter høy fylling.

Metode	Typisk enhetspris (tilleggskostnad	align="center" |Kostnadseksempler
		Antatt omfang	Tilleggskostnad pr Im dobbeltspor
Masseutskifting med steinmasser	80 - 100 kr/m3	2 m dybde	5000 - 6500 kr
		4m dybde	12000 - 15000 kr
Masseutskifting med EPS (superlette masser)	ca 350 kr/m3	2 m tykkelse (39 % vektreduksjon)	ca 11 000 kr
Lettklinkerfylling	ca 200 kr/m3	3 m lettklinkertykkelse (41 % vektreduksjon) || align="center" |ca 10 000 kr
K/C-pæler (Ø600 mm)	70 kr/Im	Lengde 20 m og 25 % dekningsgrad	ca 25 000 kr
Vertikale dren og forbelastning	25 kr/Im	c/c 1,3 m og 20 m	ca 17 000˟

˟ kostnad til forbelastning er inkludert

Effekten av setningsreduserende tiltak er sterkt avhengig av stedlige forhold og av doseringen av tiltaket. Noen typiske trekk for de to kanskje mest aktuelle tiltakene skal kort nevnes.

Effekt av lette fyllmasser

En fordel med bruk av lette fyllmasser er at det er lett å ha bra kontroll med effekten av tiltaket. Med lette fyllmasser er det i prinsippet også mulig å bygge setningsfritt. Dette krever imidlertid både bruk av lette masser som byggemateriale i fyllinga og masseutskifting med lette masser i grunnen under for å kompensere for gjenværende fyllingsvekt (kompensert fundamentering). For ei lettklinkerfylling uten masseutskifting oppnås normalt mellom 30 og 50 % setningsreduksjon. Kostnadene øker til omlag det dobbelte for å oppnå 100 % setningsreduksjon (fullt kompensert fundamentering).

Effekt av kalksementpæler

Effekten av kalksementpæler på setningene er krevende å vurdere. Både kvaliteten av selve pælene og det mekaniske samvirket mellom pælene og den ustabiliserte leira innvirker. Det er lang erfaring med metoden i Sverige og Finland, men beregningsmodellene som benyttes har likevel fortsatt svakheter og er under stadig utvikling. I Norge er det foreløpig begrenset erfaring med metoden. Da leiras egenskaper har stor innvirkning på stabiliseringseffekten, kan heller ikke erfaringene fra våre naboland overføres direkte.

I likhet med andre setningsreduserene tiltak er kalksementpæler mest kostnadseffektivt under lave fyllinger. På den annen side har lange kalksementpæler vesentlig større setningsreduserende effekt enn korte i forhold til kostnaden. På steder der det kun ønskes en liten reduksjon av setningene kan tiltaket derfor bli uforholdsmessig kostbart. Med 20 meter lange kalksementpæler vil det være mulig å oppnå en betydelig setningsreduksjon i driftsfasen, i de fleste tilfeller så mye som 60-70 %.

Prosjektering og bygging

Prosjektering etter setningskrav

Jernbaneverkets setningskrav angir hvor store setninger som maksimalt er tillatt på nye banestrekninger de første årene banen er i bruk. Setningskravene har to hensikter:

Hindre større setninger enn akseptabelt på en nyanlagt banestrekning. Bidra til lavest mulige samlede kostnader til utbygging og drift av baner på bløt grunn.

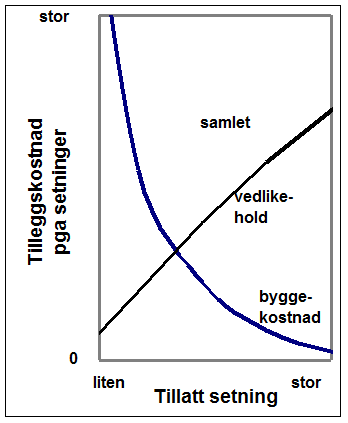
Setningskravene bygger på undersøkelser og vurderinger av hvordan byggekostnadene og vedlikeholdsbehovet påvirkes av tillatte setninger. I prinsippet er denne sammenhengen som illustrert i figur .16.

På strekninger med mye bløt grunn vil byggekostnadene øke betydelig dersom det stilles krav til et nesten setningsfritt spor. På den annen side vil vedlikeholdskostnadene øke med økende setninger.

Figur 3.16 Økte bygge- og vedlikeholdskostnader på banestrekninger med setningsproblemer avhengig av tillatte setninger. Prinsippfigur.

Jernbaneverkets nåværende setningskrav definerer minstestandarden som aksepteres for nye banestrekninger på bløt grunn. På nye anlegg hvor setningsproblemer forekommer mer sporadisk, vil det trolig være lønnsomt å prosjektere etter strengere kriterier enn minstestandarden.

Omfattende setninger i driftsfasen kan også generere så hyppige sporfeil at det kan gå ut over regulariteten av banen. Tilgjengeligheten til sporet for å utføre nødvendig sporoppretting kan være en avgjørende faktor på høytrafikkerte linjer. For slike baneanlegg kan det være behov for å fastlegge egne setningskrav.

Ved prosjektering av baner etter fastlagte setningskrav er oppgaven å sørge for at setningskravene oppnås innenfor en lavest mulig kostnadsramme. For å unngå unødige byggekostnader må underbygningen utformes slik at setningskravene tilfredsstilles og ikke slik at det oppnås et setningsfritt baneanlegg.

For at banen skal få ønsket kvalitet, er det nødvendig med en systematisk og målrettet behandling av setningsspørsmålene under prosjekteringen. Det anbefales en trinnvis framgangsmåte, f.eks. i tre faser:

1. I første fase klarlegges partier med fare for større setninger enn tillatt. 2. Deretter fastlegges steder hvor det skal iverksettes tiltak. 3. Til slutt utarbeides fundamenteringsløsninger på kritiske steder.

En slik framgangsmåte vil sikre at den største geotekniske prosjekteringsinnsatsen innrettes mot de kritiske stedene. Dette øker mulighetene for at målsettingene med setningskravene oppnås.

Også grunnundersøkelsene bør normalt utføres trinnvis. På steder med lite informasjon om grunnforholdene fra før, kan følgende opplegg anbefales:

I første omgang kartlegge alle potensielle problempunkter og skaffe grunnlag for å anslå totalbehovet for setningsreduserende tiltak. Gjennom supplerende grunnundersøkelser skaffe grunnlag for å fastlegge hvilke partier som har behov for tiltak og for valg og utforming av tiltakene på disse stedene.

Valg av kostnadseffektive løsninger

På kritiske steder må det tilstrebes å velge fundamenteringsløsninger som er mest mulig økonomisk optimale.

Valg av metode (eller kombinasjon av metoder) bør vurderes i hvert enkelt tilfelle basert på en teknisk og økonomisk vurdering av alternativer. Hvilken metode som er mest egnet avhenger i første rekke av:

grunnforhold (dybde til fast grunn og den bløte grunnens egenskaper) fyllingshøyde behovet for setningsreduksjon eventuelt forsterkningsbehov pga. dårlig stabilitet (valg av forsterkningsmetode må i så fall ses i sammenheng)

Også en del andre forhold som kan ha stor betydning for valg av tiltak må vurderes, f.eks.:

miljøhensyn overfor omgivelsene (støy, støv, avrenning) tidsaspekt for stabiliseringseffekten tilgjengelighet og adkomst for aktuelt utstyr risiko forbundet med gjennomføring og virkemåte av aktuelle løsninger

Optimal fundamenteringsløsning er heller ikke bare er et spørsmål om valg av metode, men i like stor grad spørsmål om utforming og omfang av tiltaket.

Tiltak for nødvendig setningsutjevning er normalt mer kostnadskrevende der behovet skyldes overganger i grunnforholdene enn der årsaken er varierende fyllingshøyder. Siden omfanget av nødvendige tiltak for å oppnå en gitt effekt også øker sterkt med fyllingshøyden, er det meget viktig å optimalisere bruken av tiltak godt under høye fyllinger på variable grunnforhold.

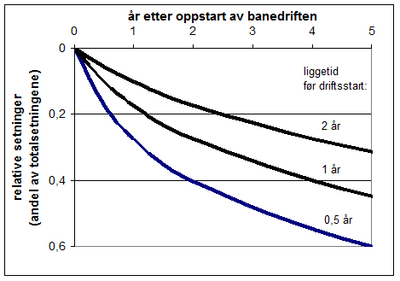
Det kan vanskelig gis konkrete råd mht valg av tiltak i ulike situasjoner ut over det som er nevnt i avsnitt 4. Ett klart råd kan imidlertid gis: Lengst mulig liggetid for fyllinger bør utnyttes maksimalt på alle jernbaneanlegg. Her er det spesielt viktig å legge ut de største fyllingene tidlig. En illustrasjon av hvordan setningsutviklingen de første driftsårene kan påvirkes av liggetiden er vist i figur .17. Særlig for de to første driftsårene vil liggetiden ha stor betydning. Det er også disse årene setningene er mest kritisk.

Figur 3.17 Lengst mulig liggetid av fyllinger bør utnyttes som setningsreduserende tiltak så langt som råd. (Figuren illustrerer hvordan typisk setningsutvikling i tidlig driftsfase avhenger av liggetiden).

Kostnadene for en generell setningsreduksjon over lengre strekninger kan bli meget store. For å begrense kostnadene er det derfor avgjørende å innrette tiltakene mot mest kritiske partier. Vanligste problempunkter er overganger mellom ulike grunnforhold samt på tilløpsfyllinger inn mot faste konstruksjoner (bruer og kulverter). Der det er hyppige overgangspartier (mer enn 3-4 pr km) vil utjevningstiltakene kunne overlappe hverandre. I så fall bør sammenhengende tiltak vurderes over en lengre strekning.

Det må også unngås å introdusere nye overgangspartier der forsterkningstiltakene avsluttes. En gradvis avtrapping av tiltakene er derfor viktig.

Nødvendig omfang av et setningsreduserende tiltak øker sterkt med fyllingshøyden. Det kan derfor være mye å spare på å legge ut store fyllinger tidlig. Under høye fyllinger er det også spesielt viktig å optimalisere tiltakene godt.

Det trengs også mer omfattende tiltak for å jevne ut overgangene mellom bløt og fastere grunn enn for å jevne ut overganger som skyldes varierende topografi (varierende fyllingshøyde). I tabell 3.7 er det vist hvordan nødvendig omfang av setningsreduserende tiltak ventes å variere på kritiske fyllingspartier med ulik karakter.

Tabell 3.7 Antatt behov for setningsreduserende tiltak langs kritiske fyllingspartier med ulik karakter etter en lineær skala fra 1-10.

Årsak til ujevn setningsutvikling		Liten Fyllingshøyde (inntil 3 m)	Stor fyllingshøyde (>5 m)
Variasjon i fyllingshøyde	Moderat	1	2
	Stor (blå)	2-3 (4)	3-4 (5)
Overgang i grunnforholdene	Gradvis	2-3	5-7
	Brå	4-5	9-10

Kontroll i byggeperioden

Som en naturlig del av den geotekniske prosjekteringen inngår det å lage et program for nødvendig oppfølging og kontroll i anleggsfasen. Behovet for geotekniske kontrollmålinger og annen oppfølging i anleggsfasen varierer imidlertid sterkt avhengig av stedlige forhold og valgte løsninger.

Generelt for underbygningsarbeider i bløt grunn vil behovene for oppfølging og kontroll være knyttet til:

dokumentasjon av prosjekteringsforutsetningene tilpasse utførelse og framdrift etter måleresultater (observasjonsmetoden) sikring av forutsatt kvalitet av arbeider i grunnen unngå eller begrense skadevirkninger på omgivelsene

Observasjoner og kontrollmålinger i byggeperioden vil også være et meget viktig bidrag til å vinne økt erfaring.

For å sikre at setningsproblemene blir håndtert slik som forutsatt vil oppfølging og kontroll i byggeperioden både være aktuelt på uforsterkede strekninger og på partier hvor det benyttes forsterkningstiltak. Eksempler på forhold som er spesielt viktige å kontrollere med tanke på setningene er:

traubunnens kvalitet (fyllingene må anlegges på ren, uforstyrret grunn) tidspunkt for utlegging av fyllingene komprimeringen av fyllingene kvaliteten av grunnforsterkningsarbeider

På kritiske fyllingsstrekninger vil setningsmålinger og poretrykksmålinger være de mest aktuelle kontrollmålingene i grunnen.

Setningsmålinger av fyllinger i byggeperioden vil gi vesentlig sikrere informasjon om forventet setningsforløp i driftsfasen. Dette er nyttig av to grunner:

Ved større setninger enn beregnet, kan det settes inn korrektive tiltak før banen tas i bruk (eksempel på et mulig tiltak er å skifte ut deler av fyllinga med lette fyllmasser). Sikrest mulig kunnskap om forventede setninger i driftsperioden er nyttig informasjon for planlegging av banedriften.

Poretrykksmålinger er et mye brukt kontrolltiltak for å sikre en forsvarlig gjennomføring av grunnarbeidene på steder med anstrengt stabilitet. Også i setningssammenheng kan det være behov for å overvåke konsolideringsprosessen under fyllinger. Spesielt gjelder det ved bruk av tiltak som skal framskynde konsolideringen og øke andelen av setninger i byggeperioden. For å ta stilling til om en forbelastning kan fjernes, vil det være til stor nytte å kjenne poretrykksutviklingen.

Gjennom oppfølging og kontroll i anleggsperioden vil det også bli satt økt fokus på forhold relatert til grunnen. Erfaringen er at dette gir bedre forståelse hos de utførende for aktuelle problemstillinger, noe som bidrar til en sikrere gjennomføring av kompliserte grunnarbeider.

LITTERATURHENVISNINGER /1/ Statens vegvesen: Veiledning til 018: Veg på bløt grunn, Oslo 1995

/2/ Statens vegvesen: Håndbok 016: Geoteknikk i vegbygging, Oslo 1992

/3/ JANBU, Nilmar: Grunnlag i geoteknikk, Tapir forlag, 1970

/4/ NVE: Vassdragshåndboka, Tapir forlag, 1998

/5/ SINTEF Vegteknikk, SINTEF Geoteknikk: Jernbanebygging på bløt grunn. Hovedprosjektrapport, Trondheim 1994