Utledning kurveveksler: Forskjell mellom sideversjoner
Hopp til navigering
Hopp til søk
| Linje 32: | Linje 32: | ||
<div style="width: 100px; margin: 0 auto;"> | <div style="width: 100px; margin: 0 auto;"> | ||
<math> | <math> | ||
R(r-x | R(r-x-rcos(\alpha)-xcos(\alpha)) = (rx+x^2)(1+cos(\alpha)) | ||
</math> | </math> | ||
</div> | </div> | ||
<div style="width: 100px; margin: 0 auto;"> | <div style="width: 100px; margin: 0 auto;"> | ||
<math> | <math> | ||
R\left | R\left (r(1-cos(\alpha))-x(1+cos(\alpha))\right ) = (rx+x^2)(1+cos(\alpha)) | ||
</math> | </math> | ||
</div> | </div> | ||
<div style="width: 100px; margin: 0 auto;"> | <div style="width: 100px; margin: 0 auto;"> | ||
<math> | <math> | ||
R\left | R\left (r\cdot\frac{1-cos(\alpha)}{1+cos(\alpha)}-x\right ) = x(r+x) | ||
</math> | </math> | ||
</div> | </div> | ||
| Linje 49: | Linje 49: | ||
<div style="width: 100px; margin: 0 auto;"> | <div style="width: 100px; margin: 0 auto;"> | ||
<math> | <math> | ||
tan(\alpha/2) | tan^2(\alpha/2)=\frac{1-cos(\alpha)}{1+cos(\alpha)} | ||
</math> | </math> | ||
</div> | </div> | ||
| Linje 56: | Linje 56: | ||
<div style="width: 100px; margin: 0 auto;"> | <div style="width: 100px; margin: 0 auto;"> | ||
<math> | <math> | ||
R\left ( | R\left (\frac{r}{x}\cdot tan^2(\alpha/2)-1\right ) = r+x | ||
</math> | </math> | ||
</div> | </div> | ||
| Linje 63: | Linje 63: | ||
<div style="width: 100px; margin: 0 auto;"> | <div style="width: 100px; margin: 0 auto;"> | ||
<math> | <math> | ||
tan(\alpha/2) = t | tan(\alpha/2) = \frac{t}{r_0} | ||
</math> | </math> | ||
</div> | </div> | ||
</br> | </br> | ||
Merk at dette er en tilnærming som kun er gyldig når stigningen i vekselen kan ses på som liten, hvilket den stort sett er i enkle veksler. | Merk at dette er en tilnærming som kun er gyldig når stigningen i vekselen kan ses på som liten, hvilket den stort sett er i enkle veksler. | ||
</br> | |||
Ved å også benytte at | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
tan(\alpha/2) = \frac{x}{t} | |||
</math> | |||
</div> | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
\frac{t}{r_0} = \frac{x}{t} | |||
</math> | |||
</div> | |||
får vi | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
R(\frac{r\cdot r_0}{t^2}\cdot\frac{t^2}{r_0^2}-1) = r+\frac{t^2}{r_0} | |||
</math> | |||
</div> | |||
og til slutt | |||
<div style="width: 100px; margin: 0 auto;"> | |||
<math> | |||
R = \frac{r\cdot r+t^2}{r-r_0} | |||
</math> | |||
</div> | |||
Sideversjonen fra 19. apr. 2021 kl. 09:16
Utledning, formel for radier, kurveveksel
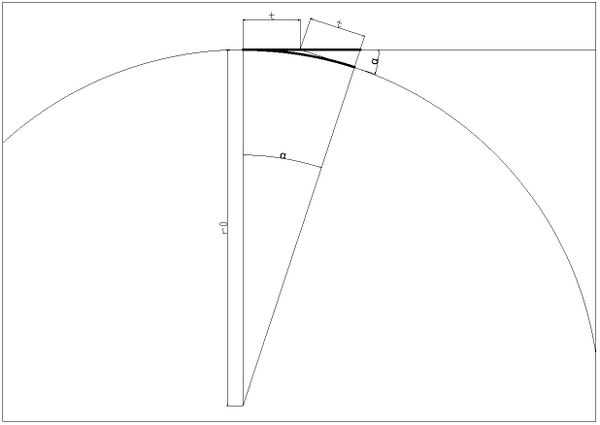
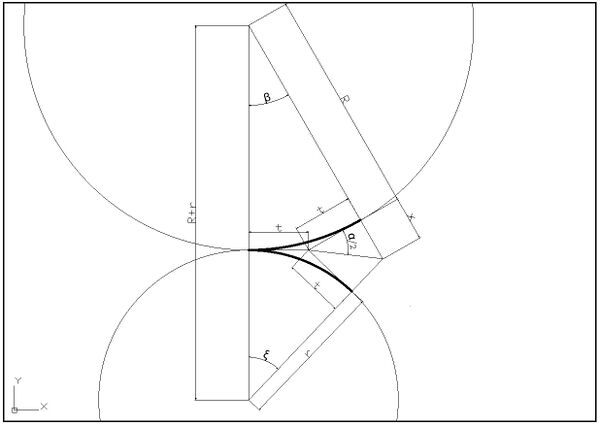
I figuren under vises geometri for en enkel sporveksel med lang kurve og en utoverbøyd kurveveksel.
Siden vinkelen er liten, antas t å være tilnærmet lik både før og etter bøying av den enkle vekselen. Ved å benytte cosinussetningen:
oppnås følgende sammenheng mellom radier og vinkel, :
Videre bearbeiding av denne ligningen gir:
Ved å benytte den trigonometriske identiteten:
gir dette videre:
Fra geometrien i den enkle vekselen, kan vi nå innføre:
Merk at dette er en tilnærming som kun er gyldig når stigningen i vekselen kan ses på som liten, hvilket den stort sett er i enkle veksler.
Ved å også benytte at
får vi
og til slutt