Bruer/Spesielle hensyn: Forskjell mellom sideversjoner
(Ny side: __NUMBEREDHEADINGS__ == Innledning== Når ei jernbanebru skal konstrueres, er det ikke bare i samme utstrekning som for andre bruer trafikkbelastningen den skal bære, som bestemmer dens d...) |
Ingen redigeringsforklaring |
||
| Linje 13: | Linje 13: | ||
== NEDBØYNING== | == NEDBØYNING== | ||
=== Krav til sikkerhet=== | === Krav til sikkerhet=== | ||
Nedbøyninger i bruer må begrenses for å forhindre store endringer i sporgeometri som i sin tur vil føre til ekstra vibrasjoner i konstruksjonene. For de fleste bruer, dvs. på strekninger der kjørehastigheten aldri vil overstige ca. 220 km/ h, er det tilstrekkelig å forvisse seg om at egenfrekvensen ligger innenfor et gitt område. For bruer der kjørehastigheten kan komme til å overstige 220 km/h, må akselerasjonen i brudekket begrenses til 3,4 m/s<sup>2</sup> for vibrasjoner opp til 20 Hz i bruer med gjennomgående ballast. | Nedbøyninger i bruer må begrenses for å forhindre store endringer i sporgeometri som i sin tur vil føre til ekstra vibrasjoner i konstruksjonene. For de fleste bruer, dvs. på strekninger der kjørehastigheten aldri vil overstige ca. 220 km/h, er det tilstrekkelig å forvisse seg om at egenfrekvensen ligger innenfor et gitt område. For bruer der kjørehastigheten kan komme til å overstige 220 km/h, må akselerasjonen i brudekket begrenses til 3,4 m/s<sup>2</sup> for vibrasjoner opp til 20 Hz i bruer med gjennomgående ballast. | ||
Det stilles også strenge krav til vridning av brudekket under trafikklast. Overskridelse av gitte verdier kan i verste fall føre til avsporing med katastrofale konsekvenser. | Det stilles også strenge krav til vridning av brudekket under trafikklast. Overskridelse av gitte verdier kan i verste fall føre til avsporing med katastrofale konsekvenser. | ||
| Linje 46: | Linje 46: | ||
Det bør også her benyttes forspenningskrefter i stagene tilsvarende den statiske påkjenningen mot landkarert. | Det bør også her benyttes forspenningskrefter i stagene tilsvarende den statiske påkjenningen mot landkarert. | ||
Figur .1 viser en prinsippskisse for landkar med friksjonsplate. | Figur 4.1 viser en prinsippskisse for landkar med friksjonsplate. | ||
[[Fil:Fig523-401.png|800px]] | |||
Figur 4.1 Landkar med friksjonsplate | Figur 4.1 Landkar med friksjonsplate | ||
| Linje 53: | Linje 54: | ||
Friksjonsplata plasstøpes eller prefabrikeres i betong og forankres til landkaret med stag. Det spennarmerte betongstaget må hele tiden være i trykk for å forhindre riss som fører til armeringskorrosjon. Dette kan være økonomisk ved at fundamentdimensjonene kan reduseres betraktelig ved store horisontallaster. | Friksjonsplata plasstøpes eller prefabrikeres i betong og forankres til landkaret med stag. Det spennarmerte betongstaget må hele tiden være i trykk for å forhindre riss som fører til armeringskorrosjon. Dette kan være økonomisk ved at fundamentdimensjonene kan reduseres betraktelig ved store horisontallaster. | ||
Kapasiteten QA på ei friksjonsplate beregnes av formel .1: | Kapasiteten QA på ei friksjonsplate beregnes av formel 4.1: | ||
QA= (Nf NE t) (p´+ a) B (4.1) | QA= (Nf NE t) (p´+ a) B (4.1) | ||
| Linje 61: | Linje 62: | ||
Nf= (r0 + ru)tan , når L Lopt og Nf =(KP – KA) z/2L + ru tan når L Lopt | Nf= (r0 + ru)tan , når L Lopt og Nf =(KP – KA) z/2L + ru tan når L Lopt | ||
KA= aktiv jordtrykkskoeffisient, se figur .2 | KA= aktiv jordtrykkskoeffisient, se figur 4.2 | ||
KP= passiv jordtrykkskoeffisient, se figur .2 | KP= passiv jordtrykkskoeffisient, se figur 4.2 | ||
Nf kan finnes fra figur .3 | Nf kan finnes fra figur 4.3 | ||
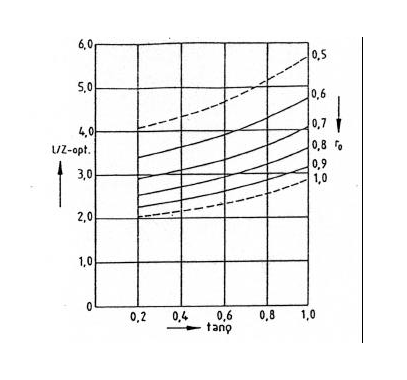
NE er endemotstandsfaktoren for friksjonsplata, og kan tas ut av figur .4. | NE er endemotstandsfaktoren for friksjonsplata, og kan tas ut av figur 4.4. | ||
Platas optimale lengde finnes ved formel .2. | Platas optimale lengde finnes ved formel 4.2. | ||
(4.2) | (4.2) | ||
| Linje 73: | Linje 74: | ||
Ruheten settes i området r0= ru= 0,7 – 0,9 | Ruheten settes i området r0= ru= 0,7 – 0,9 | ||
[[Fil:Fig523-402.png|800px]] | |||
Figur 4.2 Jordtrykkskoeffisienter (aktiv - passiv) | Figur 4.2 Jordtrykkskoeffisienter (aktiv - passiv) | ||
[[Fil:Fig523-403.png|800px]] | |||
Figur 4.3 Friksjonsfaktor | Figur 4.3 Friksjonsfaktor N<sub>F</sub> for friksjonsplate | ||
[[Fil:Fig523-404.png|800px]] | |||
Figur 4.4 Endemotstandsfaktoren N<sub>E</sub> for friksjonsplate | |||
[[Fil:Fig523-405.png|800px]] | |||
Figur 4.5 Optimal platelengde | Figur 4.5 Optimal platelengde | ||
Nødvendig forankringslengde | Nødvendig forankringslengde L<sub>tot</sub> finnes fra følgende uttrykk: | ||
(4.3) | (4.3) | ||
=== Kontinuerlig friksjonsplate fra landkar=== | === Kontinuerlig friksjonsplate fra landkar=== | ||
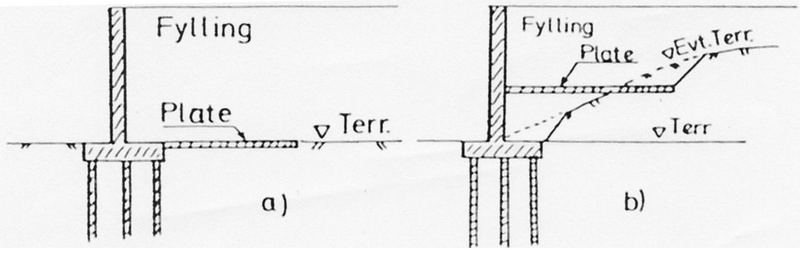
Kontinuerlige forankringsplater som går direkte over i landkarsålen eller landkarveggen, vil ta opp horisontale krefter fra landkaret ved friksjon mellom plate og underliggende jord. Siden platen henger sammen med landkarveggen vil det ikke bli noen endemotstand mot platen. Det vil heller ikke bli noen friksjonsvirkning mellom plate og overliggende jord, fordi jorden følger de bevegelsene som platen gjør. Oversiden av platen er således uvirksom. Videre vil en viss del av platelengden som ligger nærmest landkaret være lite virksom dersom plata ligger et stykke opp på landkarveggen. Det kan derfor være praktisk og økonomisk fordelaktig å lage utsparinger mellom mer eller mindre konsentrerte armeringsføringer eller strekkstag i partiet nærmest landkarveggen. Dimensjonering for øvrig utføres som for horisontale forankringsplater med stag. Figur .6 viser prinsippet for to ulike plasseringer av kontinuerlige friksjonsplater. | Kontinuerlige forankringsplater som går direkte over i landkarsålen eller landkarveggen, vil ta opp horisontale krefter fra landkaret ved friksjon mellom plate og underliggende jord. Siden platen henger sammen med landkarveggen vil det ikke bli noen endemotstand mot platen. Det vil heller ikke bli noen friksjonsvirkning mellom plate og overliggende jord, fordi jorden følger de bevegelsene som platen gjør. Oversiden av platen er således uvirksom. Videre vil en viss del av platelengden som ligger nærmest landkaret være lite virksom dersom plata ligger et stykke opp på landkarveggen. Det kan derfor være praktisk og økonomisk fordelaktig å lage utsparinger mellom mer eller mindre konsentrerte armeringsføringer eller strekkstag i partiet nærmest landkarveggen. Dimensjonering for øvrig utføres som for horisontale forankringsplater med stag. Figur 4.6 viser prinsippet for to ulike plasseringer av kontinuerlige friksjonsplater. | ||
[[Fil:Fig523-406.png|800px]] | |||
Figur 4.6 Plassering av kontinuerlige friksjonsplater | Figur 4.6 Plassering av kontinuerlige friksjonsplater | ||
| Linje 111: | Linje 111: | ||
I figurene 4.7 - 4.9 er det foretatt en oppsummering av prinsippet for de forskjellige typer forankring som er nevnt under avsnitt 3. | I figurene 4.7 - 4.9 er det foretatt en oppsummering av prinsippet for de forskjellige typer forankring som er nevnt under avsnitt 3. | ||
[[Fil:Fig523-407.png|800px]] | |||
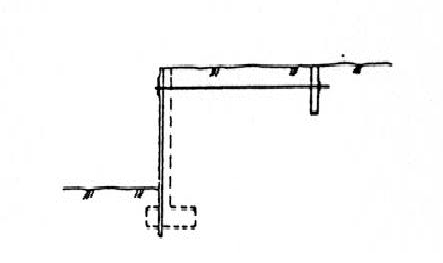
Figur 4.7 Stag til vertikal forankring basert på passivt jordtrykk | Figur 4.7 Stag til vertikal forankring basert på passivt jordtrykk | ||
| Linje 116: | Linje 117: | ||
[[Fil:Fig523-408.png|800px]] | |||
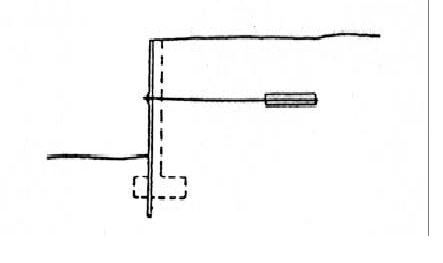
Figur 4.8 Stag til horisontal forankringsplate basert på tosidig friksjon | Figur 4.8 Stag til horisontal forankringsplate basert på tosidig friksjon | ||
[[Fil:Fig523-409.png|800px]] | |||
Figur 4.9 Avlastnings-/friksjonsplate basert på ensidig friksjon | Figur 4.9 Avlastnings-/friksjonsplate basert på ensidig friksjon | ||
| Linje 136: | Linje 136: | ||
Det er to typer uregelmessigheter en må regne med: skinnebrudd eller avbrudd i overgangen mellom spor og bru slik at sporstabiliteten ikke kan garanteres lengre. Et godt eksempel er når ballasten løsner fulgt av betraktelig forskyvning av brua slik at tilstrekkelig motstand mot sideveis forskyvning ved bruendene ikke lengre er tilstede. | Det er to typer uregelmessigheter en må regne med: skinnebrudd eller avbrudd i overgangen mellom spor og bru slik at sporstabiliteten ikke kan garanteres lengre. Et godt eksempel er når ballasten løsner fulgt av betraktelig forskyvning av brua slik at tilstrekkelig motstand mot sideveis forskyvning ved bruendene ikke lengre er tilstede. | ||
De tillatte grenseverdier for sporet er avhengig av dets konstruksjon og vedlikeholdstilstand. De tillatte grenseverdier som ERRI D 213 har kommet frem til enten for forskyvninger eller tilleggsspenninger i skinnene pga. interaksjon, er verdier som er generelt tillatt for standard sporkomponenter ved godt vedlikehold. Disse tilleggsverdier er for helsveiste UIC 60 skinner 72 | De tillatte grenseverdier for sporet er avhengig av dets konstruksjon og vedlikeholdstilstand. De tillatte grenseverdier som ERRI D 213 har kommet frem til enten for forskyvninger eller tilleggsspenninger i skinnene pga. interaksjon, er verdier som er generelt tillatt for standard sporkomponenter ved godt vedlikehold. Disse tilleggsverdier er for helsveiste UIC 60 skinner 72 N/mm<sup>2</sup> i tillatt trykkspenning i og 5 mm forskyvning av konstruksjonen ved bremsing. Tillatt tilleggsspenning i strekk er 92 N/mm<sup>2</sup>. | ||
=== Beskrivelse av fenomenet=== | === Beskrivelse av fenomenet=== | ||
| Linje 149: | Linje 149: | ||
Helsveist spor inneholder en ”sentral” sone der utvidelsen og sammentrekningen er fullstendig forhindret, og to ”puste”- soner ved hver ende på ca. 150 m lengde. Glideskjøter ved endene på helsveist spor har en 50 mm variasjon i åpning som tillater fri bevegelse av skinnene | Helsveist spor inneholder en ”sentral” sone der utvidelsen og sammentrekningen er fullstendig forhindret, og to ”puste”- soner ved hver ende på ca. 150 m lengde. Glideskjøter ved endene på helsveist spor har en 50 mm variasjon i åpning som tillater fri bevegelse av skinnene | ||
[[Fil:Fig523-410.png|800px]] | |||
Figur 4.10 Oppførsel av helsveist spor ved temperaturforandringer | Figur 4.10 Oppførsel av helsveist spor ved temperaturforandringer | ||
| Linje 156: | Linje 156: | ||
temperaturutvidelseskoeffisient | temperaturutvidelseskoeffisient | ||
TR forandring i skinnetemperatur relativ til nøytraltemperatur ( ca. | TR forandring i skinnetemperatur relativ til nøytraltemperatur ( ca. 21<sup>O</sup> ved JBV) | ||
E Elastisitetsmodul for stål (210 000 N / | E Elastisitetsmodul for stål (210 000 N/mm<sup>2</sup> ) | ||
A Tverrsnittsareal av to skinner | A Tverrsnittsareal av to skinner | ||
F Sporkraft | F Sporkraft | ||
| Linje 175: | Linje 175: | ||
En hvilken som helst bevegelse i bruoberbygningen påfører en bevegelse i sporet og indirekte i brulagrene. | En hvilken som helst bevegelse i bruoberbygningen påfører en bevegelse i sporet og indirekte i brulagrene. | ||
[[Fil:Fig523-411.png|800px]] | |||
Figur 4.11 Kurve som viser skinnespenninger forårsaket av temperaturvariasjoner i brudekket | Figur 4.11 Kurve som viser skinnespenninger forårsaket av temperaturvariasjoner i brudekket | ||
| Linje 202: | Linje 203: | ||
For ubelastet spor har den siste faktoren mye mindre verdi enn den første. | For ubelastet spor har den siste faktoren mye mindre verdi enn den første. | ||
[[Fil:Fig523-412.png|800px]] | |||
Figur 4.12 Sporets motstand som funksjon av langsgående forskyvning, u. | Figur 4.12 Sporets motstand som funksjon av langsgående forskyvning, u. | ||
Sideversjonen fra 31. aug. 2011 kl. 12:26
__NUMBEREDHEADINGS__
Innledning
Når ei jernbanebru skal konstrueres, er det ikke bare i samme utstrekning som for andre bruer trafikkbelastningen den skal bære, som bestemmer dens dimensjoner.
Følgende faktorer må også tas hensyn til ved dimensjoneringen:
tillatt nedbøyning mhp. sikkerhet og passasjerkomfort store opptredende horisontalkrefter må ivaretas glideskjøt i skinnegangen eller ikke, avhengig av bruas lengde gjensidig samspill mellom krefter i brukonstruksjonen og krefter i sporet overgangssonen mellom bru og fylling
NEDBØYNING
Krav til sikkerhet
Nedbøyninger i bruer må begrenses for å forhindre store endringer i sporgeometri som i sin tur vil føre til ekstra vibrasjoner i konstruksjonene. For de fleste bruer, dvs. på strekninger der kjørehastigheten aldri vil overstige ca. 220 km/h, er det tilstrekkelig å forvisse seg om at egenfrekvensen ligger innenfor et gitt område. For bruer der kjørehastigheten kan komme til å overstige 220 km/h, må akselerasjonen i brudekket begrenses til 3,4 m/s2 for vibrasjoner opp til 20 Hz i bruer med gjennomgående ballast.
Det stilles også strenge krav til vridning av brudekket under trafikklast. Overskridelse av gitte verdier kan i verste fall føre til avsporing med katastrofale konsekvenser.
Disse sikkerhetskrav fører med seg at ei jernbanebru må være mye stivere enn ei veibru selv om denne eventuelt skulle dimensjoneres for en like tung trafikklast.
Krav til komfort
Togpassasjerer stiller i dag høyere krav til komfort enn tidligere. Det vil si at den vertikale vognakselerasjonen ikke må overstige 1 m/s2 for at man ikke skal utsettes for ubehag. Som følge av dette må tillatt nedbøyning begrenses. Størrelsen på tillatt nedbøyning varierer med statisk system, antall spenn og spennvidde.
OPPTAK AV STORE HORISONTALKREFTER
Forankringsplater generelt
Forankringsplater benyttes for opptak av store horisontalkrefter. Slike store krefter forekommer alltid på jernbanebruer når bruoverbygningen er noen hundre meter lang.
Der byggegrunnen er dårlig, er det vanskelig og kostbart å ta vare på vertikallastene på en slik måte at ikke store setninger finner sted. Ved fundamentering av bruer på dårlig grunn, blir det nesten alltid utført pæling. Iblant ligger fjellet så dypt at svevende friksjonspæler blir valgt. Tillatt last på slike pæler er oftest liten, og det kreves mange pæler og store fundamenter.
Den største andelen av horisontallaster på jernbanebruer kommer fra bremse- og trekkreftene (akselerasjonskreftene) som utgjør opp til ca. ¼ av trafikklasten. På ei 300 m lang enkeltsporet bru skal bremselasten settes til 6000 kN, og på ei dobbeltsporet bru av samme lengde vil bremse- og trekklasten sammenlagt utgjøre opptil 7000 kN. Det er åpenbart at fundamenteringen blir komplisert og kostnadskrevende dersom grunnforholdene er dårlige.
Et alternativ til tradisjonelle metoder for å oppta horisontalkrefter, er en friksjonsplate av betong som bygges inn i fyllingen bak det ene landkaret og forankres til landkaret med stag. Når en slik plate dimensjoneres, er det nødvendig å fastsette enkelte kriterier som må oppfylles. Nedenfor gjøres en kort oppsummering av ulike typer friksjonsplater / forankringsplater og hvilke prinsipper og forutsetninger som bør ligge til grunn.
Vertikale forankringsplater
Vertikale forankringaplater er kjent fra praksis og litteratur. Strekket fra staget blir balansert ved netto differanse mellom passivt jordtrykk foran platen og aktivt jordtrykk bak platen. Ved utregning av jordtrykkskomponentene må det ved fastsettelse av ruhetsverdier (r) tas hensyn til vertikal likevekt av plata. Ved horisontale stag gir r = 0 brukbare overslagsverdier for jordtrykket. Denne dimensjoneringsmetoden, som bl.a. blir brukt ved forankrede spuntvegger, gir også for landkar-problemstillinger platedimensjoner som er håndterlige og brukbare for praktiske formål.
I praksis vil stagføring og feste i platen kreve spesiell omtanke. Da det er vanskelig å vurdere sammenhengen mellom deformasjon og mobilisert jordtrykk, bør det i praksis benyttes forspente stag med samlet forspenning tilsvarende den statiske delen av lastbidragene mot landkaret. Dette vil også gi en stivere konstruksjon og mindre forskyvninger av landkaret under de vekslende forholdene i brukstiden.
Horisontale forankringsplater med stag
Horisontale forankringsplater med stag dimensjoneres ved at strekket fra staget blir balansert av friksjonskrefter mellom plate og jord på over- og undersiden av platen. Lastkapasiteten vil øke tilnærmet lineært med økende platelengde opp til en viss grense (Lopt ) som er bestemt av størrelsen på de horisontale jordtrykkskreftene mot jordprismet over plata. Når forskjellen mellom aktivt og passivt jordtrykk er like stor som friksjonskraften mot oversiden av platen, er den optimale platelengden nådd. Ved videre økning av platelengden vil lastkapasiteten fortsatt øke tilnærmet lineært med platelengden, men da bare som et resultat av økt friksonskraft mot undersiden av platen.
Avhengig av hvilke forutsetninger man setter i beregningsmodellen, vil optimale platelengder variere fra ca. 0,5 – 3 ganger platedybden (vertikal avstand fra overflaten). Platekapasiteten er avhengig av styrkeparametrene til jorda omkring plata, vekt av overliggende masse og av ruhetsforholdene mellom plate og jord.
Det må vurderes om motstand mot endeflata skal tas med i beregningen. Forutsetningen er bl.a. at plata virkelig kan få relativ forskyvning i forhold til jorda over og foran plata. Dersom stagene er jevnt spredt over platebredden og/eller de er omstøpte for korrosjonssikring, vil virkemåten lett bli som for kontinuerlige plater på grunn av tendensen til medsleping av overliggende jord. Se avsnitt 3.3 vedr. horisontal kontinuerlig friksjonsplate.
Det bør også her benyttes forspenningskrefter i stagene tilsvarende den statiske påkjenningen mot landkarert.
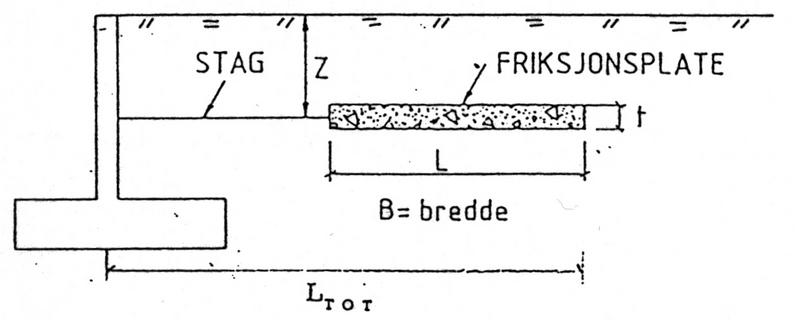
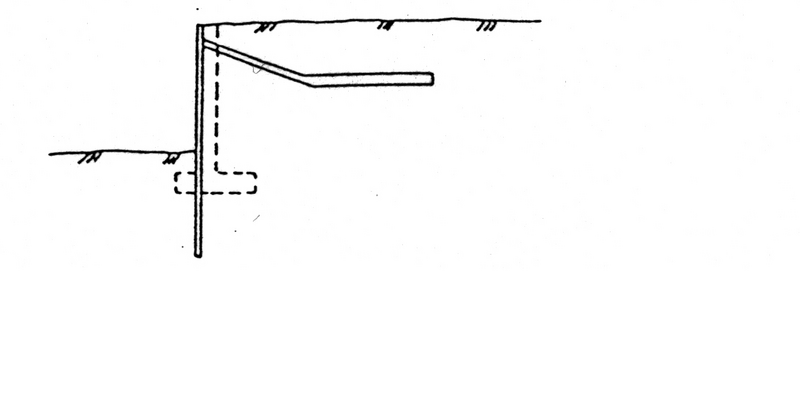
Figur 4.1 viser en prinsippskisse for landkar med friksjonsplate.
Figur 4.1 Landkar med friksjonsplate
Friksjonsplata plasstøpes eller prefabrikeres i betong og forankres til landkaret med stag. Det spennarmerte betongstaget må hele tiden være i trykk for å forhindre riss som fører til armeringskorrosjon. Dette kan være økonomisk ved at fundamentdimensjonene kan reduseres betraktelig ved store horisontallaster.
Kapasiteten QA på ei friksjonsplate beregnes av formel 4.1:
QA= (Nf NE t) (p´+ a) B (4.1)
Der Nf er friksjonsfaktoren for friksjonsplata uttrykt som:
Nf= (r0 + ru)tan , når L Lopt og Nf =(KP – KA) z/2L + ru tan når L Lopt
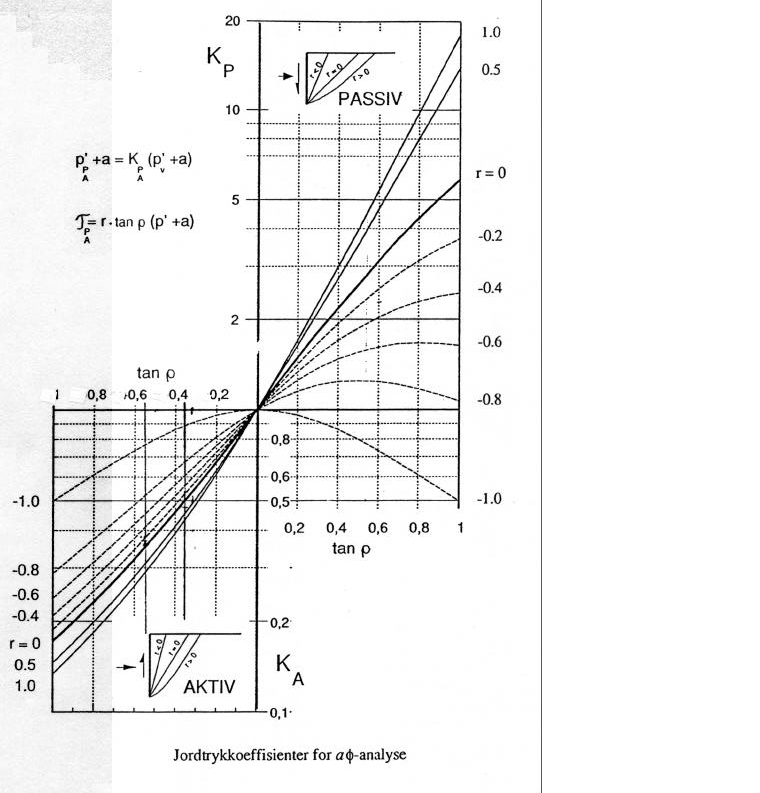
KA= aktiv jordtrykkskoeffisient, se figur 4.2 KP= passiv jordtrykkskoeffisient, se figur 4.2
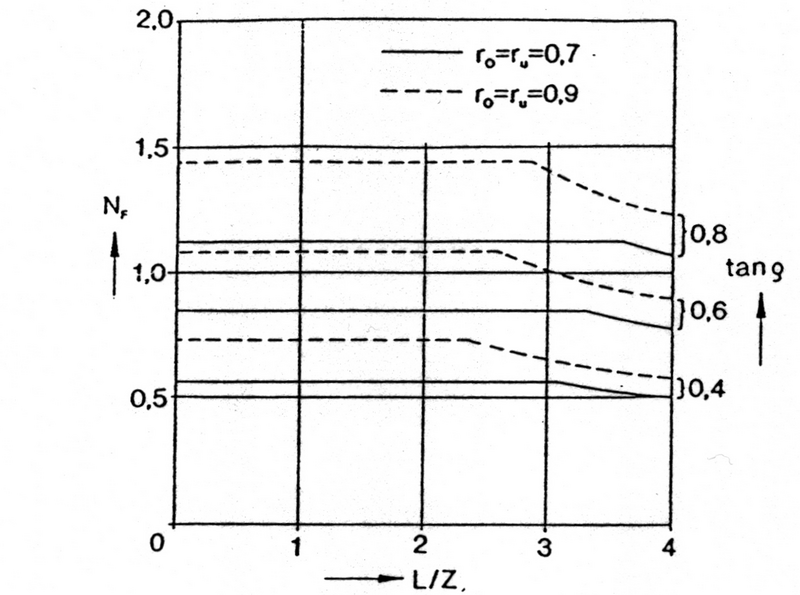
Nf kan finnes fra figur 4.3
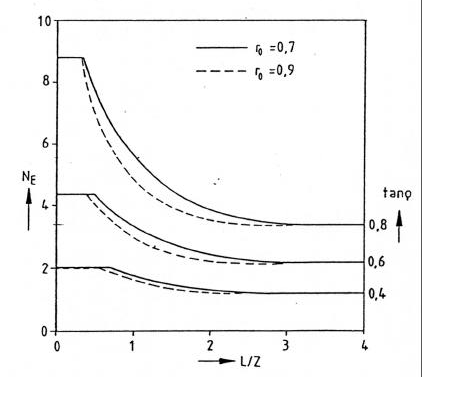
NE er endemotstandsfaktoren for friksjonsplata, og kan tas ut av figur 4.4. Platas optimale lengde finnes ved formel 4.2.
(4.2)
Ruheten settes i området r0= ru= 0,7 – 0,9
Figur 4.2 Jordtrykkskoeffisienter (aktiv - passiv)
Figur 4.3 Friksjonsfaktor NF for friksjonsplate
Figur 4.4 Endemotstandsfaktoren NE for friksjonsplate
Figur 4.5 Optimal platelengde
Nødvendig forankringslengde Ltot finnes fra følgende uttrykk:
(4.3)
Kontinuerlig friksjonsplate fra landkar
Kontinuerlige forankringsplater som går direkte over i landkarsålen eller landkarveggen, vil ta opp horisontale krefter fra landkaret ved friksjon mellom plate og underliggende jord. Siden platen henger sammen med landkarveggen vil det ikke bli noen endemotstand mot platen. Det vil heller ikke bli noen friksjonsvirkning mellom plate og overliggende jord, fordi jorden følger de bevegelsene som platen gjør. Oversiden av platen er således uvirksom. Videre vil en viss del av platelengden som ligger nærmest landkaret være lite virksom dersom plata ligger et stykke opp på landkarveggen. Det kan derfor være praktisk og økonomisk fordelaktig å lage utsparinger mellom mer eller mindre konsentrerte armeringsføringer eller strekkstag i partiet nærmest landkarveggen. Dimensjonering for øvrig utføres som for horisontale forankringsplater med stag. Figur 4.6 viser prinsippet for to ulike plasseringer av kontinuerlige friksjonsplater.
Figur 4.6 Plassering av kontinuerlige friksjonsplater I tilfelle a) ligger plata i nivå med landkarsålen, på eller negravd i opprinnelig terreng.
I tilfelle b) ligger plata i en viss høyde over sålen på opprinnelig terreng eller i bakfyllingsmassen.
For å oppnå best mulig lastkapasitet og minst mulig forskyvninger er det ved begge typer stagforankring spesielt viktig at massene rundt plata og mellom plate og landkar blir godt komprimerte.
Oppsummering
I figurene 4.7 - 4.9 er det foretatt en oppsummering av prinsippet for de forskjellige typer forankring som er nevnt under avsnitt 3.
Figur 4.7 Stag til vertikal forankring basert på passivt jordtrykk
Figur 4.8 Stag til horisontal forankringsplate basert på tosidig friksjon
Figur 4.9 Avlastnings-/friksjonsplate basert på ensidig friksjon
BRU / SPOR INTERAKSJON
Generelt
Samspillet mellom spor og bru, dvs. konsekvensene av hvordan det ene påvirker det andre, forekommer fordi de er sammenbundet uavhengig av om sporet ligger direkte på brua eller i ballast.
Samspillet, eller interaksjonen som det også kalles fører til krefter i skinnene og i den understøttende konstruksjonen og i lagrene så vel som forskyvninger i de forskjellige element i brua og i sporet.
Dersom interaksjonen er under kontroll, vil brua fortsatt fylle sin funksjon, dvs. understøtte sporet uten at sporet blir utsatt for uregelmessigheter.
Det er to typer uregelmessigheter en må regne med: skinnebrudd eller avbrudd i overgangen mellom spor og bru slik at sporstabiliteten ikke kan garanteres lengre. Et godt eksempel er når ballasten løsner fulgt av betraktelig forskyvning av brua slik at tilstrekkelig motstand mot sideveis forskyvning ved bruendene ikke lengre er tilstede.
De tillatte grenseverdier for sporet er avhengig av dets konstruksjon og vedlikeholdstilstand. De tillatte grenseverdier som ERRI D 213 har kommet frem til enten for forskyvninger eller tilleggsspenninger i skinnene pga. interaksjon, er verdier som er generelt tillatt for standard sporkomponenter ved godt vedlikehold. Disse tilleggsverdier er for helsveiste UIC 60 skinner 72 N/mm2 i tillatt trykkspenning i og 5 mm forskyvning av konstruksjonen ved bremsing. Tillatt tilleggsspenning i strekk er 92 N/mm2.
Beskrivelse av fenomenet
Ved Jernbaneverket består nå (1999) ca. 95 % av nettets sporlengde av helsveist spor.
Det er i årenes løp gjort mange studier og evalueringer av skinnespenninger og stabilitet av helsveist spor som ligger i ballast, men ikke på bruer. Ved slike studier har man undersøkt temperaturspenninger alene og kombinert effekt av temperaturspenninger og trafikkrefter.
Bruk av konstruksjonsfuger i bruer slik at de kan bevege seg relativt til det helsveiste sporet, introduserer en diskontinuitet i ballastlagets karakteristika. Denne diskontinuitet svarer for relativ bevegelse mellom ballastlaget og sporet når brudekket utvider seg eller trekker seg sammen og forårsaker krefter som påføres skinnene og brukonstruksjonen så vel som forandringer i tilleggsspenninger pga. krefter som kommer fra trafikklasten.
Prinsipper for helsveist spor i ballast
Skinnene er festet til svillene ved hjelp av elastiske festeanordninger som utøver en definert fastholdingskraft for å sikre skinnene til svillene. Denne fastholdingskraften er vanligvis så stor at alle langsgående bevegelser i skinnene overføres til svillene. Dvs. at motstanden mot skinne/sville glidning er større enn motstanden mot langsgående bevegelser som ballasten byr på. Da den frie bevegelsen av skinnene som er utsatt for termiske krefter og trafikkrefter virker motsatt til ballasten, blir skinnene utsatt for langsgående krefter. Helsveist spor inneholder en ”sentral” sone der utvidelsen og sammentrekningen er fullstendig forhindret, og to ”puste”- soner ved hver ende på ca. 150 m lengde. Glideskjøter ved endene på helsveist spor har en 50 mm variasjon i åpning som tillater fri bevegelse av skinnene
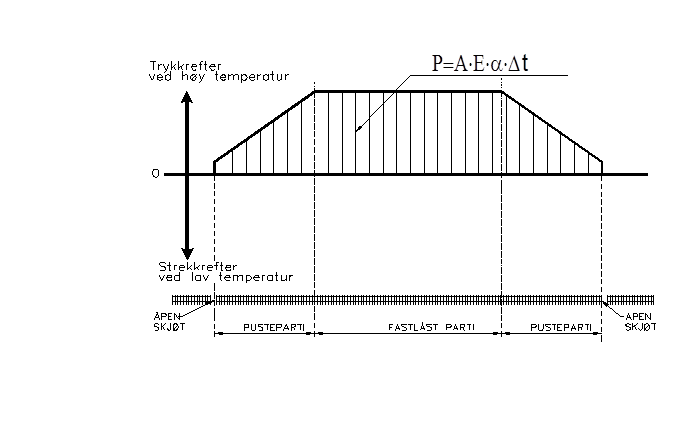
Figur 4.10 Oppførsel av helsveist spor ved temperaturforandringer
Hvor:
temperaturutvidelseskoeffisient TR forandring i skinnetemperatur relativ til nøytraltemperatur ( ca. 21O ved JBV) E Elastisitetsmodul for stål (210 000 N/mm2 ) A Tverrsnittsareal av to skinner F Sporkraft
Eksempel: TR = + 50OC og UIC 60 skinneprofil, settes til 1,0 10-5 Sporkraft (F) = E A TR = 210 000 2 7686 10-5 50 1600 kN
Virkning av ei bru under sporet
Ei bru under et helsveist spor betyr at det helsveiste sporet hviler på et underlegg som utsettes for deformasjon og bevegelse og således forårsaker forskyvninger av sporet.
Når både brua og sporet kan bevege seg, vil en hvilken som helst kraft eller forskyvning som påvirker en av dem, påføre krefter i den andre.
Interaksjon finner derfor sted mellom sporet og brua som følger:
Krefter som blir påført helsveist spor introduserer tilleggskrefter i sporet og/eller i lagrene som understøtter brua, og bevegelser i sporet og brua. En hvilken som helst bevegelse i bruoberbygningen påfører en bevegelse i sporet og indirekte i brulagrene.
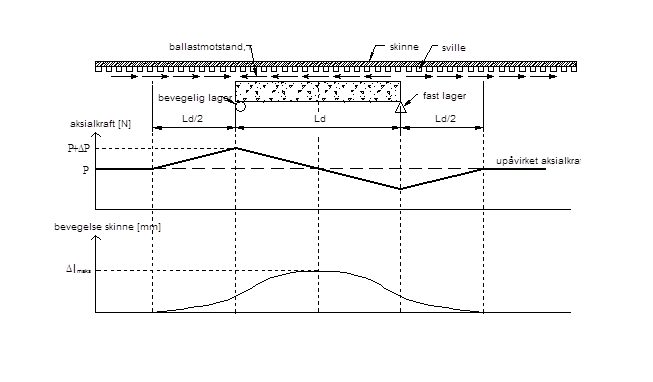
Figur 4.11 Kurve som viser skinnespenninger forårsaket av temperaturvariasjoner i brudekket
Bruparametre
Når ei bru har fast lager ved det ene landkaret og bevegelig lager ved det andre, er utvidelseslengden eller ekspansjonslengden lik avstanden mellom fast lager og bevegelig lager. Dersom brua er fastholdt et annet sted enn ved en av bruas ender, har brua to ekspansjonslengder, en til hver side om fastholdingspunktet. Dette punktet blir også kalt termisk senter, dvs. at ingen langsgående bevegelser finner sted her.
Spennvidden influerer også på samspillet mellom spor og bru fordi den vertikale lasten forårsaker langsgående forskyvning av dekket.
Bruoverbygningens motstand mot horisontal forskyvning er en fundamental parameter da den påvirker alle interaksjonsfenomener. Denne faktoren blir bestemt hovedsakelig av støttens totale stivhet. Denne er sammensatt av lagrenes stivhet, og av de forskjellige komponenter under lagrene; dvs. søylene, fundamentene og jordarten rundt fundamentene.
Bruas bøyestivhet er en parameter som i like stor grad som bruas vertikale deformasjon forskyver brudekkets øvre kant i horisontal retning. Denne deformasjonen genererer interaksjonskrefter.
Avstanden fra bruas nøytralakse til dekkets overflate og avstanden fra nøytralaksen til lagrenes rotasjonssentrum påvirker også interaksjonsfenomenet pga. bruas bøyning.
Sporparametre
Sporets motstand, k, per lengdeenhet mot langsgående forskyvning, u, er en viktig parameter. Men denne parameter er avhengig av et stort antall andre faktorer ( slike som om sporet er belastet eller ikke, om sporet ligger i ballast eller ikke, ballastens pakningsgrad og vedlikeholdsstandard.
Skinnenes tverrsnittsareal, A, er også en sporparameter.
I et spor med ballast er motstanden mot langsgående forskyvning avhengig av følgende:
Skinnenes motstand mot forskyvning relativt til svillene. Denne motstanden er gitt av skinnebefestigelsen og dens størrelse avhenger av festeanordningens effektivitet.
Sporets (dvs. sviller og skinner) motstand mot forskyvning relativt til brudekket. Denne motstand er gitt av ballastens tendens til å motstå hvilken som helst forskyvning av svillen og av friksjonen mellom ballast og brudekk.
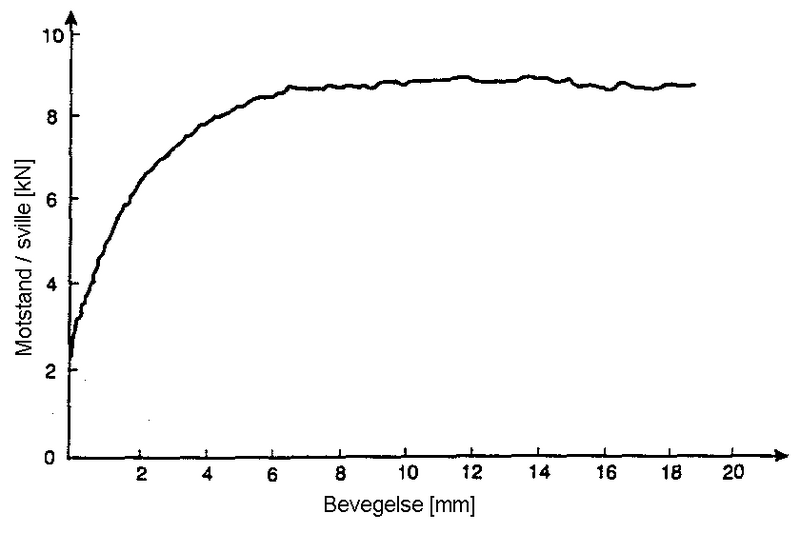
For ubelastet spor har den siste faktoren mye mindre verdi enn den første.
Figur 4.12 Sporets motstand som funksjon av langsgående forskyvning, u.
Se for øvrig jernbaneverkets læebok L532 kap. 5 ”Aksialkrefter i helsveis spor”
LITTERATURHENVISNINGER
1. Døssland, T., Forankring av støttekonstruksjonar med horisontale friksjonselement. Doktoravhandling. Institutt for geoteknikk i vegbygging,NTH, 1980 2. Statens vegvesens håndbok nr. 016 Geoteknikk i vegbygging,2.utg. 1992 3. ERRI D 213